Abstract
Many infectious diseases have seasonal outbreaks, which may be driven by cyclical environmental conditions (e.g., an annual rainy season) or human behavior (e.g., school calendars or seasonal migration). If a pathogen is only transmissible for a limited period of time each year, then seasonal outbreaks could infect fewer individuals than expected given the pathogen’s in-season transmissibility. Influenza, with its short serial interval and long season, probably spreads throughout a population until a substantial fraction of susceptible individuals are infected. Dengue, with a long serial interval and shorter season, may be constrained by its short transmission season rather than the depletion of susceptibles. Using mathematical modeling, we show that mass vaccination is most efficient, in terms of infections prevented per vaccine administered, at high levels of coverage for pathogens that have relatively long epidemic seasons, like influenza, and at low levels of coverage for pathogens with short epidemic seasons, like dengue. Therefore, the length of a pathogen’s epidemic season may need to be considered when evaluating the costs and benefits of vaccination programs.
Key words and phrases: Mathematical model, epidemics, infectious disease, vaccination, seasonality
1. Introduction
Mathematical models can be used to help understand the dynamics of infectious disease outbreaks [19, 21, 2]. With an estimate of the transmissibility of a pathogen, often summarized as R0, one can use models to gain insight into the relationship between the transmissibility of a disease, the fraction of a population it can infect, and the fraction of a population that needs to be vaccinated to prevent outbreaks [8, 2, 17, 31]. However, these relationships are less straightforward when a pathogen’s transmissibility is not constant over time.
Transmission of many pathogens is seasonal, and outbreaks tend to occur during the same time each year. Seasonal transmission can be driven by cyclical environmental (e.g., rainfall or temperature) or behavioral and demographic (e.g., school calendars or seasonal migration) forces [13, 10, 12, 23]. The length of an outbreak might therefore be constrained by the length of the season. Previous modeling work has shown that adding seasonality to disease transmission models can improve fits to annual or biennial disease cycles observed in surveillance data [27, 18], alter the multi-year dynamics of disease incidence [3, 26, 1, 15], increase understanding of disease persistence and local extinction [18], and test novel intervention strategies that take advantage of timing [30, 1, 15]. Here, we use a simple mathematical model to explore the effects that seasonal forcing could have on the effectiveness and efficiency of mass vaccination. We hypothesize that the most efficient coverage level, defined as the number of infections averted per vaccination, can be affected by seasonal forcing.
2. Mathematical model of infectious disease transmission
We model epidemics of infectious disease using a Susceptible–Infectious–Recovered (SIR) model [19] with an additional compartment to represent vaccinated individuals. The system of ordinary differential equations (ODEs) that describe the model dynamics are:
| (1) |
| (2) |
| (3) |
| (4) |
where S is the number of individuals who are susceptible to infection, V is the number who are vaccinated (and susceptible to infection), I is the number who are currently infected, R is the number who are recovered from infection (and immune to future infection), β is the transmissibility of the pathogen, γ is the recovery rate of infected individuals, and VE is the vaccine efficacy against infection. We focus our attention on epidemics which run their course in relatively short time compared to the demographic changes in the population such as influenza, cholera and dengue. As a result, a fixed population size and density-dependent transmission is assumed. Mass vaccination is modeled by initializing the model with a proportion of the population in the vaccinated compartment. Vaccinated individuals are less susceptible to infection by a factor of 1 − VE. We assume that vaccine protection is leaky, so that vaccinated individuals are not fully protected but instead are infected at a lower rate than non-vaccinated individuals.
The basic reproductive number, R0, is the average number of people that a typical infected individual infects in a fully susceptible population [2]. For an SIR model, R0 = βN/γ, where N is the total population size, which we assume to be constant. The final size p, or the fraction of people infected during an epidemic, can be computed using the final size expression 1 − p = e−R0p. In our simple model of seasonality, we assume that an epidemic only lasts for t days, then transmission stops, which is equivalent to setting β to 0 at time t. We define the size of an epidemic on day t to be the sum I + R at time t.
When a sufficient fraction of a population is vaccinated, an outbreak can not grow in size [8]. This critical vaccination threshold is . Here, we assume that protection conferred by vaccines is leaky, so vaccinated individuals have a reduced rate of infection but may be partially susceptible. When fraction f of a population is vaccinated with a leaky vaccine, the effective reproductive number, Rf, is: Rf = (1 − f)R0 + f(1 − VE)R0. The final size assuming a leaky vaccine can be found by solving: p = 1 − (1 − f)e−R0p − fe−R0(1−VE)p. The derivation of Rf and the final size of a partially vaccinated population can be found in [24, Appendix A.3].
3. Results
The pathogen’s transmissibility (which we express in terms of R0, the basic reproductive number) and serial interval (the average time between the onset of symptoms in an individual and the onset in secondary cases) can be used to compute the speed and magnitude of an epidemic.
3.1. Modeling uninterrupted epidemics
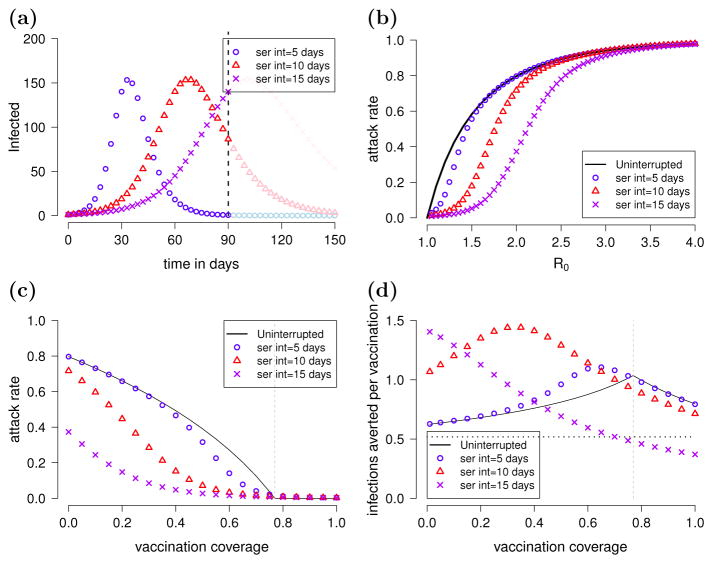
When epidemics are allowed to run their course without the effects of seasonality, the proportion of the population they infect, the attack rate, does not depend on their speed of transmission and can be computed using the final size expressions from Section 2. Increasing the serial interval, while keeping R0 constant, simply delays the peak of the epidemic but does not change the peak’s height (when the height is defined as the number of infected people at a given time rather than the incidence), or the maximum number of infected people at the epidemic peak (Figure 1a). The relationship between R0 and the attack rate does not depend on the serial interval (Figure 1b, black curve).
Figure 1.
The effects of limiting the duration of an epidemic. We modeled epidemics with an R0 of 2.0 with serial intervals of 5, 10, or 15 days. The models are initialized with a population of 1000 individuals, one of whom is initially infected. (a) The number of infected individuals over time with when the serial interval is 5 days (blue circles), 10 days (red triangles), and 15 days (purple xs). The epidemics are stopped at day 90, indicated by the vertical dashed line, to represent the end of an epidemic season. Note that the y-axis is the number of infected individuals and not infection incidence. (b) The attack rate of an epidemic vs R0. The black line shows the effect of increasing R0 on the infection attack rate when outbreaks are not interrupted using the final size expression. The same relationship is plotted when the epidemics are stopped on day 90 and the serial interval is 5 days (blue circles), 10 days (red triangles), and 15 days (purple xs). Other initial conditions were the same as in panel (a). (c) The effect of vaccine coverage on the attack rate. Initial conditions were the same as in panel (a), and vaccinated individuals are infected at rate 65% less than non-vaccinated susceptibles. The final size expression was used to compute the attack rate of uninterrupted outbreaks. The critical vaccination threshold is indicated by the vertical dashed gray line. (d) The efficiency of mass vaccination vs coverage. We define efficiency to be the number of infections averted per vaccination administered, which we would like to maximize. The horizontal dotted line represents the simplifying assumption that mass vaccination only reduces the risk of infection among vaccinated individuals (by 65%) and not among non-vaccinated individuals.
We show that when epidemics are not interrupted by seasonality, the attack rate is a concave function (the second derivative is negative) of the vaccination coverage up to the critical vaccination fraction, i.e., the attack rate of the epidemic drops more and more rapidly with increasing coverage until the critical vaccination fraction is reached (Figure 1c).
Theorem 3.1
Assuming that the vaccine is fully protective, the final size of the non-interrupted epidemic simulated with the model described in Equations 1–4 is a decreasing concave function of the vaccination coverage up to the critical vaccination threshold and becomes zero afterwards.
Proof
In the model with a perfect vaccine that protects completely, vaccinated and recovered individuals are indistinguishable. Vaccinated individuals can therefore be moved to the recovered compartment initially, i.e., R(0) > 0 and the total number of cases at the end of the epidemic is given by R(∞) − R(0). The simplified model with the vaccinated compartment removed is:
| (5) |
| (6) |
| (7) |
Dividing Equation 5 by Equation 7 implies that . Separating the variables and applying the initial conditions it leads to:
| (8) |
which converted to fractional form ( ) is
| (9) |
where is the vaccinated fraction (coverage) while is the final size, i.e., the proportion of the population which becomes infected by the end of the epidemic. Since all individuals at the end of the epidemics are vaccinated, recovered or naive susceptibles then s(∞) = 1−p−f and therefore . Differentiating twice with respect to p gives us:
| (10) |
| (11) |
| (12) |
where .
We consider the function g(x) = 1 − ex + x which appears in the numerator of . We have that g′(x) = 1 − ex < 0 and therefore g(x) is decreasing for x > 0. As a result g(x) < 0 for x > 0 since g(0) = 0. It implies that .
Similarly, let we consider h(x) = 2+x+ex(−2+x) which appears in the numerator of . We have that h′(x) = 1 − ex + xex and h″(x) = xex. Therefore h′(x) is increasing and positive for x > 0 since h′ (0) = 0. As a result h(x) is increasing and positive for x > 0 since h(0) = 0. It implies that .
Therefore, the vaccine coverage (f) is a decreasing concave function in terms of the final size (p) and the critical vaccination threshold is fcr = f(0). Moreover, by Inverse Function Theorem, the final size can be expressed as a function of the coverage (p(f)) over the interval [0, fcr]. This function is differentiable with respect to f and its derivatives satisfy and .
This completes the proof that the final size (p) is a decreasing concave function in term of the vaccine coverage (f) up to the critical vaccination threshold (fcr). It is clear that for coverage greater than fcr the final size remains zero. This completes the proof of Theorem 3.1.
3.2. Modeling seasonal epidemics
We model an epidemic season by stopping transmission after a fixed time elapses, 90 days, which could correspond to a change in seasons or another external factor that reduces transmission. If a pathogen is only transmissible for a limited time, then slower epidemics may infect fewer individuals than they would given unlimited time. Figure 1a plots three epidemic curves that have the same R0 (and thus the same attack rate) but different serial intervals. Here, we emphasize that the attack rate for an epidemic interrupted by seasonal forces is usually lower than the final size that one would expect for an uninterrupted epidemic. If the epidemic stops on day 90, a rapid epidemic might have already run its course, a slower epidemic might be interrupted after it peaks, and an even slower epidemic might be interrupted during its exponential growth phase (Figure 1a). The speed of an epidemic can therefore affect the relationship between transmissibility and the attack rate (Figure 1b). This effect is greatest when the transmissibility of a pathogen is low (R0 is close to 1) and the serial interval is long (Figure 1b). Thus, both the transmissibility (R0) and serial interval of the pathogen need to be considered when seasonal forces limit the duration of epidemics.
If epidemics are interrupted, then the relationship between vaccination coverage and the infection attack rate of the epidemic can qualitatively change. As the vaccinated proportion of a well-mixed population increases, epidemics become slower and smaller until the critical vaccination fraction is reached, at which point, outbreaks do not occur (Figure 1c).
Limiting the time during which a pathogen can be transmitted affects the relationship between vaccination coverage and the size of the epidemic. Our analysis suggests that if a pathogen’s serial interval is short relative to the length of its season, the relationship between vaccination coverage and the epidemic’s attack rate takes a sigmoid shape with an inflection point that occurs below the critical vaccination fraction (Figure 1c). With longer serial intervals, the effects of interrupting the epidemic are even larger and the attack rate may become a convex function (the second derivative is positive) of vaccination coverage (Figure 1c). The shape of this curve determines the incremental benefit of vaccinating more individuals.
Mass vaccination can become either more or less efficient as vaccination coverage increases, depending on the speed of transmission relative to the length of the epidemic season. We define the efficiency of mass vaccination to be the number of cases averted per vaccination administered. The shape of the curve describing the attack rate vs vaccination coverage (Figure 1c) determines the efficiency profile of mass vaccination (Figure 1d), which we describe more formally below.
Theorem 3.2
Consider an interrupted epidemic. The efficiency of the vaccination measured as the number of infections prevented per vaccination depends on the functional expression of the attack rate in terms of the vaccination coverage as follows:
If the final epidemic size is a concave function of the vaccination coverage, then efficiency improves with increasing vaccination coverage up to the critical vaccination threshold and worsens at higher levels.
If the final epidemic size is a linear function of the vaccination coverage, then efficiency is constant up to the critical vaccination threshold and worsens at higher levels.
If the final epidemic size is a convex function of the vaccination coverage, then efficiency decreases with increasing vaccination coverage.
If the final epidemic size is a sigmoid function of the vaccination coverage, then efficiency improves with increasing the vaccination coverage up to an \optimal value” below the critical vaccination threshold and worsens at higher levels.
Proof
The efficiency of the vaccination E is defined as the number of infections prevented divided by number of vaccinations. Therefore, where f is the vaccination coverage while p(f) and p(0) represent the final size of the epidemic with vaccination coverage f and without vaccination, respectively. We focus on E up to the critical vaccination threshold (fcr). When coverage increases beyond fcr the number of vaccinations increases while the number of prevented infections remain unchanged. Therefore E decreases and the efficiency of the vaccination always worsens.
For f ∈ (0, fcr) we have:
| (13) |
By the Mean Value Theorem there exists f̄ < f such that and .
If p(f) is a concave function then p′(f) is decreasing. As a result for f < fcr, i.e., the efficiency of the vaccination improves with increasing vaccination coverage up to the critical vaccination threshold.
If p(f) is a linear function then p′(f) is constant. Therefore and the efficiency is constant up to the critical vaccination threshold.
If p(f) is a convex function then p′(f) is increasing. As a result for f < fcr, i.e., the efficiency worsens with increasing the vaccination coverage.
Suppose p(f) is a concave function for f ∈ (0, f*) and convex function for f ∈ (f*, fcr) where f* < f. Therefore for f < f* and for f* < f < fcr and E will have a maximum at f*. The efficiency of vaccination improves with increasing vaccination coverage up to f* and worsens afterwards.
This completes the proof of Theorem 3.2.
For an uninterrupted epidemic, the concave relationship between the attack rate and coverage implies that the efficiency of mass vaccination increases as coverage increases from zero to the critical vaccination fraction, after which it decreases (Figure 1d). The efficiency decreases at high vaccination coverage levels because vaccinating in excess of the critical vaccination fraction does not prevent additional infections. Therefore, coverage at exactly the critical vaccination fraction is the most efficient.
For interrupted epidemics, the efficiency can initially either increase or decrease with increasing coverage. For interrupted epidemics with a sigmoid attack rate vs coverage curve (the curve is concave then convex), vaccination efficiency improves with increasing vaccination coverage only up to the inflection point, and the most efficient coverage levels are below the critical vaccination fraction. When an epidemic is interrupted early, during its exponential growth phase (attack rate vs coverage is a convex function), mass vaccination becomes less efficient as coverage increases, and there is no optimal coverage to reach. Note that the efficiency of mass vaccination at levels below the critical vaccination fraction is often better than that predicted for the uninterrupted epidemic. For all scenarios considered, efficiency decreases when coverage exceeds the critical vaccination fraction, which is to be expected.
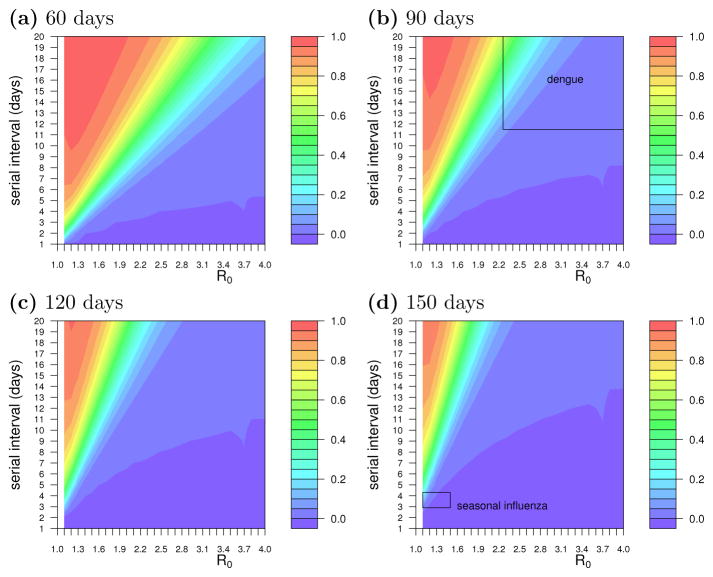
We explored how seasonality may regularly interrupt outbreaks of specific pathogens. Using the mathematical model, we plot how much of seasonal epidemics with different combinations of R0 and serial interval are potentially interrupted when the epidemic season is exactly 60 days, 90 days, 120 days, and 150 days (Figures 2a–d). As observed above, epidemics with long serial intervals and low values of R0 are the most interrupted by shorter seasons, with a nearly linear trade-off between R0 vs serial interval when following the isoclines on these plots. Seasonal influenza has a short serial interval (about 3 days [7]) and a long season in the temperate northern and southern hemispheres, from the fall through the spring (maybe as long as 8 months) [28], so influenza outbreaks are not likely to be interrupted by the end of the season (Figure 2d). This implies that the optimal vaccination coverage, in terms of infections averted per number of people vaccinated, would be close to the critical vaccination threshold. In contrast, seasonal dengue outbreaks may be limited by dengue’s long serial interval (perhaps 20 days [25]) and the limited time during which rainfall, high humidity, and high temperatures are optimal for the breeding of its primary vector, Aedes aegypti, and the rapid incubation of the virus [16, 29, 20]. Dengue season may last for up to 6 months in some regions, but the period of highest transmissibility is likely shorter and curtailed by the reduction in temperature and humidity by the end of each rainy season [4], so we conservatively assume that high dengue transmission occurs in a 3-month window (Figure 2b). If dengue epidemics are greatly curtailed by the short season, then the optimal vaccination coverage could be well below the critical vaccination threshold, though higher-than-optimal levels of coverage could still be cost-effective.
Figure 2.
The relationship between transmissibility, serial interval, and season length on the magnitude of the effect of a limited transmission season. Colors represent the proportion of an epidemic interrupted when the season is (a) 60, (b) 90, (c) 120, and (d) 150 days long for different values of R0 and the serial interval. Regions in red indicate parameters for which epidemics are completely averted by a short season, and dark blue regions correspond to parameters for which the epidemic size is not reduced by the season length. The regions of parameter space corresponding to dengue and influenza are indicated in panels (b) and (d), respectively.
4. Discussion
Using a mathematical model, we have shown how the interruption of epidemics by seasonal external drivers can have large effects on epidemic size and the effectiveness and efficiency of mass vaccination. Mass vaccination can be either more or less effective than expected, depending on when epidemics are interrupted. When seasonality is not a factor, and an epidemic exhausts itself by infecting a sufficient number of susceptibles, then vaccination coverage at the level critical vaccination fraction is efficient and averts the most infections per dose administered. Influenza, with its long season and short serial interval, might be such a pathogen, and influenza seasonality might drive the timing but not the magnitude or duration of epidemics. When a pathogen’s season length interrupts its outbreaks, then the critical vaccination fraction may not be the most efficient coverage target. We suspect that this affects epidemics of some vector-borne diseases, such as dengue, because of the relatively short season and the long serial intervals associated with incubation periods in both the host and the vector. For epidemics that are interrupted early, during their exponential growth phase, low levels of vaccination will avert the most infections per dose. For epidemics that are interrupted after their peak, while they are waning, intermediate levels of vaccination below the critical vaccination threshold are most efficient. In general, transmission of pathogens with relatively low transmissibility, long serial intervals, and short seasons are most likely to be affected by seasonal interruptions, and we suggest that this be considered when evaluating the effectiveness of mass vaccination or other interventions and when estimating transmissibility using the number of annual cases.
The simple mathematical model used here might not be appropriate for all pathogens. Pathogens with \long cycle” transmission, like cholera, may be more affected by seasonal interruption than predicted from an SIR model, which captures short cycle (person-to-person) but not long cycle (environmental) transmission. Transmission models that include long cycle transmission could be used to study seasonality of enteric pathogens [6, 5, 9], while models that explicitly include vectors, such as [22], could be used to study vector-borne pathogens. However, the SIR model is sufficient for the qualitative analyses presented here. Other major simplifying assumptions in our model are the simplified treatment of seasonality, in which a pathogen is highly transmissible during its season and not at all transmissible outside its season, and the assumption that a population is only seeded with the pathogen at the beginning of the season. The magnitude and frequency of seeding might play a significant role in seasonal epidemic dynamics, which we did not explore here. For diseases that occur less regularly in time and space, the pathogen might be introduced to a population later in the season, which we did not consider in our analyses. In addition, we only analyzed the transmission of disease during a single epidemic season. Multi-year dynamics of transmission and immunity would require more complicated models possibly specific to each pathogen and host population.
Although our results suggest that low levels of vaccination might be most \efficient” for some diseases, we do not suggest deliberately limiting vaccination coverage for the sake of efficiency. Beyond the ethical arguments that support access to vaccination for everyone [11], other public health goals, such as the local elimination of a pathogen or the prevention of disease outbreaks or invasion, still require high levels of vaccination coverage. Levels of coverage higher than the theoretical \optimal” might be required to prevent outbreaks in the real world [14]. However, excessively high coverage levels, well beyond the critical vaccination threshold, might not be the best use of resources if these levels are difficult to reach [32].
Acknowledgments
The first author is partially supported by NIH grant U54-GM111274. Both authors receive support from a contract from the Bill and Melinda Gates Foundation.
Contributor Information
Dennis L. Chao, Email: dchao@fhcrc.org.
Dobromir T. Dimitrov, Email: ddimitro@scharp.org.
References
- 1.Altizer S, Dobson A, Hosseini P, Hudson P, Pascual M, Rohani P. Seasonality and the dynamics of infectious diseases. Ecol Lett. 2006;9:467–484. doi: 10.1111/j.1461-0248.2005.00879.x. [DOI] [PubMed] [Google Scholar]
- 2.Anderson RM, May RM. Infectious Diseases of Humans: Dynamics and Control. Oxford University Press; Oxford, United Kingdom: 1991. [Google Scholar]
- 3.Aron JL, Schwartz IB. Seasonality and period-doubling bifurcations in an epidemic model. J Theor Biol. 1984;110:665–679. doi: 10.1016/s0022-5193(84)80150-2. [DOI] [PubMed] [Google Scholar]
- 4.Campbell KM, Lin CD, Iamsirithaworn S, Scott TW. The complex relationship between weather and dengue virus transmission in Thailand. Am J Trop Med Hyg. 2013;89:1066–1080. doi: 10.4269/ajtmh.13-0321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chao DL, Longini IM, Jr, Morris JG., Jr . Modeling cholera outbreaks. In: Nair GB, Takeda Y, editors. Current Topics in Microbiology and Immunology: Cholera Outbreaks. Vol. 379. Springer–Verlag; Berlin: 2014. pp. 195–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Codeço CT. Endemic and epidemic dynamics of cholera: The role of the aquatic reservoir. BMC Infect Dis. 2001;1:p1. doi: 10.1186/1471-2334-1-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cowling BJ, Fang VJ, Riley S, Malik Peiris JS, Leung GM. Estimation of the serial interval of influenza. Epidemiology. 2009;20:344–347. doi: 10.1097/EDE.0b013e31819d1092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Diekmann O, Heesterbeek JA, Metz JA. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J Math Biol. 1990;28:365–382. doi: 10.1007/BF00178324. [DOI] [PubMed] [Google Scholar]
- 9.Dimitrov DT, Troeger C, Halloran ME, Longini IM, Chao DL. Comparative effectiveness of different strategies of oral cholera vaccination in Bangladesh: A modeling study. PLoS Negl Trop Dis. 2014;8:e3343. doi: 10.1371/journal.pntd.0003343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ferrari MJ, Djibo A, Grais RF, Bharti N, Grenfell BT, Bjornstad ON. Rural–urban gradient in seasonal forcing of measles transmission in Niger. Proc Biol Sci. 2010;277:2775–2782. doi: 10.1098/rspb.2010.0536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fine P, Eames K, Heymann DL. \Herd immunity”: A rough guide. Clin Infect Dis. 2011;52:911–916. doi: 10.1093/cid/cir007. [DOI] [PubMed] [Google Scholar]
- 12.Fisman D. Seasonality of viral infections: Mechanisms and unknowns. Clin Microbiol Infect. 2012;18:946–954. doi: 10.1111/j.1469-0691.2012.03968.x. [DOI] [PubMed] [Google Scholar]
- 13.Fisman DN. Seasonality of infectious diseases. Annu Rev Public Health. 2007;28:127–143. doi: 10.1146/annurev.publhealth.28.021406.144128. [DOI] [PubMed] [Google Scholar]
- 14.Fox JP. Herd immunity and measles. Rev Infect Dis. 1983;5:463–466. doi: 10.1093/clinids/5.3.463. [DOI] [PubMed] [Google Scholar]
- 15.Grassly NC, Fraser C. Seasonal infectious disease epidemiology. Proc Biol Sci. 2006;273:2541–2550. doi: 10.1098/rspb.2006.3604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Halstead SB. Dengue virus–mosquito interactions. Annu Rev Entomol. 2008;53:273–291. doi: 10.1146/annurev.ento.53.103106.093326. [DOI] [PubMed] [Google Scholar]
- 17.Hethcote HW. The mathematics of infectious diseases. SIAM Review. 2000;42:599–653. [Google Scholar]
- 18.Keeling MJ, Grenfell BT. Understanding the persistence of measles: Reconciling theory, simulation and observation. Proc Biol Sci. 2002;269:335–343. doi: 10.1098/rspb.2001.1898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society of London Series A. 1927;115:700–721. [Google Scholar]
- 20.Lambrechts L, Paaijmans KP, Fansiri T, Carrington LB, Kramer LD, Thomas MB, Scott TW. Impact of daily temperature fluctuations on dengue virus transmission by Aedes aegypti. Proc Natl Acad Sci U S A. 2011;108:7460–7465. doi: 10.1073/pnas.1101377108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ludwig D. Final size distribution for epidemics. Math Biosci. 1975;23:33–46. [Google Scholar]
- 22.Macdonald G. The epidemiology and control of malaria. Oxford University Press; Oxford, United Kingdom: 1957. [Google Scholar]
- 23.Martinez-Bakker M, Bakker KM, King AA, Rohani P. Human birth seasonality: Latitudinal gradient and interplay with childhood disease dynamics. Proc Biol Sci. 2014;281:20132438. doi: 10.1098/rspb.2013.2438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Matrajt L, Britton T, Halloran ME, Longini IM., Jr One versus two doses: What is the best use of vaccine in an influenza pandemic? Epidemics. 2015;13:17–27. doi: 10.1016/j.epidem.2015.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Nishiura H, Halstead SB. Natural history of dengue virus (DENV)-1 and DENV-4 infections: reanalysis of classic studies. J Infect Dis. 2007;195:1007–1013. doi: 10.1086/511825. [DOI] [PubMed] [Google Scholar]
- 26.Roberts MG, Kao RR. The dynamics of an infectious disease in a population with birth pulses. Math Biosci. 1998;149:23–36. doi: 10.1016/s0025-5564(97)10016-5. [DOI] [PubMed] [Google Scholar]
- 27.Rvachev LA, Longini IM., Jr A mathematical model for the global spread of influenza. Math Biosci. 1985;75:3–22. [Google Scholar]
- 28.Schanzer DL, Langley JM, Dummer T, Viboud C, Tam TWS. A composite epidemic curve for seasonal influenza in Canada with an international comparison. Influenza Other Respir Viruses. 2010;4:295–306. doi: 10.1111/j.1750-2659.2010.00154.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Schwartz E, Weld LH, Wilder-Smith A, von Sonnenburg F, Keystone JS, Kain KC, Torresi J, Freedman DO. Seasonality, annual trends, and characteristics of dengue among ill returned travelers, 1997–2006. Emerg Infect Dis. 2008;14:1081–1088. doi: 10.3201/eid1407.071412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Stone L, Shulgin B, Agur Z. Theoretical examination of the pulse vaccination policy in the SIR epidemic model. Math and Comp Mod. 2000;31:207–215. [Google Scholar]
- 31.van den Driessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci. 2002;180:29–48. doi: 10.1016/s0025-5564(02)00108-6. [DOI] [PubMed] [Google Scholar]
- 32.Whittington D, Sur D, Cook J, Chatterjee S, Maskery B, Lahiri M, Poulos C, Boral S, Nyamete A, Deen J, Ochiai L, Bhattacharya SK. Rethinking cholera and typhoid vaccination policies for the poor: Private demand in Kolkata, India. World Development. 2009;37:399–409. [Google Scholar]