Abstract
Mammals maintain homeostatic control of their body temperature. Therefore, these organisms are expected to have adaptations that confer the ability to detect and react to both self and ambient temperature. Temperature-activated ion channels have been discovered to be the primary molecular determinants of thermosensation. The most representative group of these determinants constitutes members of the transient receptor potential superfamily, TRP, which are activated by either low or high temperatures covering the whole range of physiologically relevant temperatures. This review makes a critical assessment of existing analytical methods of temperature-activated TRP channel mechanisms using the cold-activated TRPM8 channel as a paradigm.
Keywords: DRG, dorsal root ganglion; F, Faraday; T, temperature; TG, trigeminal ganglion; TRP, transient receptor potential; R, universal gas constant; G0, Standard molar Gibbs free energy; H0, Standard molar enthalpy; Q10, temperature coefficient; S0, Standard molar entropy
Abbreviations: DRG, dorsal root ganglion; F, Faraday; G0, Standard molar Gibbs free energy; H0, Standard molar enthalpy; Q10, temperature coefficient; S0, Standard molar entropy; TG, trigeminal ganglion; TRP, transient receptor potential; T, temperature; R, universal gas constant
Introduction
Living organisms are forced to exist in an environment in which temperature is constantly changing. Since virtually all known chemical reactions display temperature dependency, biological processes are unavoidably affected by this thermodynamic intensive parameter. Hence, it is advantageous for organisms to possess adaptive mechanisms or structures that confer them a special ability for sensing ambient and potentially dangerous temperatures. If we move up the evolutionary ladder, the more complex structures and mechanisms for sensing temperature are found in mammals. The neuronal pathways that participate in thermosensation of external stimuli in mammals have been well described.1 Thermal stimuli excite sensory nerve endings of primary afferent neurons that project from trigeminal ganglia (TG) in the head and from the dorsal root ganglion (DRG) of the spinal cord to the rest of the body. Sensory nerve fibers convert thermal stimuli into action potentials that carry information to integrative centers in the spinal cord and brain. Identification and characterization of the molecular determinants of thermal sensitivity in neuronal endings has been an important undertaking in physiology for the past decades.
Propagated action potentials are initiated by a membrane depolarization at the nerve ending. Although several mechanisms have been proposed to explain the membrane depolarization evoked by cold in different tissues,2–6 there is a large body of evidence suggesting that cold and warming can promote Ca2+ influx into DRG neurons, which would imply that Ca2+ channels are involved in thermosensation.7,8 In fact, in the last decades several non-selective cation channels belonging to the transient receptor potential (TRP) superfamily have been identified as the molecular determinants in thermosensitive neurons.9–11 In addition to thermosensitive TRP channels, there are other families of proteins involved in thermosensation, such as ANO1 and ANO2 (2 Ca2+-activated Cl− channels),12 the endoplasmic reticulum Ca2+ sensor of store-operated Ca2+ entry STIM113 as well as several K+ and Na+ channels, whose thermosensitivity can modulate the excitability of neurons.1 In addition changes in the intracellular concentration of the TRP channel modulator phosphatidylinositol 4,5-bisphosphate (PIP2) contribute to the temperature detection in vivo.14 In this review, we attempt to make a critical assessment of the analytical methods of thermosensitive channel gating, focusing on one of the most extensively characterized members from a biophysical point of view, namely TRPM8.
TRP Channels
The term TRP channels comes from the discovery of a Drosophila melanogaster mutant strain with an abnormal response to light. This mutant displayed a transient electroretinogram instead of a plateau-like receptor potential typically found in the wild type.15 Because of this phenotype, the mutant was named trp (for transient receptor potential).16 The Drosophila gene responsible for the trp phenotype was cloned in 1989 and several alternative putative functions for the trp gene product were suggested, including that of a channel or receptor.17 At present, almost 30 trp-related mammalian genes have been cloned, being the majority of them cation-non-selective channels.18
TRP channels are tetramers whose monomers have 6 transmembrane spanning segments with the pore region formed by the fifth and the sixth transmembrane segment. Both the carboxyl (C)- and amino (N)-terminal are intracellular.19 The TRP channel family can be divided into 7 subfamilies according to sequence and function: TRPA (ankyrin), TRPC (canonical), TRPM (melastatin), TRPN (NOMPC), TRPML (mucolipin), TRPP (polycistin) and TRPV (vanilloid):20,21 The TRPN subfamily is not found in mammals. The TRP family displays a large structural diversity, where the main differences between subfamilies reside in the nature of the cytosolic tails. Except for TRPM4 and TRPM5, which are only permeant to monovalent cations,22 TRP channels are typically Ca2+ permeable. TRP channels are polymodal and display variable gating mechanisms (constitutively active channels, voltage-, temperature- ligand- gated channels). They are expressed in a wide variety of mammal cells, where they are involved in many physiological functions. Thus, dysfunction of these channels can cause important acquired or inherited human diseases.23
TRP Channels as Physiological Temperature Sensors
Temperature sensitivity of a channel may be characterized by the temperature coefficient Q10, which is a measure of how many times the ion channel current increases upon a 10 degrees rise in temperature. However, to be considered a physiological temperature sensor the following requirements must be met:1,24
-
1.
Steep temperature dependence: Usually expressed as a Q10 larger than 5 (or less than 0.2 in cold-activated channels) in a relevant temperature range.
-
2.
Expression in relevant cell types, potentially facing significant changes in temperature (as sensory nerve endings or keratinocytes).
-
3.
Underlying the temperature dependency of a physiological process. In other words, there must be in vivo evidence that the temperature dependence of the channel determines the effects of temperature on a physiological process or pathology.
More than 10 mammalian TRP channels meet requirement 1: TRPA1,25 TRPC5,26 TRPM2,27 TRPM3,28 TRPM4,29 TRPM5,29 TRPM8,10 TRPV1,9 TRPV2,30 TRPV3,31 and TRPV4.32,33 However only some TRP channels meet requirements 2 and 3: TRPV1, TRPM3 and TRPM5, which are heat-activated; TRPC5 and TRPM8, which are cold-activated.24 TRPA1 is a cold sensor in mice25,34-36 but it is a heat sensor in invertebrates and ancestral vertebrates37-42. In humans and monkeys TRPA1 was found to be insensitive to temperature43 however, it is sensitive to cold temperatures when reconstituted into lipid bilayers.44
TRPM8 meet the 3 requirements to be considered a physiological temperature sensor. 1) TRPM8 is strongly activated by cold temperatures,10,45 2) TRPM8 is expressed in DRG neurons and their projections to the skin.46 3) TRPM8-deficient mice show severe deficits in behavioral cold perception.47–49 In addition TRPM8 is cold activated when reconstituted in lipid bilayers, demonstrating that the channel has an intrinsic temperature sensor.50 However, temperature sensing is complemented in vivo with intracellular signaling such as changes of the levels of the TRPM8 modulator phosphatidylinositol 4,5-bisphosphate, PIP2.14,51
In this review we will first take a short journey through the classical mathematical approach to studying thermosensitive TRP channels followed by a description of the biophysics of TRPM8. Detailed discussions on molecular mechanisms for temperature activation and about the possible molecular nature of the temperature sensor can be found elsewhere.52,53
Classical Approaches to the Ion Channel Thermosensation Mechanism
In most reports concerning thermosensitive TRP channels we found that there are 2 parameters used to measure the channel´s thermosensitivity, namely the thermal coefficient Q10 and the thermal threshold Tt. A critical appraisal of these 2 parameters is given below.
Thermal coefficient (Q10)
The Q10 temperature coefficient is used to denote the n-fold increase in rate (α) of a process accompanying a 10°C increase in temperature, and it is defined as:
| (1) |
Where αT and αT+10 are the rates of a process at temperatures T and T + 10°C, respectively.
An expression for Q10 for arbitrary temperatures T2 and T1 is:
| (2) |
Where α2 and α1 are the rates determined at temperatures T2 and T1, respectively, and the dimensionless exponent is the ratio of 10 kelvin over the actual temperature difference. Note that T2 must be larger than T1 and the difference between them can be more or less than 10°C.
Equation (2) can be rewritten as:
| (3) |
Multiplying by both sides of the equation (3) we have
| (4) |
Note that the quantity between square parentheses represents the slope m of the plot of the logarithm of the kinetic rate versus the reciprocal of the absolute temperature (Arrhenius plot) expressed in kelvin:
| (5) |
The quantity before the square parentheses in equation (4) is −10/T1T2 and the product of the absolute temperatures can be approximated to the square of an average temperature T:
| (6) |
So, equation (4) can be rewritten as:
| (7) |
Equation (7) leads to the calculation of Q10 at a given temperature, when the Arrhenius plot slope is known. Equation (7) also tells us that Q10 depends on temperature even for a process characterized by a constant-slope Arrhenius plot. Therefore, it is mandatory to report Q10 together with the temperature of the determination. Conversely, a process characterized by a temperature-independent Q10 will have a non-linear Arrhenius plot
Thermal threshold
Another parameter often used to describe channel activation is the thermal threshold (Tt), that is, the temperature at which the channel begins to activate. From an experimental point of view the thermal threshold is the temperature at which TRP current reaches a magnitude equal to the background current.24 Later we will use an example to illustrate the explanation of this parameter.
The 2-State Model
The simplest classical thermodynamics approach considers that ion channel activation is well described by a 2-state model, encompassing an open (O) state and a closed (C) state with an opening rate α and a closing rate β:
According to the Eyring rate theory, α and β depend on the height of the energy barrier separating the closed and open states, which is temperature dependent according to:
| (8) |
And,
| (9) |
Where and represent the molar activation enthalpy and and the molar activation entropy associated with channel opening and closing, respectively. T is the absolute temperature in kelvin. A is the pre exponential factor, which can be assumed to be temperature-independent in the physiological temperature interval.
Q10 of rate constants
Using the Q10 definition given in equation (1), and assuming constant activation enthalpy and entropy we can calculate the Q10 value for the activation rate constant:
| (10) |
Since 10 K is small compared to T, the following approximation can be used:
| (11) |
Then, by introducing these approximations into equation (7) we obtain:
| (12) |
In the same way, the Q10 value for the closing rate is:
| (13) |
From equation (8) it can be easily demonstrated that is the slope of an Arrhenius plot of ln (α) vs 1/T; so equation (12) and (7) are the same thing.
Some important considerations about equilibrium conditions
In the 2-state model, the equilibrium constant is defined as the ratio O/C, the ratio of the probability of finding the open and the closed state in equilibrium.
| (14) |
The equilibrium constant in terms of the change of thermodynamic variables associated with the close to open transition is as follows:
| (15) |
In this equation, ΔH0 and ΔS0 are the standard molar enthalpy and the standard molar entropy of the process. Temperature dependence of K is determined by ΔH0, which is the difference between molar activation enthalpies of the close to open transition, minus the open to close transition.
| (16) |
This difference between molar activation enthalpies determines the ratio of the close to open and the open to close Q10 values. Combining equations (12) and (13), this Q10 ratio is as follows:
| (17) |
If the rate constant of the close to open transition grows faster than the reverse with a rise in temperature, Q10,α would be larger than Q10,β, and ΔH0 would be positive. Therefore, the equilibrium would be displaced toward the open state upon a K increase with a rise in temperature, according to equation (16). On the other hand, the equilibrium would be displaced toward the closed state when a Q10,β is larger than Q10,α, ΔH0 is negative and K decreases with a rise in temperature.
A Q10,K for the equilibrium constant can be defined as KT+10 / KT. This Q10 calculated from equation (15) assuming that ΔH0 and ΔS0 are independent from temperature is shown in equation (18):
| (18) |
By combining equations (16), (17) and (18) an important relationship emerges:
| (19) |
The open probability (PO) is defined as Po = O/(O + C), and is given by the following equation in terms of the equilibrium constant:
| (20) |
The open probability tends toward 1.0 for large values of K, and Po tends toward 0 for small K values. In the limit of very low probabilities Po tends toward K; therefore Q10,K can be obtained from a Q10 calculated as the ratio of the open probabilities having measured a T + 10 and T in the regime of low Po.
| (21) |
Some important experimental issues
Sensu stricto, Q10 should only be used to describe the effects of temperature on the rate of a process. In the case of ion channels this quantity is the rate of electric charge transport across the channel, i.e. the ion current. Note that the current I passing through ion channels is proportional to the product between the open probability and the unitary channel conductance gi:
| (22) |
Where N is the number of channels, and G is the total conductance, Vm is the membrane electric potential and Vi is the inversion potential. As any physical process, the unitary channel conductance is temperature dependent. However, the Q10 of gi is low and about 1.5.54-56 Then, the relation between the unitary conductances at 2 different temperatures is:
| (23) |
In addition, when determining the channel temperature dependence of thermosensitive TRP channels in, for example, a neuron, there are endogenous conductances and leak currents, which are necessary to consider. We will name the sum of these currents the “heat-activated background current” (Ibg) with low temperature dependence (Q10,bg = 2):
| (24) |
Let us assume that we have a membrane patch containing heat-activated TRP channels (Q10 = 30) with a maximal conductance of 10 nS at 50°C and Ibg = 0.5 nS. Under these experimental conditions we apply a temperature ramp from 0°C to 50°C with the membrane voltage fixed at 100 mV. Then, the total current can be written as:
| (25) |
The IT vs. temperature curve is shown in Figure 1A. By plotting the logarithm of IT vs. the reciprocal of temperature (Fig. 1B), an apparent Q10 for each temperature can be calculated from the curve slope using equation (7), as shown in Figure 1C. It can be observed that by using this method we underestimate the actual Q10 of the thermosensitive TRP channel. Figure 1C shows that at low temperatures, where the TRP channels are closed, the Q10 approaches that of the background current as expected. At higher temperatures the Q10 vs. T curve reaches a maximum of around 26 at 32 °C and then falls to the unitary channel conductance Q10. Thus, the TRP channel Q10 is grossly underestimated when this approach is used, because the actual Q10 of the TRP channel is the product of Q10,K and Q10,gi (Q10 = 45). The procedure fails because at the limit of very low open probability, where the TRP Q10 can be calculated from the slope of the Arrhenius plot, the recorded current is mainly background current. The apparent Q10 at low temperatures corresponds to the background current. At higher temperatures the TRP current becomes detectable and the apparent Q10 rises, but the TRP channels are far from the limit of very low open probability and equation (21) is no longer valid. At even higher temperatures, when TRP channels are fully open, Po becomes temperature independent and the apparent Q10 approximates that of the open channel conductance. The same caveats that apply to the Q10 obtained from temperature ramps are valid when calculating Q10s from conductance vs. voltage curves at different voltages and at 2 different temperatures (Yang and Zheng)57a. In particular, large errors in the determination of the Q10 may arise in the neighborhood of 0 mV.
Figure 1.
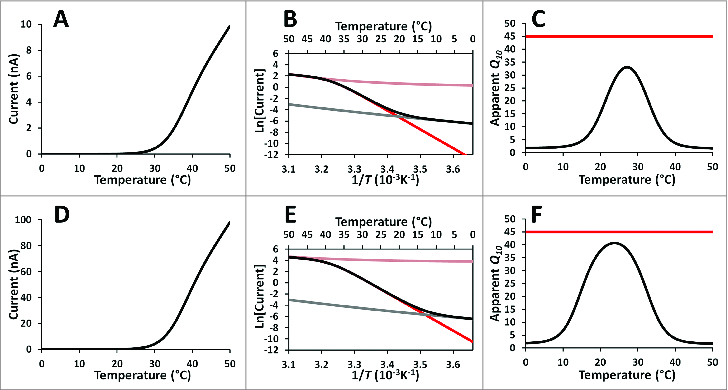
Determination of Q10 and the thermal threshold in a typical heat-activated TRP channel. (A) Simulation of a patch clamp recording of a membrane where a heat activated TRP channel is expressed. Parameters: Maximal conductance = 10 µS (at 50°C), Temperature ramp: from 0°C to 50°C. Q10,K = 30, Q10, gi = 1.5 Q10, bg = 2, conductance of background = 0.5 nS (at 50°C). (B) The same data as in A represented as the logarithm of the current (without units) vs. the reciprocal of the temperature (red line: TRP current; gray line: background current; pink line: total current changing because the temperature dependency of the unitary current if the open probability was the same as that at 50°C; black line: the total current). (C) The apparent Q10 calculated from the slope of the data in B versus the temperature reciprocal is represented by the black line (red line: total Q10 obtained from the product between Q10, K and Q10, gi at 25°C). (D) Results of a simulation as in A except that the maximal conductance of the TRP channels is 100 µS (at 50°C). (E) The same data as in D represented as the logarithm of the current vs. the reciprocal of the temperature (red line: TRP current; gray line: background current; pink line: total current changing because the temperature dependency of the unitary current if the open probability was the same as that at 50°C; black line: the total current). (F) The apparent Q10 calculated from the slope of the data in E versus the temperature is represented by the black line (red line: total Q10 obtained from the product between Q10, K and Q10, gi at 25°C).
At temperatures less than 30°C in the particular example shown in Figure 1B, the Arrhenius plot can be described as the sum of 2 tangent straight lines. The thermal threshold is defined as the temperature at which the tangent lines intersect,24 namely when the TRP current equals the background current. This value is about 33°C in the example displayed in Figure 1B. However, if TRP channel expression is higher as in Figure 1D, the thermal threshold is found at a lower temperature (Fig. 1E) and the Q10 is more accurately determined (Fig. 1F). As can be appreciated in Figure 1F, the determination of Q10, although closer to the true value, is again underestimated. From the previous analysis, it can be stated that using Q10 and the thermal threshold to describe the TRP channel has to be with caution because both values are strongly influenced by the experimental conditions, such as magnitude of the background current and the number of TRP channels in the membrane.
More striking is the case of a cold-activated TRP channel (Fig. 2). The currents in Figure 2A are simulated in the same conditions as 1A, except that he sign of the enthalpy change is negative. Interestingly, the current curve vs. temperature curve has a biphasic behavior, because while the opening probability increases with lower temperatures, the unitary conductance displays the opposite behavior. At low temperatures (˜10°C) all channels are open, Po is temperature independent (close to 1.0) and the slope of the current vs. T curve is determined by the temperature dependence of the unitary conductance. It should be recalled that the Q10 values obtained from the Arrhenius plot (as in Fig. 2B) represent values less than 1 for cold activated channels, and for clarity we have plotted the reciprocals of the calculated Q10 values (Fig. 2C). The TRP current is not detectable at higher temperatures when approaching the limit of low Po, because of the background current. At high temperatures the apparent Q10 is that of the background current. Similarly to the heat-activated channel case, when cold-activated TRP channel expression increases (Fig. 2D), the thermal threshold changes (cf., Fig. 2B and 2E) and the Q10 approaches the expected value.
Figure 2.

Determination of Q10 and the thermal threshold in a typical cold-activated TRP channel. (A) Simulation of a patch clamp recording of a membrane where a cold activated TRP channel is expressed. Parameters: Maximal conductance = 10 µS (at 0°C), Temperature ramp: from 0°C to 50°C. Q10,K = 1/30, Q10, gi = 1.5 Q10, bg = 2, conductance of background = 0.5 nS (at 50°C). (B) The same data as in A represented as the logarithm of the current vs. the reciprocal of the temperature (red line: TRP current; gray line: background current; pink line: total current changing because the temperature dependency of the unitary current if the open probability was ever the same as that at 0°C; black line: the total current). (C) The reciprocal of apparent Q10 calculated from the slope of the data in B versus the temperature reciprocal is represented by the black line (red line: reciprocal of Q10 obtained from the product between reciprocals of Q10, K and Q10, gi). (D) Results of a simulation as in A except that the maximal conductance of the TRP channels is 100 µS (at 0°C). (E) The same data as in D represented as the logarithm of the current vs. the reciprocal of the temperature (red line: TRP current; gray line: background current; pink line: total current changing because the temperature dependency of the unitary current if the open probability was the same as that at 0°C; black line: the total current). (F) The reciprocal of apparent Q10 calculated from the slope of the data in E versus the temperature reciprocal is represented by the black line (red line: reciprocal of Q10 obtained from the product of reciprocals of Q10, K and Q10, gi).
In sum, the experimental approach described here to obtain Q10 and the thermal threshold gives unreliable results. The Q10 values are underestimated and the thermal threshold is strongly dependent on the experimental conditions. The key for a successful determination of Q10 is to be able to distinguish the TRP current from the background current in the limit of very low Po. This can be done by detecting single channel events using noise analysis in membranes with many channels, as in Raddatz et al.56
The voltage-dependent 2-state Kinetic Model
Most thermosensitive TRP channels are also voltage-dependent and it is expected that depending on the characteristics of the energy landscape both rate constants should be voltage-dependent according to the following equations:
| (26) |
And,
| (27) |
Where z is the gating charge, δ is the fraction of the electric field, F is the Faraday constant and V is the membrane voltage. Using a similar procedure as in the previous section (equation 13) it is possible calculate the Q10 value of the opening rate by using the following equation:
| (28) |
and the Q10 value for the closing rate is given by the relation:
| (29) |
Similarly, it can be calculated that the Q10 value from the equilibrium constant is equal to the Q10 value from the limiting slope of the PO, and it is the ratio between the Q10 of the rates:
| (30) |
Then, Q10 can be determined from the van't Hoff plot slope as shown in Figure 3C. Note that for this model there is a family of van't Hoff curves because there is a different lnK vs. 1/T curve for each voltage.
Figure 3.
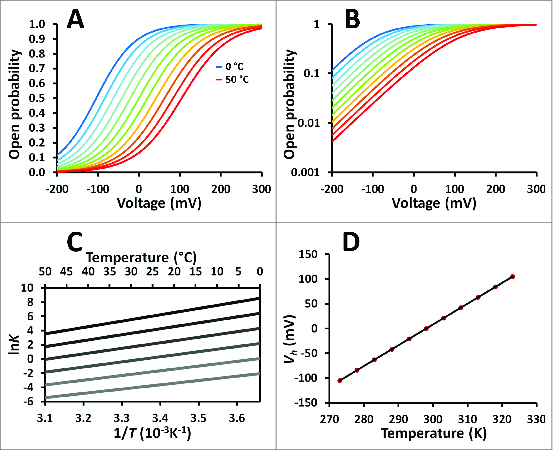
The 2-state model. (A) Conductances vs. voltage curves of a cold-activated channel with voltage dependence. Parameters: ΔH0 = −60 kJ/mol, ΔS0 = −200 J/Kmol, zδ = 0.5; temperatures: from 0 to 50°C in 5°C steps (blue-like curves represent colder temperatures and red-like curves representing warmer temperatures). (B) Same data in A plotted in a semilogarithmic graphic. (C) The van't Hoff plot family from data in A at several voltages (−200, −100, 0, 100, 200 and 300 mV, the darker line representing the most positive membrane voltage). (D) The half activation voltage versus temperature curve for the data in A.
The open probability can be written as follows:
| (31) |
Then, there is a family of Po vs. V curves, depending on the temperature at which this curve is determined as shown on Figure 3A. Semi-logarithmic plot shown on Figure 3B illustrates that at extreme negative voltages a constant limiting slope is reached according to equation 31 (Fig. 3A and 3B).
In this model, the open probability can be rewritten as follows:
| (32) |
Where Vh is the voltage at which the half maximal activation occurs. By combining equations (31) and (32) it is possible to show that Vh changes linearly with temperature according to:
| (33) |
So, ΔH0 and TΔS° can be calculated from the intercept and the slope of a linear fit to experimentally derived Vh values in function of temperature, as shown in Figure 3D.
Thermosensitive TRP channels and the change of molar heat capacity
Clapham and Miller57b suggested that ΔH0 and ΔS0 are not constant with temperature and that gating of thermosensitive TRP channels involves large changes in molar heat capacity. The relationship between change of molar heat capacity (ΔCp) and the ΔH0 and ΔS0 associated with channel opening is given by the modified Gibbs-Helmhotz equations:58
| (34) |
| (35) |
In these equations, and are the differences in standard molar enthalpy and entropy, respectively, between the open and the closed states of the channel at temperature T0.
Interestingly, equation (34) predicts that there is a temperature at which ΔH0 = 0:
| (36) |
It is evident from equation (18) (see also Latorre et al.59) that all what is needed in order to have a temperature-activated channel is a large ΔH0. At T = T0 the channel is temperature insensitive and above or below T0 the channel may be heat or cold activated, according to the ΔCp and sign (equation (36)). However, there is no experimental evidence of cold and heat activation in thermosensitive TRP channels to support that the gating of thermosensitive TRP channels involves a large change in molar heat capacity56,60-64 Conversely, a quasi-linear relation has been found between ln(K) and 1/T indicating that the ΔH0 of thermosensitive TRP channels is approximately constant at least in the physiological range. This would imply that thermosensitive TRP channels undergo a small change in molar heat capacity associated with channel opening.
Evidences for more complex models
Thus far we have focused on the study of thermosensitive ion channels as a 2-state system, but this type of approach failed to adequately describe the behavior of TRPM8, which is a widely studied cold-activated TRP channel.56,60,65,66 Equation (32) for the 2-state model predicts that Po = 1 if the membrane is sufficiently depolarized (Fig. 3A). However, it was found that the maximal open probability may be less than 1.0 and it is temperature-dependent in TRPM8.56,60 This finding can be explained with a sequential scheme including 2 closed states and one open state, where the last transition between closed and open states would depend on temperature, but would be voltage independent. In addition, TRPM8 Vh fails to be a linear function of T as predicted by equation (33), since it tends to saturate at low and high temperatures.56,59 Also, the existence of 2 exponential components upon the decay of the deactivation time course is incompatible with the 2-state model, which predicts a monoexponential decay for the activation of the open-closed transition.56,60
Allosteric Models for Thermosensitive TRP Channels
The term allosteric (αλλoσ = other, different; στερεoσ = solid, object) was introduced by Monod and Jacob67 to propose a rational mechanism for the observed cooperativity in hemoglobin's oxygen binding. In the field of thermosensitive ion channels, allosteric models assume the existence of specific domains of the channel acting as thermosensitive modules and can transit between an activated and a resting state in response to temperature changes. In these types of models this activation is allosterically linked to the pore opening.59,60,66,68,69 Allosteric models were introduced for ion channels to explain voltage and calcium activation of the large conductance calcium activated potassium channel.68,70
Allosteric models assume that the temperature sensors and the channel pore gate are separate parts of the protein structure. Brauchi et al.45,71 demonstrated that the temperature sensor of TRPM8 and TRPMV1 is located on the C-terminal domain. They interchanged the temperature sensitivity of TRPM8 and TRPV1 by swapping the C-terminal of the cold activated TRPM8 with that of the heat activated TRPV1, generates an interchange of temperature activation phenotype. PIP2, but not temperature sensitivity, disappears when positively charged residues contained in the exchanged region are neutralized.45 Furthermore, they find that the deletion of 11 amino acids in this region of TRPM8 abolished the temperature sensitivity without affect the voltage activation.45 These observations support the concept that the PIP2 biding site, temperature sensor, the voltage sensor and the channel pore gate are separate parts of the protein structure.
The dual allosteric coupling model for TRPM8
The model was used for TRPM860 and describes the channel as having 3 modules, which undergo 3 separate 2-state equilibria that interact allosterically with each other. These modules are the voltage sensor, the temperature sensor and the conduction pore (Fig. 4A). The conduction pore can have 2 alternative states: open (O) or closed (C). The equilibrium constant L of the channel is shown in equation (37):
| (37) |
Figure 4.

The allosteric models for the TRPM8 channel. (A) Schematic representation of the 2-tiered allosteric model proposed by Brauchi et al.60 (B) Open channel probability vs. voltage curves of a cold-activated channel calculated using the model proposed by Brauchi et al. Parameters: ΔH0 = −200 kJ/mol, ΔS0 = −740 J/Kmol, zJ = 0.6, C = 3047, D = 1000, Vh,J = 81 mV, L = 1.44 × 10−4; temperatures: from 0 to 50°C in 5°C steps (the blue curve represents the coldest temperature and the red curve represents the warmest temperature). (C) The same data in B plotted in semilogarithmic plot. (D) Schematic representation of the 2-tiered allosteric model proposed by Raddatz et al.56 (E) Conductances versus voltage curves of a cold-activated channel using the 2-tiered model proposed by Raddatz et al.56 Parameters: ΔH0 = −79 kJ/mol, ΔS0 = −292 J/Kmol, zJ = 0.37, C = 52.3, D = 2.3, E = 60, Vh,J = 234 mV, L = 4.3 × 10−8; temperatures: from 0 to 50°C in 5°C steps (the blue curve represents the coldest temperature and the red curve represents the warmest temperature). (F) The same data in (E) plotted in a semilogarithmic plot. (G) Schematic representation of the 3-tiered allosteric model proposed by Raddatz et al.56 (H) Conductance vs. voltage curves of a cold activated channel using the 3-tiered model proposed in (G). Parameters ΔH0 = −125 kJ/mol, ΔS0 = −435 J/Kmol, zJ = 0.35, C = 1.1, D = 7.7, E = 30, F = 1.36, G = 3.8, Vh,J = 267 mV, M = 2.5 × 10−4 L = 0.015, Temperatures: from 0 to 50°C in 5°C steps (the blue curve represents the coldest temperature and the red curve represents the warmest temperature). (I) The same data in (H) plotted in semilogarithmic plot.
This equilibrium constant is assumed to be independent of temperature and voltage, and determines the lower limit of the open channel probability.
The temperature-dependent equilibrium K constant for the resting (RT) and the active (AT) states of the temperature sensor is voltage independent, as shown in equation (38). This is the expression for the temperature sensor when the channel is closed and the voltage sensor is in the resting state:
| (38) |
The voltage-dependent equilibrium constant for the resting (RV) and the activated (AV) states of the voltage sensor is shown in equation (39). This is the expression for the voltage sensor when the channel is closed and the temperature sensor is in the resting state. J0 is the equilibrium constant at 0 mV
| (39) |
Activation of either the voltage or temperature sensor affects the pore opening. For example, when the voltage sensor is active, the equilibrium constant of the pore is multiplied by the allosteric factor D. When the temperature sensor is active, the equilibrium constant is multiplied by the allosteric factor C. When both sensors are active, the equilibrium constant for the close to open transition is the product of LCD. When both sensors are resting, the equilibrium constant for channel gating is L.
The equation for the open probability at any temperature and any membrane potential is:
| (40) |
Brauchi et al.60 modified the original Horrigan and Aldrich model70 by substituting the Ca2+ binding present in the allosteric model for the BK channel with temperature sensor activation. In this case there is only one voltage sensor, which contrasts with what is assumed in the model put forth by Horrigan and Aldrich,70 which considers 4 voltage sensors and 4 Ca2+ sensors, based on the homotetrameric structure of the BK channels. In addition, the interactions between temperature and voltage sensors were not included. The model produces a family of Po vs voltage curves as shown in Figure 4B. When the same data was plotted in a semilogarithmic plot, the curves were not straight lines at very negative voltages, as can be appreciated in Figure 4C, cf. Figure 3B which was plotted for the voltage-dependent 2-state kinetic model. Moreover, the open channel probability becomes voltage-independent at extreme negative voltages. Parameters used to plot Figure 3B and C were taken from Brauchi et al.60
This model assumes that activation of either sensor would additively change the standard molar free energy difference of the C-O transition and can reproduce the steady-state behavior of TRPM8 in a wide range of conditions. One of the highlights of this model is that the allosteric linkage between activation of any sensor and the pore opening predicts that temperature (or voltage) sensor activation is not strictly necessary for channel opening and that these stimuli can act independently from each other. When both sensors at rest the equilibrium constant for the close to open transition is L = 4.4 × 10−4, which implies an open channel probability, Po = 4.4 × 10−4. When the voltage sensor is fully activated and the temperature sensor is at rest the equilibrium constant is LD. With D = 1000, Po = 0.30. When the temperature sensor is fully activated and the voltage sensor is at rest the equilibrium constant is LC. With C = 3047, Po = 0.57. When the temperature and sensors are fully activated the equilibrium constant is LCD and Po = 1.0. In this model with the values assigned to L, C and D neither temperature nor voltage alone can fully activate the channel. The model assumes that there are independent domains within the channel structure that behaves as a temperature and voltage sensor in thermosensitive TRP channels that would be able to convert thermal or electric energy into mechanical work in order to open the channel.
Enthalpy and entropy changes associated with TRPM8 temperature sensor activation were both negative, as expected from the discussion of the 2-state model ΔH0 = −200 kJ/mol, ΔS0 = −740 J/Kmol, and the allosteric coupling factor is 3047 However, the same effect of temperature on open channel probability would be obtained with positive enthalpy and entropy changes, if the allosteric coupling factor C was 1/3047, such that the channel closes when the temperature sensor gets activated. This point was raised by Jara-Oseguera and Islas72 and Yao et al.62
The thermodynamic analysis contains information richer than the temperature factor Q10 which can be calculated from ΔH0 obtained for temperature sensor equilibrium constant, using equation 18. The Q10 calculated for the enthalpy change of −200 kJ/mol is 15. The large enthalpy change of −200 kJ/mol implies a large molecular rearrangement involving the creation of many non-covalent bonds during channel opening. The large enthalpy change is compensated by a large negative entropy change of −740 J/Kmol, The ratio ΔH0/ΔS0 is the temperature at which the temperature sensor is half-activated., provided the voltage sensor is at rest. In this case this temperature is −3°C. The magnitude and sign of the entropy change is consistent with an open channel state which is more ordered than the closed state.
Raddatz et al.56 compared the goodness of a global fit to the “one sensor” model with a global fit to a 2-tiered 4-voltage and 4-temperature sensor model (Figure 4D-F plotted using the parameters reported by Raddatz et al.56). This model works better in describing the equilibrium results than the Brauchi et al. model60 specially on the open channel probability at very negative voltages (Fig. 4F). In addition, the sum of the square residuals was 3.1 for the Brauchi et al. (2004) model60 and felt to 2.1 in the case of the Raddatz et al. (2014) model.56 However, there are some kinetics results that cannot be explained by this allosteric model, as we discuss in the next section.
The three-tiered allosteric model for TRPM8
The TRPM8 time course of deactivation is not a first order process, and a 2 exponential decay is necessary to describe its time course. A double exponential time course for deactivation is predicted in a C0-C1-O kinetic scheme, in which the forward rate in the C-O transition is different from zero.73 These transitions are described by the equilibrium constant M and L as shown in the model depicted in Figure 4G and in equations(41) and (42):
| (41) |
| (42) |
The voltage sensor and the temperature sensor operate in the same way as in the 2-tiered allosteric model. The equilibrium constants for the resting (RT) and the active (AT) states of each temperature sensor and each voltage sensor are identical to equations (38) and (39), respectively.
Similarly, the activation of one module affects the other. For example, the activation of one voltage sensor multiplies M and L equilibria by allosteric factors D and F, respectively. The activation of one temperature sensor multiplies M and L by allosteric factors C and G, respectively. E is an allosteric factor that describes the interaction between both sensors.
The equation for the open probability at any temperature and any membrane potential is:
| (43) |
This model produces a conductance vs voltage curves as are display if Figure 4H-I plotted using the parameters reported by Raddatz et al.56 The activation of both sensors additively affects the standard molar free energy of the C0-C1 and C1-O transitions and can reproduce the steady-state behavior of TRPM8 in a wide range of conditions. Even though the fit to the experimental steady state does not improve compared with mode of Figure 4D, this model is able to account for the complex channel kinetics.
Conclusions
The classical approaches used to describe the thermosensitivity of ion channels consist of 2 parameters: the thermal coefficient Q10 and the thermal threshold. We have shown that both parameters must be used with extreme caution because obtained values are strongly dependent on the precise experimental conditions.
Within the thermosensitive proteins in mammals, the TRP channels represent a very extended and important family. We have focused on a well-studied thermosensitive TRP member, namely the cold-activated TRPM8 channel, which has been extensively studied in terms of mathematical modeling of temperature and voltage coupling to the channel gating. Evidence has been presented in support of the inadequacy of the classical 2-state or linear sequential models, in which voltage and temperature sensors are strictly coupled to the pore domain, as they fail to describe the complex behavior of the gating of this channel. In contrast, allosteric models have more accurately described TRPM8 gating, possibly posing a general rule for all polymodal TRP channel receptors.
Disclosure of Potential Conflicts of Interest
No potential conflicts of interest were disclosed.
Funding
This study was funded by grant FONDECYT 1150273 and 1110430 (To R. Latorre). The Centro Interdisciplinario de Neurociencia de Valparaíso (CINV) is a Millennium Institute supported by the Millennium Scientific Initiative of the Ministerio de Economía, Fomento y Turismo (Chilean Government).
References
- 1.Vriens J, Nilius B, Voets T. Peripheral thermosensation in mammals. Nat Rev Neurosci 2014; 15:573-89; PMID:25053448; http://dx.doi.org/ 10.1038/nrn3784 [DOI] [PubMed] [Google Scholar]
- 2.Spray DC. Metabolic dependence of frog cold receptor sensitivity. Brain Res 1974; 72:354-9. Available at: http://www.ncbi.nlm.nih.gov/pubmed/4545716; PMID:4545716; http://dx.doi.org/ 10.1016/0006-8993(74)90881-6 [DOI] [PubMed] [Google Scholar]
- 3.Pierau F, Torrey P, Carpenter DO. Mammalian cold receptor afferents: role of an electrogenic sodium pump in sensory transduction. Brain Res 1974; 73:156-60; PMID:4407843; http://dx.doi.org/ 10.1016/0006-8993(74)91015-4 [DOI] [PubMed] [Google Scholar]
- 4.Kobayashi S, Takahashi T. Whole-cell properties of temperature-sensitive neurons in rat hypothalamic slices. Proc Biol Sci 1993; 251:89-94; PMID:8096083; http://dx.doi.org/ 10.1098/rspb.1993.0013 [DOI] [PubMed] [Google Scholar]
- 5.Reid G, Flonta M. Cold transduction by inhibition of a background potassium conductance in rat primary sensory neurones. Neurosci Lett 2001; 297:171-4. PMID:11137755; http://dx.doi.org/ 10.1016/S0304-3940(00)01694-3 [DOI] [PubMed] [Google Scholar]
- 6.Askwith CC, Benson CJ, Welsh MJ, Snyder PM. DEG/ENaC ion channels involved in sensory transduction are modulated by cold temperature. Proc Natl Acad Sci U S A 2001; 98:6459-63 PMID:11353858; http://dx.doi.org/ 10.1073/pnas.111155398 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Reid G, Babes A, Pluteanu F. A cold- and menthol-activated current in rat dorsal root ganglion neurones: properties and role in cold transduction. J Physiol 2002; 545:595-614PMID:12456837; http://dx.doi.org/ 10.1113/jphysiol.2002.024331 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Suto K, Gotoh H. Calcium signaling in cold cells studied in cultured dorsal root ganglion neurons. Neuroscience 1999; 92:1131-5. Available at: http://www.ncbi.nlm.nih.gov/pubmed/10426551; PMID:10426551; http://dx.doi.org/ 10.1016/S0306-4522(99)00063-9 [DOI] [PubMed] [Google Scholar]
- 9.Caterina MJ, Schumacher MA, Tominaga M, Rosen TA, Levine JD, Julius D. The capsaicin receptor: a heat-activated ion channel in the pain pathway. Nature 1997; 389:816-24; PMID:9349813; http://dx.doi.org/ 10.1038/39807 [DOI] [PubMed] [Google Scholar]
- 10.Mckemy DD, Neuhausser WM, Julius D. Identification of a cold receptor reveals a general role for TRP channels in thermosensation. Nature 2002; 416:52-8; PMID:11882888 [DOI] [PubMed] [Google Scholar]
- 11.Hjerling-Leffler J, Alqatari M, Ernfors P, Koltzenburg M. Emergence of functional sensory subtypes as defined by transient receptor potential channel expression. J Neurosci 2007; 27:2435-43; http://dx.doi.org/ 10.1523/JNEUROSCI.5614-06.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Cho H, Yang YD, Lee J, Lee B, Kim T, Jang Y, Back SK, Na HS, Harfe BD, Wang F, et al.. The calcium-activated chloride channel anoctamin 1 acts as a heat sensor in nociceptive neurons. Nat Neurosci 2012; 15:1015-21; PMID:22634729; http://dx.doi.org/ 10.1038/nn.3111 [DOI] [PubMed] [Google Scholar]
- 13.Xiao B, Coste B, Mathur J, Patapoutian A. Temperature-dependent STIM1 activation induces Ca2+ influx and modulates gene expression. Nat Chem Biol 2011; 7:351-8; PMID:21499266; http://dx.doi.org/ 10.1038/nchembio.558 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Liu B, Qin F. Functional control of cold- and menthol-sensitive TRPM8 ion channels by phosphatidylinositol 4,5-bisphosphate. J Neurosci 2005; 25:1674-81; http://dx.doi.org/ 10.1523/JNEUROSCI.3632-04.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cosens DJ, Manning A. Abnormal Electroretinogram from a Drosophila Mutant. Nature 1969; 224:285-7; PMID:5344615; http://dx.doi.org/ 10.1038/224285a0 [DOI] [PubMed] [Google Scholar]
- 16.Minke B, Wu CF, Pak WL. Induction of photoreceptor voltage noise in the dark in Drosophila mutant. Nature 1975:84-7; PMID:810728; http://dx.doi.org/ 10.1038/258084a0 [DOI] [PubMed] [Google Scholar]
- 17.Montell C, Rubin GM. Molecular characterization of the Drosophila trp locus: a putative integral membrane protein required for phototransduction. Neuron 1989; 2:1313-23. Available at: http://www.ncbi.nlm.nih.gov/pubmed/2516726; PMID:2516726; http://dx.doi.org/ 10.1016/0896-6273(89)90069-X [DOI] [PubMed] [Google Scholar]
- 18.Gees M, Owsianik G, Nilius B, Voets T. TRP channels. Compr Physiol 2012; 2:563-608; PMID:23728980; http://dx.doi.org/ 10.1002/cphy.c110026 [DOI] [PubMed] [Google Scholar]
- 19.Gaudet R. TRP channels entering the structural era. J Physiol 2008; 586:3565-75; PMID:18535090; http://dx.doi.org/ 10.1113/jphysiol.2008.155812 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Montell C. The TRP superfamily of cation channels. Sci STKE 2005; 2005:re3; PMID:15728426; http://dx.doi.org/ 10.1126/stke.2722005re3 [DOI] [PubMed] [Google Scholar]
- 21.Clapham DE, Julius D, Montell C, Schultz G. International Union of Pharmacology. XLIX. Nomenclature and structure-function relationships of transient receptor potential channels. Pharmacol Rev 2005; 57:427-50; PMID:16382100; http://dx.doi.org/ 10.1124/pr.57.4.6 [DOI] [PubMed] [Google Scholar]
- 22.Launay P, Fleig A, Perraud A, Scharenberg AM, Penner R, Kinet J. TRPM4 is a Ca2+ activated nonselective cation channel mediating cell membrane depolarization. Cell 2002; 109:397-407; PMID:12015988 [DOI] [PubMed] [Google Scholar]
- 23.Nilius B, Owsianik G, Voets T, Peters JA. Transient receptor potential cation channels in disease. Physiol Rev 2007; 87:165-217; http://dx.doi.org/ 10.1152/physrev.00021.2006 [DOI] [PubMed] [Google Scholar]
- 24.Voets T. Quantifying and modeling the temperature-dependent gating of TRP channels. Rev Physiol Biochem Pharmacol 2012; 162:91-119; PMID:22298025; http://dx.doi.org/ 10.1007/112_2011_5 [DOI] [PubMed] [Google Scholar]
- 25.Story GM, Peier AM, Reeve AJ, Eid SR, Mosbacher J, Hricik TR, Earley TJ, Hergarden AC, Andersson DA, Hwang SW, McIntyre P, et al.. ANKTM1, a TRP-like channel expressed in nociceptive neurons, is activated by cold temperatures. Cell 2003; 112:819-29. Available at: http://www.ncbi.nlm.nih.gov/pubmed/12654248; PMID:12654248; http://dx.doi.org/ 10.1016/S0092-8674(03)00158-2 [DOI] [PubMed] [Google Scholar]
- 26.Zimmermann K, Lennerz JK, Hein A, Link AS, Kaczmarek JS, Delling M, Uysal S, Pfeifer JD, Riccio A, Clapham DE. Transient receptor potential cation channel, subfamily C, member 5 (TRPC5) is a cold-transducer in the peripheral nervous system. Proc Natl Acad Sci U S A 2011; 108:18114-9; PMID:22025699; http://dx.doi.org/ 10.1073/pnas.1115387108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Togashi K, Hara Y, Tominaga T, Higashi T, Konishi Y, Mori Y, Tominaga M. TRPM2 activation by cyclic ADP-ribose at body temperature is involved in insulin secretion. EMBO J 2006; 25:1804-15; PMID:16601673; http://dx.doi.org/ 10.1038/sj.emboj.7601083 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Vriens J, Owsianik G, Hofmann T, Philipp SE, Stab J, Chen X, Benoit M, Xue F, Janssens A, Kerselaers S, et al.. TRPM3 is a nociceptor channel involved in the detection of noxious heat. Neuron 2011; 70:482-94; PMID:21555074; http://dx.doi.org/ 10.1016/j.neuron.2011.02.051 [DOI] [PubMed] [Google Scholar]
- 29.Talavera K, Yasumatsu K, Voets T, Droogmans G, Shigemura N, Ninomiya Y, Margolskee RF, Nilius B. Heat activation of TRPM5 underlies thermal sensitivity of sweet taste. Nature 2005; 438:1022-5; PMID:16355226; http://dx.doi.org/ 10.1038/nature04248 [DOI] [PubMed] [Google Scholar]
- 30.Caterina MJ, Rosen TA, Tominaga M, Brake AJ, Julius D. A capsaicin-receptor homologue with a high threshold for noxious heat. Nature 1999; 398:436-41; PMID:10201375; http://dx.doi.org/ 10.1038/18906 [DOI] [PubMed] [Google Scholar]
- 31.Xu H, Ramsey IS, Kotecha SA. , Magdalene MM, Chong JA, Lawson D, Ge P, Jeremiah Lilly J, Silos-Santiago I, Xie Y, et al. TRPV3 is a calcium-permeable temperature-sensitive cation channel. Nature 2002; 418:181-6; PMID:12077604; http://dx.doi.org/ 10.1038/nature00850.1 [DOI] [PubMed] [Google Scholar]
- 32.Liedtke W, Choe Y, Martí-Renom MA, Bell AM, Denis CS, Sali A, Hudspeth AJ, Friedman JM, Heller S. Vanilloid receptor-related osmotically activated channel (VR-OAC), a candidate vertebrate osmoreceptor. Cell 2000; 103:525-35. Available at: http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=2211528&tool=pmcentrez&rendertype=abstract; PMID:11081638; http://dx.doi.org/ 10.1016/S0092-8674(00)00143-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Güler AD, Lee H, Iida T, Shimizu I, Tominaga M, Caterina M. Heat-evoked activation of the ion channel, TRPV4. J Neurosci 2002; 22:6408-14; PMID:12151520; http://dx.doi.org/20026679 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bandell M, Story GM, Hwang SW, Viswanath V, Eid SR, Petrus MJ, Earley TJ, Patapoutian A. Noxious cold ion channel TRPA1 is activated by pungent compounds and bradykinin. Neuron 2004; 41:849-57. Available at: http://www.ncbi.nlm.nih.gov/pubmed/15046718; PMID:15046718; http://dx.doi.org/ 10.1016/S0896-6273(04)00150-3 [DOI] [PubMed] [Google Scholar]
- 35.Sawada Y, Hosokawa H, Hori A, Matsumura K, Kobayashi S. Cold sensitivity of recombinant TRPA1 channels. Brain Res 2007; 1160:39-46; PMID:17588549; http://dx.doi.org/ 10.1016/j.brainres.2007.05.047 [DOI] [PubMed] [Google Scholar]
- 36.Karashima Y, Talavera K, Everaerts W, Janssens A, Kwan KY, Vennekens R, Nilius B, Voets T. TRPA1 acts as a cold sensor in vitro and in vivo. Proc Natl Acad Sci U S A 2009; 106:1273-8; PMID:19144922; http://dx.doi.org/ 10.1073/pnas.0808487106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hamada FN, Rosenzweig M, Kang K, Pulver SR, Ghezzi A, Jegla TJ, Garrity PA. An internal thermal sensor controlling temperature preference in Drosophila. Nature 2008; 454:217-20; PMID:18548007; http://dx.doi.org/ 10.1038/nature07001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kang K, Panzano VC, Chang EC, Ni L, Dainis AM, Jenkins AM, Regna K, Muskavitch MA, Garrity PA. Modulation of TRPA1 thermal sensitivity enables sensory discrimination in Drosophila. Nature 2012; 481:76-80; http://dx.doi.org/ 10.1038/nature10715 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Neely GG, Keene AC, Duchek P, Chang EC, Wang QP, Aksoy YA, Rosenzweig M, Costigan M, Woolf CJ, Garrity PA, et al.. TrpA1 regulates thermal nociception in Drosophila. Zars T, ed. PLoS One 2011; 6:e24343; PMID:21909389; http://dx.doi.org/ 10.1371/journal.pone.0024343 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Viswanath V, Story GM, Peier AM, Petrus MJ, Lee VM, Hwang SW, Patapoutian A, Jegla T. Opposite thermosensor in fruitfly and mouse 2003; 423:822-3; PMID:12815418 [DOI] [PubMed] [Google Scholar]
- 41.Saito S, Nakatsuka K, Takahashi K, Fukuta N, Imagawa T, Ohta T, Tominaga M. Analysis of transient receptor potential ankyrin 1 (TRPA1) in frogs and lizards illuminates both nociceptive heat and chemical sensitivities and coexpression with TRP vanilloid 1 (TRPV1) in ancestral vertebrates. J Biol Chem 2012; 287:30743-54; PMID:2791718; http://dx.doi.org/ 10.1074/jbc.M112.362194 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Gracheva EO, Ingolia NT, Kelly YM, Cordero-Morales JF, Hollopeter G, Chesler AT, Sánchez EE, Perez JC, Weissman JS, Julius D. Molecular basis of infrared detection by snakes. Nature 2010; 464:1006-11; PMID:20228791; http://dx.doi.org/ 10.1038/nature08943 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Chen J, Kang D, Xu J, Lake M, Hogan JO, Sun C, Walter K, Yao B, Kim D. Species differences and molecular determinant of TRPA1 cold sensitivity. Nat Commun 2013; 4:2501; PMID:24071625; http://dx.doi.org/ 10.1038/ncomms3501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Moparthi L, Survery S, Kreir M, Simonsen C, Kjellbom P, Högestätt ED, Johanson U, Zygmunt PM. Human TRPA1 is intrinsically cold- and chemosensitive with and without its N-terminal ankyrin repeat domain. Proc Natl Acad Sci U S A 2014; 111:16901-6; PMID:25389312; http://dx.doi.org/ 10.1073/pnas.1412689111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Brauchi S, Orta G, Mascayano C, Salazar M, Raddatz N, Urbina H, Rosenmann E, Gonzalez-Nilo F, Latorre R. Dissection of the components for PIP2 activation and thermosensation in TRP channels. Proc Natl Acad Sci U S A 2007; 104:10246-51; PMID:17548815; http://dx.doi.org/ 10.1073/pnas.0703420104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Dhaka A, Earley TJ, Watson J, Patapoutian A. visualizing cold spots: TRPM8-expressing sensory neurons and their projections. J Neurosci 2008; 28:566-75; PMID:18400897; http://dx.doi.org/ 10.1523/JNEUROSCI.3976-07.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bautista DM, Siemens J, Glazer JM, Tsuruda PR, Basbaum AI, Stucky CL, Jordt SE, Julius D. The menthol receptor TRPM8 is the principal detector of environmental cold. Nature 2007; 448:204-8; PMID:17538622; http://dx.doi.org/ 10.1038/nature05910 [DOI] [PubMed] [Google Scholar]
- 48.Colburn RW, Lubin ML, Stone DJ, Wang Y, Lawrence D, D'Andrea MR, Brandt MR, Liu Y, Flores CM, Qin N. Attenuated cold sensitivity in TRPM8 null mice. Neuron 2007; 54:379-86; PMID:17481392; http://dx.doi.org/ 10.1016/j.neuron.2007.04.017 [DOI] [PubMed] [Google Scholar]
- 49.Dhaka A, Murray AN, Mathur J, Earley TJ, Petrus MJ, Patapoutian A. TRPM8 is required for cold sensation in mice. Neuron 2007; 54:371-8; PMID:17481391; http://dx.doi.org/ 10.1016/j.neuron.2007.02.024 [DOI] [PubMed] [Google Scholar]
- 50.Zakharian E, Cao C, Rohacs T. Gating of transient receptor potential melastatin 8 (TRPM8) channels activated by cold and chemical agonists in planar lipid bilayers. J Neurosci 2010; 30:12526-34; PMID:20844147; http://dx.doi.org/ 10.1523/JNEUROSCI.3189-10.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Rohács T, Lopes CMB, Michailidis I, Logothetis DE. PI(4,5)P2 regulates the activation and desensitization of TRPM8 channels through the TRP domain. Nat Neurosci 2005; 8:626-34; http://dx.doi.org/ 10.1038/nn1451 [DOI] [PubMed] [Google Scholar]
- 52.Baez D, Raddatz N, Ferreira G, Gonzalez C, Latorre R. Gating of thermally activated channels. Curr Top Membr 2014; 74:51-87; http://dx.doi.org/ 10.1016/B978-0-12-800181-3.00003-8 [DOI] [PubMed] [Google Scholar]
- 53.Latorre R, Zaelzer C, Brauchi S. Structure-functional intimacies of transient receptor potential channels. Q Rev Biophys 2009; 42:201-46; PMID:20025796; http://dx.doi.org/ 10.1017/S0033583509990072 [DOI] [PubMed] [Google Scholar]
- 54.Horn R, Vandenberg CA, Lange K. Statistical analysis of single sodium channels. Effects of N-bromoacetamide. Biophys J 1984; 45:323-35; http://dx.doi.org/ 10.1016/S0006-3495(84)84158-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Rodríguez BM, Sigg D, Bezanilla F. Voltage gating of Shaker K+ channels. The effect of temperature on ionic and gating currents. J Gen Physiol 1998; 112:223-42. Available at: http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=2525751&tool=pmcentrez&rendertype=abstract. Accessed February26, 2015; http://dx.doi.org/ 10.1085/jgp.112.2.223 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Raddatz N, Castillo JP, Gonzalez C, Alvarez O, Latorre R. Temperature and voltage coupling to channel opening in transient receptor potential melastatin 8 (TRPM8). J Biol Chem 2014; 289:35438-54; ttp://dx.doi.org/ 10.1074/jbc.M114.612713 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.a. Yang F, Zheng J. High temperature sensitivity is intrinsic to voltage-gated potassium channels. eLife 2014; e03255; http://dx.doi.org/10.7554/eLife.03255; b. Clapham DE, Miller C. A thermodynamic framework for understanding temperature sensing by transient receptor potential (TRP) channels. Proc Natl Acad Sci U S A 2011; 108:19492-7; PMID:22109551; http://dx.doi.org/ 10.1073/pnas.1117485108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Prabhu N V, Sharp KA. Heat capacity in proteins. Annu Rev Phys Chem 2005; 56:521-48; http://dx.doi.org/ 10.1146/annurev.physchem.56.092503.141202 [DOI] [PubMed] [Google Scholar]
- 59.Latorre R, Brauchi S, Orta G, Zaelzer C, Vargas G. ThermoTRP channels as modular proteins with allosteric gating. Cell Calcium 2007; 42:427-38; PMID:17499848; http://dx.doi.org/ 10.1016/j.ceca.2007.04.004 [DOI] [PubMed] [Google Scholar]
- 60.Brauchi S, Orio P, Latorre R. Clues to understanding cold sensation: thermodynamics and electrophysiological analysis of the cold receptor TRPM8. Proc Natl Acad Sci U S A 2004; 101:15494-9; PMID:15492228; http://dx.doi.org/ 10.1073/pnas.0406773101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Voets T, Droogmans G, Wissenbach U, Janssens A, Flockerzi V, Nilius B. The principle of temperature-dependent gating in cold- and heat-sensitive TRP channels. Nature 2004; 430:748-54; http://dx.doi.org/ 10.1038/nature02732 [DOI] [PubMed] [Google Scholar]
- 62.Yao J, Liu B, Qin F. Modular thermal sensors in temperature-gated transient receptor potential (TRP) channels. Proc Natl Acad Sci U S A 2011; 108:11109-14; PMID:21690353; http://dx.doi.org/ 10.1073/pnas.1105196108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Yao J, Liu B, Qin F. Pore turret of thermal TRP channels is not essential for temperature sensing. Proc Natl Acad Sci U S A 2010; 107:E125; author reply E126-7; http://dx.doi.org/ 10.1073/pnas.1008272107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Liu B, Hui K, Qin F. Thermodynamics of heat activation of single capsaicin ion channels VR1. Biophys J 2003; 85:2988-3006; http://dx.doi.org/ 10.1016/S0006-3495(03)74719-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Voets T, Owsianik G, Janssens A, Talavera K, Nilius B. TRPM8 voltage sensor mutants reveal a mechanism for integrating thermal and chemical stimuli. Nat Chem Biol 2007; 3:174-82; PMID:17293875; http://dx.doi.org/ 10.1038/nchembio862 [DOI] [PubMed] [Google Scholar]
- 66.Matta JA, Ahern GP. Voltage is a partial activator of rat thermosensitive TRP channels. J Physiol 2007; 585:469-82; PMID:17932142; http://dx.doi.org/ 10.1113/jphysiol.2007.144287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Monod J, Jacob F. General conclusions: teleonomic mechanisms in cellular metabolism, growth, and differentiation. Cold Spring Harb Symp Quant Biol 1961; 26:389-401. Available at: http://symposium.cshlp.org/content/26/389.extract. Accessed September3, 2014; http://dx.doi.org/ 10.1101/SQB.1961.026.01.048 [DOI] [PubMed] [Google Scholar]
- 68.Cox DH, Cui J, Aldrich RW. Allosteric gating of a large conductance Ca-activated K+ channel. J Gen Physiol 1997; 110:257-81. Available at: http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=2229366&tool=pmcentrez&rendertype=abstract; PMID:9276753; http://dx.doi.org/ 10.1085/jgp.110.3.257 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Cui Y, Yang F, Cao X, Yarov-Yarovoy V, Wang K, Zheng J. Selective disruption of high sensitivity heat activation but not capsaicin activation of TRPV1 channels by pore turret mutations. J Gen Physiol 2012; 139:273-83; PMID:22412190; http://dx.doi.org/ 10.1085/jgp.201110724 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Horrigan FT, Aldrich RW. Coupling between voltage sensor activation, Ca2+ binding and channel opening in large conductance (BK) potassium channels. J Gen Physiol 2002; 120:267-305; PMID:12198087; http://dx.doi.org/ 10.1085/jgp.20028605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Brauchi S, Orta G, Salazar M, Rosenmann E, Latorre R. A hot-sensing cold receptor: C-terminal domain determines thermosensation in transient receptor potential channels. J Neurosci 2006; 26:4835-40; http://dx.doi.org/ 10.1523/JNEUROSCI.5080-05.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Jara-Oseguera A, Islas LD. The role of allosteric coupling on thermal activation of thermo-TRP channels. Biophys J 2013; 104:2160-9; PMID:23708356; http://dx.doi.org/ 10.1016/j.bpj.2013.03.055 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Goldman L. On the extraction of kinetic rate constants from experimental data. Biophys J 1991; 60:519-23; http://dx.doi.org/ 10.1016/S0006-3495(91)82080-X [DOI] [PMC free article] [PubMed] [Google Scholar]


