The emergence of functional microcircuits in visual cortex

Abstract

Sensory processing occurs in neocortical microcircuits in which synaptic connectivity is highly structured^1–4 and excitatory neurons form subnetworks that process related sensory information^5,6. However, the developmental mechanisms underlying the formation of functionally organized connectivity in cortical microcircuits remain unknown. Here we directly related patterns of excitatory synaptic connectivity to visual response properties of neighbouring layer 2/3 pyramidal neurons in mouse visual cortex at different postnatal ages, using two-photon calcium imaging in vivo and multiple whole-cell recordings in vitro. Although neural responses were highly selective for visual stimuli already at eye opening, neurons responding to similar visual features were not yet preferentially connected, indicating that the emergence of feature selectivity does not depend on the precise arrangement of local synaptic connections. After eye opening, local connectivity reorganised extensively, as more connections formed selectively between neurons with similar visual responses, and connections were eliminated between visually unresponsive neurons, while the overall connectivity rate did not change. We propose a unified model of cortical microcircuit development based on activity-dependent mechanisms of plasticity: neurons first acquire feature preference by selecting feedforward inputs before the onset of sensory experience – a process that may be facilitated by early electrical coupling between neuronal subsets^7–9 – after which patterned input drives the formation of functional subnetworks through a redistribution of recurrent synaptic connections.

Intrinsic and experiential factors guide the patterning of neural pathways and the establishment of sensory response properties during postnatal development^10–12. During this time, neural circuit refinement is thought to depend on the elimination of initially exuberant projections and/or selective formation of new connections^13,14. However, the mechanisms governing the emergence of structured connectivity in local cortical microcircuits, where dendrites and axons overlap extensively, remain uncertain. Moreover, it is not clear whether the organisation of synaptic connections between nearby neurons is established early and inherently linked to the formation of receptive fields (RFs) before the onset of sensory experience or whether the mature patterns of recurrent connectivity appear only after the formation of RFs as a result of correlated activity induced by feedforward drive from the sensory periphery. Here we investigate these questions in networks of layer 2/3 pyramidal cells in mouse primary visual cortex (V1) — where neighbouring neurons exhibit a diversity of preference for visual features^5,15–17 — by determining how local synaptic connectivity relates to visual response properties during development.

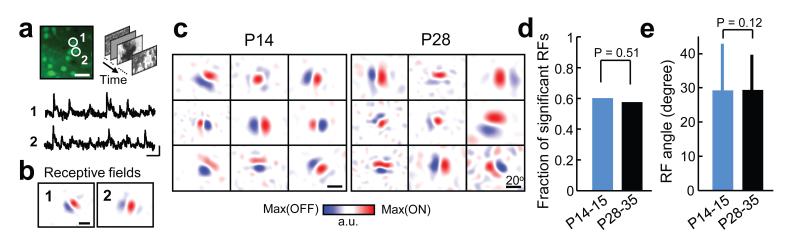
Stimulus selective responses in V1 are observed at eye opening^18–22, but the extent to which detailed RFs are established by this time remains unclear. To characterize the spatial RF structure of L2/3 neurons in V1 at eye-opening (P14 – 15) and in more mature mice (P28 – 35), we used in vivo two-photon calcium imaging²³ in monocular V1 to obtain spatial RFs by reverse correlation^16,17,24 of static natural images and spiking responses inferred from calcium signals²⁵ (see Methods, Fig. 1a,b), and fitted a two-dimensional Gabor function to the RFs (Supplementary Fig. 1). At eye-opening, L2/3 neurons exhibited a diversity of RF spatial structures that resembled those of mature V1 neurons (Fig. 1c, Supplementary Fig. 1a). The proportion of neurons with significant linear RFs was similar between the two age groups (Fig. 1d, P14 – 15, 60%, 191 out of 317; P28 – 35, 58%, 201 out of 348, P = 0.51, Chi-squared test), as was the angle of visual space subtended by RFs (Fig. 1e, mean visual angle along the long RF axis ± s.d., P14 – 15, 29.3 ± 13.6°; P28 – 35, 29.4 ± 10.3°, P = 0.12, rank-sum test; see also Supplementary Fig. 1b,c). The similarity of RF structures was shown by the overlapping distributions of standard RF measures of n_x(=σ_xf) and n_y(=σ_yf), which, respectively, express the width and length of the fitted Gabor in units of the underlying grating period (see Methods, Supplementary Fig. 1d, median n_x, P14 – 15, 0.31; P28 – 35, 0.32, P = 0.14; median n_y, P14 – 15, 0.20; P28 – 35, 0.20, P = 0.41, rank-sum test). For comparison, the orientation tuning of neurons responsive to drifting gratings was slightly but significantly broader at eye-opening than in more mature V1 (Supplementary Fig. 2a,b; median orientation selectivity index (OSI), P13 – 15, 0.62 vs P 22 – 26, 0.68, P = 2.39 × 10⁻³⁴, rank-sum test). Neuronal responses at eye-opening, however, exhibited higher variability to repeated presentation of the preferred grating stimulus (coefficient of variation) than in more mature animals (Supplementary Fig. 2c; mean CV ± s.d., P13 – 15,: 0.93 ± 0.36 vs P22 – 26, 0.71 ± 0.30, P=1.17 × 10⁻³⁰⁴, rank-sum test), indicating that responses in immature animals were less reliable despite the presence of clearly defined RFs and orientation selectivity.

Figure 1. Responses of layer 2/3 pyramidal cells in mouse visual cortex are highly feature selective at eye-opening.

a, Example of OGB-labelled region at P14 (left, scale bar, 30 μm) with calcium transients of two cells obtained with two-photon microscopy (below, scale bars, 20 s, 10 % ΔF/F) in response to natural image sequences. b, Linear receptive fields (RFs) of the neurons in a obtained by regularized reverse correlation (see Methods); scale bars, 20°. c, RFs of neurons from two mice at different ages. d,e, Fractions of neurons with significant RFs (d, chi-squared test) and RF size (e, rank-sum test) at eye-opening and in more mature V1. Error bars show s.d.; n = 4 mice P14 – 15, 5 mice P28 – 35.

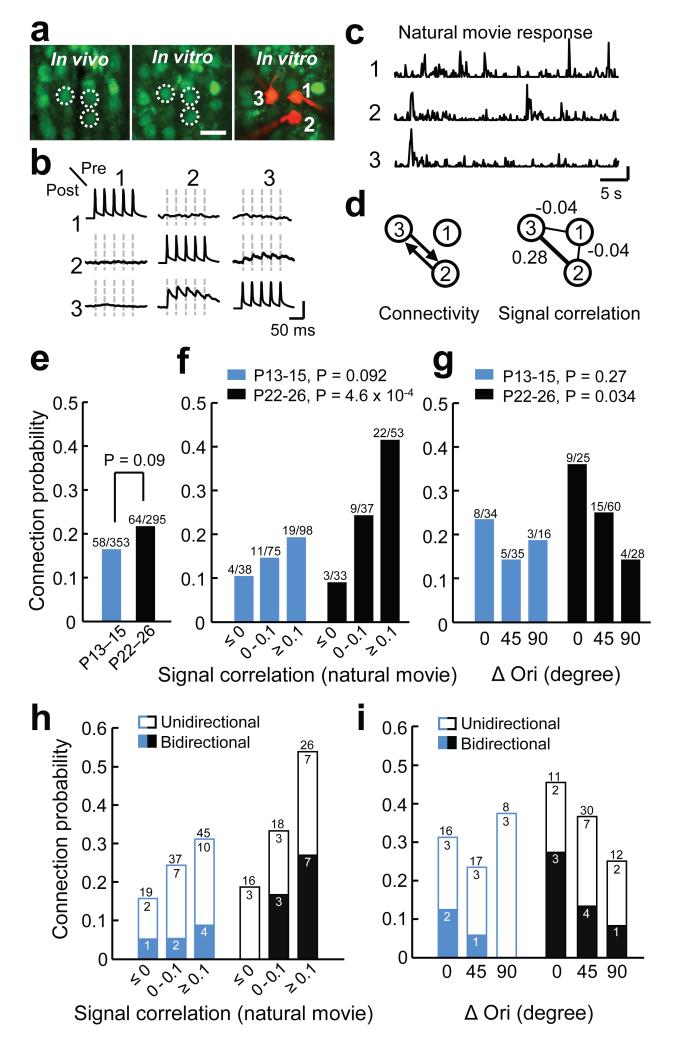
The similarity of spatial RF properties in immature and older V1 suggests that the organization of feedforward connections²⁶ was largely established by the time of eye-opening. We next tested whether synaptic connectivity of neurons in the local cortical network is functionally specific when vision begins. We combined in vivo two-photon calcium imaging in V1 and subsequent multiple whole-cell recordings in slices of the same tissue⁵ (Fig. 2). We first imaged calcium signals at consecutive depths within L2/3 to characterize the responses to natural movies and drifting gratings of all neurons within a volume of approximately 285×285×40–120 μm³. We then carried out simultaneous whole-cell recordings in vitro from two to six neighboring L2/3 pyramidal neurons separated by less than 50 μm (Fig. 2a,b; mean distance ± s.d., P13 – 15, 24 ± 9 μm; P22 – 26, 25 ± 10 μm). We recorded from a total of 143 and 140 neurons in the slice at P13 – 15 and P22 – 26, respectively, which were identified in the in vivo image stack by image registration based on affine transformation⁵ (Fig. 2a). Synaptic connectivity was assessed by evoking action potentials in each neuron sequentially while searching for the presence of excitatory postsynaptic potentials (EPSP) in the other neurons (Fig. 2b) This approach allowed us to relate the probability of finding connections between pairs of L2/3 neurons to the correlation of their average responses to natural movies (signal correlation, Fig. 2c,d,f,h) and to the differences in their preferred orientation (Fig. 2g,i). We used natural-movie signal correlation for comparison of response similarity not only because it was a good predictor of the similarity of their linear RFs (Supplementary Fig. 3), but because it also likely captures the similarity of feature selectivity in neurons with nonlinear RFs, which could not be estimated by reverse correlation.

Figure 2. Functionally specific connectivity between L2/3 pyramidal cells is not apparent at eye opening.

a, Example triplet of neurons shown in a transformed in vivo image (left), the same neurons in the brain slice (middle) and during whole-cell recordings (right); scale bar, 30 μm. b, Membrane potential recordings from neurons shown in a. Evoked spikes and average traces of postsynaptic potentials. Dashed lines indicate timing of presynaptic spikes. Scale bars, 80 mV, 0.8 mV. c, Peristimulus time histogram of spikes inferred from calcium signals of the three neurons in response to a natural movie sequence (averages of six repetitions); scale bar 0.02 a.u. d, Schematics of synaptic connectivity and in vivo signal correlations during natural movies for the three neurons. e, Overall connectivity rates at eye-opening and in more mature V1; Chi-squared test. f, Relationship between connection probability and signal correlation of neuronal pairs significantly responsive to the natural movie across age; Cochran-Armitage test. g, Relationship between connection probability and difference in preferred orientation (ΔOri) among pairs in which both neurons were responsive and orientation selective (OSI > 0.4). h,i, The probability of observing uni- or bidirectionaly connected pairs as function of either signal correlation (h) or ΔOri (i); n = 13 mice at P13 – 15, and 18 mice at P22 – 26.

The overall rate of connectivity was not significantly different between the two age groups (Fig. 2e, P13 – 15, 16.4%, 58 of 353 connections tested; P22 – 26, 21.7%, 64 of 295 connections tested, P = 0.09, Chi-squared test). Among the recorded neurons, 73% (104 out of 143) and 56% (79 out of 140) exhibited significant responses to the natural movie (see Methods). As we reported previously⁵, among responsive L2/3 pyramidal cells, the connection probability increased steeply with increasing signal correlation at P22 – 26 (Fig. 2f, P = 4.6 × 10⁻⁴, Cochran-Armitage test). This was not the case at P13 – 15 (P = 0.092), when a much weaker trend was observed. Specifically, there were twice as many connections between highly correlated neuronal pairs (signal correlation ≥ 0.1) in older V1 than at eye opening (Fig. 2f, P13 – 15, 19.4%, 19 of 98 tested vs P22 – 26, 41.5%, 22 of 53 tested, P = 0.0035, Chi-squared test). Therefore, the functional selectivity of synaptic connections increased in the period after eye-opening, as more connections formed selectively between neurons responding to similar stimulus features.

We further examined the refinement of connection specificity by relating the connection rate between reliably responsive and orientation tuned neurons (Fig. 2g, P13 – 15, 43.4%, 62 out of 143; P22 – 26, 57.9%, 81 out of 140, see Methods) to the difference in their preferred orientation. A significant decreasing relationship between connection probability and the difference in preferred orientation was present in more mature V1 but not at eye-opening (Fig. 2g; P13 – 15, P = 0.27; P22 – 26, P = 0.034, Cochran-Armitage test). Together, these results indicate that at eye-opening the organization of synaptic connections between nearby L2/3 pyramidal neurons exhibits only weak functional specificity. After the onset of visual experience, connectivity increases specifically between neurons coding for similar visual features.

Previous studies suggest that bidirectional recurrent connections are overexpressed in some cortical networks^2,4 and they are most frequent between L2/3 pyramidal cell pairs with similar visual responses in mature V1⁵. We examined whether a similar organization of bidirectional motifs is already present at eye-opening. In contrast to mature mice, visually naive mice did not exhibit a larger proportion of bidirectionally connected pairs between neurons with highly correlated responses to the natural movie (Fig. 2h; P13 – 15, P = 0.27; P22 – 26, P = 0.01, Cochran-Armitage test). Similar trends were found between neurons preferring similar orientations (Fig. 2i; P13 – 15, P = 0.13; P22 – 26, P = 0.11, Cochran-Armitage test). Therefore, this statistical feature of pairwise connectivity also refines after eye-opening, such that a greater proportion of neurons with similar visual responses become bidirectionally connected (Fig. 2h,i).

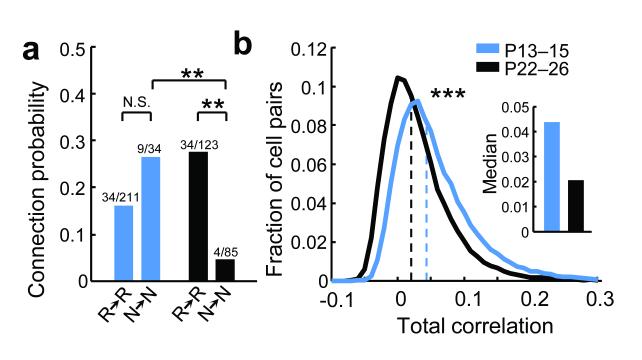
We next tested for developmental changes in recurrent connectivity between neurons not reliably responsive to visual stimuli, which were encountered at similar proportions at both age groups (fraction of non-significantly responsive neurons to repeated presentations of the natural movie: P13 – 15, 39%, 4133/10509 neurons; P22 – 26, 44%, 4691/10662). At P22 – 26, non-responsive neurons connected to each other at much lower rates than responsive neurons (Fig. 3a, P < 0.01, Tukey’s HSD multiple comparison test among proportions). At P13 – 15, however, both responsive and non-responsive neurons formed recurrent connections at similar rates (Fig. 3a, P > 0.05). These data suggest that connections between L2/3 neurons not driven effectively by visual stimuli are selectively eliminated after eye-opening (Fig. 3a, P < 0.01). This non-specific connection scheme at eye-opening is consistent with the statistics of population activity during visual stimulation, which showed a two-fold higher total pairwise firing rate correlation at P13 – 15 than at P22 – 26 (Fig. 3b, median correlation, P13 – 15, 0.044 vs P22 – 26, 0.021, P < 10⁻³⁰⁷, rank-sum test). Higher activity correlations at eye-opening may allow connections to be maintained between neurons not reliably driven by visual stimuli. These connections are then lost as activity in the V1 network becomes progressively less correlated.

Figure 3. Developmental elimination of recurrent connections between non-responsive neurons.

a, Connection probability between neurons significantly responsive to the natural movie (R→R) and between non-responsive neurons (N→N) at two ages; ** indicates P < 0.01, Tukey’s HSD multiple comparison test among proportions. b, Distribution of pair-wise time-varying inferred firing rate correlation coefficients for all responsive cell pairs (to natural movies) separated by < 50 μm; *** indicates P < 10⁻³⁰⁷, rank-sum test).

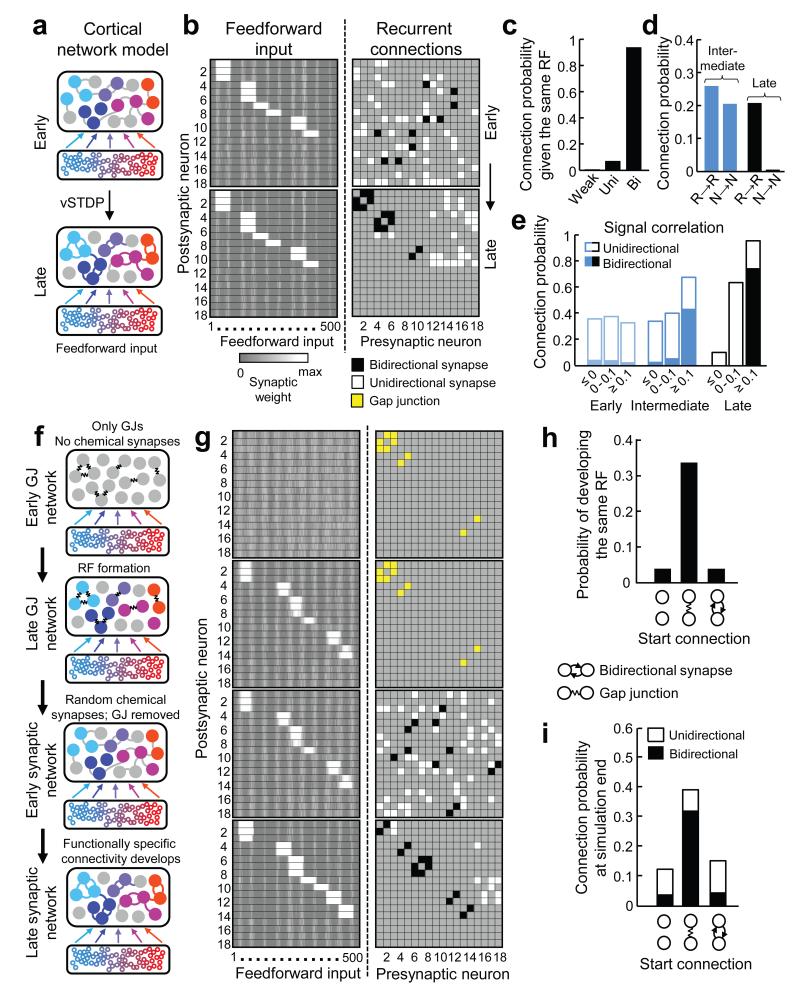
To obtain a mechanistic insight into the refinement of local recurrent connectivity after eye-opening, we constructed a network model of the neocortex based on activity-dependent synaptic plasticity²⁷. The model consists of a recurrently connected cortical network of 18 excitatory and five inhibitory integrate-and-fire neurons (see Methods). Cortical neurons received feedforward input from 500 presynaptic neurons, a subset of which exhibited spatially correlated activity during each iteration of the simulation (Fig. 4a). The weights of both recurrent and feedforward synapses were updated by a voltage-based spike-timing-dependent plasticity (vSTDP) learning rule²⁷. Initially, neurons were seeded with RFs (see Methods) while the weights of the recurrent network were drawn randomly from a uniform distribution (Fig. 4b, upper panels). Excitatory neurons in the recurrent network with the same RFs developed strong, mostly bidirectional connections (Fig. 4b,c; 93.2%; proportions taken across 50 simulations). There was a strong decrease in connectivity between neurons that were not responsive to feedforward input (Fig. 4d; from 20.5% near the beginning to 0.6% at the end of the simulation) but not between neurons which were both responsive to feedforward input (from 26.0% to 20.7%), consistent with experimental observations (Fig. 3a). To further compare the model’s behaviour with our experimental data we froze the feedforward and recurrent weights at three time points and measured the signal correlation between all responsive neuronal pairs. Higher signal correlations between neurons predicted a higher rate of connectivity at later but not earlier stages of network development (Fig. 4e, Fig. 2f). The model also predicted the increase in bidirectional connections between neurons with high signal correlations at later stages of development (Fig. 4e, Fig. 2h). These simulations suggest that feedforward connection patterns determine the structure of recurrent connectivity by activity-dependent mechanisms of synaptic plasticity.

Figure 4. Feedforward input structure determines the functional organization of recurrent connectivity.

a, Schematic of the network model of functional microcircuit development based on voltage-based spike-timing dependent plasticity (vSTDP) (see text for details). At simulation start, cortical neurons were randomly connected, but received spatially clustered input from a subset of presynaptic neurons. Both feedforward and recurrent connections were updated via the vSTDP rule (see Methods). b, Synaptic weight matrices of feedforward (left, reordered for display purposes) and recurrent (right) connections from an example network at the beginning and end of the simulation. Recurrent synaptic connections were classified as weak (light grey), unidirectional (white) and bidirectional (black). c, Probability of observing weak, uni- or bidirectional connections at simulation end between neurons that start with the same RF. d, Connection probability of responsive (R→R) and non-responsive (N→N) neuronal pairs during and at the end of the simulation. e, Relationship between connection probability and feed-forward input-driven signal correlation at three time points in the simulation. f, Schematic of different stages of network model extended earlier in development. g, Synaptic weight matrices from example gap-junction network model. The recurrent network is initially connected with GJs (yellow) in the absence of chemical synapses. With time, neurons selected a spatially clustered set of feedforward inputs (RFs). Gap junctions were then removed and recurrent chemical connections were randomly assigned. The simulation was then continued as in a and b. h, Probability of developing RFs from the same set of feedforward inputs for pairs with no recurrent connections, GJs or early bidirectional connections (data from separate simulations) at the start of the simulation. i, Probability of developing shared connections depended on the starting connectivity. Data in c,d,e,h,i are from 50 network simulations.

Our results indicate that RFs exist before mature patterns of recurrent connectivity. However, transient electrical coupling via gap junctions (GJs) between clonally related neurons contributes to shared feature selectivity and raises the possibility that intracortical connectivity may precede and instruct RF formation^7,9,28. We extended our network model earlier in time to examine the mechanisms by which GJ coupling may influence the emergence of RFs and recurrent connectivity. In this model, early recurrent connectivity in the cortical network was provided by electrical gap junctions (Fig. 4f,g) while recurrent excitatory chemical synapses did not exist, approximating the organization of the mouse neocortex in the first postnatal week⁷. Early feedforward connections were randomly assigned (Fig. 4f,g) and their weights were updated according to the vSTDP rule. Cell pairs were more likely to stabilize the same set of feedforward inputs (i.e. develop the same RF) if they had been connected by gap junctions (Fig. 4h; GJ coupled, 31.6%, 79/250 pairs; not GJ coupled, 4.1%, 305/7400; P < 0.001, Chi-squared test; 50 simulations). We then removed the gap junctions, which disappear by the second postnatal week in mouse V1⁷, and assigned random recurrent synaptic connections to neurons in the cortical network (Fig. 4f,g). Neurons sharing the same RF formed strong synaptic connections (Fig. 4c,g). Therefore, the functional specificity of recurrent connections was influenced indirectly by early GJ motifs (Fig. 4i), as electrically coupled neurons were first likely to develop the same RFs before becoming synaptically connected. Separate simulations initiated with chemical connections revealed that modifiable bidirectional chemical connections had no influence on either the formation of RFs or recurrent connectivity at the end of the simulation (Fig. 4h,i; probability of developing same RF: not connected, 5.5%, 270/4918; bidirectional chemical connections, 3.8%, 11/288; P = 0.22, Chi-squared test; 50 simulations). Therefore, early initial biases in cortical connectivity may only influence functional circuit development if they exist as strong and stable connections when feedforward inputs are being selected. Although the absolute connectivity rates found experimentally were not perfectly replicated (Fig. 2f versus Fig. 4e), the connection probability between cells with similar visual responses was higher when assessed deeper in the acute slice, where connections are more likely to be preserved during cutting (Supplementary Fig. 6 of ref. 5).

We found that the functional specificity of local connections in mouse V1 was not apparent at eye-opening despite the occurrence of highly selective responses to visual features. While the overall rate of synaptic connectivity did not change after eye-opening, connections redistributed according to the following rules: more connections were added preferentially between neurons responding most similarly to visual stimuli, while connections were eliminated between cells not reliably responsive to visual stimulation. This result is surprising given existing theories of neural circuit formation, which suggest either that connections are initially exuberant and subsequently ‘prune’ away^10,13 or that synapse number increases after the onset of sensory experience^11,14. Instead, in local L2/3 networks we find a balanced restructuring of connectivity after eye-opening. It remains to be seen whether similar mechanisms contribute to the elaboration of long-range connections in visual cortex of rodents and higher mammals^22,29,30.

Functionally specific connection patterns between L2/3 pyramidal cells appear to be instructed by feedforward input (e.g. from layer 4 or the visual thalamus) only after RF formation. Our network model suggests that correlated firing driven by feedforward activity increases the functional specificity of recurrent connections by activity-dependent mechanisms of synaptic plasticity, which leads to the preferential formation of synapses between any neurons sharing similar RFs. The model can additionally explain how electrically coupled neurons early in development first develop similar feature selectivity and then preferential recurrent connectivity^7,9,28 (Fig. 4g-i).

Our data suggest that functionally organized connectivity between L2/3 pyramidal neurons is not necessary for establishing elemental RF properties at eye-opening. Instead, it may contribute to the amplification of visually driven responses and thereby increase the robustness and reliability of cortical representation of sensory input with age (Supplementary Fig. 2c), which may be facilitated by the preferential formation of bidirectional connections between neurons with similar stimulus preferences (Fig. 2h,i). The role of inhibition for the maturation of visual responsiveness remains to be determined.

In conclusion, the patterning of recurrent cortical connectivity through the feedforward-driven activity-dependent redistribution of connections may be a fundamental rule by which neurons link up into assemblies that process related information.

Methods

Animals and surgical procedures

All experimental procedures were carried out in accordance with institutional animal welfare guidelines and licensed by the UK Home Office. Experiments were performed on C57Bl/6 mice aged postnatal days 13 – 15 and 22 – 35. Mice were initially anesthetized with a mixture of fentanyl (0.05 mg/kg), midazolam (5.0 mg/kg), and medetomidin (0.5 mg/kg). At the time of imaging, the injectable anesthetic had mostly worn off and light anesthesia was maintained by isoflurane (0.3 −0.5%) in a 60:40% mixture of O₂:N₂O delivered via a small nose cone. Surgery was performed as described previously¹⁵. Briefly, a small craniotomy (1 – 22mm) was carried out over primary visual cortex and sealed after dye injection with 1.6% agarose in HEPES-buffered artificial cerebrospinal fluid (ACSF) and a cover slip.

In vivo two-photon calcium imaging

For bulk loading of cortical neurons, the calcium-sensitive dye Oregon Green BAPTA-1 AM (OGB-1 AM, Molecular Probes) was first dissolved in 4 μl DMSO containing 20% Pluronic F-127 (Molecular Probes), and further diluted (1/11) in dye buffer (150 mM NaCl, 2.5 mM KCl, and 10 mM HEPES [pH 7.4]) to yield a final concentration of 0.9 mM. Sulforhodamine 101 (SR 101, 50μM, Molecular Probes) was added to the solution for experiments in C57Bl/6 mice to distinguish neurons and astrocytes³¹. The dye was slowly pressure injected into the monocular region of right visual cortex at a depth of 170 – 200 μm with a micropipette (3–5 MΩ, 3 – 10 psi, 2–4 min) under visual control by two-photon imaging (×10 water immersion objective, Olympus). Activity of cortical neurons was monitored by imaging fluorescence changes with a custom-built microscope and a mode-locked Ti:sapphire laser (Mai Tai, Spectra-Physics) at 830 nm or 930 nm through a ×40 water immersion objective (0.8 NA, Olympus). Scanning and image acquisition were controlled by custom software written in LabVIEW (National Instruments).

Visual stimuli were generated using MATLAB (Mathworks) Psychophysics Toolbox^32,33, and displayed on a LCD monitor (60 Hz refresh rate) positioned 20 cm from the left eye, roughly at 45 degree to the long axis of the animal, covering ~105 × 85 degrees of visual space. At the beginning of each experiment, the appropriate retinotopic position in visual cortex was determined using small grating stimuli at 12 – 24 neighboring positions. The monitor was repositioned such that the preferred retinotopic position of most imaged neurons was roughly in the middle of the monitor.

Imaging frames of 256×256 pixels were acquired at 7.6 Hz while presenting different visual stimuli, including naturalistic images and movies, and drifting gratings (see sections below for details). After each recording, the focal plane and imaging position was checked and realigned with the initial image if necessary. In combined in vivo functional imaging and in vitro connectivity assaying experiments, to obtain visually evoked responses from all neurons in a cortical volume of approximately 285×285×40 – 120 μm³, images were recorded at 7 to 18 cortical depths with a spacing of 7 μm, starting at ~110 μm below cortical surface, corresponding to superficial layer 2/3 in mouse V1.

Image sequences were aligned for tangential drift and analyzed with custom programs written in MATLAB and LabVIEW. Recordings with significant brain movements, vertical drift, or both, were excluded from further analysis. Cell outlines were detected using a semi-automated algorithm based on morphological measurements of cell intensity, size, and shape, and subsequently confirmed by visual inspection. After erosion of the cell-based regions of interest (ROIs) (to minimize influence of the neuropil signal around the cell bodies), all pixels within each ROI were averaged to give a single time course (ΔF/F), which was additionally high-pass filtered at a cut-off frequency of 0.02 Hz to remove slow fluctuations in the signal. Spike trains were inferred from calcium signals using a fast non-negative deconvolution method which approximates the maximum a posteriori spike train for each neuron, given the fluorescence observations³⁴. This method yields spike probabilities (or inferred firing rate) that linearly related to the number of action potentials per imaging frame²⁵.

Receptive field measurement

Receptive field data were acquired from four mice at eye-opening (P14 – 15) and five mature mice (P28 – 35). Naturalistic image sequences (between 1440 and 2700 individual images) were presented on the monitor during two-photon calcium imaging. Images were shown at 2s intervals (0.5s presentation time, interleaved by 1.5s grey screen) for a total presentation time of between 0.83-1.5 hrs. After the onset of each natural image, 15 imaging frames were recorded at 7.6Hz before presenting the next image. For each cell in the imaged region, the response to an image was calculated in the following way. Spike probabilities were inferred from calcium signals using the fast non-negative deconvolution method described above. For each visual stimulus, k (=1,…,N), and each cell, i (=1,…,C), the response to the stimulus can be expressed r(k,i,j) where j=1,…,15 are the 15 imaging frames. An average population response was calculated $R\left(j\right)=\frac{\left({\Sigma }_k{\Sigma }_{i}r\right(k,i,j\left)\right)}{\mathit{NC}}$. If the imaging frame J denotes the frame during which the peak average population response occurred (so that R(J)=max_j{R(j)}), then the response of cell i to stimulus k was defined $\frac{{\Sigma }_{j=J-1}^{J+1}r(k,i,j)}{3}$.

To estimate linear receptive fields, a regularized pseudoinverse method²⁴ was used for reverse correlating neuronal responses with images of natural scenes. This algorithm regularizes the inverse problem by introducing a two-dimensional smoothness constraint on the linear receptive field; namely, the constraint is that the Laplacian of the RF should be close to zero at all points (▽²RF = 0). This method introduces a regularization parameter, λ, which balances the emphasis to be placed on fitting the data and the emphasis to be placed on the smoothness constraint.

Since this method introduces a free parameter λ, we performed the following analysis to choose the regularization parameter. For each cell and each regularization parameter, the naturalistic images and associated responses were separated into training (75% of the data) and test (remaining 25% of the data) data sets. Training data sets were chosen randomly and the remaining 25% of the data was placed into the test data set. Linear RFs were then calculated using the training data, and a sigmoid nonlinearity, described by the equation

$$P\left(x\right)=\frac{A}{1+\mathit{exp}(-\mathit{ax}+\beta )},$$

(where A is the amplitude, α determines the slope, and β determines the offset of the sigmoid) was then fit to the training data to convert the linear predictions made by the RF into neuronal spike probabilities. Response predictions to the naturalistic images of the test data set were then made and the correlation coefficient between the actual and predicted responses was taken as a measure of RF prediction performance. This procedure was carried out for each cell and each regularization parameter 100 times. For each cell, the regularization parameter that maximized the RF prediction performance was chosen.

To assess whether the receptive field for a particular cell was significant, the response vector to the naturalistic image sequence was randomly shuffled and the reverse correlation was performed again using the same regularization parameter, λ. This procedure was repeated 100 times to produce 100 shuffled receptive fields, RF_shuffled. From these shuffled receptive fields the mean, μ_shuffled, and standard deviation, σ_shuffled across all pixels were calculated. A receptive field was defined to be significant if there were pixels which had absolute values > μ_shuffled + 6σ_shuffled.

For Gabor fitting we used only the RFs determined as significant by the previous analysis. The RF was parameterized in MATLAB by fitting a two-dimensional Gabor function using the Levenberg-Marquardt algorithm. The Gabor function is described by:

$$G(x^{\prime },y^{\prime })=A\mathit{exp}\left(-\frac{x^{\prime 2}}{2{\sigma }_x^2}-\frac{y^{\prime 2}}{2{\sigma }_y^2}\right)\mathit{cos}(2\pi {\mathit{fx}}^{\prime }+\phi ),$$

where,

$$x^{\prime }=(x-c_x)\mathit{cos}\theta -(y-c_y)\mathit{sin}\theta ,$$

$$y^{\prime }=(x-c_x)\mathit{sin}\theta +(y-c_y)\mathit{cos}\theta .$$

These equations describe an underlying two-dimensional cosine grating parameterized by θ (orientation), f (spatial frequency) and φ (phase), which is enveloped by a two-dimensional Gaussian function parameterized by A (amplitude), (c_x,c_y) (centre of the Gaussian) and and σ_x and σ_y (standard deviations of the Gaussian perpendicular to and parallel to the axis of the grating, respectively). Gabor fits were individually inspected to make sure they matched the RF (some Gabor fits were excluded at this point since they did not provide a good match to the RF: juveniles 3/191 (1.6%), adults 6/201 (3%)).

To quantify the shape of RFs, the dimensionless measures n_x = σ_xf and n_y = σ_yf were used³⁵. These values express the size of the Gaussian envelope in terms of the wavelength of the underlying cosine grating. For instance, n_x = 1 indicates that the standard deviation of the Gaussian perpendicular to the grating is equal to half a cycle of the underlying cosine grating. To get a measure of the size of the RF (Fig. 1, Supplementary Fig. 1), the visual angle subtended by the Gabor fit along the axis perpendicular to the direction of the cosine grating was calculated. That is, if the eye of the mouse is located at (0,0,0)cm in space, the centre of the monitor at (0,0,d) (where d is the shortest distance of the mouse eye from the screen), the centre of the Gabor fit to the RF at (c_x,c_y,d), and the angle of orientation of the cosine grating on the screen is θ, then the visual angle, α, subtended by the Gabor was calculated as:

$$\alpha =\text{arccos}\left(\frac{\mathit{u}\cdot \nu }{\Vert \mathit{u}\Vert \Vert \nu \Vert }\right)$$

where u = (c_x – σ_x cosθ, c_y + δ_x sinθ,d), v = (c_x + σ_x cosθ, c_y – σ_x sinθ,d). RF similarity was calculated as the pixel-pixel correlation coefficient.

Natural-movie signal correlation

Natural movies consisted of 40 s sequences of either moving scenes in a mouse cage or compilations David Attenborough’s Life of Mammals (BBC), adjusted to 70 % mean contrast, continuously looped 6 times. Visual responsiveness to natural movies was determined by the following procedure. For all stimulus repetitions, inferred spike trains were moving-average filtered with a time window of 3 frames (~0.394 s). The smoothed firing rates at corresponding points of the stimulus were then treated as groups and tested for differences by one-way ANOVA. Neurons with P-value less than 0.01 (i.e. those that exhibited consistently elevated firing during at least one period of stimulus presentation) were considered significantly visually responsive. For pairs of significantly responsive neurons, the signal correlation was calculated as the Pearson’s correlation coefficient of the averaged responses to the stimulus.

Orientation tuning

To measure the orientation preference and selectivity of neurons, square-wave gratings (0.035 cycle/degree, 2 cycle/s, 100% contrast) drifting in eight different directions were randomly interleaved, with the grating standing for 1.4–1.9 s before moving for 0.9–1.5 s (six repetitions per grating). Responsive neurons that exhibited consistently elevated firing during at least one time point of presentation of each grating were identified by one-way ANOVA. Among cells responsive to grating stimuli (P-value < 0.05), the mean of inferred firing rate of during the presentation of a drifting grating was taken as the response to each stimulus. From each trial, we obtained one orientation tuning curve, and neurons were defined as reliably responsive if the mean cross-correlation between all pairs of curves obtained from different trials was above 0.1. Responses from different trials were then averaged to obtain the average orientation tuning curve for each neuron. This orientation tuning curve was then Fourier interpolated to 360 points, and the preferred direction was determined by the angle at which the interpolated tuning curve attained its maximum. The preferred orientation was taken as the modulus of the preferred direction to 180 degrees. Orientation selectivity index (OSI) was calculated as (R_best − R_ortho)/(R_best + R_ortho), where R_best is the interpolated response to the preferred direction, and R_ortho is the average of interpolated responses to the directions orthogonal to best responding direction. When relating connection probability to orientation selectivity, neurons were defined as orientation selective if OSI >0.4. For quantifying neuronal response reliability we calculated the coefficient of variation (standard deviation/mean) from responses to the optimal grating direction.

In vitro whole-cell recording

We carried out imaging experiments followed by whole-cell recordings in vitro at P13 – 15 and P22 – 26, using approach as described previously⁵. After two-photon calcium imaging of visual responses in vivo, small volumes of red fluorescent microspheres (Lumafluor) were injected into the imaged region to facilitate identification of the region in the slice tissue. The mouse brain was then rapidly removed to and dissected in ice-cold artificial cerebrospinal fluid (ACSF) containing 125 mM NaCl, 2.5 mM KCl, 1 mM MgCl₂, 1.25 mM NaH₂PO₄, 2 mM CaCl₂, 26 mM NaHCO₃, 25 mM Dextrose; osmolarity 315-325 mOsm, bubbled with 95% O₂/5% CO₂, pH 7.4. Visual cortex slices (300 μm) were cut coronally (HM 650 V Vibration Microtome, MICROM) and were incubated at 34 °C for thirty minutes before they were transferred to the recording chamber. The slice containing the imaged region was identified by the presence of OGB-1 green fluorescence and the red microsphere injection site. To reveal the relative locations of cells, a detailed morphological stack of the slice was acquired with a custom-built microscope and a mode-locked Ti:sapphire laser (Chameleon, Coherent) at 830 nm through a ×16 water immersion objective (0.8 NA, Nikon). Scanning and image acquisition were controlled by custom software written in LabVIEW (National Instruments). Whole cell recordings from two to six cells were carried out in regions identified by visually comparing image stacks obtained in vivo and in vitro, using red fluorescent microspheres and the pial surface as reference. Recordings were carried out in 28°C ACSF, using Multiclamp 700B amplifiers (Axon Instruments) and data was acquired using custom software running in Igor Pro (WaveMetrics Inc.)³⁶ or MATLAB. Recording pipettes were filled with internal solution containing 5 mM KCl, 115 mM K-Gluconate, 10 mM K-HEPES, 4 mM MgATP, 0.3 mM NaGTP, 10 mM Na-Phosphocreatine, 0.1% w/v Biocytin, 40 μM Alexa Fluor 594; osmolarity 290–295 mOsm, pH 7.2. Junction potential was not corrected for. The chloride reversal potential was ~−85.2 mV. Cells were approached under visual guidance using laser-scanning Dodt contrast. After breakthrough, the presence of synaptic connections was tested by evoking five spikes at 30 Hz in each cell, repeated 30 to 120 times, while searching for postsynaptic responses. PPR was calculated as the amplitude of the second evoked EPSP over that of the first one. After connectivity mapping, step currents from −125/250 pA to 350/700 pA were injected at 25/50 pA increments. Pyramidal neurons were identified according to morphology in Alexa 594 filled image stacks (Fig. 2a), regular-spiking pattern on current injection and spike half-width (> 1 ms), and in the presence of connections, depolarizing postsynaptic potentials (Fig. 2b). To match the same neurons imaged in vivo and recorded from in vitro, we performed three-dimensional image registration of in vivo and in vitro image stacks by affine transformation using custom-written MATLAB software subsequent to the experiment.

Connection probabilities were calculated as the number of connections detected over the number of potential connections assayed. Probability of unidirectional and bidirectional connections were calculated as the number of unidirectionally and bidirectionally connected pairs over the total number of pairs respectively. To relate connectivity to functional properties, the asymptotic Cochran-Armitage test for trend was used to test for significance of linear trends³⁷. Pairs in which a high quality recording was achieved in only one cell (e.g. the other cell was too depolarized/unhealthy, or the seal resistance was less than 1 GΩ) connectivity was assayed only in the direction from the unhealthy cell to the healthy cell only, given that spikes could be evoked in both cells. Data from these pairs were included in the analysis of connection probability, but not in the analysis of probability of finding bidirectional or unidirectional pairs. Only neuronal pairs in which both neurons were located at >60 μm depth from slice surface and with an inter-soma distance of <50 μm were included in the analysis.

The strength and short term plasticity of synapses were also measured because these synaptic parameters affect the efficacy of presynaptic firing on postsynaptic partners. Connections between L2/3 pyramidal cells in P13 – 15 mice were significantly stronger (Supplementary Fig. 4a; median EPSP amplitude, P13 – 15, 0.41 mV vs P22 – 26, 0.20 mV, P = 2.9 × 10⁻⁴, rank-sum test), and paired-pulse ratio (PPR) significantly lower (Supplementary Fig. 4b; median PPR, P13 – 15, 0.87, vs P22 – 26, 1.13, P = 6.2 × 10⁻⁴, rank-sum test) than in P22 – 26 mice, in line with previous reports³⁸. However, in both age groups there was no significant correlation between EPSP amplitude or PPR with signal correlation or difference in preferred orientation (Supplementary Fig. 4c-f). Part of the connectivity data was published previously in ref. 5.

Neuron model

In the network model, the dynamics of membrane potential u(t) of model neurons is described by the Adaptive Exponential Integrate-and-Fire (AdEx) model³⁹

$$C\frac{d}{\mathit{dt}}u=-g_L(u-E_L)+g_L{\Delta }_T{e}^{\frac{u-V_T}{{\Delta }_T}}-w_{\mathit{ad}}+z+I,$$

where C is the membrane capacitance, g_L the leak conductance, E_L the resting potential and I the stimulating current. The exponential term describes the activation of sodium current. The parameter Δ_T is called the slope factor and V_T the threshold potential. A hyperpolarizing adaptation current is described by the variable w_ad with dynamics

$${\tau }_{w_{\mathit{ad}}}\frac{d}{\mathit{dt}}{w}_{\mathit{ad}}=a(u-E_L)-w_{\mathit{ad}},$$

where τ_wad is the time constant of the adaption of the neuron and α a parameter. Upon firing the variable u is reset to a fixed value V_reset whereas w_ad is increased by an amount b. An additional current z, which is set to a value I_sp immediately after a spike occurs and decays otherwise with a time constant τ_z,

$${\tau }_z\frac{d}{\mathit{dt}}z=-z$$

was used to account for spike afterpotential⁴⁰. Refractoriness is modelled with an adaptive threshold V_T which starts at V_Tmax after a spike and decays to V_Trest with a time constant τ_VT,

$${\tau }_{V_T}\frac{d}{\mathit{dt}}{V}_T=-\left(V_T-V_{T_{\text{rest}}}\right).$$

Parameters for the neuron model were taken from³⁹ for the AdEx, τ_z was set to 40 ms in agreement with^36,41 and kept fixed throughout all simulations (see Table 1).

Table 1.

Parameters for the neuron model

Parameter		Value
C	membrane capacitance	281 pF
gL	leak conductance	30 nS
EL	resting potential	−70.6 mV
ΔT	slope factor	2 mV
VTrest	threshold potential at rest	−50.4 mV
τwad	adaptation time constant	144 ms
a	subthreshold adaptation	4 nS
b	spike triggered adaptation	0.0805 pA
Isp	spike current after a spike	400 pA
τz	spike current time constant	40 ms
τvT	threshold potential time constant	50 ms
VTmax	threshold potential after a spike	−30.4 mV

Plasticity model

Our plasticity model exhibits separate additive contributions to the plasticity rule, one for LTD and another one for LTP⁴². For the LTD part, we assumed that presynaptic spike arrival at synapse t induces depression of the synaptic weight w_i by an amount $-A_{\mathit{LTD}}{\left[{\stackrel{‒}{u}}_{-}\right(t)-{\theta }_{-}]}_{+}$. The brackets []₊ indicate rectification, i.e. any value ${\stackrel{‒}{u}}_{-}<{\theta }_{-}$ does not lead to a change⁴³. The quantity ${\stackrel{‒}{u}}_{-}\left(t\right)$ is an exponential low-pass filtered version of the postsynaptic membrane potential u(t) with time constant τ_:

$${\tau }_{-}\frac{d}{\mathit{dt}}{\stackrel{‒}{u}}_{-}\left(t\right)=-{\stackrel{‒}{u}}_{-}\left(t\right)+u\left(t\right).$$

Since the presynaptic spike train is described as a series of short pulses at time $t_i^n$ where t is the index of the synapse and n an index that counts the spike, $X_i\left(t\right)={\Sigma }_n\delta (t-t_i^n)$, we have for depression

$$\frac{d}{\mathit{dt}}{w}_i^{-}=-A_{LTD}\left(\overline{\overline{u}}\right)X_i\left(t\right){[{\stackrel{‒}{u}}_{-}-{\theta }_{-}]}_{+}\text{if}{w}_i>w_{\mathit{min}},$$

where $A_{\mathit{LTD}}\left(\overline{\overline{u}}\right)$ is an amplitude parameter that is under the control of homeostatic processes⁴⁴, depending on the mean depolarization ${\stackrel{‒}{u}}_{-}$ of the postsynaptic neuron, averaged over a time scale of 1 second. The time scale of 1 second is not critical (100 seconds or more would be more realistic for homeostasis), but convenient for the numerical implementation.

For the LTP part, we assumed that each presynaptic spike at the synapse w_i increases the trace ${\stackrel{‒}{x}}_i\left(t\right)$ of some biophysical quantity, which decays exponentially with a time constant τ_x^45,46

$${\tau }_x\frac{d}{\mathit{dt}}{\stackrel{‒}{x}}_i\left(t\right)=-{\stackrel{‒}{x}}_i\left(t\right)+X_i\left(t\right),$$

where X_i(t) is the spike train defined above. Potentiation is given by

$$\frac{d}{\mathit{dt}}{w}_i^{+}=+A_{\mathit{LTP}}{\stackrel{‒}{x}}_i\left(t\right){[u-{\theta }_{+}]}_{+}{[{\stackrel{‒}{u}}_{+}-{\theta }_{-}]}_{+}\text{if}{w}_i<w_{\mathit{max}}.$$

Here, A_LTP is a free amplitude parameter fitted to electrophysiology data and ${\stackrel{‒}{u}}_{+}\left(t\right)$ is another low-pass filtered version of u(t) similar to ${\stackrel{‒}{u}}_{-}\left(t\right)$ but with a shorter time constant τ₊. Thus positive weight changes can occur if the momentary voltage u(t) surpasses a threshold θ₊ and, at the same time the average value ${\stackrel{‒}{u}}_{+}\left(t\right)$ is above θ₋.

The final rule used in the simulation was

$$\frac{d}{\mathit{dt}}{w}_i=-A_{\mathit{LTD}}\left(\overline{\overline{u}}\right)X_i\left(t\right){[{\stackrel{‒}{u}}_{-}-{\theta }_{-}]}_{+}+A_{\mathit{LTP}}{\stackrel{‒}{x}}_i\left(t\right){[u-{\theta }_{+}]}_{+}{[{\stackrel{‒}{u}}_{+}-{\theta }_{-}]}_{+},$$

combined with hard bounds w_min ≤ w_i ≤ w_min. For network simulation, $A_{\mathit{LTD}}\left(\stackrel{‒}{u}\right)=A_{\mathit{LTD}}\frac{{\overline{\overline{u}}}^2}{u_{\mathit{ref}}^2}$, where $u_{\mathit{ref}}^2$ is a reference value.

Network simulation

In all simulations, five hundred presynaptic Poisson neurons with firing rates $v_i^{\mathit{pre}}(1\le i\le 500)$ were connected to 18 postsynaptic excitatory neurons. The input rates ${\nu }_i^{\mathit{pre}}(1\le i\le 500)$ followed a Gaussian profile, i.e. ${\nu }_i^{\mathit{pre}}=\mathit{Ae}\frac{-{(i-\mu )}^2}{2{\sigma }^2}$, with variance σ = 10 and amplitude A = 30. The center μ of the Gaussian shifted randomly every 100 ms between ten equally distributed positions, each position occurring with equal probability. Circular boundary conditions were assumed, i.e. neuron t = 500 was considered as neighbour of neuron t = 1. Five inhibitory neurons were each driven by 14 excitatory neurons and each projected onto 11 excitatory neurons. These connections were chosen randomly and were fixed with a weight equal to 1. Feedforward connections onto the inhibitory neurons were drawn from a uniform distribution on the interval [0,0.5] and were fixed for the duration of the simulation. The reference value was set to $u_{\mathit{ref}}^2=70{\mathit{mV}}^2$. Parameters were chosen as in Table 2. The excitatory recurrent connections were plastic under the same rule and with the same parameters as the feedforward connections (Table 2), but the amplitudes A_LTP and A_LTD were reduced by a factor of 100.

Table 2.

Parameters for the plasticity model

Parameter		Value
θ−	LTD/LTP voltage threshold for ${\stackrel{‒}{u}}_{-}∕{\stackrel{‒}{u}}_{+}$	−70.6 mV
θ+	LTP voltage threshold for u(t)	−45.3 mV
ALTD	LTD amplitude parameter	14 × 10−5 mV−1
ALTP	LTP amplitude parameter	8 × 10−5 mV−2
τx	${\stackrel{‒}{x}}_i\left(t\right)$ time constant	15 ms
τ−	${\stackrel{‒}{u}}_{-}\left(t\right)$ time constant	10 ms
τ+	${\stackrel{‒}{u}}_{+}\left(t\right)$ time constant	7 ms

In the first set of simulations, feedforward weights were initialized with receptive fields (weights taken from previous test simulations took values between 0 and 3 which were also the hard bounds). At the beginning of the simulation, recurrent excitatory connection weights were drawn randomly from a uniform distribution on the interval [0,0.75] (hard bounds were set to 0 and 0.75). At each time point during the simulation, noise current (Gaussian white noise) was injected into each cell independently in the recurrent network. In this and all subsequent networks, the model was run for 20s of simulated time to allow the homeostatic dynamical variables to settle before the recurrent synaptic weights were reinitialized. The simulations were then run for another 1000s.

To calculate signal correlations in the network at three different time points (at the reinitialization of recurrent excitatory chemical synapses, 1 s of simulation time later, and end of the simulation), the weights were frozen and the same stimuli were played in order to assess the firing rate correlations across neurons. Two neurons were considered to be bidirectionally connected if both synaptic weights between them were >0.6, and unidirectionally connected if only one was >0.6.

Responsiveness was determined in the following way: the feedforward weights onto each neuron were summed, to produce a single value for each cell. These values were then plotted on a histogram, which displayed a bimodal distribution. A threshold value was chosen in between the two peaks of this bimodal distribution, to separate the cells into responsive and non-responsive. Feedforward weights were manually checked to make sure no cells with clear RFs were missed. Neuronal pairs whose RFs had a correlation coefficient of >0.85 were defined to have the same RF.

The recurrent gap-junction network began so that neurons 1 and 2 were electrically coupled together, neurons 3 and 4 together and neurons 5 to 7 together, and was run in this state for 200s. There were no chemical synapses during this time. The gap junction model was taken from⁴⁷. The current from neuron i to j was defined as I_ij(t) = α∑_iδ(t – t_i) – g_gap[u_j(t) – u_i(t)], where g_gap was chosen to be 2 and α such that the spikelet was about 2mV. The network was in this state for 200s of simulation time (after the initial 20s settling time), at which point gap junctions were removed and replaced with recurrent excitatory chemical connections with weights drawn randomly from a uniform distribution on the interval [0,0.75]. After this time point Gaussian white noise current stimulation was again provided to each cell in the recurrent network. The network was then run for another 800s.

The comparison chemical network was run in the same manner as the gap-junction network except that a recurrent chemical network, with weights drawn randomly from a uniform distribution on the interval [0,0.75], replaced the recurrent gap-junction network during the first 200s, and there was no replacement of the recurrent weights after this 200s.