Functional organization of excitatory synaptic strength in primary visual cortex

Abstract

The strength of synaptic connections fundamentally determines how neurons influence each other’s firing. Excitatory connection amplitudes between pairs of cortical neurons vary over two orders of magnitude, comprising only very few strong connections among many weaker ones^1–9. Although this highly skewed distribution of connection strengths is observed in diverse cortical areas^1–9, its functional significance remains unknown: it is not clear how connection strength relates to neuronal response properties, nor how strong and weak inputs contribute to information processing in local microcircuits. Here we reveal that the strength of connections between layer 2/3 (L2/3) pyramidal neurons in mouse primary visual cortex (V1) obeys a simple rule—the few strong connections occur between neurons with most correlated responses, while only weak connections link neurons with uncorrelated responses. Moreover, we show that strong and reciprocal connections occur between cells with similar spatial receptive field structure. Although weak connections far outnumber strong connections, each neuron receives the majority of its local excitation from a small number of strong inputs provided by the few neurons with similar responses to visual features. By dominating recurrent excitation, these infrequent yet powerful inputs disproportionately contribute to feature preference and selectivity. Therefore, our results show that the apparently complex organization of excitatory connection strength reflects the similarity of neuronal responses, and suggest that rare, strong connections mediate stimulus-specific response amplification in cortical microcircuits.

To determine the relationship between connection strength and neuronal responses, we used a combination of two-photon calcium imaging in vivo and whole-cell recordings in vitro in L2/3 of mouse V1¹⁰ (Fig. 1). We first examined how connection strength relates to the degree of correlated firing between pairs of neurons. We obtained pairwise correlation coefficients of responses to a sequence of static natural images (see Methods) from L2/3 neurons labelled with the calcium-sensitive indicator OGB-1 (ref. 11; imaged volumes ~260 × 260 × 56 μm; Fig. 1a, b). The distribution of pairwise response correlations was highly skewed: correlations were generally low, and only a small fraction of pairs were highly correlated during visual stimulation (median correlation coefficient: 0.012; mean correlation coefficient ± s.d.: 0.021 ± 0.051; range: −0.12 to 0.67; Fig. 1c; Extended Data Fig. 1).

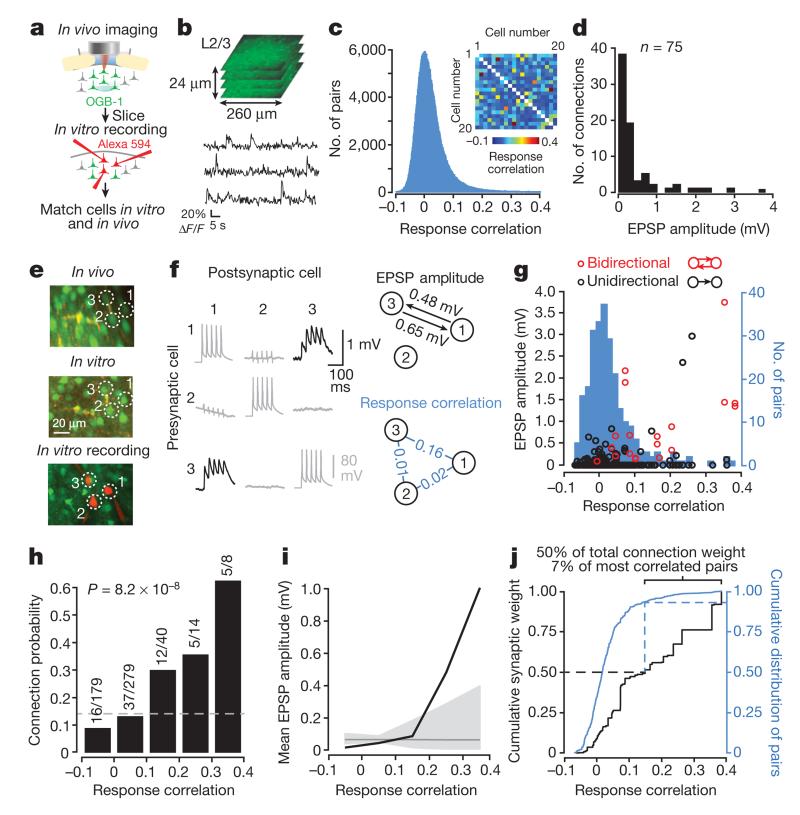
Figure 1. Excitatory connection strength reflects the similarity of pyramidal cell firing in vivo.

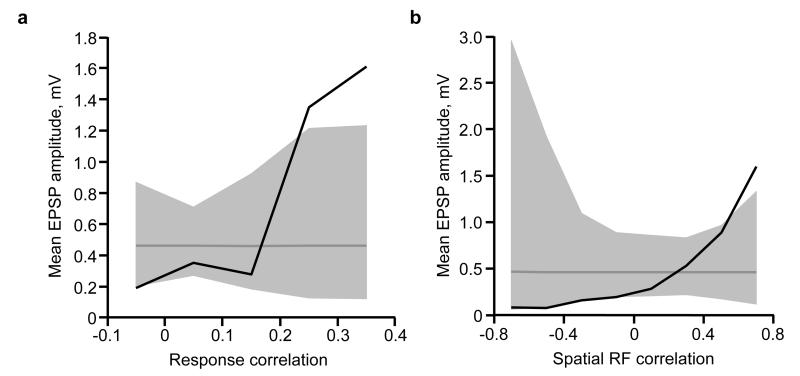
a, Schematic of experimental protocol. b, Somatic calcium signals were sampled simultaneously from all neurons within a small volume of cortex (~260 × 260 × 24 μm). Two such volumes were recorded in each experiment. c, The distribution of pairwise response correlation coefficients for all imaged cell pairs. Inset, example matrix of correlation coefficients of pairwise responses from 20 neurons within a single imaged volume. d, Distribution of excitatory postsynaptic potential (EPSP) amplitudes (n = 75 connections). e, Example triplet of neurons shown in a transformed in vivo image (upper), in the brain slice (middle) and during whole-cell recordings (lower). f, Left, average postsynaptic potential traces of neurons in e. Black traces, connected; grey traces, unconnected; evoked presynaptic spikes are along the diagonal. In some traces, capacitative stimulation artefacts coincide with presynaptic spikes. Right, synaptic connectivity and response correlation coefficients of neurons in e. g, EPSP amplitude plotted against pairwise response correlation coefficient for bidirectionally (red) and unidirectionally (black) connected pairs. Underlying histogram shows the distribution of pairwise response correlation coefficients (blue, right y axis). h, Relationship between connection probability and pairwise response correlation. Grey dashed line, mean connection probability. Connection probability increased with response correlation (P = 8.2 × 10⁻⁸; Cochran–Armitage test). i, Mean connection amplitude (including unconnected pairs) plotted against response correlation (bin size = 0.1). Grey line, mean EPSP amplitude of all pairs. Grey shaded region represents the 95% confidence interval of the expected mean, estimated by repeated random reshuffling of the EPSP amplitudes among all cell pairs in the data set. j, Black trace, cumulative distribution of synaptic weight with respect to response correlation. A value of 1 corresponds to the linear sum of all EPSPs (33.34 mV). Blue trace, cumulative distribution of pairwise response correlation coefficients (right y axis).

We next identified the same OGB-1-filled neurons in acute slices (Fig. 1e), and targeted up to six neurons for simultaneous whole-cell recording to assess their synaptic connectivity (Fig. 1e, f; see Methods). A total of 203 pyramidal cells (across 17 mice) recorded in the slice were identified in the in vivo image stacks, and the overall connection rate was 75/520 (0.14). Consistent with previous reports^1–9, the distribution of excitatory postsynaptic potential (EPSP) amplitudes was highly skewed (median EPSP amplitude: 0.19 mV; mean EPSP amplitude ± s.d.: 0.45 ± 0.68 mV; Fig. 1d).

Neurons with more similar responses were much more likely to connect (P = 8.2 × 10⁻⁸, Cochran–Armitage test for trend; Fig. 1g, h), consistent with previous observations¹⁰. Importantly, response correlation was closely related to EPSP amplitude: the strongest connections were found between neuronal pairs with the highest response correlations (Fig. 1g, i; Extended Data Fig. 2a), while neurons with negatively correlated responses tended not to connect or formed only weak connections (response correlation > 0.2, median amplitude of connected pairs: 1.38 mV, n = 10; response correlation < 0, median amplitude: 0.12 mV, n = 16; P = 6.8 × 10⁻⁴, Wilcoxon rank-sum test; Fig. 1g). The close correspondence between response correlation and mean connection amplitude was apparent both when including (Fig. 1i) or excluding unconnected pairs (Extended Data Fig. 2a). Indeed, the majority of total synaptic weight was concentrated in the minority of connections between highly correlated pairs (7% most correlated pairs accounted for 50% of the total synaptic weight; Fig. 1j), further emphasizing the highly non-random arrangement of connection amplitudes. Together, these data suggest that the long-tailed distribution of cortical connection weights arises from a simple rule: neurons with highly correlated responses form strong connections, and neurons with uncorrelated responses connect rarely, and only weakly.

In visual cortex, strong response correlations may be explained by one of several shared visual response properties. To understand how connection strength relates to visual feature preference, we characterized the spatial linear receptive field (RF) structure for each neuron in the imaged populations (Fig. 2a; see Methods). The linear RF describes the relative position of ON (response to light increments) and OFF (response to light decrements) subfields in visual space, and thus provides information about visual features to which a neuron is most sensitive, including their orientation, phase, spatial frequency and size. RFs of nearby cortical neurons were highly diverse within each imaged population in L2/3^12–15 (example region in Fig. 2b). We quantified RF similarity as the pixel-to-pixel correlation coefficient between pairs of RF maps. RF correlations were close to zero for the majority of pairs, and only a small fraction of neurons exhibited highly similar or highly dissimilar RFs (Fig. 2c).

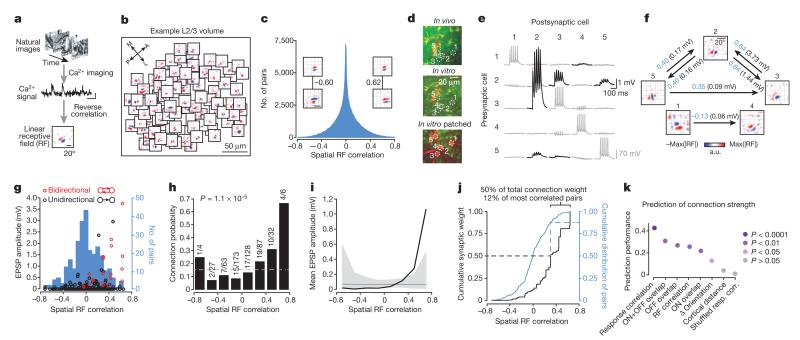
Figure 2. Organization of excitatory connection strength with respect to linear RF properties.

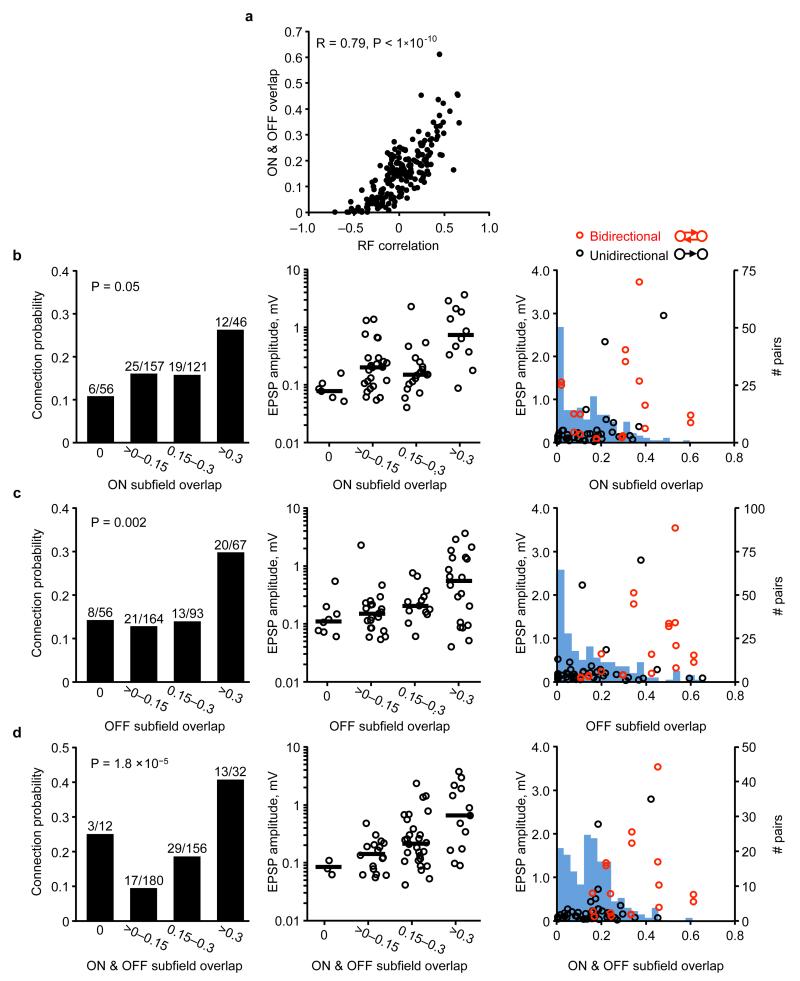
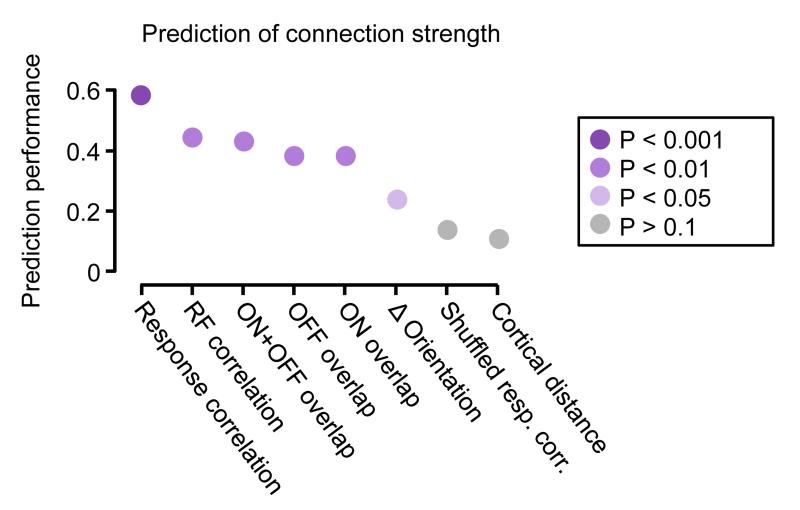
a, RFs obtained by regularized reverse correlation of responses to a sequence of static natural images (see Methods; scale bars: calcium trace, 20% ΔF/F, 5 s, RF, 20°). b, RFs distributed across an example imaged region (collapsed over cortical depth, 150–174 μm below cortical surface), revealing a large diversity of RFs. c, Distribution of spatial RF correlation coefficients for all recorded cell pairs. Inset, example RFs for two pairs of neurons and their correlation coefficients. Typically, negatively correlated RFs had similar orientation but opposite phase preference. d, Example quintuplet of neurons shown in the transformed in vivo image (upper), in the brain slice (middle) and during whole-cell recordings (lower). e, Average postsynaptic potential traces of neurons in d. Black traces, connected; grey traces, unconnected; evoked presynaptic spikes are along the diagonal. f, Synaptic connectivity and RFs of neurons in d. Arrows indicate a synaptic connection. Values indicate the correlation coefficient of RF maps (blue) and the amplitude of the connection (EPSP, black). a.u., arbitrary units. g, EPSP amplitude plotted against RF correlation for bidirectionally (red) and unidirectionally (black) connected pairs. Underlying histogram shows the distribution of pairwise RF correlations (blue, right y axis). h–j, Same as Fig. 1h–j for the RF correlation coefficient. k, Similarity of shared neuronal properties ranked according to how well they predict connection amplitude (including unconnected pairs). Prediction performance and P values were calculated using a Monte-Carlo analysis (see Methods). Disc colour indicates P value.

By assessing connectivity between neurons with linear RFs (Fig. 2d–f), we found that connections between neuronal pairs with more similar RF structure were stronger (Fig. 2g, i; Extended Data Fig. 2b) and much more frequent (Fig. 2h) than connections between pairs with uncorrelated or negatively correlated RFs. The minority of connections observed between neurons with the most similar RFs accounted for a large fraction of the total synaptic weight (50% of total synaptic weight between 12% of pairs with the most correlated RFs; Fig. 2j). RF correlation was closely related to the degree of ON and OFF subfield overlap (R = 0.79, P < 1 × 10⁻¹⁰; Extended Data Fig. 3a), and both connection strength and connection probability increased with larger ON and OFF overlap (Extended Data Fig. 3b–d). Indeed, these measures of RF similarity predicted connection strength much better than cortical distance and even the difference in orientation preference (Fig. 2k; Extended Data Fig. 4; see Methods). Nonetheless, pairwise response correlation was the best predictor of connection strength (Fig. 2k); this is not surprising as pairwise response correlation includes additional information about shared response properties not captured by the linear RF¹⁶.

The preferential, strong connectivity between correlated neurons was further emphasized when considering the reciprocity of connections (Figs 1g and 2g, Extended Data Fig. 5). Connections between bidirectionally connected pairs generated larger EPSPs than unidirectionally connected pairs, consistent with previous reports^3,4,17, and the RF maps of bidirectionally connected neurons were significantly more correlated than RFs of unidirectionally connected or unconnected pairs (Extended Data Fig. 5).

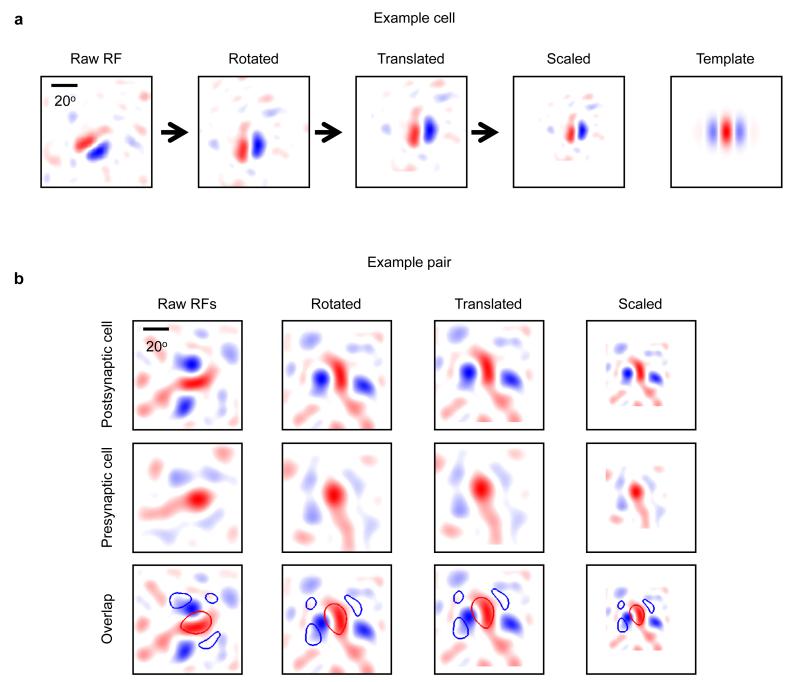
Only a small fraction of neuronal pairs in the local V1 network shared a similar RF structure (7.5% of pairs with RF correlation > 0.4; Fig. 2j). Thus, connections between neurons with non-matching RFs (RF correlation < 0.4, 61/75 or 81% of all measured connections) greatly outnumbered the connections between neurons with similar RFs (RF correlation > 0.4, 14/75 or 19% of all measured connections). Given this large RF diversity of local inputs, we next sought to estimate the combined visual feature preference of the net synaptic excitation an individual neuron receives from the L2/3 network. We combined data from all pairs of connected neurons after rotating, translating and scaling each postsynaptic RF to match a normalized RF structure¹⁸ (Extended Data Fig. 6a; see Methods). The same transformation was applied to the RFs of the presynaptic neurons (Extended Data Fig. 6b), and we considered the sum of these transformed presynaptic RFs, weighted by the amplitude of the connections, to indicate net synaptic input. The structure of this weighted presynaptic RF sum closely resembled the structure of the normalized postsynaptic RF (correlation between presynaptic RF sum and postsynaptic RF sum: R = 0.73, n = 45 pairs; Fig. 3a, top row; Extended Data Fig. 7). This input specificity did not result from a bias in the structure of RFs in the local population because the RF sum of the unconnected neurons was very different (R = −0.38, n = 227; Fig. 3a, bottom row; Extended Data Fig. 8). Therefore, despite the majority of inputs arising from neurons with mismatched RFs, the combined local excitatory drive onto pyramidal cells in L2/3 has a RF structure that closely matches that of the receiving neuron.

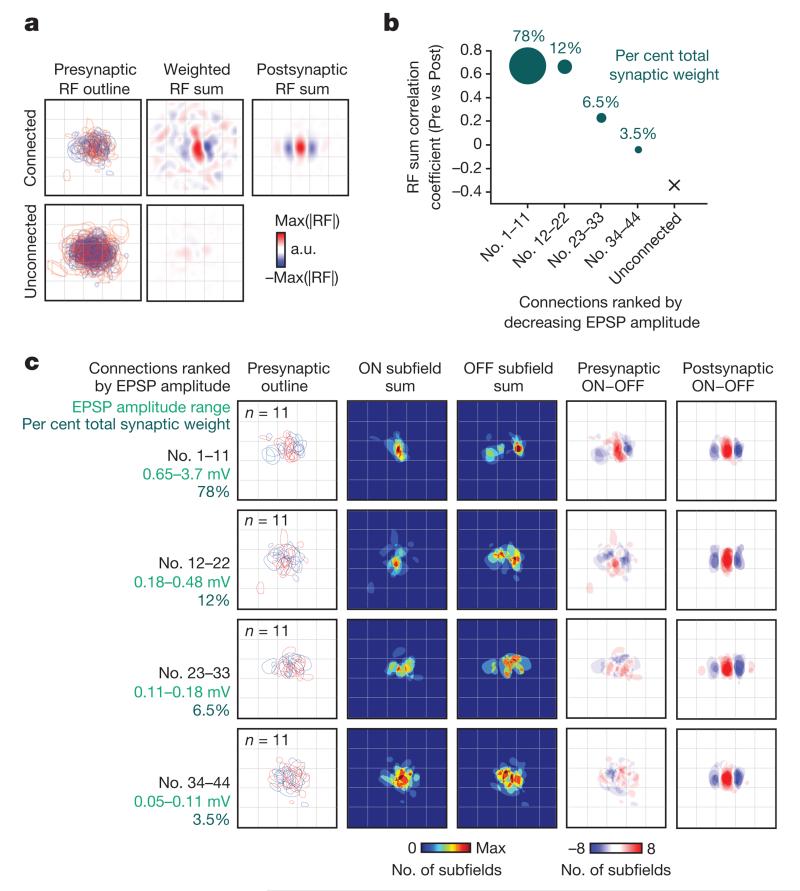
Figure 3. Combined synaptic input from the local L2/3 cortical network matches the RF structure of the receiving neuron.

a, Top left, presynaptic RF outlines overlaid in normalized visual space (after rotation, translation and scaling of the postsynaptic RF; see text, Methods and Extended Data Fig. 7). Red outline indicates an ON subfield, blue outline indicates an OFF subfield. Bottom left, superimposed RF outlines for neurons assessed presynaptically, but which did not connect. Top middle, sum of presynaptic RFs. Each presynaptic RF was weighted by the EPSP amplitude from the pre- to the postsynaptic neuron. Bottom middle, RF sum for unconnected neurons assessed presynaptically. Top right, RF sum of the postsynaptic neurons. Before summing, each postsynaptic RF was weighted by the EPSP amplitude from the presynaptic to the postsynaptic neuron. b, Each point indicates the correlation between the presynaptic RF sum (weighted by the EPSP amplitude) and the corresponding postsynaptic RF sum, when including only connections in quarters of the connection amplitude distribution. The RF sum of the strongest 25% of inputs has the highest correlation with the postsynaptic RF (R = 0.67). This correlation value falls with decreasing connection strength. Disc area and values above represent the total synaptic weight accounted for by each quarter of the connection amplitude distribution. c, Relationship between ON and OFF subfields of connected pre- and postsynaptic neurons, ranked and displayed according to EPSP amplitude. Left column, presynaptic RF outlines of neurons grouped in quarters ranked by decreasing EPSP amplitude. Middle-left and middle columns, sum of binarized presynaptic ON and OFF subfields, respectively. Middle-right column, subtraction of summed OFF from summed ON subfields for presynaptic neurons. Right column, subtraction of summed OFF from summed ON subfields for postsynaptic neurons.

How do connections of different strengths contribute to this feature-specific excitation from the local network? The RFs of the strongest 25% of inputs (n = 11), which accounted for 78% of the overall synaptic weight, were highly similar to the postsynaptic RF (correlation of weighted RF sums, pre- versus postsynaptic, R = 0.67; Fig. 3b). Further, the ON and OFF subfields of the strongest inputs closely matched the ON and OFF subfields of the postsynaptic RF, with very few mismatches (Fig. 3c, top row). Both the similarity between summed pre- and postsynaptic RFs (Fig. 3b), as well as the ON and OFF subfield overlap (Fig. 3c, middle rows), progressively decreased for weaker connections, and there was little common structure to the input from the weakest 25% of connections (Fig. 3c, bottom row). This indicates that feature-matched excitation from the local L2/3 network is dominated by only a small fraction of strong inputs that a pyramidal neuron receives.

We next sought to understand how local excitatory inputs contribute to the response and stimulus selectivity of a neuron’s membrane potential in L2/3. In mouse V1, a simple cell’s subthreshold response to drifting grating stimuli^19–23 is characterized by two components that are determined by the angle and phase of the grating in relation to its RF (Fig. 4a). Namely, a large amplitude depolarization evoked at all orientations (F0 component, Fig. 4a–d), and an orientation-tuned membrane potential modulation locked to the grating phase (F1 component). The F1 component contributes directly to the firing response of a neuron, since spikes occur at the peaks of the large modulation (Fig. 4b). To estimate the contribution of local inputs to the F0 and F1 components, we generated a model informed by the experimentally measured RF properties and connectivity within L2/3 (see Methods). In the model network, a single neuron received input from all others in the population, and the input connection strength was drawn from the experimentally determined distribution relating RF correlation to connection strength (Fig. 4e, f). Despite receiving no direct feedforward input, simulated neurons displayed qualitatively similar membrane potential responses to L2/3 neurons recorded in vivo (Fig. 4g, compare to Fig. 4c), including a large depolarization (F0) at all stimulus orientations (Fig. 4g, h), and a highly modulated membrane potential response (F1) to the preferred but not the non-preferred orientation (Fig. 4g, h). These results suggest that local connections contribute to the stimulus selectivity of L2/3 neurons by providing tuned excitation that modulates the membrane potential in a manner qualitatively similar to that observed in vivo^19–23.

Figure 4. Simulation of local L2/3 excitatory input to single neurons qualitatively predicts the dynamics of membrane depolarization to drifting grating stimuli.

a, Schematic of characteristic membrane potential (V_m) response to gratings drifting across a neuron’s RF in mouse V1. Both the preferred and the orthogonal stimuli evoke large membrane depolarizations (F0). V_m modulation (F1) is strongest when the grating and the RF are matched in orientation, and the grating cycles in and out of phase with the RF. b, Example in vivo whole-cell V_m recording from a L2/3 pyramidal cell during presentation of oriented gratings drifting in eight different directions. Black and grey arrows indicate preferred and orthogonal orientations, respectively. c, Average V_m response of the same neuron in b after spike removal. d, F0 and F1 components of V_m response to drifting gratings normalized to the preferred stimulus for neuron in b and c (left), and averaged across the population of recorded neurons (n = 24, right). e, Left, schematic of network model, showing input to a single L2/3 neuron from an example L2/3 neuronal population. Right, connection strengths were sampled from the experimentally measured relationship between EPSP amplitude and RF correlation (Fig. 2g). f, Responses for each presynaptic neuron were generated using a linear/nonlinear/Poisson model by correlating the visual input (drifting grating stimuli) with its experimentally measured RF (see Methods). Firing rates were weighted by their connection strengths (e) and summed to generate a time-varying V_m for each postsynaptic neuron. g, Example V_m response of a simulated neuron receiving input from the model L2/3 network. h, F0 and F1 components of the V_m response from the example simulated neuron in g (left) or from the population of simulated neurons (right, n = 4,633). i, V_m response of example simulated neuron in g when including only the strongest 25% of connections (top, blue trace) or weakest 75% of connections from the model network (bottom, purple trace). j, Same as d and h but for V_m responses driven by the strongest 25% of connections (blue) or weakest 75% of connections (purple).

We then systematically varied the relative fractions of strong and weak connections in the simulated network to estimate how connections of different strengths contribute to the F0 and F1 response components (Extended Data Fig. 9). For instance, removing the strongest 25% of connections from the model (equivalent to including the weakest 75% of connections; Fig. 4i, j, purple traces) essentially eliminated the modulated F1 component of the response (95% reduction in the modulation amplitude at the preferred orientation). In contrast, removing the weakest 75% of connections (leaving the strongest 25% connections; Fig. 4i, j, blue traces) decreased the mean depolarization (F0 component) by 23%, but only slightly affected the F1 component (5% decrease in modulation amplitude at the preferred orientation). This means that the membrane potential modulation of a L2/3 neuron in response to drifting gratings is weakly influenced by the majority of local inputs it receives, which contribute only partly to the broadly-tuned depolarization. In contrast, the orientation- and phase-selective response is predominantly influenced by a small subset of other L2/3 neurons with similar RF structure, which provide strong, feature-matched excitation at the preferred orientation.

We describe a simple rule governing how the long-tailed distribution of excitatory connection strength — observed in diverse cortical areas^1–9 — is organized with respect to the functional properties of cortical neurons. In L2/3 of mouse V1, pyramidal neurons with correlated responses to visual stimuli connect preferentially with strong and often reciprocal connections, whereas neurons with uncorrelated or anti-correlated responses connect infrequently with weak connections. The fact that there are only very few strong connections in neocortical circuits reflects the low number of cell pairs with highly correlated responses. Therefore, the strength of synaptic coupling mirrors the strength of functional coupling, a relationship which may arise from correlation-based learning rules^15,24.

Our results suggest that infrequent, strong connections play a prominent role in cortical computation. While a L2/3 pyramidal neuron receives inputs from many neurons with diverse response properties (for example, receptive fields) in the local V1 network, the majority of the synaptic drive is provided by only a small fraction of strong inputs from cells with the most similar responses to visual stimuli. These rare but powerful inputs provide strongly tuned excitation, and therefore directly contribute to a neuron’s selectivity by amplifying responses to specific visual features.

This circuit architecture—comprising strong recurrent excitation within ensembles of neurons with similar RFs—may additionally amplify (and perhaps prolong²⁵) population-level responses to particular sensory stimuli^{19,20,26–29}, and thus promote effective information transmission to multiple postsynaptic targets. In contrast, the matrix of more numerous, weaker connections, which only generate a small fraction of total excitation in the L2/3 network, may facilitate local contextual interactions and serve as a substrate for plasticity—for example, when particular visual feature combinations become behaviourally relevant.

METHODS

Animals and surgical procedures

All experimental procedures were carried out in accordance with institutional animal welfare guidelines, and licensed by the UK Home Office.

In vivo two-photon calcium imaging

Experiments were performed in 17 C57Bl/6 mice of both sexes, aged P22–26. Please note that we applied no randomization or blinded assignment of animals to groups and no animals were excluded from any analyses. The number of experimental preparations used in the analysis was chosen according to previous studies^10,13. Mice were initially anaesthetized with a mixture of fentanyl (0.05 mg per kg), midazolam (5.0 mg per kg), and medetomidine (0.5 mg per kg). Surgery was performed as described previously³⁰. Briefly, we made a small craniotomy (1–2 mm) over primary visual cortex and, after dye injection, sealed it with 1.6% agarose in HEPES-buffered artificial cerebrospinal fluid (ACSF) as well as a cover slip. At the time of imaging, the injectable anaesthetic had mostly worn off and light anaesthesia was maintained by isoflurane (0.3–0.5%) in a 60:40% mixture of O₂:N₂O delivered via a small nose cone.

For bulk loading of cortical neurons, we first dissolved the calcium-sensitive dye Oregon Green BAPTA-1 acetyloxymethyl ester (OGB-1 AM, Molecular Probes) in 4 μl DMSO containing 20% Pluronic F-127 (Molecular Probes), and then diluted (1/11) in dye buffer (150 mM NaCl, 2.5 mM KCl, and 10 mM HEPES, pH 7.4), resulting in a final concentration of 0.9 mM. In order to distinguish neurons and astrocytes, we added sulforhodamine 101 (SR 101, 50 μM, Molecular Probes) to the solution³¹. With a micropipette (3–5 MΩ) the dye was slowly pressure-injected (3–10 psi, 2–4 min) into the monocular region of right visual cortex at a depth of 170–200 μm under visual control by two-photon imaging (×16, 0.8 numerical aperture water immersion objective, Nikon). Activity of cortical neurons was monitored by two-photon imaging of OGB-1 fluorescence changes with a B-Scope microscope (Thorlabs) and a mode-locked Ti:sapphire laser (Mai Tai, Spectra-Physics) at 830 nm through a ×40, 0.8 numerical aperture water immersion objective (Olympus).

Visual stimuli were generated using MATLAB (Mathworks) Psychophysics Toolbox^32,33, and displayed on an LCD monitor (60 Hz refresh rate) positioned 20 cm from the left eye, roughly at 45 degrees to the long axis of the animal, covering ~110 × 84 degrees of visual space. At the beginning of each experiment, the appropriate retinotopic position in visual cortex was determined using small grating stimuli at 12 positions arranged in a 4 × 3 grid. The monitor was repositioned such that the preferred retinotopic position of most imaged neurons was roughly in the middle of the monitor.

Imaging frames of 512 × 512 pixels were acquired at 27.9 Hz in Scanimage 4.0 while presenting different visual stimuli, including movies and static naturalistic images (see sections below for details). A piezo z-scanner (PI P-726 PIFOC) was used to rapidly move the objective in the z axis and acquire 4 image planes, each separated by 8 μm in depth. Thus a single imaged plane (acquired in 35.8 ms) was part of an imaged volume acquired in 143 ms (6.98 Hz). Before recording the first volume, a reference image was acquired. After each recording, the imaging position in the x and y axis was checked and realigned with the initial image if necessary. To obtain visually evoked responses from all neurons in a cortical volume of 263 × 255 × 56 μm, two volumes were recorded, starting at ~135 μm below the cortical surface, corresponding to superficial layer 2 in mouse V1.

After aligning image sequences to correct for tangential drift we analysed them with customized programs written in MATLAB. A semi-automated algorithm was used to detect cell outlines, which were subsequently confirmed by visual inspection. This algorithm was based on morphological measurements of cell intensity, size, and shape. The cell-based regions of interest (ROIs) were then eroded (to reduce the influence of the neuropil signal around the cell bodies as far as possible), and all pixels within each ROI were averaged to yield a time course (ΔF/F) for each neuron; to remove slow fluctuations in the signal, this single time course was subsequently high-pass filtered at a 0.02 Hz cut-off frequency. A fast non-negative deconvolution method approximating the maximum a posteriori spike train for each neuron, given the fluorescence observations³⁴, was used to infer spike trains from calcium signals. This method yields spike probabilities (or inferred firing rate) that are linearly related to the number of action potentials per imaging frame³⁵.

In vitro whole-cell recording

After in vivo imaging experiments, whole-cell recordings in vitro were performed using an approach as described previously^10,13. After two-photon calcium imaging in vivo, red fluorescent microspheres (Lumafluor) were injected into the imaged region to facilitate identification of the same region in sliced tissue. We then rapidly removed the mouse brain, dissected it in ice-cold artificial cerebrospinal fluid (ACSF) containing 125 mM NaCl, 2.5 mM KCl, 1 mM MgCl₂, 1.25 mM NaH₂PO₄, 2 mM CaCl₂, 26 mM NaHCO₃, 25 mM dextrose; osmolarity 315–325 mOsm, bubbled with 95% O₂/5% CO₂, pH 7.4. Visual cortex slices (300 μm) were cut coronally on a microtome (VT1200S, Leica Biosystems) and were incubated at 34 °C for thirty minutes before being transferred to the recording chamber. We identified the slice containing the imaged region by the red microsphere injection site and the presence of OGB-1 green fluorescence. To identify the cells’ relative locations, a detailed morphological stack of the slice was obtained with a custom-built microscope and a mode-locked Ti:sapphire laser (Vision-S, Coherent) at 830 nm through a ×16 water immersion objective (0.8 numerical aperture, Nikon). Scanning and image acquisition were controlled by custom software written in LabVIEW (National Instruments). To match the neurons recorded in vitro with the neurons imaged in vivo, three-dimensional image registration of in vivo and in vitro image stacks was carried out through an affine transformation using custom-written MATLAB software. We performed simultaneous whole-cell recordings, in 28 °C ACSF, from two to six cells in regions identified in the in vivo stack. Recordings were made using Multiclamp 700B amplifiers (Axon Instruments) and acquired using custom software running in MATLAB. Recording pipettes were mounted on remote-controlled motorised micromanipulators (MicroStar, Scientifica), and filled with internal solution containing 5 mM KCl, 115 mM K-gluconate, 10 mM K-HEPES, 4 mM MgATP, 0.3 mM NaGTP, 10 mM Na-phosphocreatine, 40 μM Alexa Fluor 594; osmolarity 290–295 mOsm, pH 7.2. Junction potentials were not corrected. The chloride reversal potential was ~−85.2 mV. Cells were approached under visual guidance using laser-scanning Dodt contrast and two-photon imaging. To test for the presence of synaptic connections, five spikes at 30 Hz were evoked in each cell, repeated 30 to 120 times, while searching for postsynaptic responses. EPSP amplitudes were calculated by averaging the data points within 1 ms around the first peak depolarization value. After connectivity mapping, step currents from −50 pA to 700 pA were injected at 50 pA increments. Pyramidal neurons were identified according to morphology in Alexa Fluor 594 filled image stacks, spike half-width (>1 ms), regular-spiking pattern on current injection, and in the presence of connections, depolarizing postsynaptic potentials.

Connection probabilities were calculated as the number of connections detected over the number of potential connections assayed. Traces in which large stimulation artefacts occurred were excluded from the analysis. For pairs in which a high quality recording was achieved in only one cell (for example, the other cell was too depolarized/unhealthy, or the seal resistance was less than 1 GΩ), connectivity was assayed only in the direction from the unhealthy cell to the healthy cell, given that spikes could be evoked in both cells. Data from these pairs were included in the analysis of connection probability, but not in the analysis of bidirectional or unidirectional pairs.

In vivo whole-cell recordings

Experiments were performed in 9 C57Bl/6 mice of both sexes, aged P29–40. Mice were initially anesthetized with a mixture of fentanyl (0.05 mg per kg), midazolam (5.0 mg per kg), and medetomidine (0.5 mg per kg). The skull was exposed and a metal head-plate was attached with dental cement. A small craniotomy (1–2 mm) was carried out over primary visual cortex, based on stereotaxic coordinates. The dura was removed and the cortex was kept moist with cortex buffer solution (125 mM NaCl, 5 mM KCl, 10 mM glucose, 10 mM HEPES, 2 mM MgSO₄, and 2 mM CaCl₂, pH 7.4).

A silver reference electrode was fixed in place using 2% agarose in cortex buffer under the skin of the neck. Recording pipettes were made using thick-walled filamentous borosilicate glass capillaries (G150F-3, Harvard apparatus) using a horizontal (Sutter, P1000) or vertical (Narashige, PC10) puller adjusted to produce a tip size of approximately 1 μm and resistance of 5–7 MΩ when filled with intracellular solution containing: 120 mM K-gluconate, 4 mM NaCl, 40 mM HEPES, 2 mM MgATP, 0.3 mM NaGTP; osmolarity 295 mOsm, pH 7.4 or 135 mM K-gluconate, 10 mM KCl, 10 mM HEPES, 4 mM MgATP, 0.3 mM NaGTP, 10 mM Na-phosphocreatine; osmolarity 295 mOsm, pH 7.4.

Recording pipettes were mounted on a remote-controlled motorised micromanipulator (‘Junior’, Luigs & Neuman) and orientated at an elevation of approximately 45° from horizontal. The signal was amplified using a Multiclamp 700B amplifier (Molecular Devices), processed by a 50/60 Hz noise eliminator (Humbug, Digitimer) and digitized at 20 kHz by an 18-bit ADC/DAC board (National Instruments) and low-pass filtered at 6 kHz. Data acquisition was controlled by a computer running either Igor Pro (Wavemetrics)/Neuromatic (Jason Rothman, UCL) or a custom MATLAB program. Data were digitally stored for off-line analysis.

Recordings were made using the blind whole-cell patch technique³⁶. Neurons were targeted at a depth of 150–300 μm below the pial surface (estimated using the reading of the micromanipulator). After a neuron was encountered and whole-cell access was achieved, the recording was switched to current-clamp configuration (0 pA holding current) and data acquired at 10 kHz. Junction potentials were not corrected.

Visual stimuli were generated using MATLAB Psychophysics Toolbox, and displayed on a 43 × 23 cm LCD monitor with a refresh rate of 60 Hz. The monitor was located 16 cm from the eye, and covered ~106 × 71 degrees of the visual space. At the beginning of each experiment, a coarse retinotopic map was acquired for each neuron. Patches of moving black and white gratings were presented in 28 different locations on a grey background, in a pseudorandom order (stimulus duration: 600 ms; interstimulus interval: 400 ms). The monitor position was adjusted to centre the RF on the middle of the screen.

Test visual stimuli consisted of square-wave gratings of 4 orientations drifting in 8 evenly spaced directions spanning 0–360°. Stimulus orientation was perpendicular to drift direction. Stimuli of 50% contrast were presented in a fixed sequence, with the direction of drift increasing in 135° increments. Spatial and temporal frequencies of all stimuli were 0.04 cycles per degree and 3 cycles per s, respectively. Drifting gratings (1.67 s) were interspersed with stationary gratings of 1.67 s. Stationary gratings were of the same orientation as the subsequent drifting grating. The entire stimulus sequence was repeated 5–10 times.

Analysis was restricted to a window commencing 250 ms after the onset of each drifting stimulus and lasting for 1,333 ms (that is, 4 cycles of the 3 Hz square wave grating). The onset of the analysis window was delayed relative to the start of the stimulus in order to avoid the neuron’s initial onset response.

Spike thresholds were localized to the maximum second differential within the 5 ms period preceding the action potential peak and spike timing was recorded at 0.1 ms precision. For each spike the subthreshold trace was capped at the threshold value (from the point of threshold until the point at which the membrane potential passed back below this value). If spikes occurred within 10 ms of each other the trace was capped until the membrane potential passed below threshold following the last spike. After spike removal subthreshold traces were smoothed using a 7-ms sliding window.

The baseline membrane potential of each recording block was defined as follows. The pre- and post-stimulus baseline conditions were divided into 1-s sections and the minimum membrane potential observed during each section was averaged to give the baseline of that recording session. The amplitude of depolarization (F0 component) and modulation (F1 component) in response to drifting gratings was measured in the following way: a sine wave function given by σ(t)= A sin (2πft + φ) + B, where f is the temporal frequency of the drifting gratings (3 Hz), and A, B and φ are free parameters, was fit to the membrane potential during the analysis window, averaged over all trials of a given stimulus orientation. The amplitude component (F0) was taken as the depolarization B from the baseline membrane potential, and the modulation component (F1) was taken as the amplitude of the sine-wave fit, A.

Receptive field measurement

We displayed natural image sequences (1800 individual images) at 1.4 s intervals (0.4 s presentation time, interleaved by 1 s grey screen). After the onset of each natural image, we recorded 10 imaging frames at ~7 Hz before the next image was presented. For each imaged cell, spike probabilities were inferred from calcium signals using the fast non-negative deconvolution method described above. The response to an image was calculated in the following way: for each visual stimulus, k(1, … ,N), and each cell, i(1, … ,C), the response to the stimulus can be expressed r(k,i,j) where j=1, … ,10 are the 10 imaging frames. A response value of cell i to stimulus k was then defined as $\frac{{\sum }_{j=3}^{5}r\left(k,i,j\right)}{3}$.

To estimate linear RFs, we used a regularized pseudoinverse method³⁷ to reverse-correlate neuronal responses with natural images. This algorithm regularizes the inverse problem by introducing a two-dimensional smoothness constraint on the linear RF; specifically, the constraint is that the Laplacian of the RF should be close to zero at all points (▽² RF = 0). This method introduces a regularization parameter, λ, which balances the emphasis to be placed on fitting the data and the emphasis to be placed on the smoothness constraint.

The following analysis was performed to choose the regularization parameter. For each cell and each value of the regularization parameter, we separated the natural images and associated responses into training data sets (75% of the data) and test data sets (the remaining 25% of the data). The images included in the training set were chosen randomly and the remaining 25% of the images were placed into the test set. We then calculated linear RFs using the training data, and fit a sigmoid nonlinearity, which can be described by the equation

$$P\left(x\right)=\frac{A}{1+\exp \left(-\alpha x+\beta \right)}$$

(where A is the amplitude, α determines the slope, and β determines the offset of the sigmoid) to the training data in order to convert the linear predictions made by the RF into neuronal spike probabilities. We then used the linear RF and nonlinearity to predict responses to the natural images of the test set and took the correlation coefficient between the actual and predicted responses as a measure of RF prediction performance. We performed this procedure 100 times for each cell and each value of the regularization parameter. For each cell, we chose the regularization parameter that maximized the RF prediction performance. Using this procedure, 42% of neurons, 1,969/4,743, had fraction of explained variance >10% (range: 22–59%, 17 experiments), comparable to previous reports (48%, 222/463, in ref. 13), where fraction of explained variance is defined as 100 (R²), where R is the Pearson’s product-moment correlation coefficient between the actual and predicted responses.

To assess whether the RF for a particular cell was significant, we randomly shuffled the response vector to the natural image sequence and performed the reverse correlation again using the same regularization parameter, λ. This procedure was repeated 100 times to produce 100 shuffled RFs, RF_shuffled. From these shuffled RFs the mean, μ_shuffled, and standard deviation, σ_shuffled across all pixels were calculated. A RF was defined to be significant if there were pixels which had absolute values μ_shuffled + Lσ_shuffled, where L (the ‘significance level’) denotes the number of standard deviations from the mean. The fraction of neurons with RFs with significance level >5 was 53% (2,532/4,743, range: 34–68%, 17 experiments).

The RF was parameterized by fitting a two-dimensional Gabor function using the Levenberg–Marquardt algorithm. The Gabor function is described by

$$G\left(x^{\prime },y^{\prime }\right)=A\exp \left(-\frac{x^{\prime 2}}{2{\sigma }_x^2}-\frac{y^{\prime 2}}{2{\sigma }_y^2}\right)\cos \left(2\pi f{x}^{\prime }+\phi \right)$$

where

$$\begin{array}{c}\hfill x^{\prime }=\left(x-c_x\right)\cos \theta -\left(y-c_y\right)\sin \theta \hfill \\ \hfill y^{\prime }=\left(x-c_x\right)\sin \theta +\left(y-c_y\right)\cos \theta \hfill \end{array}$$

These equations describe an underlying two-dimensional cosine grating parameterized by θ (orientation), f(spatialfrequency) and φ (phase), which is enveloped by a two-dimensional Gaussian function parameterized by A (amplitude), (c_x,c_y) (centre of the Gaussian) and σ_x and σ_y (standard deviations of the Gaussian perpendicular to and parallel to the axis of the grating, respectively).

The pixel–pixel Pearson’s correlation coefficient was used as a measure of RF similarity. To compare the difference in orientation preference, the two-dimensional Fourier transform of each RF was taken, $\mathcal{F}\left\{\mathrm{RF}\right\}$. An orientation tuning curve for each neuron was calculated by interpolating the power value of the Fourier spectrum, ${\mid \mathcal{F}\left\{\mathrm{RF}\right\}\mid }^2$ around a circle with radius equal to the dominant spatial frequency of the RF (also derived from the two-dimensional Fourier transform). The Gabor fits were used to compare the amount of ON and OFF subfield overlap between pairs of neurons (Fig. 2 and Extended Data Figs 4 and 5). In this case, ON subfields were defined as the region in which pixels of the Gabor fit were >20% of maximum absolute value, max(abs(Gabor fit)). Similarly, OFF subfields were defined as the region in which pixels of the Gabor fit were <20% of the negative of the maximum absolute value, – max(abs(Gabor fit)). The amount of overlap was defined as

$$\text{overlap}=\frac{\mid A\cap B\mid }{\mid A\cup B\mid }$$

where A and B are the regions of visual space covered by the presynaptic (say, A) and postsynaptic (say, B) ON, OFF, or both subfields.

General statistical analyses

All statistical tests used in the manuscript were non-parametric, with no assumptions concerning normality or of equal variances. Statistical tests used are described in the manuscript or in the figure legends.

Statistical analysis of connectivity predictions

To determine which aspects of neuronal responses predict connection strength we performed the following analysis. Each pairwise similarity metric (for instance, difference in orientation preference or RF correlation) was ordered such that higher values indicated higher similarity between two neurons. Our test hypothesis (H1) was that there was a positive (linear) correlation between the similarity metric and observed connection weights. Our null hypothesis (H0) was that connections are drawn randomly from the measured distribution of connection strengths. The prediction performance value of a pairwise similarity metric was defined as the Pearson’s product-moment correlation coefficient between the similarity metric and the observed synaptic weights, PP_O = corr(p,o), where p and o are the vectors of the metric and observed connection weights, respectively. To measure the prediction for difference in orientation preference, we combined connection amplitude data from a previous publication, in which orientation was measured using drifting oriented gratings (see refs. 10 and 15), and the RF data, where orientation was measured using the Fourier analysis described above. Only neurons with RFs having a significance level >4.3 (see above) were included in the analysis for subfield overlap and orientation preference.

We estimated P values for this hypothesis using a Monte-Carlo analysis. We generated random permutations of the observed connections and connection strengths (50 permutations were generated for each observed connection). For each permutation, we calculated the prediction performance, PP_R = corr(o,r) where o and r are the vectors of observed and randomly permuted connection weights, respectively. The P values for hypothesis H1 were then estimated as the proportion of prediction performance values, PP_R that were higher than the value PP_O.

Receptive field transformation

To allow us to pool RF data across neurons, we normalized postsynaptic RFs by first defining a template RF, which was a vertical Gabor with 0 degree phase (that is, centred on an ON domain; see Extended Data Fig. 6). A Gabor was fit to the RF of each postsynaptic neuron, and then rotated, translated and scaled so that the ON subfield was centred on the template’s ON subfield. We used the parameters of this transformation to transform the RFs of all simultaneously recorded presynaptic (whether connected or not) and postsynaptic cells.

The RF outlines used for display (Fig. 3, Extended Data Figs 6, 7 and 8) were calculated in the following way. The maximum pixel value obtained by the RF was defined as Peak_ON, and the minimum pixel value obtained by the RF was defined as Peak_OFF. If ∣Peak_ON∣ > ∣Peak_OFF∣, then a contour (ON subfield outline) was traced at a value 0.2Peak_ON. The OFF subfield outline was then defined as the contour at (0.7 – 0.5(Peak_OFF/Peak_ON))Peak_OFF. If ∣Peak_OFF∣ > ∣Peak_ON∣, then a contour (OFF subfield outline) was traced at a value 0.2Peak_OFF. The ON subfield outline was then defined as the contour at (0.7 – 0.5(Peak_ON/Peak_OFF))Peak_ON.

Predicting single-neuron membrane potential responses in a L2/3 network simulation

We used the statistics of recurrent cortical connections measured in our experimental work to predict the feature selectivity of local recurrent inputs to individual L2/3 neurons. The model was used to predict the subthreshold membrane potential of each neuron in response to drifting oriented gratings presented to the network.

To predict inputs in response to drifting gratings, we pooled all RFs measured experimentally into a single population (n = 4,633 neurons) by shifting RFs so that the mean RF centre location of each experiment was aligned. Thus, the observed RF scatter for each experiment was retained. We simulated the presentation of 100% contrast, drifting sinusoidal gratings with temporal frequency of 3 Hz (cycles per s) and spatial frequency 0.04 cycles per degree, in 8 equally spaced directions from 0° to 360°.

Network connections were generated by taking each neuron in turn as a postsynaptic neuron, and assigning input connections from all other neurons according to the similarity between the pre- and postsynaptic RFs. We used the relationship between RF correlation and connection amplitude (Fig. 2g) to assign weights to each simulated connection (see schematic in Fig. 4e). Each network simulated the input only to a single postsynaptic neuron. Every network instance was normalized to have the same total weight. The contributions from the strongest 25% of inputs and the weakest 75% of inputs were additionally examined by setting all other weights to zero.

Responses for each neuron in the population were generated using a linear/nonlinear model. The parameters of this model were derived for each neuron in the population during estimation of the linear RF (see Methods above). The linear output in response to a particular grating orientation and phase was estimated by correlating the grating stimulus with the RF of a given neuron. The nonlinear sigmoidal transfer curve fit during RF estimation (see Methods above), was used to convert the linear output into a mean firing-rate at each time point of the simulation (Fig. 4e). The firing rates from all presynaptic neurons were then weighted by their connection strengths and summed to generate a time varying membrane potential (V_m) of the postsynaptic neurons (Fig. 4f). No external (for example, feedforward) input was applied to the postsynaptic neuron. The membrane potential for a given postsynaptic neuron was estimated by integrating an R–C membrane model, with input resistance R_in = 140 MΩ, capacitance C = 120 pF. Membrane potential traces produced in this way were analysed identically to membrane potential traces obtained in vivo (see above).

Extended Data

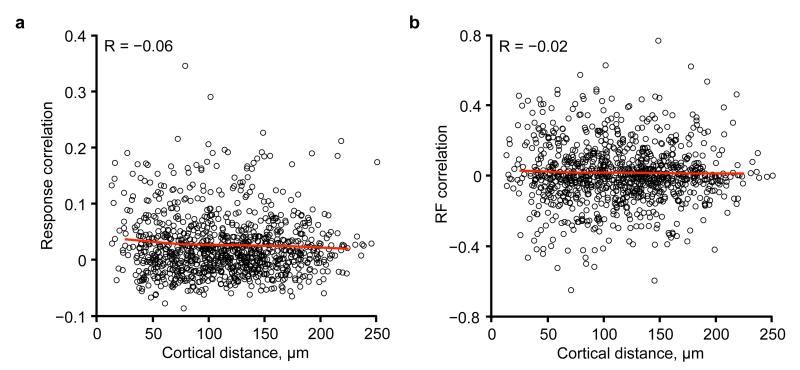
Extended Data Figure 1. Relationship between response correlation coefficient or RF correlation and cortical distance.

a, Pairwise response correlation coefficient plotted as a function of cortical distance, for an example region, indicates only a weak relationship between response correlation and cortical distance (R = −0.06). Red line denotes mean value of response correlation in 50 μm bins of cortical distance. b, Pairwise RF correlation plotted as a function of cortical distance, for the same example region as in a. Again, only a weak relationship was observed (R = −0.02).

Extended Data Figure 2. Relationship between mean connection amplitude and response correlation or RF correlation.

a, Black trace, mean connection amplitude (excluding unconnected pairs) plotted against response correlation. Dashed grey line indicates mean EPSP amplitude of all connections. Grey shaded region represents the 95% confidence interval of the expected mean, estimated by repeated random reshuffling of the EPSP amplitudes among all cell pairs in the data set. Connections were binned with ranges from −0.1 to 0, 0 to 0.1, and so on. b, Black trace, mean connection amplitude (excluding unconnected pairs) plotted against RF correlation. Dashed grey line indicates mean EPSP amplitude of all connections. Grey shaded region represents the 95% confidence interval of the expected mean, estimated by repeated random reshuffling of the EPSP amplitudes among all cell pairs in the data set. Connections were binned with ranges from −0.8 to −0.6, −0.6 to −0.4, and so on.

Extended Data Figure 3. Relationship between connectivity and RF subfield overlap.

a, The amount of ON and OFF subfield overlap (see Methods) was strongly correlated to the overall RF similarity as measured by RF correlation (R = 0.79, P < 1 × 10⁻¹⁰). b, Left panel, connection probability increased with increasing ON subfield overlap (P = 0.05; Cochran–Armitage test). Middle panel, EPSP amplitudes categorized into bins of ON overlap. Black line, median EPSP amplitude for each bin. Right panel, EPSP amplitude plotted against ON overlap. Red data points, bidirectional connections. Black data points, unidirectional connections. Underlying histogram shows frequency of recorded cell pairs as a function of ON overlap. c, Same as b, but for OFF overlap (P = 0.002; Cochran–Armitage test). d, Same as b, but for combined ON and OFF overlap (P = 1.8 × 10⁻⁵; Cochran–Armitage test). P values from the Cochran–Armitage test. To perform the Cochran–Armitage test, the bins at 0 and >0–0.15 were considered together, so that groups were evenly spaced.

Extended Data Figure 4. Similarity of shared neuronal properties ranked according to how well they predict connection amplitude, when excluding unconnected pairs.

Prediction performance and P values were calculated using a Monte-Carlo analysis (see Methods). Colours of the discs indicate P values.

Extended Data Figure 5. Relationship between bidirectional and unidirectional connections and RF properties.

a, EPSP amplitude plotted against RF correlation from bidirectionally (red) and unidirectionally connected pairs (black). Replotted from Fig. 2g. b, EPSP amplitude for bi- or unidirectional connections. Bidirectional connections were stronger than unidirectional connections (median connection amplitude: 0.44 mV for bidirectional connections, n = 22; 0.16 mV for unidirectional connections, n = 50; P = 4.4 × 10⁻⁴, Wilcoxon rank-sum test). c, RF correlation for bidirectionally connected, unidirectionally connected and unconnected pairs. The RFs of bidirectionally connected pairs were more correlated than those of unidirectionally connected or unconnected pairs (median RF correlation: 0.3 for bidirectionally connected pairs, n = 11; 0.04 for unidirectionally connected pairs, n = 50; P = 0.002; and −0.02 for unconnected pairs, n = 191, P = 5.3 × 10⁻⁵), although unidirectionally connected pairs did not have higher RF correlations than unconnected pairs (P = 0.18, Wilcoxon rank-sum test). d, Mean EPSP amplitude versus RF correlation for all (yellow), unidirectionally (black) or bidirectionally (red) connected pairs. There was a positive relationship between RF correlation and connection amplitude for both unidirectional and bidirectional connections.

Extended Data Figure 6. Method of RF normalization.

a, We normalized postsynaptic RFs to a template RF that was a vertical Gabor with 0 degree phase and an arbitrary but fixed spatial frequency (far right). A Gabor was fit to the RF of each postsynaptic neuron, and then rotated, translated and scaled so that the ON subfield was centred on the template’s ON subfield and the spatial frequencies matched. The same transformation was applied to presynaptic RFs of any simultaneously patched neurons. b, Transformation of the RF from an example postsynaptic neuron (upper row), and for the RF for its connected presynaptic neuron (middle row). Bottom row shows presynaptic RF outline overlaid on the postsynaptic RF at each step in the transformation.

Extended Data Figure 7. Overlay of RFs between connected neurons.

Presynaptic RF outline overlaid on the postsynaptic RF for all the connected pairs after performing normalization of the pre- and postsynaptic RFs to the RF template (n = 45). Numbers indicate connection amplitude.

Extended Data Figure 8. Overlay of RFs between unconnected neurons.

Assessed presynaptic RF outlines overlaid on the assessed postsynaptic RF for a representative set of unconnected pairs after normalization to the RF template.

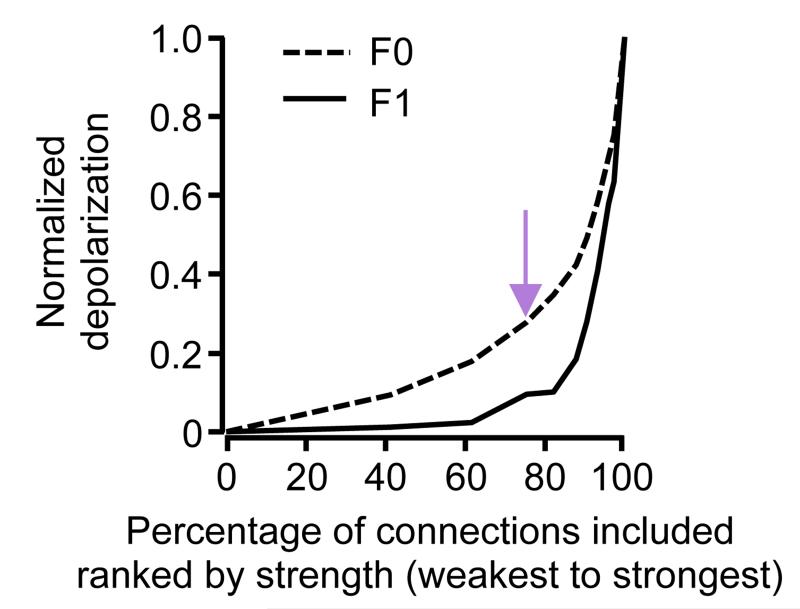
Extended Data Figure 9. Contribution of strong and weak connections to membrane potential depolarization.

Removal of an increasingly larger fraction of the strongest inputs from the L2/3 model steeply reduces the large modulation component (F1) but more gradually reduces the mean depolarization component (F0). Model from Fig. 4d. Purple arrow indicates the weakest 75% of connections, as shown in Fig. 4i, j.