Ensemble Learning Approaches to Predicting Complications of Blood Transfusion

Abstract

Of the 21 million blood components transfused in the United States during 2011, approximately 1 in 414 resulted in complication [1]. Two complications in particular, transfusion-related acute lung injury (TRALI) and transfusion-associated circulatory overload (TACO), are especially concerning. These two alone accounted for 62% of reported transfusion-related fatalities in 2013 [2]. We have previously developed a set of machine learning base models for predicting the likelihood of these adverse reactions, with a goal towards better informing the clinician prior to a transfusion decision. Here we describe recent work incorporating ensemble learning approaches to predicting TACO/TRALI. In particular we describe combining base models via majority voting, stacking of model sets with varying diversity, as well as a resampling/boosting combination algorithm called RUSBoost. We find that while the performance of many models is very good, the ensemble models do not yield significantly better performance in terms of AUC.

I. Introduction

Despite being a frequently employed routine medical practice, blood product transfusion is still associated with a small but severe risk of complication. Two adverse reactions in particular, transfusion-related acute lung injury (TRALI) and transfusion-associated circulatory overload (TACO), described in [3], are especially problematic: Between 2009 and 2013, TRALI accounted for 30–45% of reported transfusion-related fatalities, and TACO accounted for 13–34% [2]. Furthermore, recent studies [4, 5] of a non-cardiac surgical patient subpopulation found that those experiencing TACO or TRALI stay in both the ICU and hospital roughly twice as long as those who do not, and have in-hospital mortality rates that are respectively 3.5 and 10 times greater. Consequently, these adverse events not only put the patients at a much higher risk of mortality and poor quality of life outcomes, but also lead to increased utilization of healthcare services potentially leading to an increase in healthcare cost and expenditure.

Because of these considerations, having the ability to predict the risk of TRALI and TACO – prior to an episode of transfusion – may potentially benefit patients, providers as well as the overall healthcare system. This is one of the specific aims of research in our group. We emphasize that this a priori prediction goal is distinct from studies that have looked at risk factors for both TRALI and TACO.

In a previous work [6], we constructed several learning models, hereafter called base models, built on a dataset collected by Clifford et al. [4, 5]. One particularly appealing aspect of this dataset is the physician-adjudicated “ground truth” for patients suffering TACO/TRALI. That is, after employing novel screening techniques, each of the retrospectively-considered cases flagged as potential TACO or TRALI episodes were reviewed by a panel of physicians, including further expert review in case of disagreement. This provides a compelling reference for whether or not a patient suffered either TACO or TRALI.

One of the particular challenges of both this dataset as well as the field in general is a severe class imbalance between those patients suffering an adverse reaction and those that are transfused without complication. To whit, after pre-processing, out of 3398 observations in the set only 143 (~4%) suffered adverse reactions. While a triumph for medicine, this presents a non-trivial practical difficulty for prediction algorithms.

In the current work, we describe combining the previously built base models into ensemble models and their resulting impact on prediction. Our results suggest that the new ensemble models do not statistically significantly outperform top base models.

II. Dataset and Base Models

A. Dataset

The initial study population consisted of all non-cardiac surgical patients receiving general anesthesia that were present in Mayo Clinic’s perioperative datamart [4, 5]. This database contains near real-time patient data from monitored-care environments, and includes details relating to a variety of patient vital signs, history, procedure details and other relevant factors. All patients in the study population had previously given signed consent for the use of their medical records for research purposes, and the Mayo Clinic Institutional Review Board approved the study before its onset.

Following [4, 5], this study more specifically includes all adult non-cardiac surgical patients who received blood product transfusions in either 2004 or 2011. Exclusions are carefully described in the references, but summarized briefly patients were excluded if their conditions would preclude a clean ruling as to the presence of TACO/TRALI. For example, because TACO and TRALI are characterized by lung injury, patients with preoperative respiratory failure were excluded.

For further details regarding the dataset, including descriptive statistics and a discussion of the choice of years, we refer the reader to the above references.

B. Base Models

Considering our goal of predicting the likelihood of an adverse reaction before performing a transfusion, our base analysis proceeded as follows: Beginning with the raw data as described above, we first removed all variables which violated predictive causality, namely those that included information which would not be available pre-transfusion. For example, anything measured after blood products were transfused was excluded. Continuous variables were normalized to zero mean and unit variance. Categorical variables with many levels were condensed into reduced sets, and several variables with similar medical implications, such as degrees of liver disease, were also combined into single predictors. Furthermore, several types of specific transfusion products (e.g. plasma and cryoprecipitate) were condensed into unified factors. A list of included predictors can be found in Table I.

Table I.

Predictors

ACEI Use	Age
ARB Use	ASA number
Aspirin (preOp)	Beta Blocker Use
Clopidogrel Use	Diuretic (preOp)
Emergency vs Elective Surgery	Fluid Ratio
Gender	Height
Hist Coronary Artery Disease	Hist Congestive Heart Failure
Hist Chronic Kidney Disease	Hist Diabetes
Hist Chronic Obs. Pulmonary Disease	Hist Liver Disease
Hist Myocardial Infarction	Sepsis (preOp)
Mixed or Non-RBC Transfusion	Hist Smoking
Statin Use	Surgical Specialty
Warfarin Use	Weight
Year

The response variable considered is adverseEvent = TACO or TRALI. We found it necessary to combine both TACO and TRALI responses into a single category due to the low prevalence of TRALI in our dataset.

Given the above predictors and response we trained 8 base models, including logistic regression (glm), flexible discriminant analysis (fda), C5.0 (C5.0), bagged CART (treebag), sparse linear discriminant analysis (slda), support vector machine with radial basis kernel (svmR), single-hidden-layer feed-forward neural network (nnet), and random forest (rf). Discussions of these algorithms can be found in [7]. All models were trained using the well known statistical software R [8] making particular use of the caret package [2]. After dividing the data into training (70%), evaluation (10%), and final test (30%) sets, the training set was oversampled using the SMOTE algorithm [9]. Oversampling, discussed below, is necessary due to the low prevalence of true-positive cases of adverse reactions. Three repeats of ten-fold cross-validation were then performed over a grid of possible model parameters using the training set. Care was taken to ensure all models were trained on identical samples of the training set. From this the optimal parameters for a given model were selected. Selection was done by comparing AUC’s, and in the case of similar AUC’s choosing the most parsimonious model. Additionally, using the evaluation set, optimal class probability thresholds were determined by first constructing ROC curves then choosing a threshold that maximized similarity to a perfect two-class model (i.e. sensitivity and specificity both equal to unity). Performance of models based on the optimized threshold and a naïve threshold of 50% of the predicted scores was then evaluated on the final test set.

III. Oversampling

One important characteristic in our dataset is a dramatic class imbalance between patients responding adversely to transfusion (the minority class) and those presenting no complications (the majority class). Specifically, the entire dataset contained only 143 observations of adverse events out of a total of 3398 observations, roughly a 4% prevalence. Following a class-balanced data allocation using the percentages described in Section II, the final test set included 28 adverse events out of 650 observations.

One technique commonly employed to mitigate the consequences of such a class imbalance is that of oversampling. Oversampling methods alter a dataset in such a way as to bring the minority and majority classes to similar proportions. While there are a variety of possible approaches, in the current study we chose to build our base models using training sets oversampled via the SMOTE [9] method. SMOTE enhances the training set by using a nearest-neighbors algorithm to create artificial-but-similar observations of the minority class while also down-sampling observations of the majority class. These two actions in concert balance the majority and minority classes, and frequently improve models’ predictive performance [10].

While we used SMOTE for training the base models, one of our ensemble models is based on the RUSBoost [11] algorithm. This algorithm implements a different sampling technique called random under-sampling. In random under-sampling, observations of the majority class are removed until balance is achieved.

IV. Ensemble Learning

Ensemble learning is a general term for the concept of combining the predictions of several learning models, frequently presumed weak, into a single “ensemble” model. The ensemble model is often found to yield better performance [7]. Common approaches to ensemble learning include bagging, boosting, and stacking, amongst others [7].

Briefly, bagging takes different random samples of data, trains models on the different samples, and then either averages or votes on the results. It is frequently used with low bias / high variance learners like decision trees, with a goal of reducing the overall variance.

Boosting in contrast begins by constructing a single model on a dataset, then producing a series of new models, iteratively training each new model on the observations that were misclassified by the previous model in the series. The process is continued until a stopping condition is met. In practice, new models are not trained solely on previously-misclassified observations, but rather on new datasets that have been resampled to include a proportionally greater number of observations of the misclassified points.

Stacking consists of training a new meta-learning model, or combiner, on the predictions of the base models.

Here we consider two forms of ensemble learning, majority-vote bagging and stacking, as well as a hybrid ensemble/oversampling algorithm called RUSBoost.

A. Majority Vote

This straightforward ensemble technique simply counts the class predictions of all base models and assigns a class based on the majority opinion. This is a direct application of bagging, but can be distinguished from other common forms, e.g. the bagging internal to a random forest, in that it combines the results of distinct families of algorithms.

B. Stacking

Stacking consists of training a new model, frequently called a combiner, on the probabilities produced by the base models. Specifically, one trains the combiner on the probabilities that result from the base models learning the training set. To predict using the stacked model, one first predicts using the base models, then feeds these predicted probabilities into the combiner.

An important concept in deploying stacked models is the choice of base models to include in the ensemble. If the base models are always in agreement the stacked model will realize no performance benefit.

We chose diverse models in two ways. First, the base models that we began with are diverse in algorithm. For example our base model choices include a linear model, a bagged tree model, a boosted tree model, a neural network, a support vector machine, a regression splines model, discriminant analysis and a random forest. Some of these models include implicit feature selection or regularization schemes; others include internal bagging or boosting. This variety of learning methods thus produces a set with a natural degree of diversity.

Second, among these relatively diverse models we chose a maximally diverse subset. We did this via k-means clustering on an agreement matrix (described below), as well as hierarchical clustering on the Euclidean distance between base model predictions on the evaluation set. We found both methods produced very similar maximally diverse model sets.

Details of the clustering are as follows: For the k-means model clustering we first predicted all n = 8 base models on the evaluation set. We then created an “agreement matrix,” which is an n × n matrix with each element consisting of the fraction of observations where a given pair of models predicted the same patient outcome. Clustering using k = 4 produced a set of diverse models. For hierarchical model clustering, we formed a model-dissimilarity matrix by taking the predicted probabilities of the base models on the evaluation set and calculating the Euclidean distance between each models’ set of probabilities. We then used hierarchical clustering on this dissimilarity matrix to produce a set of diverse models. This set was very similar to the set found by k-means hence we chose a hybrid of the two which consisted of the rf, nnet, and fda models described above.

For the combiner model we trained logistic regression on both the set of all base models (stackAllGLM) as well as the diverse set of base models (stackDivGLM). In addition using the diverse set we trained random forest (stackDivRF), and Bayesian generalized linear (stackDivBayes) models.

C. RUSBoost

RUSBoost is an algorithm specifically designed to target class-imbalanced datasets. It combines the benefits of the AdaBoost model [12] with those of random-undersampling (RUS). It is similar to the SMOTEBoost [13] algorithm but uses undersampling at each boosting step in place of SMOTE. The two suggested advantages are that random undersampling is a less complicated algorithm than SMOTE, and that the datasets produced by RUS are smaller than those produced by SMOTE, thus resulting in shorter computational time. We made use of the Stephen Carnagua’s implementation of RUSBoost [14].

V. Results

A. Receiver-Operator Curves

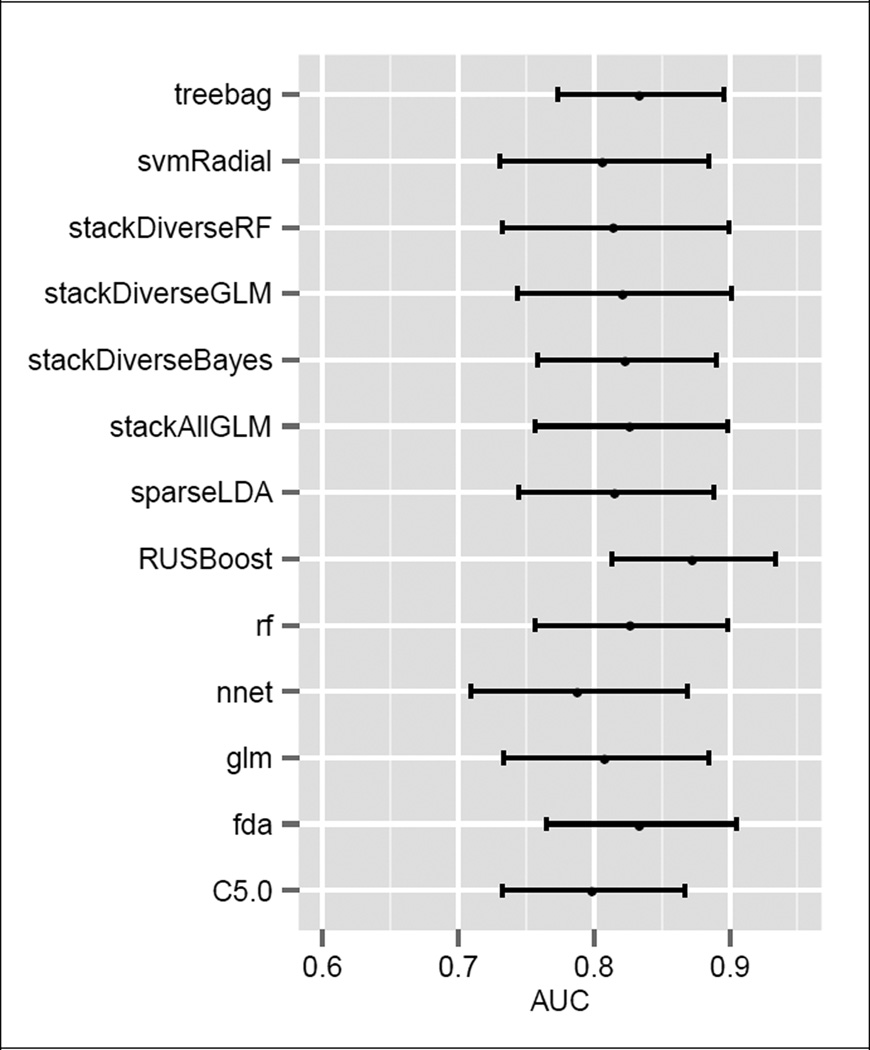
Test set AUC’s and their 95% confidence intervals are shown for all models in Fig. 1. The confidence intervals were calculated via bootstrap using 2000 class-stratified sample passes. By AUC, the top performing model was RUSBoost, with an AUC of 0.87. The worst performing model by AUC was the majority vote, with a score of 0.74.

Figure 1.

Final Test AUC’s with 95% Confidence Intervals

We compared the areas under the final test ROC’s using DeLong’s method [15]. We found no statistical difference between top performers. We also compared the ROC curves directly using Venkatraman’s method [16], again finding no statistically significant difference between top performers.

B. Sensitivity

All of the classifiers we considered produce both probabilities that a patient will suffer an adverse reaction as well as a final yes/no adverse reaction prediction. One can therefore tune the sensitivity of a model by varying the probability threshold at which a patient is predicted to react adversely. We investigated model performance under alternate class probability thresholds by using test set ROC’s to choose thresholds which were maximally similar to a perfect model (e.g. sensitivity and specificity both equal to unity). The results for both 50% and alternate thresholds are shown in Tables II and III.

Table II.

Test Set Results Using Alternate Probability Thresholds

	AUC	Sensitivity	Specificity Accuracy	Accuracy
RUSBoost	0.87	0.93	0.64	0.65
fda	0.83	0.86	0.66	0.67
C5.0	0.80	0.86	0.60	0.61
treebag	0.83	0.82	0.71	0.71
sparseLDA	0.82	0.82	0.73	0.73
rf	0.83	0.82	0.71	0.71
stackDivRF	0.82	0.82	0.68	0.69
stackFullGLM	0.83	0.79	0.72	0.73
stackDivGLM	0.82	0.79	0.71	0.72
stackDivBayes	0.82	0.79	0.73	0.73
majorityVote	NA	0.79	0.73	0.73
svmRadial	0.81	0.75	0.72	0.72
glm	0.81	0.71	0.74	0.74
nnet	0.79	0.61	0.79	0.78

Table III.

Test Set Results Using Naive (50%) Thresholds

	AUC	Sensitivity	Specificity Accuracy	Accuracy
RUSBoost	0.87	0.64	0.89	0.88
fda	0.83	0.75	0.81	0.81
treebag	0.83	0.61	0.80	0.79
rf	0.83	0.71	0.78	0.78
stackFullGLM	0.83	0.79	0.75	0.75
stackDivBayes	0.82	0.64	0.81	0.81
stackDivGLM	0.82	0.71	0.81	0.80
sparseLDA	0.82	0.71	0.76	0.76
stackDivRF	0.82	0.71	0.80	0.80
glm	0.81	0.71	0.76	0.76
svmRadial	0.81	0.57	0.80	0.79
C5.0	0.80	0.57	0.81	0.80
nnet	0.79	0.68	0.78	0.77
majorityVote	NA	0.68	0.81	0.80

VI. Conclusion

We have employed three ensemble learning methods with the goal of improving the accuracy of predicting two complications of blood transfusion, TACO and TRALI. We found that the while the ensemble methods did not statistically significantly outperform the top base models, the results from both base and ensemble models are quite encouraging, with AUC’s of the top 5 averaging 0.84 and sensitivities between 0.82 and 0.92.

Given the class imbalance present in the data, extensions to the current work that are likely to be helpful may include introducing a cost sensitive learning approach to the base models [10]. We are also working to expand the observations in our dataset.

We are hopeful that this research will lay the foundation for deployable predictive models of adverse reactions to blood transfusion, enhancing clinical practice and aiding in the delivery of high quality medical care.