Advances in Quantification of Meniscus Tensile Mechanics Including Nonlinearity, Yield, and Failure

Abstract

The meniscus provides crucial knee function and damage to it leads to osteoarthritis of the articular cartilage. Accurate measurement of its mechanical properties is therefore important, but there is uncertainty about how the test procedure affects the results, and some key mechanical properties are reported using ad hoc criteria (modulus) or not reported at all (yield). This study quantifies the meniscus' stress–strain curve in circumferential and radial uniaxial tension. A fiber recruitment model was used to represent the toe region of the stress–strain curve, and new reproducible and objective procedures were implemented for identifying the yield point and measuring the elastic modulus. Patterns of strain heterogeneity were identified using strain field measurements. To resolve uncertainty regarding whether rupture location (i.e., midsubstance rupture versus at-grip rupture) influences the measured mechanical properties, types of rupture were classified in detail and compared. Dogbone (DB)-shaped specimens are often used to promote midsubstance rupture; to determine if this is effective, we compared DB and rectangle (R) specimens in both the radial and circumferential directions. In circumferential testing, we also compared expanded tab (ET) specimens under the hypothesis that this shape would more effectively secure the meniscus' curved fibers and thus produce a stiffer response. The fiber recruitment model produced excellent fits to the data. Full fiber recruitment occurred approximately at the yield point, strongly supporting the model's physical interpretation. The strain fields, especially shear and transverse strain, were extremely heterogeneous. The shear strain field was arranged in pronounced bands of alternating positive and negative strain in a pattern similar to the fascicle structure. The site and extent of failure showed great variation, but did not affect the measured mechanical properties. In circumferential tension, ET specimens underwent earlier and more rapid fiber recruitment, had less stretch at yield, and had greater elastic modulus and peak stress. No significant differences were observed between R and DB specimens in either circumferential or radial tension. Based on these results, ET specimens are recommended for circumferential tests and R specimens for radial tests. In addition to the data obtained, the procedural and modeling advances made in this study are a significant step forward for meniscus research and are applicable to other fibrous soft tissues.

1. Introduction

The meniscus performs the critical function of distributing knee loads over articular cartilage and protecting it from overload. Meniscus damage impairs this function and may necessitate meniscectomy to resolve pain or mechanical symptoms, greatly increasing the risk of osteoarthritis. Due to the consequences of a mechanically compromised meniscus, there is a great interest in developing methods to repair or replace damaged meniscus [1–5]. These efforts depend on accurate quantification of normal meniscus mechanics, damage, and failure. Mechanical property measurements must be reliable and functionally relevant, and procedural factors which affect the outcome of mechanical tests must be identified and controlled. These challenges merit careful attention; they have not been entirely solved for fibrous soft tissue in general or meniscus specifically. The specific objectives of this study are to quantify the meniscus' nonlinear mechanics, in the process resolving several issues pertaining to their quantification, and to determine the benefits and disadvantages of several popular specimen shapes for tensile testing.

The meniscus, like all fibrous soft tissues, has a nonlinear stress–strain curve in tension. It is also anisotropic, necessitating testing in multiple loading directions. The meniscus is compliant at low strain (the toe region of the stress–strain curve), stiffens as strain increases (the so-called linear region), undergoes a loss of stiffness (strain-softening), and finally ruptures. The strain-stiffening is attributed to the incremental recruitment of collagen fibers [6]. The nonlinearity of the stress–strain curve, which affects the toe region in particular, is usually left unparameterized, making it difficult to carry out tasks such as predicting the meniscus' in situ mechanical response. Some studies have modeled the nonlinear mechanics of the meniscus using an exponential or a piecewise quadratic and linear formulation [6–10]. These phenomenological models, although they make mechanical predictions possible, are difficult to interpret in terms of meniscus structure or pathology. In this study, we quantify the stress–strain curve up to the strain-softening regime using a structural model based on the concept of sequential fiber recruitment [11].

Meniscus mechanics are also quantified using nonmodel parameters. Historically, these have only included elastic modulus (slope of the stress–strain curve), peak strain (ultimate tensile strain), and peak stress (ultimate tensile strength) [1,7,10,12–20]. These metrics are useful and, compared to model-based approaches, are simple to measure. However, the elastic modulus is difficult to define due to the nonlinear stress–strain response of the meniscus. It is usually calculated using a linear regression fit of the linear region [7,10,15–18,21–23], but there is no part of the stress–strain curve that is truly linear. The assignment of a linear region is thus rather arbitrary and so varies from study to study. The criteria used for assignment are often left unspecified, and human judgment on a case-by-case basis appears to tacitly be the most common procedure. The studies which reproducibly define the yield point do so using a strain or stress range relative to the peak value. While this solution is practical, it makes the linear region covariate with the peak point rather than specific to the stress–strain curve's shape. The chosen range must be tweaked from study to study to ensure it corresponds to a region with quasi-linear behavior. The meaning of an elastic modulus obtained by fitting the linear region thus also varies. A related problem is identification of the transition from strain-stiffening to strain-softening, i.e., the yield point. This transition is a potentially important transition in function. The yield point has not yet been reported for meniscus. In this study, we implement a procedure for measuring the meniscus' elastic modulus and yield point based on the stress–strain curve's shape, which should prove more robust than existing methods.

In an ideal tensile test, the specimen ruptures in the middle of the gauge region, away from the grips. This is called midsubstance rupture. It is desirable because the grips create local stresses by applying clamping force and restricting specimen deformation [24–26]. Rupture at or near the grip line thus occurs under different conditions than midsubstance rupture and measures a potentially different failure process. The local grip stresses are complex and difficult to quantify, so tissue tests resulting in the rupture of the gripped region are usually discarded [12,15,18]. However, few studies report the rupture location; those that do so only report that midsubstance ruptures were used and do not specify the rules by which midsubstance ruptures were identified. As a practical matter, classification of a rupture in a tissue specimen as a midsubstance or gripped region rupture is seldom clear. Tissue specimens are usually small, and ruptures can involve a large part of the specimen length. Many ruptures involve both the midsubstance and gripped regions [15,22]. To help resolve uncertainty regarding how rupture locations should be identified, in this study we classified rupture locations in detail with illustrated definitions so that these classifications can be reproduced in future work. To help determine which rupture types should be considered valid test outcomes, we also compared mechanical test outcomes between rupture types.

Dogbone (DB)-shaped (also known as dumbbell-shaped) specimens are used to compensate for local grip-induced stresses by reducing the cross-sectional area in the specimen midsubstance, thus increasing its stress and the likelihood of midsubstance rupture. If the rupture is sufficiently far from the grip line that the local grip stresses have diffused into a uniform stress field, the midsubstance rupture is expected to be independent of grip effects (i.e., Saint–Venant's principle). Thus, DBs in principle provide results unconfounded by grip effects and have been incorporated into test standards for many industrial materials (e.g., metal, plastic, and leather) [27–29]. They accordingly are the de facto standard for tensile tests of meniscus and other fibrous soft tissues [15,18–20,23,30]. Rectangular specimens are also used, though, and may be preferable when specimens are only a few millimeters long [12,16,31,32]. However, for fibrous soft tissues, it is not clear whether the DB shape actually prevents grip effects from influencing test outcomes. Abatement of local grip stresses from the grips to the midsubstance region is unlikely in the (by necessity) short length of most tissue specimens [25,33,34]. To resolve the question of which specimen shape is preferable for meniscus testing, we compared DB specimens with rectangular specimens. Strain fields were measured to elucidate the role of grip-associated local stresses and other local stress sources.

The meniscus, due to the arc of its circumferential fibers, poses an additional complication: the inner side and outer corners of standard fiber-aligned circumferential DB specimens and rectangle (R) specimens have fibers that insert into only one grip. Therefore, we also compared these specimen shapes to a nonstandard expanded tab (ET) shape [17]. The ET shape has elongated grip-region tabs that follow the arc of the meniscus fibers and are meant to ensure that all fibers which cross the grip line have sufficient length inside the grips to be securely clamped. Quantitatively, the ET specimens are hypothesized to have a greater proportion of fibers loaded by the tensile test and thus greater apparent stiffness and strength.

In summary, the objective of this study was to comprehensively quantify the nonlinear mechanical properties of the meniscus in uniaxial tension and resolve several experimental issues regarding quantification procedure, rupture location, and specimen shape. Since the meniscus bears multiaxial loads, tensile tests were done in both the circumferential and radial directions. The mechanical properties reported in this study as well as the advances made regarding (i) structure-based modeling of the nonlinear toe region, (ii) yield and modulus quantification, (iii) rupture location classification, (iv) local strain field heterogeneity, and (v) choice of specimen shape are each a significant step forward for meniscus research and, importantly, are applicable to fibrous soft tissues in general.

2. Methods

2.1. Specimen Preparation and Tensile Test Protocol.

Meniscus specimens were prepared for uniaxial tensile testing in both the circumferential and radial directions (Fig. 1). Bovine menisci were purchased from Animal Technologies, Inc., Tyler, TX and stored at −20 °C. Both medial and lateral menisci were used. The source animals were all greater than 3 years old. Specimens were cut from the center (mid-circumferential, mid-radial, and mid-axial region) of the meniscus. While whole, the meniscus was measured and the placement of the specimen boundary was planned. Both sides of the meniscus were then planed using a cryomicrotome to obtain the desired specimen thickness. The specimen's curved edges were cut with a biopsy punch, and the straight edges were cut with a 130 mm histology trimming knife or, for tight work, a #15 scalpel. The target dimensions were adapted on a specimen-specific basis to accommodate anatomic variation between animals such that the same anatomic region was sampled in all cases. For example, in an especially narrow meniscus, the width of a circumferential specimen or the length of a radial specimen was reduced to avoid the inner or outer regions. In a meniscus with a short anterior–posterior distance, and hence sharp fiber arcing, circumferential specimens were cut with reduced length to preserve grip-to-grip fiber continuity. Specimen cross-sectional area (i.e., thickness and width) was measured with a scanning laser displacement sensor (factory-specified z accuracy < 16 μm and x and y accuracy < 11 μm) [11,35].

Fig. 1.

Meniscus specimen shapes used in this study and their dissection locations. The specimen and meniscus outlines are printed at 1:2 scale. The specimen outlines match the median dimensions used in this study. The gray-shaded regions of the specimen were clamped by the grips. The dashed lines schematically illustrate the curved path of the meniscus' fibers.

Circumferential tests used ET, R, and DB-shaped specimens (Fig. 1). The ET shape was meant to improve the grip-to-grip fiber continuity in the circumferential specimens by elongating the gripped tabs on the inner side of the meniscus, accommodating the arc of the circumferential fibers into the grips. Circumferential specimen dimensions were as follows: Specimen thickness was 1.3 ± 0.4 mm. ET specimens were 37 ± 2 mm long and 7.1 ± 2.5 mm wide in the midsubstance, with 1.5 mm radius fillets. The uniform-width midsection was 12.2 ± 1.8 mm long, and the grip-to-grip length was 17.1 ± 2.4 mm. R specimens were 28 ± 4 mm long, 7.7 ± 1.4 mm wide, and the grip-to-grip length was 14.8 ± 3.6 mm. DB specimens were 28 ± 4 mm long and 8.8 ± 1.5 mm wide, with a 4.3 ± 1 mm wide midsubstance and 2 mm radius semicircular cutouts. Their grip-to-grip length was 15.4 ± 3.2 mm.

Radial tests used R and DB specimens (Fig. 1). Radial specimen dimensions were as follows: Specimen thickness was 1.7 ± 0.2 mm. R specimens were 12.4 ± 2.6 mm long, 5.5 ± 1.0 mm wide, and had 7.8 ± 1.6 mm grip-to-grip length. DB specimens were 11.9 ± 1.6 mm long and 6.8 ± 0.8 mm wide, with a 3.8 ± 1.1 mm wide midsubstance. They had a grip-to-grip length of 8.3 ± 0.8 mm.

Prepared specimens were mounted in aluminum grips with 0.031 in tall 60 deg serrated teeth. A double layer of 400 grit cloth sandpaper was used to protect the specimen from the grips' teeth. The grips were tightened via bolts (2 per grip) to a standardized torque (8 in lb; 4–40 thread) [36,37]. The grips were kept aligned by a rigid guide while the specimen was mounted and the grips tightened. The grips were then left to sit for 10 min and tightened again to the target torque. The torque dropped to about 2 in lb during this 10 min time. The surface of each specimen was speckle coated with Verhoeff's stain before it was mounted on the mechanical tester to facilitate digital image correlation for strain analysis. The grips were then removed from the rigid guide and attached to an Instron 5943 tensile tester. Up to this point, the specimen was kept under gauze moistened with phosphate-buffered saline (PBS) except while being manipulated.

The specimen was loaded with a 20 kPa preload; the specimen length at this load was considered the undeformed length. Ten cycles of preconditioning to 4% strain were applied, followed by a displacement-controlled ramp to rupture. The displacement rate was 0.5 mm/s (quasi-static) for all tests. Video was recorded for each test at $\sim$ 15 fps with a field of view of 1280 × 960 pixels and a scale of $\sim$ 30 pixel/mm. The total testing time from removal of the damp gauze through preconditioning and rupture was approximately 5 min. Circumferentially loaded ET specimens were tested in either air (5 in the final dataset) or PBS (14 in the final dataset). Other shapes were tested in air alone, except for one circumferentially loaded R specimen tested in PBS. Both test environments produced nearly identical stress–strain responses with no significant difference with respect to any measured parameters (Fig. 2 and Table 1). Furthermore, the magnitude of the (nonsignificant) differences between tests in air and PBS were small relative to the differences observed between specimen shapes (compare Table 1 and Fig. 7 or Table 3). Since there was no effect of test environment on the mechanical response, at least for this < 5 min test duration, results from tests in air and PBS were pooled.

Fig. 2.

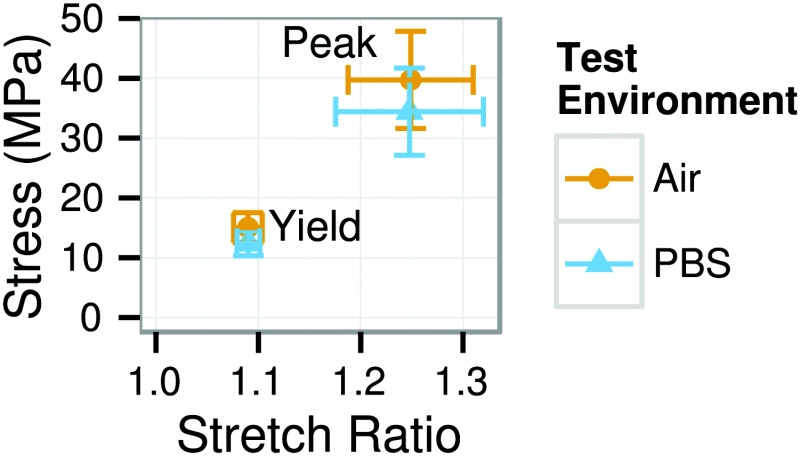
Mean and standard deviation of yield and peak points for circumferential ET specimens by test environment. The stress–strain response of specimens tested in air and PBS did not differ with respect to these points or any other measured parameter (see Table 1 for other parameters).

Table 1.

Mechanical parameters compared between circumferential ET specimens tested in air and PBS. There was no significant difference with respect to any parameter, and the 95% confidence intervals for potential differences are small.

	Air (Mean ± SD)	PBS (Mean ± SD)	Difference (95% CI)
${\overline{\lambda }}_c$	1.033 ± 0.010	1.04 ± 0.01	− 0.017 to 0.008
${\lambda }_c^{\text{SD}}$	0.016 ± 0.004	0.020 ± 0.004	−0.008 to 0.001
kf (MPa)	264 ± 35	238 ± 48	−19 to 71
Yield strain	0.09 ± 0.02	0.09 ± 0.01	−0.02 to 0.02
Yield stress (MPa)	15 ± 3	12 ± 2	−0.43 to 5.66
Modulus (MPa)	271 ± 41	231 ± 43	−9.36 to 91.20
Peak strain	0.28 ± 0.08	0.28 ± 0.09	−0.10 to 0.10
Peak stress (MPa)	40 ± 8	34 ± 7	−4.58 to 15.22

Fig. 7.

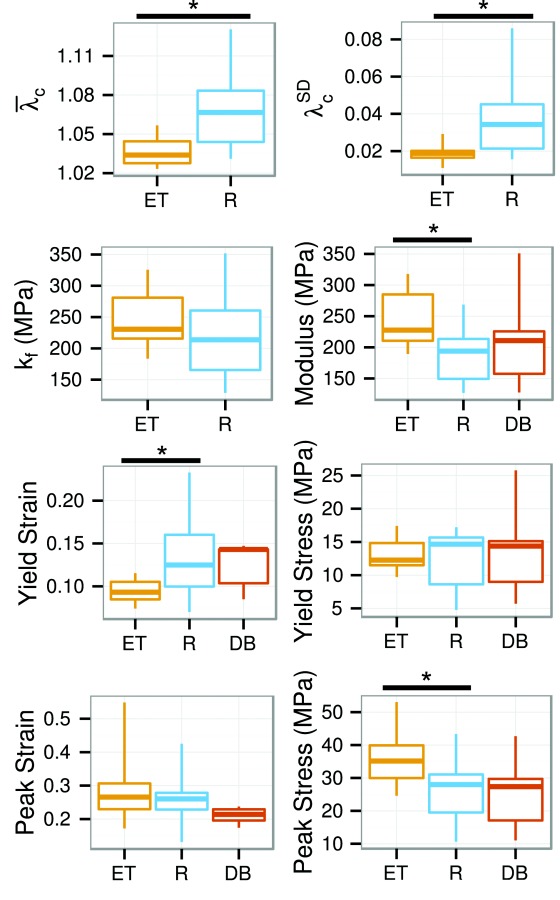
Fiber recruitment model and stress–strain results for circumferentially stretched ET, R, and DB specimens. Significant differences between specimen shapes are marked with a bar and asterisk. The ET specimens showed differences indicating more complete and rapid fiber recruitment.

Table 3.

Fiber recruitment model and stress–strain results by loading direction and specimen shape

	Circumferential			Radial
	ET	R	DB	R	DB
${\overline{\lambda }}_c$	1.04 ± 0.01a	1.07 ± 0.03a
${\lambda }_c^{\text{SD}}$	0.019 ± 0.004a	0.04 ± 0.02a
kf (MPa)	245 ± 45	215 ± 65
Modulus (MPa)	241 ± 45a	189 ± 48a	215 ± 86	21 ± 13	19 ± 10
Yield strain	0.09 ± 0.01a	0.13 ± 0.05a	0.12 ± 0.03	0.17 ± 0.05	0.18 ± 0.07
Yield stress (MPa)	13 ± 2	12 ± 5	14 ± 8	1.79 ± 0.83	2.0 ± 1.0
Peak strain	0.28 ± 0.09	0.26 ± 0.08	0.21 ± 0.03	0.47 ± 0.13	0.38 ± 0.07
Peak stress (MPa)	36 ± 8a	27 ± 10a	26 ± 12	4.9 ± 2.7	3.6 ± 1.6

^aThis value is significantly different between tests of circumferential ET and R specimens.

2.2. Specimen Characteristics and Specimen Exclusion.

Sixty-seven bovine menisci were used for this study. From these menisci, 95 specimens were cut and tested. Specimens ruptured in a variety of ways, so ruptures were classified according to the following definitions (illustrated in Fig. 3):

Fig. 3.

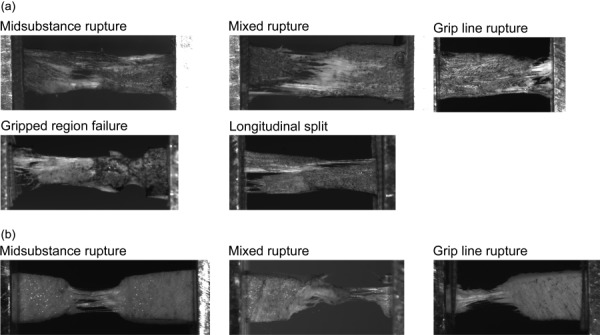
Classification scheme for types of specimen rupture. Circumferential specimens (a) ruptured in two more ways than the radial specimens (b). Gripped region failures and longitudinal splits were considered invalid and excluded from mechanical analysis.

• Midsubstance rupture: The line of rupture did not cross or touch either grip line.

• Mixed rupture: The line of rupture touched or crossed a grip line, but did not qualify as any of the following rupture types. A mixed rupture can be thought of as a mix of midsubstance rupture and grip-related rupture.

• Grip line rupture: The line of rupture was entirely within $\sim$ 1 mm of the grip line, but did not enter the gripped region.

• Gripped region rupture: Rupture occurred inside the grips, and the rupture did not qualify as a longitudinal split.

  Longitudinal split: The line of rupture bisected the specimen lengthwise.

Counts of tests ending in each rupture type are given in Table 2 for each specimen shape and loading direction. Gripped region ruptures were excluded from further analysis because the stress field within the grips is unknown. Similarly, tests ending in longitudinal splits were excluded because the stress across the rupture surface is unknown. Counts of tests ending with valid and excluded rupture types are given in Table 2.

Table 2.

Specimen counts by rupture type, test axis, and specimen shape before and after excluding invalid ruptures and duplicate specimens from the same meniscus

		Circumferential			Radial
		ET	R	DB	R	DB
Valid failures	Midsubstance rupture	6 (25%)	0 (0%)	1 (9%)	6 (24%)	5 (42%)
	Mixed rupture	10 (42%)	11 (48%)	4 (36%)	4 (16%)	2 (17%)
	Grip line rupture	4 (17%)	5 (22%)	2 (18%)	14 (56%)	4 (33%)
Total	20 (83%)	16 (70%)	7 (64%)	24 (96%)	11 (92%)
Excluded failures	Gripped region failure	4 (17%)	5 (22%)	4 (36%)	0 (0%)	0 (0%)
	Longitudinal split	0 (0%)	2 (9%)	0 (0%)	0 (0%)	0 (0%)
	No rupture	0 (0%)	0 (0%)	0 (0%)	1 (4%)	1 (4%)
Total	4 (17%)	7 (30%)	4 (36%)	1 (4%)	1 (8%)
Both	Total	24 (100%)	23 (100%)	11 (100%)	25 (100%)	12 (100%)
Discarded duplicates	Total	1	4	2	16	3
Final dataset	Total	19	12	5	8	8

After these exclusions, the sample set still included some duplicate specimens of the same shape cut from the same meniscus. (These duplicates were originally prepared with the aim of doing paired tests, but fair paired comparisons were not possible due to the variety of rupture outcomes.) To avoid considering within-meniscus covariance in the analysis, these duplicates were excluded first by dropping grip line ruptures, then at random, until each remaining specimen in each shape category came from a unique meniscus (Table 2). The final specimen counts used in each group for analysis, after all exclusion criteria were applied, are given in the last row of Table 2. The circumferential DB specimen count is low because, as the experiment proceeded, many issues with this shape became apparent (see Sec. 4.8). We consequently phased out the use of DB specimens.

2.3. Data Analysis.

Strain was measured using grip-to-grip displacement (grip strain) and reported in the form of the stretch ratio ($\lambda =l/l_0$, where $l$ is the current length and $l_0$ is the undeformed length) or Lagrange strain ($E_{\mathit{x}\mathit{x}}=1/2[{\lambda }^2-1]$). Stress was calculated using the initial cross-sectional area of the narrowest region of the specimen. The stress–strain curve was quantified by fitting it to a fiber recruitment model developed to represent the toe region (see Sec. 2.4) and by measuring yield strain, yield stress, tangent modulus at yield, strain at peak stress (peak strain), and peak stress (Fig. 4, top half). The yield point was defined as the first inflection point in the stress strain curve [38], which was identified by fitting a cubic smoothing spline (using the SMOOTH.SPLINE function in R 3.2 [39] with spar = 1.0) to the prepeak stress–strain curve and taking its first derivative to obtain a smooth tangent modulus curve (Fig. 4, bottom half). This procedure equates yield with a proportional limit.

Fig. 4.

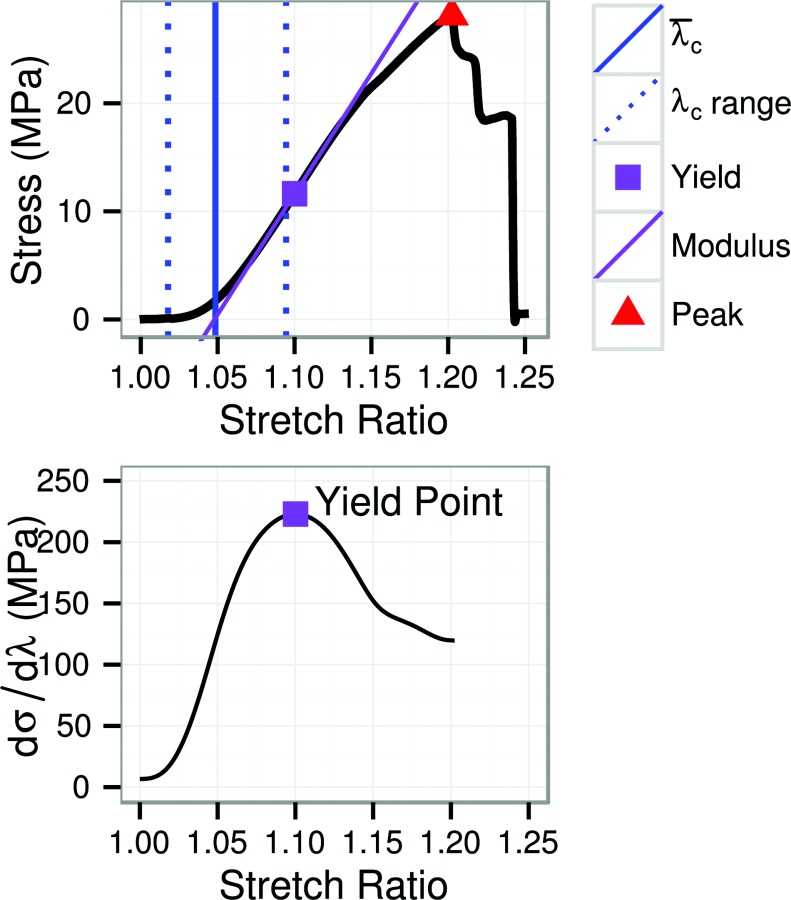
A representative stress–strain curve for circumferential ET specimens with the fiber recruitment range (the 0.025 and 0.975 quantiles of ${\lambda }_c$), mean fiber recruitment stretch (${\overline{\lambda }}_c$), yield point, and peak point marked. The lower plot shows the pointwise tangent modulus curve (the first derivative of the stress–strain curve), the first local maximum of which was identified as the yield point. Both plots share the same x-axis.

Strain fields were measured from video records of each test by digital image correlation using Vic-2D 2009 (Correlated Solutions). An image taken between the preconditioning and ramp to failure steps was used as the zero-strain reference point. The correlation window was 0.7 mm × 0.7 mm. All strain fields were plotted in the reference space.

2.4. Fiber Recruitment Model.

The nonlinear stress–strain response of circumferentially loaded specimens was quantified using a fiber recruitment model [11,40,41]. The model represents the tissue as an assembly of linear stiffness fibers aligned with the loading axis. Since radial specimens have fibers primarily perpendicular to the loading direction, the model was not applied to these tests. Sequential recruitment of fibers is represented by making the stretch at which each fiber starts to bear load, λ_c, a randomly distributed variable. Here, λ_c is called the fiber recruitment stretch. In other work, it is usually called the uncrimping stretch, but in this work we interpret λ_c as representing fiber reorientation into the loading direction as well as fiber uncrimping. Although the fibers are linear, the randomly distributed recruitment causes a nonlinear response.

Fibers are assumed to have linear stiffness k_f and bear no load in compression, such that the stress in the fibers is

$${\sigma }_f=\{\begin{array}{ccc}{k}_f{\mathrm{\epsilon }}_f& \hspace{1em}& {\mathrm{\epsilon }}_f\ge 0\\ 0& \hspace{1em}& {\mathrm{\epsilon }}_f<0\end{array}$$ (1)

where ${\mathrm{\epsilon }}_f$ is the fiber strain. The fiber stiffness k_f is assumed to be the same across all fibers. The fiber strain is related to the fiber recruitment stretch λ_c and the tissue stretch $\lambda$ by

$${\mathrm{\epsilon }}_f=\frac{1}{2}\left(\frac{{\lambda }^2}{{\lambda }_c^2}-1\right)$$ (2)

The variation in fiber recruitment stretch (i.e., fiber initial state) is given by the probability density function

$$G\left({\lambda }_c\right)={({\lambda }_c-1)}^{\alpha -1}\frac{e^{-({\lambda }_c-1)/\beta }}{{\beta }^{\alpha }\Gamma (\alpha )}$$ (3)

which is a gamma distribution with shape parameter $\alpha$, location parameter = 1, and scale parameter $\beta$ ($\Gamma$ is the gamma function). The mean recruitment stretch (${\overline{\lambda }}_c$) and the square root of the variance of the recruitment stretch (${\lambda }_c^{\text{SD}}$) were calculated to make the physical meaning of the model clearer. They are related to the distribution parameters by

$${\overline{\lambda }}_c=\alpha \beta +1$$ (4)

and

$${\lambda }_c^{\text{SD}}=\sqrt{\alpha {\beta }^2}$$ (5)

The overall tissue stress $\sigma$ is given by integration over the fiber population

$$\sigma =\frac{k_f}{2}{\int }_1^{\lambda }G\left({\lambda }_c\right)\left(\frac{{\lambda }^2}{{\lambda }_c^2}-1\right)d{\lambda }_c$$ (6)

This fiber recruitment model was fit to the preyield stress–strain curve (the model is purely elastic) using the Levenberg–Marquardt algorithm implemented in SciPy [42]. The variables ${\overline{\lambda }}_c$, ${\lambda }_c^{\text{SD}}$, and k_f were used to report the model fit and compare specimen shapes.

2.5. Statistics and Inference.

Comparisons between the specimen shapes were done separately for circumferential and radial tests using the fiber recruitment model variables (for circumferential specimens only) and the five stress–strain curve summary statistics (for both radial and circumferential specimens). Circumferential tests of ET, R, and DB specimens were compared by ANOVA, followed by Tukey's honest significant difference test (HSD) post-hoc tests if indicated. Fiber recruitment model parameters were compared between ET and R specimens using Mann–Whitney–Wilcoxon tests. Radial tests of R and DB specimens were compared by two-sided Welch t-tests. The significance threshold was set at p = 0.05 for all the comparisons. Boxplots show median (bar), first/third quartile (box), and min/max (whiskers) values. Unless otherwise noted, summary statistics are mean ± SD.

3. Results

3.1. Stress–Strain Curves, Yield, and Rupture.

Stress–strain curves are plotted by failure type and specimen shape in Fig. 5. The stress–strain curves display the nonlinear response typical of fibrous soft tissues. Subjective visual interpretation would place the yield point at about 3/4 of the peak stress, which is the point at which the loss of stiffness has caused visual deflection of the curve. However, the objectively measured yield point (the inflection point of the stress–strain curve) is placed at about 1/3 of the peak stress, within the subjectively linear region. This placement is precisely at the point of transition from strain-stiffening to strain-softening (e.g., Fig. 4). This definition of yield has structural significance in that the tangent modulus at yield was nearly identical to the fiber modulus k_f from the fiber recruitment model (Fig. 6). Yield therefore represents the point at which the model predicts complete fiber recruitment.

Fig. 5.

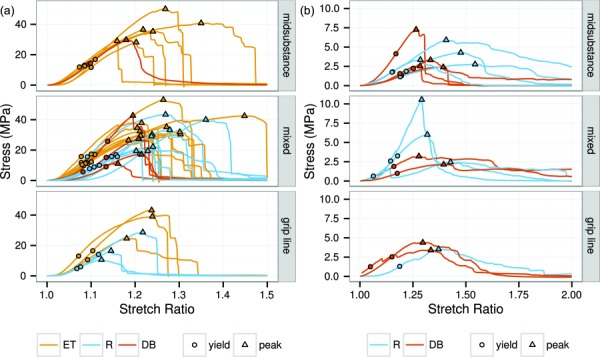
Stress–strain curves for the circumferential and radial specimens by rupture type and specimen shape. The yield and peak stress points are marked. (a) Circumferential and (b) radial.

Fig. 6.

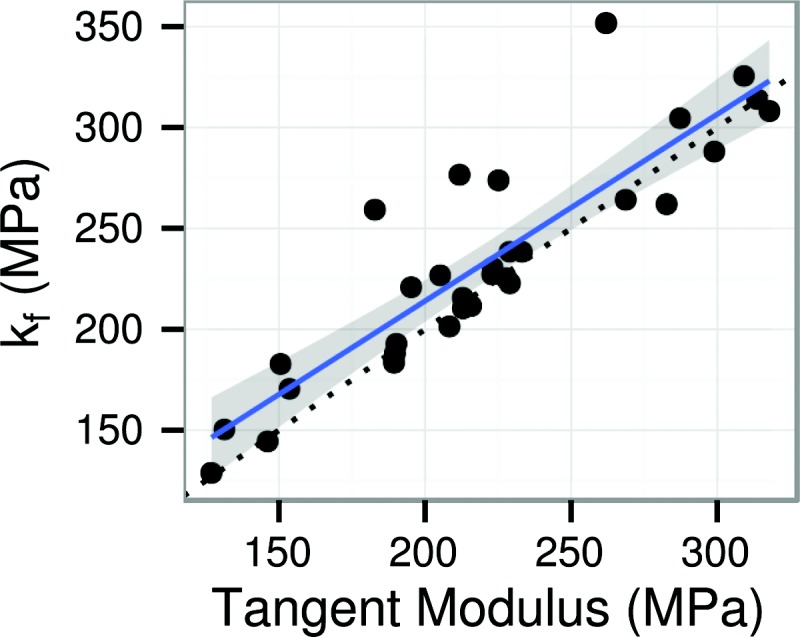
Fiber modulus (k_f) was strongly correlated with tangent modulus at yield (r [95% CI] = 0.77–0.94 by Pearson correlation). The solid line and shaded region are the best-fit line and its 95% confidence interval. The dotted black line illustrates a 1:1 relationship (slope = 1 and intercept = 0).

Most circumferentially loaded specimens ruptured with an abrupt, near-total release of stress, which was preceded by strain-softening (Fig. 5(a)). Qualitatively, there were no differences in the stress–strain curves between midsubstance, mixed, and grip line ruptures. In terms of rupture morphology, circumferentially loaded ET specimens failed mostly by mixed and midsubstance rupture (2/3 of all tests run), with the remainder split between grip line ruptures and gripped region ruptures (Table 2). In contrast, no circumferentially loaded R specimens failed by midsubstance rupture. About half failed by mixed rupture, 20% by grip line rupture, and 30% by gripped region failure or longitudinal splitting. DB specimens showed a distribution of rupture types similar to the R specimens. Note that these ratios of rupture type by specimen shape are calculated from the total number of tests (i.e., with no exclusions). The mechanical analyses use the subset of specimens with valid ruptures and cut from different menisci (Sec. 2.2).

Radially loaded specimens, in contrast to circumferentially loaded specimens, ruptured with a gradual postpeak decrease in stress (Fig. 5(b)). Radial specimens, as expected from their fiber orientation, were much less stiff and strong than the circumferential specimens (compare Fig. 5(a) and Fig. 5(b)). Similar to the circumferential specimens, the stress–strain curves of radial specimens did not differ by rupture type. Midsubstance, mixed, and grip line ruptures were all common.

3.2. Effect of Specimen Shape on Mechanical Properties.

The fiber recruitment model produced excellent fits for all of the ET specimens (RMS error = 0.03 ± 0.02 MPa). Fits of ET specimen data were also physically plausible, with fiber recruitment starting in the toe region and ending before the yield point (Fig. 4). The rectangle specimens also had good model fits in a purely numeric sense (RMS error = 0.05 ± 0.02 MPa), but five (out of 12) had fiber recruitment ranges extending below zero strain and above the yield point. The DB specimens all exhibited similarly wide fiber recruitment ranges or, in two (out of five) cases, did not even have a unique solution. Due to the low fit quality for DB specimens, they were dropped from the model-based analysis. Both the mean recruitment stretch (${\overline{\lambda }}_c$) and the square root of the variance of the recruitment stretch (${\lambda }_c^{\text{SD}}$) were significantly less in ET specimens than in R specimens (Fig. 7). The model's fiber modulus (k_f) was not significantly different between the two shapes. The more rapid fiber recruitment and superior model fits evidenced by the ET specimens support our hypothesis that the ET shape is more effective at ensuring fiber loading.

The yield and peak points from the circumferential tests were also significantly affected by the specimen shape. ET specimens had 0.04 lesser yield stretch, 50 MPa greater tangent modulus, and 9 MPa greater peak stress than R specimens, as well as narrower distributions for the yield stretch and yield stress (Fig. 7). Yield points for ET specimens consequently form a tight cluster on the stress–strain plots, visibly separate from the yield points for the other shapes (Fig. 5(a)). The peak points were broadly distributed for all the specimen shapes. The stress–strain curve metrics for the circumferential DB specimens were not significantly different from the ET or R specimens, but were qualitatively similar to the R specimens and dissimilar to the ET specimens. Radially loaded specimens had no significant differences in yield or peak points between specimen shapes (Fig. 8). Nor did the radial stress–strain curves display any qualitative differences between specimen shapes (Fig. 5(b)). Differences between specimen shapes are summarized in Table 3.

Fig. 8.

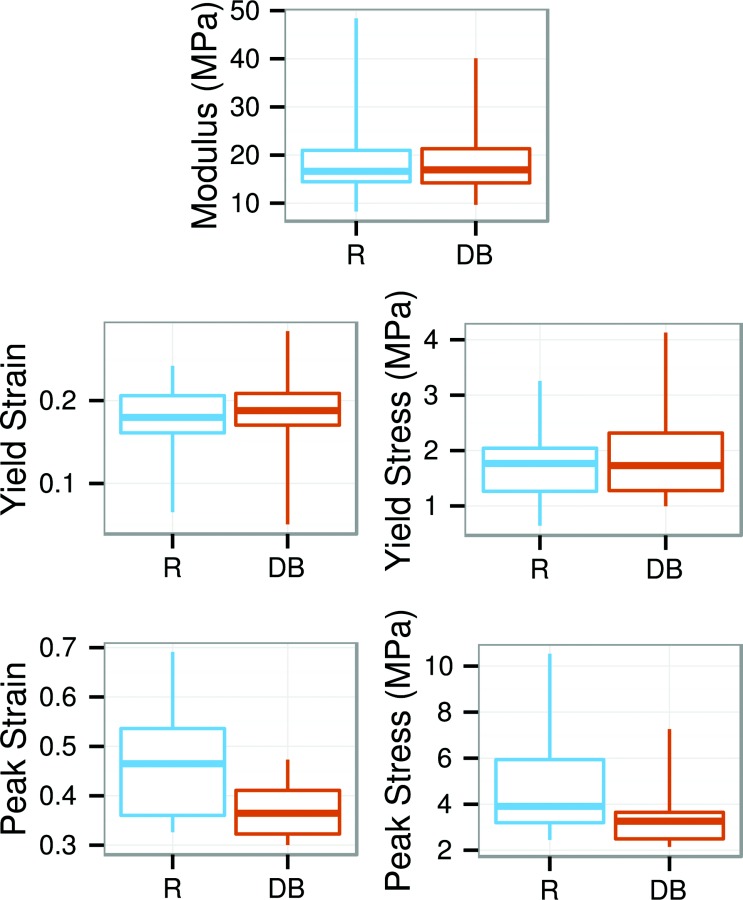
Stress–strain results for radially stretched R and DB specimens. There were no significant differences between specimen shapes.

3.3. Strain Fields.

Circumferential tests resulted in inhomogeneous strain fields for each strain component. Longitudinal strain (E_xx) fields, shown at the yield point in Fig. 9, had spotlike regions (about 0.5 mm in diameter) of greater than average strain. In many cases (but not a majority), longitudinal strain was unevenly distributed over the scale of the whole specimen, e.g., one end of the specimen might have greater strain than the other (Fig. 9(a)).

Fig. 9.

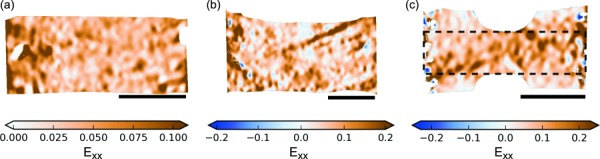
Representative longitudinal strain (E_xx) fields at yield for the circumferentially loaded specimens. In (c), the dashed outline over the DB's strain field indicates the loaded region, which has potential grip-to-grip fiber continuity. The flared margins outside this outline are the shielded region, which has no grip-to-grip continuous fibers and exhibits less longitudinal strain than the loaded region. Color scales are truncated at the 0.05 and 0.95 quantiles. The scale bars are 5 mm long. (a) ET, (b) R, and (c) DB.

Shear strain (E_xy) fields for circumferentially loaded specimens were also inhomogeneous, with longitudinal bands (about 0.5 mm wide) of alternating positive and negative shear strain that resembled the pattern of fascicles on the specimen surface (Figs. 10(a) and 10(c)). These shear bands sometimes extended from one grip to the other, but usually ended partway across the specimen.

Fig. 10.

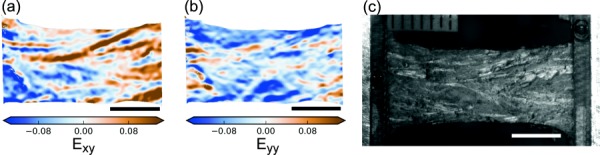
Representative (a) shear strain (E_xy) and (b) transverse strain (E_yy) field at yield for the circumferential specimens with (c) the corresponding camera image of the specimen. An ET specimen is shown. The bands in the E_xy field qualitatively match the fascicle boundaries visible in the camera image. The color scales are truncated at the 0.05 and 0.95 quantiles. The scale bars are 5 mm long.

Transverse strain (E_yy) fields from the circumferentially loaded specimens had pockets of concentrated strain similar to the E_xx strain concentrations, but more elongated (Fig. 10(b)). These pockets were sometimes so elongated that they resembled the bands in the E_xy field. The transverse strain fields always included regions of tensile strain; these tensile strain concentrations were usually of similar magnitude to the compressive strain and could cover up to half the specimen area.

Qualitatively, there were no differences between ET and R strain fields under circumferential loading, but the margins of the DB specimens' flared ends had lesser longitudinal strain compared to the central region (Fig. 9). This lack of stress and strain redistribution was confirmed by specifically labeling the part of the specimen with potential grip-to-grip fiber continuity (dotted outline in Fig. 9(c)) and comparing strain in this region (the “loaded region”) to that in the margins of the flared ends (the “shielded regions”). In all cases, median strain in the shielded regions was less than in the loaded region, with divergence occurring early in the test ( < 5% grip strain). A representative case is shown in Fig. 11. At the point of peak stress, longitudinal strain in the shielded region was about half of that in the loaded region. The E_xy and E_yy fields did not show a strain shielding effect; rather, the boundary between the shielded and loaded regions tended to develop large E_xy and E_yy strains.

Fig. 11.

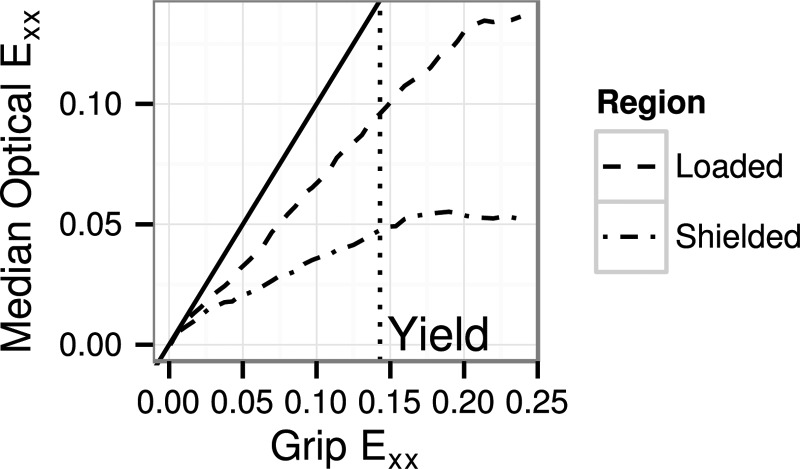
Representative plot of the longitudinal strain (E_xx) in a DB specimen measured optically (y-axis) and by grip displacement (x-axis). The median optical strain in the central region (the loaded region), which has grip-to-grip fiber continuity, is much greater than in the flared ends of the specimen (the shielded region), which contain severed fibers. See Fig. 9(c) for a diagram of these regions. The line of 1:1 correspondence between optical and grip strain is marked by a solid black line. Optical strain is approximately linearly correlated with grip strain up to and a little past the yield point.

Radially loaded specimens, whether R or DB, had smoother E_xx fields than the circumferentially loaded specimens, but often had large, irregularly shaped strain concentrations (Fig. 12). The E_xy fields were organized into large regions of somewhat homogeneous positive and negative shear. They did not exhibit the banding evident in the circumferentially loaded specimens. The E_yy fields were almost entirely compressive, with small strain concentrations like those seen in the E_xx fields of the circumferentially stretched specimens. The radially loaded DB specimens did not exhibit the strain shielding effect that was present in the circumferentially loaded DB specimens (compare Fig. 9(c) and Fig. 12(a)).

Fig. 12.

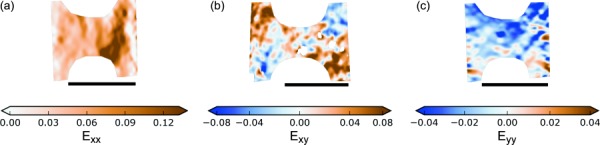
Representative longitudinal (E_xx), shear (E_xy), and transverse (E_yy) strain fields for radially stretched DB specimens at yield. The strain fields for radially stretched R specimens are similar. The scale bars are 5 mm long.

4. Discussion

4.1. Overview.

This study met its objective of providing a more complete quantification of the meniscus' uniaxial tensile mechanics than was previously available. The preyield stress–strain response was quantified using a fiber recruitment model, which performed very well, justifying attribution of the meniscus' nonlinearity in circumferential tension to sequential fiber recruitment. The yield point was measured for the first time, and the modulus was quantified using a new procedure that is objective and reproducible. Circumferential specimens showed striking bands of shear strain and transverse tension that appeared to follow fascicle boundaries, supporting the notion that rupture occurs along these boundaries. These strain field inhomogeneities traverse the midsubstance and near-grip regions, indicating that the complex loads on the gripped ends of the specimen do not redistribute into homogeneous midsubstance loading. Nor does a narrow central region ensure midsubstance rupture, as evidenced by the ubiquitous involvement of the near-grip region in ruptures of DB and ET specimens. Our hypothesis that ET specimens would more effectively grip and load fibers than specimens with narrower tabs was confirmed. ET specimens showed enhanced stiffness and strength in circumferential stretch as well as earlier and more rapid fiber recruitment. They are therefore recommended for circumferential tension tests of meniscus.

4.2. Fiber Recruitment Model and Stress–Strain Nonlinearity.

A fiber recruitment model was used to parameterize the meniscus' nonlinear stress–strain curve for fiber-aligned (circumferential) tension up to the yield point. The nonlinearity of the stress–strain curve is represented by sequential recruitment of linear fibers. A fiber is recruited when it starts to bear load due to uncrimping, rotation into the loading direction, or some other reason. The model showed excellent fits for ET and R specimens, with residuals 2 orders of magnitude less than the fitted data. DB specimens could not be fit; this and other issues associated with DB specimens are discussed in Sec. 4.8. The good fits for ET and R specimens indicate that the meniscus' circumferential tensile response is consistent with an assembly of linear fibers.

The fiber recruitment model was also consistent with key functional aspects of the meniscus' stress–strain curve. In the circumferential ET specimens, which most effectively load the meniscus fibers, the yield point consistently coincided with the point at which almost all the fibers were recruited. The tangent modulus at yield was, on average, the same as the fiber modulus k_f (Fig. 6), further supporting the interpretation that yield occurs at the point of maximum fiber recruitment. The data also show that both the preyield stress–strain curve and its derivative are nonlinear (Fig. 4); the model reflects both nonlinearities. The fiber recruitment model thus has a strong structural interpretation that is consistent with nonmodel metrics for the stress–strain curve, and it is a good option for modeling the uniaxial tensile mechanics of meniscus.

4.3. Yield Point.

The yield point was defined in this study as the first inflection point of the stress–strain curve. There is no standard or rigorous definition of yield for fibrous soft tissues. Colloquially, it refers to the onset of decreasing stiffness with increasing strain (i.e., a proportional limit) or the onset of plastic strain. Quantitatively, yield has been defined as the point of first divergence from the linear region [43–45], the point at which the slope subjectively decreases [46,47], or the intersection of a line parallel to the linear region but offset by a certain strain or displacement [48–50]. Defining the yield point relative to the linear region poses the problem of how to identify the linear region of a curve which is nonlinear from beginning to end. Defining the yield point instead as the first inflection point of the stress–strain curve is objective, reproducible, and consistent with the commonly held meaning of yield. The use of a smoothing spline interpolant makes the method robust to noise and variations in sampling rate. Calculation of derivatives by finite differences is also an option, but is less robust to these effects. The yield point obtained by the inflection point method occurs at lesser strain and stress than would probably be determined by eye (for example, a subjectively estimated yield point in Fig. 4 would probably be 3/4 up the curve). The definition used here marks a clear transition from strain-stiffening to strain-softening (Fig. 4).

The mechanisms that cause loss of stiffness (strain-softening) subsequent to yield are not yet clear. The yield point may indicate the onset of damage, perhaps by the onset of interfibrillar sliding [52]. Onset of structural damage occurs in ligament at about 5% strain [51]. Tendon fascicles also show elongation without increase in stress at about this strain threshold [52]. These thresholds are somewhat lower than the yield strain observed here for meniscus, but tendon fibers are quite well aligned with the tensile axis from the start of the test. Meniscus fibers have more orientational dispersion and may require more tissue strain before they are recruited and stretched to this putative damage threshold. More study is necessary to test the hypothesis that the yield point represents the onset of damage.

4.4. Radial Specimens and Tie Fibers.

A few radial specimens had much greater peak stress and a more abrupt reduction in stress postpeak than the others (Fig. 5). These sharp stress peaks may indicate the presence of radial tie fibers. The meniscus contains radially oriented tie fibers that increase its radial tensile strength and stiffness [20,53]. Since these fibers are randomly distributed with millimeter-scale separation and are not necessarily parallel to the specimen plane, only a few specimens in this study would be expected to contain tie fibers. This is consistent with the low number of radial tests with sharply peaked stress–strain curves. The peak stress values from these sharply peaked curves are in the range previously observed in tests of radial meniscus specimens containing radial tie fibers [20].

4.5. Comparison With Prior Work.

Mechanical properties of meniscus from the literature are given in Table 4 for circumferential specimens and Table 5 for radial specimens. For the sake of comparison, we listed only properties from the center part of the meniscus (the location we tested). Few studies report a complete set of mechanical properties; only modulus is consistently reported. There is great variation in the reported values. Since there is great diversity between studies regarding species, medial/lateral side, specimen thickness, method for quantifying modulus, method for measuring strain, and specimen shape, a large degree of variation is to be expected. Mechanical properties may vary with the side of the knee (medial/lateral) and anterior/posterior position, although reports conflict between studies [10,13,16,18]. Of these studies, Tissakht and Ahmed [10] had the greatest statistical power and found no statistical anterior/posterior or medial/lateral effect for circumferential specimens. We verified (by two-way ANOVA with specimen shape and medial/lateral side as factors) that there was no confounding medial/lateral effect in our present work. Modulus has been reported to be greater for thinner specimens, but the authors attributed this to specimen selection effects [15]. Bursac et al. [16] used twice the thickness of Tissakht and Ahmed [10], but obtained similar modulus values for human meniscus. We verified (by linear regression) that the limited range of thickness variation in our present work did not impact our measurements.

Table 4.

Comparison of the current and prior circumferential uniaxial tensile tests. Values are listed for the center region (anterior–posterior axis) unless otherwise indicated.

Reference	Species	Side	Shape	Modulus (MPa)	Peak strain (%)a	Peak stress (MPa)	Environment	Strain measurement
Present study	Cow	Both	ET	241 ± 43	25 ± 7	36 ± 8	Mixed	Grip displacement
Present study	Cow	Both	R	190 ± 49	23 ± 6	27 ± 10	Air	Grip displacement
Present study	Cow	Both	DB	215 ± 86	19 ± 2	26 ± 12	Air	Grip displacement
Proctor et al. [18]b	Cow	Medial	DB	140 ± 80	NA	NA	Bath	Gauge lines
Anderson et al. [22]b	Sheep	Medial	DB	239 ± 97	12 ± 3	24 ± 3	Bath	Gauge lines
Tanaka et al. [17]c	Sheep	Medial	ET	187 ± 32	36 ± 2	36 ± 5	Mist	Grip displacement
Stabile et al. [7]	Sheep	Medial	Unknown	67 ± 30	NA	NA	Air	Gauge markers
Tanaka et al. [17]	Pig	Medial	ET	209 ± 35	30 ± 5	38 ± 8	Mist	Grip displacement
LeRoux and Setton [32]	Dog	Medial	R	68 ± 28	NA	NA	Bath	Optical
Sweigart and Athanasiou [12]	Rabbit	Medial	R	157 ± 49	NA	22 ± 7	Mist	Grip displacement
Fithian et al. [56]d	Human	Both	DB	161 ± 37	NA	NA	Unknown	Gauge lines
Tissakht and Ahmed [10]d	Human	Both	R	63 ± 11	27 ± 7	12 ± 2	Humid chamber	Grip displacement
Lechner et al. [15]	Human	Medial	DB	84 ± 24	NA	NA	Bath	Gauge lines
Tanaka et al. [17]	Human	Medial	ET	98 ± 22	22 ± 4	12 ± 2	Mist	Grip displacement
Bursac et al. [16]d	Human	Both	R	73 ± 15	NA	NA	Bath	Grip displacement

^aCauchy (engineering) strain.

^bAverage of reported anterior and posterior values.

^cSkelatally immature animals.

^dAverage of reported medial and lateral values.

Table 5.

Comparison of the current and prior radial uniaxial tensile tests. Values are listed for the center region (anterior–posterior axis) unless otherwise indicated.

Reference	Species	Side	Shape	Modulus (MPa)	Peak strain (%)a	Peak stress (MPa)	Environment	Strain measurement
Present study	Cow	Both	R	21 ± 14	39 ± 9	5 ± 3	Air	Grip displacement
Present study	Cow	Both	DB	17 ± 11	32 ± 5	4 ± 2	Air	Grip displacement
Proctor et al. [18]b	Cow	Medial	DB	5 ± 2	NA	NA	Bath	Gauge lines
Skaggs et al. [20]	Cow	Medial	DB	35 ± 20	17 ± 6	3 ± 2	Bath	Gauge lines
LeRoux and Setton [32]	Dog	Lateral	R	11 ± 4	NA	NA	Bath	Optical
Tissakht and Ahmed [10]c	Human	Both	R	6 ± 2	44 ± 25	2 ± 1	Humid chamber	Grip displacement

^aCauchy (engineering) strain.

^bAverage of anterior and posterior values.

^cAverage of reported medial and lateral values.

Some of the variation in modulus is caused by variation in modulus definitions. For example, our modulus definition produces values 16 ± 16 MPa greater than Lechner et al. [15] for circumferential tests and 2 ± 4 MPa greater for radial tests. Note that the distributions of these differences are skewed positive because some stress–strain curves are not even quasi-linear in the chosen stress range of Lechner et al. One of the advantages of measuring the tangent modulus at yield is that it handles highly nonlinear curves well.

Peak stress from the circumferentially tested specimens from large quadrupeds was greater for sheep ET specimens [17] than sheep DB specimens [22] (Table 4). This is consistent with the specimen shape effects observed in our present work. Peak strain values have large ranges of variation, but are generally consistent within both circumferential (Table 4) and radial studies (Table 5), with a few outliers. The lesser peak strain reported by Anderson et al. [22] for circumferential tests and by Skaggs et al. [20] for radial tests may be due to calculation of strain using gauge lines rather than grip-to-grip displacement. Variation in peak strain may also be caused by the difficulty of standardizing the zero-strain point, as strain is sensitive to the choice of preload. Strain can also be applied inadvertently during specimen mounting. Stress values are more consistent.

Human specimens show lesser modulus and peak stress than nonhuman animals in circumferential testing, regardless of the specimen shape (Table 4). Age-related deterioration in the human meniscus specimens could reasonably be suspected as an explanation for this effect, but Tissakht and Ahmed [10] used specimens aged 29–45 years and reported near-identical values to Tanaka et al. [17], who used specimens aged 67–84 years. Despite this, the lesser modulus and peak stress in human specimens could still be caused by age-related deterioration if it occurs prior to the fourth decade of life. This would not be unprecedented; aspects of intervertebral disk degeneration are well underway by the fourth decade [54,55]. Alternatively, humans may simply possess less stiff meniscus tissue.

4.6. Rupture Location.

A midsubstance rupture is considered desirable because it implies that the test result is unaffected by local grip-associated stresses. In this study, most specimens did not fail by midsubstance rupture (Table 2), but the stress–strain curves of midsubstance ruptures were not clearly different from the mixed or grip line ruptures (Fig. 5). Even the gripped region failures and longitudinal splits, which were excluded from formal analysis, did not have qualitatively different stress–strain curves, despite the ruptures extending inside the gripped region. Previously, comparison between at-grip and midsubstance ruptures in tendon has also shown no difference [57]. It is not clear why at-grip and midsubstance ruptures do not appear mechanically different. In the present study, grip-associated strain inhomogeneities do extend to the midsubstance (discussed further in Sec. 4.7), so all ruptures may have been affected by the grips to some degree.

4.7. Strain Field Inhomogeneity, Grip Effects, and Damage.

The observed strain fields were extremely heterogeneous. Circumferential specimens developed intense shear bands that followed a pattern similar to the fascicles (Fig. 10). We interpret these shear strain bands as caused by sliding between adjacent fascicles. Meniscus failure in uniaxial tension tends to occur by shear along a fascicle boundary [13], consistent with the interdigitating fiber pull-out observed here (Fig. 3(a)). Circumferential–radial shear has also been hypothesized to be important in the development of vertical meniscus tears [13,58]. Future work is required to definitively relate patterns of strain field inhomogeneity to meniscus structure and damage mechanisms.

Some of these strain field inhomogeneities—in particular, bands of longitudinal strain (Fig. 9(b)) and, more commonly, shear strain and transverse strain (Fig. 10)—spanned the near-grip and midsubstance regions in tests of the circumferential specimens. This is direct evidence that complex local stresses in the gripped region probably do not dissipate into an even stress field in the midsubstance, i.e., Saint–Venant's principle does not apply. In anisotropic, inhomogeneous materials, such as the meniscus, the spatial extent of local stress effects, such as grip effects, is much greater than for isotropic, homogeneous materials [33,34,59,60]. Due to the limited size of the meniscus, it is probably not possible to cut a specimen long enough for the midsubstance to be free of grip effects. Local stress effects almost certainly apply in situ as well. The capability to treat the meniscus as a highly anisotropic, inhomogeneous material with complicated boundary conditions will be important to make useful predictions for in vivo mechanics.

One specific effect produced by the grips was to prevent transverse deformation at either end of the specimen. The ends of the specimen thus cannot contract along with the midsubstance; this creates local stresses at the grip line [24,25]. Consequently, many circumferential specimens exhibited small ruptures, separate from the main rupture site, at one of the corners formed by the specimen and the grip face. For example, the patches of tensile strain visible in the transverse strain fields (Figs. 10(b) and 12(c)) are probably caused by the grips preventing transverse contraction. Transverse tension produced by this effect could damage interfascicle interfaces required for longitudinal load transfer.

4.8. Choice of Specimen Shape.

We hypothesized that ET specimens would be more effective at gripping and loading fibers than specimens with narrower tabs. This hypothesis was confirmed. In circumferential tension, ET specimens showed fiber recruitment at lesser stretch (${\overline{\lambda }}_c$) and over a smaller stretch interval (${\lambda }_c^{\text{SD}}$), lesser yield stretch, greater tangent modulus at yield, and greater peak stress than R specimens (Fig. 7). Lesser ${\overline{\lambda }}_c$ and ${\lambda }_c^{\text{SD}}$ indicate that the ET specimens recruited fibers more rapidly. Since yield occurs at about the point of maximum fiber recruitment, more rapid fiber recruitment explains the lesser yield stretch. The combination of greater modulus and peak stress in the ET specimens, but similar peak strain, indicates that ET specimens recruited a greater number of fibers per unit area, thus increasing the apparent modulus, but that individual fibers ruptured at about the same tissue strain regardless of specimen shape. Strain has been previously hypothesized to be the key failure metric for fibrous soft tissue [61], with peak stress determined by the combination of modulus and peak strain [34,62]. The ET specimens are capable of recruiting more fibers because the ETs allow curved fibers on the inner side of the specimen to extend deep into the grips and thus be securely gripped; the other specimen shapes sever these fibers or grip them insecurely. Since the fiber recruitment model fits both the ET and R specimens well, fiber recruitment can be considered the dominant mechanical mechanism for both shapes.

It is likely that the same differences in modulus, yield strain, and peak stress between ET and R specimens also exist between ET and DB specimens and were just not detected due to the sample's statistical power. For circumferential specimens, this study was powered to detect differences of 1.1 standard deviation (SD) for the ET–R comparison ($\beta$  = 0.8), and this was about the magnitude of the detected differences. The ET–DB comparison was powered to detect differences of only 1.5 SD, and the R–DB comparison was powered to detect differences of 1.6 SD. However, the close similarity between the distributions of variables for R and DB specimens (Fig. 7) suggests that any undetected difference is small. This is true for the radial tests as well (Fig. 8). The radial R–DB comparison was powered to detect differences of 1.5 SD. It is reasonable to conclude that the R and DB specimens have similar yield point, modulus, and peak point, and the ET specimens differ from both by the same amount.

The purpose of the DB shape is to increase stress in the narrow part and thus ensure failure at that location; it did not achieve this (Table 2). DBs are known to be ineffective at ensuring midsubstance failure in tests of synthetic fiber-reinforced composites; rectangles are preferred [63–65]. The inability of the DB shape to ensure midsubstance failure in the circumferential tests was probably in part because the grip line was unevenly loaded, with strain-shielded regions (Fig. 9(c)). Skaggs et al. hypothesized the existence of this strain-shielding effect as the cause of at-grip failures in DB-shaped specimens of annulus fibrosus [34]. The location of failure may also be controlled by inhomogeneous tissue strength, which could be exacerbated by severing of internal structures while cutting the specimen. Still, the juxtaposition of strain-shielded and loaded regions creates severe shear and transverse strain. The addition of these deformations is probably why the fiber recruitment model could not fit the DB specimen stress–strain response. Although no other specimen shape ensured midsubstance failure either, the strain-shielded regions in the DB specimens are disadvantageous.

The DB specimen shape has an additional disadvantage regarding the calculation of cross-sectional area: the width of a DB specimen varies. Since ruptures may occur anywhere along the specimen length (Fig. 3), it is not obvious which cross-sectional area to use for stress calculations. We used the central minimum width, which in circumferential specimens is the width of the loaded region (Fig. 9) and so is reasonably accurate for this case. However, using the minimum width for the radially stretched DB specimens may have caused some overestimation of stress. The other specimen shapes have equal cross-sectional area throughout the intergrip length and so do not pose this ambiguity.

Changing the DB specimen shape and the way it is mounted can mitigate its disadvantages. A DB specimen with a long, parallel-sided gauge region may function similarly to a rectangle if the flared ends are wholly within the grips, as in Ref. [23]. The parallel sides eliminate cross-sectional area variation, and placing the flared ends inside the grips prevents them from causing strain-shielded regions.

In general, circumferential testing of meniscus is best done using ET specimens due to their enhanced fiber recruitment and increased apparent strength. The principle value of the ET specimen shape lies in accommodating the meniscus' fiber curvature. Unlike a DB specimen, its wide tabs are almost entirely inside the grips, and the gauge region consequently is similar to that of a rectangle specimen (Fig. 1). In materials without curved fibers, rectangles would probably produce identical results. The ET specimen shape does consume more tissue area than a plain rectangle, making it difficult to cut multiple specimens from the same meniscus or test small subregions. However, it readily accommodates different inner/outer and distal/proximal locations. Anterior/posterior variation is more limited; only the mid-anterior, center, and mid-posterior regions are amenable. For testing of the extreme anterior or posterior locations, we suggest gripping the bony insertion as in Ref. [31] and using an ET on the opposite end. In radial testing of meniscus, fiber curvature is not relevant, so rectangles are the best choice.

4.9. Choice of Strain Measurement.

Grip strain was used for the stress–strain curves rather than optical strain. There are several prior examples of this [9,11]. Although optical strain is in principle preferable to grip strain because it measures actual tissue deformation, the extreme heterogeneity of the strain fields (Figs. 9, 10, and 12) makes it difficult to convert the strain fields to a single summary strain value. The range of optical strain values broadens greatly as the test progresses (Fig. 13). Local overstrain and shear discontinuities in particular are major difficulties; Should the entire strain field be used or just the part that coincides with the site of rupture? If the site of rupture is used, its extent is not obvious. Overstrain can also change the appearance of the specimen surface sufficiently to cause the digital image correlation to fail. In this study, since we discarded all tests with observed grip slip, the grip strain is a fair summary of the overall tissue strain (Fig. 13) and has the advantages of clarity and reproducibility. However, the optical strain fields are a rich source of information and methods should be developed to unlock their potential.

Fig. 13.

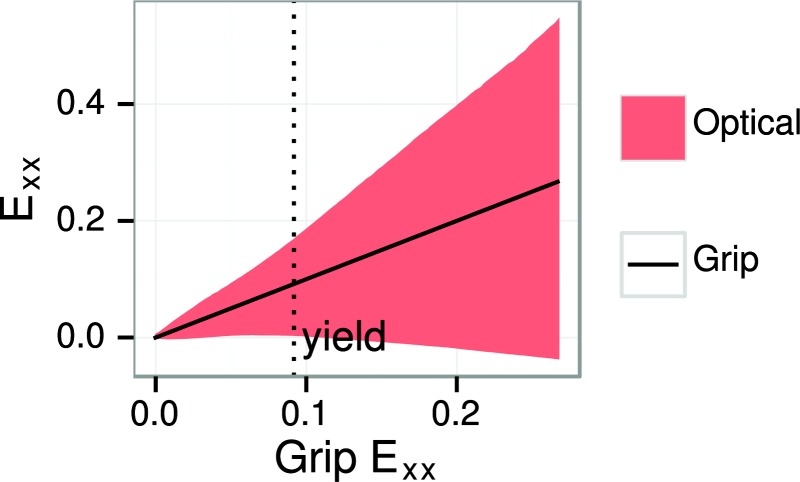
Optical longitudinal strain 0.05/0.95 interquartile range (shaded region) compared with grip strain (solid black line). The optical strain range broadens in proportion to the applied grip strain. This is a representative example; in other cases, the optical strain range may broaden nonlinearly. The plot shows data up to the peak point.

5. Conclusion

This study represented the preyield uniaxial tensile response of the meniscus with a fiber recruitment model, providing a quantitative link between the meniscus' fiber structure and its nonlinear stress–strain response. The elastic modulus was quantified using a new procedure that consistently measures the same functional region of the stress–strain curve and is simple enough to be used as a routine method for measuring elastic modulus in soft tissue testing. This method is more robust to variation in mechanical behavior than a linear fit of a chosen stress or strain range. Through this procedure, we quantified the meniscus' (previously unreported) yield point. We also quantified peak stress and strain. Together, these metrics are useful as functional targets for meniscus replacements or repair procedures, to compare disease states, or as diagnostic markers. Strain fields revealed significant heterogeneity in the strain response, which grew as the test progressed. Most interestingly, bands of shear strain and transverse strain occurred in the same pattern as the fascicles, suggesting interfascicle shear as an important deformation and damage mechanism. Local stresses (e.g., grip effects) and non-midsubstance ruptures appear endemic to fibrous soft tissue testing, and DB specimens do not resolve these issues. Due to fiber curvature in the meniscus, it is recommended to use ET specimens for circumferential tension tests. The tabs ensure that as many fibers as possible are securely gripped, producing more rapid and complete fiber recruitment, lesser yield strain, and greater peak stress. Rectangular specimens are suitable for radial tension tests. Although this study makes significant strides in measurement of the meniscus' mechanics, more work needs to be done to develop procedures for fibrous soft tissue testing and to quantify processes of damage and failure.

Nomenclature

DB =

dogbone

ET =

expanded tab

E_xx =

longitudinal Lagrange strain

E_xy =

shear Lagrange strain

E_yy =

transverse Lagrange strain

k_f =

fiber stiffness

R =

rectangle

$\lambda$ =

stretch ratio

${\overline{\lambda }}_c$ =

mean fiber recruitment stretch

${\lambda }_c^{\text{SD}}$ =

square root of the variance of the fiber recruitment stretch

σ =

first Piola–Kirchhoff stress