On Buckling Morphogenesis

Abstract

Cell-generated mechanical forces drive many of the tissue movements and rearrangements that are required to transform simple populations of cells into the complex three-dimensional geometries of mature organs. However, mechanical forces do not need to arise from active cellular movements. Recent studies have illuminated the roles of passive forces that result from mechanical instabilities between epithelial tissues and their surroundings. These mechanical instabilities cause essentially one-dimensional epithelial tubes and two-dimensional epithelial sheets to buckle or wrinkle into complex topologies containing loops, folds, and undulations in organs as diverse as the brain, the intestine, and the lung. Here, I highlight examples of buckling and wrinkling morphogenesis, and suggest that this morphogenetic mechanism may be broadly responsible for sculpting organ form.

Introduction

Evolution has generated an enormous diversity of biological form. This diversity is readily apparent in the variety of body plans, pigmentation patterns, and appendage morphologies observed in nature. Hidden beneath this surface diversity, however, is a remarkable similarity of form. All organisms need a central processing unit, an ability to digest food into key nutrients, and a mechanism to acquire oxygen from their surrounding environment. Despite their different functions, the human brain, mouse gut, and bird lung all share one special feature: the tissues that make up these organs have an undulated topology, one that arises from an initially flat sheet of cells during embryonic development (Fig. 1). These simple sheets are transformed in the embryo into complex three-dimensional structures through the process of morphogenesis.

Fig. 1.

Schematics of cortical folding in the brain, villus morphogenesis in the small intestine, and branching morphogenesis in the airways of the lung

Over the past 50 years, studies in developmental biology have unlocked several of the biochemical and genetic mysteries that underlie morphogenesis. Morphogens and signaling pathways have been identified, gene regulatory networks parsed together, differentiation programs elucidated [1–3]. In parallel, biological systems must obey Newton's laws. Physical forces need to be generated to sculpt something as complex as a brain or a kidney from a simple sheet or tube of tissue, and the mechanisms by which cells exert forces on their surroundings to accomplish morphogenesis have unsurprisingly received much interest [4,5]. Cells can actively change their shapes and pull against their neighbors by contracting their actomyosin cytoskeletons [6–8], switching positions at a local level and thereby altering the mesoscale morphology of the tissue [9].

In this way, cells actively exert forces on their surroundings in order to change the shape of a tissue. Recent studies have revealed that morphogenesis can also be accomplished by passive mechanical forces, induced by elastic or viscoelastic instabilities [10,11]. For example, the wavy edges of cabbage leaves can form as a result of the elastic instability induced by growth at the margin of the leaf itself, no genetic blueprints are needed to instruct the cells to move out of the plane of the body of the leaf [12]. Findings from a variety of model organisms now suggest that the brain, gut, and lung (amongst other organs) form complex topologies as a result of similar mechanical instabilities.

Tissue Folding—Topological Similarities

To achieve their transport requirements, most animal bodies are divided into systems of tubes—pipes that are lined by epithelial cells, which provide barrier function, secretory capacity, and (inside–outside) polarity. At the macroscopic level, epithelial tubes fit into the body cavity by folding or looping along their length, like a garden hose spooled around a reel. For example, the human epididymis is a 6-m (20-foot)-long tube that connects the testicle to the vas deferens, and is coiled on itself to fit this entire length within the dorsal surface of the testicle. This space-filling organization is reminiscent of that of the intestines, which are looped and folded such that they are confined within the abdominal cavity. At the microscopic level, the surface area of the epithelial walls of these tubes can also be increased by folding, all while maintaining a constant length for the tube and a small volume for the organ. The gut forms finger-like extensions called villi that project into the lumen, leading to a 30-fold increase in the surface area available for absorbing nutrients. The cerebral cortexes of large mammals are folded inward, which increases the surface area of this important region of the brain. In a similar topology, the airway epithelium of the mammalian lung folds outward into a branched, tree-like architecture; this arrangement is also observed in the ducts of secretory organs like the salivary and mammary glands and the collecting ducts of the kidney. Folded epithelial sheets and tubes are thus widely observed across organs and phyla. Here, I describe studies that suggest that some of these tissues fold through passive mechanical instabilities rather than genetically encoded active cellular movements.

Mechanics of Buckling and Wrinkling

Epithelial tissues are thin. The epithelial cells themselves are ∼10 μm in height (<1 μm to 25 μm across various epithelia), but packed into sheets that can extend up to centimeters or meters in length and width. This geometry primes epithelial tissues to respond to mechanical forces. In particular, thin materials are susceptible to mechanical instabilities that cause large deformations resulting in buckling or wrinkling [13,14]. Buckling is the process by which in-plane compression of a thin object results in its out-of-plane bending (Fig. 2). This problem has been considered extensively for thin elastic beams of finite length that are actively compressed at their two ends by some force [15]. When compressed, the beam deforms with a characteristic curvature k that depends in part on the force exerted at the two ends of the beam, its length, and its thickness. This buckling relieves in-plane strains while the compressive forces are applied; as soon as the force is removed, the beam relaxes back into its unbuckled geometry.

Fig. 2.

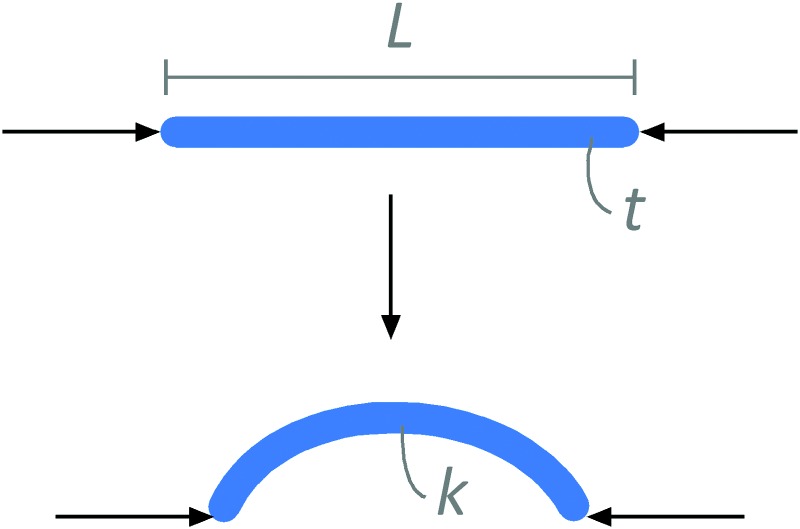
Compressive forces induce buckling of linear rods. The curvature of the buckle, k, depends in part on the thickness of the rod, t.

Epithelial sheets do not exist in isolation. These initially flat tissues are almost always conformally adherent to an adjacent tissue, the mesenchyme, which is comprised of less well-ordered cells that are dispersed within an extracellular matrix (Fig. 3(a)). This arrangement is similar to that of layered films and sheets observed in nonliving systems [16]. When compressed longitudinally along one dimension (uniaxial compression), a thin film that is floating on a liquid or soft elastic foundation will first respond by forming parallel wrinkles or undulations along its surface that are oriented perpendicular to the axis of compression (Fig. 3(b)). The wrinkles form because buckling of the film causes the foundation to deform; the wavelength λ of the wrinkles depends in part on the thickness t of the film. If the compressive forces are high enough, these wrinkles will then form larger folds, a process that depends on the bending energy of the film (which is a function of its Young's modulus E, Poisson ratio ν, and thickness t) and the gravitational energy of the foundation (which is a function of the relative densities ρ between the fluids above and below the film and the force of gravity g) [17]. Interestingly, antisymmetric folds are energetically favorable and stable unless tension is applied to the sheet [18]. (As an analogy, consider applying plastic wrap on the surface of an open container of leftover soup.)

Fig. 3.

Epithelial tissues form sheets of packed cells, similar to layered films. (a) The basal surface of epithelial sheets adheres to a basement membrane, which itself is adjacent to a loosely packed mesenchyme. (b) Thin sheets supported by a (visco)elastic foundation will form wrinkles out of the plane of the membrane when placed under compression. The wavelength of the wrinkling, λ, depends of the thickness of the sheet, its mechanical properties, and those of the foundation.

Compression thus induces in-plane stresses that can only be relieved if the film wrinkles out of its original two-dimensional plane and into a three-dimensional configuration. This problem has also been investigated extensively in the context of stratified layers of viscoelastic materials (including tectonic plates) under compression [19,20]. Compression does not always need to be applied externally to induce wrinkling, however. If the film grows nonuniformly, this growth will also induce in-plane stresses within the film that will cause it to wrinkle [13]. Even more simply, if the film grows uniformly under confinement (such that it is growing faster than its underlying foundation), it will also wrinkle.

Biological Examples of Buckling and Wrinkling During Morphogenesis

Based on their geometries, epithelial tissue buckling could arise from differential rates of growth, either within a layer of cells or between adjacent layers. For the cerebral cortex, it has been suggested that the surface folds because the cortical plate grows more quickly than the tissue beneath it, thereby causing the outer surface to buckle [21]. This increased growth could arise both from proliferation of the cortical cells proper as well as from any spreading of the tissue that might result from cells intercalating within it from deeper layers [22].

A similar mechanism has been proposed to explain how the initially straight intestinal tube, which is essentially a one-dimensional rod, forms the looping structure of the gut [23]. In this case, the gut tube grows in length faster than does the mesentery to which it is attached [24]; this differential growth (between tissues) is thought to be physically sufficient to place the tube under compression and induce it to buckle [23,25]. The topology of the looping—that is, the size and spacing between the loops of the tube—was found to depend on the elastic properties of the intestinal tube, the elastic properties of the mesentery, and the relative mismatch in strain (Fig. 4(a)). Relative differences in the shape and density of the cells in the left versus the right side of the mesentery also appear to bias the direction of the buckling, thereby generating left-right asymmetry of the gut [26,27].

Fig. 4.

Buckling/wrinkling morphogenesis of developing epithelia. (a) Looping of the vertebrate small intestine depends on the mechanical properties of the intestinal tube and the mesentery, and their relative rates of growth. With permission from Ref. [23]. (b) The luminal surface of the small intestinal epithelium morphs from smooth, to longitudinal ridges, to zigzags, to villi at the same time as the smooth muscle differentiates around the basal surface of the tube. With permission from Ref. [30]. (c) Growth of the embryonic dental epithelium under confinement might cause it to buckle into the surrounding mesenchyme. With permission from Ref. [36]. (d) The terminal end of the embryonic airway epithelium bifurcates into two daughter branches as a result of spatially patterned differentiation of airway smooth muscle. When smooth muscle differentiation is inhibited, the growing airway epithelium forms buckles instead of a bifurcation, suggesting that the smooth muscle constrains the instability. Adapted from Ref. [59].

Mechanical instability can thus drive the macroscale morphogenesis of the intestine, an organ that is approximately 7.5 -m (∼25 feet) long in the adult human. A similar process appears to play a role in the formation of the micrometer-scale structures of the intestinal villus. The inner surface of the gut tube is lined by a layer of epithelial cells that provide the absorptive function of the intestine. In the embryo, this epithelial layer is initially flat but undergoes a series of morphogenetic movements that give rise to finger-like protrusions known as intestinal villi, thus increasing its surface area [28]. In the mature intestine, the inner-most epithelial layer is surrounded by three layers of smooth muscle; these layers of stiffer tissue form sequentially in the embryo at the same time as the epithelium folds sequentially into longitudinal ridges, zigzag folds, and finally into villi (Fig. 4(b)). In the 1950s, it was proposed that contraction of the intestinal smooth muscle caused the epithelium to buckle into villi [29], but more recent work combining experiments and mathematical modeling has suggested that the sequential differentiation of the three layers of smooth muscle, which constrains the growing epithelium, is sufficient to induce the different stages of villus morphogenesis [30–32]. Here, buckling of the epithelium depends on its constrained growth and the pattern of development of the smooth muscle layers that ensheathe it. In this case, the dynamics of microscale epithelial buckling are directed by the patterns and rates of differentiation of the surrounding nonepithelial tissue.

Importantly, this process not only bends the intestinal mucosa into villi but also serves to instruct the intestinal stem cells to localize to the crypts that form at the base of each villus [33]. This appears to arise from the simple change in geometry of the tissue—the currogated undulations create sinks for morphogens that are secreted by the epithelial cells, leading to a concentration gradient along the length of the villus. So something as simple as constrained growth of the epithelium not only directs its morphogenesis but also its pattern of differentiation.

A similar growth-induced instability is thought to play a role in the early stages of morphogenesis of the tooth. Here, an epithelial bud folds inward to form a cap structure (Fig. 4(c)); this process is known as the bud-to-cap transition. The molecular regulation of the bud-to-cap transition has been intensely investigated, and involves reciprocal signaling between the epithelium and mesenchyme through molecules including fibroblast growth factor (FGF), sonic hedgehog (SHH), bone morphogenetic protein (BMP), and Wnts [34]. These signals were once thought to lead to spatial patterns of proliferation within the dental epithelium, such that highly proliferative regions grew faster than the adjacent cells and thus formed the protruding bulges of the cap [34,35]. However, a recent study has revealed that proliferation within the epithelium is essentially uniform prior to the bud-to-cap transition [36]. As with the cortical folds and intestinal villi, instead it appears that the dental epithelium proliferates at a higher rate than its adjacent mesenchyme, thus placing the epithelium under compression and causing it to buckle into the cap geometry. An analogous buckling model has been proposed for the later stages of tooth development, which generates the number and shape of the cusps that form the crown of the tooth [37].

Development of the branched architecture of the airways of the lung also requires concerted, reciprocal signaling between the epithelium and its surrounding mesenchyme. As in morphogenesis of the tooth, embryonic development of the lung is regulated by signaling through FGFs, BMPs, and Wnts, among other proteins [38,39]. In this case, however, the epithelium folds outward in a process known as branching morphogenesis to generate the complex, three-dimensional geometry of the airway epithelial tree [40], a structure with as many as 2²³—approximately 8 × 10⁶—terminal ends! In the mammalian lung, the epithelium begins as a wish-bone shaped structure, with the trachea bifurcating into the left and right primary bronchi. These initially simple tubes form new branches along their lateral surfaces in a process known as domain branching, and split at their ends into two equivalent daughter buds in a process known as terminal bifurcation (Fig. 4(d)) [41]. The signals that govern branching of the epithelium have been elucidated in part by using ex vivo culture systems, in which the embryonic airway epithelium is denuded of mesenchyme and embedded within a three-dimensional gel of extracellular matrix [42,43]. Using this approach, it was found that FGF10 in particular acts as an important signal for branching of the airway epithelium [44,45]. Adding FGF10 to mesenchyme-free airway epithelium caused it to fold into the surrounding gel [46,47], reminiscent of branching in vivo. In mice, FGF10 appeared to be expressed adjacent to newly forming branches [46], and deleting it genetically disrupted lung development [48,49], so the prevailing hypothesis was that FGF10 induced a subset of epithelial cells to proliferate in a specific direction [50] and thus form a branch [51].

Intriguingly, adding exogeneous FGF10 to mesenchyme-free airway epithelium induces morphogenesis [46], despite the fact that in this system the epithelium is bathed in a uniform concentration of the growth factor agonist. Similarly, expressing Fgf10 uniformly within the embryonic pulmonary mesenchyme in Fgf10-null mice still leads to what has been interpreted as normal airway morphogenesis [52]. These results suggest that spatially patterned epithelial growth is not the physical mechanism underlying shape change in the epithelium. Consistently, proliferation within the epithelium is uniform until after the branches have already formed [53,54], similar to the findings for bud-to-cap transition in the tooth. Instead, a combination of experiment and mathematical modeling has shown that uniform growth of the epithelium, when constrained by a surrounding gel, is sufficient to induce a mechanical instability that causes the tissue to buckle, and thereby form what had previously been assumed to be a genetically controlled branching architecture [53]. As with the morphogenesis of the cortical folds, intestinal villi, and tooth anlagen, the higher order three-dimensional epithelial structure results because the epithelial tissue grows faster than its surroundings, causing compressive stresses that force it to deform out of its original two-dimensional plane.

This of course begs the question: How does the airway epithelium form a branch in vivo? If FGF10 induces uniform epithelial growth [54], and uniform growth causes the epithelium to buckle, then how are terminal bifurcations achieved? Analysis of intact embryonic lungs suggests the answers to these questions. Similar to the embryonic intestine, the airway epithelium undergoes morphogenesis at the same time as the mesenchyme is differentiating into various tissue types, including smooth muscle [55–58]. Timelapse analysis of embryonic lungs from transgenic mice that express red fluorescent protein (RFP) downstream of the alpha-smooth muscle actin (αSMA) gene promoter revealed that nascent smooth muscle cells form at the future cleft site of the epithelial bud prior to its bifurcation (Fig. 4(d)) [59]. Surgically removing the smooth muscle from the basal surface of the epithelium in the middle of the bifurcation process caused the epithelium to pop back into a smooth morphology, suggesting that the epithelium is under compression during its morphogenesis. Preventing smooth muscle differentiation blocked terminal bifurcation of the epithelium, and instead caused the epithelium to buckle, similar to the morphogenesis of mesenchyme-free epithelium in culture (Fig. 4(d)) [53]. These data suggest that in the intact embryonic lung, the tendency of the growing airway epithelium to buckle is constrained by the simultaneous differentiation of the surrounding smooth muscle, which instead directs the epithelium to fold specifically at its midline to form two daughter buds. It is possible that the spatial heterogeneity in mechanical properties of the mesenchyme surrounding the growing epithelium, such as would be introduced by spatially patterned smooth muscle differentiation, directs its morphogenesis.

How to Achieve Stereotyped Patterns of Folds?

As described above, evidence is mounting for a general mode of tissue morphogenesis that results from mechanical instabilities that arise when a growing epithelial tissue is constrained within or between a foundation of mesenchyme. The beauty of this folding mechanism is that it does not require that each fold be specified a priori in the genome—the patterns of bends, loops, branches, and folds could emerge entirely from the mechanical properties and relative growth rates of the tissues. One open question that remains, however, is how can this mechanical mechanism result in precise tissue architectures? That is, how does one achieve stereotypy with buckling morphogenesis? For example, the branches of the airways of the lungs are identical between individuals within a given species—How can buckling lead to such complexity and order?

The answer to this question may also lay in the examination of nonliving materials. The locations of folds within buckled systems are influenced by several physical factors, including the initial geometry of the unfolded structure as well as spatial heterogeneities in stiffness, thickness [60], and expansion. In the developing embryo, landmarks might serve to constrain buckling of epithelial sheets, such as smooth muscle in the lung. Alternatively, the buckling epithelium might be directed by a tether, such as the mesentery in the developing gut [26,27]. Consistent with this idea, separating the dorsal mesentery from the gut tube, either surgically or enzymatically, causes the looped intestine to uncoil into a straight tube, supporting the idea that the mesentery serves as a compressional tether for the gut [23].

It is worth pointing out that the idea that unequal growth could give rise to buckling during tissue morphogenesis was postulated long ago, most famously by Wilhelm His in the 1870s [61] and then again by D'Arcy Thompson in 1917 [4]. It has taken more than 100 years for us to have the technical abilities to test these ideas definitively, and it is likely that more tissues will be found to form as a result of mechanical instabilities. In-depth understanding of the relative roles played by passive mechanical forces and buckling or wrinkling will require continued combination of experimental systems and computational models.

Nomenclature

BMP =

bone morphogenetic protein

E =

Young's modulus (Pa)

FGF =

fibroblast growth factor

g =

force of gravity

k =

characteristic curvature

RFP =

red fluorescent protein

SHH =

sonic hedgehog

t =

thickness of film or epithelial sheet (μm)

αSMA =

alpha-smooth muscle actin

λ =

wavelength (μm)

ν =

Poisson ratio

ρ =

relative density