Prediction of In Vivo Knee Joint Loads Using a Global Probabilistic Analysis

Abstract

Musculoskeletal models are powerful tools that allow biomechanical investigations and predictions of muscle forces not accessible with experiments. A core challenge modelers must confront is validation. Measurements of muscle activity and joint loading are used for qualitative and indirect validation of muscle force predictions. Subject-specific models have reached high levels of complexity and can predict contact loads with surprising accuracy. However, every deterministic musculoskeletal model contains an intrinsic uncertainty due to the high number of parameters not identifiable in vivo. The objective of this work is to test the impact of intrinsic uncertainty in a scaled-generic model on estimates of muscle and joint loads. Uncertainties in marker placement, limb coronal alignment, body segment parameters, Hill-type muscle parameters, and muscle geometry were modeled with a global probabilistic approach (multiple uncertainties included in a single analysis). 5–95% confidence bounds and input/output sensitivities of predicted knee compressive loads and varus/valgus contact moments were estimated for a gait activity of three subjects with telemetric knee implants from the “Grand Challenge Competition.” Compressive load predicted for the three subjects showed confidence bounds of 333 ± 248 N, 408 ± 333 N, and 379 ± 244 N when all the sources of uncertainty were included. The measured loads lay inside the predicted 5–95% confidence bounds for 77%, 83%, and 76% of the stance phase. Muscle maximum isometric force, muscle geometry, and marker placement uncertainty most impacted the joint load results. This study demonstrated that identification of these parameters is crucial when subject-specific models are developed.

Introduction

Musculoskeletal models are powerful tools that allow subject-specific investigations of biomechanical quantities that are not measurable in vivo, and predictions of the effects of clinical treatments [1–4]. The main challenge of subject-specific modeling is the lack of validation strategies, because predicted outcomes of musculoskeletal models can rarely be compared to measurable experimental data [5]. In particular, when muscle forces are involved in model predictions, two quantities measurable in vivo have been used to verify the reliability and accuracy of the model: (1) muscle electromyography (EMG) signals that allow for a mostly qualitative comparison of muscle activity [6,7] and (2) joint loads measured with instrumented joint implants that allow for an indirect validation of muscle forces [8–12]. Instrumented implants have significantly enhanced the awareness of the ability of musculoskeletal models to predict contact loads with surprising accuracy [9,13–15]. In particular, blinded predictions of total knee replacement (TKR) contact loads on an instrumented tibial component were possible due to the Grand Challenge Competition, which made joint load, human movement, and imaging data sets available to the scientific community [13].

All previous attempts to match experimental contact loads have used deterministic models whose final output depended on several input parameters necessarily estimated from the available data (e.g., joint kinematics, segment inertial parameters or musculotendon parameters). However, deterministic musculoskeletal models are characterized by an intrinsic uncertainty that is often ignored. For example, segment masses cannot be directly measured from the subject and are often estimated with scaling techniques. Musculoskeletal models are usually developed and validated with the purpose of predicting and estimating biomechanical quantities not measurable in vivo. If an accurate estimate of an output is obtained by means of a model with intrinsic uncertainty, there is no guarantee that future estimates of the model will be accurate in different conditions. Therefore, it is important to take into account this variability in order to assess the robustness of a model.

Many studies have partially included model uncertainty and analyzed its influence on biomechanical outputs of interest. When the possible amount of an uncertainty is not available, the sensitivity of a particular output (e.g., joint kinematics, muscle moment arms, muscle function) to the change of an uncertain input (e.g., musculoskeletal geometry, musculotendon properties, joint axis location) can be quantified and provide valuable insights into the possible effects of lack of knowledge [5,16,17]. The impact of the uncertainty in different input parameters on several outputs of interest has been analyzed for musculotendon parameters [18–22], musculotendon geometry [23–25], joint center location [26], degree of freedom classification [27], joint models [28–30], skin marker placement [30], and pose estimation algorithms [31]. On the other hand, when the amount of possible uncertainty is known, an accurate evaluation of the output variability can be quantified. In particular, uncertainty has been evaluated in video motion capture marker placement [32], segment inertial parameters [33,34], kinematics and muscle origin-insertion location [35].

While many studies have used probabilistic tools to analyze the effect of uncertain parameters on the output of interest [18–31], few of them have performed probabilistic analyses that combine multiple uncertainties belonging to different categories of parameters (described hereafter simply as “global”) [36,37]. These global analyses allow a more complete investigation of the overall reliability of a model. Valente et al. [37] used a full limb MRI-informed musculoskeletal model in opensim that included uncertainties of anatomical landmark location, muscle attachments sites, and maximum muscle tension. Myers et al. [36] used a scaled-generic musculoskeletal model in opensim that included marker placement error, segment inertial parameters uncertainty, and Hill-type muscle parameters uncertainty. However, Myers et al. [36] did not account for variability in muscle geometry and did not investigate the impact of the included uncertainties on joint reaction forces. Moreover, these two studies used data from a single healthy subject and did not perform a quantitative validation of their results because joint load measurements were not available for the subjects.

The present study proposes a global probabilistic analysis to investigate the influence of uncertainty in multiple parameters of a musculoskeletal model on knee joint load while simulating level gait for three TKR patients. The goals of this study are: (1) to include common sources of uncertainty present in a musculoskeletal model in a probabilistic framework with realistic input distributions while predicting the TKR contact loads of patients with telemetric implants; (2) to quantify the influence of each input uncertainty on the desired output (knee contact loads) and therefore to identify the most critical parameters whose knowledge must be improved to develop more accurate subject-specific models; and (3) to compare the obtained variability of the prediction to the available in vivo contact loads. This will allow an estimate of the musculoskeletal model's reliability for prediction of muscle forces and knee joint loads.

Methods

Experimental Data.

Walking data of three subjects (169.0 ± 2.6 cm, 71.7 ± 6.0 kg) implanted with an instrumented TKR from the Grand Challenge Competition was used [13]. The three subjects walked at similar self-selected speed (1.2, 1.1 and 1.0 m/s, respectively). The first subject was implanted with an instrumented tibial prosthesis with four uniaxial load cells to allow the measurement of medial and lateral contact forces separately [38]. The other two subjects were implanted with telemetric implants that allowed the measurement of knee contact forces in six degrees of freedom by means of a single load cell [39]. The available data includes video motion capture marker locations, ground reaction forces, and tibiofemoral contact forces.2 A modified Cleveland Clinic marker set that included extra markers on the feet and trunk was used for motion data collection [13]. Surface EMG signals were also collected for the major muscles spanning the knee of each subject.

Baseline Musculoskeletal Model.

A previously developed musculoskeletal model with a total of 10 segments and 92 musculotendon units was modified in opensim to obtain the baseline model for this study [40,41]. The lower limbs included a ball-and-socket hip joint and a revolute ankle joint. In the current study, the knee joint was modified to implement a coupled mechanism (one degree-of-freedom) with translations of tibia and patella prescribed by the knee flexion angle [42]. In addition, a varus/valgus degree of freedom of the tibia with respect to the femur was introduced in the knee model for subsequent analysis of uncertainty in lower limb coronal alignment and was fixed to zero in the baseline model. The geometry of the quadriceps muscles in the original opensim model was refined to insert on the tibial tubercle with via points placed on the superior and inferior poles of the patella [43]. This enabled resultant quadriceps force to be correctly included in the calculation of tibiofemoral contact forces in opensim. Via point locations of the quadriceps were manually adjusted to assure that the moment arm of each of the musculotendon units lied inside the mean ± std area of the patellar tendon moment arm measurements presented by Krevolin et al. [44]. Finally, geometry and properties of the two gastrocnemius musculotendon units (medialis and lateralis) of the original model were replaced with the gastrocnemius units from the musculoskeletal model of Arnold et al. [42], as these better matched the moment arms measured by Buford et al. [45].

Body segment dimensions and inertial properties were scaled to the subjects using scale factors calculated from motion capture marker locations. The dimensions of the scaled segments were also checked by comparing them to the CT images of the subjects' implanted lower limb.

Baseline joint kinematics and inverse dynamics for each subject were determined with opensim. To achieve the pose of the subject, the recorded marker locations are matched to virtual markers on the kinematic model of the subject. This matching technique is performed by solving a weighted least squares problem that minimizes marker errors at each time frame [41]. Net forces and moments needed at the joints to achieve the desired motion were obtained through the inverse dynamics solution. Baseline muscle forces were predicted with a static optimization technique that solves the equations of motion while minimizing the summed muscle activations squared at each time frame [46]. Baseline joint loads were calculated in opensim from the inverse dynamics and muscle forces by calculating loads exchanged between segments through a free body diagram analysis [43].

Probabilistic Workflow.

A previously developed Probabilistic Toolbox [36] that alters opensim input files within a Monte Carlo simulation was customized to introduce the desired uncertainty in the baseline model's parameters. The uncertainty of all the parameters considered in this study was propagated to the joint contact analysis through the stages of the workflow (Fig. 1). In particular, four main sources of uncertainty were taken into account: the uncertainty (1) in the motion capture marker placement on the anatomical landmarks, (2) in the coronal alignment, (3) in the segment inertial parameters, and (4) in the Hill-type muscle model parameters and in muscle geometry.

Fig. 1.

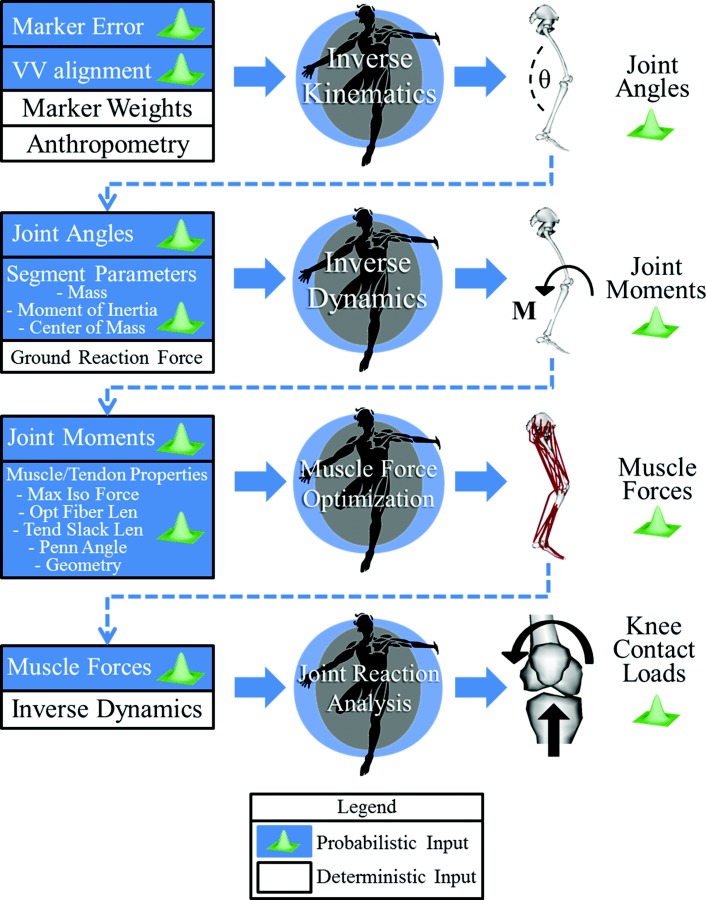
Workflow of the study. Monte Carlo analyses were performed with opensim at each step of a pipeline that included inverse kinematics, inverse dynamics, muscle force prediction with static optimization and joint reaction analysis. Every probabilistic input was described as a normal distribution with standard deviations from the literature. Specific description of each uncertainty can be found in Table 1 (marker placement), Table 2 (Inertial parameters) and Table 3 (muscle paths and properties). Only uncertainty in tibiofemoral alignment (VV alignment) is not described in a table since it is a single distribution with null mean and std of 2.5 deg [47]. The propagation of the uncertainties was obtained by using output distributions of each step as input uncertainty for following steps. The final output of the workflow was knee compressive load and varus/valgus contact moment.

• (1)Marker placement: Errors in marker placement result from the inherent uncertainty that occurs when an examiner places a marker on the skin relative to a palpated bony landmark. This uncertainty was modeled as a constant offset between the anatomic landmark and the marker [36]. Marker placement uncertainty was modeled by sampling the magnitude of the offset in each direction from a normal distribution. Previously reported intra-examiner variances were used [32] for anatomical landmarks present both in the marker set used in this study and in the marker set used by Della Croce et al. [32] (Table 1 ). To assess intra-examiner precision, the same examiner performed the anatomical landmark identification six times and the standard deviation (std) across the six measurements was calculated. For markers in the present study that were not described by Della Croce et al. [32], two different stds were used. To represent the uncertainty along the two directions of the anatomical plane (either sagittal, coronal, or transverse) that best represents the surface tangent to the anatomical landmark, the average of the maximum stds in Della Croce et al. [32] was used (7.9 mm). Along the direction perpendicular to that same surface, the average of the minimum stds in Della Croce et al. [32] was used (3.7 mm). The uncertainties calculated this way were applied also to the markers on the foot because the patients in our study wore shoes, which likely created greater uncertainty than the subjects in Della Croce et al. [32] who were barefoot. Although uncertainty in marker placement occurs during the experimental session, they were more easily accounted for by perturbing the location of the virtual markers in the local coordinate system of the corresponding segment on the musculoskeletal model. Since the kinematics were resolved by minimizing the distance between experimental and virtual markers, perturbations in the virtual or experimental marker location have the same effect on joint angles.
• (2)Limb alignment in the coronal plane: Although an implant aligned to the mechanical axis of the lower limb is usually the surgical objective, it can be challenging to achieve. Coronal alignment, besides affecting the survivorship of the implant [47], influences the distribution of the tibiofemoral contact load on the lateral and medial side [48]. The uncertainty in this postoperative tibiofemoral angle was included in the present study. The varus/valgus degree of freedom was introduced in the knee model and locked to a constant offset sampled from a normal distribution with null mean and std of 2.5 deg, since this is the std of the postoperative tibiofemoral alignment for 6070 TKA patients reported by Fang et al. [47].
• (3)Inertial parameters: Body segment parameters are usually estimated by considering them linearly proportional to their dimensions, obtained by scaling a general model according to marker distance ratios. This approximation of the actual parameters does not account for other factors such as mass distribution, density and amount of soft tissue. Therefore, uncertainties in mass, moment of inertia, and center of mass location of the lower limb segments were modeled by perturbing the parameters of the baseline scaled model with estimated variances [34] (Table 2 ). Rao et al. [34] calculated variability in inertial parameters by estimating them with six different parameter identification models. Input distributions for the current study were defined using baseline model parameters as the means and stds defined by coefficients of variation (COV = std/mean) from Rao et al. [34]. Inertial parameters of the pelvis and the segments of the upper body were not perturbed because they do not influence the calculation of ankle, knee and hip net joint moments calculated via inverse dynamics, and consequently do not significantly affect the prediction of muscle forces and joint reaction loads in the lower limb [36].
• (4)
  Muscle path and parameters: Musculotendon units were modeled as Hill-type muscles. A Hill-type muscle is completely described by: (a) its path, (b) the active and passive force-length relationships [49], (c) the force–velocity relationship [40] and (d) four parameters (maximum isometric force, optimal fiber length, tendon slack length, and pennation angle) [50]. While force–length and force–velocity relationships are consistent among different muscles and subjects [51,52], there can be significant variability in muscle path and parameters. Uncertainties in Hill-type muscle parameters of 20 musculotendon units were modeled by sampling them from input distributions defined according to the dataset in Ward et al. [53] (Table 3 ), where means and stds of physiological cross-sectional area (PCSA), fiber length ($L_f$), and pennation angle ($\alpha$) from 21 cadavers are presented. Since maximum isometric force ($F_M^o$) can be calculated as PCSA times muscle tension [54], the COVs from PCSA measurements by Ward et al. [53] were used to calculate stds for maximum isometric forces by multiplying them times the baseline values (considered the mean values). Fiber lengths by Ward et al. [53] were obtained by first measuring a raw fiber length ($L_f^{\prime }$) from three to five regions in each muscle and scaling it with a sarcomere length-based ratio [55]

  $$L_f=\frac{2.7\cdot L_f^{\prime }}{L_s}$$ (1)

  where $L_s$ is the bundle sarcomere length measured by laser diffraction from each muscle region, and 2.7 μm represents the optimum sarcomere length for human muscles [55]. Therefore, the fiber length measured by Ward et al. [53] is an approximation of optimal fiber length, since this is the length at which most of the sarcomeres are at their optimal length. The baseline optimal fiber length values were used as mean values of the input distributions, and stds were calculated by means of the fiber length COVs from the cited dataset [53]. COVs from pennation angle measurements were used to calculate stds for this parameter. Since tendon slack length ($L_T^S$) variability was not found in the literature, this parameter was calculated from the sampled optimal fiber length and pennation angle by keeping a constant musculotendon total length

  $$L_{T\text{pert}}^S=L_{T\text{bl}}^S-(L_{M\text{pert}}^o-L_{M\text{bl}}^o)*\hspace{0.17em}\text{cos}({\alpha }_{\text{pert}})$$ (2)

  where the subscripts pert and bl indicate the perturbed value and the baseline value, respectively [56].

Table 1.

Uncertainty in marker placement relative to anatomical landmarks expressed in opensim coordinate systems (based on Della Croce et al. [32]). Bold stds represent anatomical landmarks directly investigated in Della Croce et al. Nonbold stds were selected according to the anatomical plane that best represents the surface tangent to the anatimical landmark. Along the two directions of this plane, a std of 7.9 mm was used (average of maximum stds in Della Croce et al.). Along the direction perpendicular to the same surface, a std of 3.7 mm was used instead (average of minimum stds in Della Croce et al.).

Marker	Std (mm)
Pelvis	x	y	z
L ASIS	3.4	4	11
R ASIS	10	11.5	14.5
L PSIS	2.8	8.3	7.5
R PSIS	5.7	10.7	4.6

Patella	x	y	z
Patella	3.7	7.9	7.9

Femur	x	y	z
Thigh Sup	7.9	7.9	3.7
Thigh Inf	7.9	7.9	3.7
Thigh Lat	3.7	7.9	7.9

Tibia	x	y	z
Shank Sup	3.3	3.3	3.3
Shank Inf	3.7	7.9	7.9
Shank Lat	7.9	7.9	3.7

Foot	x	y	z
Heel	3.7	7.9	7.9
Toe	7.9	3.7	7.9
Toe Lat	7.9	3.7	7.9
Toe Med	7.9	3.7	7.9

Table 2.

Uncertainty in body segment parameters. Inertia tensor and center of mass components are expressed in opensim coordinate systems (based on Rao et al. [34]).

		COV (std/mean)			Std (mm)
		Inertia tensor			COM
Body	Mass	x	y	z	x	y	z
Femur	0.138	0.22	0.22	0.22	3.4	6.8	3.4
Tibia	0.065	0.1	0.1	0.1	3.8	7.5	3.8
Talus	0.07	0.225	0.3	0.2	0.3	0.2	0.2
Calcaneus	0.07	0.225	0.3	0.2	4.2	2.1	2.1
Toes	0.07	0.225	0.3	0.2	1.4	0.7	0.7

Table 3.

Uncertainty in muscle parameters. Bold stds for origin and insertion locations are from Duda et al. [57]. For origin and insertion locations not investigated in Duda et al. [57], a std of 5 mm along each axis was used according to the range of landmark location errors reported in White et al. and Kepple et al. [58,59]. A std of 5 mm along each axis was also used for all the via points of the 20 muscles included in the study.

				std (mm)
	COV (std/mean)			Origin			Insertion
Muscle	$F_M^o$	$L_M^o$	$\alpha$	x	y	z	x	y	z
Rectus Femoris	0.37	0.17	0.25	5	5	5	5	5	5
Vastus Intermedius	0.41	0.20	1.00	14	50	13	5	5	5
Vastus Lateralis	0.46	0.18	0.37	15	22	4	5	5	5
Vastus Medialis	0.35	0.24	0.23	11	38	15	5	5	5
Semimembranosus	0.41	0.27	0.23	5	5	5	5	5	5
Semitendinosus	0.42	0.21	0.38	5	5	5	5	5	5
Biceps Fem Long Head	0.42	0.47	0.27	5	5	5	5	5	5
Biceps Fem Short Head	0.33	0.19	0.29	10	18	5	5	5	5
Gastrocnemius Lateralis	0.34	0.16	0.26	9	15	10	5	5	5
Gastrocnemius Medialis	0.27	0.19	0.44	4	23	12	5	5	5
Soleus	0.29	0.23	0.36	5	5	5	5	5	5
Psoas	0.30	0.14	0.30	5	5	5	7	11	7
Iliacus	0.34	0.17	0.37	5	5	5	6	13	7
Tibialis Anterioris	0.28	0.12	0.32	5	5	5	5	5	5
Gluteus Medius Ant	0.43	0.21	0.84	5	5	5	8	12	6
Gluteus Medius Centr	0.43	0.21	0.84	5	5	5	8	12	6
Gluteus Medius Pos	0.43	0.21	0.84	5	5	5	8	12	6
Gluteus Maximus Ant	0.26	0.16	1.20	5	5	5	16	41	13
Gluteus Maximus Centr	0.26	0.16	1.20	5	5	5	13	27	13
Gluteus Maximus Pos	0.26	0.16	1.20	5	5	5	7	43	15

Uncertainty in the paths of the same 20 muscles was included by perturbing the location of muscle attachments and via points. Uncertainty in muscle attachments on the femur (origins of vasti, biceps femoris short head, gastrocnemius medialis and lateralis, and insertions of glutei maximus, glutei medialis, psoas and iliacus) were modeled according to the variability reported in a cadaver study with six specimens whose femur lengths were scaled to a mean model to allow interspecimen comparison [57]. Attachment and via point locations not investigated by Duda et al. [57] were perturbed in all directions according to a normal distribution with a 5 mm std, comparable to the range of landmark location errors reported in the literature [58,59] (Table 3).

Output variability of joint kinematics, net joint torques, muscle forces, and joint contact loads was determined with opensim by performing several combined Monte Carlo analyses (Fig. 1). In particular, the output variability of each step was used as the input distribution for the following step (e.g., joint kinematics outputs from the kinematics Monte Carlo analysis were used as one of the random inputs for inverse dynamics, static optimization, and joint reaction analysis).

Data Analysis.

The 5–95% confidence bounds of the output variables (joint kinematics, kinetics, muscle forces, and joint contact loads) were calculated at each time frame, which represents the region in which the true result would lie with a confidence of 90%. Mean and std of the 5–95% confidence bounds were used to evaluate an average impact of the uncertainties on the analyzed output [36]. The relative contribution of each source of uncertainty was assessed by comparing the sizes of the confidence bounds when only single sources of uncertainty were included in the Monte Carlo analysis. When mean and std of muscle force bounds were calculated, only time frames when the muscle was active were included. A total of 15 Monte Carlo analyses were performed for each subject to assess the relative contribution of each source of uncertainty to output kinematics, kinetics and muscle forces: three inverse kinematics analyses in which just inverse kinematics was performed (perturbing marker location, tibiofemoral alignment, and both); four inverse dynamics analyses in which inverse dynamics was performed (perturbing marker location, tibiofemoral alignment, inertial parameters, and all of them combined); eight static muscle optimization analyses in which static muscle optimization was performed (perturbing marker location, tibiofemoral alignment, inertial parameters, muscle paths, maximum isometric force, fiber properties, pennation angle, and all of them combined). Joint contact loads were estimated for each static optimization solution of each Monte Carlo analysis.

One thousand simulations per Monte Carlo analysis ensured convergence for the main outputs: knee superior/inferior (compressive) force and varus/valgus contact moment 5–95% confidence bounds. Specifically, means and stds of output confidence bounds lay within 1% of each final mean and std over the last 100 simulations for every Monte Carlo analysis [22,37]. When maximum isometric force and/or muscle path were perturbed, a limited number of simulations (always less than 2% of the total number for each Monte Carlo analysis) failed because of the muscular system's weakness. However, every failed simulation was replaced by another simulation to ensure a total of 1000 simulations per Monte Carlo analysis.

Sensitivity of knee loads was assessed by calculating the Pearson Product-Moment Correlation between the input parameter and the two compressive loading peaks that normally occur during gait. Significant correlations were divided into three groups according to their absolute value: weak ($0.2<|r|<0.4$), moderate ($0.4<|r|<0.6$), and strong ($|r|>0.6$). The slope of each correlation was also calculated and multiplied by the standard deviation of the input uncertainty to assess the potential influence of the input parameter on the analyzed output. Sensitivity was evaluated for Monte Carlo analyses where only individual groups of parameters were perturbed (e.g., only maximum isometric force of all the muscles) in order to assess the influence of a single parameter in comparison to other parameters of the same kind. Therefore, a total of six additional Monte Carlo analyses were performed per each subject to evaluate sensitivity: one with only marker and coronal alignment uncertainties, one with only BSP uncertainty, and one for each source of uncertainty in the muscles (maximum isometric force, fiber parameters, pennation angles, and muscle path).

Root mean square (RMS) errors and squared Pearson Product-Moment Correlations were calculated between joint loads predicted with the baseline musculoskeletal model and joint loads measured from the subjects [13,14]. The percentage of the stance phase in which loads measured by the telemetric implants were within the predicted 5–95% confidence bounds was also calculated. EMG signals were first processed with a 10–400 Hz band-pass eighth order Butterworth filter, then rectified and filtered with a 6 Hz low-pass second order Butterworth filter, and finally, normalized to signals collected during maximum voluntary contractions [60]. The processed EMG signals were used to confirm predicted muscle forces were appropriate.

Intersubject differences were identified through comparison of 5–95% confidence bounds and sensitivity analysis results for the three subjects. For each subject, input variables were ranked from largest to smallest according to the mean 5–95% bounds they produced on each output (kinematics, kinetics and joint loads). In addition, rankings were compared among subjects of most affected outputs when all input variables were perturbed. Finally, moderate and strong correlations between input variables and the first and second joint load peaks during the gait cycle were compared between subjects.

Results

5–95% Confidence Bounds

Kinematics.

The impact of marker placement error and coronal alignment on kinematics was quantified by the size of the 5–95% confidence bounds of each joint angle (Fig. 2(a)). For the three subjects, the degree of freedom with the largest mean bound size was hip flexion/extension (8.4 ± 0.5 deg for subject 1).

Fig. 2.

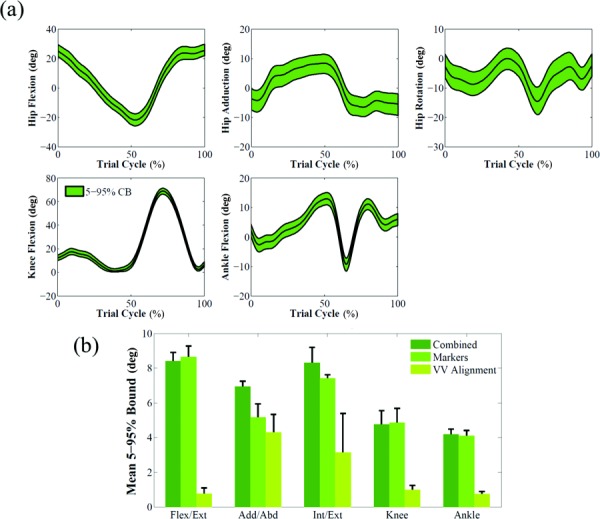
(a) Effect of marker and limb coronal alignment uncertainties shown as 5–95% confidence bounds on joint angles for subject 1. The baseline results are represented by the black line. (b) Mean and standard deviation of 5–95% Bounds for each individual source of uncertainty that affected kinematics (subject 1).

The impact of marker placement error was higher than coronal alignment for all joint angles of the lower limb, with a maximum of 11.3 times higher than coronal alignment for hip flexion/extension angle of subject 1 (Fig. 2(b)).

Kinetics.

The confidence bounds of net joint moments quantified the impact of marker placement, coronal alignment and BSP uncertainties on inverse dynamics (Fig. 3(a)). Bounds for hip flexion/extension moment (5.7 ± 1.8 Nm) and hip internal/external rotation (2.0 ± 0.9 Nm) in subject 1 were the largest and smallest bounds, respectively. Marker placement error had the most significant impact also on all joint moments for the three subjects except internal/external rotation of the hip of subject 1, on which coronal alignment had the largest effect (Fig. 3(b)).

Fig. 3.

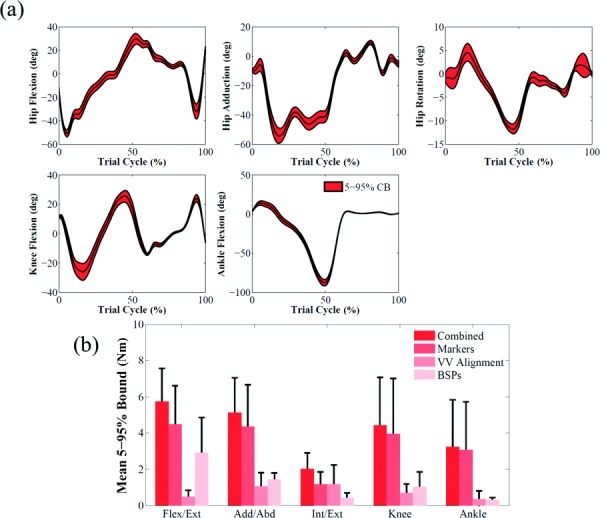
(a) Effect of marker, limb coronal alignment, and body segment parameters uncertainties shown as 5–95% confidence bounds on joint moments for subject 1. The baseline results are represented by the black line. (b) Mean and standard deviation of 5–95% Bounds for each individual source of uncertainty that affected inverse dynamics (subject 1).

Muscle Forces.

By combining all the uncertainties in the workflow (Fig. 1), soleus presented bounds substantially larger than other muscles (e.g., 500 ± 362 N for subject 1) (Fig. 4(a)). Other musculotendon actuators with average 5–95% confidence bounds above 250 N were psoas (305 ± 235 N), iliacus (297 ± 229 N), medial gastrocnemius (264 ± 287 N), anterior gluteus medius (273 ± 192 N), and central gluteus medius (262 ± 176 N) (Fig. 4(a)).

Fig. 4.

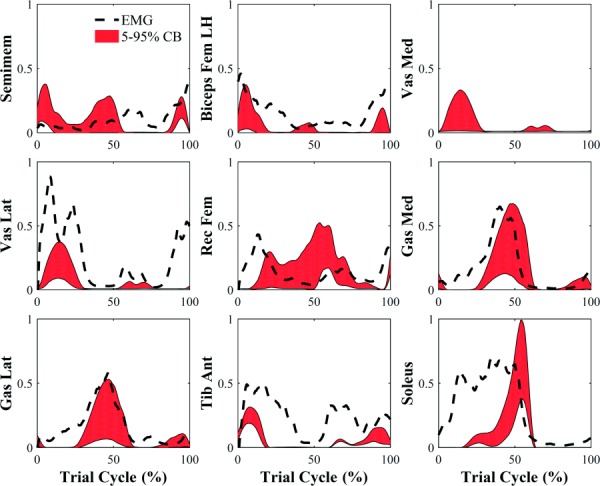
Effect of all sources of uncertainty shown as 5–95% confidence bounds on muscle activation predictions for subject 1. Activation confidence bounds are compared to processed EMG signals (black dashed line). Vastus medialis processed EMG signal was not included in the graph because it was not considered reliable.

Joint Loads.

Knee compressive load and varus/valgus contact moment of subject 1 showed confidence bounds of 333 ± 248 N (Fig. 5(a)) and 16 ± 11 Nm (Fig. 6(a)), respectively, when all the sources of uncertainty were considered. The variables that had a substantially higher impact on muscle forces and knee loads were muscle maximum isometric force and muscle fiber path (Fig. 5(b)). Their contribution to compressive load variation was 3.4 and 2.5 times higher than the contribution of marker placement error, which was the third most impactful variable. Varus/valgus contact moment bounds were also influenced by coronal alignment uncertainty (80% of muscle maximum isometric force influence) (Fig. 6(b)).

Fig. 5.

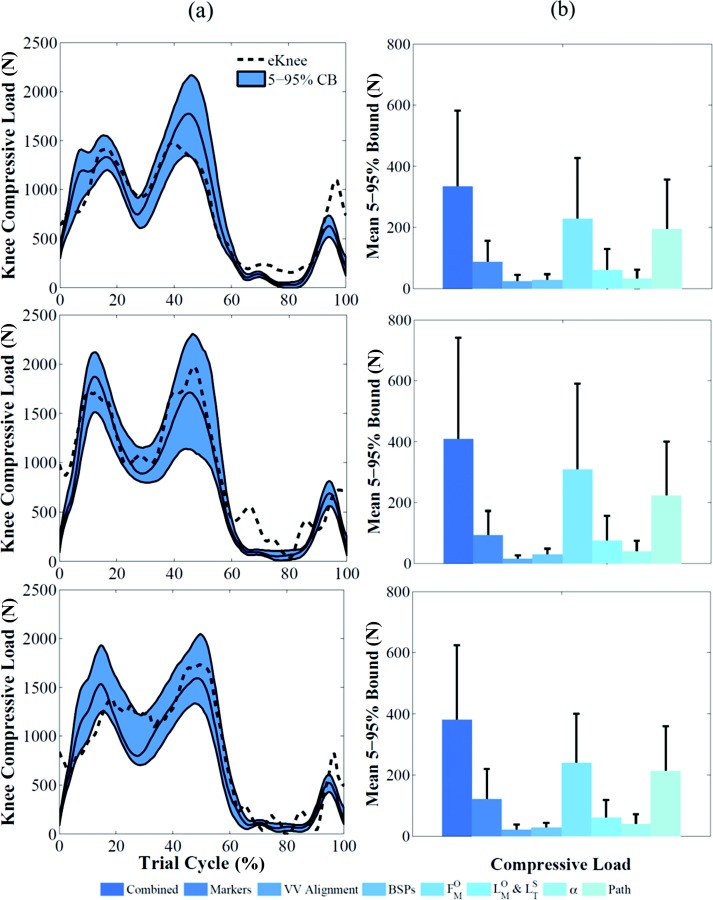
(a) Effect of all the uncertainties shown as 5–95% confidence bounds on knee compressive load for the three subjects. The baseline results are represented by the solid black line. Corresponding measured data are represented by the black dashed line. (b) Mean and standard deviation of 5–95% bounds for each individual source of uncertainty that affected compressive loads for the three subjects.

Fig. 6.

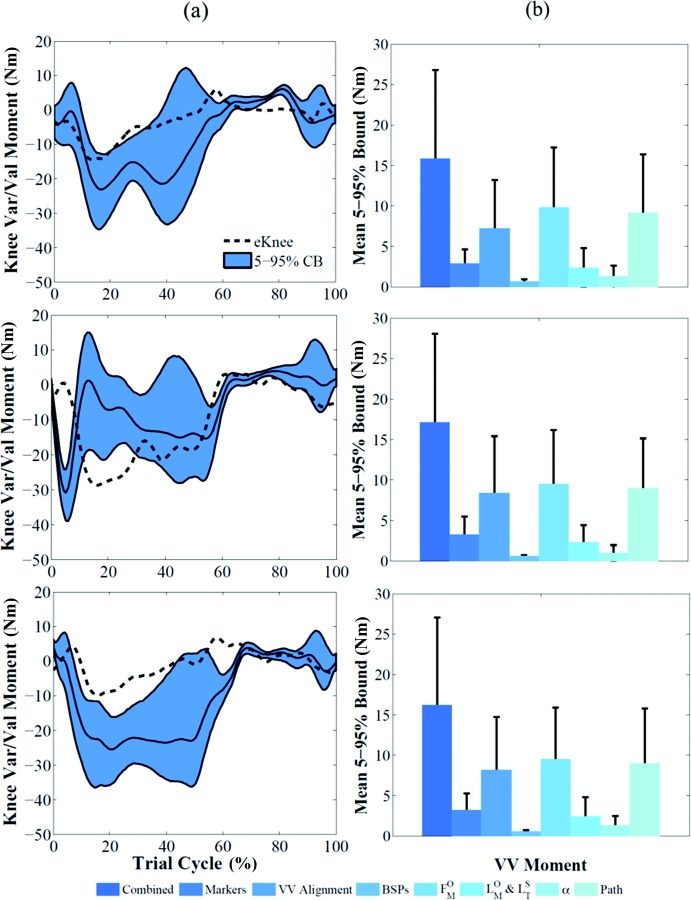
(a) Effect of all the uncertainties shown as 5–95% confidence bounds on varus/valgus contact moment for the three subjects. The baseline results are represented by the solid black line. Corresponding measured data are represented by the black dashed line. (b) Mean and standard deviation of 5–95% bounds for each individual source of uncertainty that affected contact moment for the three subjects.

Sensitivity Analysis.

When only the marker placement and coronal alignment uncertainties were included in the Monte Carlo analysis, compressive load for subject 1 was just moderately correlated to the anterior/posterior location of the right Thigh Inferior marker at its first peak, and to the anterior/posterior location of the right ASIS marker (see Table 4 for correlations and responses to 1 std change in the input parameters). Strong correlations between alignment in the coronal plane and both peaks of varus/valgus contact moment were found. Tibial inertial parameters showed the highest correlations when only BSP uncertainties in subject 1 were investigated, but relatively small impacts on the outputs were observed (Table 4).

Table 4.

Correlations and 1std changes between joint load peaks and input variables that presented a correlation $|r|>0.4$ for subject 1. Italic and bold values represent moderate ($0.4<|r|<0.6$) and strong ($|r|>0.6$) correlations, respectively. Corresponding 1std changes present the same format. Vas Lat PP4 = path point of the vastus lateralis muscle fiber on the distal patella. A/P = antero/posterior, S/I = superior-inferior, M/L = medio-lateral, V/V = varus/valgus.

First peak
	Correlation						1std change
Variable	Compressive load			V/V moment			Compressive load			V/V moment
R.Thigh.Inf A/P	0.4			0.02			24.11			0.07
Coronal alignment	0.26			−0.91			15.76			−4.14
Body	Mass	Inertia	COM	Mass	Inertia	COM	Mass	Inertia	COM	Mass	Inertia	COM
Tibia A/P	0.71	−0.03	−0.61	0.33	−0.14	0.23	3.38	−0.12	−2.89	0.05	−0.02	0.03
Tibia S/I		−0.03	−0.13		0.03	−0.17		−0.16	−0.6		0	−0.03
Tibia M/L	−0.04	−0.15	0.06	−0.84	−0.21	−0.7	0.01	−0.12
Muscle	$F_M^o$	$L_M^o$	α	$F_M^o$	$L_M^o$	α	$F_M^o$	$L_M^o$	α	$F_M^o$	$L_M^o$	α
Vas Lat	−0.08	−0.1	−0.01	0.78	0.62	−0.06	−3.13	−0.65	−0.05	2.88	0.59	−0.02
Vas Med	−0.28	−0.75	0.07	−0.39	−0.67	0.18	−11.14	−4.9	0.42	−1.45	−0.64	0.07
Glut Med Ant	0.52	−0.16	−0.76	−0.3	0.06	0.88	20.9	−1.05	−4.73	−1.11	0.06	0.32
Vas Lat PP4 M/L	0.43			0.69			23.79			2.72

Second peak
	Correlation						1std change
Variable	Compressive load			V/V moment			Compressive load			V/V moment
R.ASIS A/P	0.43			0.01			24.17			0.03
Coronal alignment	−0.23			−0.96			−12.8			−4.68
Body	Mass	Inertia	COM	Mass	Inertia	COM	Mass	Inertia	COM	Mass	Inertia	COM
Femur A/P	−0.57	0.03	−0.44	−0.12	0.04	−0.03	−3.69	0.2	−2.85	−0.02	0.01	0
Femur S/I		−0.05	0.23		−0.01	−0.01		−0.31	1.53		0	0
Femur M/L	−0.29	−0.17	0.02	0.03	−1.85	−1.1	0	0.01
Tibia A/P	0.29	0.02	0.32	0.25	−0.02	0.16	1.86	0.16	2.07	0.04	0	0.03
Tibia S/I		0.03	−0.16		0.03	−0.19		0.18	−1.03		0.01	−0.03
Tibia M/L	−0.1	−0.12	−0.01	−0.9	−0.65	−0.76	0	−0.14
Muscle	$F_M^o$	$L_M^o$	α	$F_M^o$	$L_M^o$	α	$F_M^o$	$L_M^o$	α	$F_M^o$	$L_M^o$	α
Gas Lat	−0.06	−0.01	0.05	0.48	0.33	−0.03	−11.21	−0.31	1.62	3.1	0.41	−0.03
Gas Med	−0.54	−0.69	0.88	−0.77	−0.71	0.92	−100.1	−36.08	26.53	−4.93	−0.89	1.08

Several significant correlations were found when only individual muscle parameters were perturbed in subject 1. The muscles that showed the strongest correlation to first and second peaks of compressive load were vastus medialis (maximum isometric force) and anterior gluteus medius (pennation angle) for the first peak, and gastrocnemius medialis (fiber parameters and pennation angle) for the second peak (Table 4). The varus/valgus contact moment was strongly affected by vastus lateralis (maximum isometric force and fiber parameters) and vastus medialis (fiber parameters) at its first peak, and by gastrocnemius medialis (maximum isometric force, fiber parameters, and pennation angle) at its second peak (Table 4).

Validation.

Simulation of walking for the three subjects produced RMS errors of 218 N ($r^2$ = 0.85), 229 N ($r^2$ = 0.91), and 229 N ($r^2$ = 0.85), respectively, between compressive load predicted by the baseline deterministic model and the measured value. The measured loads were within the predicted 5–95% confidence bounds (mean ± 2 std) for 77%, 83%, and 76% of the stance phase. The 5–95% bounds size of compressive load for the three subjects was 43 ± 12%, 50 ± 15%, and 55 ± 18% (mean ± std) of the deterministic prediction during the stance phase. RMS error between measured and predicted varus/valgus moments was 8 Nm ($r^2$ = 0.53), 12 Nm ($r^2$ = 0.11), and 14 Nm ($r^2$ = 0.37) for the three subjects (Fig. 5(a)). The measured moments were within the confidence bounds for 73%, 51%, and 25% of the stance phase (Fig. 6(a)).

Timing and magnitude of processed EMG signals were consistent with estimated muscle activation 5–95% confidence bounds (Fig. 4). Specifically, knee flexors were active at the beginning and end of the gait cycle, whereas knee extensors and ankle plantarflexors were active in correspondence of the first and second peaks of the knee compressive force, respectively.

Comparison Between Subjects.

When 5–95% confidence bounds of kinematics outputs were compared, the ranking of most affected degrees of freedom was consistent among subjects, with marker placement error having a larger impact than tibiofemoral alignment on all degrees of freedom (Fig. 2(b)). Similarly, marker placement error had the largest impact on kinetics outputs when the three subjects were compared (Fig. 3(b)). Joint loads 5–95% bounds showed the same ranking for the three subjects (Figs. 5(b) and 6(b)). Uncertainty in maximum isometric force had consistently the largest impact on both compressive force and varus/valgus moment; tibiofemoral alignment and BSP uncertainties consistently had the smallest influence on compressive force and varus/valgus moment, respectively.

Intersubject differences were revealed in the muscles when results from the sensitivity analysis were compared across subjects. Similar to subject 1, only a few individual marker placement uncertainties showed moderate correlation with joint load in subjects 2 and 3. Uncertainties in coronal alignment and in medio-lateral (M-L) location of tibial center of mass were strongly correlated with both peaks of varus/valgus moment for all the subjects. The muscles that showed strong correlations with the first peak of compressive load were different among subjects: vastus medialis (subject 1), anterior gluteus medius (subjects 1 and 3), and semimembranosus (subjects 2 and 3). Varus/valgus moment first peak was strongly correlated to changes in parameters of vastus lateralis, vastus medialis and anterior gluteus medius for subjects 1 and 3, and to biceps femoris long head, semimebranosus, and central gluteus maximus for subject 2. Conversely, all muscle parameters of gastrocnemius medialis were either moderately or strongly correlated to the predicted second peak of both compressive load and varus/valgus contact moment for all the subjects.

Discussion

A global probabilistic analysis that evaluated the influence of experimental and model uncertainties on joint kinematics, joint dynamics, muscle forces, and knee contact loads was presented. Marker misplacement strongly influenced the calculated joint kinematics and net torques, whereas muscle maximum isometric force and muscle path had the largest impact on muscle forces and compressive load variability. These results demonstrate the necessity of including subject-specific musculoskeletal parameters and geometry for the assessment of joint loading.

The 5–95% confidence bounds of the predicted compressive load captured the general shape and timing of the experimental contact force for the analyzed activity with RMS errors and $r^2$ values comparable to Grand Challenge competitors [14]. The compressive loads measured in vivo were within the bounds for most of the stance phase (77%, 83% and 76% for the three subjects). In particular, the predicted bounds captured the experimental value at the two peaks (weight acceptance and contralateral heel strike). Only during the swing phase of gait was the compressive load consistently underestimated by the model, although the trend of the predicted bounds was clearly similar to the measured load (Fig. 5). This may be explained by a muscle activation strategy used by the subjects that includes muscle co-contractions that was not enforced in the static optimization algorithm and can be interpreted as preparatory mechanism of joint stabilization [61].

Predicted varus/valgus contact moments for the three subjects were generally less accurate than compressive loads. Correlation between deterministic predictions and experimental measurements were significant for all subjects (p < 0.05) but $r^2$ values were on average 0.34. Measured values were captured by confidence bounds for 73%, 51%, and 25% of the stance phase. These results show that the musculoskeletal model and the optimization technique used in this study to solve the muscle redundancy problem provide satisfying predictions of muscle force allocation among main muscle groups (quadriceps, hamstrings, gastrocnemius), whereas predictions of the distribution of load on the tibia may require more sophisticated estimates of muscle forces, contact point location and the inclusion of passive tissues such as the tibiofemoral ligaments.

There are limitations of our study that should be considered. First, although several sources of uncertainty were included in the probabilistic analysis, some features of the model remain uncertain. For example, the employed scaling technique affects inertial parameters, muscle fiber parameters, muscle attachment, and via point locations, segment dimensions and joint center locations according to marker-based ratios. While uncertainty in inertial, muscle fiber parameters and muscle geometry was addressed in the present study, uncertainty sources such as segment dimensions and joint location may influence simulation outputs but were left out to focus the investigation on the most common sources of uncertainty.

The second limitation was that maximum isometric forces of muscles in the same limb were not assumed to be correlated. Correlations were not taken into account in this study because no quantitative data was found in the literature to support this assumption (e.g., similar scaling of the maximum isometric force of the medial and lateral gastrocnemius). If correlations between fiber strengths of the same muscle group were included, maximum isometric force uncertainty might have a smaller impact on varus/valgus contact moment because activation distribution among fibers on the medial and lateral sides of the knee might be more similar. Although the modeled uncertainty in maximum isometric force was significant and a limited number of simulations failed for not achieving dynamic equilibrium, its source [53] was considered the most complete dataset with the given information about the subjects (measurements from 21 cadavers).

The third limitation of this study was related to the input data used to model the uncertainty in muscle path. Moment arms, which represent the effectiveness of a muscle in generating force or torque along a degree of freedom, are mainly defined by the geometry of the muscle and therefore by the location of the attachments and via points used to describe it in the model [22]. Uncertainty in attachment and via point locations not investigated by Duda et al. [57] was modeled with a normal distribution with a 5 mm std that is an approximation of the uncertainty in locating an anatomical landmark and estimating attachment sites as points from irregular areas on the surface of the bones [58,59]. However, straightforward scaling does not account for all intersubject variability in muscle size, shape, and path point sites [62]. Since a 5-mm std has a significant impact on joint loads, we assume that greater uncertainty in attachment sites would produce even larger output bounds.

The combined effect of all the included sources of uncertainty significantly impacted joint load. Different sources of uncertainty had significantly different impacts on the analyzed outputs. Valente et al. stated that uncertainties in parameter identification of their subject-specific model had a moderate effect on model predictions (knee compressive load included) and that no specific parameter was crucial to model robustness [37]. However, Valente et al. measured muscle cross-sectional area using full lower limb MRI that allowed better identification of muscle maximum isometric force values and, consequently, a smaller uncertainty. In addition, other musculotendon parameters (optimal fiber length, tendon slack length, and pennation angle) were not modeled. These parameters were shown to have a significant effect on muscle force and function predictions [21,22,36]. Myers et al. showed that muscle force predictions were mostly influenced by uncertainty in muscle parameters and, in particular, by tendon slack length variability [36]. In the present study maximum isometric force and muscle path points location had the highest impact on muscle forces and compressive load, whereas tendon slack length was less impactful (27% of maximum isometric force bounds size for subject 1). This can be explained by the different input distributions used by Myers et al. First, maximum isometric force uncertainty was chosen from a cadaver study that included just two specimens [63]; second, tendon slack length was included by using the COVs specified in Ward et al. for optimal fiber length. However, variability in fiber parameters can be assumed to have a stronger influence on muscle forces when activities with high range of motion and muscle length changes are analyzed (e.g., squat, chair rise).

The three input uncertainties that had the largest impact on compressive load were maximum isometric force, muscle path, and joint kinematics. Estimates of muscle and joint loading might be improved by more accurate subject-specific determination of these inputs. Maximum isometric force derived from measurements in cadavers is most often tuned in musculoskeletal models to match measurements of isometric and isokinetic torque. This strategy can be used to obtain baseline maximum isometric values by averaging results for different subjects [40], and also to tune subject-specific strength values to peak torques measured during isometric contractions [64]. Alternatively, subject-specific maximum isometric forces have been estimated from the physiological cross-sectional area of the muscle obtained from MRI or CT images [37,65,66]. However, image-based models can be expensive and especially challenging and time-consuming to create. Correlations between muscle strength and anthropometric measurements could be used to assess subject-specific parameters or reduce the intersubject variability in probabilistic analyses. Relationships between 35 lower limb muscles to height and body mass were investigated in a group of 24 young, healthy subjects using MRI [66] and several correlations between the volumes of muscle groups and the product of body mass and height were observed. However, Handsfield et al. acknowledged their results cannot be generalized to all humans because many factors like inactivity, disease-related atrophy or obesity can affect muscle volumes in different populations [66]. An increase of publicly available musculoskeletal parameter data is needed for more rendering of subject-specific parameters from population-based databases.

The second most impactful uncertainty in this study was muscle geometry. This variable has a large influence on muscle force predictions because it determines the moment arm of the muscle, and therefore its effectiveness in joint torque generation. Muscle attachment and via point location also influences the joint load calculation since it affects muscle lines of action, and therefore the joint force direction. Muscle attachment sites and geometry can be identified from MRI images to obtain more realistic subject-specific moment arms and lines of action [37,62,67]. However, the geometric description of a muscle cannot be reduced to one single joint configuration because muscles wrap around many structures (especially bones and other muscles) and take on different shapes. Models with linear representations of muscle fibers that make use of via points and wrapping surfaces provide moment arms in good agreement with average values measured in vitro [68], but an intrinsic uncertainty remains in subject-specific moment arms.

Inaccuracies of marker-based measurement of joint kinematics are challenging to overcome. Techniques such as videofluoroscopy allow submillimeter and sub-degree accuracy [69]. However, this solution is not always accessible and requires subject exposure to X-ray. In addition, it is limited to acquisitions of a single joint at a time, and tracking kinematics involves time-consuming manual work. Therefore, the need for noninvasive accurate solutions is still a priority. Results from the present work show that joint kinematics and subsequent calculation of joint loads can be affected by uncertainty in single markers, which demonstrates the importance of quantifying and accounting for this kind of uncertainty when drawing conclusions.

When results of the probabilistic analysis were compared between the three subjects, relevant differences were not observed in the relative contribution of input distribution groups to the output variability size. The most notable difference was related to the muscles correlated to compressive load and varus/valgus contact moment first peaks: while for subjects 1 and 3 the peaks showed strong correlations with vasti parameters, high correlations to hamstrings were observed for subject 2. This can be partially explained by the need of a higher hip extension torque during weight acceptance (i.e., when the first joint load peaks occur) in subject 2. The similarity among subjects strengthens the conclusion of the present study that correct identification of subject-specific maximum isometric forces, muscle geometries, and marker placements is more crucial than for the other perturbed parameters when muscle forces and joint loads are estimated.

In conclusion, our study demonstrated that uncertainty in the large number of parameters that must be estimated to perform a pipeline of biomechanical analyses with a commonly used musculoskeletal model has a significant impact on joint kinematics, muscle forces and contact loads. Results for subjects with TKR during gait were most sensitive to uncertainties in kinematics, muscle strength, and muscle geometry. Although better subject-specific measurements may provide more precise knowledge of these inputs and improve estimates of muscle and joint loads, demonstrating the reliability of these estimates requires evaluation of uncertainty.