Comparative Risk Predictions of Second Cancers after Carbon-Ion Therapy versus Proton Therapy

Abstract

The purpose of this work was to propose a theoretical framework that enables comparative risk predictions for second cancer incidence after particle-beam therapy for different ion species for individual patients, accounting for differences in relative biological effectiveness (RBE) for the competing processes of tumor initiation and cell inactivation. Our working hypothesis was that using carbon-ion therapy instead of proton therapy would show a difference in the predicted risk of second cancer incidence in the breast for a sample of Hodgkin lymphoma (HL) patients. We generated biologic treatment plans and calculated relative predicted risks of second cancer in the breast using two proposed methods: a full model derived from the linear-quadratic model and a simpler linear-no-threshold model. For our reference calculation, we found the ratio of predicted risk of breast cancer incidence for carbon-ion versus proton plans <R_c/R_p> to be 0.75±0.07 but not significantly smaller than 1 (p=0.180). Our findings suggest that second cancers risks are, on average, comparable between proton therapy and carbon-ion therapy.

1. Introduction

A worldwide milestone has recently been reached that over 100,000 cancer patients have now been treated with proton therapy and more than 13,000 patients have been treated with carbon-ion therapy (PTCOG 2014). These high-energy particle beams can often achieve excellent disease control while delivering minimal radiation dose to healthy tissue near cancer targets [43]. This is important because patients can sometimes experience devastating side effects of radiation, including second primary cancers, lung fibrosis, cardiac toxicity, and infertility [37]. Recently, a patient-outcome study investigated second cancer incidence after therapy with photons or protons [4], and from those data it appears that protons offer a significantly lower rate of carcinogenesis than photons. Due to the sharper physical dose gradients [47] and differential relative biological effectiveness (RBE) [12], carbon-ion therapy might provide reduced dose to normal tissues compared to proton therapy [12,18,38]. However, the capacity of high LET radiation to induce late effects is much less understood than that of low LET radiation and could increase risks of second cancer after radiotherapy.

To estimate risks of tumor initiation after exposure to radiation, many works rely on epidemiological studies of atomic bomb survivors and follow up of cancer survivors [9,45] and recommend a linear-no-threshold risk model [32]. However, at higher radiation doses, cell sterilization may lead to a non-linear decrease of cancer risk. Furthermore, the carcinogenesis process may itself exhibit non-linear dose response, as seen clearly in in-vivo experiments, e.g., induction of tumors in mice [5,44] and seen in in-vitro cell transformation experiments [48]. These findings have inspired the development of nonlinear risk models [39], which have been used to estimate second cancer risks after modern radiotherapy techniques [33].

To estimate risks after ion-beam therapy, a method of calculating RBE for tumor initiation by ions is needed. Since the exact mechanism of cancer induction by radiation is not known, it is not possible to assume the same RBE will hold for different endpoints, e.g., cell sterilization versus tumor initiation. For instance, Barendsen [2] demonstrated the variety in RBE as a function of LET for different DNA damage endpoints. To understand RBE for cell transformation, several studies were carried out in in-vitro assays [31,48]. Additionally, Alpen et al. [1] reported the RBE for tumor initiation in the Harderian gland of mice for various ions. Given this composite body of knowledge, RBE for ion beams is seen to depend not only on the particle LET but also on the ion species [17]. One recent radiation-risk model [7] accounts explicitly for the effects of particle species and LET, but the model is designed for astronauts. Similarly, Manem et al. [30] derived a model for second cancer risk estimation after ion therapy but did not consider realistic patient treatment factors such as variable dose and LET spectra present within patient anatomy.

In this paper, we propose a theoretical framework that enables comparative risk predictions for second cancer incidence after particle-beam therapy for different ion species for individual patients. We used this framework to test the working hypothesis that using carbon ion therapy instead of proton therapy would show a systematic difference in the predicted risk of second cancer incidence in the breast for female Hodgkin lymphoma (HL) patients. We calculated relative predicted risks of second cancer in the breast using two new methods, one derived from the linear-quadratic (LQ) model and another, simpler model derived from the linear-no-threshold model for cancer incidence. We further investigated the sensitivity of our risk predictions to uncertainties in our RBE model parameters.

2. Methods

2.1. Patient Sample

We selected patient records for 9 women with stage II HL diagnoses and bulky disease targets localized above the diaphragm. We chose to study this disease because of its high incidence in young adults, its favorable response to therapy, and because a significant risk of radiation-induced second cancer persists many years after therapy [10]. Data collection was approved by the University of Texas MD Anderson Cancer Center (Houston, TX) institutional review board.

2.2. Biologically Optimized Treatment Planning

Biologic treatment planning for scanned proton therapy and scanned carbon ion therapy was performed using the TRiP98 treatment planning system (TPS) [25,27] and the Local Effect Model [41] in its recent implementation Version IV (LEMIV) [12,16,18,41]. For all patients, scanned proton and scanned carbon treatment plans were prepared as follows.

1. Tables of the RBE for cell sterilization (RBE_s) were computed using LEMIV. We estimated α/β ratios of 8 Gy for the HL target [36] and 3 Gy for breast [39,49]. These tables consisted of RBE values for carbon and all lighter ions (including fragments) down to hydrogen at various kinetic energies. Those values along with physical beam data were used as input to TRiP98 to allow calculation of RBEs-weighted dose for particle fields of mixed ion species and mixed LET [26].

2. Scanned proton and carbon fields were planned to irradiate the clinical target volume (CTV) using a single anterior-to-posterior beam direction [21]. Ion pencil beams had focal spot sizes (in air) of 12.4 ± 1.7 mm full-width at half-maximum (FWHM) for protons and 7.0 ± 0.3 mm FWHM for carbon ions, typical of centers with active scanning beam delivery.

3. Particle numbers were optimized to provide a prescribed uniform RBE-weighted dose of 36 Gy (RBE) given in 2 Gy (RBE) fractions [22].

4. Absorbed doses, RBE_s-weighted doses, and dose-averaged LET were calculated in each CT voxel for the proton and carbon fields [24-26].

2.3. Calculation of Relative Risks of Second Cancer Incidence

We calculated the ratio (R_c/R_p) of predicted risk of breast cancer incidence for each patient after proton (p) and carbon (c) therapy as

$$\frac{R_c}{R_p}=\frac{\langle T_c{S}_c\rangle }{\langle T_p{S}_p\rangle }$$ (1)

where T is the probability of a tumor-initiating event occurring in a cell (or voxel) and S is the probability that a cell survives after irradiation. The brackets indicate that we averaged voxel calculations of TS over all voxels in the breast for carbon and proton plans before identifying the ratio, similar in concept to that of “organ equivalent dose” [35,40]. For the tumor-initiating term, we investigated 2 models. The first model, which we refer to as the “full model,” was derived using a linear-quadratic framework as

$$T=1-\exp \{-n[{\mu }_x{d}_i{\mathrm{RBE}}_T+{\nu }_x{\left(d_i{\mathrm{RBE}}_T\right)}^2]\}$$ (2)

where n is the number of fractions, μ_x and ν_x are the linear and quadratic terms, respectively, for tumor initiation by a given dose of x rays (x), d_i is the single-fraction absorbed dose from ions (i) to each voxel in the breast, and RBEt is the RBE for tumor initiation, which in general depends on LET, particle species, and dose. For this study, we considered a plausible range of μ_x/ν_x to be 1-5 Gy and assumed a reference value of 3 Gy with μ_x of 0.0226 [breast cancers per 30 person-years per Gy (RBE)], corresponding to an exposed age of 20 years and an attained age of 50 years [39]. For the full model, we express the dose dependence of RBEt as

$${\mathrm{RBE}}_T=\frac{\sqrt{{\mu }_x^2+4{\nu }_x\left({\mu }_i{d}_i+{\nu }_i{d}_i^2\right)}-{\mu }_x}{2{\nu }_x{d}_i}.$$ (3)

which can be derived in the LQ framework considering RBEt = d_x/d_i under the condition of equal biologic effect, where ${\mu }_i{d}_i+{\nu }_i{d}_i^2={\mu }_x{d}_x+{\nu }_x{d}_x^2$ (cf. Supplement 1). The linear term μ_i is found by μ_i = μ_x RBE_t,α, where RBE_t,α represents the RBE for ions to initiate tumors at very low absorbed doses (the limit as dose approaches zero). For both protons and carbon-ions, we evaluated the case when ν_i = ν_x, as might be expected for lower LET radiation, and we also evaluated the opposite extreme case when the quadratic component was negligible (ν_i = 0), as might be expected for high LET radiation [14]. For the RBE_t,α term, we assumed a linear LET dependence

$${\mathrm{RBE}}_{T,\alpha }=1+k\mathrm{LET}$$ (4)

where k depends on ion species [3,8,15,20]. We assumed further a constant linking factor between the coefficient k for proton and carbon ions, k_p = κ k_c, accounting that the RBE of protons increases with LET faster than that for carbon ions [15,38]. For our reference case, we chose k_c = 0.09 μm/keV and κ = 5. For sensitivity testing, the parameter k_c was varied within the interval 0.01 < k_c < 0.49 μm/keV, reflecting a plausible range for RBE_t,α between 2 and 50 for carbon ions at 100 keV/μm. Further, we investigated the sensitivity of our results to variable κ in the range of 1-10.

The second model for tumor initiation, which we refer to as the “simple model,” was derived using a linear-no-threshold approach and neglecting dose dependence on RBE_t as

$$T={\mu }_{x}n{d}_i{\mathrm{RBE}}_{T,\alpha }.$$ (5)

Thus, this simple model assumes that the probability of tumor initiation increases in a simple linear fashion with dose and increases with LET. In the simple model, the exact value of μ_x does not affect the ratio of risk since it mathematically cancels out (cf. Equation 1).

Assuming that only surviving breast cells pose risk for tumor induction, we used a standard linear-quadratic survival calculation

$$S=\exp \left\{-n\left[\alpha d_i{\mathrm{RBE}}_S+\beta {\left(d_i{\mathrm{RBE}}_S\right)}^2\right]\right\},$$ (6)

where RBE_s was calculated using the treatment planning system using an α/β for breast cell sterilization of 3 Gy, and our reference α value was set to 0.067 Gy⁻¹ [39]. We also investigated the effect of variable cell sensitivity on our findings, considering a plausible range for α of 0.01-0.1 Gy, based on values reported in the literature for a broad range of human tissues [13].

2.4. Statistical Analysis

We first analyzed differences in the mean RBE_s-weighted doses to organs-at-risk near the HL target. Second, we analyzed the ratio of risk of second cancer incidence in the breast. Significance was assessed using a (nonparametric) two-sided Sign Test; differences having a p statistic less than 0.05 were considered significant.

3. Results

3.1. Comparison of biologically optimized treatment plans

A comparison of proton and carbon ion treatment plans is shown in Figure 1 for HL Patient #1. Compared to the proton plan, the carbon plan shows a more rapid falloff of the high dose region. Interestingly, the carbon treatment plan shows a thin, halo-shaped region of overdose in healthy tissue near the CTV on all sides, due to the different radiosensitivity of the HL tumor and the surrounding normal tissue. In addition, a non-zero exit dose is seen for carbon, due to fragmentation of the carbon projectiles. Differences between the carbon and proton plans for Patients #2 - #9 were similar to those seen for Patient #1.

Figure 1.

RBE_s-weighted dose from proton (left) and carbon ion (right) treatment plans for HL Patient #1. Contours shown for the CTV (T), right breast (RB), left breast (LB), lung (L), esophagus (E), spinal cord (C), and heart (H).

Table 1 reports the mean RBE_s-weighted organ doses to the breast, heart, lung, esophagus, and spinal cord, averaged over the 9 patients. We found a significant (p=0.004) advantage for carbon-ions over protons for sparing the breast, heart, and lung, a slight (insignificant) advantage for sparing the esophagus, and a slight (insignificant) disadvantage for the spinal cord, due to the exit dose of the carbon fragmentation tail.

Table 1.

Mean and standard error for RBE_S-weighted dose (D) to organs near the target for carbon (c) versus proton (p) plans for 9 HL patients. Sig. indicates whether a ratio was significantly different than 1.

Organ	Dp [Gy (RBE)]	Dc [Gy (RBE)]	Dc/Dp	Sig.	p
Breast	3.40 ± 0.85	2.15 ± 0.65	0.63	yes	0.004
Heart	6.06 ± 1.51	4.42 ± 1.32	0.73	yes	0.004
Lung	6.45 ± 0.98	4.80 ± 0.76	0.74	yes	0.004
Esophagus	11.10 ± 2.46	9.79 ± 2.32	0.88	no	0.18
Cord	0.40 ± 0.11	0.84 ± 0.16	2.1	no	0.508

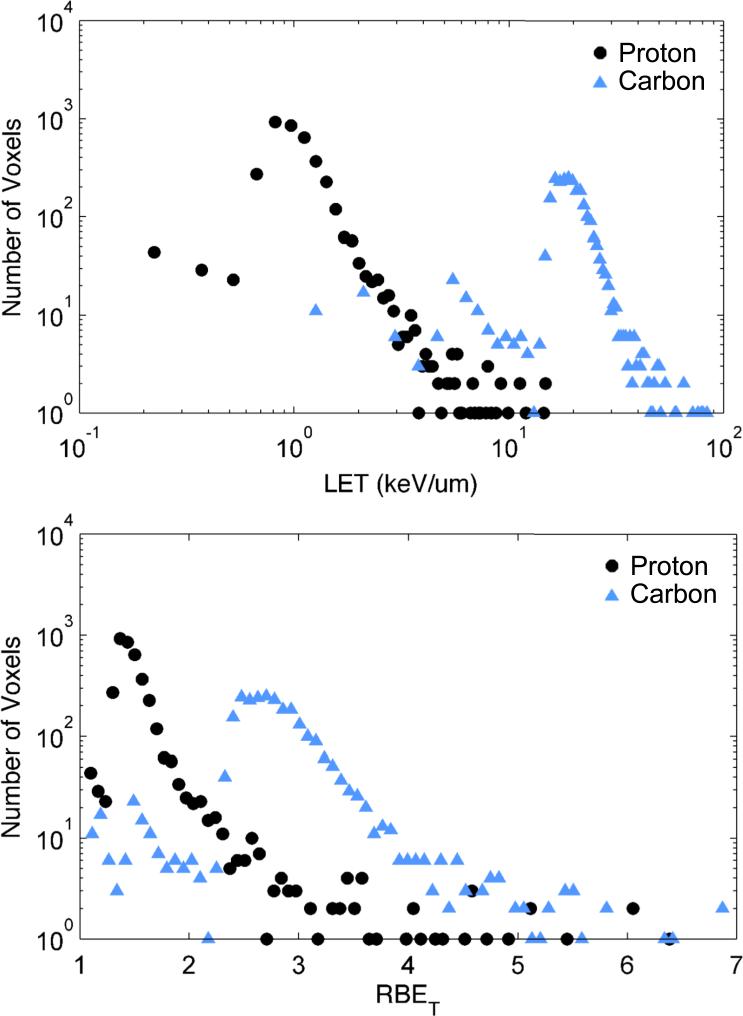
Histograms of dose-averaged LET for all breast voxels for all patients are shown in Figure 2 (a). Importantly, the vast majority of values of dose-averaged LET were lower than typical values of LET where saturation effects in RBE are known to occur, namely near 20-30 keV/μm for protons and near 100-200 keV/μm for carbon ions. Corresponding histograms of predicted RBE_t are shown in Figure 2 (b) for the reference case parameters (cf. Table 2).

Figure 2.

Histograms (top) of dose-averaged LET in breast voxels for all 9 patients. Corresponding histograms of RBE_T in each voxel shown (bottom) for reference case parameters of the full model.

Table 2.

Sensitivity analysis of the mean ratio of risk <R_c/R_p> to plausible variation in model parameters. Parameters varied with respect to the reference case (Ref.) are indicated in the leftmost column. SE indicates standard error. Sig. indicates whether a ratio of risk was significantly different than 1.

Variables	Model	α (Gy−1)	μx/νx (Gy)	ν i	kc (μm/keV)	κ	<Rc/Rp>	SE	Sig.	p
Ref.	Full	0.067	3	ν x	0.09	5	0.75	0.07	no	0.180
κ	Full	0.067	3	ν x	0.09	1	0.92	0.08	no	0.180
	Full	0.067	3	ν x	0.09	10	0.62	0.06	yes	0.004
kc	Full	0.067	3	ν x	0.01	5	0.51	0.05	yes	0.004
	Full	0.067	3	ν x	0.19	5	0.85	0.08	no	0.180
	Full	0.067	3	ν x	0.49	5	0.87	0.08	no	0.180
μx/νx	Full	0.067	1	ν x	0.09	5	0.69	0.06	yes	0.004
	Full	0.067	5	ν x	0.09	5	0.76	0.07	no	0.180
α	Full	0.01	3	ν x	0.09	5	0.68	0.05	yes	0.004
	Full	0.1	3	ν x	0.09	5	0.74	0.08	no	0.180
ν i	Full	0.067	3	0	0.09	5	0.80	0.07	no	0.180
kc and κ	Simple	0.067	-	ν x	0.01	1	0.55	0.05	yes	0.004
	Simple	0.067	-	ν x	0.09	1	1.18	0.11	yes	0.039
	Simple	0.067	-	ν x	0.19	1	1.87	0.17	yes	0.039
	Simple	0.067	-	ν x	0.49	1	3.31	0.30	yes	0.004
	Simple	0.067	-	ν x	0.01	5	0.52	0.05	yes	0.004
	Simple	0.067	-	ν x	0.09	5	0.88	0.08	no	0.180
	Simple	0.067	-	ν x	0.19	5	1.10	0.11	no	0.508
	Simple	0.067	-	ν x	0.49	5	1.38	0.14	yes	0.039
	Simple	0.067	-	ν x	0.01	10	0.50	0.05	yes	0.004
	Simple	0.067	-	ν x	0.09	10	0.66	0.06	yes	0.039
	Simple	0.067	-	ν x	0.19	10	0.73	0.07	yes	0.039
	Simple	0.067	-	ν x	0.49	10	0.80	0.08	no	0.180

3.2. Relative risks of second cancer incidence in breast

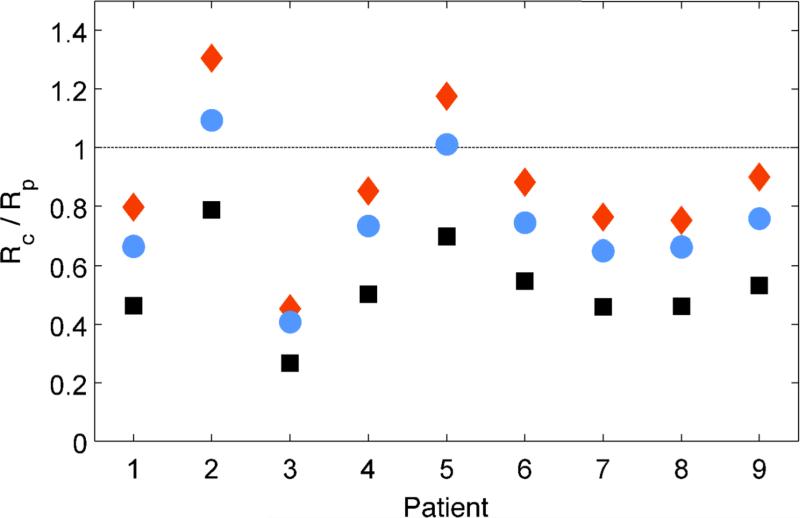
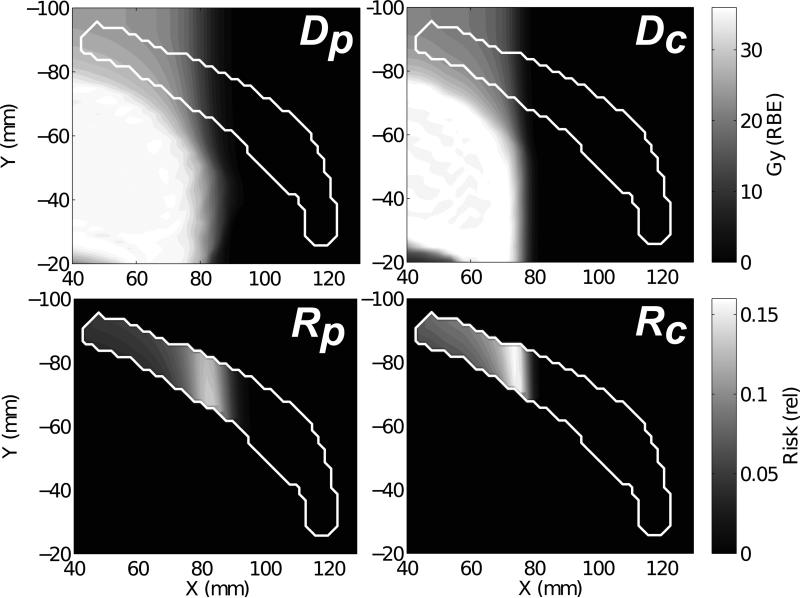
Predicted ratios of risk (R_c/R_p) of breast cancer incidence for the 9 HL patients receiving scanned carbon ion versus scanned proton therapy are shown for a subset of model parameters in Figure 3. For the full model with our reference case parameters (cf. Table 2), the mean and standard error of the ratio of risk for all patients was <R_c/R_p> = 0.75 ± 0.07, in favor of carbon-ion therapy but not significant (p = 0.180). The simple model predictions (cf. Equation 5) are also shown in Figure 3 for values of α, μ_x/ν_x, ν_i, and κ equal to those from the reference case, but with variable k_c of 0.01 - 0.09 μm/keV. For clarity, we remark that the simple model predictions included in Figure 3 correspond to RBE_t ranging from 2-10 for carbon ions at 100 keV/μm. Figure 4 shows spatial maps of predicted risks in the left breast in comparison to the RBE_s-weighted dose. Areas of relatively high risk are seen qualitatively for both modalities near the lateral beam penumbra.

Figure 3.

Predicted ratio of risk (R_c/R_p) for breast cancer incidence for the 9 HL patients receiving scanned carbon versus scanned proton therapy. Blue circles show reference-case predictions using the full model (cf. Equation 2). Orange diamonds show simple model predictions (cf. Equation 5) for k_c = 0.09 μm/keV and κ = 5, which we considered as a likely upper bound for RBE_t for therapeutic doses. Black squares show simple model predictions but with a k_c of 0.01 μm/keV and κ of 5, which we considered as a lower plausible bound for RBE_t.

Figure 4.

RBE_s-weighted dose (D) distribution in the left breast (white contour) from proton (p) and carbon (c) treatment plans for HL Patient #1. Corresponding voxelized risks (R) of second cancer incidence shown below for reference case parameters of the full model.

The results of our sensitivity analysis are included in Table 2. The data indicate the mean predicted ratio of risk <R_c/R_p> was highly dependent on the biological model parameters and, in many cases, was not significantly different than 1. However, for the full model, <R_c/R_p> was always less than 1, and we observed for 7 out of 9 patients that carbon-ion therapy provided a lower predicted risk of second cancer incidence than proton therapy, no matter the exact biological parameters used in this study. For the simple model, some parameter sets (lower κ and higher k_c) led to opposite results in favor of proton therapy. While we expected those parameters were less plausible than our reference case, we included them for completeness of sensitivity testing and acknowledge that under those extreme conditions, the major findings of our work would change. Looking at the overall trends in Table 2, we found that <R_c/R_p> was, generally, (1) lower when dose effects on RBE_t were included using the full model compared with the simple model, (2) lower with higher κ, (3) increased with higher k_c, (4) higher with higher μ_x/ν_x, (5) higher with higher α, and (6) lower with higher ν_i. By far, <R_c/R_p> depended most strongly on k_c and κ.

4. Discussion

We found that the predicted risk of second cancer incidence in the breast after carbon-ion therapy versus proton therapy was highly dependent on the patient and disease anatomy, the biological parameters used in our risk model, and the absorbed dose within the simple model formalism applied. The results using our full model indicate that, on average, carbon ion therapy offers a lower predicted risk of second cancer incidence in the breast for female HL patients compared to proton therapy, but differences were not significant. We interpret this trend to mean that smaller volumes of breast tissue were exposed to carbonion radiation than proton radiation, and that condition, along with the sterilization of cells in the high-dose, high-LET portion of the radiation field, outweighed the increased risk of tumor induction predicted at higher LET. This interpretation is in general agreement with the study of Durante et al. [11], which reported lower chromosomal aberrations in circulating lymphocytes for patients treated with carbon-ion versus photon therapy. Due to the large underlying biological uncertainties, the uncertainties in the model of RBE_t, and the variation seen among patients, it is difficult to draw strong conclusions from this study. Nonetheless, our findings indicate an important trend, and our interval of calculated risk ratios suggest that it could be better to use carbon ion therapy instead of proton therapy for some patients to reduce second cancer risks.

A particular strength of this work was that we performed the first in-silico comparison of carbon ion therapy versus proton therapy for HL patients. Another strength was that we calculated relative risks of second cancer incidence after particle-beam therapy on a voxelized basis considering (1) absorbed dose, (2) dose-averaged LET, (3) cell sterilization, and (4) variable RBE for tumor initiation. In addition, we performed sensitivity tests to understand the robustness of the risk predictions to uncertainties in biological model parameters.

This study had several limitations. First, we used a linear RBE versus LET model for tumor induction, expected to fail at high LET when second-order (e.g., saturation) effects might occur. Given the scarcity of knowledge regarding tumor induction as a function of LET, we decided that a linear relation was the simplest relation to assume, and, in this work, we only applied this model to relatively low LET values found in the breast in the beam entrance path. Second, we did not account for secondary neutron production [19,23,28,34]. We include Supplement 2 to show that neutron exposures would not greatly affect our findings for breast in the primary beam path. However, further work is needed to accurately model dose and LET distributions outside the primary field. Third, we estimated risks based on a simplistic model of tumor induction using linear and linear-quadratic formalisms that essentially rely on a core simplistic concept of a “tumor-initiating event.” We acknowledge that cancer formation is a multistage process that involves multiple temporal and functional domains. More detailed risk modeling approaches have been developed [29,46]; [42] that provide a more mechanistic picture and are likely more physiologically realistic. Such an approach might also be desirable to understand risks after hypofractionated therapy, where the LQ model's relevancy is debated, for example, due to macroscopic (or systemic) tissue disruptions unique to higher fraction doses. However, we avoided such complex models and chose a simpler framework for two major reasons: (1) The aforementioned parameters all must be estimated or fit to epidemiological data that are simply not available for patients treated using multiple ion species, and (2) we only considered the ratios of risk on paired data sets, meaning we only focused on differences in radiation-induced initiation between proton therapy and carbon-ion therapy and assume all other host factors are identical. Thus, the increased complexity would not be expected to change relative trends found in our study. To better understand this, we did investigate the influence of a non-targeted effects model [6] and found minimal impact on our risk predictions.

In conclusion, we proposed a new methodology for comparative predictions for second cancer risks after ion-beam therapy. We explicitly modeled the biological effectiveness of the particle beams to induce the competing processes of tumor initiation and cell inactivation on a voxelized basis throughout the patient anatomy including fractionation effects on cell survival. Our findings suggest that second cancer risks are, on average, comparable between proton therapy and carbon-ion therapy but vary among patients. Thus, individual patient risk predictions are likely beneficial to screen patients that would most benefit from carbon-ion therapy or from proton therapy.

Summary.

This work proposes a theoretical framework that enables comparative risk predictions for second cancer incidence after particle-beam therapy for different ion species. We modeled the biological effectiveness of ions to initiate second cancers on a voxelized basis for individual patients, considering variations in dose and linear energy transfer. Our methods may be used to identify which patients from a cohort are likely better candidates for carbon-ion therapy versus proton therapy.