Summary
We consider the joint modelling, analysis and prediction of a longitudinal binary process and a discrete time-to-event outcome. We consider data from a prospective pregnancy study, which provides day level information regarding the behaviour of couples attempting to conceive. Reproductive epidemiologists are particularly interested in developing a model for individualized predictions of time to pregnancy (TTP). A couple’s intercourse behaviour should be an integral part of such a model and is one of the main focuses of the paper. In our motivating data, the intercourse observations are a long series of binary data with a periodic probability of success and the amount of available intercourse data is a function of both the menstrual cycle length and TTP. Moreover, these variables are dependent and observed on different, and nested, timescales (TTP is measured in menstrual cycles whereas intercourse is measured on days within a menstrual cycle) further complicating its analysis. Here, we propose a semiparametric shared parameter model for the joint modelling of the binary longitudinal data (intercourse behaviour) and the discrete survival outcome (TTP). Further, we develop couple-based dynamic predictions for the intercourse profiles, which in turn are used to assess the risk for subfertility (i.e. TTP longer than six menstrual cycles).
Keywords: Binary data, Discrete survival, Empirical Bayes predictions, Semiparametric models, Shared parameter models
1. Introduction
Fecundity is defined as the biologic potential of men and women for reproduction and is often measured by estimating the probability of pregnancy in each menstrual cycle among couples having regular unprotected intercourse (Gini, 1928). Estimating fecundity is challenging, in part, given the effect that varying patterns of sexual intercourse may have on the length of an attempt at pregnancy (Stanford and Dunson, 2007). Clinical guidance is sometimes sought to aid couples in timing acts of intercourse around ovulation to minimize the time that is needed to achieve pregnancy. There is little empirical evidence delineating the timing of intercourse relative to ovulation, resulting in a generalized clinical recommendation to have intercourse every other day (Practice Committee of the American Society for Reproductive Medicine, 2013). Understanding the relationship between fecundity, intercourse behaviour and other relevant covariates is increasingly relevant given population level changes in the sociodemographic characteristics of reproductive-aged couples such as an increase in age at first pregnancy (Mathews and Hamilton, 2002). This may be associated with reduced intercourse activity, longer time to pregnancy (TTP), an increased prevalence of infertility or a combination of all these factors (de La Rochebrochard and Thonneau, 2003; Dunson et al., 2004).
Our main objective in this paper is to model intercourse behaviour, a binary longitudinal process, and TTP, a survival outcome, jointly, with a view towards prediction of both processes. Our modelling procedure is motivated by a scientific interest in understanding the change in the probability of intercourse over time, the distribution of TTP and in predicting a couple’s risk for subfertility (TTP more than six cycles).
Thus far, TTP prediction models have not incorporated day level intercourse information despite its being a necessary criterion for pregnancy. Bortot et al. (2010) used a model for the length of the follicular phase of the menstrual cycle to predict the probability of conception. A limitation of their prediction model was that they treated the intercourse behaviour as fixed, as no model for intercourse behaviour over the whole menstrual cycle was available. McLain et al. (2012) predicted TTP by using the estimated average number of acts of intercourse in the fertile window, which is defined as the days of the menstrual cycle where intercourse can lead to pregnancy. Consequently, one needs to develop methods that will assess the intercourse behaviour over the entire menstrual cycle and to study its effect on TTP, so that couples requiring clinical investigation or intervention can be helped.
To address the objectives of this paper, we utilize data from a prospective pregnancy cohort study that we introduce in Section 1.1. We also discuss the analytical challenges in considering intercourse behaviours over the entire menstrual cycle.
1.1. Prospective pregnancy studies and analytical issues with intercourse data
We utilized data from the Oxford conception study (OCS) (Pyper et al., 2006), which is one of a few prospective cohort studies with preconception enrolment of women who were attempting to become pregnant. The women in the OCS provided daily level information on acts of inter-course, menstrual bleeding, smoking and alcohol consumption, along with couple level baseline covariates. These women were prospectively followed for the number of menstrual cycles that it took them to become pregnant (i.e. human chorionic gonadotropin confirmed pregnancy on the day of expected menses), which is known as their TTP, or a maximum of six menstrual cycles. Other examples of prospective pregnancy cohort studies include the ‘Longitudinal in-vestigation of fertility and environment’ (Buck Louis et al., 2011b), the fertili study (Colombo and Masarotto, 2000) and the Billings study (Colombo et al., 2006).
Next, we discuss key methodological issues that arise in the analysis of intercourse data in prospective pregnancy studies. Each woman is observed for a random number of menstrual cycles (i.e. her TTP, which is subject to right censoring due to loss to follow-up), with a random number of observations per menstrual cycle. Here, TTP and the probability of intercourse depend on various unobserved variables that include libido and daily stressors, as well as a host of external factors like endocrine disrupting pollutants that potentially impact both male intercourse behaviour (Burnett, 2008) and female fecundity (Buck et al., 2002; Buck Louis et al., 2011a). Moreover, TTP and menstrual cycle length are dependent possibly because of common unmeasured covariates (Jensen et al., 1999; Small et al., 2010). Thus, the total number of observations of intercourse is a function of two random processes (i.e. menstrual cycle lengths and TTP) which are dependent.
Previous analyses of day level intercourse data have demonstrated that couples are more likely to have intercourse around ovulation regardless of their intentions about pregnancy (Bullivant et al., 2004; Wilcox et al., 2004), possibly because of an increase in the level of libido or testosterone before ovulation. This results in a periodic pattern of the probability of intercourse, where each menstrual cycle may have a maximum probability of intercourse close to the day of ovulation. As can be seen in Fig. 1, the relationship between day relative to ovulation and the probability of intercourse is non-linear. Since the structure of the relationship is unknown, we use semiparametric cubic B-splines to relate day relative to ovulation and probability of intercourse. To account for the heterogeneity of the probability of intercourse profile between women (possibly caused by heterogeneity in their hormone profiles), we allow for subject-specific random effects for the height and peak (i.e. amplitude) of the cubic B-spline curves.
Fig. 1.
Average number of acts of intercourse on non-bleeding days by the day relative to ovulation (——), along with the longitudinal hormonal patterns of luteinizing hormone (------) and oestrone-3-glucuronide (·-·-·-) scaled to (0,1)
The day relative to ovulation is equal to 0 for the day of ovulation, −1 for the day before ovulation, 1 for the day after ovulation, etc. For each cycle, a fertility monitor uses urinary measurements of luteinizing hormone and oestrone-3-glucuronide to identify impending ovu-lation within 24 h (see Fig. 1). In approximately 10% of cycles, however, the fertility monitor did not detect a day of ovulation. For cycles with unknown day of ovulation, the day relative to ovulation (which is used in our model) cannot be calculated. A missing day of ovulation is an indication that a cycle may have low hormone variability, which in turn could result in a less variable pattern of the probability of intercourse across the menstrual cycle. Ignoring such cycles (i.e. using listwise deletion) may bias results towards cycles with more variable probabilities of intercourse. Our modelling procedure accounts for cycles with unknown day of ovulation to avoid biased results.
The outline of the paper is as follows. In Section 2, we present our data structure and notation. In Section 3, we give our proposed models for intercourse and TTP and the shared parameter model framework. In Section 4, we discuss how to implement joint predictions with the shared parameter model framework using a Monte Carlo empirical Bayes technique. In Section 5, we present our analysis and prediction of the OCS data by splitting it into training and test sets. In Appendix A, we present some technical derivations for our proposed shared parameter model, and in Appendix B we present the details of our estimation procedure.
2. Data structure and notation
This section introduces the data structure and the associated notation that will be used through-out the paper. We present below the fully observed data from the OCS prospective pregnancy study that will be used in the methods proposed.
Typically, women who have enrolled in prospective pregnancy studies (e.g. the OCS) are followed from baseline up to a maximum time point τ (six menstrual cycles in the OCS) at which observation is administratively censored.
During the follow-up, daily intercourse behaviour is measured with Xd denoting the indicator of an act of intercourse on day d of the study.
During the follow-up, the TTP is also evaluated. The quantity is a discrete survival out-come T, indicating the number of menstrual cycles that it took to become pregnant.
The menstrual cycle timescale can be ‘linked’ to the daily timescale through the observed lengths of each menstrual cycle measured in days. The length (in days) of the jth menstrual cycle is denoted by Kj (which is also the maximum number of observations of intercourse in menstrual cycle j). We denote by Yj the follicular phase length that is associated with the jth menstrual cycle.
Let T * denote the TTP and C denote the time to censoring, both measured in menstrual cycles. Note that the latter corresponds to the number of menstrual cycles for which a woman is observed without pregnancy until time τ : Let T = min(T *, C) and Δ = I(T * > C) where I(·) is the indicator function.
Let denote the total number of observable days of intercourse behaviours. Note that no intercourse data are observed after the day of a positive pregnancy test. Furthermore, let X = {X1, …, XN } denote the collection of observable intercourse indicators. However, as shown in Fig. 1 we want to account for the nesting of daily timescales within a menstrual cycle in modelling intercourse. Accordingly, we relabel intercourse in-formation with a nested time index, i.e. X = {Xjk : 1 ≤k ≤Kj ; 1 ≤j ≤T } where Xjk denotes the intercourse indicator on the kth day of the jth menstrual cycle. We use similar time indexing for all daily level covariates of interest.
3. Shared parameter model for longitudinal binary and discrete survival outcomes
We present a shared parameter framework for joint modelling of longitudinal binary data and discrete survival which incorporates the underlying characteristics that are exhibited by these processes. Shared parameter models were introduced in Wu and Carroll (1988) in the general framework of longitudinal data with missingness (see also Ten Have et al. (1998) and Pulkstenis et al. (1998) for related work). One advantage of the shared parameter model framework is that the joint models for intercourse and TTP can be used to predict jointly the probability of intercourse on a given day and the probability distribution of the TTPs. In this section, we give the details of the specific submodels for the intercourse fX(X|b; θ) and the TTP fT (T |b; κ), where θ and κ denote the unknown parameters and b denotes a shared random effect.
3.1. Model for the pattern of intercourse
Here, we seek to develop a model for intercourse that allows the probability to be periodic, varying according to an unknown function within each menstrual cycle. An important aspect of our intercourse model is the cubic B-splines component to account for the periodic non-linear relationship between the probability of intercourse and time, and a mixed model to account for between-subject heterogeneity in the height and peak of the B-splines.
Let
where Xijk is the intercourse indicator for the ith subject on the kth day of the jth menstrual cycle and pijk = Pr(Xijk = 1|Zijk, Wij, Yij, bi; θ) has the functional form
| (3.1) |
with
Here Zijk and Wij are covariate vectors, bi1 and bi2 are random effects, β and ϕ are vectors of regression parameters, g(·) is a smooth function, Yij is the follicular phase length and logit(p) = log{p/(1 − p)}. We estimate g by using cubic B-splines with , Where {B1(·), …, BL(·)} are B-spline basis functions of degree 3.
As discussed in Section 1, variation in hormones across the menstrual cycle contributes to a heterogeneous within-cycle probability of intercourse (i.e. variability in pijk by k; see Fig. 1). This is represented in equation (3.1) by g(k − Yij ) and φij, where k − Yij is the day relative to ovulation and Yij is the follicular phase length. Here, φij represents the peakedness parameter, and bi2 the peakedness random effect. Note that φij is constrained to be positive; the minimum value of 0 indicates that the probability of intercourse has no within-cycle variability. Similar shape invariant mixed models of human hormonal profiles have been considered by Wang et al. (2003) and Albert and Hunsberger (2005) (see also Ding and Wang (2008)).
3.2. Model for time to pregnancy
Next we give a model for the TTP which is a discrete survival model that modifies the hazard function as in Sundaram et al. (2012) accounting for whether a couple put themselves at risk for pregnancy. We assume that the survival outcome, namely TTP, has a discrete hazard
with a complementary log–log-link
| (3.2) |
where Uij is a covariate vector, γ and ξ are vectors of regression parameters and Vij is an indicator that subject i is at risk for an event in menstrual cycle j. As proposed in Sundaram et al. (2012), we modify the hazard by using to identify whether a couple were at risk for pregnancy if intercourse occurred in the fertile window, which is defined here as from day −6 to day 1 relative to ovulation. It is well studied through day-specific conception probabilities that acts on differing days relative to ovulation have a different influence on the probability of conception in a cycle; see for example Dunson and Stanford (2005). So, additionally to the Vij -term we assess the effect of intercourse behaviour through the term ξ. The parameters ξ = (ξ1, ξ2) capture the effect of the intercourse profile on hazard for conception in that cycle. Here, ξ1 is associated with bi1 and captures the effect of the overall chance of having intercourse on a day whereas ξ2 is associated with bi2 and captures the effect of a surge (or lack thereof) in intercourse activity around ovulation. We also include a time-dependent intercept in Uij giving model (3.2) a flexible semiparametric structure. This model is equivalent to the grouped version of the continuous time proportional hazards model (Fahrmeir and Tutz, 2001). The corresponding probability mass and survivor functions are given respectively by
and
In the absence of the at-risk indicator, the complementary log–log-link has also been used in TTP modelling by Scheike and Jensen (1997) and Scheike et al. (1999).
3.3. Joint model for intercourse and time to pregnancy
We next present our proposed joint model for intercourse and TTP. In our context, the number of longitudinal observations N and the intercourse behaviour X are dependent. More precisely, a woman’s value of N is related to her intercourse behaviour X through her TTP; see point (f) in Section 2, i.e. N is a random variable that may potentially be informative for X: Using arguments similar to those in section 5.16 of Cox (2006), by conditioning on N and the random effects, and assuming that the parameters for the distribution of N and those of the TTP and the intercourse behaviour are variation independent, we have
| (3.3) |
where θ and κ are the unknown parameters in the models for intercourse and TTP respectively. Observe that expression (3.3) essentially says that the contribution of N to the log-likelihood of X and T is a term that is independent of the parameters of interest (θ, κ), and in deriving expression (3.3) we have also used the framework of the shared parameter models. We provide the details of the derivation of the above expression specifically for our setting in Appendix A.
3.4. Missing data
In practice, observations are subject to missingness. We focus on two types of missingness that are encountered in our data. These two types of missingness are
missingness of ovulation, i.e. the length of follicular phase in some menstrual cycles is unknown, and
intermittent missingness of the intercourse indicators X.
We first focus on the follicular phase length missingness. For cycles with known follicular phase length, we assume that Yij is observed without error. Let Yi = {Yiobs, Yimis} where Yiobs and Yimis denote the observed and missing Yij respectively, and Rij = 1 if the ith woman’s jth follicular phase length is missing and Rij = 0 otherwise. We include a model on the Yij s due to their informative missingness (as discussed in Section 1.1), and their presence in pijk. We assume that Yij ~ log-normal(νi, σ2) where νi = ν + σb3 bi3 and bi3 > is a random effect. For a cycle with Rij = 1, we integrate over the follicular phase lengths with respect to the log- normal distribution. Note that, biologically, follicular phase length cannot be longer than the menstrual cycle length; however, we found it reasonable to ignore this restriction. We assume that bi = (bi1, bi2, bi3) ~ MVN(0, D), where D is a correlation matrix with off-diagonal elements denoted by ρjk. The Gaussian random-effects assumption has been shown to be robust to misspecification for estimation (see Song et al. (2002), Hsieh et al. (2006) and Rizopoulos et al. (2008)) and prediction (see McCulloch and Neuhaus (2011) and Albert (2012)). In Appendix A, we present details of an adaptive Gaussian quadrature inference method that was used in our data analysis, which we describe briefly below.
To estimate the likelihood of the observed intercourse values, TTP and follicular phase lengths we integrate over unobserved variables. If subject i has no missing follicular phase lengths, this amounts to integrating over bi with respect to fb(·; D). If subject i has missing follicular phase lengths, we integrate with respect to {bi, Yimis} with respect to fb(·; D) and the distribution of Yimis|bi. As a result, the likely values for Yimis are determined by the intercourse behaviour (through the pijks) and Yiobs (through bi3). Here, {bi, Yimis} can be integrated out by using adaptive Gaussian quadrature. An analytic file with all the programs and data used to implement our analyses can be obtained from
Another type of missingness that occurs in practice is the intermittent missingness of the longitudinal process X: We assume that, given the TTP and the menstrual cycle lengths, the intermittent missingness is independent of b as well as the other relevant processes. This is quite reasonable in our motivating example because intermittently missed observations were sporadic and predominantly due to missed diary entries on random days (e.g. due to forgetting to record information). Moreover, the fraction of days where such missingness occurred was small (less than 1%). So our results will probably be robust to a violation of the above assumption. Note that, under such missingness, expression (3.3) still holds.
In light of the various modelling assumptions that are made in our procedure, sections B and C of the on-line supplementary materials contain discussion and exploratory analysis of the model assumptions.
4. Prediction
In this section, we develop methods for predictions of longitudinal and survival outcomes with shared parameter models when time varying covariates are present via a Monte Carlo empirical Bayes procedure. Our method of prediction is applicable when the model proposed has been fitted by using training data, and partial information on the subjects is available. The partial information is denoted by 𝒟ij0 for the history up to menstrual cycle j0 for subject i. Let ψ̂ denote an estimate of the parameter vector ψ = {θ, κ, D, ν, σ}, with variance estimate denoted by Σ̂. Prediction for menstrual cycle j0 + 1 is of interest only if the couple have not achieved pregnancy, so we use Ti = j0 and Δi = 0. We assume that Rij = 0 for j = 1, …, j0; the extension to include missing Yij is straightforward.
Given 𝒟ij<sub>0</sub> and ψ̂, the posterior distribution of bi is
| (4.1) |
Estimates of bi can be made via the posterior mode
The covariance matrix of b̃ ij<sub>0</sub>, which is denoted by Ψ̂ij0, can be estimated from the Hessian matrix of the log-posterior distribution evaluated at b̃ij<sub>0</sub>. We use the posterior mode, instead of the posterior mean, because it does not require the estimation of the normalizing constant of the posterior density.
Given ψ̂, b̃ and Yij, prediction of pijk, which is denoted as p̃ijk, can be made by inputting the estimates into equation (3.1). In our data analysis we include the act of intercourse on the previous day in the fixed effect design matrix. Prediction will be done for an entire cycle of data, so lagged intercourse observations will be unknown for all except the first day. As a result, we use p̃ij(k+1)|l = P(Xij(k+1)=1|Xijk =l, b̃; θ̂); then given p̃ijk predictions can be made sequentially via p̃ij(k+1) = p̃ijk p̃ij(k+1)|1+(1 − p̃ijk) p̃ij(k+1)|0. For the survival outcome, we focus on
| (4.2) |
the conditional survivor function, which can be estimated by using λi(j|b; κ) in expression (3.2). Here, λi(j|b; κ) =0 if Vij =0, where Vij is a function of the Xijk. As a result, we estimate
The predicted hazard for the ith subject’s jth cycle is
We then estimate the conditional survivor by using the first-order approximation
Owing to the unknown follicular phase lengths, we use a Monte Carlo scheme to estimate the marginal expectations of pijk and πi(j|j0). This method is also useful for estimating confidence intervals that are associated with the prediction estimates. To do so, we must account for the uncertainty that is associated with ψ̂, the empirical Bayes estimate b̃ij0 and the future follicular phase lengths Yij. Following arguments given in Rizopoulos (2001), we estimate the distribution of pijk and πi(t|j0) by assuming that ψ̂MVN(ψ̂, Σ̂), and bi ~ t4(b̃ij0, ψ̂ij0 ) where t4 denotes a multivariate t-distribution with 4 degrees of freedom. Using this assumption, Monte Carlo samples of p̂ijk and π̂i(j|j0) for j=j0+1, …, jmax can be made as follows.
Draw ψ(l) ~ MVN.(ψ̂, Σ̂) and b(l)i ~ t4(b̃ij0, ψ̂ij0 ).
Draw for j=j0+1, …, jmax.
Compute p̂ (l)ijk and π̂(l)i(t|j0) by using ψ̂(l), b(l)i and (Y(l)ij0+1, …, Y(l)ijmax).
We repeat (a)–(c) for l=1, …,L. The prediction analysis in Section 5.2 used L=2000. We present the mean values of the Monte Carlo samples, which we denoted by p̂ijk and π̂ (t|j0), along with 95%-quantile-based confidence intervals.
Once values have been predicted for the test data set, the prediction performance is quantified with receiver operating characteristic (ROC) curves of empirically estimated sensitivity, P(p̂ijk> c|Xijk =1), versus specificity, P(p̂ijk ≤ c|Xijk =0), for all c∈[0, 1], and the area under the ROC curve, AUC. Further, we look at the calibration of the prediction by plotting
| (4.3) |
for cl=l=20 with l=1, …, 20. Here, PPl and OPl are the empirical estimated E(p̂ijk|cl−1 ≤ p̂ijk< cl) and E(Xijk|cl−1 ≤ p̂ijk <cl) respectively. The prediction estimates are properly calibrated if PPl ≈OPl for all l.
5. Analysis of the Oxford stress and time-to-pregnancy study
In this section, we present an analysis of a subset of the OCS data that were discussed in Section 1.1. The data that are presented here include n = 338 women, 1064 cycles and 24214 days of information. This analysis does not include 36 women who were excluded from the analysis because of missing values for maternal age, parity or pregnancy status. In this analysis, we are interested in assessing the association between exposures, probability of intercourse and TTP, along with predicting women’s intercourse profiles and TTP survival estimates. To estimate the predictive error in our model, we randomly split the data into training (two-thirds) and test (one-third) sets. First, we analyse the training set comprising 225 women contributing 703 cycles and 16289 days (an average of 72.7 observations per woman). Secondly, we use the model fitted to present dynamic predictive intercourse profiles, and risk for subfertility for the remaining 113 woman and 7925 days in the test set.
The model that is presented for the analysis of the test data was chosen with a combination of Akaike information criterion AIC, ROC curves and AUC. AIC was used to determine whether covariates improved the model fit. We found that including some covariates that are unknown prospectively (e.g. lag variables) improved AIC but did not result in a gain in AUC for the test data, since they are unknown and must be averaged over while predicting prospectively in time. Sections C and D of the on-line supplementary materials contain details on how the final model was selected (including knot selection) and a full list of parameter estimates with standard errors respectively.
5.1. Analysis of the training set
Using the notation of Section 3, the probability that intercourse occurs on cycle j, day k, for woman i was modelled by using the form in equation (3.1) with Zijk = (1, Xijk−1, SMKijk, ALCijk, BLDijk, WKNDijk, PARi, AGEi, PARi*AGEi)′ (see Laumann et al. (2000) and Wilcox et al. (2004) for discussion on factors that are associated with intercourse). The definition of all variables is contained in Table 1. We modelled the distribution of TTP with model (3.2), where Uij = {I(j = 1),…, I(j = 6), PARi, AGEi }, and For follicular phase lengths, we assume Yi·~IID log-normal(νi, σ2) where νi =ν +σb3bi3. We found that setting ρ13=ρ23=0 in D had a better fit than a model that included ρ13 and ρ23. In the model fitting portion we tested for the presence of various trends in intercourse behaviour by cycle number. The final model includes covariates j* = j − 1 and j*2 in the peakedness portion of the intercourse model (j* is used to help the identifiability of the peakedness parameters). The final model had 10 interior knots at {−13, −10, −7, −4, −2, 1, 4, 7, 10, 13} days relative to ovulation, corresponding to the percentiles of the observed k − Yij (see section C of the on-line supplementary materials for further details). We assumed that g(·) was constant outside −20 and 50 days relative to ovulation. Standard errors of estimates were calculated from a numerical approximation to the observed Fisher information matrix. We compare our results with those of a generalized linear model (GLM) and a generalized non-linear mixed model (GNLMM) that included all covariates and the cubic B-splines function. For these models for cycles with missing follicular phase length we use a fixed Yij = 14 days corresponding to the follicular phase length in an ideal menstrual cycle. This is motivated by common practice of assuming that an ideal menstrual cycle is of length 28 days and the ovulation is assumed to occur mid-cycle (approximately around day 14) (Dominik et al., 2001). The GNLMM also included a random intercept.
Table 1.
Definitions of fixed effect covariates
| Effect | Definition | Type |
|---|---|---|
| Xijk−1 Lag 1 | intercourse indicator | Day varying |
| ALC | Indicator of alcohol consumption | Day varying |
| BLD | Indicator of menstrual bleeding | Day varying |
| SM | K Indicator of smoking | Day varying |
| WKND | Indicator of a Friday, Saturday or Sunday | Day varying |
| PAR | Indicator whether the women had at least 1 live birth | Baseline |
| AGE | Age of the female partner minus 31.5 years | Baseline |
In Table 2, we present the intercourse submodel estimates, standard errors and 95% Wald-type confidence intervals for the method proposed, a GLM and a GNLMM. The biggest factor in the probability of intercourse was BLDijk, the menstrual bleeding indicator. The other covariates that had a significant effect on the probability of intercourse were Xijk−1, ALCijk and PARi*AGEi. There was no significant cycle effect on the peakedness, but AIC did prefer a model with these components to a model without. There are noticeable differences between the model proposed versus the GLM and GNLMM in the value of the intercept estimate β̂0, which is lower in the models that do not account for joint modelling with TTP. This was expected since people having less intercourse contribute more cycles of data (longer TTPs). Another marked difference is in the direction of the lag 1 value in the model proposed and the GNLMM, versus the GLM. The positive direction for the lag parameter in the GLM is not unexpected since, without a baseline random effect, it is the only way to increase the marginal probability of intercourse E(pijk) for highly active couples. We also believe that the performance of the GLM and GNLMM would also be impacted by not accounting for variability in follicular phase length.
Table 2.
Estimates θ̂ and 95% confidence intervals for intercourse outcome with the proposed method, GNLMM and GLM
| Results for proposed model
|
Results for GNLMM
|
Results for GLM
|
||||
|---|---|---|---|---|---|---|
| θ̂ | 95% confidence interval | θ̂ | 95% confidence interval | θ̂ | 95% confidence interval | |
| Intercept | −1.02 | (−1.39, −0.65) | −1.51 | (−2.16, −0.86) | −1.41 | (−2.04, −0.78) |
| Lag 1 | −0.21 | (−0.3, −0.12) | −0.12 | (−0.19, −0.03) | 0.26 | (0.17, 0.33) |
| SMK | −0.22 | (−0.47, 0.02) | −0.18 | (−0.40, 0.04) | 0.01 | (−0.10, 0.13) |
| ALC | 0.18 | (0.08, 0.28) | 0.18 | (0.09, 0.26) | 0.05 | (−0.03, 0.14) |
| BLD | −2.20 | (−2.41, −1.99) | −2.06 | (−2.26, −1.86) | −1.88 | (−2.08, −1.68) |
| WKND | 0.07 | (−0.002, 0.15) | 0.09 | (0.011, 0.17) | 0.09 | (0.021, 0.16) |
| PAR | −0.15 | (−0.35, 0.05) | −0.12 | (−0.31, 0.06) | −0.10 | (−0.17, −0.02) |
| AGE | −0.02 | (−0.05, 0.01) | −0.02 | (−0.04, 0.00) | −0.01 | (−0.02, 0.00) |
| AGE*PAR | −0.07 | (−0.11, −0.02) | −0.06 | (−0.10, −0.02) | −0.05 | (−0.07, −0.04) |
| j* | 0.09 | (−0.04, 0.22) | — | — | ||
| j*2 | −0.02 | (−0.04, 0.01) | — | — | ||
In Table 3, we display the results for the standard deviations and correlation of the random effects, and the TTP parameters. All the standard deviations were significantly greater than 0, and there was a substantial negative correlation between b1 and b2. The negative correlation is a result of couples who target their act of intercourse acts to fall within the fertile window and have little intercourse otherwise, versus couples who have consistent intercourse throughout the menstrual cycle. The estimates of ξ1 and ξ2 show that there is a significant dependence between the baseline b1 and peakedness b2 random effects and TTP. The estimates suggest that those with a positive baseline or peakedness random effect become pregnant faster. However, those women random effects that are large in absolute value but opposite in sign (e.g. b1= c and b2= −c) have TTP characteristics that are not markedly different from a woman with b1=b2=0. The results indicate that, for a fixed b1 =0, a 35-year-old nulliparous (i.e. no previous live birth) woman with better-than-average intercourse behaviour (b2 = 1) has a median TTP of four cycles. However, if she has lower-than-average intercourse behaviour (b2 = −1) the median TTP is 10 cycles (assuming that γj = γ6 for j = 7, 8, …). Further graphical examples are given in section D of the on-line supplementary materials.
Table 3.
Estimates θ̂ and 95% confidence intervals for the proposed model†
|
D-parameters
|
TTP parameters
|
||||
|---|---|---|---|---|---|
| θ̂ | 95% confidence interval | θ̂ | 95% confidence interval | ||
| σb1 | 0.84 | (0.67, 1.00) | γPAR | 0.57 | (0.22, 0.92) |
| ρ12 | −0.64 | (−0.84, −0.44) | γAGE | −0.26 | (−0.43, −0.09) |
| σb2 | 0.62 | (0.51, 0.73) | ξ1 | 0.24 | (0.03, 0.44) |
| σb3 | 2.49 | (2.12, 2.86) | ξ2 | 0.30 | (0.05, 0.55) |
The GNLMM estimated σb1 as 0.71 with 95% confidence interval (0.56, 0.86).
5.2. Prediction for test data set
Using estimates for the models that were built in the previous section, we predicted intercourse probability profiles and TTP characteristics for the test data set. We use the first cycle of data to implement the Monte Carlo empirical Bayes estimation procedure that was detailed in Section 4. For the GLM and GNLMM we used a fixed 14-day follicular phase length. The GNLMM used empirical Bayes estimates of the baseline random effect. For time varying covariates SMKijk and ALCijk, we imputed the empirical probabilities of these indicators by using 𝒟i1. For BLDijk we used the bleeding pattern that was observed in the first cycle.
The performance of the prediction is quantified by using calibration curves, ROC curves and AUC. The AUC and ROC curve will quantify the quality of the rankings that are generated by each specific model, whereas the calibration curves assess any bias in the predictive estimates. In Fig. 2(a), we present a calibration curve, which plots PPl against OPl given in expression (4.3), and in Fig. 2(b) an ROC curve, for the GLM, GNLMM and the model proposed. The calibration of the model proposed and the GNLMM are similar, and both are superior to the GLM. The rankings of the probabilities improved substantially with the proposed method versus the standard approaches. The AUC of the models was 0.796, 0.725 and 0.679 for the model proposed, GNLMM and GLM respectively. Using the model proposed, which incorporates a model for follicular phase length to account for missingness, leads to a 17.3% and 9.8% improvement in AUC over respectively the GLM and GNLMM with a fixed 14 days to account for missing follicular phase lengths.
Fig. 2.

(a) Calibration curve of PP/ versus OP/ given in expression (4.3) and (b) ROC curves: both compare a GLM (·-·-·-), a GNLMM (------) and the proposed model (——) for the test data set; AUC for the proposed model was 0.796 for the GNLMM 0.725 and for the GLM 0.679
Using the methods in Section 4, we estimated predictive intercourse profiles with 95% confidence intervals, for the second and third cycles of two women with identification numbers 1135 and 1468 (Fig. 3).Woman 1135 has a particularly low value of b̃i2, indicating a flatter, more consistent probability profile, whereas woman 1468 has a particularly high value of b̃i2, indicating a highly peaked probability profile. The empirical Bayes estimates were based on 𝒟i1 and 𝒟i2 for the second and third cycles respectively. Menstrual bleeding’s effect on the probability of intercourse can be seen in the sharp decrease in p̂ for the beginning days for woman 1135. These figures demonstrate the flexibility of the proposed semiparametric mixed model of binary data. Allowing for heterogeneity in the peakedness is critical for our outcome.
Fig. 3.
Dynamic individualized predictive profiles by using the proposed model (——) with 95% pointwise confidence intervals (------) and the true realizations (●) (empirical Bayes estimates of unknowns utilized 𝒟i1 for cycle 2, and 𝒟i2 for cycle 3): (a) cycle 2, woman 1135; (b) cycle 3, woman 1135, (c) cycle 2, woman 1468; (d) cycle 3, woman 1468
We were further interested in predicting the probability of subfertility (i.e. TTP longer than 6 cycles). Let Ũij denote the predicted covariates for cycle j. The form of the predicted conditional survivor function is given by
| (5.1) |
We predict the probability that a couple are subfertile conditionally on one and two cycles of information, i.e. π(6|1) and π(6|2) respectively. We did not include women with Ti = 1 or Ti < 6 with Δi = 0, which left 65 women available for the prediction analysis. We compare the predictions that are given in equation (5.1) with a semiparametric discrete survival model with complementary log–log-form, where the sum of the intercourse values over the fertile window , parity and age were included as covariates, along with the Vij at-risk indicator. Cycles with missing Yij used a fixed 14 days. We used the average number of acts of intercourse over the fertile window of the first j0 menstrual cycles to predict π(j|j0) with the discrete survival model.
The sensitivity P{π̂i(6|j) > c|Ti > 6} and specificity P{π̂i(6|j) ≤ c|Ti ≤ 6} for j =1, 2 c ∈ [0, 1], are displayed in Fig. 4 for the method proposed and the standard discrete survival model. For the method proposed AUC for π̂i(6|1) and π̂i(6|2) is 0.707 and 0.714 respectively; the corresponding values for the standard method are 0.565 and 0.588. This indicates that AUC for the method proposed is 25.1% and 21.4% higher than that for the standard approach, when conditioning on one and two cycles of data. For the method proposed π̂i(6|1) ranks women with subfertility higher than women without 70.7% of the time. This shows the efficacy of the proposed model in accurately predicting longitudinal and survival processes.
Fig. 4.

ROC curve for predicting the probability Ti >6 by (a) π̂i(6|1) and by (b) π̂i(6|2) with the proposed method (——) and the standard approach (·-·-·-): AUC for the proposed method and standard approach is (0.707, 0.714) and (0.565, 0.588) respectively
6. Summary and discussion
In this paper, we have proposed a semiparametric shared parameter model for the analysis and prediction of intercourse behaviour (a longitudinal process) and TTP (a discrete time-to-event process). The total number of observations of intercourse can be viewed as having nested time-scales, where we observe a series of intervals with varying numbers of observations per interval. The shared parameter model framework was beneficial in our scenario, since it allowed for the joint analysis and prediction of the longitudinal and survival processes.
The training set portion of our data analysis found that there was a significant dependence between the shared baseline and peakedness intercourse random effects and TTP. This dependence-was in the hypothesized direction, where people with higher rates of intercourse behaviour became pregnant faster than those with lower rates of intercourse behaviour. Our proposed semiparametric peakedness model successfully accounted for the non-linear trend between the probability of intercourse and day relative to ovulation (see Fig. 3). By including a model on the follicular phase lengths we could integrate out their effect when unknown, and in the prediction analysis. The test portion showed how a Monte Carlo empirical Bayesian procedure could be used to obtain point predictions and to estimate predictive error. Such an approach, where the estimation of the parameters is done via a likelihood-based method and prediction via a Bayesian approach, is quite common in practice and has been shown to have desirable properties (Proust-Lima and Taylor, 2009; Rizopoulos, 2011) in the context of joint modelling of longitudinal and time-to-event data analysis. However, a full Bayesian approach and a comparison vis à vis our approach including computational cost is worth investigating in the future. The predictive model of intercourse behaviour can be used in future attempts of TTP prediction (see the on-line supplementary materials for a full list of parameter estimates and standard errors). One could alternatively predict TTP by using the intercourse observations in the fertile window and the survival model that was proposed by Sundaram et al. (2012). However, owing to the unknown follicular phase lengths, this model would still require a model for intercourse observations outside the fertile window, adding to its complexity.
Our work is relevant for the development of couple-specific intercourse and TTP prediction models and offers promise to help couples to minimize the time required to achieve pregnancy by addressing sexual intercourse behaviours. Further, preconception counsellors can use current methods of targeting acts of intercourse (see Scarpa and Dunson (2007) and Bortot et al. (2010)) for those with predicted intercourse or fecundity problems to maximize their success in pregnancy. AUC for our TTP prediction was slightly lower than the AUC of 0.77 that was found in the TTP prediction in McLain et al. (2012) that was based on menstrual cycle characteristics. Their results predicted the TTP for a different data set and focused on the relationship between menstrual cycle length and TTP. Morework is needed in evaluating the predictive benefits of multiple longitudinal processes with a relationship to a survival outcome (Rizopoulos and Ghosh, 2011).
Supplementary Material
Acknowledgments
This research was supported in part by the Intramural Research Program of the National Institute of Health, Eunice Kennedy Shriver National Institute of Child Health and Human Development. This work was completed while the first author was a Research Fellow with Dr Sundaram. The authors also acknowledge that this study utilized the high performance computational capabilities of the Biowulf Linux cluster at the National Institutes of Health, Bethesda, Maryland (http://biowulf.nih.gov). The authors thank the Joint Editor, the Associate Editor and two reviewers for comments and suggestions that considerably improved this paper.
Appendix A: Shared parameter models
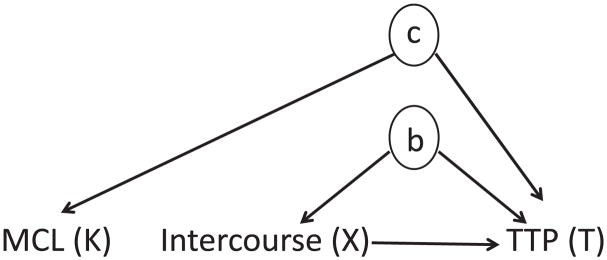
In this section, we provide details concerning our joint model formulation and provide justification for expression (3.3) in our framework of shared parameter models. Observe that N, as defined in point (f) of Section 2, depends both on the TTP and on the menstrual cycle lengths. We look to simplify the dependence structure by using the current biological understanding of the dependence structure of intercourse, TTP and menstrual cycle length. More precisely, we assume that there are unobserved latent variables b (e.g. unmeasured factors such as libido and stress level) that relate intercourse and TTP, and unobserved latent variables c (e.g. unmeasured female reproductive hormones such as luteinizing hormone and oestrogen) that relate the TTP and menstrual cycle length, whereas intercourse and menstrual cycle length may be indirectly related through the TTP (see Fig. 5 for a visual representation of these dependences). In view of this, we make the following assumptions.
Assumption 1. Given b and the TTP, intercourse acts are independent of the menstrual cycle lengths.
Assumption 2. Given the TTP, the menstrual cycle lengths are independent of b.
Fig. 5.
Schematic representation of the underlying random processes of interest: intercourse X, observed intercourse Xobs, menstrual cycle length K and TTP T :
 , latent variables representing the unobserved shared random effect b, and the unobserved covariates c that relate K and T
, latent variables representing the unobserved shared random effect b, and the unobserved covariates c that relate K and T
In Fig. 5, we include a latent variable c (e.g. unmeasured female reproductive hormones) that induces dependence between K and T. It should be noted that conditioning on T in the distribution of K could create dependence between K and b. Note that T is an outcome of b (directly) and menstrual cycle length (indirectly through c), which is commonly referred to as a collider. It is well known in the epidemiological literature (Rothman et al., 2008) that, when a collider is conditioned on, dependence between two otherwise independent variables is generated. For example, there may be dependence between menstrual cycle length and b after conditioning on TTP. However, this dependence would be attenuated by the strength of the relationships between T and c, followed by K and c. Consequently, we assume that the relationship between K and b given T is negligible. Thus, assumptions 1 and 2 are reasonable in our context.
We shall now establish expression (3.3), i.e.
where θ and κ are the unknown parameters in the models for intercourse and TTP respectively. For this, note that the joint distribution of the longitudinal process X, N and T under the shared parameter framework can be expressed as
Note that is a function of two random processes T and KT. So, we have
| (A.1) |
| (A.2) |
Note that we derived equation (A.2) from equation (A.1) as a consequence of assumptions 1 and 2. Consequently,
Appendix B: Inference method
In this section, we present a maximum likelihood method using adaptive Gaussian quadrature to estimate the parameter vector ψ ={θ, κ, D, ν, σ}.We use the formulation of the data structure that was introduced in Sections 2 and 4. For subject i we observe 𝒟i = {Xi, Zi, Wi, Ui, Yi, Ri, Ti, Δi} where Xi is a vector of the longitudinal binary outcome, Zi, Wi and Ui are the design matrices and Ri={Ri1, …,RiTi} is a vector of indicators that delineates Yi into observed and missing portions. To estimate ψ, we use expression (3.3). Under these assumptions the likelihood for subject i is
| (B.1) |
where , and 𝒟 = {𝒟1, …, 𝒟n}. We use adaptive Gaussian quadrature to evaluate expression (B.1), which is based on the conditional likelihood for subject i:
where a = {b, Yimis}. For each candidate value of ψ, say ψ = ψc, we estimate
| (B.2) |
and
where , for all i = 1, …, n. Following Pinheiro and Bates (1995) the integral in expression (B.1) is approximated by a weighted sum of L(ψ|𝒟i, a) evaluated at Gaussian quadrature nodes centred and scaled by ãi and H̃i respectively, for i = 1, 2, …, n. To calculate ψ̂ = arg maxψ log{L(ψ|𝒟)} we used the numerical optimization routine optim in R (R Development Core Team, 2012). Section E of the on-line supplementary materials contains the R code.
In the on-line supplementary materials we present further details on our inference method and results of a simulation study. In our simulation study we tested the performance of a model that is similar to that presented here. Our adaptive Gaussian quadrative method was fitted with five, 10 and 15 quadrature nodes. We found that when 10 quadrature nodes were used the estimates of the parameters had little bias, and a numerical approximation to the Hessian matrix provided standard error estimates that were relatively similar to the Monte Carlo standard error. Wald-type confidence intervals yielded converged probabilities that were close to the nominal 0.95-level. We did not find that 15 quadrature nodes were significantly superior to 10 quadrature nodes. As a result, we used 10 quadrature nodes in our analysis.
Footnotes
Additional ‘supporting information’ may be found in the on-line version of this article:
‘Supplementary materials for: “Joint analysis of longitudinal and survival data measured on nested time-scales using shared parameter models: an application to fecundity data”’.
References
- Albert PS. A linear mixed model for predicting a binary event from longitudinal data under random effects misspecification. Statist Med. 2012;31:143–154. doi: 10.1002/sim.4405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albert PS, Hunsberger S. On analyzing circadian rhythms data using non-linear mixed models with harmonic terms. Biometrics. 2005;61:1115–1120. doi: 10.1111/j.0006-341X.2005.464_1.x. [DOI] [PubMed] [Google Scholar]
- Bortot P, Masarotto G, Scarpa B. Sequential predictions of menstrual cycle lengths. Biostatistics. 2010;11:741–755. doi: 10.1093/biostatistics/kxq020. [DOI] [PubMed] [Google Scholar]
- Buck GM, Vena JE, Greizerstein HB, Weiner JM, McGuinness B, Mendola P, Kostyniak PJ, Swanson M, Bloom MS, Olson JR. Pcb congeners and pesticides and female fecundity, New York state angler prospective pregnancy study. Environ Toxicol Pharmcol. 2002;12:83–92. doi: 10.1016/s1382-6689(02)00026-1. [DOI] [PubMed] [Google Scholar]
- Buck Louis GM, Rios LI, McLain AC, Cooney MA, Kostyniak PJ, Sundaram R. Persistent organochlorine pollutants and menstrual cycle characteristics. Chemosphere. 2011a;85:1742–1748. doi: 10.1016/j.chemosphere.2011.09.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buck Louis GM, Schisterman EF, Sweeney AM, Wilcosky TC, Gore-Langton RE, Lynch CD, Boyd Barr D, Schrader SM, Kim S, Chen Z, Sundaram R on behalf of the LIFE Study. Designing prospective cohort studies for assessing reproductive and developmental toxicity during sensitive windows of human reproduction and development—the LIFE Study. Paed Perntl Epidem. 2011b;25:413–424. doi: 10.1111/j.1365-3016.2011.01205.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullivant SB, Sellergren SA, Stern K, Spencer NA, Jacob S, Mennella JA, McClintock MK. Women’s sexual experience during the menstrual cycle: identification of the sexual phase by noninvasive measurement of luteinizing hormone. J Sex Res. 2004;41:82–93. doi: 10.1080/00224490409552216. [DOI] [PubMed] [Google Scholar]
- Burnett AL. Environmental erectile dysfunction: Can the environment really be hazardous to your erectile health? J Androl. 2008;29:229–236. doi: 10.2164/jandrol.107.004200. [DOI] [PubMed] [Google Scholar]
- Colombo B, Masarotto G. Daily fecundability: first results from a new data base. Demog Res. 2000;3(5) [PubMed] [Google Scholar]
- Colombo B, Mion A, Passarin K, Scarpa B. Cervical mucus symptom and daily fecundability: first results from a new database. Statist Meth Med Res. 2006;15:161–180. doi: 10.1191/0962280206sm437oa. [DOI] [PubMed] [Google Scholar]
- Cox DR. Principles of Statistical Inference. Cambridge: Cambridge University Press; 2006. [Google Scholar]
- Ding J, Wang JL. Modeling longitudinal data with nonparametric multiplicative random effects jointly with survival data. Biometrics. 2008;64:546–556. doi: 10.1111/j.1541-0420.2007.00896.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dominik R, Zhou H, Cai J. A statistical model for the evaluation of barrier contraceptive efficacy. Statist Med. 2001;20:3279–3294. doi: 10.1002/sim.965. [DOI] [PubMed] [Google Scholar]
- Dunson DB, Baird DD, Colombo B. Increased infertility with age in men and women. Obstet Gyn. 2004;103:51–56. doi: 10.1097/01.AOG.0000100153.24061.45. [DOI] [PubMed] [Google Scholar]
- Dunson DB, Stanford JB. Bayesian inferences on predictors of conception probabilities. Biometrics. 2005;61:126–133. doi: 10.1111/j.0006-341X.2005.031231.x. [DOI] [PubMed] [Google Scholar]
- Fahrmeir L, Tutz G. Multivariate Statistical Modelling based on Generalized Linear Models. 2. New York: Springer; 2001. [Google Scholar]
- Gini C. In: Fields JC, editor. Premierès recherces sur la fécondabilité de la femme; Proc. Int. Math. Congr; Toronto. Aug. 11th–16th, 1924; Toronto: University of Toronto Press; 1928. pp. 889–892. [Google Scholar]
- Hsieh F, Tseng YK, Wang JL. Joint modeling of survival and longitudinal data: likelihood approach revisited. Biometrics. 2006;62:1037–1043. doi: 10.1111/j.1541-0420.2006.00570.x. [DOI] [PubMed] [Google Scholar]
- Jensen TK, Scheike T, Keiding N, Schaumburg I, Grandjean P. Fecundability in relation to body mass and menstrual cycle patterns. Epidemiology. 1999;10:422–428. doi: 10.1097/00001648-199907000-00011. [DOI] [PubMed] [Google Scholar]
- de La Rochebrochard E, Thonneau P. Paternal age > 40 years: an important risk factor for infertility. Am J Obstet Gyn. 2003;189:901–905. doi: 10.1067/s0002-9378(03)00753-1. [DOI] [PubMed] [Google Scholar]
- Laumann E, Gagnon J, Michael R, Michaels S. The Social Organization of Sexuality: Sexual Practices in the United States. Chicago: University of Chicago Press; 2000. [Google Scholar]
- Mathews T, Hamilton BE. Mean age of mother, 1970–2000. Natn Vitl Statist Rep. 2002;51:1–13. [PubMed] [Google Scholar]
- McCulloch CE, Neuhaus JM. Prediction of random effects in linear and generalized linear models under model misspecification. Biometrics. 2011;67:270–279. doi: 10.1111/j.1541-0420.2010.01435.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLain AC, Lum KJ, Sundaram R. A joint mixed effects dispersion model for menstrual cycle length and time-to-pregnancy. Biometrics. 2012;68:648–656. doi: 10.1111/j.1541-0420.2011.01711.x. [DOI] [PubMed] [Google Scholar]
- Pinheiro JC, Bates DM. Approximations to the log-likelihood function in the nonlinear mixed-effects model. J Computnl Graph Statist. 1995;4:12–35. [Google Scholar]
- Practice Committee of the American Society for Reproductive Medicine. Optimizing natural fertility: a committee opinion. Fertil Steril. 2013;100:631–637. doi: 10.1016/j.fertnstert.2013.07.011. [DOI] [PubMed] [Google Scholar]
- Proust-Lima C, Taylor JMG. Development and validation of a dynamic prognostic tool for prostate cancer recurrence using repeated measures of posttreatment psa: a joint modeling approach. Biostatistics. 2009;10:535–549. doi: 10.1093/biostatistics/kxp009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pulkstenis EP, Ten Have TR, Landis JR. Model for the analysis of binary longitudinal pain data subject to informative dropout through remedication. J Am Statist Ass. 1998;93:438–450. [Google Scholar]
- Pyper C, Bromhall L, Dummett S, Altman DG, Brownbill P, Murphy M. The Oxford conception study design and recruitment experience. Paed Perntl Epidem. 2006;20:51–59. doi: 10.1111/j.1365-3016.2006.00771.x. [DOI] [PubMed] [Google Scholar]
- R Development Core Team. R: a Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing; 2012. [Google Scholar]
- Rizopoulos D. Dynamic predictions and prospective accuracy in joint models for longitudinal and time-to-event data. Biometrics. 2011;67:819–829. doi: 10.1111/j.1541-0420.2010.01546.x. [DOI] [PubMed] [Google Scholar]
- Rizopoulos D, Ghosh P. A bayesian semiparametric multivariate joint model for multiple longitudinal outcomes and a time-to-event. Statist Med. 2011;30:1366–1380. doi: 10.1002/sim.4205. [DOI] [PubMed] [Google Scholar]
- Rizopoulos D, Verbeke G, Molenberghs G. Shared parameter models under random effects mis-specification. Biometrika. 2008;95:63–74. [Google Scholar]
- Rothman K, Greenland S, Lash T. Modern Epidemiology. Boston: Wolters Kluwer Health; 2008. [Google Scholar]
- Scarpa B, Dunson DB. Bayesian methods for searching for optimal rules for timing intercourse to achieve pregnancy. Statist Med. 2007;26:1920–1936. doi: 10.1002/sim.2846. [DOI] [PubMed] [Google Scholar]
- Scheike TH, Jensen TK. A discrete survival model with random effects: an application to time to pregnancy. Biometrics. 1997;53:318–329. [PubMed] [Google Scholar]
- Scheike TH, Petersen JH, Martinussen T. Retrospective ascertainment of recurrent events: an application to time to pregnancy. J Am Statist Ass. 1999;94:713–725. [Google Scholar]
- Small CM, Manatunga AK, Klein M, Dominguez CE, Feigelson HS, McChesney R, Marcus M. Menstrual cycle variability and the likelihood of achieving pregnancy. Rev Environ Hlth. 2010;25:369–378. doi: 10.1515/reveh.2010.25.4.369. [DOI] [PubMed] [Google Scholar]
- Song X, Davidian M, Tsiatis AA. A semiparametric likelihood approach to joint modeling of longitudinal and time-to-event data. Biometrics. 2002;58:742–753. doi: 10.1111/j.0006-341x.2002.00742.x. [DOI] [PubMed] [Google Scholar]
- Stanford JB, Dunson DB. Effects of sexual intercourse patterns in time to pregnancy studies. Am J Epidem. 2007;165:1088–1095. doi: 10.1093/aje/kwk111. [DOI] [PubMed] [Google Scholar]
- Sundaram R, McLain AC, Buck Louis GM. A survival analysis approach to modeling human fecundity. Biostatistics. 2012;13:4–17. doi: 10.1093/biostatistics/kxr015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ten Have TR, Kunselman AR, Pulkstenis EP, Landis JR. Mixed effects logistic regression models for longitudinal binary response data with informative drop-out. Biometrics. 1998;54:367–383. [PubMed] [Google Scholar]
- Wang Y, Ke C, Brown MB. Shape-invariant modeling of circadian rhythms with random effects and smoothing spline anova decompositions. Biometrics. 2003;59:804–812. doi: 10.1111/j.0006-341x.2003.00094.x. [DOI] [PubMed] [Google Scholar]
- Wilcox A, Day Baird D, Dunson DB, Mc Connaughey DR, Kesner JS, Weinberg CR. On the frequency of intercourse around ovulation: evidence for biological influences. Hum Reprodn. 2004;19:1539–1543. doi: 10.1093/humrep/deh305. [DOI] [PubMed] [Google Scholar]
- Wu MC, Carroll RJ. Estimation and comparison of changes in the presence of informative right censoring by modeling the censoring process. Biometrics. 1988;44:175–188. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.