A Coupled Lumped-Parameter and Distributed Network Model for Cerebral Pulse-Wave Hemodynamics

Abstract

The cerebral circulation is unique in its ability to maintain blood flow to the brain under widely varying physiologic conditions. Incorporating this autoregulatory response is necessary for cerebral blood flow (CBF) modeling, as well as investigations into pathological conditions. We discuss a one-dimensional (1D) nonlinear model of blood flow in the cerebral arteries coupled to autoregulatory lumped-parameter (LP) networks. The LP networks incorporate intracranial pressure (ICP), cerebrospinal fluid (CSF), and cortical collateral blood flow models. The overall model is used to evaluate changes in CBF due to occlusions in the middle cerebral artery (MCA) and common carotid artery (CCA). Velocity waveforms at the CCA and internal carotid artery (ICA) were examined prior and post MCA occlusion. Evident waveform changes due to the occlusion were observed, providing insight into cerebral vasospasm monitoring by morphological changes of the velocity or pressure waveforms. The role of modeling of collateral blood flows through cortical pathways and communicating arteries was also studied. When the MCA was occluded, the cortical collateral flow had an important compensatory role, whereas the communicating arteries in the circle of Willis (CoW) became more important when the CCA was occluded. To validate the model, simulations were conducted to reproduce a clinical test to assess dynamic autoregulatory function, and results demonstrated agreement with published measurements.

1. Introduction

The brain has unique abilities to maintain adequate CBF under various physiologic and pathologic conditions, such as rapid changes of blood or ICP, and arterial occlusion. Important features of intracranial hemodynamics include, (1) cerebral autoregulation (CA) [1–3], (2) cortical anastomosis that can transfer blood between different regions of brain, (3) communicating arteries that form the CoW to redistribute blood supply, and (4) multiple arterial blood sources (carotid and vertebral arteries). The functions of these are highly coupled, and nonlinearly related to CSF and ICP dynamics. Moreover, the blood distribution and pulse-wave dynamics in cerebral arteries can be affected by flow and pressure dynamics in large systemic arteries. Due to these factors, quantitative modeling of the intracranial hemodynamics is a rich topic.

Hemodynamics simulation is typically achieved using models of varying dimensionality. In 3D models, the velocity and pressure fields are fully resolved in space and time through computational fluid–structure dynamics simulations. These simulations are computationally expensive, but necessary if localized flow structures need to be resolved. When a more regional or global assessment of blood flow is sought, LP and 1D models are appropriate, especially in assessing pressure and flow waveforms. LP models typically represent the behavior of a collection of vessels by electrical analogs [4]. Recently, Ursino and Giannessi [5] applied a LP network model to represent carotid and basilar arteries and segments in the CoW. The cerebral arteries were connected to six peripheral vascular beds coupled with models for autoregulation, cortical anastomoses, CSF circulation, and ICP. This model enabled the study of blood flow distributions and transient effects of pathological conditions (e.g., hypercapnia) and carotid artery compression. Similar to LP models, a system of differential equation can be derived to describe global effects of cerebral autoregulation. Gonzalez-Fernandez and Ermentrout [6] modeled CA²⁺ variations in smooth muscle and reproduced vasomotions observed in cat cerebral arteries by Harder [7,8]. Later, David et al. [9] investigated myogenic and metabolic autoregulation, and showed that the latter mechanism is the dominant mechanism for cerebral autoregulation in response to carbon dioxide variation. LP and theoretical models do not incorporate topological properties of arteries however, and are thus not able to describe wave propagation effects. The measurement of such effects has become important in patient monitoring with the increased prevalence of diagnostic devices such as transcranial Doppler and continuous intracranial or arterial blood pressure monitoring.

To capture wave propagation phenomena, distributed 1D models are used [10] whereby the governing (Navier–Stokes) equations for blood flow in each arterial segment are reduced to the axial coordinate and then a deformable tube network is constructed through appropriate junction conditions. In such settings, LP models are often coupled at the terminal segments of the 1D domain to represent downstream vascular beds. A similar approach is adopted here. Important work in modeling CBF on the pulse-waveform level with patient-based vessel geometry was performed by Alastruey et al. [11] using a 1D deformable pipe network. This model considered the first generation of arteries past the CoW and coupled three-element Windkessel models at the outlets. In a subsequent publication [12], the three-element Windkessel models were extended to include autoregulatory function to investigate how anatomical variation of the CoW restored CBF after a sudden carotid occlusion. Using similar models, Köppl et al. [13] also recently studied the impact of varying degrees of unilateral stenoses of a carotid artery to CBF. The three-element based CA models used in the aforementioned studies demonstrated the ability of CA to recover and maintain blood flow following carotid artery occlusion. Liang et al. [14] considered more sophisticated cerebral LP model in addition to heart and lung models for their 1D study to describe cerebral hyperperfusion syndrome after carotid artery surgery. These models however did not consider the influences of distal collateral flow, ICP and CSF, which can be essential elements influencing intracranial hemodynamics. A review of computational models of blood flow to the brain and how variations in arterial geometry can influence the perfusion in the cerebral vasculature can be found in Ref. [15].

In this study, we developed an integrated computational framework to assess the effects of clinical tests and pathological conditions (e.g., occlusion or compression of arteries) on CBF distribution, pulse-wave propagation, and ICP. For this, we extended the recent study by Connolly et al. [16], which incorporated Ursino's autoregulation models [17,18] into downstream LP models of a 1D flow domain. Specifically, we extend the 1D network to include proximal arteries for accurate calculation of blood distribution and pulse-wave propagation. We also incorporated improvements to the LP CA model by considering the cortical anastomoses [5]. Moreover, we provide a comparison between popular pressure–area coupling used in the 1D domain for pulse-wave analysis. The model developed could be coupled with model-driven statistical inference approaches to provide a model-based data fusion of clinical data to monitor cerebral hemodynamics for patients under neurocritical care.

The remainder of this paper is organized as follows. First, we present the basic formulations used in this study. In the results, these methods are used to investigate waveform dynamics, including comparison between two popular pressure constituent models based on Laplace's law. The role of CA and distal collateral pathways are compared when the MCA or CCA are occluded. The role of CA is further analyzed when both CCAs are compressed with various strengths; this procedure has been used to reduce cerebral embolic load during transcatheter aortic-valve implantation. Finally, the model is applied to the transient hyperemic response test (THRT) [19] and compared with available data in the literature.

2. Numerical Procedures

2.1. Vascular Model.

Pressure and flow wave propagation can be modeled in the major arteries by representing each arterial segment as a deformable tube. A diagram of the arterial network used in this study is shown in Fig. 1(a). The following vessel segments are considered in the model: aorta (#1, 2, 4, 8; AORT), brachiocephalic (#3; BRC), subclavian (#7, 9; SC), brachial (#15, 16; BR), common carotid (#5, 6; CCA), internal carotid (#11, 12, 18, 21; ICA), external carotid (#10, 13; ECA), vertebral (#14, 17; VERT), basilar (#22; BAS), posterior communicating (#19, 20; PcoA), anterior communicating (#31; AcoA), middle cerebral (#23, 24; MCA), anterior cerebral (#25, 26, 29, 30; ACA), and posterior cerebral arteries (#27, 28, 32, 33; PCA). Below, “R” and “L” in front of the vessel abbreviations denote the right and left side of the body, respectively. The reference state geometries (length and diameter when transmural pressure is zero) and mechanical properties of the vessels are adopted from physiological data in Refs. [11] and [20–22] and listed in Table 1. We consider occlusions of the MCA and CCAs at the locations marked with the $\times$ in Fig. 1(a).

Fig. 1.

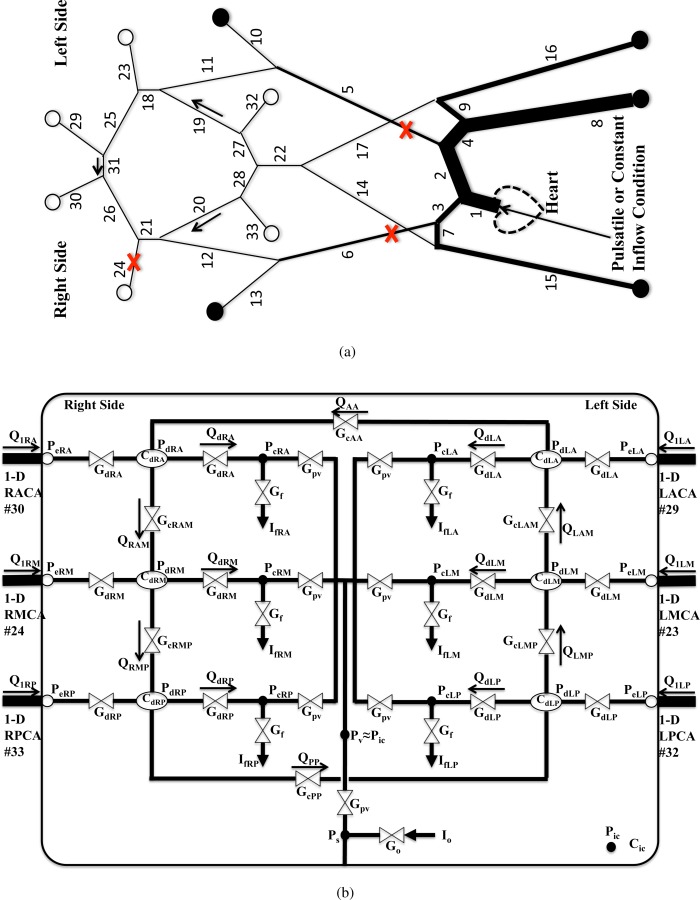
(a) Schematic of the 1D arterial network. Outflow boundaries marked with $○$ are coupled with the LP network in (b), and boundaries marked with $•$ are coupled to three-element Windkessel models. Locations where A ₀ is varied are marked with $\times$. (b) Schematic of the LP network model, which includes CA. The bounding box represents intracranial space, and a single ICP model is shared by the six cerebral distal vascular bed models inside the intracranial space.

Table 1.

The cross section area A ₀, length L, elasticity constant $\beta =\sqrt{\pi }{h}_{0}E/(1-{\sigma }^2)$, reference PWV $c_0=\sqrt{\beta /2\rho A_0^{1/2}}$, peripheral resistance R, and compliance C of each vessel in the 1D network model shown in Fig. 1(a), based upon the physiological data collected by previous studies [11,16,20–22]. A ₀ for AcoA and PcoA have been adjusted to match physiological blood flow flux through the communicating arteries.

		A 0	L	β	c 0	Peripheral R	Peripheral C
Vessel	ID	(cm2)	(cm)	(Pa)	(m/s)	(109  Pa · s m−3)	$({10}^{-10}\hspace{0.17em}{\text{Pa}}^{-1}\hspace{0.17em}{\mathrm{m}}^3)$
Aorta (I)	#1	4.52	4.00	1540	5.87	—	—
Aorta (II)	#2	3.94	2.00	1190	5.34	—	—
Aorta (III)	#4	3.60	3.90	1090	5.22	—	—
Aorta (IV)	#8	3.14	15.6	1040	5.29	0.180	38.7
Brachiocephalic	#3	1.21	3.40	755	5.72	—	—
Subclavian	#7,9	0.562	3.40	633	6.34	—	—
Brachial	#15,16	0.510	42.2	633	6.50	2.68	2.58
CCA	#5,6	0.196	17.70	595	8.00	—	—
ICA (I)	#11,12	0.126	17.70	945	11.3	—	—
ICA (II)	#18,21	0.126	0.500	1890	15.9	—	—
ECA	#10,13	0.0707	17.70	718	11.3	5.43	1.27
VERT	#14,17	0.0581	14.8	642	11.3	—	—
Basilar artery	#22	0.0824	2.90	1510	15.8	—	—
MCA	#23,24	0.0642	11.9	1360	16.0	—	—
ACA (I)	#25,26	0.0430	1.20	1100	15.9	—	—
ACA (II)	#29,30	0.0452	10.3	1130	15.9	—	—
PCA (I)	#27,28	0.0360	0.500	1020	16.0	—	—
PCA (II)	#32,33	0.0346	8.60	982	15.9	—	—
AcoA	#31	0.00800	0.300	718	19.6	—	—
PcoA	#19,20	0.00800	1.50	680	19.0	—	—

Terminal branches are coupled with three-element Windkessel models (marked with $•$) or with CA models (marked with $○$) that themselves are internally coupled. Specifically, the elements of the cerebral LP network are shown schematically in Fig. 1(b). The six cerebral distal vascular beds are coupled by collateral pathways and are also commonly coupled within a single ICP model. Further details about the elements are shown, and modeling of the autoregulatory functions is covered in Sec. 2.6.

2.2. Mass and Momentum Conservation.

The 1D equations for blood flow and pressure in a deformable tube have been derived in numerous publications under various assumptions. We use the formulation derived in Ref. [23]. The basic assumption is that the transverse velocities are small compared with the axial. Upon applying this assumption and integrating the Navier–Stokes equations over the cross section, the conservation of mass and momentum in the axial direction is reduced to

$$\frac{\partial A}{\partial t}+\frac{\partial AU}{\partial x}=0$$ (1)

$$\frac{\partial U}{\partial t}+(2\alpha -1)U\frac{\partial U}{\partial x}+(\alpha -1)\frac{U^2}{A}\frac{\partial A}{\partial x}=-\frac{1}{\rho }\frac{\partial p}{\partial x}+\frac{2\mu }{\rho R}{\left[\frac{\partial u}{\partial r}\right]}_R$$ (2)

where x and r are the axial and radial coordinates, R and A are the vessel's radius and cross section area, U is the transverse average of the axial velocity u, and p is the transversely averaged pressure. The blood density ρ and apparent viscosity μ are assumed constant, and

$$\alpha (x,t)=\frac{2\pi }{A{U}^2}{\int }_0^R{u}^{2}r\mathrm{d}r$$

To compute α and the wall shear rate $\partial u/\partial r{|}_R$, we need to know how u depends on r. As proposed in Ref. [24], we assume a velocity profile of the form

$$u(r,x,t)=\frac{\gamma +2}{\gamma }U(x,t)\left[1-{\left(\frac{r}{R}\right)}^{\gamma }\right]$$

from which it can be shown that $\gamma = \hspace{0.17em}(2-\alpha )/(\alpha -1)$. Note that the Poiseuille (parabolic) velocity profile is represented by γ = 2 leading to $\alpha =4/3$. In most arteries, the profile is more blunt than parabolic and higher values for γ are appropriate, which typically produce $\alpha \approx 1$. Consulting Eq. (2), it is clear that, for $\alpha \approx 1$, the nonlinearity in the momentum equation can be reduced (but not eliminated) so that

$$\frac{\partial U}{\partial t}+\frac{\partial }{\partial x}\left(\frac{1}{2}{U}^2+\frac{p}{\rho }\right)=\frac{2\mu }{\rho R}{\left[\frac{\partial u}{\partial r}\right]}_R$$ (3)

This form of the momentum equation is used henceforth in the results, as well as parameter values of γ = 9, $\rho =1.05\times {10}^3\hspace{0.17em}\text{kg}\hspace{0.17em}{\mathrm{m}}^{-3}$, and $\mu =4.05\times {10}^{-3}\hspace{0.17em}\text{Pa}\cdot \mathrm{s}$.

2.3. Pressure–Vessel Area Relationship.

For the above formulation of flow in a compliant tube, the unknown variables are U, p, and A. To close the system of equations, various constitutive relations between p and A have been employed, see, e.g., Refs. [22,25,26]. Mostly commonly, the constitutive relation is of a thin elastic and isotropic tube governed by Laplace's law; however, even this model has been treated differently. Starting from the standard form of Laplace's law

$$p-p_0=\frac{h}{R}\tau =\frac{h}{R}\frac{E}{1-{\sigma }^2}\frac{R-R_0}{R_0}$$ (4)

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{Eh\sqrt{\pi }}{1-{\sigma }^2}\frac{1}{A_0}\frac{R_0}{R}(\sqrt{A}-\sqrt{A_0})$$ (5)

where h is the vessel thickness, p ₀ is the external pressure, R ₀ is the vessel radius at zero transmural pressure (p = p ₀), τ is the circumferential (hoop) stress, E is Young's modulus, and σ is Poisson's ratio. By assuming $R_0/R\approx 1$

$$p-p_0=\frac{{\beta }^{*}}{A_0}\left(\sqrt{A}-\sqrt{A_0}\right)$$ (P1)

where ${\beta }^{*}=(\sqrt{\pi }hE)/(1-{\sigma }^2)$. This elastic relation has been employed in many recent 1D [11,25,27] models.

If we do not directly apply $R_0/R\approx 1$ explicitly in the above formula, Laplace's law gives

$$p-p_0=\frac{h}{R}\tau =\frac{h}{R}\frac{E}{1-{\sigma }^2}\frac{R-R_0}{R_0}=\beta \left(\frac{1}{\sqrt{A_0}}-\frac{1}{\sqrt{A}}\right)$$ (P2)

where $\beta =\sqrt{\pi }hE/(1-{\sigma }^2)$. This pressure model has been used by Olufsen et al. [28] and Steele et al. [29]. These two formulas (Eqs. (P1) and (P2)) represent different functional dependencies between pressure (and, e.g., wave speed) and cross-sectional area. Below, we explore how these two constitutive models affect the pulse-wave quantities in practical applications to systemic blood flow modeling.

2.4. Characteristic Variable and Wave Intensity Analysis (WIA).

Boundary conditions for a hyperbolic system (Eqs. (1), (3), and (P1) or (P2)) are often handled by separating propagating waves into incoming and outgoing ones by characteristic variable analysis. This analysis also facilitates WIA [30], which quantifies the amount of forward and backward traveling flow quantities. In this section, important equations for this analysis are recalled.

Using Eqs. (1), (3), and the distensibility $D=(1/A)(\mathrm{d}A/\mathrm{d}p)$, a nonconservative form of the governing equations can be derived with an inviscid approximation (see, e.g., Ref. [27]). In canonical coordinates, the wave equations are derived

$$\frac{\partial W_{\pm }}{\partial t}+{\lambda }_{\pm }\frac{\partial W_{\pm }}{\partial x}=0$$ (6)

where ${\lambda }_{\pm }=U\pm c,\hspace{0.17em}c=1/\sqrt{\rho D}$, and characteristic variables $W_{+}$ and $W_{-}$ can be determined by

$$W_{\pm }={\int }_{U_0=0}^U\mathrm{d}U\pm {\int }_{A_0}^A\frac{\text{c}}{\text{A}}\mathrm{d}A=U\pm {\int }_{A_0}^A\frac{\text{c}}{\text{A}}\mathrm{d}A$$ (7)

where U ₀ and A ₀ are at the reference state when the transmural pressure is zero.

The two pressure models discussed in Sec. 2.3 result in different values for c and $W_{\pm }$. The distensibility and wave speed $c^{*}$ using the (P1) model [25,27] become

$$D^{*}=\frac{2A_0}{\beta \sqrt{A}},\hspace{1em}{c}^{*}=\frac{1}{\sqrt{\rho D^{*}}}=\sqrt{\frac{{\beta }^{*}}{2\rho A_0}}{A}^{1/4}$$ (8)

When A = A ₀, the wave speed is consistent with the Moens–Korteweg formula ($c\sim \sqrt{\mathit{h}\mathit{E}/\rho A^{1/2}}$); however, the wave speed increases with an increase of A, which is opposite from the Moens–Korteweg formula. The characteristic variables are

$$W_{\pm }^{*}=U\hspace{0.17em}\pm \hspace{0.17em}4(c^{*}-c_0)=U\hspace{0.17em}\pm \hspace{0.17em}4\sqrt{\frac{\beta }{2\rho A_0}}\left(A^{1/4}-A_0^{1/4}\right)$$ (9)

Using the (P2) model, the distensibility D and the wave speed c are computed as

$$D=\frac{2\sqrt{A}}{\beta }, c=\frac{1}{\sqrt{\rho D}}=\sqrt{\frac{\beta }{2\rho A^{1/2}}}$$ (10)

which is consistent with the Moens–Korteweg formula. The characteristic variables are

$$W_{\pm }=U\hspace{0.17em}\pm \hspace{0.17em}4\sqrt{\frac{\beta }{2\rho }}\left(\frac{1}{A_0^{1/4}}-\frac{1}{A^{1/4}}\right)$$ (11)

Characteristic analysis has been employed to derive WIA, which is typically applied when blood pressure and velocity measurements are available at the same vessel location with an approximated pulse-wave velocity (PWV). The characteristic variables can be expressed by P and U using Eq. (7).

$$W_{\pm }=U\hspace{0.17em}\pm \int \frac{\mathrm{d}P}{\rho c}$$ (12)

The differences of W, P, and U in time are

$$\mathrm{d}{W}_{\pm }=\mathrm{d}U\hspace{0.17em}\pm \frac{\mathrm{d}P}{\rho c},\hspace{1em}\mathrm{d}P=\frac{\rho c}{2}(\mathrm{d}{W}_{+}-\mathrm{d}{W}_{-}),\hspace{1em}\mathrm{d}U=\frac{1}{2}(\mathrm{d}{W}_{+}+\mathrm{d}{W}_{-})$$ (13)

The wave intensity can then be defined as

$$\mathrm{d}I\left(t\right)=\mathrm{d}P\left(t\right)\mathrm{d}U\left(t\right)=\frac{\rho c}{4}(\mathrm{d}{W}_{+}^2-\mathrm{d}{W}_{-}^2)$$ (14)

which indicates the dominance of forward or backward waves at a given location. The forward and backward components of pressure and velocity can be found by $\mathrm{d}{W}_{\pm }=\mathrm{d}U\pm (\mathrm{d}P/\rho c)=\mathrm{d}{U}_{\pm }\pm (\mathrm{d}{P}_{\pm }/\rho c)$. This gives the water hammer equation $\mathrm{d}{P}_{\pm }=\pm \rho c\mathrm{d}{U}_{\pm }$. The same relations can also be derived by a control volume approach [31]. If the PWV c can be estimated, forward and backward components of differences of P, U, and I can be computed by

$$\mathrm{d}{P}_{\pm }=\frac{1}{2}(\mathrm{d}P\pm \rho c\mathrm{d}U),\hspace{1em}\mathrm{d}{U}_{\pm }=\frac{1}{2}(\mathrm{d}U\pm \frac{\mathrm{d}P}{\rho c}),\hspace{1em}\mathrm{d}{I}_{\pm }=\mathrm{d}{P}_{\pm }\mathrm{d}{U}_{\pm }$$ (15)

Note that $\mathrm{d}I=\mathrm{d}{I}_{+}+\mathrm{d}{I}_{-}$ is satisfied. To a linear approximation, forward and backward components of pressure and velocity waveforms are computed by summation

$$P_{\pm }(t)=\sum _0^t\mathrm{d}{P}_{\pm }(t)+P_{0\pm }, U_{\pm }(t)=\sum _0^t\mathrm{d}{U}_{\pm }(t)+U_{0\pm }$$ (16)

where $P_{0\pm }$ and $U_{0\pm }$ are the initial state.

2.5. Inflow and Vessel Junction Conditions.

The hyperbolic system of partial differential equations (Eqs. (1), (3), and (P1) or (P2)) is solved in each vessel segment of Fig. 1(a) with inflow/outflow boundary conditions and vessel junction relations. The conservations of mass and total pressure are enforced at the vessel junctions. The spatially and temporally evolving flow variables and cross section area at each uniformly discretized cell are solved with a finite volume method using a $\text{second}$ -order spatial scheme and a two-step Adams–Bashforth temporal scheme.

For inlet boundary conditions, heart beats are modeled using a periodic inflow rate $Q_{\text{in}}(t)$ at the ascending aorta (#1) that is immediately downstream of the aortic valve. Each cardiac cycle consists of a half sine wave with a peak value ${\widehat{Q}}_{\text{max}}=430\hspace{0.17em}\text{ml}\hspace{0.17em}{\mathrm{s}}^{-1}$ and a duration $t_s=0.3\hspace{0.17em}\mathrm{s}$ (systole), and zero for the rest of the period (diastole).

$$Q_{\text{in}}\left(t\right)=\{\begin{array}{cc}{\widehat{Q}}_{\text{max}}\hspace{0.17em}\text{sin}\left(\frac{\pi t}{t_s}\right)\hfill & \text{for}\hspace{0.5em}0\le t\le t_s\hfill \\ 0\hfill & \text{for}\hspace{0.5em}{t}_s<t<t_c\hfill \end{array}$$ (17)

where $t_c=0.9\hspace{0.17em}\mathrm{s}$. The closure of the aortic valve is modeled by the zero flow rate, which acts as a numerical reflector and generates the expected dicrotic notch in pulse-waveform solutions. We note that a clinically measured flow waveform at the ascending aorta was not chosen, since such measured data contain reflected waves that would become redundant with those generated by the model, leading to spurious results.

The coupling between the 1D domain and LP outflow model is established through the characteristic analysis (Eq. (11)) at their interface. This process requires terminal pressure P_e. P_e is calculated from the three-element Windkessel model at systemic outlets, and by $P_e=Q_d/(2G_d)+P_d$ at cerebral outlets. Calculation of Q_d, G_d, and P_d will be discussed in Sec. 2.6. Once P_e is calculated, terminal vessel area and velocity are calculated by Eq. (P1) or (P2) and the forward characteristic $W_{+}$. $W_{+}$ at the terminal mesh node is linearly extrapolated from the two upstream values. Various approaches have been used for coupling of 1D with LP models. Some of recent works can be found in Refs. [32–35].

2.6. Cerebral Autoregulation Model.

Outflow boundaries of cerebral arteries (marked with $○$ in Fig. 1(a)) are coupled with autoregulation models adapted from Refs. [5,16,18,36]. These models represent distal vascular territories downstream of ACA, MCA, and PCA. A schematic diagram of the CA LP model for the intracranial space is shown in Fig. 1(b). All distal vascular models are coupled with a single ICP model with intracranial compliance C _ic. In the diagram, G_d and C_d are the conductance and compliance of the pial/small arterial beds, respectively. G _pv is the conductance from the capillary to the venous bed. G_f and G_o are the conductances for the formation and reabsorption of the CSF, respectively. I_f and I_o denote the production rate and outflow (reabsorption) of CSF, respectively. The venous bed is collapsible and often modeled as a Starling resistor. Here, we have assumed that the venous pressure P_v is same as ICP P _ic. The pressures P_e, P_d, P_c, and P_s correspond to the pressures at the 1D outflow, pial/small arterial beds, capillary, and the sagittal sinus, respectively. Subscripts A, M, and P denote distal territories downstream of the ACA, MCA, and PCA, respectively. The model also includes distal collateral flow pathways. G_c represents the conductance of the cortical collateral vessels with additional subscripts denoting the brain regions coupled.

Vascular regions are represented by a lumped vessel model, and the relation between transmural pressure and wall tension is first applied following Laplace's law:

$$P_d{r}_d-P_{\text{ic}}(r_d+h_d)=T_d$$ (18)

where r_d and h_d are the lumped distal vessel radius and wall thickness, respectively. T_d is the wall tension, decomposed into three components such that

$$T_d=T_e+T_v+T_m$$ (19)

where T_e is the passive elastic tension, T_v is the viscous tension. T_m is the active tension that is produced by the smooth muscle contraction in response to an autoregulation stimulus. T_e is calculated as $T_e={\sigma }_e{h}_d$, where the stress σ_e assumes an exponential functional form of r_d as

$${\sigma }_e={\sigma }_{e0}\left[\text{exp}\left(K_{\sigma }\frac{r_d-r_{d0}}{r_{d0}}\right)-1\right]-{\sigma }_{\text{coll}}$$ (20)

where ${\sigma }_{e0},\hspace{0.17em}{K}_{\sigma }$, and $r_{d0}$ are constant model parameters. σ _coll is used to allow the vessel to have a moderate negative tension before collapsing. T_v is related to the viscous force introduced by the blood flow and modeled as $T_v={\sigma }_v{h}_d$, where the viscous stress is ${\sigma }_v=(\eta /r_{v0}) (\mathrm{d}{r}_d/\mathrm{d}t)$ with η being a constant model parameter as well.

The active tension T_m is a function of r_d. Its regulation is modeled by modulating its maximal tension T ₀ in the following way:

$$T_m=T_0(1+M)\text{exp}\left(-{\left|\frac{r_d-r_m}{r_t-r_m}\right|}^{n_m}\right)$$ (21)

where M is the CA activation factor, which varies between $[-1, 1]$ with M = 1 denoting maximal vasoconstriction, M = −1 maximal vasodilation, and M = 0 the neutral state. T ₀, r_m, r_t, and n_m are model parameters. In essence, M responds to maintain CBF. The control function is modeled using a first-order low pass system (characterized by time constant t _CA and gain G _CA), which filters the raw fluctuations subject to a sigmoid function that limits the excessive changes. Namely, the internal state x of the filter is expressed as

$$t_{\text{CA}}\frac{\mathrm{d}x}{\mathrm{d}t}=-x+G_{\text{CA}}\frac{Q_d-Q_n}{Q_n}$$ (22)

where Q_d is the CBF at each cerebral territory (anterior, middle, and posterior), and Q_n is the target flow rate. M is then calculated by

$$M=\frac{e^{2x}-1}{e^{2x}+1}$$ (23)

In addition to the above autoregulatory mechanism, cortical anastomosis becomes important when cerebral arteries are occluded. Following Ursino and Giannessi [5], we consider distal collateral connections between the anterior and middle (AM) territories, middle and posterior (MP) territories, as well as anterior to anterior (AA) and posterior to posterior (PP) flows across the hemispheres (Fig. 1(b)). Q_d is calculated using the flow rate from the 1D domain at each outlet (Q ₁), as well as distal collateral flows (Q _AA, Q _AM, Q _MP, and Q _PP) as follows:

$$Q_{\text{dRA}}=Q_{1\text{RA}}+Q_{\text{AA}}-Q_{\text{RAM}},Q_{\text{dLA}}=Q_{1\text{LA}}+Q_{\text{LAM}}-Q_{\text{AA}}$$ (24)

$$Q_{\text{dRM}}=Q_{1\text{RM}}+Q_{\text{RAM}}-Q_{\text{RMP}},Q_{\text{dLM}}=Q_{1\text{LM}}+Q_{\text{LMP}}-Q_{\text{LAM}}$$

$$Q_{\text{dRP}}=Q_{1\text{RP}}+Q_{\text{RMP}}-Q_{\text{PP}},Q_{\text{dLP}}=Q_{1\text{LP}}+Q_{\text{PP}}-Q_{\text{LMP}}$$

where Q _RAM denotes collateral flow from anterior to middle cerebral territory in the right cerebral hemisphere, determined by the pressure difference between two distal regions ($P_{\text{dRA}}-P_{\text{dRM}}$) and collateral conductance (G _cRAM). Q _RMP, Q _PP, Q _LMP, Q _LAM, and Q _AA are computed similarly.

$$Q_{\text{RAM}}=G_{\text{cRAM}}(P_{\text{dRA}}-P_{\text{dRM}}),Q_{\text{LAM}}=G_{\text{cLAM}}(P_{\text{dLM}}-P_{\text{dLA}})$$ (25)

$$Q_{\text{RMP}}=G_{\text{cRMP}}(P_{\text{dRM}}-P_{\text{dRP}}),Q_{\text{LMP}}=G_{\text{cLMP}}(P_{\text{dLP}}-P_{\text{dLM}})$$

$$Q_{\text{PP}}=G_{\text{cPP}}(P_{\text{dRP}}-P_{\text{dLP}}),Q_{\text{AA}}=G_{\text{cAA}}(P_{\text{dLA}}-P_{\text{dRA}})$$

To complete the model, the volume changes within the intracranial compartment are balanced.

$$C_{\text{ic}}\frac{\mathrm{d}{P}_{\text{ic}}}{\mathrm{d}t}=\sum _{k=1}^6\left(\frac{\mathrm{d}{V}_k}{\mathrm{d}t}+I_{f_k}\right)-I_o$$ (26)

where V_k is the blood volume for a modeled vascular territory, with k representing the six cerebral distal beds. Below, variables with the subscript k denote the quantity for each vascular territory. The volume change balance equation becomes

$$\frac{\mathrm{d}{V}_k}{\mathrm{d}t}=2K_v{r}_{d_k}\frac{\mathrm{d}{r}_{d_k}}{\mathrm{d}t}=G_{d_k}(P_{e_k}-P_{d_k})-G_{d_k}(P_{d_k}-P_{c_k})+\Delta Q_{{\text{coll}}_k}$$ (27)

where K_v is a constant parameter, and $\Delta Q_{{\text{coll}}_k}$ is the collateral flow from Eq. (25). $G_{d_k}$ is one half of vascular conductances of the modeled vascular territory. It is related to $r_{d_k}$ as $G_{d_k}=K_g{r}_{d_k}^4$, where K_g is a constant parameter. In the above formulation, CSF production rate ($I_{f_k}$) is modeled with a constant conductance (G_f) as $I_{f_k}=G_f(P_{c_k}-P_{\text{ic}})H(P_{c_k}-P_{\text{ic}})$, where H is the Heaviside function. In a similar fashion, CSF outflow (I_o) is modeled with a constant outflow conductance (G_o) as $I_o=G_o(P_{\text{ic}}-P_s)H(P_{\text{ic}}-P_s)$ with P_s representing the sagittal sinus pressure.

C _ic in Eq. (26) represents the craniospinal compliance that has been shown to be a nonlinear function of ICP, $C_{\text{ic}}=1/(K_e|P_{\text{ic}}-P_{\text{icn}}|+(1/C_m))$ [36]. A simplified model is adopted here for the cerebral venous bed. The collapsible nature of the venous bed makes it behave like a Starling resistor indicating that the venous pressure equals ICP at locations of cerebral venous collapse. Thus, blood flow to the venous bed can be specified as $G_{\text{pv}}(P_{c_k}-P_{\text{ic}})$, where G _pv is the conductance from the capillary to the location of collapse.

In summary, there are three state variables for each cerebral outlet: r_d, P _ic, and x. The input of the model is Q ₁. State equations of x and P _ic are given in Eqs. (22) and (26). However, explicit equations of r_d have to be obtained by solving a set of linear algebraic equations with $\mathrm{d}{r}_d/\mathrm{d}t$, P_d, and P_c as unknowns, which are given by

$$2K_v{r}_d\frac{\mathrm{d}{r}_d}{\mathrm{d}t}=G_d(P_e-P_d)-G_d(P_d-P_c)+\Delta Q_{\text{coll}}$$ (28)

$$P_d{r}_d=T_e+T_m+P_{\text{ic}}(r_d+h)+\frac{\eta h}{r_{v0}}\frac{\mathrm{d}{r}_d}{\mathrm{d}t}$$ (29)

$$P_c=\frac{G_{\text{pv}}}{G_{\text{pv}}+G_d}{P}_{\text{ic}}+\frac{G_d}{G_{\text{pv}}+G_d}{P}_d$$ (30)

The baseline values for these parameters were adopted from previous studies [5,16,17,36] and are listed in Table 2. Note that, for basal flow conditions, the target flow rate Q_n of MCA, ACA, and PCA were set to $2.2\hspace{0.17em}\text{ml}\hspace{0.17em}{\mathrm{s}}^{-1},\hspace{0.17em}1.48\hspace{0.17em}\text{ml}\hspace{0.17em}{\mathrm{s}}^{-1}$, and $1.14\hspace{0.17em}\text{ml}\hspace{0.17em}{\mathrm{s}}^{-1}$, respectively. K_v is specified such that the baseline blood volume in distal arteries is $10\hspace{0.17em}{\text{cm}}^3$.

Table 2.

The baseline values of autoregulatory LP distal vascular bed model

$r_{d0}=0.015\hspace{0.17em}\text{cm}$	$t_{\mathit{C}\mathit{A}}=10\hspace{0.17em}\mathrm{s}$
$h_{d0}=0.003\hspace{0.17em}\text{cm}$	$G_{\mathit{C}\mathit{A}}=10\hspace{0.17em}\text{mm}\hspace{0.17em}{\text{Hg}}^{-1}$
${\sigma }_{e0}=0.1425\hspace{0.17em}\text{mm}\hspace{0.17em}\text{Hg}$	$G_{\mathit{p}\mathit{v}}=0.189\hspace{0.17em}\text{mm}\hspace{0.17em}{\text{Hg}}^{-1}{\mathrm{s}}^{-1}\text{ml}$
$k_{\sigma }=10.0$	$G_f=7.0\times {10}^{-5}\hspace{0.17em}\text{mm}\hspace{0.17em}{\text{Hg}}^{-1}{\mathrm{s}}^{-1}\text{ml}$
${\sigma }_{\mathit{c}\mathit{o}\mathit{l}\mathit{l}}=62.79\hspace{0.17em}\text{mm}\hspace{0.17em}\text{Hg}$	$G_{\mathit{c}\mathit{A}\mathit{A}}=4.0\times {10}^{-2}\hspace{0.17em}\text{mm}\hspace{0.17em}{\text{Hg}}^{-1}{\mathrm{s}}^{-1}\text{ml}$
$T_0=2.16\hspace{0.17em}\text{mm}\hspace{0.17em}\text{Hg}\hspace{0.17em}\text{cm}$	$G_{\mathit{c}\mathit{P}\mathit{P}}=1.0\times {10}^{-2}\hspace{0.17em}\text{mm}\hspace{0.17em}{\text{Hg}}^{-1}{\mathrm{s}}^{-1}\text{ml}$
$r_m=0.027\text{cm}$	$G_{\mathit{c}\mathit{A}\mathit{M}}=9.0\times {10}^{-3}\hspace{0.17em}\text{mm}\hspace{0.17em}{\text{Hg}}^{-1}{\mathrm{s}}^{-1}\text{ml}$
$r_t=0.018\hspace{0.17em}\text{cm}$	$G_{\mathit{c}\mathit{M}\mathit{P}}=8.0\times {10}^{-3}\hspace{0.17em}\text{mm}\hspace{0.17em}{\text{Hg}}^{-1}{\mathrm{s}}^{-1}\text{ml}$
$n_m=1.83\hspace{0.17em}\text{cm}$	$P_{\mathit{a}\mathit{n}}=100\hspace{0.17em}\text{mm}\hspace{0.17em}\text{Hg}$
$\eta =232\hspace{0.17em}\text{mm}\hspace{0.17em}\text{Hg}\hspace{0.17em}\mathrm{s}$	$G_o=3.17\times {10}^{-4}\hspace{0.17em}\text{mm}\hspace{0.17em}{\text{Hg}}^{-1}{\mathrm{s}}^{-1}\text{ml}$
$K_v=7.40\times {10}^3\hspace{0.17em}\text{cm}$	$P_s=6.0\hspace{0.17em}\text{mm}\hspace{0.17em}\text{Hg}$
$K_{\mathit{g}\mathit{M}}=1.05\times {10}^6{(\text{mm}\hspace{0.17em}\text{Hg}\hspace{0.17em}\mathrm{s}\hspace{0.17em}\text{cm})}^{-1}$	$Q_{\mathit{n}\mathit{M}}=2.2\hspace{0.17em}\text{ml}\hspace{0.17em}{\mathrm{s}}^{-1}$
$K_{\mathit{g}\mathit{A}}=7.50\times {10}^5{(\text{mm}\hspace{0.17em}\text{Hg}\hspace{0.17em}\mathrm{s}\hspace{0.17em}\text{cm})}^{-1}$	$Q_{\mathit{n}\mathit{A}}=1.48\hspace{0.17em}\text{ml}\hspace{0.17em}{\mathrm{s}}^{-1}$
$K_{\mathit{g}\mathit{P}}=5.90\times {10}^5{(\text{mm}\hspace{0.17em}\text{Hg}\hspace{0.17em}\mathrm{s}\hspace{0.17em}\text{cm})}^{-1}$	$Q_{\mathit{n}\mathit{P}}=1.14\hspace{0.17em}\text{ml}\hspace{0.17em}{\mathrm{s}}^{-1}$
$K_e=0.077\hspace{0.17em}{\text{ml}}^{-1}$	$P_{\mathit{i}\mathit{c}\mathit{n}}=9.5\hspace{0.17em}\text{mm}\hspace{0.17em}\text{Hg}$
$C_m=1.37\hspace{0.17em}\text{mm}\hspace{0.17em}{\text{Hg}}^{-1}\text{ml}$

Age or pathological conditions can degrade CA. To investigate the role of the cerebral autoregulation, we consider both healthy (baseline) and impaired CA cases. The degree of the impairment of the CA can be controlled by varying the gain parameter G _CA in Eq. (22). G _CA of the healthy (baseline) case was considered to be $G_{\text{CA}}=10\hspace{0.17em}\text{mm}\hspace{0.17em}{\text{Hg}}^{-1}$ following previous studies by Ursino. By contrast, we also test the totally impaired case with $G_{\text{CA}}\approx 0$ such that the second term of the right hand side of Eq. (22) becomes negligible at all six cerebral outlets. Partially and/or locally impaired cases were studied by varying G _CA but not reported here for brevity.

3. Results

The modeling framework discussed above was used to investigate the hemodynamic effects of cerebral autoregulation and collateral blood flows in healthy and pathological conditions. In Sec. 3.1, pulse-wave propagation through the arterial network is discussed using the two pressure–area models. In Sec. 3.2, the role of cortical collateral blood flow, communicating arteries, and cerebral autoregulation are examined under MCA and CCA occlusion. In Sec. 3.3, the dynamic assessment of the cerebral autoregulation by the compression–decompression of the CCA (THRT [19]) is presented. In the results below, the baseline condition will correspond to no occlusion and fully functional autoregulation.

3.1. Pulse-Wave Analysis.

Figure 2 presents pulse-waveform results for the baseline model, including comparison of results from the two (P1 and P2) pressure–area relations. Similar analysis can be found in the supplemental results which are available under “Supplemental Data” tab for this paper on the ASME Digital Collection for the case of RMCA occlusion. The top two rows plot the PWV and pressure waves in various arteries over the cardiac cycle. Velocity and wave intensity results are displayed in the bottom two rows for the P2 model only.

Fig. 2.

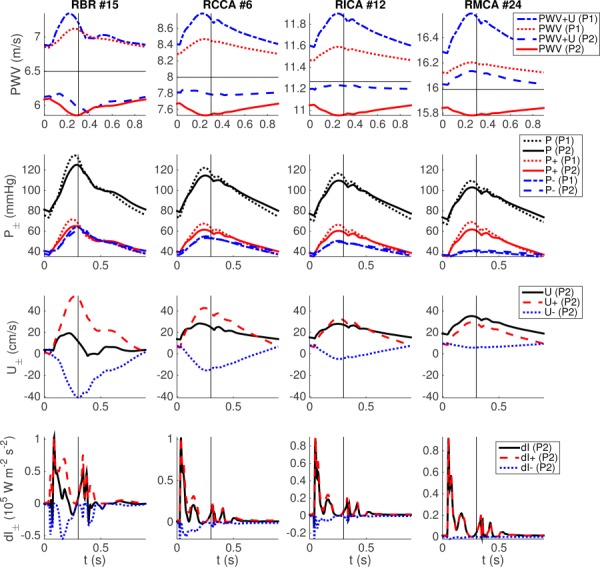
Waveforms in the RBR, RCCA, RICA, and RMCA. The first two rows compare waveforms resulting from the P1 and P2 pressure–area models, including (first row) PWV and total pulse-wave propagation speed (PWV + U), as well as (second row) full (P), forward (P+), and backward (P−) components of pressure. The third and fourth rows, respectively, plot the full, forward, and backward components for velocity and wave intensity. Horizontal lines denote the reference PWV $(c_0=\sqrt{\beta /2\rho A_0^{1/2}})$. Vertical lines denote aortic-valve closure.

PWV is used clinically to estimate arterial stiffness and is highly correlated with various cardiovascular conditions such as hypertension [37,38]. There is significant difference in PWV between the P1 and P2 models. PWV using the P1 model (first row, dotted lines) varies in proportion to the blood pressure (second row, dotted lines with larger magnitudes), whereas PWV using the P2 model (first row, solid lines) demonstrates the opposite trend. PWV values are consistently less than the reference PWV $c_0=\sqrt{\beta /(2\rho A_0^{1/2})}$ (first row, horizontal lines) using the P2 model, whereas the opposite is true for the P1 model. These differences are reduced somewhat in the RICA and RMCA (third and fourth column), as these arteries are stiffer and of smaller caliber than the RBR and RCCA (first and second column). Local wave propagation speed can be calculated by adding PWV and local blood flow velocity U. The P2 model (first row, dashed lines) presents relatively flat propagation speed throughout the cardiac cycle, which approaches c ₀ for the smaller RICA and RMCA arteries. Alternatively, the P1 model (first row, dotted-dashed lines) produces large fluctuations in wave propagation speed throughout the cardiac cycle. We note that the trends between pressure and PWV in Fig. 2 should not be related to long-term and global effects of arterial stiffening, which increases both mean pressure and PWV. Both P1 and P2 models can properly describe this phenomenon by applying larger β ($=(\sqrt{\pi }hE)/(1-{\sigma }^2)$).

Global pulse-wave propagation speeds can be estimated from the pressure waveforms using the foot-to-foot method [39]. The distances from the inflow (aortic root) to the RBR (#15) and RMCA (#24) are divided by the delay times for minimum pressure in the respective arteries. These values are listed in Table 3 and compared to the values computed from the vessel properties (distance and c ₀). Consistent with the above results, the two pressure–area models demonstrate significant differences. Results from the P2 model are close to the characteristic values, whereas the P1 model shows $8–16\%$ larger values than the characteristic values.

Table 3.

The average PWV from inflow to RBR (#15) and RMCA (#24) are calculated by the distance and travel time using $c_0=\sqrt{\beta /(2\rho A_0^{0.5})}$. This is compared with the estimates using two simulations with P1 and P2 models. Differences from the reference PWVs are shown in the parenthesis.

Distance	$c_0=\sqrt{\beta /(2\rho A_0^{0.5})}$	P1 model	P2 model
$L=32.4\hspace{0.17em}\text{cm}$ (inflow to RBR)	6.18 (m/s)	7.2 (16.5%)	6.35 (2.75%)
$L=47.7\hspace{0.17em}\text{cm}$ (inflow to RMCA)	9.86 (m/s)	10.7 (8.52%)	9.93 (0.71%)

Reflections.

The waveform of blood flow quantities is a superposition of forward and backward traveling waves, at least under a linear approximation theory. Thus, large differences in PWV between the two pressure–area models suggest potential differences in waveform morphology. The transmural pressure and its forward and backward components are shown on the second row in Fig. 2. For the current vessel geometry and a physiologically realistic peripheral resistance, the P2 model (solid lines with larger magnitudes) appears to attain more physiologic results. For example, brachial pressure varies between $76.6–121.8 \text{mm}\hspace{0.17em}\text{Hg} (\Delta p\approx 45 \text{mm}\hspace{0.17em}\text{Hg})$ for the P2 model, whereas for the P1 model (dotted lines with larger magnitudes) demonstrates larger variation between $71.3–130.4\hspace{0.17em}\text{mm}\hspace{0.17em}\text{Hg}(\Delta p\approx 60 \text{mm}\hspace{0.17em}\text{Hg})$.

Using Eq. (16), forward and backward pressure components can be calculated. Since $P_{0\pm }$ is not available, $P_{0\pm }=P_0/2$ has been used as in Ref. [40]. Due to low peripheral resistance in the cerebral vascular bed, the backward pressure variations at the MCA and ICA are relatively small compared to the forward pressure. However, at the brachial artery, large wave reflection occurs. This is also observed in the velocity waveforms, as shown in the third row of Fig. 2. The strong reflection from the BR arteries propagates to the cerebral arteries and generates pressure peaks in addition to the systolic and dicrotic notch. These are observed in the full and forward pressure and velocity waveforms by the P2 model at CCA, ICA, and MCA (a small hump after the dicrotic notch $t\approx 0.5\hspace{0.17em}\mathrm{s}$, most evident in Fig. 3). These peaks are not observed in the backward wave component in these vessels, confirming that they originate from proximal arteries. The P1 model does not show these additional pressure peaks. Wave intensity ($\mathrm{d}I$) demonstrates consistent results (Fig. 2, fourth row). For example, the RBR demonstrates large $\mathrm{d}{I}_{-}$, which makes $\mathrm{d}I$ negative at early, late, and immediately after, systole. RICA and RMCA show very small $\mathrm{d}{I}_{-}$. Clinical measurements of wave intensities at the aorta [41] and carotid artery [42] have similarly shown two positive peaks during early systole and toward the end of ejection, and negative values between these two peaks. The numerical study of Alastruey et al. [31] also demonstrated similar results.

Fig. 3.

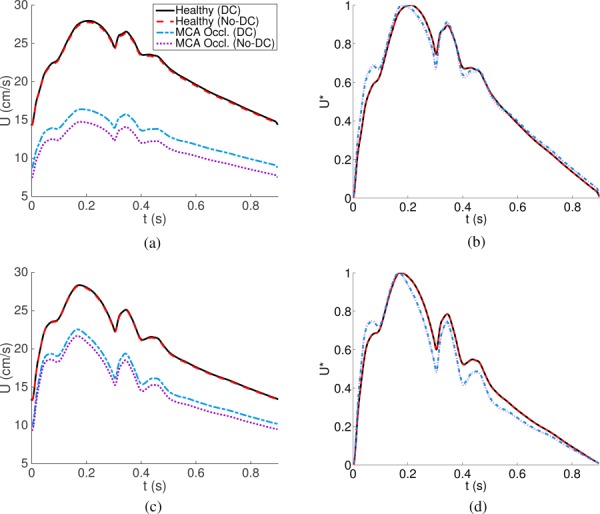
Flow velocities at the middle sections of RICA (top left) and RCCA (bottom left), and their normalized quantities ($U^{*}=(U-\text{min}(U))/(\text{max}(U)-\text{min}(U))$, right) are shown for the healthy and RMCA occlusion conditions. They are compared with (DC) and without (No-DC) distal collateral pathways.

MCA Occlusion.

With MCA occlusion (supplemental results which are available under “Supplemental Data” tab for this paper on the ASME Digital Collection), backward pressure at the MCA is considerably increased, and overall pressure is increased proximally in the ICA and CCA. Higher backward velocity and intensity due to the occlusion reduce the velocity and wave intensity at the ICA and CCA. Blood quantities at the brachial arteries were not found to be affected by MCA occlusion.

Recent studies [16,43] have suggested that the waveforms of blood flow velocity can be used to diagnose cerebral vasoconstriction and vasodilation. Figure 3 shows flow velocities and their normalized quantities at the middle sections of RICA and RCCA under healthy conditions and under RMCA occlusion. With MCA occlusion, both ICA and CCA show a significant decrease of the flow velocity, and the role of distal collateral flow (Sec. 3.2) becomes important. Due to the small blood flow rate, distal collateral flow does not affect the waveform shape. For better comparison of the waveform variation, the velocities are normalized such that systolic maximum and diastolic minimum values become 1 and 0, respectively. With the MCA occlusion, the first hump between t = 0 and 0.1 is pronounced both at ICA and CCA. Values at the valleys (both ICA and CCA) and peaks (CCA) after the systolic peak are relatively reduced with the occlusion. This is due to the negative contribution of the reflected backward wave component during and after the systolic peak.

3.2. Collateral Blood Flow and Autoregulation.

Under normal conditions, flow through the cortical collateral arteries is thought to be insignificant, however flow through these arteries can increase in response to significant differences in distal vascular pressure (Pd), e.g., during ischemia. Table 4 lists flow rates (absolute or relative) at the main cerebral arteries (ACA, MCA, and PCA), communicating arteries (AcoA and PcoA), and in the distal territories. The baseline condition, as well as full occlusions of the RMCA, RCCA, and both CCAs, is considered. The flow rates are compared between cases with (*) and without (No-DC**) distal collateral flow. In order to examine the role of CA function, impaired CA conditions were additionally tested for all cases, and the results are listed in the supplemental results which are available under “Supplemental Data” tab for this paper on the ASME Digital Collection.

Table 4.

Flow rates and proportions at major cerebral arteries (ACAs, MCAs, and PCAs) and communicating arteries (AcoA and PcoAs) for baseline conditions, and for occlusion of RMCA, RCCA, or both CCAs

Case	Q	RACA	LACA	RMCA	LMCA	RPCA	LPCA	All	AcoA	RPcoA	LPcoA
Baseline	$Q_{1H} (\text{ml}/\mathrm{s})$	1.47	1.47	2.21	2.21	1.11	1.11	9.58	−0.031	−0.022	−0.012
Conditions	$\frac{Q_{1H}}{Q_{\text{tot}H}} (\%)$	15.3	15.3	23.1	23.1	11.6	11.6	100	−0.325	−0.230	−0.127
RMCA	$\frac{Q_1}{Q_{1H}} (\%)$	110	101	0	103	107	98.3	80.0	942	543	139
Occlusion*	$\frac{Q_d}{Q_{1H}} (\%)$	100	101	13.1	100	100	100	—	—	—	—
(No-DC**)	$\frac{Q_1}{Q_{1H}} (\%)$	103	101	0	100	101	101	77.8	1030	535	154
RCCA	$\frac{Q_1}{Q_{1H}} (\%)$	71.2	105	72.3	102	101	96.6	90.1	−7880	−3910	−408
Occlusion*	$\frac{Q_d}{Q_{1H}} (\%)$	86.3	92.8	75.3	97.4	98.3	98.3	—	—	—	—
(No-DC**)	$\frac{Q_1}{Q_{1H}} (\%)$	79.7	95.4	72.3	97.8	98.3	98.3	88.8	−8220	−3970	−350
Both CCA	$\frac{Q_1}{Q_{1H}} (\%)$	25.4	25.4	27.6	27.6	103	103	44.3	0	−5570	−10,100
Occlusion*	$\frac{Q_d}{Q_{1H}} (\%)$	25.8	25.8	30.7	30.7	95.7	95.7	—	—	—	—
(No-DC**)	$\frac{Q_1}{Q_{1H}} (\%)$	25.5	25.5	28.4	28.4	97.4	97.4	43.5	0	−5650	−10,200

$Q_{\text{tot}H}\hspace{0.17em}=\hspace{0.17em}9.59\hspace{0.17em}\text{ml}/\mathrm{s}$ is the combined efferent cerebral artery at baseline. Flow rates are compared with (*) and without (No-DC**) distal collateral flow. For cases with distal collateral flow, Q_d is also listed. Note that $Q_1=Q_d$ without collateral flow (cf. Fig. 1).

RMCA Occlusion.

For baseline conditions, flow rates at the MCA, ACA, and PCA are close to the target state of the CA distal vascular bed model, and blood flow rates through communicating arteries (Table 4, first rows, far right) and distal collateral vessels (not shown) are insignificant. When the RMCA is occluded, the distal vascular pressure (P _dRM) decreases significantly, and this increases distal collateral flow from the anterior and posterior regions (increased $-Q_{\text{RMP}}$ and Q _RAM in Eqs. (24) and (25), negative sign indicates opposite the flow direction in Fig. 1). $Q_d-Q_1$ represents the amount of distal collateral blood flow and under occlusion of the RMCA, the distal RMCA territory receives $\approx 13\%$ of normal MCA flow through the distal collateral vessels (Table 4, RMCA occlusion*); this collateral flow leads to increased flow through the RACA and RPCA.

Impaired cortical collateral blood flow was also studied. In this case (“No-DC**” under RMCA occlusion), the blood flow rates at the RMCA and its distal territory become zero, implying a critical ischemic event. There are slight changes in flow rates at other cerebral arteries due to blood flow rerouting through the CoW. In the absence of CA, this rerouting leads to overflow in the RACA and RPCA, however including CA enables proper maintenance of blood flow to the territories (for impaired CA conditions, see supplemental results which are available under “Supplemental Data” tab for this paper on the ASME Digital Collection).

RCCA Occlusion.

Occlusion of the RCCA (Table 4, RCCA occlusion) affects flow rates of both the RMCA and RACA directly. In this case, flow rates at communicating arteries in the CoW increase significantly (40 to 80 times more than healthy condition). When the RCCA is occluded, flow to the RACA is reduced by 29%, hence 71% of the baseline flow is maintained by the communicating arteries. This is similarly true for the RMCA, which also maintains 72% of baseline flow upon RCCA occlusion.

The influence of distal collateral pathways is more profound for recovering flow in the anterior territory. Namely, the distal collateral vessels recover approximately 15% of baseline flow in the RACA territory (i.e., nearly 1/2 of the total loss due to RCCA occlusion). However, distal collateral pathways are only able to recover approximately 3% of baseline flow in the RMCA territory. This is consistent with clinical observations as the MCA territory is relatively isolated distally, and the distal collateral pathways between the left and right anterior regions are better developed.

Upon RCCA occlusion, active vasodilation via CA in the RACA and RMCA territories reduced distal resistance significantly. This promoted blood flow from the left to right side through communicating arteries than the cases with impaired CA. Downstream territories of LACA and LMCA also reduced resistances to maintain blood flow. Overall, the healthy CA condition was able to maintain 90% of Q _{tot H} during total occlusion of the CCA, whereas the impaired CA condition was able to maintain 78% of Q _{tot H}. See supplemental results which are available under “Supplemental Data” tab for this paper on the ASME Digital Collection for additional data on impaired CA conditions.

Dual CCA Occlusion.

Compression of the CCAs is used in the clinical setting for various purposes. For example, this is sometimes performed to reduce the risk of cerebral embolization during transcatheter aortic-valve implantation, as well as during the evaluation of autoregulation function. We performed simulations with various compressions of the CCAs and examined the changes to the flow rates at main cerebral arteries under healthy and impaired (G _CA = 0) CA conditions.

Figure 4 shows the change of the flow rates at the RCCA, RMCA, RACA, RVERT, and at all cerebral outlets versus percent occlusion of the CCAs (values for left side arteries are similar). The flow velocity at the narrowed portion of the CCA is also shown. The CCA flow rate is not significantly affected by the compression until roughly a 70% occlusion, i.e., $A_{0\text{post}}/A_{0\text{pre}}\approx 30\%$. For $A_{0\text{post}}/A_{0\text{pre}}<0.1$, the flow rate decreases rapidly to 0 as $A_{0\text{post}}/A_{0\text{pre}}$ is reduced to 0. The CCA has a large initial caliber ($A_{0\text{pre}}$), thus moderate compression of the artery does not significantly increase resistance compared to distal vascular resistance. However, as the compression progresses beyond $A_{0\text{post}}/A_{0\text{pre}}\approx 0.1$, the resistance of the occluded segment becomes dominant resulting in a significant reduction in CCA flow. This can most clearly be observed by inspection of the CCA velocity versus compression ratio (bottom right). When $A_{0\text{post}}/A_{0\text{pre}}>0.1$, the overall resistance does not alter volumetric flow, and hence velocity increases proportional to area reduction. However, as $A_{0\text{post}}/A_{0\text{pre}}$ is reduced further, overall resistance increases, which decreases volumetric flow and leads to a rapid decrease in velocity.

Fig. 4.

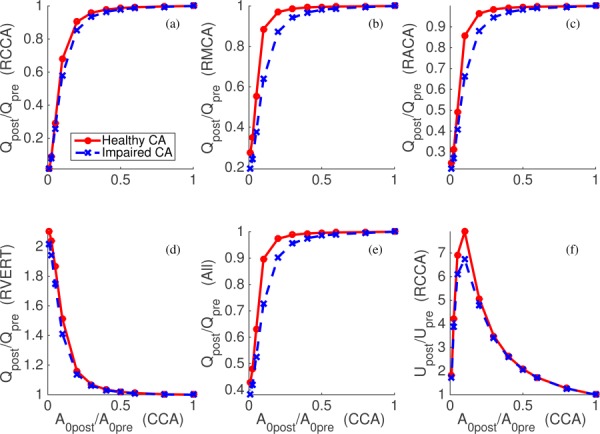
The changes of flow rates at the RCCA (a), RMCA (b), RACA (c), RVERT (d), all cerebral outlets (e), and velocity at the narrowed RCCA (f) due to the compression of both CCAs. Horizontal axes denote the baseline area of the narrowed portion of the RCCA compared to the initial baseline area. Solid and dashed lines represent the cases with healthy and unhealthy autoregulation cases, respectively.

As shown in Fig. 4, normal and impaired CAs demonstrated the most noticeable differences when $A_{0\text{post}}/A_{0\text{pre}}$ = 10–30%. Impaired autoregulation did not significantly affect CCA flow (upper-left panel); normal CA demonstrated a maximum of $\approx 8\%$ larger flow rate versus impaired CA over all range of occlusion percentage. However, differences were more pronounced at the MCA and ACA (top middle and right of Fig. 4). When $A_{0\text{pre}}/A_{0\text{post}}=0.1$, the MCA flow rate was reduced to $\approx 90\%$ and $\approx 65\%$ of the baseline condition with normal and impaired CA, respectively. During total occlusion of both CCAs, the combined flow rate to all cerebral outlets was reduced to 40% of the initial state (Table 4), with $\approx$ 75% reductions in flow to the MCAs and ACAs. Compensatory flow to the ACA and MCA territories was supplied by an increase in VERT flow, yet this increase did not affect PCA flow.

Figure 5 shows the activation factor M, active tension T_m, lumped distal radius r_d (downstream of the RMCA), and ICP versus compression ratio for the CCAs. With normal CA, M and T_m decrease as $A_{0\text{post}}/A_{0\text{pre}}$ is reduced by compression (Fig. 5, left). The CA mechanism reaches the vasodilation limit (M = −1 and T_m = 0) when $A_{0\text{post}}/A_{0\text{pre}}$ becomes 5%. r_d and ICP increase by $\approx 50\%$ (Fig. 5, right) until CA reaches its limit, then when $A_{0\text{post}}/A_{0\text{pre}}<0.05$ both r_d and ICP decrease. This nonmonotonic behavior of the lumped distal radius and ICP is due to the fast reduction of the flow rate after the CA limit is reached. As shown in Eqs. (26) and (27), ICP is directly related to r_d. A slight difference between r_d and ICP variation is due to the contribution of other cerebral distal vasculature and the production of CSF. With impaired CA, r_d and ICP decrease due to the flow rate reduction.

Fig. 5.

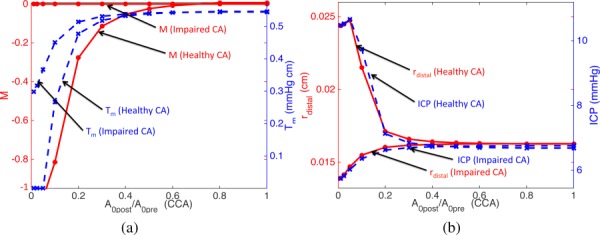
The activation factor M (solid lines, left vertical axis) and active tension T_m (dashed lines, right vertical axis) (left). Distal radius (solid lines, left vertical axis) and ICP (dashed lines, right vertical axis) (right). M, T_m, and r_d are from downstream of RMCA. Both healthy and impaired CA cases are shown. Horizontal axes denote the reference area of the constricted portion of the RCCA compared to the initial reference area.

3.3. The Dynamic Assessment of the Cerebral Autoregulation.

The function of cerebral autoregulation is often monitored for patients with brain damage in order to prevent secondary damage to the injured brain [44,45]. The dynamic assessment of CA (dCA) quantifies the fast modifications in CBF in relation to rapid alterations in arterial blood pressure [3]. These changes can be assessed using the THRT, in which compression–decompression of a CCA is performed and resulting flow changes in the MCA are monitored using transcranial Doppler [19].

The nominal diameter of the RCCA is $0.5\hspace{0.17em}\text{cm}$, and the compression–decompression (modeled by controlling A ₀) was applied to the middle subsegment of the RCCA over a length of $2\hspace{0.17em}\text{cm}$. From the upstream to downstream, the lengths of three subsegments of the RCCA are $3\hspace{0.17em}\text{cm},\hspace{0.17em}2\hspace{0.17em}\text{cm}$, and $12.7\hspace{0.17em}\text{cm}$. A 95% reduction was applied to A ₀ of the middle segment for $7\hspace{0.17em}\mathrm{s}$ to represent the THRT. The MCA vessel diameter was also reduced to 80% of the value in Table 1 to match the range of flow velocity in Ref. [46].

Figure 6 compares the flow velocity at the RMCA measured in vivo by transcranial Doppler (TCD) during THRT [46] (left) and predicted by the present model (right). Although the in vivo data contain measurement noise and breathing effects, the simulation accurately captures the essential autoregulatory features. Both figures present a rapid decrease of the MCA flow velocity in response to the compression, a gradual increase of the velocity while the same level of compression lasts for $7\hspace{0.17em}\mathrm{s}$, a rapid overshoot immediately after the decompression, and a delayed recovery to the initial state.

Fig. 6.

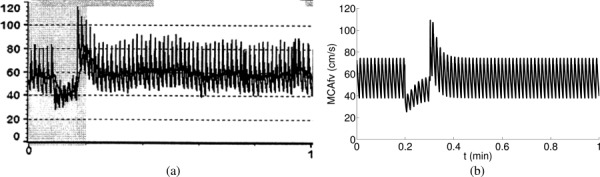
Flow velocity at the RMCA measured in vivo using TCD with compression–decompression of right CCA (left) (Reproduced with permission from Smielewski et al. [46]. Copyright 1996 by Wolters Kluwer Health, Inc.) and predicted by the present model (right).

4. Discussion

We have presented a multiscale approach for CBF modeling, which involves coupling of a 1D nonlinear blood flow solver with a sophisticated cerebral autoregulation LP vascular bed model. The CA model enables the computation of pressure and flow rates at distal cerebral vessels, distal collateral blood flow, CSF dynamics, and ICP. The combined framework was used to explore pulse-wave dynamics under healthy conditions, as well as occlusions of the MCA and CCAs.

The model described is dependent on several parameters that are patient dependent. Prior studies have investigated to some degree sensitivity analysis [16]. In general, parameters were chosen to be physiologically reasonable and similar to prior published data. Because exhaustive sensitivity analysis is cost prohibitive, a more global approach was taken whereby gross aspects of the modeling (e.g., autoregulation, distal collateral flow, constitutive model, etc.) were varied and differences reported. General trends reported above are expected to be robust to finer scale uncertainties in chosen parameters, nonetheless, the availability of patient specific parameter information will likely lead to greater prediction capability in clinical settings.

Two popular pressure constituent models based on Laplace's law were compared. The magnitudes and waveforms of hemodynamic quantities (pressure and velocity) and PWV were found to be significantly affected by the choice of pressure–area model. For the given physiological parameters, the P2 model appeared to produce more realistic pressure magnitudes and waveforms. The derivation of the P1 model uses the $A/A_0\simeq 1$ approximation explicitly. Without such assumption, the P2 model results in PWV that is consistent with the Moens–Korteweg formula. However, we note that the comparison of two pressure models is not conclusive, since both models assume a constant elasticity for each vessel segment, which in fact is a function of the strain condition of the vessel wall. Thus, both models are (implicitly) restricted to small deformations. Also, the magnitude of pulse pressure is determined by multiple factors, such as the amplitude of the prescribed aortic flow rate, the stiffness of large arteries, and the peripheral resistances [31,47]. Nevertheless, the elastic model dominates the blood-vessel wall interactions even in more advanced viscoelastic models, thus the differences between the two popular models considered in this study motivates additional investigation on the validation of the models.

In addition to the pressure magnitudes, the P2 model showed a second peak during diastole, which is typically observed in measurements. In vivo, peaks in pressure or flow waveforms originate from wave reflections in the entire peripheral vasculature. These reflections are superimposed on each other and transmitted through the aorta to the cerebral arteries to generate the additional peaks. The magnitude and timing of these peaks are determined by both the stiffness of large arteries and the resistances of distal vascular beds. The systemic arteries are simplified in the present model with the assumption that pulse-wave travel times within truncated vessels are much smaller than the cardiac cycle. Recently, Epstein et al. [48] investigated the effect of a reduction in the number of arterial segments in a given distributed 1D model on the shape of the simulated pressure and flow waveforms. They replaced downstream 1D arteries with LP models and found good agreement in the shape of the waveforms between the original and reduced models. It still remains to be confirmed using clinical measurements whether the present model reasonably captures the major characteristics of pressure waves in the cerebral arteries. Additionally, the viscoelastic property of artery wall is another factor affecting the contour of simulated pressure wave [49–51] that may be necessary to consider.

Velocity waveforms at RICA and RCCA were examined under normal (healthy) conditions and during MCA occlusion. Normalized waveforms show evident morphological changes due to the occlusion, including relative decrease of the magnitudes during and after the systolic peak compared to the magnitude before the peak. This is due to the negative contribution of the reflected wave component during and after the systolic peak. Accurate and continuous monitoring of cerebral vasculature status is very important to treat neurocritical care unit patients. The velocity waveform changes due to the distal vascular occlusion may enable the development of such monitoring system [16,43].

Simulations were conducted to examine the role of proximal and distal collateral blood pathways. When the MCA is occluded, the distal collateral vessels have an important role. Previous experiments with rats [52,53] have shown that the caliber of cortical collaterals increases by $\approx 50\%$ during prolonged ischemia of the MCA territory. Local blood flow returned close to normal value due to this change. Ursino and Giannessi [5] modeled this aspect by gradual decrease of collateral resistances in their LP model study. They reported $\approx 15\%$ of normal MCA flow passing through anterior-to-middle and posterior-to-middle distal collateral pathways during the MCA occlusion. This value increased to $\approx 45\%$ with the vasodilation of the distal collaterals. Our study did not consider such vasodilated cortical collaterals, and $\approx 13\%$ of normal MCA flow rate was observed through the distal collaterals, which is similar to the findings in prior studies before active vasodilation of the collaterals.

The communicating arteries in the CoW become important when the CCA is occluded. Peak flow rates of $\approx 2.8\hspace{0.17em}\text{ml}/\mathrm{s}$ and $\approx 1.0\hspace{0.17em}\text{ml}/\mathrm{s}$ were observed at the AcoA and RPcoA, respectively, when the RCCA was occluded. These flow rates are consistent with a recent study by Köppl et al. [13] which reported $\approx 3.2\hspace{0.17em}\text{ml}/\mathrm{s}$ and $\approx 1.5\hspace{0.17em}\text{ml}/\mathrm{s}$ for peak systolic flow rates at the AcoA and RPcoA, respectively, for severe RCCA stenosis (95% area reduction). We note that their study used 2 × larger vessel areas for the communicating arteries than the present study, which may explain the observed differences, in addition to the more sophisticated CA model in our study. Alastruey et al. [11] also observed similarly large increases of flow rates in the communicating arteries (20 to 80 times more flow rates than the cases with complete CoW) when ACA or PCA are absent in the CoW. In the present study, we have considered a complete CoW structure, which can only be found in about 50% of the population [54]. Anatomical variation in the CoW has been shown to significantly affect the regulatory capability of the cerebral circulation [11,14,15], which motivates additional studies on this topic with the present model.

The model is also used to examine the CBF distribution and ICP variation during the compression of both CCAs, which is a minimally invasive approach to reduce the cerebral embolization during transcatheter aortic valve implantation (TAVI). Despite the increasing popularity of TAVI, there have not yet been thorough investigations on the strategies to reduce the risk for the neurological events [55]. Our results show that the total CBF is reduced to 40% and ICP increases by $\approx 50\%$ during the CCA compression. This suggests that the compression should be carefully considered for patients who are vulnerable with the large ICP variations.

Simulations for the compression–decompression of a CCA (the dynamic assessment of cerebral autoregulation, dCA) were conducted. The results show a favorable agreement with a published clinical measurement for healthy conditions [46]. The simulation is capable of reproducing all important features of dCA. Most importantly, a rapid overshoot and delayed recovery to the initial state of the MCA flow velocity are accurately captured.

This modeling delivers insights to the meanings of morphological features of CBF and ICP pulsatile waveforms. There have been an extensive studies of morphological features of these pulses using pure data-driven approaches [56,57]. In addition, the developed model could be coupled with model-driven statistical inference approaches to provide a model-based data fusion of clinical data to monitor cerebral hemodynamics for patients under neurocritical care [36,43].