Abstract
Myocardial microstructures are responsible for key aspects of cardiac mechanical function. Natural myocardial deformation across the cardiac cycle induces measurable structural alteration, which varies across disease states. Diffusion tensor magnetic resonance imaging (DT-MRI) has become the tool of choice for myocardial structural analysis. Yet, obtaining the comprehensive structural information of the whole organ, in 3D and time, for subject-specific examination is fundamentally limited by scan time. Therefore, subject-specific finite-element (FE) analysis of a group of rat hearts was implemented for extrapolating a set of initial DT-MRI to the rest of the cardiac cycle. The effect of material symmetry (isotropy, transverse isotropy, and orthotropy), structural input, and warping approach was observed by comparing simulated predictions against in vivo MRI displacement measurements and DT-MRI of an isolated heart preparation at relaxed, inflated, and contracture states. Overall, the results indicate that, while ventricular volume and circumferential strain are largely independent of the simulation strategy, structural alteration predictions are generally improved with the sophistication of the material model, which also enhances torsion and radial strain predictions. Moreover, whereas subject-specific transversely isotropic models produced the most accurate descriptions of fiber structural alterations, the orthotropic models best captured changes in sheet structure. These findings underscore the need for subject-specific input data, including structure, to extrapolate DT-MRI measurements across the cardiac cycle.
Keywords: cardiac structure, image-based modeling, diffusion tensor MRI, cardiac biomechanics, small animal modeling
Introduction
There is a profound link between ventricular structure and mechanical cardiac function, which has been consistently observed experimentally and clinically. The structure of myocyte aggregation is a key contributor to wall thickening (the driver of stroke volume), circumferential strain, and torsion [1–5]. Some of these kinematics already serve or have an expanding role, as clinical functional indicators [6–9]. Several animal experiments have shown that cardiac structure is altered in disease states, for example, fiber orientation has been used to detect interstitial tissue fibrosis, to quantify the extent and progression of tissue damage due to ventricular infarction, and to assess changes after surgical restoration [10–13]. In humans, observations of in vivo cardiac structure using DT-MRI alterations show potential for detection and quantification of tissue damage and its consequences in terms of variations in strain patterns and local perfusion [14–16]. With improvements in numerical techniques, fundamental aspects of myocardial structure have been integrated with computational biomechanics to derive significant observations regarding stress distribution and contractility, as well as the optimization of devices and surgical techniques [3,11,17–19]. Thus, precise knowledge of myocardial structure is crucial for understanding cardiac function in health, monitoring disease progression, and predicting cardiac functional behavior.
Ventricular structure has been elucidated by a variety of means including histology, electron microscopy, and DT-MRI [20–22]. The latter has become the tool of choice because it is nondestructive, does not use ionizing radiation, and it is inherently 3D. In DT-MRI, the average orientations of myocardial structures at each voxel can be extracted from the principal directions, or eigenvectors, of the DT [21–24]. Specifically, myocardial fiber orientations have been correlated to the first eigenvector, while the secondary eigenvalue has been associated with the general direction of myocardial sheets [21,25]. A third direction orthogonal to the first two describes the so-called sheet-normal direction [24]. Since it requires two scalar angles to specify a directional vector in 3D, these structural orientations are often expressed in terms of angles projected along the cardiac longitudinal, circumferential, and radial planes. For clarity, the imaging planes and the convention of the angles used in the current work for representing fiber and sheet orientations are detailed in Fig. 1.
Fig. 1.
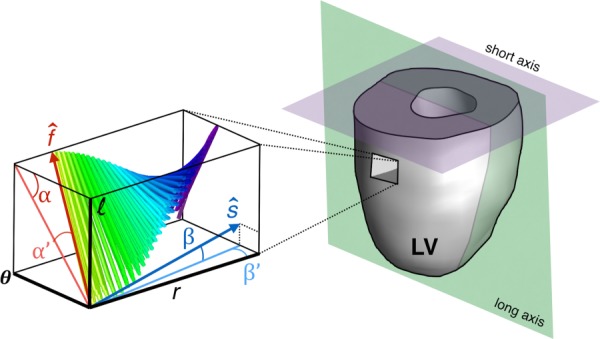
Angular quantification of fiber and sheet structures in the LV. The local fiber () or sheet direction () can be expressed numerically as rotations about a coordinate system defined by the local circumferential, radial, and longitudinal direction (θ, r, and l, respectively). The fiber orientation is described by the helix α (which takes on negative values on the epicardium) and transverse α′ angles. A similar approach can be used to express sheet orientation (β and β′). The idealized imaging planes (long and short axes) approximately coincide with the longitudinal–radial plane and circumferential–radial plane near the midventricle.
The dynamic myocardial structure, particularly at systole and diastole, has been studied with DT-MRI both in vivo, as well as ex vivo with the aid of isolated heart preparations. The changes between the two cardiac cycle points are generally described using basic geometrical models relating fiber shortening and wall thickening through conservation of volume [26], with the most evident changes consisting of an overall longitudinal fiber alignment in systole with respect to diastole [1,27,28]. Specifically, with the wall thickness normalized, systolic fiber structure has a steeper transmural rate of change of the fiber helical angle α. In terms of whole-ventricle histograms, the fiber transverse angle α′ converges toward zero in diastole [1,16]. Dynamic information about the sheet orientation is more scarce, but a distinct reconfiguration of the sheet transverse angle β has been observed as a shift from having relatively large populations of voxels near larger angles at diastole, toward a larger concentration near 0 deg at systole [14,29].
The advent of in vivo DT-MRI, now also available for rats and midsized animals [30], has opened the door for unprecedented studies of structural dynamics and mechanisms to examine underlying key aspects of cardiac function linked to variability and disease characterization. However, obtaining a complete description of the structural dynamics of the beating whole heart still faces severe technical and experimental challenges. In particular, tradeoffs between scan resolution and acquisition time in current in vivo DT-MRI have limited the available structural data to single imaging slices and cardiac cycle points [14,31,32]. Detailed true 3D, let alone 4D (the fourth dimension being time), assessments of the myocardial structure in the whole heart remain elusive. As a first step toward the ultimate goal of 4D imaging of the structure of the myocardium, a basic premise of the current study is that the limited available structural information can be employed to extrapolate temporal evolution with the aid of computational biomechanics.
Although computational models of ventricular mechanics have long existed, many of them with outstanding descriptive and predictive power, little research has been focused on the design and experimental validation of models dedicated to studying predictions of dynamic structural behavior. Instead, the role of ventricular structure in the context of numerical simulations has been considered mostly from a sensitivity standpoint, whereby the performance of computer simulations, particularly using the FE discretization, has been measured against global metrics like pressure and volume, and to some extent, stress and strain distribution [2,5,17,33]. Many of these previous studies have yielded an improved understanding regarding the role of parameterization and distribution of helical structure in ventricular modeling and have pointed to the need for further investigation regarding the role of additional aspects of structural characterization on the performance of computational models [5,26,33,34]. However, direct validation of simulated structural changes against experimental measurements (both kinematic and structural dynamics) remains lacking.
The main objectives for this research are to identify a suitable numerical approach and to apply it toward extrapolating a discrete set of initial structural DT-MRI information temporally across the cardiac cycle. The first step is intended to prioritize the practical considerations needed to capture left-ventricular (LV) structural dynamics and also to address some of the ambiguities surrounding the nature and net effect of sheet structures on simulated deformation, through a systematic evaluation of selected structural dynamic simulations against subject-specific experimental data. The second step serves as a demonstration of the applicability of the method beyond validation points, by integrating estimated structural dynamics with common visualization techniques of cardiac structure.
Methods
Overview.
Extrapolation of DT-MRI data depends on tissue deformation information and the manner in which this information is applied to deform (or warp) images. This study focused on three aspects of the numerical simulation of structural alterations: material assumptions, inclusion of subject-specific data, and application of simulated deformation to DT-MRI. To evaluate different extrapolation strategies arising from four subject-specific FE simulations and two warping approaches, the simulated results (a total of eight approaches per subject) were compared against an experimental benchmark composed of in vivo CINE and displacement-encoded MRI as well as DT-MRI of isolated rat hearts (n = 3). This last measurement allowed experimental characterization of 3D myocardial structure in states associated with early diastole (EAD), end diastole (ED), and end systole (ES). Care was taken to ascertain that the isolated heart retained its in vivo gross morphology by preserving intraventricular volume. DT-MRI at EAD provided an initial set of structural data for the simulations, whereas ED and ES were designated as the extrapolation targets.
Animal Procedures.
All animal protocols were approved by the Institutional Animal Care and Use Committee at the University of Utah in accordance to the Guide for the Care and Use of Laboratory Animals issued by the US National Institutes of health (NIH Publication No. 85-23, rev. 1996). For in vivo MRI, adult male Sprague Dawley rats (n = 3, 300 ± 25 weight) were anesthetized with 1–3% isoflurane and 0.6–0.9 L/min O2 and placed inside the imaging RF coil. Continuous monitoring of vital signs (respiration, temperature, electrocardiogram, and oxygen saturation) was performed using a magnetic resonance (MR)-compatible physiological monitoring system (SA Instruments, Stony Brook, NY).
After completion of in vivo imaging protocols, the animal was euthanized via rapid exsanguination under deep isoflurane anesthesia (5%) according to approved standard operating procedures. The heart was rapidly extracted, cannulated at the aorta, suspended vertically, and perfused retrograde in a custom-made MRI-compatible, temperature-controlled perfusion chamber initially with 100% oxygenated Tyrode's solution (in mM: NaCl 140.0, glucose 11.0, KCl 5.4, HEPES 5.0, CaCl2 1.8, and MgCl2 1.0) at 90 mm Hg at a flow rate of 15 mL/min with a positive displacement pump (Cole-Parmer, Item# EW-77120-42). A balloon was placed in the ventricle to control volume based on in vivo readings for each subject, and a small perforation was made in the pulmonary vein to allow perfusion fluid outflow. Continuous pressure, temperature, and electrical activity measurements were used to adjust perfusion rates depending on the state of the heart.
The desired cardiac states for DT-MRI were emulated by perfusing the isolated heart with appropriate cardioplegic solutions and adjusting the volume of the intraventricular balloon based on in vivo measurements [1,27,29]. For EAD, a KCl solution (in mM: NaCl 105.0, KCl 25.0, glucose 11.0, HEPES 10.0, and MgCl2 1.0) was used with the balloon deflated to allow the myocardium to remain relaxed. For ED, the heart was similarly arrested, but the balloon was adjusted to the ED volume. Contracture at ES was induced by adding LiCl (in mM: LiCl 125.0, glucose 11.0, HEPES 10.0, KCl 5, CaCl2 2.5, and MgCl2 1.0). All solutions were titrated to pH 7.4 and kept at 37 °C for the duration of the experiments, and bovine serum albumen (4 mg/L) was added to achieve osmotic equilibrium. Approximately 15 min of perfusion time was administered at each change of solution prior to imaging to achieve tissue equilibrium.
Magnetic Resonance Image Acquisitions.
For in vivo imaging, the animal was placed prone inside a 72-mm ID quadrature volume RF coil in a Bruker Biospec 7 T imaging instrument (Bruker Biospin, Billerica, MA). The dynamic morphology of the heart, for biomechanical modeling, was obtained via retrospectively gated fast low angle shot (FLASH) CINE (eight-short slices spanning the left ventricle, 20.0 ms repetition time (TR), 2.0 ms echo time (TE), flip angle 15 deg, 40 × 40 mm field of view (FOV), 96 × 96 matrix size). For validating biomechanical simulations, displacement-encoding with stimulated-echoes scans (DENSE, 20.0 ms TR, 2.0 ms TE, 40 × 40 mm FOV, 96 × 96 matrix size, and 0.7 cycles/mm motion encoding gradients in each read, phase, and slice directions) [35,36] were performed to measure deformation on three 3.0 mm-thick short-axis slices at the base, middle, and apex of the LV. In Vivo scan time included 8 min for the anatomical FLASH CINE sequence and 45 min for the DENSE acquisitions for a total of approximately 1 h and 10 min scan time per animal including preparation time.
For ex vivo imaging, the perfused isolated heart was imaged using the custom-built integrated (19 mm) loop-gap RF coil in the perfusion chamber. At each emulated cardiac state, DT-MRI was acquired using a velocity-compensated, multishot segmented EPI sequence (FOV 36.3 × 36.3 mm, 128 × 128 pixels, four slices, TR 2000 ms, TE 20 ms, 24 encoding directions with 900 s/mm2 b-value). Additional slices were acquired for morphological characterization using a FLASH sequence (256 × 256 pixels, four long slices, four short slices, TR 10 ms, TE 1.5 ms, 30 deg flip angle). Total scan time in the isolated heart apparatus was approximately 25 min divided into DT-MRI (6 min per state), FLASH (2 min per state), and scout acquisitions. For tractography visualization, after the isolated heart preparation, the specimens were fixed and scanned at high resolution over night (3D spin echo sequence, FOV 30 × 30 × 30 mm, 128 × 128 × 128 pixels, 2000 ms TR, 20 ms TE).
Image Postprocessing.
The anatomical images were semi-automatically segmented (Amira, FEI Life Sciences, Hillsboro, OR). Ventricular volumes were approximated via Simpson's rule. DENSE phase images (after k-space subtraction and low-pass filtering) were unwrapped using a fuzzy logic approach, and offset corrected using registration of magnitude images [36,37]. The displacements were used to calculate the average systolic circumferential and radial strain (with ED as the reference) at each slice based on the principal components of the Green-Lagrange strain, as well as slice rotations and longitudinal torsion according to previous studies in rat hearts [38,39]. The DT and principal directions were computed from diffusion-weighted images using a nonlinear least-squares reconstruction protocol [40].
Computational Modeling and Boundary Conditions.
Approximately 75% of the myocardial volume of the LV, from the apex to approximately two-thirds of the distance to the base, was organized into a FE domain composed of linear hexahedral elements (TrueGrid, XYZ Applications, Livermore, CA) using semi-automatically labeled images obtained from long- and short-axes anatomical MRI (Amira, FEI Life Sciences, Hillsboro, OR). Labeled data were combined to create a single surface by means of implicit spline fitting [41]. The final mesh, after evaluating models from about 3000–13,200 elements, was composed of approximately 8000 elements after performing a 3% convergence analysis using maximum first principal strains and maximum effective shear under 4 kPa (30 mm Hg) pressurization on the LV cavity. For simulation of the validation points, the endocardial LV surface was pressurized to 2.3 kPa (17 mm Hg) and 15 kPa (113 mm Hg) for ED and ES, respectively. For simulation of the whole cardiac cycle, pressure and volume load curves were constructed based on a confidence interval of in vivo volume measurements and pressure waveforms of the healthy rat heart extracted from the literature [42]. Additional constraining was achieved by surrounding the LV with a block made of a low-stiffness, compressible support material and applying the boundary conditions shown in Fig. 2 [43]. The additional mesh was also applied to facilitate interpolation of displacements near the LV outer surface. (Supporting material was modeled as Neo-Hookean with modulus of elasticity of 0.01 kPa, and Poisson ratio of 0—A tenfold change on support material stiffness had no discernible effects on the solution.)
Fig. 2.
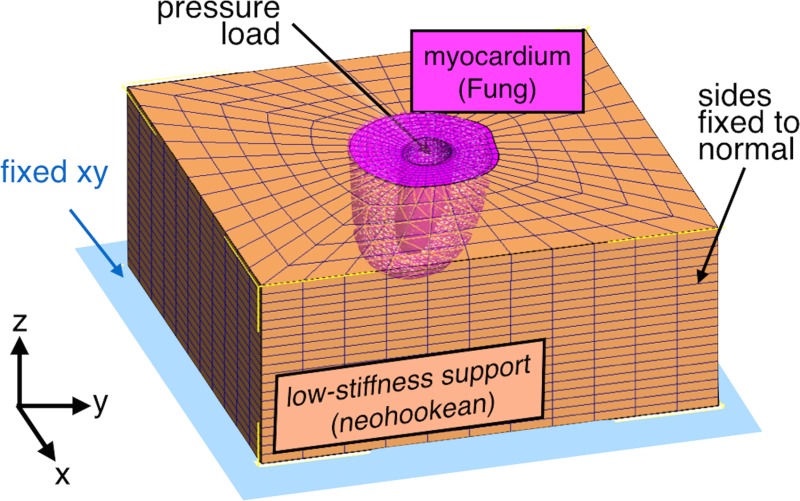
Representative FE model of the LV wall. The myocardium was represented as a mesh extracted from anatomical imaging embedded in a support block. LV mechanics were represented by a Fung-type constitutive model, and the surroundings were composed of a compliant and compressible material. The boundary conditions included the displacement constraints shown and a hydrostatic pressure in the endocardial surface.
Myocardial Constitutive Relationships.
A single Fung-type strain energy function was used to model all the material representations of passive constitutive behavior in this study [44,45]. The myocardium is assumed to be homogeneous across the ventricular volume, hyperelastic, and nearly incompressible. The strain energy, , was assumed to follow:
| (1) |
where is the material's bulk modulus set at 200 kPa, , and is the spatially dependent gradient of the material deformation map. For the myocardium in the local coordinate system defined by fiber and sheet structures
| (2) |
The coefficients and – defined the stiffness and isotropy with respect to the components of the deviatoric Green-Lagrange strain tensor in local coordinates, i.e., where for fiber, sheet and sheet-normal, respectively. To enable comparison on the deviatoric behavior of the different decoupled constitutive models, Lagrangian augmentation iterations were added to enforce incompressibility by keeping changes of volume under 1% regardless of material symmetry [46]. The four variations of FE models of the rat left ventricle were constructed using the following material symmetry models determined by strategic choice of material coefficients:
An isotropic material model (hereafter referred to as “isotropic” case) was used for the passive myocardium and contraction in the circumferential direction and was designed to represent basic geometrical changes disregarding the contribution from a realistic structural modeling. In this case, and .
The myocardial tissue was assumed to be transversely isotropic (“transversely isotropic” case) with a fiber structure characterized by linear transmural variation of α from −60 deg at the epicardium to 60 deg at the endocardium, and similarly for α′, except from −20 deg to 20 deg. A nominal, population-based approximation of fiber structure based on the literature [47,48] is assumed, without taking into consideration material model of the sheet structure.
A “subject-specific transversely isotropic” material was used, but a fiber distribution is generated from DT-MRI data for the animal.
An “orthotropic” material model was used to allow inclusion of subject-specific sheet structure from DT-MRI.
The values of the material coefficients used to define isotropic and transversely isotropic behavior were based on previous studies on perfused heart preparations of rat hearts [45]. Due to the lack of experimental data on the shear response of perfused cardiac tissue of rats, orthotropic shear response was based on shear experimental data from dog tissue [49]. To reduce the effects of biological variability on material coefficients, was adjusted to match the simulated response to the measured ED volume of each subject [11,50]. The material coefficients prior to subject-specific scaling are listed in Table 1, and response curves are shown in Fig. 3. A frame-invariant formulation of the strain energy function was used to integrate Eqs. (1) and (3) into the solver [51]. The FE simulations used both passive and active representations of cardiac tissue available in the febio software suite [52]. Active stress generation responsible for ventricular contraction was modeled with an implementation of active contraction based on a steady-state specialization of the time-varying elastance modification to Hill's active muscle contraction model [53,54], which is briefly described in the Appendix.
Table 1.
Material coefficient sets for passive myocardium. In some cases, material coefficients are repeated to produce the desired material symmetry depending on one of the four simulation approaches (cases (ii) and (iii) have identical coefficients, but differ in structural arrangement).
| (kPa) | |||||||
|---|---|---|---|---|---|---|---|
| Isotropic | 0.35 | 9.2 | 9.2 | 9.2 | 7.4 | 7.4 | 7.4 |
| Trans. isotropica | 1.3 | 9.2 | 2 | 2 | 3.7 | 2 | 3.7 |
| Orthotropic | 0.75 | 20.2 | 1.4 | 0.3 | 8.1 | 6.0 | 3.7 |
Coefficients obtained from perfused rat heart data [45].
Fig. 3.
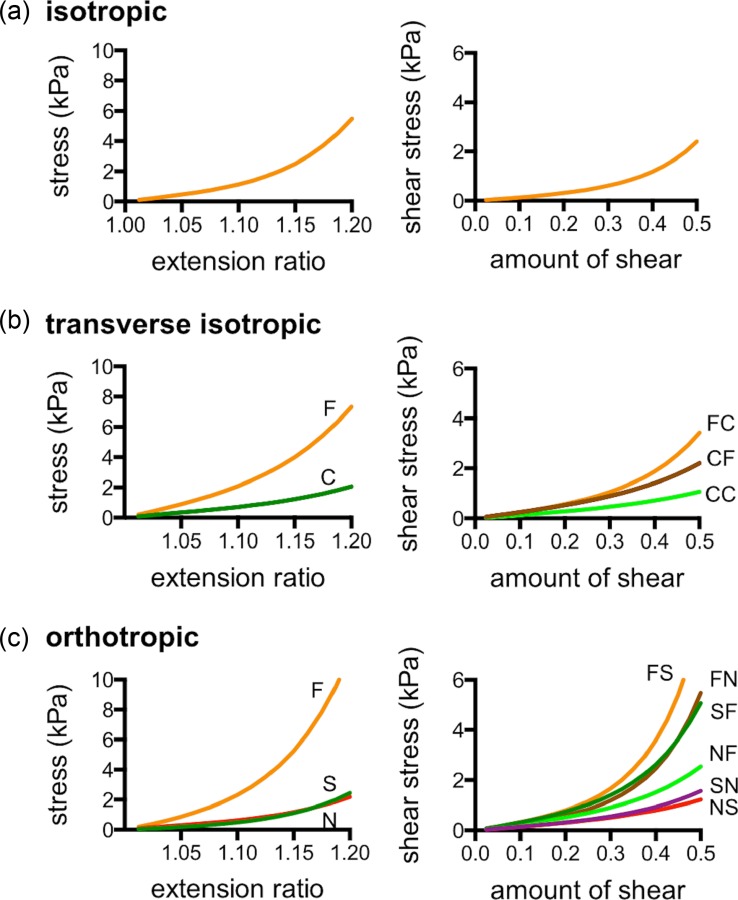
Material symmetry assumptions. The simulation cases included three material behavior models: isotropic (a), transverse isotropic (b), where the fiber (F) and cross-fiber (C) directions exhibit different responses, and orthotropic (c), where shear response was defined in terms in the local fiber (F), sheet (S), and sheet-normal (N) directions.
Inclusion of Structural Information.
To incorporate structural information into the FE model, a local coordinate system was constructed using a distribution of potentials, described as the Laplace Dirichlet method for structural definition [55]. However, instead of a rule-based approach, structural information was defined from DT-MR-based volumetric polynomials with respect to the radial and longitudinal coordinates and (see Fig. 1) assuming circumferential symmetry. Then, the angular value at each element was used to rotate the longitudinal or radial direction (defined as the gradients and ) into alignment with the local fiber or sheet orientation, respectively. The polynomial form and order, N, were defined based on spatial angular distributions, and previous investigations [56–58], in terms of coefficients , , , and where , as
| (3) |
| (4) |
| (5) |
| (6) |
For the isotropic case, all structural coefficients were zero, as well as for the transversely isotropic case except = −60, = 120, = −20, and = 40. The coefficient sets for the subject-specific transversely isotropic and orthotropic cases are listed in Table 2.
Table 2.
Fiber and sheet distribution coefficients for subject-specific modeling obtained from fitting DT-MRI data
| Fiber | Sheet | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Subject | () | () | () | () | ||||||||||||
| (deg) | (deg) | (deg) | (deg) | |||||||||||||
| Rat 1 | 75.6 | 126 | −153 | 152 | 730 | −619 | −59.7 | 473 | −702 | −4.61 | −315 | 639 | −38.0 | 47.0 | −101 | 107 |
| Rat 2 | 54.1 | 77.8 | −103 | 308 | 830 | 233 | −44.8 | 110 | −851 | −36.0 | −497 | 480 | 49.3 | −44.2 | −170 | 151 |
| Rat 3 | 100 | 109 | −162 | 569 | 1068 | −1639 | −67.0 | 1084 | −1051 | 10.9 | −653 | 639 | 55.9 | −55.4 | −181 | 165 |
Extrapolation and Visualization of Myocardial Structures.
For each FE prediction of cardiac deformation, angular measures of fiber and sheet structures were obtained by regenerating the gradients that define the local coordinate system using current (deformed) nodal positions, and using inverse isoperimetric mapping [59] to obtain warped DT-MRI slices. Two different approaches of deforming DT-MRI (which also appear in the previous literature [60,61]), “rotation-only” and “full deformation,” were performed and compared. In the rotation-only approach, the simulation-generated deformation map ( and represents reference and current coordinates, respectively) was applied to displace (or ), and then to produce rotation according to
| (7) |
where uppercase indicates the vector is in the reference configuration, and was obtained from single-value decomposition of the deformation gradient
| (8) |
In the full-deformation approach, the structural vectors were translated in the same manner, but the direct application of the deformation gradient or
| (9) |
ensued rotation and shear. Thus, each of the four FE predictions yielded two approximations of the structural alterations observed experimentally. Comparison of transmural alterations between simulated and experimental measurements was performed by calculating transmural helical angle slope and construction of histograms for the eight predictions of structural alterations as described in recent literature [1,14,16].
Results
Gross Morphology of Isolated Hearts.
Over the total experimental time of 40–50 min from excision to completion of the last ex vivo image acquisition, electrical activity and regular pressure pulsations indicating organ viability were briefly observed during solution change intervals in between imaging protocols. The LV volumes (see also Fig. 4) of the isolated hearts were (n = 3, mean ± SD, in μL) 127 ± 17, 383 ± 72, and 76 ± 23, compared to 132 ± 68, 310 ± 38, and 82 ± 23 for the same hearts in vivo at EAD, ED, and ES, respectively. The wall thicknesses of the isolated hearts were (in mm) 3.2 ± 0.6, 1.8 ± 0.6, and 3.7 ± 0.2, compared to 2.8 ± 0.3, 2.0 ± 0.1, and 3.6 ± 0.2 measured in vivo at the same states. These results indicate that, except for the tendency toward higher ventricular volume due to slight overinflation of the balloon at ED, the gross morphology of the isolated perfused hearts was in excellent agreement with their in vivo counterparts.
Fig. 4.
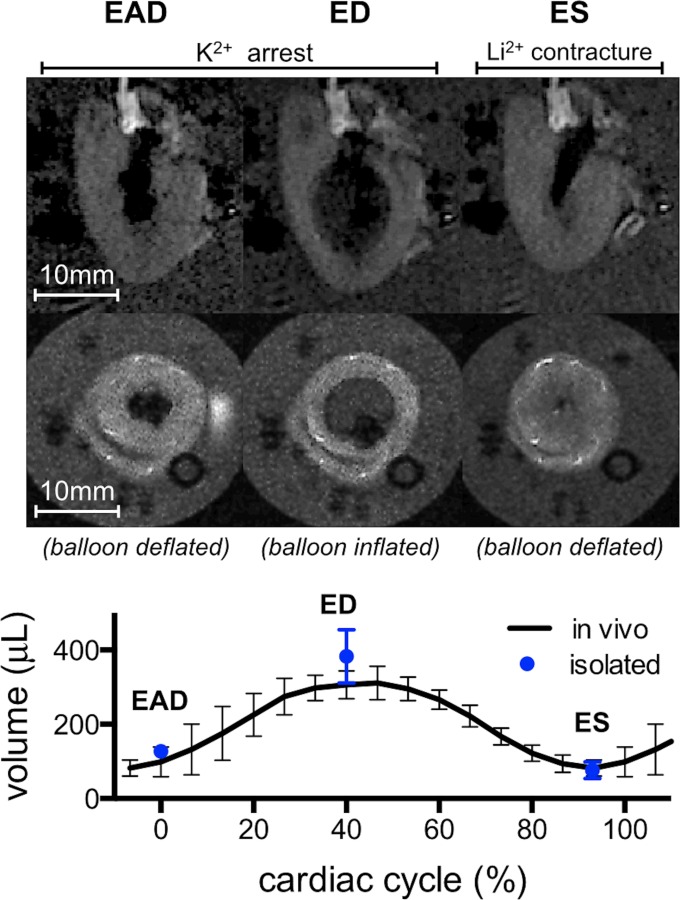
Gross morphology of an isolated arrested heart. Long and short axes MRI of the LV (top two rows, see also Fig. 1) revealed morphological alterations consistent with the targeted cardiac states. Compared to EAD, balloon inflation at ED produced volume increase and wall thinning, whereas deflation at ES caused volume decrease and wall thickening. The volumes of the isolated perfused hearts were quantitatively similar to those seen in vivo.
In Vivo Cardiac Kinematics.
Ejection fraction (EF) in the live animals (n = 3) was measured to be 0.71 ± 0.04 (mean ± SD). Circumferential strain in the base, midventricle, and apex of the LV was − 0.23 ± 0.05, −0.27 ± 0.04, and −0.28 ± 0.04, respectively. Radial strain values in the corresponding locations were 0.55 ± 0.06, 0.57 ± 0.06, and 0.49 ± 0.07. Longitudinal torsion was 1.3 ± 0.8 deg/mm based on slice rotations of −15.9 deg ± 3.3 at the base, −14.2 deg ± 4.3 at the midventricle, and −11.5 deg ± 3.5 at the apex. These values agreed with the previous studies on healthy rats of similar size [39,62].
Structural Variations of Isolated Heart Preparation.
The total transmural change of helical angle averaged over the entire myocardium and across all animals (n = 3) at ES was approximately 26 ± 8% larger than the same measurement at ED, which is consistent with the longitudinal alignment described in previous studies [16,29]. The histograms of helical distribution in Fig. 5 showed a larger population near zero for ED than ES. Fiber transverse angle distribution showed increased circumferential alignment during systole (larger population about zero). The clearest difference in structural distribution was seen on the sheet angle histogram, which showed a marked increase in pixel count near zero at ES. Similar characteristic observations have been made in previous DT-MRI studies using isolated heart preparations [14,16].
Fig. 5.
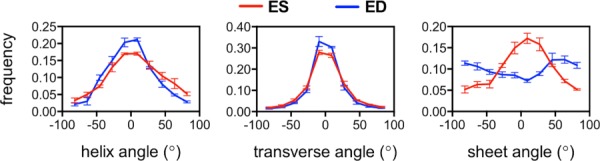
Histogram representation of structural angles populations at ED and ES from ex vivo DT-MRI (n = 3). Compared to ED, systolic helix angle population is more concentrated at higher angles, which indicates longitudinal alignment. During diastole, the transverse fiber angle population increases near 0 deg, which indicates alignment in the circumferential direction. Sheet angle distribution is markedly different between both states and tends to concentrate about zero at ES in comparison to ED, which has a different concavity.
Simulated Myocardial Kinematics.
A partial list of the key parameters associated with simulated LV deformation averaged over the subject-specific models (n = 3) for each of the four simulation strategies and in vivo is listed in Table 3 for (i) isotropic, (ii) transversely isotropic, (iii) subject-specific transversely isotropic, and (iv) subject-specific orthotropic cases. The FE predictions of volumetric changes were in excellent agreement with in vivo measurements, with errors of less than 10% in end-diastolic volume (EDV) and end-systolic (ESV) volume and EF for all cases. Not surprisingly, the isotropic model grossly underestimated the amount of systolic longitudinal torsion, but the remaining three models with more realistic fiber distribution had the tendency of overestimating it. There was also good agreement in terms of circumferential strain values, although the mild longitudinal change observed experimentally (larger in vivo strain at the base compared to the apex) was reversed likely due to the boundary conditions. Some systematic variation in terms of radial strain was observed, whereby the measures fell below the in vivo measurements in case (i) and above in the remaining cases. Parameter identification resulted in reduction of the stiffness parameter c in all cases except case (iii) where the reduction was insignificant. In general, simulations provided a good description of ventricular volume and rotation, but strain values differed depending on the fiber structure modeling approach.
Table 3.
Average measurements of kinematic parameters. Tissue deformation information metrics were averaged across the subjects (n = 3), and each of the simulation case groups.
| Parameter | Unit | In Vivo | Case (i) | Case (ii) | Case (iii) | Case (iv) |
|---|---|---|---|---|---|---|
| ESV | μL | 82 ± 22 | 95 ± 35 | 104 ± 21 | 100 ± 22 | 103 ± 25 |
| EDV | μL | 310 ± 38 | 298 ± 47 | 311 ± 30 | 313 ± 38 | 302 ± 31 |
| EF | μL | 0.71 ± 0.10 | 0.69 ± 0.09 | 0.67 ± 0.03 | 0.68 ± 0.03 | 0.66 ± 0.05 |
| Torsion | deg/mm | 1.3 ± 0.8 | 0.07 ± 0.04 | 1.73 ± 0.14 | 2.17 ± 0.35 | 2.24 ± 0.44 |
| (base) | — | −0.28 ± 0.04 | −0.28 ± 0.02 | −0.24 ± 0.09 | −0.28 ± 0.01 | −0.28 ± 0.02 |
| (mid) | — | −0.27 ± 0.04 | −0.28 ± 0.02 | −0.24 ± 0.09 | −0.29 ± 0.02 | −0.28 ± 0.02 |
| (apex) | — | −0.23 ± 0.05 | −0.29 ± 0.02 | −0.25 ± 0.07 | −0.30 ± 0.01 | −0.29 ± 0.01 |
| (base) | — | 0.49 ± 0.07 | 0.26 ± 0.12 | 0.68 ± 0.27 | 0.75 ± 0.09 | 0.74 ± 0.12 |
| (mid) | — | 0.57 ± 0.06 | 0.43 ± 0.11 | 0.66 ± 0.30 | 0.77 ± 0.09 | 0.82 ± 0.12 |
| (apex) | — | 0.55 ± 0.06 | 0.41 ± 0.14 | 0.64 ± 0.18 | 0.75 ± 0.20 | 0.75 ± 0.20 |
| kPa | — | 25 ± 8 | 56 ± 4 | 53 ± 14 | 44 ± 9 | |
| kPa | — | 0.14 ± 0.09 | 0.95 ± 0.48 | 0.77 ± 0.31 | 0.27 ± 0.17 |
Simulated Structural Alterations.
Computation time for the structural alteration simulations was approximately 60, 30, 25, and 60 min for cases (i), (ii), (iii), and (iv), respectively. Each numerical simulation ((i)–(iv)) produced a set of tissue deformation results subsequently used to warp the initial DT-MRI data either using the rotation-only method or the full-deformation method. Histograms of the simulated structural alterations using the rotation-only approach appear in Fig. 6. The isotropic case, (i), yields no visible changes in helix, transverse, or sheet angle population. The remaining cases, particularly the subject-specific transversely isotropic and orthotropic cases, showed fiber structure alterations that suggest circumferential alignment of transverse angles in ED, which is more consistent with the experimental observations. Sheet angle population remains unchanged regardless of the simulation case.
Fig. 6.
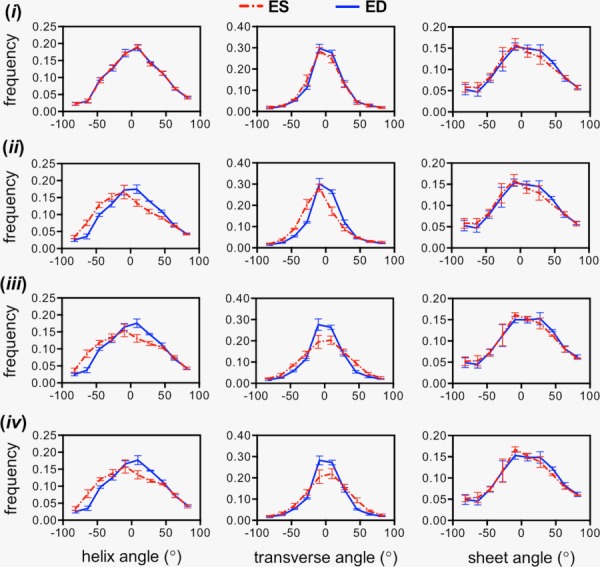
Averaged histograms of structural angle populations (n = 3) using the rotation-only approach to transform DTI data from an initial time point to ED and ES. The deformation results from case (i) (top row) do not show any difference between states, i.e., overlapping lines, constituting a poor prediction with respect to the experimental observations in Fig. 5. Cases (ii)–(iv) (rows 2–4, left column) produced similar helix angle distribution alterations that suggest longitudinal alignment at ES. Transverse angle alterations (middle column) are more realistic in cases (iii) and (iv). The rotation-only approach produced no visible differences in sheet angle distributions (right column).
Results obtained using the full-deformation approach appear in Fig. 7. The helix angle population for the isotropic case (i) follows a pattern consistent with the transmural slope, where there is a markedly different distribution compared to the rotation-only method. Distribution changes of the same angular measure in the other cases are similar to that obtained with the rotation-only method and also consistent with slope measurements, in that helical changes were less pronounced on the subject-specific transversely isotropic case. Circumferential alignment of transverse angles can be observed in all the simulation cases. Unlike the rotation-only approach, sheet distribution changes were present in the transversely isotropic (ii), subject-specific transversely isotropic (iii), and orthotropic (iv) models appearing to be slightly more evident in the last, although not to the same extent as the alterations observed experimentally.
Fig. 7.
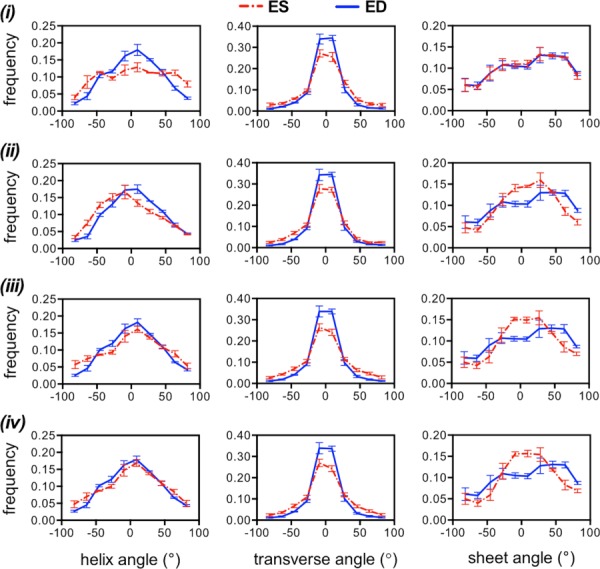
Averaged histograms of structural angle populations (n = 3) using the full-deformation approach to transform DTI data from an initial time point to ED and ES. Helix angle populations (left column) varied depending on the simulation strategy with (ii) and (iii) appearing to be closer to the experimental measurements in Fig. 5. Transverse angle populations (middle column) appeared to be identical regardless of the simulation approach. Sheet angle populations (right column) improved with the sophistication of the material model with (i) being the poorest (no difference between ED and ES) and (iv) being the best (largest change in concavity).
An inherent limitation of histograms is that they do not contain information regarding the spatial patterns of the myocardial structure, which may serve as an additional performance metric of the simulations. The use of histograms arises from MRI volumetric averaging and idealization on LV shape and effectively limits quantitative comparison to experimental data. As a partial remedy, Table 4 shows a comparison of transmural fiber helix angle slopes obtained by simulation at ED and ES. While all of the systolic values show some degree of longitudinal alignment, values obtained by applying rotation-only deformation vary more widely among simulation cases with (i) being the smallest at 3% and (ii) being the largest at 30%, compared to 26% observed in vivo. Using full deformation, case (i) largely overestimates the measurement, and case (iv) underestimates it. Case (iv) also underestimates the longitudinal alignment using the rotation-only approach. Cases (ii) and (iii) show reasonable agreement with the experimental observations. Combined with the histograms in Figs. 6 and 7, the results in Table 4 suggest that case (iii), i.e., the subject-specific transversely isotropic model, is the most appropriate for deforming the myocardial fiber structure between cardiac cycle states.
Table 4.
Mean transmural helix angle slope from extrapolated slices based on each of the FE simulation case groups (columns) and warping approaches (rows). Percent change in vivo was approximately 26%.
| Unit | Case (i) | Case (ii) | Case (iii) | Case (iv) | ||
|---|---|---|---|---|---|---|
| Rotation-only | ED | deg | 107 ± 24 | 117 ± 27 | 113 ± 28 | 113 ± 28 |
| ES | deg | 110 ± 15 | 151 ± 33 | 138 ± 32 | 131 ± 29 | |
| Changea | % | 3 | 30 | 22 | 16 | |
| Full deformation | ED | deg | 92 ± 24 | 102 ± 27 | 95 ± 23 | 101 ± 26 |
| ES | deg | 145 ± 48 | 134 ± 29 | 117 ± 26 | 114 ± 25 | |
| Changea | % | 58 | 31 | 23 | 13 |
Note: Values shown correspond to mean ± SD.
Measured with respect to ED.
Some examples of extrapolation beyond the verification points can be seen in Fig. 8 where the nodal locations have been readjusted for a more realistic representation of cardiac motion (fixed apex). The initial DT-MRI information at EAD is shown at zero time followed by some frames of the simulated progression using case (iii) across the cardiac cycle. At each time, there is a corresponding change in volume and wall thickness, as well as fiber rotations, which are more evident at 60% and ES where element deformation can be observed in the model, and a larger area of helix angles close to −90 (lighter shades) can be seen near the epicardium. Similar observations can be made on the tractography representation of ED and ES shown in Fig. 9, where the epicardial longitudinal alignment of helical structure can be seen directly.
Fig. 8.
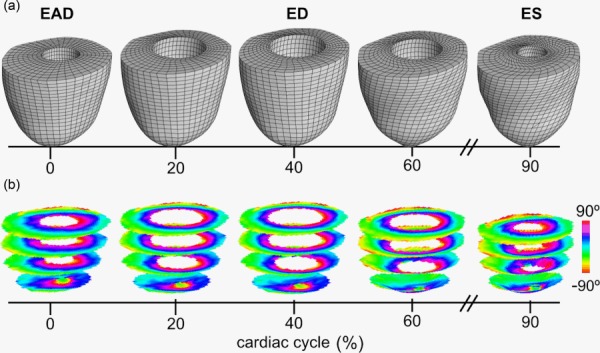
Warping DTI data across the cardiac cycle. The FE model (a) was used to generate deformation estimates at times beyond the validation points (ED and ES) using simulation approach (iii). The modeling approach follows a realistic temporal representation of pressure, volume, and contractility via FE modeling by using an image-based, subject-specific transversely isotropic material model. The warped image slices showing helical angle maps (b) show contraction-induced shortening and some angle variation indicative of longitudinal alignment.
Fig. 9.
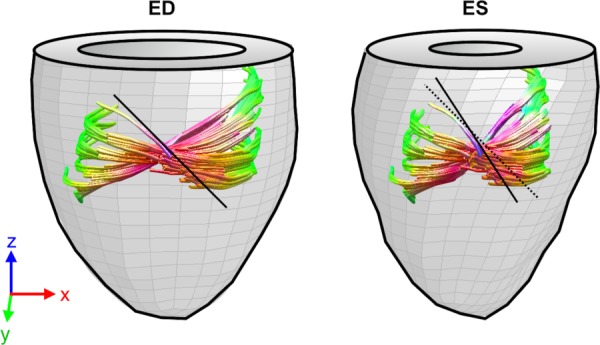
Deformed tracts of a collection of fibers in a longitudinal isocline along the radial direction. Comparing the local inclination of an epicardial fiber tract at ED (black line, left), with respect to its warping configuration at ES (right) showed longitudinal alignment typical of systolic structural state.
Discussion
This study has demonstrated the conceptual feasibility of temporal extrapolation (and by extension spatial interpolation) of DT-MRI data by implementing subject-specific FE mechanical simulations and using the results to warp imaging data by application of the deformation gradient from continuum mechanics evaluated in a pixel lattice. Deformation maps needed to simulate structural dynamics are fundamentally dissimilar from the transformations used in DTI atlas generation [61], in that dynamic changes in myocardial structure are strictly promoted by physical cardiac motion. Therefore, modeling parameters must include imaging (e.g., warping approach) and tissue deformation (e.g., material properties and mechanical loads) considerations. Likewise, results ought to be interpreted based on the imaging modality as well as the quality of the deformation prediction. As a case in point, interpretation of the results in Figs. 6 and 7 in light of tissue kinematics, such as the strain and torsion measures shown in Table 3, can be used to categorize different approximations of structural alteration even if direct structural measurements are not available. A starting point is volume and volumetric variations (such as EF). However, as shown in Table 3, the ability to achieve simulated LV volumes similar to those in vivo regardless of the modeling strategy is in agreement with previous studies, which for the most part show that pressure and volume can be relatively insensitive to structural variations [2,33]. Radial strain (associated with wall thickening) was more sensitive to structural information, and the subject-specific models (cases (iii) and (iv)) had the tendency to overestimate experimental values, partially confirming previous speculations [33]. In the context of this study, radial strain serves as an indicator of the mechanism for LV volume variation, in which the cases with realistic structural input (cases (ii)–(iv)) was mediated by wall thickening, unlike the isotropic material case (i) where cavity volume changed due to elongation. This distinction can be used to avoid misinterpreting the results. For instance, direct application of the deformation gradient to warp data using case (i) yielded ES longitudinal alignment and ED circumferential alignment (Fig. 7, top), even though the model completely disregarded myocardial fiber and sheet distribution. This is because each of the components of the fiber orientation vector was stretched by different amounts, resulting in an angular change. Even though acquisition of strain measurements needed for rigorous kinematic validation of the models will, in practice, require additional time, the results indicate that simulations can be used to recreate similar alterations in structural angle populations when DT-MRI information is adequately warped.
Comparing the rotation-only with the full-deformation results indicates that, for the more realistic cases (ii)–(iv), fiber structure alterations, i.e., helical and transverse angle distributions, seem to be, respectively, mediated largely by rotation, since transmural slopes (Table 3) and histograms (Figs. 6 and 7) show similar distribution regardless of the warping approach. The same cannot be said for the sheet angle population, which appears to be mediated mostly by transmural shear. Among the simulated cases, the orthotropic model (iv) has the most visible alteration of sheet angle with the subject-specific transversely isotropic case (iii) being a close second. These models have in common that subject-specific structural information was used as structural input. These data may be required if sheet deformation is the subject of study, e.g., to simulate structural alteration in hearts with hypertrophic cardiomyopathy, because it is possible that the distinct structural alterations between ED and ES caused by the disease [14] may be associated with shear stiffening in the transmural direction. In terms of the trends of structural dynamics observed in this study, the subject-specific models tended to be the most accurate, although a reasonable approximation could be obtained more quickly with a population-based transversely isotropic model (case (iii)).
Being an initial exploration, a fundamental limitation of this study is its qualitative nature. Although consistent numerical quantifications were used whenever possible, it is currently difficult to state precisely the accuracy of the simulated structural alterations. Thus, the interpretation of results was limited to the evidence which was clearly visible. Second, this study included intricate experimental as well as numerical components containing several assumptions; the most important includes the effectiveness of the isolated heart preparation and the numerical simulation. Despite possible limitations introduced by the isolate heart preparation, the presented extrapolation method is still expected to be valid due to its applicability to in vivo DTI data, because high-resolution 3D coverage across the cardiac cycle is likely to continue to be limited by prohibitive scan time [31,32]. In terms of the numerical simulations, the ventricle was assumed to be homogeneous and stress-free in its unloaded configuration, these assumptions were invoked partly due to the lack of experimental data needed to include these features into the models, although preliminary numerical studies indicate that myocardial residual stress has a relatively small effect on ventricular deformation [11,63,64]. Nevertheless, cases ((iii) and (iv)) include some spatial heterogeneity, at least from a structural sense.
This research can proceed in several future directions. First, there are some areas of additional study involving integration with in vivo DT-MRI results. Using this imaging technology may reduce the experimental error associated with the isolated heart and will be a more suitable alternative to validate structural atlases of the living heart. Further understanding regarding the influence of orthogonality, which is inherently present in DT-MRI, on cardiac dynamic structure measures would be needed to elucidate the dependency of fiber and sheet structures in the presence of shear deformation. For example, fiber deformation due to shear could manifest as overestimation of transmural helix angle slopes in experimental data, which may explain discrepancies observed in the magnitude of simulated and observed longitudinal alignments. There are also improvements to be made from a numerical perspective, such as the inclusion of mechanics-based image registration to warp the results, which would facilitate point-to-point comparison of structural data for error quantification, and mesh construction with quadratic elements to improve mesh convergence and increase computational efficiency. Finally, incorporation of the right ventricle can be feasible by combining the computational strategy presented here with high-resolution vivo DT-MRI.
Acknowledgment
The authors would like to thank Samer Merchant and Osama Abdullah from the Small Animal Imaging Facility at the University of Utah. Dr. Jeffrey Weiss, Steve Maas, and Dave Rawlins at the Musculoskeletal Research Laboratories (University of Utah) are gratefully acknowledged for their assistance with computational mechanics. Additional thanks to Garvin Tran, David Zou, and Adam Schmidt for laboratory assistance. This work was supported by the National Health Institutes (Grant Nos. R01 HL092055 and S10 RR023017).
Glossary
Nomenclature
- =
sarcomere length difference weight
- =
relative stiffness coefficient
- =
material coefficients in Fung-type strain energy function
- =
tension development loading curve
- =
peak calcium concentration
- =
components of the Green-Lagrange strain tensor
- =
calcium sensitivity
- =
fiber index
- =
unit vector in the local fiber direction in current configuration
- =
unit vector in the local fiber direction in reference configuration
- =
deformation gradient
- =
determinant of deformation gradient
- =
bulk modulus
- =
coefficients for fiber angle distribution polynomials
- =
coefficients for sheet angle distribution polynomials
- =
current sarcomere length
- =
longitudinal coordinate
- =
zero-tension sarcomere length
- =
sheet-normal index
- N =
polynomial order
- =
exponential term in Fung-type strain energy function
- =
radial coordinate
- =
rotation matrix
- =
sheet index
- =
time
- =
total Cauchy stress
- =
maximum sarcomere tension
- =
strain energy function
- =
current coordinates
- =
reference coordinates
- α =
helix angle
- α′ =
transverse, or imbrication, angle
- β =
sheet angle
- β′ =
transverse-like angular measure of sheet structure
- =
deformation map
Appendix
Additional information regarding the steady-state specialization of the time-varying elastance modification to Hill's active muscle contraction model used to include contractile stress into the FE simulations can be obtained from previous studies [53,54,63]. In short, the total simulated Cauchy stress tensor results from superimposed contributions from the passive material response and an active component along
| (A1) |
The active component was defined as a function of fiber stretch and a scaling parameter , which determines the shape of the activation curve [45]
| (A2) |
where the maximum activation stress = 135.7 kPa was based on the isometric tension at the peak intracellular calcium concentration, = 4.35 μM. Calcium sensitivity, , was modeled with respect to the maximum calcium concentration = 4.35 μM, the zero-tension sarcomere length, = 1.58 μm, an experimentally derived weight = 4.75 μm−1 and the current sarcomere length, , resulting from scaling the resting sarcomere length (1.2 μm) by the fiber stretch
| (A3) |
This model can be incorporated onto the passive material model in febio software suite, through a mixture of solids [52].
Contributor Information
Arnold David Gomez, Bioengineering Department, University of Utah, SMBB Room 1037, 36 S. Wasatch Drive, Salt Lake City, UT 84112, e-mail: arnold.david.gomez@utah.edu.
David A. Bull, Cardiothoracic Division, Surgery Department, University of Utah, 30 N 1900 E RM 3B205, Salt Lake City, UT 84132-2101, e-mail: david.bull@hsc.utah.edu
Edward W. Hsu, Bioengineering Department, University of Utah, SMBB Room 1242, 36 S. Wasatch Drive, Salt Lake City, UT 84112, e-mail: edward.hsu@utah.edu
References
- [1]. Hales, P. W. , Schneider, J. E. , Burton, R. A. B. , Wright, B. J. , Bollensdorff, C. , and Kohl, P. , 2012, “ Histo-Anatomical Structure of the Living Isolated Rat Heart in Two Contraction States Assessed by Diffusion Tensor MRI,” Prog. Biophys. Mol. Biol., 110(2–3), pp. 319–330. 10.1016/j.pbiomolbio.2012.07.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2]. Arts, T. , Bovendeerd, P. , Delhaas, T. , and Prinzen, F. , 2003, “ Modeling the Relation Between Cardiac Pump Function and Myofiber Mechanics,” J. Biomech., 36(5), pp. 731–736. 10.1016/S0021-9290(02)00451-7 [DOI] [PubMed] [Google Scholar]
- [3]. Bovendeerd, P. H. , Arts, T. , Huyghe, J. M. , van Campen, D. H. , and Reneman, R. S. , 1992, “ Dependence of Local Left Ventricular Wall Mechanics on Myocardial Fiber Orientation: A Model Study,” J. Biomech., 25(10), pp. 1129–1140. 10.1016/0021-9290(92)90069-D [DOI] [PubMed] [Google Scholar]
- [4]. Waldman, L. K. , Nosan, D. , Villarreal, F. , and Covell, J. W. , 1988, “ Relation Between Transmural Deformation and Local Myofiber Direction in Canine Left Ventricle,” Circ. Res., 63(3), pp. 550–562. 10.1161/01.RES.63.3.550 [DOI] [PubMed] [Google Scholar]
- [5]. Arts, T. , Costa, K. D. , Covell, J. W. , and McCulloch, A. D. , 2001, “ Relating Myocardial Laminar Architecture to Shear Strain and Muscle Fiber Orientation,” Am. J. Physiol. Heart Circ. Physiol., 280(5), pp. H2222–H2229. [DOI] [PubMed] [Google Scholar]
- [6]. Rüssel, I . K. , Götte, M. J. W. , Bronzwaer, J. G. , Knaapen, P. , Paulus, W. J. , and van Rossum, A. C. , 2009, “ Left Ventricular Torsion: An Expanding Role in the Analysis of Myocardial Dysfunction,” JACC Cardiovasc. Imaging, 2(5), pp. 648–655. 10.1016/j.jcmg.2009.03.001 [DOI] [PubMed] [Google Scholar]
- [7]. Abraham, T. P. , and Nishimura, R. A. , 2001, “ Myocardial Strain: Can We Finally Measure Contractility?,” J. Am. Coll. Cardiol., 37(3), pp. 731–734. 10.1016/S0735-1097(00)01173-6 [DOI] [PubMed] [Google Scholar]
- [8]. Hoit, B. D. , 2011, “ Strain and Strain Rate Echocardiography and Coronary Artery Disease,” Circ. Cardiovasc. Imaging, 4(2), pp. 179–190. 10.1161/CIRCIMAGING.110.959817 [DOI] [PubMed] [Google Scholar]
- [9]. Axel, L. , Montillo, A. , and Kim, D. , 2005, “ Tagged Magnetic Resonance Imaging of the Heart: A Survey,” Med. Image Anal., 9(4), pp. 376–393. 10.1016/j.media.2005.01.003 [DOI] [PubMed] [Google Scholar]
- [10]. Strijkers, G. J. , Bouts, A. , Blankesteijn, W. M. , Peeters, T. H. J. M. , Vilanova, A. , van Prooijen, M. C. , Sanders, H. M. H. F. , Heijman, E. , and Nicolay, K. , 2009, “ Diffusion Tensor Imaging of Left Ventricular Remodeling in Response to Myocardial Infarction in the Mouse,” NMR Biomed., 22(2), pp. 182–190. 10.1002/nbm.1299 [DOI] [PubMed] [Google Scholar]
- [11]. Walker, J. C. , Ratcliffe, M. B. , Zhang, P. , Wallace, A. W. , Fata, B. , Hsu, E. W. , Saloner, D. , and Guccione, J. M. , 2005, “ MRI-Based Finite-Element Analysis of Left Ventricular Aneurysm,” Am. J. Physiol. Heart Circ. Physiol., 289(2), pp. H692–H700. 10.1152/ajpheart.01226.2004 [DOI] [PubMed] [Google Scholar]
- [12]. Abdullah, O. M. , Drakos, S. G. , Diakos, N. A. , Wever-Pinzon, O. , Kfoury, A. G. , Stehlik, J. , Selzman, C. H. , Reid, B. B. , Brunisholz, K. , Verma, D. R. , Myrick, C. , Sachse, F. B. , Li, D. Y. , and Hsu, E. W. , 2014, “ Characterization of Diffuse Fibrosis in the Failing Human Heart Via Diffusion Tensor Imaging and Quantitative Histological Validation,” NMR Biomed., 27(11), pp. 1378–1386. 10.1002/nbm.3200 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13]. Schmitt, B. , Fedarava, K. , Falkenberg, J. , Rothaus, K. , Bodhey, N. K. , Reischauer, C. , Kozerke, S. , Schnackenburg, B. , Westermann, D. , Lunkenheimer, P. P. , Anderson, R. H. , Berger, F. , and Kuehne, T. , 2009, “ Three-Dimensional Alignment of the Aggregated Myocytes in the Normal and Hypertrophic Murine Heart,” J. Appl. Physiol., 107(3), pp. 921–927. 10.1152/japplphysiol.00275.2009 [DOI] [PubMed] [Google Scholar]
- [14]. Ferreira, P. F. , Kilner, P. J. , McGill, L.-A. , Nielles-Vallespin, S. , Scott, A. D. , Ho, S. Y. , McCarthy, K. P. , Haba, M. M. , Ismail, T. F. , Gatehouse, P. D. , de Silva, R. , Lyon, A. R. , Prasad, S. K. , Firmin, D. N. , and Pennell, D. J. , 2014, “ In Vivo Cardiovascular Magnetic Resonance Diffusion Tensor Imaging Shows Evidence of Abnormal Myocardial Laminar Orientations and Mobility in Hypertrophic Cardiomyopathy,” J. Cardiovasc. Magn. Reson., 16(1), p. 87. 10.1186/s12968-014-0087-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15]. Axel, L. , Wedeen, V. J. , and Ennis, D. B. , 2014, “ Probing Dynamic Myocardial Microstructure With Cardiac Magnetic Resonance Diffusion Tensor Imaging,” J. Cardiovasc. Magn. Reson., 16(1), p. 89. 10.1186/s12968-014-0089-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16]. Stoeck, C. T. , Kalinowska, A. , von Deuster C., Harmer, J. , Chan, R. W. , Niemann, M. , Manka, R. , Atkinson, D. , Sosnovik, D. E. , Mekkaoui, C. , and Kozerke, S. , 2014, “ Dual-Phase Cardiac Diffusion Tensor Imaging With Strain Correction,” PLoS One, 9(9), p. e107159. 10.1371/journal.pone.0107159 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17]. Rijcken, J. , Bovendeerd, P. H. , Schoofs, A. J. , van Campen, D. H. , and Arts, T. , 1999, “ Optimization of Cardiac Fiber Orientation for Homogeneous Fiber Strain During Ejection,” Ann. Biomed. Eng., 27(3), pp. 289–297. 10.1114/1.147 [DOI] [PubMed] [Google Scholar]
- [18]. Yang, C. , Tang, C. , Haber, I. , Geva, T. , and del Nido, P. J. , 2009, “ In Vivo MRI-Based 3D FSI RV/LV Models for Human Right Ventricle and Patch Design for Potential Computer-Aided Surgery Optimization,” Comput. Struct., 85(11–14), pp. 988–997. 10.1016/j.compstruc.2006.11.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19]. Wenk, J. , Ge, L. , and Zhang, Z. , 2013, “ A Coupled Biventricular Finite Element and Lumped-Parameter Circulatory System Model of Heart Failure,” Comput. Methods Biomech. Biomed. Eng., 16(8), pp. 807–818. 10.1080/10255842.2011.641121 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20]. LeGrice, I . J. , Smaill, B. H. , Chai, L. Z. , Edgar, S. G. , Gavin, J. B. , and Hunter, P. J. , 1995, “ Laminar Structure of the Heart: Ventricular Myocyte Arrangement and Connective Tissue Architecture in the Dog,” Am. J. Physiol. Circ. Physiol., 269(2), pp. H571–H582. [DOI] [PubMed] [Google Scholar]
- [21]. Hsu, E. W. , Muzikant, A. L. , Matulevicius, S. A. , Penland, R. C. , and Henriquez, C. S. , 1998, “ Magnetic Resonance Myocardial Fiber-Orientation Mapping With Direct Histological Correlation,” Am. J. Physiol. Heart Circ. Physiol., 274(5), pp. H1627–H1627. [DOI] [PubMed] [Google Scholar]
- [22]. Scollan, D. F. , Holmes, A. , Winslow, R. , and Forder, J. , 1998, “ Histological Validation of Myocardial Microstructure Obtained From Diffusion Tensor Magnetic Resonance Imaging,” Am. J. Physiol. Heart Circ. Physiol., 275(6), pp. H2308–H2318. [DOI] [PubMed] [Google Scholar]
- [23]. Helm, P. A. , Tseng, H.-J. , Younes, L. , McVeigh, E. R. , and Winslow, R. L. , 2005, “ Ex Vivo 3D Diffusion Tensor Imaging and Quantification of Cardiac Laminar Structure,” Magn. Reson. Med., 54(4), pp. 850–859. 10.1002/mrm.20622 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24]. Tseng, W.-Y. I. , Wedeen, V. J. , Reese, T. G. , Smith, R. N. , and Halpern, E. F. , 2003, “ Diffusion Tensor MRI of Myocardial Fibers and Sheets: Correspondence With Visible Cut-Face Texture,” J. Magn. Reson. Imaging, 17(1), pp. 31–42. 10.1002/jmri.10223 [DOI] [PubMed] [Google Scholar]
- [25]. Helm, P. , Beg, M. F. , Miller, M. I. , and Winslow, R. L. , 2005, “ Measuring and Mapping Cardiac Fiber and Laminar Architecture Using Diffusion Tensor MR Imaging,” Ann. N. Y. Acad. Sci., 1047, pp. 296–307. 10.1196/annals.1341.026 [DOI] [PubMed] [Google Scholar]
- [26]. Hunter, P. J. , McCulloch, A. D. , and ter Keurs, H. E. , 1998, “ Modelling the Mechanical Properties of Cardiac Muscle,” Prog. Biophys. Mol. Biol., 69(2–3), pp. 289–331. 10.1016/S0079-6107(98)00013-3 [DOI] [PubMed] [Google Scholar]
- [27]. Chen, J. , Liu, W. , Zhang, H. , Lacy, L. , Yang, X. , Song, S.-K. , Wickline, S. A. , and Yu, X. , 2005, “ Regional Ventricular Wall Thickening Reflects Changes in Cardiac Fiber and Sheet Structure During Contraction: Quantification With Diffusion Tensor MRI,” Am. J. Physiol. Heart Circ. Physiol., 289(5), pp. H1898–H1907. 10.1152/ajpheart.00041.2005 [DOI] [PubMed] [Google Scholar]
- [28]. Smerup, M. , Partridge, J. , Agger, P. , Ringgaard, S. , Pedersen, M. , Petersen, S. , Hasenkam, J. M. , Niederer, P. , Lunkenheimer, P. P. , and Anderson, R. H. , 2013, “ A Mathematical Model of the Mechanical Link Between Shortening of the Cardiomyocytes and Systolic Deformation of the Left Ventricular Myocardium,” Technol. Health Care, 21(1), pp. 63–79. 10.3233/THC-120710 [DOI] [PubMed] [Google Scholar]
- [29]. Lohezic, M. , Teh, I. , Bollensdorff, C. , Peyronnet, R. , Hales, P. W. , Grau, V. , Kohl, P. , and Schneider, J. E. , 2014, “ Interrogation of Living Myocardium in Multiple Static Deformation States With Diffusion Tensor and Diffusion Spectrum Imaging,” Prog. Biophys. Mol. Biol., 115(2–3), pp. 213–225. 10.1016/j.pbiomolbio.2014.08.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30]. Welsh, C. , Di Bella, E. , and Hsu, E. , 2015, “ Higher-Order Motion-Compensation for In Vivo Cardiac Diffusion Tensor Imaging in Rats,” IEEE Trans. Med. Imaging, 34(9), pp. 1843–1853. 10.1109/TMI.2015.2411571 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31]. Lau, A. Z. , Tunnicliffe, E. M. , Frost, R. , Koopmans, P. J. , Tyler, D. J. , and Robson, M. D. , 2015, “ Accelerated Human Cardiac Diffusion Tensor Imaging Using Simultaneous Multislice Imaging,” Magn. Reson. Med., 73(3), pp. 995–1004. 10.1002/mrm.25200 [DOI] [PubMed] [Google Scholar]
- [32]. Nielles-Vallespin, S. , Mekkaoui, C. , Gatehouse, P. , Reese, T. G. , Keegan, J. , Ferreira, P. F. , Collins, S. , Speier, P. , Feiweier, T. , de Silva, R. , Jackowski, M. P. , Pennell, D. J. , Sosnovik, D. E. , and Firmin, D. , 2013, “ In Vivo Diffusion Tensor MRI of the Human Heart: Reproducibility of Breath-Hold and Navigator-Based Approaches,” Magn. Reson. Med., 70(2), pp. 454–465. 10.1002/mrm.24488 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33]. Carapella, V. , Bordas, R. , Pathmanathan, P. , Lohezic, M. , Schneider, J. E. , Kohl, P. , Burrage, K. , and Grau, V. , 2014, “ Quantitative Study of the Effect of Tissue Microstructure on Contraction in a Computational Model of Rat Left Ventricle,” PLoS One, 9(4), p. e92792. 10.1371/journal.pone.0092792 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34]. Usyk, T. P. , Mazhari, R. , and McCulloch, A. D. , 2000, “ Effect of Laminar Orthotropic Myofiber Architecture on Regional Stress and Strain in the Canine Left Ventricle,” J. Elasticity Phys. Sci. Solids, 61(1–3), pp. 143–164. 10.1023/A:1010883920374 [DOI] [Google Scholar]
- [35]. Aletras, A. H. , Ding, S. , Balaban, R. S. , and Wen, H. , 1999, “ DENSE: Displacement Encoding With Stimulated Echoes in Cardiac Functional MRI,” J. Magn. Reson., 137(1), pp. 247–252. 10.1006/jmre.1998.1676 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36]. Kim, D. , Gilson, W. D. , Kramer, C. M. , and Epstein, F. H. , 2004, “ Myocardial Tissue Tracking With Two-Dimensional Cine Imaging: Development and Initial Evaluation,” Radiology, 230(3), pp. 862–871. 10.1148/radiol.2303021213 [DOI] [PubMed] [Google Scholar]
- [37]. Costantini, M. , 1998, “ A Novel Phase Unwrapping Method Based on Network Programming,” IEEE Trans. Geosci. Remote Sens., 36(3), pp. 813–821. 10.1109/36.673674 [DOI] [Google Scholar]
- [38]. Gomez, A. D. , Merchant, S. S. , and Hsu, E. W. , 2014, “ Accurate High-Resolution Measurements of 3-D Tissue Dynamics With Registration-Enhanced Displacement Encoded MRI,” IEEE Trans. Med. Imaging, 33(6), pp. 1350–1362. 10.1109/TMI.2014.2311755 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39]. Liu, W. , Ashford, M. W. , Chen, J. , Watkins, M. P. , Williams, T. A. , Wickline, S. A. , and Yu, X. , 2006, “ MR Tagging Demonstrates Quantitative Differences in Regional Ventricular Wall Motion in Mice, Rats, and Men,” Am. J. Physiol. Heart Circ. Physiol., 291(5), pp. H2515–H2521. 10.1152/ajpheart.01016.2005 [DOI] [PubMed] [Google Scholar]
- [40]. Rohmer, D. , Sitek, A. , and Gullberg, G. T. , 2007, “ Reconstruction and Visualization of Fiber and Laminar Structure in the Normal Human Heart From Ex Vivo Diffusion Tensor Magnetic Resonance Imaging (DTMRI) Data,” Invest. Radiol., 42(11), pp. 777–789. 10.1097/RLI.0b013e3181238330 [DOI] [PubMed] [Google Scholar]
- [41]. Rouhani, M. , and Sappa, A. D. , 2011, “ Implicit B-Spline Fitting Using the 3L Algorithm,” 18th IEEE International Conference on Image Processing (ICIP), Brussels, Belgium, Sept. 11–14, pp. 893–896 . 10.1109/ICIP.2011.6116702 [DOI] [Google Scholar]
- [42]. Pacher, P. , Nagayama, T. , Mukhopadhyay, P. , Bátkai S., and Kass, D. A. , 2008, “ Measurement of Cardiac Function Using Pressure-Volume Conductance Catheter Technique in Mice and Rats,” Nat. Protoc., 3(9), pp. 1422–1434. 10.1038/nprot.2008.138 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43]. Veress, A. I. , Gullberg, G. T. , and Weiss, J. A. , 2005, “ Measurement of Strain in the Left Ventricle During Diastole With Cine-MRI and Deformable Image Registration,” ASME J. Biomech. Eng., 127(7), pp. 1195–1207. 10.1115/1.2073677 [DOI] [PubMed] [Google Scholar]
- [44]. Costa, K. D. , Holmes, J. W. , and Mcculloch, A. D. , 2001. “ Modelling Cardiac Mechanical Properties in Three Dimensions,” Philos. Trans. R. Soc. A Math. Phys. Eng. Sci., 359(1783), pp. 1233–1250. 10.1098/rsta.2001.0828 [DOI] [Google Scholar]
- [45]. Omens, J. H. , MacKenna, D. A. , and McCulloch, A. D. , 1993, “ Measurement of Strain and Analysis of Stress in Resting Rat Left Ventricular Myocardium,” J. Biomech., 26(6), pp. 665–676. 10.1016/0021-9290(93)90030-I [DOI] [PubMed] [Google Scholar]
- [46]. Maas, S. , Rawlings, D. , Weiss, J. A. , and Ateshian, G. A. , 2014, febio: Finite Elements for Biomechanics-Theory Manual, University of Utah, Salt Lake City, UT. [Google Scholar]
- [47]. Healy, L. J. , Jiang, Y. , and Hsu, E. W. , 2011, “ Quantitative Comparison of Myocardial Fiber Structure Between Mice, Rabbit, and Sheep Using Diffusion Tensor Cardiovascular Magnetic Resonance,” J. Cardiovasc. Magn. Reson., 13(1), p. 74. 10.1186/1532-429X-13-74 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48]. Gilbert, S. H. , Benoist, D. , Benson, A. P. , White, E. , Tanner, S. F. , Holden, A. V. , Dobrzynski, H. , Bernus, O. , and Radjenovic, A. , 2012, “ Visualization and Quantification of Whole Rat Heart Laminar Structure Using High-Spatial Resolution Contrast-Enhanced MRI,” Am. J. Physiol. Heart Circ. Physiol., 302(1), pp. H287–H298. 10.1152/ajpheart.00824.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49]. Dokos, S. , Smaill, B. H. , Young, A. A. , and LeGrice, I. J. , 2002, “ Shear Properties of Passive Ventricular Myocardium,” Am. J. Physiol. Heart Circ. Physiol., 283(6), pp. H2650–H2659. 10.1152/ajpheart.00111.2002 [DOI] [PubMed] [Google Scholar]
- [50]. Sun, K. , Stander, N. , Jhun, C.-S. , Zhang, Z. , Suzuki, T. , Wang, G.-Y. , Maythem, S. , Wallace, A. W. , Tseng, E. E. , Baker, A. J. , Saloner, D. , Einstein, D. R. , Ratcliffe, M. B. , and Guccione, J. M. , 2009, “ A Computationally Efficient Formal Optimization of Regional Myocardial Contractility in a Sheep With Left Ventricular Aneurysm,” ASME J. Biomech. Eng., 131(11), pp. 1–21. 10.1115/1.3148464 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51]. Ateshian, G. A. , and Costa, K. D. , 2009, “ A Frame-Invariant Formulation of Fung Elasticity,” J. Biomech., 42(6), pp. 781–785. 10.1016/j.jbiomech.2009.01.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52]. Maas, S. A. , Ellis, B. J. , Ateshian, G. A. , and Weiss, J. A. , 2012, “ febio: Finite Elements for Biomechanics,” ASME J. Biomech. Eng., 134(1), p. 011005. 10.1115/1.4005694 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53]. Guccione, J. M. , and McCulloch, A. D. , 1993, “ Mechanics of Active Contraction in Cardiac Muscle—Part I: Constitutive Relations for Fiber Stress That Describe Deactivation,” ASME J. Biomech. Eng., 115(1), pp. 72–81. 10.1115/1.2895473 [DOI] [PubMed] [Google Scholar]
- [54]. Guccione, J. M. , Waldman, L. K. , and McCulloch, A. D. , 1993, “ Mechanics of Active Contraction in Cardiac Muscle—Part II: Cylindrical Models of the Systolic Left Ventricle,” ASME J. Biomech. Eng., 115(1), pp. 82–90. 10.1115/1.2895474 [DOI] [PubMed] [Google Scholar]
- [55]. Bayer, J. D. , Blake, R. C. , Plank, G. , and Trayanova, N. A. , 2012, “ A Novel Rule-Based Algorithm for Assigning Myocardial Fiber Orientation to Computational Heart Models,” Ann. Biomed. Eng., 40(10), pp. 2243–2254. 10.1007/s10439-012-0593-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56]. Gilbert, S. H. , Benson, A. P. , Li, P. , and Holden, A. V. , 2007, “ Regional Localisation of Left Ventricular Sheet Structure: Integration With Current Models of Cardiac Fibre, Sheet and Band Structure,” Eur. J. Cardiothorac. Surg., 32(2), pp. 231–249. 10.1016/j.ejcts.2007.03.032 [DOI] [PubMed] [Google Scholar]
- [57]. Streeter, D. D. , Vaishnav, R. N. , Patel, D. J. , Spotnitz, H. M. , Ross, J. , and Sonnenblick, E. H. , 1970, “ Stress Distribution in the Canine Left Ventricle During Diastole and Systole,” Biophys. J., 10(4), pp. 345–363. 10.1016/S0006-3495(70)86306-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58]. Geerts, L. , Bovendeerd, P. , Nicolay, K. , and Arts, T. , 2002, “ Characterization of the Normal Cardiac Myofiber Field in Goat Measured With MR-Diffusion Tensor Imaging,” Am. J. Physiol. Heart Circ. Physiol., 283(1), pp. H139–H145. 10.1152/ajpheart.00968.2001 [DOI] [PubMed] [Google Scholar]
- [59]. Yuan, K.-Y. , Huang, Y.-S. , Yang, H.-T. , and Pian, T. H. H. , 1994, “ The Inverse Mapping and Distortion Measures for 8-Node Hexahedral Isoparametric Elements,” Comput. Mech., 14(2), pp. 189–199. 10.1007/BF00350284 [DOI] [Google Scholar]
- [60]. Peyrat, J.-M. , Sermesant, M. , Pennec, X. , Delingette, H. , Xu, C. , McVeigh, E. R. , and Ayache, N. , 2007, “ A Computational Framework for the Statistical Analysis of Cardiac Diffusion Tensors: Application to a Small Database of Canine Hearts,” IEEE Trans. Med. Imaging, 26(11), pp. 1500–1514. 10.1109/TMI.2007.907286 [DOI] [PubMed] [Google Scholar]
- [61]. Alexander, D. C. , Pierpaoli, C. , Basser, P. J. , and Gee, J. C. , 2001, “ Spatial Transformations of Diffusion Tensor Magnetic Resonance Images,” IEEE Trans. Med. Imaging, 20(11), pp. 1131–1139. 10.1109/42.963816 [DOI] [PubMed] [Google Scholar]
- [62]. Bachner-Hinenzon, N. , Ertracht, O. , Leitman, M. , Vered, Z. , Shimoni, S. , Beeri, R. , Binah, O. , and Adam, D. , 2010, “ Layer-Specific Strain Analysis by Speckle Tracking Echocardiography Reveals Differences in Left Ventricular Function Between Rats and Humans,” Am. J. Physiol. Heart Circ. Physiol., 299(3), pp. H664–672. 10.1152/ajpheart.00017.2010 [DOI] [PubMed] [Google Scholar]
- [63]. Phatak, N. S. , Maas, S. A. , Veress, A. I , Pack, N. A., Di Bella , E. V. R., and Weiss , and J. A., 2009, “ Strain Measurement in the Left Ventricle During Systole With Deformable Image Registration,” Med. Image Anal., 13(2), pp. 354–361. 10.1016/j.media.2008.07.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64]. Wang, H. M. , Luo, X. Y. , Gao, H. , Ogden, R. W. , Griffith, B. E. , Berry, C. , and Wang, T. J. , 2014, “ A Modified Holzapfel-Ogden Law for a Residually Stressed Finite Strain Model of the Human Left Ventricle in Diastole,” Biomech. Modell. Mechanobiol., 13(1), pp. 99–113. 10.1007/s10237-013-0488-x [DOI] [PMC free article] [PubMed] [Google Scholar]


