Three-Dimensional Strains in Human Posterior Sclera Using Ultrasound Speckle Tracking

Abstract

Intraocular pressure (IOP) induced strains in the peripapillary sclera may play a role in glaucoma progression. Using inflation testing and ultrasound speckle tracking, the 3D strains in the peripapillary sclera were measured in nine human donor globes. Our results showed that the peripapillary sclera experienced through-thickness compression and meridional stretch during inflation, while minimal circumferential dilation was observed when IOP was increased from 10 to 19 mmHg. The maximum shear was primarily oriented in the through-thickness, meridional cross sections and had a magnitude slightly larger than the first principal strain. The tissue volume had minimal overall change, confirming near-incompressibility of the sclera. Substantial strain heterogeneity was present in the peripapillary region, with local high strain areas likely corresponding to structural heterogeneity caused by traversing blood vessels. These 3D strain characteristics provide new insights into the biomechanical responses of the peripapillary sclera during physiological increases of IOP. Future studies are needed to confirm these findings and investigate the role of these biomechanical characteristics in ocular diseases.

Introduction

Glaucoma is an ocular pathology that leads to vision loss. Clinically, glaucoma is characterized by damage to the optic nerve, which is responsible for transmitting visual signals from the retina to the brain. It is known that such damage is related to the IOP, as many studies have confirmed the benefit of lowering IOP in glaucoma patients, even in those without an overly high IOP [1,2]. Damage to the optic nerve initiates at the optic nerve head (ONH) [3], i.e., the site where the axons of the retinal ganglion cells exit the eye. However, the detailed mechanisms responsible for the optic nerve damage remain largely unknown.

The mechanical characteristics of the ONH and their interplay with IOP have been considered important factors in glaucoma development and progression [4]. In the human eye, the retinal ganglion cell axons make a turn from the inner surface of the retina to exit the scleral canal through a fenestrated extracellular matrix called the lamina cribrosa (LC). The LC has been the focus of many computational modeling [5,6] and histomorphology studies [7], as its microstructure and mechanical properties likely have a significant influence on the mechanical insults experienced by the optic nerve. The peripapillary sclera, which surrounds the scleral canal, is also of particular interest because it too could significantly influence the stresses and strains acting on the neural tissue [8].

Using optical imaging, the surface strains of the peripapillary sclera during inflation in human and monkey eyes have been characterized, showing significant variation due to location [9] and age [9,10]; and the collagen microstructure likely underlies the heterogeneous tensile strain responses [11]. Our laboratory has reported the through-thickness distribution of both tensile and compressive strains in porcine and human eyes [12–15]; however, little is known about the 3D deformation throughout the volume of the posterior sclera.

The microstructure of the peripapillary sclera is complex, and most notable is the annulus ring formed by in-plane collagen fibers surrounding the scleral canal that is believed to constrain scleral canal expansion [16]. In addition, there are many small traversing arteries and nerves (called the “short posterior ciliary arteries and nerves”) and a circular arterial ring (called the “circle of Zinn-Haller”), which provides blood supply to the anterior portions of the ONH [17,18]. Because of these structural complexities, heterogeneous and complex mechanical behavior is expected in this region and a full 3D characterization would be desirable. Our goal in this study was to experimentally characterize the 3D strain states of the peripapillary sclera in human donor eyes under IOP elevations within the physiological range.

Three-dimensional ultrasound speckle tracking has been used to measure the deformation of cornea [19], arteries [20], and cardiac muscles [21]. We have developed a high-frequency ultrasound method to acquire volumetric scans and measure the complex internal strains in the sclera surrounding the ONH. We implemented a data acquisition system with automated 3D imaging and synchronized data storage, and a 3D speckle tracking algorithm that determines the 3D displacement vectors for tissue grid points within the scanned volume and reconstructs the full strain tensor from the displacement gradients. We performed validation studies to analyze the displacement and strain accuracy of the 3D method [22]. Simulated whole voxel and subvoxel displacements in the presence of simulated random electrical noise showed an absolute error less than 0.01 voxel in all scanning directions for 0, 0.5, 1, and 2 voxel translations. Simulated ultrasound radiofrequency data for uniform strains (also with simulated random electrical noise) showed a high correlation between true strains and calculated strains in the range of 0.1–5.0% (R²> 0.997). The performance in the direction of sound propagation (i.e., axial) was consistently better than the performance in the directions in the orthogonal plane (i.e., lateral and elevational), while the lateral and elevational directions had similar performance. The better performance in the axial direction was due to its higher spatial resolution (30 μm) and higher scanning density (1.5 μm). The lateral direction (perpendicular to the axial direction within the 2D imaging plane) and the elevational direction (perpendicular to the 2D imaging plane) shared the same spatial resolution (62.5 μm) and scanning density (20 μm), which resulted in similar displacement and strain accuracy. For true strains of 1.0–5.0%, the accuracy was better than 6% error for all directions. For true strains of 0.1% and 0.5%, the percent error was 4–10% in the axial direction and 21–26% in the lateral and elevational directions. We also found that the error was a rather consistent bias toward smaller values than the true strain. For example, at true strains of 0.5% and 0.6%, the calculated strains were 0.39% and 0.50%, respectively; although both strains were underestimated, the difference remained about the same as the true difference (i.e., 0.1%). At true strains of 2.0% and 2.1%, the calculated strains were 1.93% and 2.02%, respectively; again, different by about 0.1%. These results suggested that the approach could robustly resolve a small strain difference, although the relative errors at the small strains became larger. Based on simulations of true volume ratios of 0.86–1.17 (the ratio between the deformed volume and the original volume), the accuracy for volume ratio measurement was shown to be consistently high (lower than 0.5% error) at all simulated true strain levels (i.e., 0.1–5.0%).

This high performance of ultrasound speckle tracking in strain estimation is explained by its relatively high spatial resolution combined with high displacement sensitivity resulting from dense sampling and interpolation. The ultrasound speckle tracking method we employ is performed using the reflectance radiofrequency data that is sampled densely both in time and space. With our current setting, the signal in the axial direction is sampled at a rate of 500 million samples per second, which corresponds to an axial voxel size of 1.5 μm. Laterally, we acquire 384 A-lines within an 8.0 mm window to achieve a lateral voxel size of 20 μm, and the same sampling density is used in the elevational direction. The speckle tracking algorithm interpolates the cross-correlation coefficients over 60 times, which is equivalent to but computationally more efficient than the interpolation of the RF data for the scanned volume, to achieve subvoxel accuracy in displacement calculation.

Using the 3D speckle tracking method, we measured the 3D inflation response of the human sclera in this study and quantified the principal and maximum shear strains for a dense grid of tissue points covering the volume of the peripapillary sclera. This 3D approach allowed us to delineate the tensile, compressive, and shear deformations and their spatial heterogeneities in the peripapillary sclera, providing a more complete evaluation than surface or 2D cross-sectional methods to characterize the strain states near the ONH, which may help us better understand the biomechanical pathways of optic nerve damage.

Materials and Methods

Nine eyes from human donors (24–73 years old, mean ± SD: 55.2 ± 16.8 years old) were obtained from the Lions Eye Bank of West Central Ohio (Dayton, OH). All donors were Caucasian with eight males and one female. The eyes were recovered within 8 hrs postmortem and stored in a moist container at 4 °C until experimental use. All experiments were performed within 72 hrs postmortem to avoid changes in tissue biomechanical properties [23]. The anterior segment was removed using a 7.5 mm trephine, and the intraocular structures were removed as well. The ocular shell was clamped at the location of trephination using a custom-built pressurization chamber [13] and immersed in 0.9% saline during measurements (Fig. 1). The real-time images displayed on the monitor of the ultrasound imaging system were used to ensure that the tissue was within the focal zone of the transducer beam. The IOP was controlled using an elevated column filled with phosphate buffered saline (PBS) connected to the pressurization chamber, and monitored continuously with a pressure sensor (P75, Harvard Apparatus).

Fig. 1.

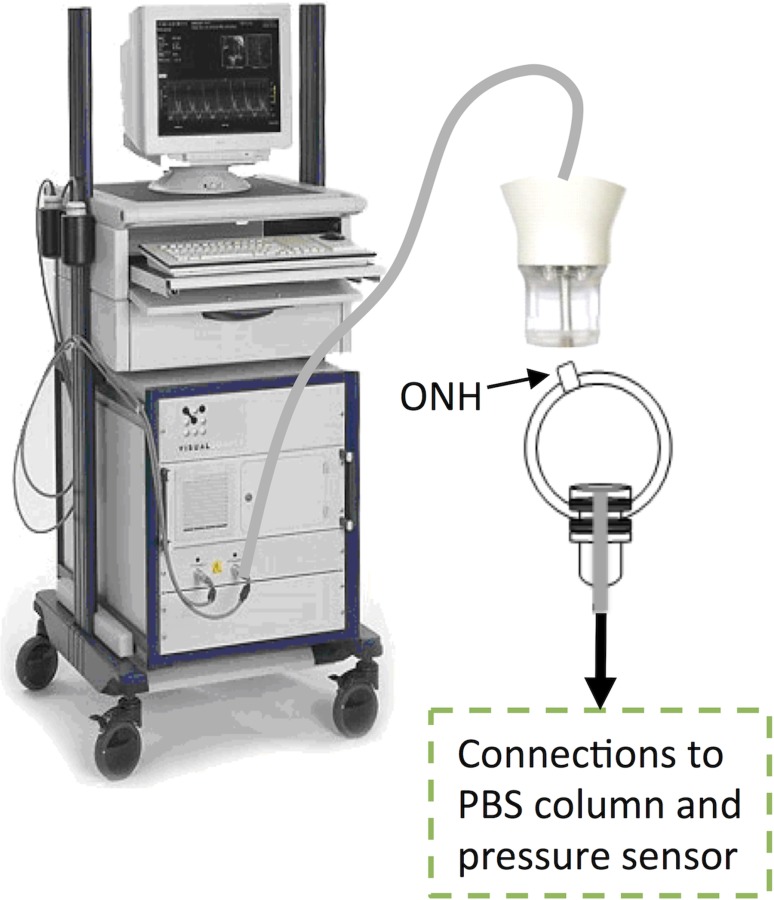
Experimental setup of the human donor scleral shell measured with the Vevo 660 high-frequency ultrasound system. ONH: optic nerve head. The shell was clamped near the corneoscleral junction, away from the measured posterior sclera; and immersed in PBS. The ultrasound probe was not in contact with the tissue during scanning.

Each globe was preconditioned using five sinusoidal pressure cycles from 5 to 30 mmHg. After preconditioning, the globe was equilibrated at a reference pressure of 10 mmHg for 30 min. Inflation tests were then performed with four pressure steps: 11.5, 13, 15, and 19 mmHg. These pressure steps were chosen based on prior testing to ensure successful speckle tracking and reduce total scanning time. Separate inflation tests were performed on the nasal and temporal sides of the ONH (order randomized for each eye). After a 7-min equilibration period at each pressure level, a 55 MHz ultrasound probe (Vevo 660, VisualSonics Inc.) was used to acquire a volume of ultrasound radiofrequency data.

Figure 2 illustrates an ultrasonic volume scan on the nasal side of the ONH. The 3D volume was built from consecutive 2D frames of radiofrequency data. An automated actuator (431 Series, Newport) was used to move the ultrasound probe in the inferior to superior or superior to inferior direction (randomized for each eye). The actuator step size was 20 μm, and a 2D scan was obtained at each incremental step of the transducer movement. The 2D scans were decomposed back to 1D A-lines and then individual voxels to reconstruct the 3D volume. The total volume, combining the nasal and temporal halves, formed a dome centered at the ONH. The data acquisition and actuator were controlled simultaneously by a customized labview program (National Instruments). As shown in Fig. 2, the three orthogonal axes of lateral (X), axial (Y), and elevational (Z) form a Cartesian coordinate system.

Fig. 2.

Illustration of the scanned volume (white region) on nasal side of the ONH. Y is the axial direction (direction of sound propagation), X is the lateral direction (direction perpendicular to Y in the cross-sectional plane), and Z is the elevational direction (i.e., direction of step motor translation). S: superior, N: nasal, I: inferior, T: temporal.

The distributive displacements for a rectangular grid of tissue points within the scleral volume were calculated using a 3D ultrasound speckle tracking algorithm. Overlapping kernels (620 × 76.5 × 620 μm³, lateral × axial × elevational) were defined in the scanned volume and their centers represent the grid points to be tracked during inflation. The new location of each grid point in the deformed volume was found based on the maximum cross-correlation coefficient with spline interpolation for subvoxel resolution, similar to the procedure used in the 2D speckle tracking [15]. The search window was defined in the deformed volume and centered at the original kernel. The size of the search window was chosen to be 1220 × 151.5 × 1220 μm³, which was found to be sufficient for the expected range of deformation of the human sclera between the experimental pressure steps. A kernel overlap of 75% in all directions was used (i.e., the step size between adjacent grid points was one fourth of the kernel size in that direction) to achieve the high spatial resolution of the strain maps, resulting in a total of about 200,000–300,000 grid points for each scanned volume whose displacement vectors were calculated at each inflation pressure.

The strains were estimated using a 3D least squares method to fit the displacement gradients to the measured displacement data as follows:

$$\begin{array}{c}u=\frac{\partial u}{\partial x}x+\frac{\partial u}{\partial y}y+\frac{\partial u}{\partial z}z+C_1\\ v=\frac{\partial v}{\partial x}x+\frac{\partial v}{\partial y}y+\frac{\partial v}{\partial z}z+C_2\\ w=\frac{\partial w}{\partial x}x+\frac{\partial w}{\partial y}y+\frac{\partial w}{\partial z}z+C_3\end{array}$$ (1)

where u, v, and w are the displacement components obtained from ultrasound speckle tracking, x, y, and z are the grid point coordinates, and the C_i's are local intercept constants used during fitting. The Green strain tensor for each grid point was then calculated using the displacement gradients. Equations for the E_xx and E_xy tensor components are shown below:

$$E_{\mathit{x}\mathit{x}}=\frac{\partial u}{\partial x}+\frac{1}{2}\left[{\left(\frac{\partial u}{\partial x}\right)}^2+{\left(\frac{\partial v}{\partial x}\right)}^2+{\left(\frac{\partial w}{\partial x}\right)}^2\right]$$ (2)

$$E_{\mathit{x}\mathit{y}}=\frac{1}{2}\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)+\frac{1}{2}\left(\frac{\partial u}{\partial x}\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\frac{\partial v}{\partial y}+\frac{\partial w}{\partial x}\frac{\partial w}{\partial y}\right)$$ (3)

Similar equations were used to find the E_yy, E_zz, E_xz, and E_yz components of the strain tensor. With all components calculated for the Green strain tensor, the eigenvalues and eigenvectors yielded the principal strains and vectors. The three principal strains were sorted in decreasing order with the first principal strain, ε₁, being the largest positive principal strain. Using the principal strain magnitudes, the maximum shear strain magnitude and volume ratio were calculated as follows [24]:

$${\gamma }_{\max }=\frac{1}{2}({\epsilon }_{\max }-{\epsilon }_{\min })$$ (4)

$$\mathrm{VR}=(1+{\epsilon }_1)(1+{\epsilon }_2)(1+{\epsilon }_3)$$ (5)

where γ_max is the maximum shear strain, VR is the volume ratio, and ε₁, ε₂, and ε₃ are the three principal strains calculated from the Green strain tensor. Maps of strain magnitudes, strain vectors, and volume ratios throughout the scanned volume were plotted using a 3D visualization software, paraview (Kitware Inc. & Los Alamos Labs). Average values for the principal strains, maximum shear strains, and volume ratios were calculated for the entire scanned volume in each eye at each pressure level during the inflation.

In order to explore the microstructural correspondence of the heterogeneous strains observed in the human peripapillary sclera, a donor eye (59-year-old, male, Caucasian) previously stored at −80 °C for several weeks was thawed and 3D-scanned at the nasal side, following the same inflation protocol described earlier. After several additional months of frozen storage at −80 °C, the specimen was fixed in 10% formaldehyde for 24 hrs. Twenty serial sections (3–5 μm thick) of the ONH and the peripapillary sclera were obtained from posterior to anterior at intervals of 50 μm beginning at the scleral outer surface. The tissue sections were stained with Masson's Trichrome. Due to the frozen storage, the strain data from this specimen was not included in the analysis of the nine eyes measured within 72 hrs postmortem.

Results

The radiofrequency data acquired from each eye was reconstructed into 3D volumes and plotted in paraview (Fig. 3). Since the 3D ultrasound scanning was performed for half of the posterior dome each time, dividing from a central meridian at the ONH (as illustrated by the white region in Fig. 2), the scanned volume included regions of half of the optic nerve, the scleral canal (or dura), and the peripapillary sclera. The transverse (Fig. 3(b)) and coronal (posterior–anterior) sections (Fig. 3(c)) obtained from the reconstructed 3D volume clearly delineate the scleral canal (dashed curves). Because a stub of the optic nerve external to the scleral surface was present during the scanning, its irregular surface and the dense dural sheath generated substantial acoustic attenuation so that the ultrasonic scattering within the optic nerve and the LC was often too weak to detect. These regions appeared blank in the scanned volume when visualized in paraview (Figs. 3(b) and 3(c)). The scanning reached the scleral canal, and the tapering of the peripapillary sclera thickness was often discernable in the transverse view (Fig. 3(b)).

Fig. 3.

(a) The reconstructed 3D volume of the nasal side of a donor eye, (b) a transverse cross section of the eye showing the span of the scanning into the ONH. Acoustic signals were poor inside ONH due to attenuation from the irregular surface of the optic nerve stub and the dural sheath. The tapering of the sclera (*) was often seen, (c) a coronal cross section of the eye showing the circular scleral canal.

The principal strains (magnitudes and vectors) were calculated at each tissue grid point in the scanned volume of the donor eyes. Although the principal strains were heterogeneous across the scanned volume in the same eye, a general trend was consistent in all eyes: that is, the first principal strain was positive and varied from 0.9% to 4.7% in the tested eyes at 19 mmHg; the second principal strain had very small magnitudes and varied from −0.3% to 0.1%; the third principal strain was negative and largest in magnitude (2.0–5.3%). This trend in principal strain magnitudes was observed at all pressure levels, and the first and third principal strains were highly correlated (Pearson correlation, R = −0.97, p < 0.001, at 19 mmHg) and showed an increase in magnitude with increasing IOP (Fig. 4).

Fig. 4.

Principal strains at different pressures in each donor eye ((a)–(c)) and averaged over all tested eyes (d). The legend shows donor age (y.o.: years old).

Based on the principal strains, the magnitudes of the maximum shear strain and volume ratios were calculated at each grid point as well. The maximum shear strain in each eye is shown in Fig. 5(a), showing an increasing trend with IOP. At 19 mmHg, the maximum shear ranged from 1.57 ± 0.53% to 5.11 ± 1.80%, with an average of 2.78 ± 1.30% in all donor eyes. The volume ratios showed a decreasing trend with IOP in all eyes (Fig. 5(b)), and all values were slightly lower than 1 except in one eye (24-year-old donor) at the first inflation pressure. At 19 mmHg, the volume ratio ranged from 0.986 to 0.998 across all nine eyes.

Fig. 5.

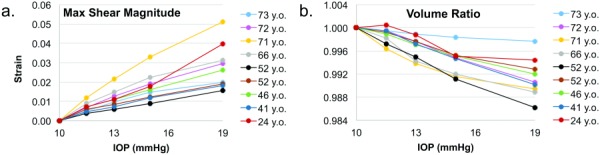
Maximum shear (a) and volume ratios (b) at different pressures in each donor eye. The legend shows donor age (y.o.: years old).

To evaluate the strain distributions throughout the scanned volume, serial strain maps in the coronal planes were obtained at different depths from the posterior surface. The principal and maximum shear strain maps are shown for a representative eye (66 y.o., male, Caucasian, Fig. 6). The average principal strains reported in Fig. 4 show an overall pattern consistent with the cross-sectional views: the first principal was largely positive (greenish yellow in most areas with red regions showing large positive strains), the third principal was largely negative (greenish blue in most areas with dark blue regions showing large negative strains), and the second principal was consistently close to zero throughout the volume (evenly green). The cross-sectional images also revealed a substantial degree of strain heterogeneity through the depth of the sclera. The patterns of high-strain regions were consistent for the first and third principals and the max shear (i.e., approximately the same areas had higher strains in all three types of strains). The second principal appeared to be evenly small throughout the scanned volume.

Fig. 6.

Serial strain maps at 13 mmHg at different depth from the posterior surface on the temporal side of a human eye (66 years male Caucasian). The strain map is overlaid on the scanned volume cropped at the plane of strain map. The small void in the scanned volume was caused by strong acoustic shadowing from tissue debris on the specimen surface.

Ultrasound images showed that the high-strain regions were often co-localized with regions of substantially different echogenicity, i.e., lower acoustic scattering, suggesting that these regions were structurally distinct from the highly reflective collagenous stroma (Figs. 7(a) and 7(b)). Histology analysis was performed in one eye to explore the structural correspondence of strain heterogeneity. Serial coronal histology sections of this eye showed an arterial circle approximately 200–800 μm from the edge of the scleral canal (Fig. 7(c)). The estimated depth of the plane at the arterial ring to the tangential plane at the scleral surface was about 500 μm. Serial strain maps of similar cross sections in this eye showed a circular pattern of high-strain regions surrounding the scleral canal (Fig. 7(b)), suggesting a correspondence between the arterial circle and increased strains.

Fig. 7.

Low acoustic scattering regions (white arrow heads) in ultrasound B-mode images (a) were co-localized with increased first principal strains (black arrow heads) in (b). The histology of this eye (c) showed the arterial circle of Zinn-Haller (white arrows).

Localized high-strain regions were observed in the internal stroma of all measured eyes. Cross-sectional strain maps from three representative donor eyes are shown (Fig. 8), including eyes with the lowest and highest average strains, and that of the youngest donor. The corresponding maps of volume ratios from the same cross sections are also plotted (Fig. 8). The volume ratio values showed a heterogeneous distribution, with regions of small gains or losses in volume. The overall heterogeneous patterns of the volume ratios largely matched those of the first principal strains, but a high strain region could experience either a volume increase or decrease.

Fig. 8.

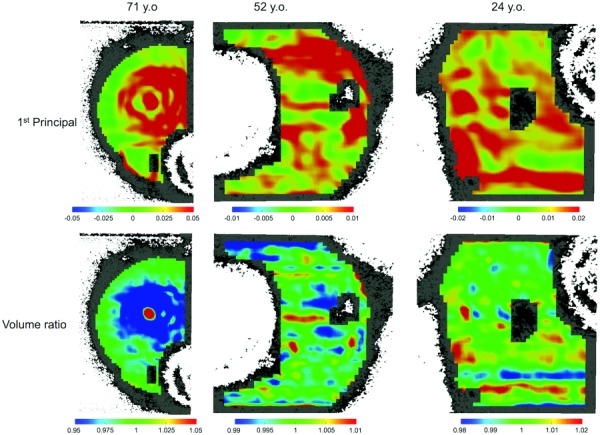
Strain and volume ratio maps from three representative donors. The 71-year-old had the highest average strains. The 52-year-old had the lowest average strains. The 24-year-old, the youngest donor in the tested group, is also shown. The color bars are adjusted for each individual plot to show within-specimen heterogeneity.

To evaluate the orientations of the principal strains, the principal vectors were also plotted at the grid points. Throughout the volume, the first principal vectors were largely oriented in the in-plane meridional direction (Fig. 9(a)), the third principal vectors were largely oriented in the through-thickness direction (Fig. 9(c)), and the second principal vectors had a predominantly in-plane circumferential arrangement around the ONH (Fig. 9(b)). The circumferential arrangement of the second principals was consistently observed in other tested eyes and more examples are shown (Fig. 10). As defined, the maximum shear is oriented in the plane of the maximum (i.e., first) and minimum (i.e., third) principals but rotated by 45 deg from the principal vectors (Fig. 11).

Fig. 9.

Vector directions (green lines) at grid points for (a) first principal, (b) second principal, and (c) third principal strains. The large orange arrows indicate (a) meridional, (b) circumferential, and (c) through-thickness directions, which align with the predominant vector directions in each plot. The grid points were down-sampled for visual clarity.

Fig. 10.

The second principal vectors in three donor eyes, consistently showing the predominant circumferential orientation

Fig. 11.

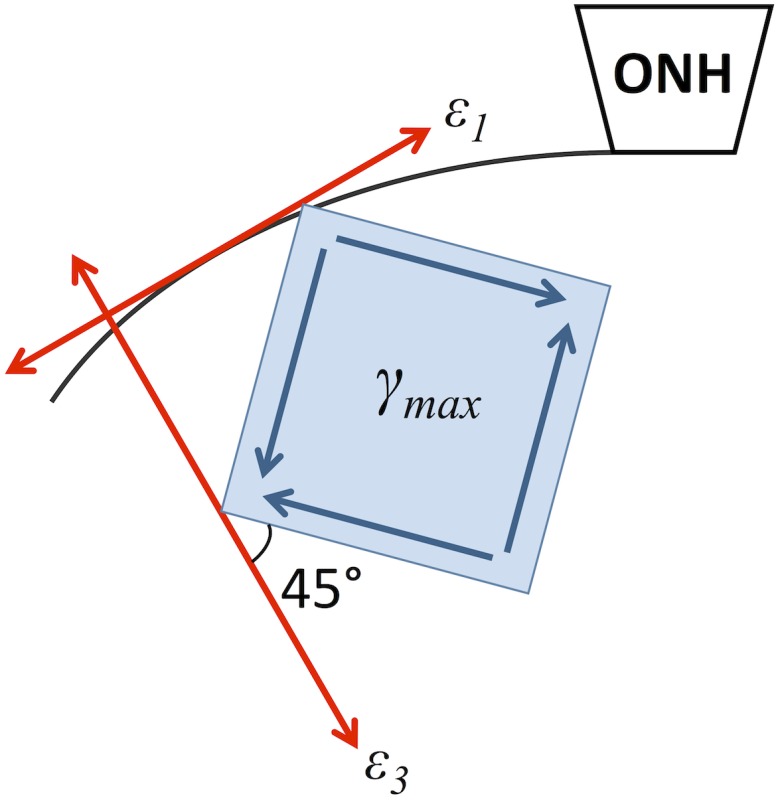
The predominant orientation of the maximum shear in the peripapillary sclera. The red arrows represent the predominant directions of the maximum (ε₁) and minimum (ε₃) principal strains. The maximum shear is oriented 45 deg from the principal strain vectors.

Discussion

In this study, a 3D ultrasound speckle tracking technique was used to characterize the deformation of the peripapillary sclera during physiological IOP increases in human donor eyes. A high frequency ultrasound probe was used to obtain volumetric scans of the peripapillary sclera centered at the ONH. All components of the 3D Green strain tensor were calculated for a dense grid of tissue points covering the scanned scleral volume, using the displacement data obtained from ultrasound speckle tracking. The coordinate-independent principal and maximum shear strains were then evaluated.

The primary findings of the study are as follows. The 3D strain data showed that the peripapillary sclera experienced compression largely along the through-thickness direction and tensile stretch of almost equal magnitude largely along the meridional direction during IOP increase from 10 to 19 mmHg. The strain along the circumferential direction to the ONH was small in magnitude suggesting minimal circumferential expansion in this region when IOP increased from 10 to 19 mmHg. These strain patterns resulted in a maximum shear largely out-of-plane and almost 45-deg to the scleral surface.

Both the first principal (tensile) and the third principal strain (compressive) increased gradually in magnitude as the eye was inflated from 10 to 19 mmHg and the pressure–strain relationship appeared rather linear (Fig. 4). Compared to previous studies, this more linear appearance can be explained by the use of a higher initial pressure and a smaller pressure range in the current study. In order to reach a meaningful IOP elevation within several hours of 3D scanning experiments, we opted to start the inflation at 10 mmHg, which shifted the pressure–strain curve just above the toe region and into the more linear region (see Fig. 5 in Ref. [25] for an example of the human sclera inflation response from 1.5 to 25 mmHg). The typical initial pressure in previous studies was 1.5 mmHg [10] or 5 mmHg [9], which included the much more compliant phase and transition to the less compliant phase showing a nonlinear response. Moreover, the pressure range used in the current study was small compared to previous studies testing up to 45 mmHg. Within the smaller pressure range, our data showed a trend of decreasing Δstrain/Δpressure slope at increasing pressures (Fig. 4(d)): the slope for the first principal was 0.39%/mmHg between 10 and 11.5 mmHg, 0.25%/mmHg between 11 and 13 mmHg, 0.24%/mmHg between 13 and 15 mmHg, and 0.23%/mmHg between 15 and 19 mmHg. The decrease in slope indicated a nonlinear trend, which could likely become more pronounced when higher pressures are reached. Although the pressure range was limited, the results were useful in understanding the behavior of human peripapillary sclera during mild IOP elevations from a normal baseline.

The second principal strain (predominantly along the circumferential direction, Fig. 10) had much smaller magnitudes than the first and third principals, and increased but remained small as the pressure increased (Fig. 4(b)). The marked contrast between the circumferential and meridional responses was unlikely an artifact of poorer measurement accuracy in one in-plane direction than the other, because the circumferential or meridional direction was not strictly aligned with any scanning directions, i.e., both were scanned as lateral and elevational depending on the location. Our validation studies showed that the strain measurement accuracy was similar for the two in-plane directions [22]. Previous surface strain measurements have reported very small circumferential strains (∼0.5%) in human donor eyes when inflated to a higher IOP [10,26]. Given the relatively high initial pressure (10 mmHg) used in the current study, it is plausible that the circumferential strains were minimal within the relatively small pressure increase. This outcome likely reflects the collagen organization in the peripapillary sclera. Wide-angle X-ray scattering studies have shown a preferred circumferential orientation of collagen fibers forming an annulus ring surrounding the human scleral canal [27]. Our results suggested that this microstructural arrangement may be highly effective in preventing circumferential increase of the scleral canal opening during mild IOP elevations from a normal baseline.

The 3D strain measurements showed peripapillary sclera compression during physiological increases of IOP (∼3% compression on average for a pressure increase from 10 to 19 mmHg), an outcome similar to our findings in 2D cross-sectional studies. Rada et al has reported a surprising presence of the “cartilage proteoglycan,” aggrecan, in human sclera, and speculated that the sclera must regularly experience substantial compression to express a proteoglycan that is known to resist compression [28]. Later, the same group reported a higher concentration of aggrecan in the posterior sclera and its unreduced levels during aging, despite the decrease of other proteoglycans starting from the fourth decade of life [29]. It was also observed that lumican–aggrecan complexes accumulate over age which may contribute to the age-associated changes in scleral mechanical properties and permeability [30]. Previous mechanical testing in dissected scleral buttons has shown that the through-thickness compressive modulus in the human sclera can be 100 times less than the in-plane tensile modulus [31,32]. Larger than normal compressive strains, either due to an increase in IOP or decrease in compressive stiffness, may potentially lead to the compression of the traversing arteries in the posterior eye that feed the ONH and the choroid, disrupting the blood flow to these structures. The compressive strains in our study exhibited a variance across the donor eyes at the same IOP elevation, suggesting individual differences in compressive stiffness.

An important result from this study was the quantification of shear strains in the intact peripapillary sclera during increases of IOP. Using shear testing on dissected bovine scleral specimens, a previous study showed that the posterior sclera had a stiffer response to in-plane shear compared to out-of-plane shear [33]. Our results showed that the maximum shear was primarily out-of-plane (in the planes formed by the meridional and through-thickness directions) and at an angle about 45 deg to the scleral surface (Fig. 11). In the human cornea, it has been shown that the shear modulus is lower than both the compressive and tensile moduli, and decreases in the posterior stroma which has less anterior–posterior collagen interweaving [34]. The anisotropic collagen structure in the peripapillary sclera, the predominantly in-plane interweaving of collagen fibers, and the material discontinuity at the scleral canal (a stiffer sclera and a weaker LC) are all possible structural factors responsible for the high levels of shear present in this region.

The presence of significant shear in the peripapillary sclera suggests the need to better understand its shear properties and their potential involvement in ocular pathologies. Computational studies have predicted large shear at the ONH [35]. To our best knowledge, the current study is among the first to report experimental data showing significant shear deformation in the peripapillary sclera during IOP elevation. Although significant shear in itself may be a normal mode of deformation in the peripapillary sclera and not necessarily associated with glaucoma neuropathy, structural or material changes could cause excessive shear in focal regions contributing to IOP-related mechanical insult at the ONH. A recent in vivo morphological study of the ONH using spectral-domain optical coherence tomography showed more prevalent optic disc tilt, i.e., the peripapillary sclera bending, correlated with the location of visual field defects in a group of patients that suffered from optic nerve damage with normal IOP, known as “normal tension” glaucoma [36]. These patients also showed greater ONH torsion, i.e., a larger skew of the long axis of the ONH disk with respect to the vertical meridian of the eye [36]. These morphological findings, combined with the findings in the present study that the peripapillary sclera region predominantly experiences shear deformation during IOP elevations, suggest a potential involvement of shear in the pathophysiology of normal tension glaucoma. It will be interesting for future studies to compare the 3D deformation characteristics, especially shear, in normal tension glaucoma eyes with normal eyes.

The first and third principal strains, as well as the maximum shear, all displayed a significant level of heterogeneity in most tested eyes (Figs. 6 and 8). Local high strains caused a large variance through the depth of the tissue. These localized high strains were unlikely caused by measurement noise because the 3D method has high accuracy for strains in these ranges (i.e., a few percent). These strain heterogeneities are likely an outcome of the structural heterogeneities in this region of the sclera. As described earlier, many short posterior ciliary arteries and nerves traverse this region, creating structural and material variations in the otherwise collagenous sclera. For example, the arterial circle of Zinn-Haller of about 40–80 μm in diameter is found embedded in the human peripapillary sclera [37], surrounding the ONH and providing the main blood supply to the anterior LC [18]. As shown in Fig. 7, the specimen with a circular high-strain area in the peripapillary sclera showed the presence of the arterial circle of Zinn-Haller at approximately the same location in histology. The increased strains during IOP elevation may represent compression and distortion of these vessels, contributing to glaucoma progression through both the biomechanical and vascular pathways. Future microstructural analyses in a larger number of specimens are needed to confirm the structural correspondence of the heterogeneous strain patterns and their in vivo relevance. These internal high strain regions also contribute to the larger average meridional strains (first principal) we found in the peripapillary sclera compared to the surface strains reported earlier [9,10].

Age has been identified as a factor associated with scleral stiffening [10,26,38] due to increased nonenzymatic collagen cross-linking. We did not find a significant trend with age in the average principal strains in the limited number of specimens tested in this study, but the presence of the high strain areas seemed to have a significant influence on the average response. For example, the eye that exhibited largest average strains (from a 71-year-old donor, Figs. 4(a) and 4(c)) showed a large area of high strains in the strain maps (Fig. 8), possibility due to a large portion of the scanned volume occupied by vessels or other structural heterogeneities in this eye. The youngest eye (24-year-old donor) also had a fairy large strain response as compared to most of the older eyes (Figs. 4(a) and 4(c)). Future studies in a larger sample size are needed to evaluate age-associated changes in both structure and mechanical responses.

By mapping the volume ratios (i.e., the ratio of deformed volume over original volume), this study is also one of the first to experimentally characterize the compressibility of the sclera. Incompressibility (i.e., no volume change) during deformation has often been assumed in computational models but direct measurement data is scarce. Judging from the measured volume ratios in the present study, the values were near unity, supporting the overall near-incompressibility assumption. In most eyes, the average volume ratio values were slightly less than 1, suggesting an overall small volume loss during inflation, likely due to initial postmortem swelling of the sclera. Evaluating the distributive volume ratios over the scanned volume, some fluctuations of values between higher and lower than unity were observed, suggesting local volume change although the range of variance was still small (e.g., 0.95–1.05 in the eye that had the largest range of volume ratios). This result supports the validity of the incompressibility assumption for modeling the peripapillary sclera.

The current study has several limitations. First, the outer region near the edge of the scanned volume was often slightly outside the transducer focal zone and therefore the spatial resolution was poorer for these regions. Although this is unavoidable due to the curved shape of the sclera, the peripapillary sclera region, which was the focus of the present study, was largely within the transducer focal zone during the 3D scans. Second, imperfect ultrasound probe placement with respect to the ONH during the scans sometimes led to differences in volume size for the nasal and temporal halves. In addition, slight rotation of the probe with respect to the mounted eye may introduce some variance in the reference coordinates for calculating the Green strain tensor. This highlights the advantage of using principal strains, which are independent of the coordinate system, especially in future studies comparing the responses from different groups of eyes (e.g., glaucomatous versus normal). Third, the equilibration time between pressure steps might not be sufficient and tissue creep could have influenced the measured strains. A 15-min equilibration time was typically used in previous studies for tissue recovery between inflation cycles [9,10]. Because the current study used a much smaller pressure step (only a few mmHg), we chose a shorter equilibration time in order to complete all measurements in one eye in about 5 hrs. Future studies are needed to verify tissue equilibrium and measurement repeatability, and investigate the effect of creep. Fourth, the orientation of the principal vectors and the maximum shear was qualitatively evaluated in the present study based on the vector plots. Future work will develop a coordinate transform algorithm to quantify the circumferential, meridional, and through-thickness strains.

In summary, this study reported 3D strains in the peripapillary sclera of nine human donor eyes inflated from 10 to 19 mmHg. Our results showed that the peripapillary sclera experienced through-thickness compression, meridional stretch, and minimal circumferential deformation, under this pressure increase. Significant shear was present, and there was little overall volume change during deformation, confirming near-incompressibility. Substantial strain heterogeneity was found in this region, likely due to its microstructural heterogeneities. Future studies with more quantitative analysis in a larger sample size are needed to confirm these initial findings. The peripapillary sclera's ability to handle IOP-related deformation may have important implications in the ONH's homeostasis and stability, and weaknesses in handling compression, tension, and/or shear may all contribute to optic nerve damage and glaucomatous susceptibility.