Population Coding by Electrosensory Neurons

Abstract

Sensory stimuli typically activate many receptors at once and therefore should lead to increases in correlated activity among central neurons. Such correlated activity could be a critical feature in the encoding and decoding of information in central circuits. Here we characterize correlated activity in response to two biologically relevant classes of sensory stimuli in the primary electrosensory nuclei, the electrosensory lateral line lobe, of the weakly electric fish Apteronotus leptorhynchus. Our results show that these neurons can display significant correlations in their baseline activities that depend on the amount of receptive field overlap. A detailed analysis of spike trains revealed that correlated activity resulted predominantly from a tendency to fire synchronous or anti-synchronous bursts of spikes. We also explored how different stimulation protocols affected correlated activity: while prey-like stimuli increased correlated activity, conspecific-like stimuli decreased correlated activity. We also computed the correlations between the variabilities of each neuron to repeated presentations of the same stimulus (noise correlations) and found lower amounts of noise correlation for communication stimuli. Therefore the decrease in correlated activity seen with communication stimuli is caused at least in part by reduced noise correlations. This differential modulation in correlated activity occurred because of changes in burst firing at the individual neuron level. Our results show that different categories of behaviorally relevant input will differentially affect correlated activity. In particular, we show that the number of correlated bursts within a given time window could be used by postsynaptic neurons to distinguish between both stimulus categories.

INTRODUCTION

Behaviorally relevant stimuli are encoded by changes in firing rates of neurons across regions of relevant sensoria. As a result, sensory stimuli should also produce changes in the rate of correlated activity among neurons. Correlated activity could be a critical mechanism used in the discrimination of different categories of sensory stimuli. In particular, theoretical studies have shown that correlations between the activities of neighboring neurons can have significant effects on information coding (Johnson 1980; Schneidman et al. 2003, 2006; Snippe 1992; Sompolinsky et al. 2001). However, there is much debate as to the role of correlated activity in neural coding as this will depend in general on how information from a neural population is decoded by higher centers (Averbeck and Lee 2006; Latham and Nirenberg 2005; Nirenberg and Latham 2003). Studies on systems with well-characterized anatomy, easily described natural stimuli, and known decoding mechanisms are thus likely to advance our knowledge as to how action potential patterns from neural populations code for natural stimuli.

Gymnotiform weakly electric fish use perturbations of a self-generated electric field, the electric organ discharge (EOD), to interact with their environment (Turner et al. 1999). Epidermal electroreceptors and associated afferent neurons encode amplitude modulations of their EOD as changes in firing rate (Bastian 1981a; Scheich 1973; Turner et al. 1999) and relay this information to pyramidal cells within the electrosensory lateral line lobe (ELL) (Fortune 2006; Sawtell et al. 2005; Turner et al. 1999; Zakon 2003). There are two pyramidal cell types: E-cells are excited by increased EOD amplitude, while I-cells are inhibited (Saunders and Bastian 1984). These cells have been well characterized both in vitro (Berman and Maler 1998; Turner et al. 1994) and in vivo (Bastian 1981b; Bastian and Nguyenkim 2001; Saunders and Bastian 1984). Natural electrosensory stimuli consist of EOD modulations caused by prey and those caused by conspecifics. While prey stimuli are spatially localized and contain low temporal frequencies (Nelson and MacIver 1999), communication stimuli are spatially diffuse and can contain a wide range of temporal frequencies (Heiligenberg 1991; Zupanc and Maler 1993). Previous studies have shown that single pyramidal cells will respond differentially to stimuli with differing spatial extents (Chacron 2006; Chacron et al. 2003, 2005a; Doiron et al. 2003).

Pyramidal cells also have properties that promote the firing of high-frequency packets of action potentials (bursts) both in vitro (Fernandez et al. 2005; Lemon and Turner 2000; Oswald et al. 2004; Turner et al. 1994) and in vivo (Bastian and Nguyenkim 2001; Gabbiani et al. 1996; Metzner et al. 1998; Oswald et al. 2004). Pyramidal cell bursts have been linked to the processing of prey-like stimulus patterns (Oswald et al. 2004) and feedback pathways have also been implicated in the control of bursts as well as oscillatory spike train dynamics (Bastian and Nguyenkim 2001; Doiron et al. 2003).

Here we characterized correlated activity in pyramidal cell pairs under baseline (i.e., unperturbed EOD), prey-like, and conspecific-like stimulation. The paper is organized as follows. We first quantify correlated activity under baseline conditions. We then show how prey and conspecific-like stimuli alter this correlated activity. These changes are shown to be due to changes in the burst firing of each cell. Finally, we show that the number of synchronous bursts in a given time window could be used by downstream neurons to distinguish between both stimulus categories.

METHODS

Experimental preparation

The weakly electric fish Apteronotus Leptorhynchus was used exclusively in this study. Fish were housed in groups of 3–10 in 150-l tanks, water temperature was maintained between 26 and 28°C, and water resistivity varied between 2,000 and 5,000 Ω·cm. Experiments were performed in a 39 × 44 × 12-cm-deep Plexiglass aquarium with water recirculated from the animal’s own tank. Animals were artificially respirated with a continuous water flow of 10 ml/min. Surgical techniques were the same as those described previously (Bastian 1996a,b), and all procedures were in accordance with animal care and use guidelines of the University of Oklahoma.

Recording

Extracellular dual or triple recordings from pyramidal cells were made with two or three metal-filled micropipettes (Frank and Becker 1964). Recording sites as determined from surface landmarks and recording depth were limited to the centrolateral and lateral segments of the ELL only. We note that a previous study focusing exclusively in the centromedial segment found that pyramidal cell correlations were exclusively stimulus driven (Krahe et al. 2002). However, anatomical results suggest that receptive field overlap is smallest in the centromedial segment and greatest in the centrolateral and lateral segments (L. Maler, personal communication). Therefore it was expected that the level of correlated activity in the absence of stimulation was the greatest in the centrolateral and lateral segments. Extracellularly signals were digitized at 10 kHz using a CED 1401 amplifier with Spike2 software (Cambridge Electronic Design, Cambridge, UK). Spikes were detected with custom-written software in Matlab (Mathworks, Natick, MA).

We used the following technique to record from pyramidal cell pairs that displayed correlated activity. First, one recording electrode was advanced into the brain and a stable single-unit recording was established. We positioned a local dipole in the center of this cell’s receptive field and gave a 4-Hz sinusoidal AM (SAM; see following text). We then advanced a second electrode until we could hear background multi-unit activity driven by the SAM. A second single-unit recording was then established within this region, and, typically, cell pairs recorded using this technique displayed correlated activity under baseline conditions (i.e., in the absence of EOD AMs). On the other hand, activities of cells encountered outside the region within which we could hear the modulation of multi-unit activity were usually not correlated with the activity from the first recording under baseline conditions. Signals from each recording electrode were amplified via separate differential preamplifiers (WPI DAM50) and by careful adjustment of a common indifferent electrode the artifact due to the ongoing EOD was largely eliminated (see original records of Fig. 2A). Each unit was used in at most three pairs.

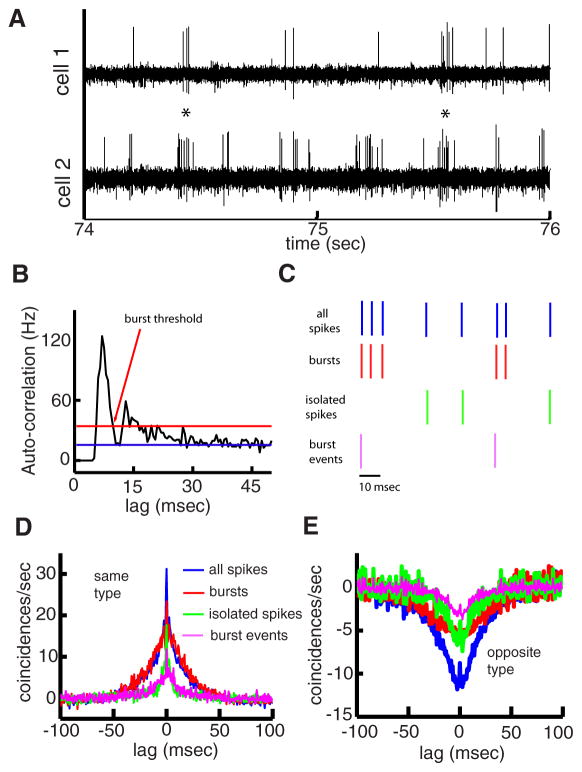
FIG. 2.

Pyramidal cell activity consists of correlated bursts. A: extracellular recording from a pair of I-type pyramidal cells. B: auto-correlogram of an example cell with expected value from a Poisson process (blue) and 99.9% confidence interval (red). The burst threshold value is indicated by the arrow. C: illustration of the procedure used to separate the spike train (blue) into bursts (red), isolated spikes (green), and burst events (purple) using the interspike interval (ISI) threshold determined. If n consecutive ISIs are all smaller than the burst threshold, then all associated spikes are considered to be part of the burst. The remaining spikes are considered isolated spikes. Burst events are obtained by taking only the 1st spike of each burst. D: population-averaged (n = 75) CCGs obtained from the full spike trains (blue), burst spike trains (red), isolated spike trains (green), and burst event spike trains (purple) for same-type pyramidal cell pairs (EE and II). E: population-averaged (n = 45) CCGs obtained from the raw spike trains (blue), burst spike trains (red), isolated spike trains (green), and burst event spike trains (purple) for opposite-type (EI) pyramidal cell pairs.

Stimulation

The electric organ of Apteronotus consists of modified motoneurons. Consequently, the EOD remains intact after neuromuscular blockade, and all experiments were performed by modulating the animal’s natural EOD. Baseline conditions thus refer to conditions under which the animal’s natural EOD is unmodulated. The stimulation protocol was described previously in detail (Bastian et al. 2002). Stimuli consisted of random amplitude modulations of animal’s own EOD and were obtained by multiplying a Gaussian band limited (0–120 Hz, 8th-order Butterworth filtered) white noise with an EOD mimic. The EOD mimic consisted of a train of single sinusoids with frequency slightly higher than that of the EOD and phase locked to the zero-crossings of the animal’s own EOD. The resulting signal (0 mean amplitude) was then added to the animal’s EOD with either local or global geometry that mimic prey and conspecific-related stimuli, respectively. With global geometry, the stimulus was presented via two silver-silver-chloride electrodes located 19 cm on each side of the animal (Fig. 2A). Note that, for this geometry, the ipsi- and contralateral sides of the animal experience instantaneous amplitude modulations of opposite sign but of identical spectral content. However, the change in EOD amplitude on each side is approximately spatially homogeneous (Bastian et al. 2002). With local geometry, the stimulus was presented via a dipole (2-mm tip spacing) 2–3 mm lateral to the animal and positioned within the receptive field center overlap of each pyramidal cell pair. Local and global stimulus intensities were essentially the same as those used previously (Bastian et al. 2002; Chacron 2006; Chacron et al. 2005a) and typical contrasts used ranged between 5 and 20%. Each noise sample lasting 20 s was presented five times to obtain sufficient data. It should be noted that male fish routinely gave behavioral responses (chirps) when the noise stimulus was presented with global geometry as previously described (Doiron et al. 2003).

Pharmacology

To block feedback signals from higher-order electrosensory nuclei, micropressure ejection techniques were used to focally apply the glutamate antagonist 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX) within the ELL molecular layer containing the apical dendritic trees of each cell within a given pair (Bastian 1993; Bastian and Nguyenkim 2001; Bastian et al. 2004; Chacron 2006; Chacron et al. 2005a). Multibarrel pipettes were pulled to a fine tip and subsequently broken to a total tip diameter of 10 μm. One barrel was filled with a 1 mM solution of CNQX, while the other was filled with a 1 mM glutamate solution. After recording from a well-isolated pyramidal cell pair, the pressure pipette was slowly advanced into an appropriate region of the ELL molecular layer while periodically ejecting “puffs” of glutamate (duration = 100 ms, pressure = 40 psi). As described previously, proximity to a recorded cell will result in short-latency excitation of that cell. After correct placement, CNQX was delivered as a single dose or as a series of 10 pulses (duration = 100 ms, pressure = 40 psi). This treatment typically resulted in altered pyramidal cell activity lasting about 5 min. Note that previous studies have shown that the diffusion is contained within the molecular layer and thus does not reach the basilar dendrites of E-type pyramidal cells (Bastian 1993).

Data analysis

All analyses were performed in Matlab (Mathworks, Natick, MA). There are two types of pyramidal cells: E-cells respond to increases in EOD amplitude, while I-cells respond to decreases in EOD amplitude (Saunders and Bastian 1984), and we recorded from EE, II, and EI pairs. From the spike time sequence we created a binary sequence X(t) with binwidth dt = 0.5 ms and set the content of each bin to equal the number of spikes the time of which fell within that bin. We then computed the autocorrelogram of each cell as $A(\tau )={\sum }_{i=1}^{N_1}{X}_1(t)X_1(t+\tau )/(\mathrm{d}tT{f}_1)$. T and f₁ are the recording time and cell’s firing rate, respectively. The cross-correlogram (CCG) between two cells was computed as $C(\tau )={\sum }_{i=1}^{N_1}{X}_1(t)X_2(t+\tau )/(\mathrm{d}tT{f}_1)-f_2$ and is expressed in coincidence/s, where f₁, f₂ are the firing rates of cells 1 and 2, respectively. Here X_a(t) and f_a are the binary sequence obtained from the spike train and the firing rate of cell a, respectively.

Note that the sum is performed over the spikes of cell 1. We note that the labeling of cells within the pair is completely arbitrary and that we could just as easily compute the CCG by averaging over the spikes of cell 2. The particular cell used for averaging does not matter for our data as the CCGs were symmetric with respect to lag 0. The cross-correlation coefficient was computed for each cell pair as described by (Shadlen and Newsome 1998)

$$R=\frac{{\langle C(\tau )\rangle }_{\tau }}{{\langle A_1(\tau )-f_1\rangle }_{\tau }^{\frac{1}{2}}{\langle A_2(\tau )-f_2\rangle }_{\tau }^{\frac{1}{2}}}$$

Where 〈…〉τ denotes averaging over τ. Note that R ranges between −1 and 1. We also computed the cross-spectrum between both activities as P(f) = 〈Ŷ₁(f) Ŷ₂(f)〉, where Ŷ_1.2(f) are the fourier transforms of X_1,2(t) (Chacron et al. 2005b).

Many studies have highlighted the need to distinguish between correlations that are solely attributable to the stimulus (signal correlations) and correlation that are not (noise correlations) (Gawne and Richmond 1993; Palm et al. 1988; Perkel et al. 1967; Schneidman et al. 2003). A standard technique to separate these correlations consists of computing the CCG from cell activities obtained during the same stimulus trial and the CCG from cell activities obtained during different, or shifted, stimulus trials. As such, for local and global stimulation, we computed the raw CCG between cells 1 and 2 for each pair as

$$C_{\text{row}}(\tau )=\frac{1}{5}\sum _{i=1}^5\sum _{j=1}^{N_1}[X_{1,i}(t)X_{2,i}(t+\tau )]/(\mathrm{d}t{T}_i{f}_{1,i})-f_{2,i}$$

where X_a,i is the binary sequence of cell a during stimulus trial i, f_a,i[r] is the firing rate of cell a during stimulus trial i, and T_i is the duration of stimulus trial i. The shift predictor is a measure of signal correlations and was computed as (Palm et al. 1988; Perkel et al. 1967)

$$C_{\text{signal}}(\tau )=\frac{1}{10}\sum _{i=1}^5\sum _{j<1}\sum _{k=1}^{N_1}[X_{1,i}(t)X_{2,j}(t+\tau )]/(\mathrm{d}t{T}_i{f}_{1,i})-f_{2,j}$$

The noise CCG was then obtained by subtracting the shift predictor from the raw CCG: C_noise(τ) = C_raw(τ) − C_signal(τ). As such, the noise CCG measures the correlation between the variability in each neuron’s response to repeated presentations of the same stimulus (Gawne and Richmond 1993).

We defined spike bursts as sequences of action potentials separated by a minimum (threshold) interspike interval (ISI). The burst threshold for each cell was obtained in the following manner. We computed the autocorrelogram A(τ) as described previously. The expected bin content for a Poisson process whose firing is equal to that of the cell studied was computed as y = fT, where f is the cell’s mean firing rate and T is the recording time. We then computed the 99.9% confidence interval on the expected Poisson bin count as the smallest m satisfying (Abeles 1982)

$$\sum _{i=0}^m\frac{e^{-y}{y}^m}{m!}>0.999$$

The burst threshold was then taken as the smallest value of lag τ for which A(τ) crossed m/(dtTf) from above (Fig. 2, B and C). The burst threshold for each cell was computed from that cell’s activity in the absence of stimulation (i.e., no amplitude modulations but normal EOD present). We then used the burst threshold as an ISI threshold value for classifying spikes as either being part of a burst or not (Chacron et al. 2004; Gabbiani et al. 1996; Metzner et al. 1998; Oswald et al. 2004). If n consecutive ISIs were smaller than the threshold value, then the n + 1 spikes associated with these ISIs were considered to be part of the same burst. Spikes that were not part of a burst were considered isolated. We also looked at burst events by taking only the first spike of each burst. Bursts typically consisted of two to five spikes as observed before (Bastian and Nguyenkim 2001; Gabbiani et al. 1996; Oswald et al. 2004). As such, we decomposed each binary sequence X(t) into its burst X_burst(t), isolated X_isolated(t), and burst event X_events(t), components and computed CCGs as described in the preceding text. We used the same burst threshold to separate spike trains obtained under local and global stimulation into their burst spike, burst event, and isolated spike components. The burst fraction for each individual cell was computed as the number of spikes belonging to bursts divided by the total number of spikes. For each cell pair consisting of cells 1 and 2, we computed the pair-averaged burst fraction as BF = BF₁/2 + BF₂/2 where BF_a is the individual burst fraction of cell a. We also computed the burst event fraction as the number of burst events divided by the total number of events (burst events + isolated spikes). For each cell pair consisting of cells 1 and 2, we computed the pair-averaged burst event fraction as BEF = BEF₁/2 + BEF₂/2 where BEF_a is the individual burst event fraction of cell a.

We computed the number of coincident events during a time window W by integrating the CCG between −W/2 and W/2 for each pair. We then used signal detection theory (Green and Swets 1966) to quantify the ability of an ideal observer to distinguish between synchronous events under prey and conspecific stimulation. In particular, we computed the discriminability d′

$${\mathrm{d}}^{\prime }=\frac{\mid {\mu }_{\text{prey}}-{\mu }_{\text{conspecific}}\mid }{\sqrt{\left(\frac{{\sigma }_{\text{prey}}^2+{\sigma }_{\text{conspecific}}^2}{2}\right)}}$$

where μ_prey, μ_conspecific are the pair averaged numbers of synchronous events for prey-like stimulation and conspecific-like stimulation, respectively. σ_prey, σ_conspecific are the SDs for prey-like and conspecific-like stimulation, respectively.

RESULTS

Pyramidal cells display correlated activity in the absence of stimulation

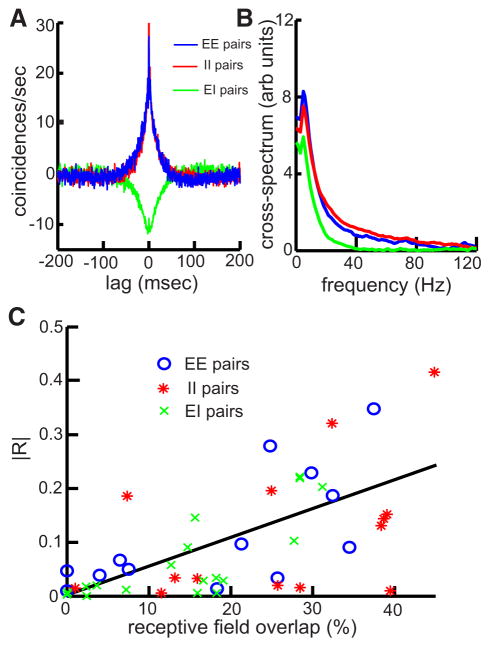
We recorded from neighboring ELL pyramidal cells in vivo and often found correlated activity in the absence of stimulation (Fig. 1). We quantified these baseline correlations using the CCG and found positive correlations for same-type pairs (i.e., pairs for which both cells are E-type, EE, or pairs for which both cells are I-type, II; Fig. 1A). In contrast, we found negative correlations for opposite-type pairs (i.e., pairs for which one cell is E-type and the other is I-type; Fig. 1A). The CCGs obtained were symmetric, broad in nature, and were quantified using the cross-correlation co-efficient R (Shadlen and Newsome 1998), which ranges between −1 and 1. We obtained R_EE = 0.32 ± 0.17 (n = 34), R_II = 0.33 ± 0.18 (n = 41), and R_EI = −0.30 ± 0.17 (n = 45). As no significant difference was seen between EE and II pairs (P = 0.92, t-test, df = 74), we grouped them into one category (same-type pairs) for the remainder of the study. Finally, the magnitude of R was not significantly different between all pair types (1-way ANOVA, F = 0.21, df = 119, P = 0.81). We also quantified correlated activity in the frequency domain using the cross-spectrum, the Fourier transform of the CCG (see METHODS). Population-averaged cross-spectra were qualitatively similar for all pair types (Fig. 1B) and contained power predominantly at low frequencies (<20 Hz) reflecting the broad CCGs. We note that as these correlations were observed in the absence of stimulation, they are not to be considered as noise correlations (see following text).

FIG. 1.

Pyramidal cells display correlated activity in the absence of stimulation. A: population-averaged cross-correlograms (CCGs) obtained for EE (blue, n = 34), II (red, n = 41), and EI (green, n = 45) pyramidal cell pairs. B: population-averaged cross-spectra obtained for EE (blue, n = 34), II (red, n = 41), and EI (green, n = 45) pyramidal cell pairs. C: cross-correlation coefficient R as a function of receptive field overlap for EE (black), II (red), and EI (green) pyramidal cell pairs. There was a significant relationship between R and the amount of receptive field overlap (r = 0.68, P < 10⁻³, n = 38).

As commonly observed in many sensory systems, ELL pyramidal cells have antagonistic center-surround receptive field organization (Bastian et al. 2002; Shumway 1989). We mapped pyramidal cell receptive fields as done previously (Bastian et al. 2002) and quantified the amount of receptive field center overlap. As in other systems (Mastronarde 1983; Meister et al. 1995), there was a significant linear relationship between the amount of correlated activity and receptive field overlap (Fig. 1C, r = 0.68, P < 10⁻³). Typically, cell pairs showing less than ~20% overlap in receptive field area showed negligible correlated activity. Our results also showed that the receptive fields from these cell pairs were located >15 mm apart. Anatomical studies show that neighboring pyramidal cells share receptor afferent input (L. Maler, personal communication), and this common input is a likely cause for the observed correlation under baseline conditions.

Correlated activity consists of synchronous or anti-synchronous bursts

Inspection of the raw data revealed that pyramidal cell tended to fire packets of action potentials (bursts) in synchrony for same-type pairs (Fig. 2A, asterisks) and anti-synchrony for opposite-type pairs. It thus seemed that burst firing played a role in correlated activity. We isolated the spikes that are part of a burst (burst spikes) from spikes that are not (isolated spikes) in each spike train using an ISI criterion (Bastian and Nguyenkim 2001; Chacron et al. 2004; DeBusk et al. 1997; Gabbiani et al. 1996; Metzner et al. 1998; Oswald et al. 2004; Reinagel et al. 1999). We computed the autocorrelogram of each cell’s spike train (Fig. 2, B and C), and the threshold ISI was chosen as the value of lag at which the autocorrelogram crossed the 99.999% Poisson confidence interval from above for the first time (Fig. 2B). Each spike train was separated into bursts, isolated spikes, and burst events (i.e., only the 1st spike of each burst was kept; Fig. 2C) using the threshold ISI, and we computed the CCG between the bursts, isolated spikes, and burst event trains obtained from each cell pair. Our results show that the CCG computed from the burst train resembled the one obtained from all spikes for same-type pairs (Fig. 2D, compare blue and red). However, the CCG obtained from isolated spikes was narrower (Fig. 2D green). Finally, the CCG obtained from burst events resembled the one obtained from isolated spikes (Fig. 2D, compare green and purple). These results suggest that the broad nature of the CCG results from the presence of bursts in each spike train. Similar results were seen for opposite-type pairs (Fig. 2E).

Prey and conspecific stimuli have opposite effects on correlated activity

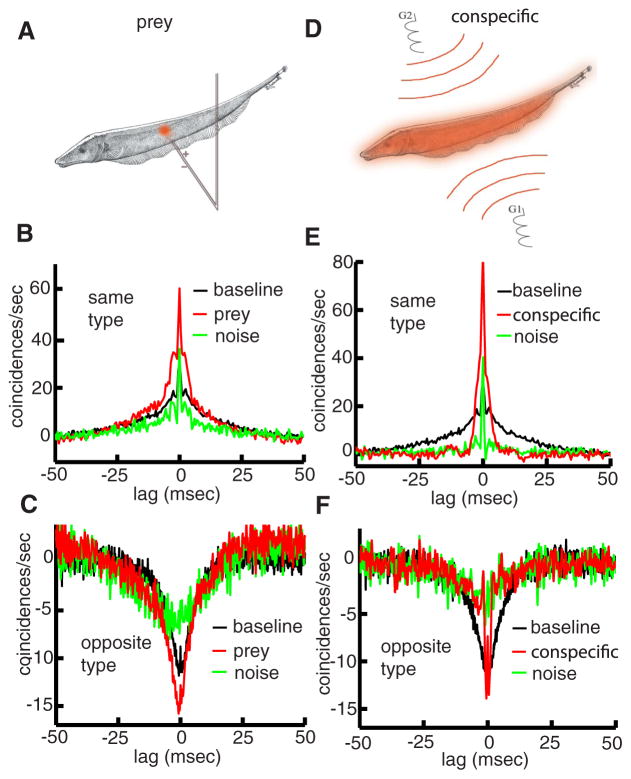
We mimicked prey stimuli by applying AMs of the EOD through a local dipole (Fig. 3A). In general, prey-like stimuli increased correlated activity in pyramidal cells pairs of same type (Fig. 3B, compare black and red) and opposite type (Fig. 3C, compare black and red) with respect to baseline conditions. Changes in CCGs were quantified by computing changes in the absolute cross-correlation coefficient |R| and data from same-and opposite-type pairs were pooled. On average, prey-like stimulation increased |R| by 42.57% relative to baseline conditions (P < 10⁻³, pairwise t-test, n = 38).

FIG. 3.

Stimulus-modulated correlations in pyramidal cells. A: illustration of local prey-like stimulation. In this geometry, the stimulus was delivered using a dipole positioned within the receptive field center overlap of the cell pair studied. B: population-averaged (n = 25) CCGs under prey-like stimulation (red), no stimulation (black) for same-type pyramidal cell pairs. The noise CCG is also shown (green). C: population-averaged (n = 13) CCGs under conspecific-like stimulation (red), no stimulation (black) for opposite-type pyramidal cell pairs. The noise CCG is also shown (green). Note that the CCGs were low-pass filtered (cutoff frequency: 200 Hz, 8th-order Butter-worth filter) for illustration purposes. D: illustration of global conspecific-like stimulation. In this geometry, the stimulus was delivered between electrodes G1 and G2. E: population-averaged (n = 25) CCGs under conspecific-like stimulation (red), no stimulation (black) for same-type pyramidal cell pairs. The noise CCG is also shown (green). F: population-averaged (n = 13) CCGs under conspecific-like stimulation (red), no stimulation (black) for opposite-type pyramidal cell pairs. The noise CCG is also shown (green).

We mimicked conspecific-related stimuli by applying AMs via two electrodes lateral to the animal thereby globally stimulating the skin surface (Fig. 3D). Despite the fact that this geometry provides similar stimuli to both cells’ entire receptive fields, we saw a net decrease in correlated activity. The CCG obtained under conspecific-like stimuli was narrower than the one obtained under baseline conditions for both same-type (Fig. 3E, compare black and red) and opposite-type (Fig. 3F, compare black and red) pairs. Despite the fact that conspecific-like stimulation could increase the occurrence of near-synchronous spikes (0 lag), we found that this stimulation geometry reduced |R| by 24.85% (P < 10⁻³, pairwise t-test, n = 38) with respect to baseline activity. Moreover, correlated activity as measured by |R| was significantly higher under prey-like stimulation than conspecific-like stimulation (P < 10⁻³, pairwise t-test, n = 38; Fig. 4A).

FIG. 4.

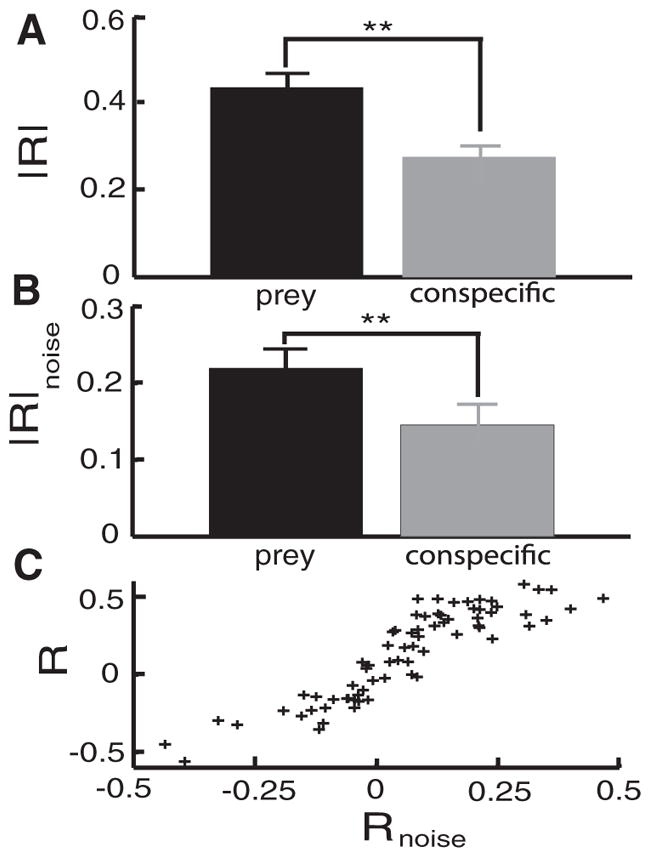
Pyramidal cells activity is more correlated under prey-like stimulation than conspecific-like stimulation. A: population-averaged absolute cross-correlation coefficient |R| for prey-like and conspecific-like stimulation. B: population-averaged absolute cross-correlation coefficient |R|_noise for prey-like and conspecific-like stimulation. C: R vs. R_noise from all pairs under prey and conspecific-like stimulation. The strong and significant linear relationship between both quantities (r = 0.9, P ≪ 10⁻³, n = 114) indicates that changes in correlated activity are at least in part due to changes in noise correlations. **, statistical significance using a pairwise t-test at the P = 0.01 level and with n = 38.

To understand how prey and conspecific stimuli could have opposite effects on correlated activity in pyramidal cells, we decomposed the CCG into two components: the one that is solely attributable to the fact that both neurons are receiving the same stimulus (signal correlations) and the component not attributable to stimulation (noise correlations) (Gawne and Richmond 1993; Schneidman et al. 2003). Noise correlations reflect correlations between the variabilities of each neuron’s response to repeated presentations of the same stimulus (Gawne and Richmond 1993; Palm et al. 1988; Perkel et al. 1967). Our results show that the noise CCG under prey-like stimulation was similar in shape to the CCG obtained under baseline conditions (Fig. 3, B and C, compare black and green). As such, we conclude that the increased correlated activity seen under prey-like stimulation results mainly from increased signal correlations (i.e., from the fact that both neurons receive the same stimulus). In contrast, we found that the noise CCG was small under conspecific-like stimuli (Fig. 3, E and F, green). We quantified changes in the noise CCG by computing the cross-correlation coefficient R_noise and found that R_noise was greater under prey-like stimulation than conspecific-like stimulation (P < 10⁻³, pairwise t-test, n = 38; Fig. 4B). Furthermore, we observed a strong relationship between the measures R and R_noise when data were pooled from all pairs with prey- and communication-like stimulation (Fig. 4C). We conclude that the reduced correlated activity seen under conspecific-like stimulation is due in part to reduced noise correlations. Finally, we note that the differential effects of prey- and conspecific-like stimulation on correlated activity are not due to changes in pyramidal cell firing rate (f_prey = 18.14 ± 8.22 Hz, f_conspecific = 18.75 ± 8.24 Hz, P = 0.21, pairwise t-test, n = 76).

Altered correlated activity results from altered burst firing

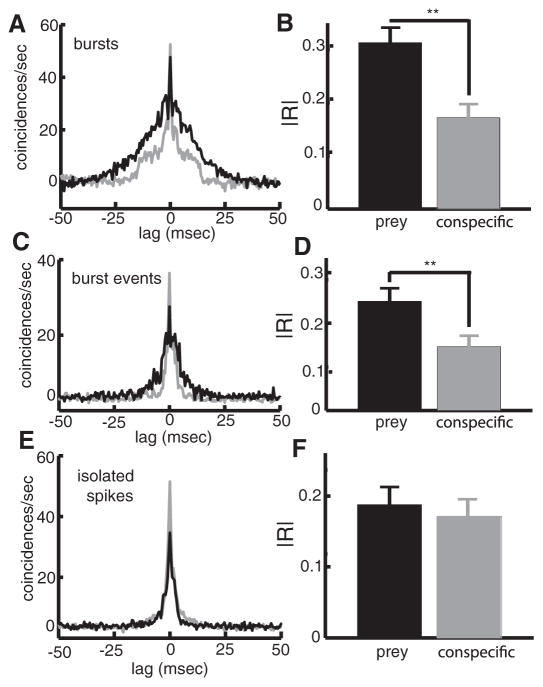
We analyzed the detailed structure of correlated activity during prey- and conspecific-like stimulation by separating the spike trains into their burst and isolated spikes components. For bursts, the CCGs obtained under conspecific-like stimulation were on average narrower than those obtained under prey-like stimulation (Fig. 5A). This was reflected in the fact that |R| values obtained from the burst CCGs were significantly larger under prey-like stimuli (Fig. 5B, P < 10⁻³, pairwise t-test, n = 38). To verify that these changes were not simply due to increases in the number of spikes within the bursts during prey-like stimulation, we computed the CCGs from burst events (i.e., only the 1st spike within each burst). The CCG from burst events under prey-like stimulation were also broader than the ones obtained during conspecific-like stimulation (Fig. 5C). |R| values obtained from these CCGs were also, on average, significantly greater under prey-like stimulation compared with conspecific-like stimulation (Fig. 5D, , P < 10⁻³, pairwise t-test, n = 38). Finally, we computed CCGs from isolated spikes, and our results show that they have qualitatively similar shapes under prey- and conspecific-like stimulation (Fig. 5E), and |R| values obtained from these CCGs were not significantly different (Fig. 5F, , P = 0.1, pairwise t-test, n = 38).

FIG. 5.

Changes in burst dynamics underlie the changes in correlated activity seen under prey-like and conspecific-like stimulation. A: population-averaged CCGs obtained from burst spikes under prey-like and conspecific-like (stimulation; note that the CCGs from EI pairs were inverted when computing the population average). B: population-averaged absolute cross-correlation coefficient |R| for burst spikes under prey-like and conspecific-like stimulation were significantly different. C: population-averaged CCGs obtained from burst events (i.e., only the 1st spike of a burst) under prey-like and conspecific-like (stimulation; note that the CCGs from EI pairs were inverted when computing the population average). D: population-averaged absolute cross-correlation coefficient |R| for burst events under prey-like and conspecific-like stimulation were significantly different. E: population averaged CCGs obtained from isolated spikes under prey-like (blue) and conspecific-like (stimulation). F: population-averaged absolute cross-correlation co-efficient |R| for isolated spikes under prey-like and conspecific-like stimulation were not significantly different. **, statistical significance using a paiwise t-test at the P = 0.01 level with n = 38.

We also computed the average number of spikes within a burst (see METHODS) and obtained 2.81 ± 0.63 for local stimulation and 2.31 ± 0.36 for global stimulation. Although the difference was statistically significant (P < 10⁻³, pairwise t-test, n = 76), it consisted of less than one extra spike per burst. Although small, this difference in the average number of spikes per burst is nevertheless expected to contribute to the change seen in correlation structure contingent on prey versus conspecific-like stimulation. We conclude from these results that changes in pyramidal cell burst firing are responsible for the changes in correlated activity.

Pyramidal cell’s burst firing is antagonized by conspecific-like stimulation and promoted by prey-like stimulation

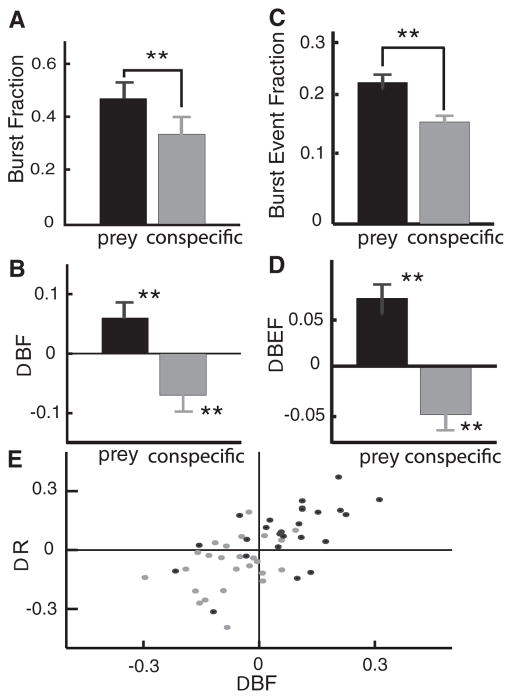
We quantified the tendency of individual pyramidal cells to burst by computing the burst fraction (i.e., the fraction of ISIs that are smaller than the burst threshold). Our results show that pyramidal cells had burst fractions that were significantly greater under prey-like stimulation as compared with conspecific-like stimulation (Fig. 6A). Furthermore, a comparison with the burst fractions obtained in the absence of stimulation revealed increased bursting under prey-like stimulation and reduced bursting under conspecific-like stimulation (Fig. 6B), which is consistent with increased correlation under the former and decreased correlation under the latter (Fig. 3). We also computed the burst event fraction, BEF, where bursts were treated as unitary events (see METHODS). We obtained similar results for the burst event fraction which was also significantly greater under prey-like stimulation than conspecific-like stimulation (Fig. 6C). Furthermore, the burst event fraction also increased for prey-like stimulation and decreased for conspecific-like stimulation with respect to levels observed under baseline activity (Fig. 6D).

FIG. 6.

Changes in burst firing underlie changes in correlated activity. A: population-averaged (n = 38) burst fractions BF under prey-like and conspecific-like stimulation. B: population-averaged (n = 38) burst event fractions BEF under prey-like (blue) and conspecific-like stimulation. C: changes in burst fraction from baseline levels (black, prey-like-baseline; gray, conspecific-like-baseline) were statistically significant. D: changes in burst event fraction from baseline levels (black, prey-like-baseline; gray, conspecific-like-baseline) were also statistically significant. E: changes in R vs. changes in BF for prey-like-baseline (black) and conspecific-like-baseline (gray). There was a strong and significant linear relationship between both quantities. Statistical significance (asterisks) was ascertained using a pairwise t-test at the P = 0.01 level with n = 38.

The influence of bursting on correlated activity was further supported by a significant linear relationship between the change in the cross-correlation coefficient R and the change in the burst fraction BF (Fig. 6C; R = 0.56, P < 10⁻³, n = 50). There was also a significant linear relationship between the change in the cross-correlation coefficient R and the change in the burst event fraction (data not shown, R = 0.34, P = 0.004, n = 50). These results demonstrate a clear and strong link between correlated activity and burst firing in pyramidal cells. Moreover, since both the burst fraction and burst event fractions displayed similar behavior, changes in correlated activity are primarily due to changes in the actual number of bursts rather than the number of spikes per burst.

Feedback regulation of burst firing and correlated activity

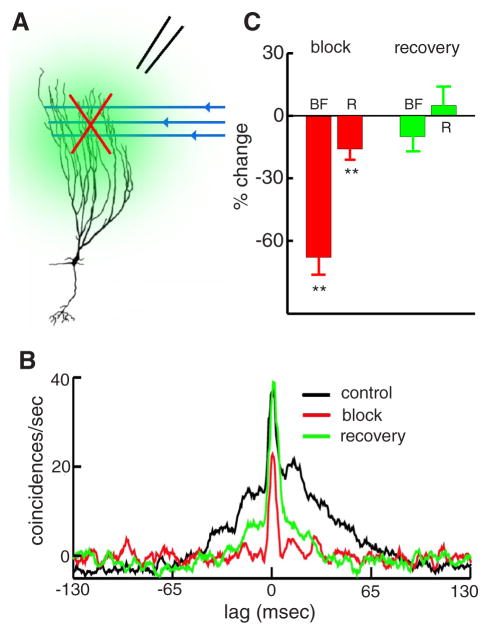
The strong link between burst firing and correlated activity suggests that the former can regulate the latter. Previous results have shown that burst firing in single pyramidal cells can be reduced by blocking feedback input to pyramidal cell apical dendrites (Bastian and Nguyenkim 2001). To test whether this reduced burst firing would lead to reduced correlated activity, we reversibly blocked parallel fiber input to pyramidal cells using the non-N-methyl-D-aspartate (NMDA) glutamate receptor antagonist 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX, see METHODS) as illustrated (Fig. 7A). CNQX blockade under baseline conditions eliminated the broad component of the cross-correlation leaving only the narrow peak typical of the isolated spike cross-correlation (Fig. 7B, black and red). Partial recovery from the CNQX treatment occurred for this cell pair (Fig. 7B, green). Changes in burst fraction and in the cross-correlation coefficient, contingent on CNQX treatment, were seen (Fig. 7C): the burst fraction BF was reduced by nearly 70%, on average, and as a consequence R was also significantly reduced by ~20% on average. We note that CNQX treatment caused reductions in firing rate that averaged 37%. However, changes in firing rate alone cannot account for the changes observed in the CCG as they cannot explain the change in CCG width. Eighteen of the 21 cell pairs studied with CNQX blockade were followed through recovery at which point both burst fraction BF and the cross-correlation coefficient R returned to near their control values (Fig. 7C). This reversible blockade of feedback input demonstrates that correlated activity is a direct function of each cells tendency to burst. This also suggests that feedback pathways have the potential to modulate correlated activity in pyramidal cells but additional studies are required to verify this.

FIG. 7.

Influence of burst firing on correlated activity. A: illustration of the experimental procedure to reversibly block feedback input from parallel fibers unto pyramidal cells. A pressure pipette is lowered close to the recording site and is used to eject 6-cyano-7-nitroquinoxalene-2,3-dione (CNQX), thereby blocking parallel fiber feedback input unto pyramidal cells. B: CCGs in the absence of stimulation under control (black), block (red), and recovery (green). C: changes in burst fraction BF and cross-correlation coefficient R during the block (red) and after recovery (green). Feedback blockade significantly reduced both BF and R, and both quantities returned to values that were not significantly different from those obtained under control conditions. Statistical significance was ascertained using a pairwise t-test at the P = 0.01 level with n = 21 for block data and n = 18 for recovery data.

We also attempted CNQX blockade under conspecific-like stimulation. No consistent result was seen. Instead this treatment typically produced small increases or decreases in |R| relative to conspecific-like stimulation prior to blockade. On average |R| increased by only 1.1% (P = 0.95, pairwise t-test, n = 6). Previous studies have shown that CNQX decreases the firing rate as well as burst firing in single pyramidal cells (Bastian and Nguyenkim 2001). In addition, this treatment eliminates the striking differences normally seen in response to communication-like stimulation versus prey-like stimuli; the former become similar to the latter (i.e., burst firing increases) (Bastian et al. 2004; Chacron 2006; Chacron et al. 2005a). Thus the lack of significant changes in correlated activity during conspecific-like stimulation before and during CNQX blockade likely results from these opposing changes in the cells’ tendency to burst.

Distinguishing between prey and conspecific stimuli using synchronous bursts

Finally, we quantified the ability of an ideal observer to distinguish between prey and communication stimuli based on the number of synchronous events in a given time window using the discriminability d′ (Green and Swets 1966). Our results show that the discriminability obtained from all spikes was maximal for a time window of ~75 ms (Fig. 8). Using synchronous bursts gave rise to a discriminability that was comparable to that obtained with all spikes (Fig. 8, compare red and blue). However, using synchronous isolated spikes gave rise to a much smaller discriminability (Fig. 8, green). This is a direct consequence of the fact that prey- and communication-like stimulation lead to differences in the structure of correlated bursts rather than correlated isolated spikes (Fig. 5, E and F). These results, coupled with the previous description of higher-order neurons that receive direct input from pyramidal cells and preferentially respond to spike bursts (Rose and Fortune 1999), suggest that that changes in the number of synchronous bursts in a given time window could be used to distinguish between prey and conspecific stimuli.

FIG. 8.

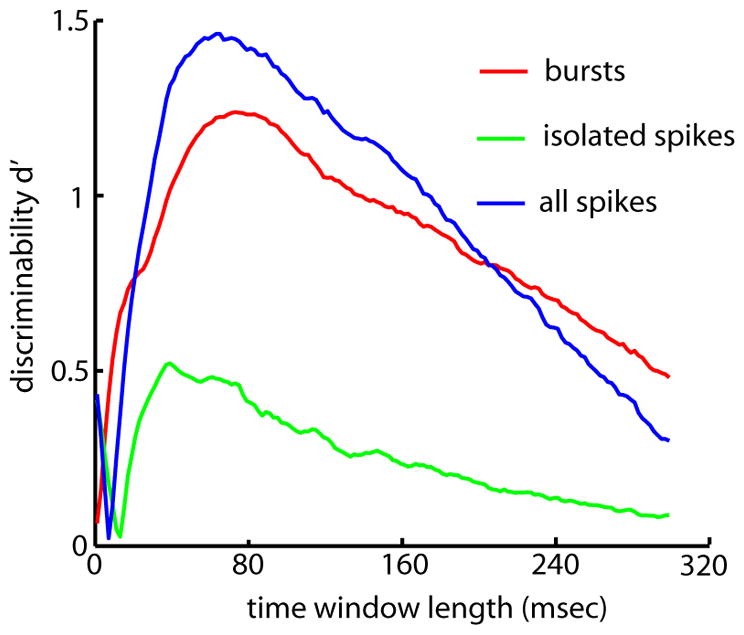
Distinguishing between prey and conspecific stimuli using synchronous bursts. Discriminability d′ as a function of the time window length for all spikes (blue), bursts (red), and isolated spikes (green).

DISCUSSION

Summary of results

We have quantified correlated activity in pyramidal cell pairs within the ELL. We found that the baseline activities of pyramidal cell pairs the receptive fields of which had sufficient overlap were correlated positively for same-type pairs and negatively for opposite-type pairs. Separation of the spike train into its burst and isolated spike components revealed that correlated activity was mostly due to synchronous burst firing. We then explored the effects of behaviorally relevant spatial stimulation patterns on pyramidal cell correlated activity. While prey-like stimuli gave rise to increased correlation with respect to no stimulation, conspecific-like stimuli gave rise to decreased correlation with respect to no stimulation. We decomposed the CCGs into their signal and noise components. Our results showed that the increased correlation seen under prey-like stimulation was mostly due to increased signal correlations. However, the decrease in correlated activity seen under conspecific-like stimulation was in part due to decreased noise correlations. We decomposed the spike trains into their burst and isolated spike components and found that changes in correlated activity were positively correlated with changes in burst firing. That feedback from higher centers could alter burst firing as well as correlated activity was demonstrated by pharmacological blockade of glutamatergic input to pyramidal cell apical dendrites. Finally, we quantified the ability of an ideal observer to distinguish between prey and conspecific stimuli. We found that the performance was very good based on synchronous bursts alone and only marginally improved when the entire spike train was considered. This raises the possibility that correlated bursts might provide an efficient channel for distinguishing prey from conspecific stimuli.

Correlated activity under baseline conditions

Contrary to previous findings (Krahe et al. 2002), we found that pyramidal cells displayed correlations both in the absence and presence of stimulation. This difference in results is probably due to the fact that our recordings were from different ELL segments than those of Krahe et al. (2002). As in other sensory systems (Meister et al. 1995; Puchalla et al. 2005), pyramidal cells with overlapping receptive fields displayed broad CCGs in the absence of stimulation that were positive for same-type pairs (EE and II) and negative for opposite-type pairs (EI). The overall magnitude of these correlations was not significantly different among the different pair types. Since anatomical studies have shown that neighboring pyramidal cells within the segments that we studied receive common receptor afferent input (L. Maler, personal communication), it is likely that this shared input causes the correlated activity that we observed. A detailed examination revealed that correlated activity in pyramidal cells in the absence of stimulation consisted mostly of nearly synchronous bursts for same-type pairs and anti-synchronous bursts for opposite-type pairs.

Differential correlated activity in the electrosensory system

Our results have shown that correlated activity, including noise correlations, is dependent on the stimulus and thus most likely is dependent on the behavioral context. Recent reviews have highlighted the need for understanding the structure of noise correlations in the CNS (Averbeck and Lee 2004, 2006) to understand population coding. Although the effect of such correlations on information has been shown to be small for neuron pairs (Averbeck and Lee 2006; Nirenberg et al. 2001), recent results suggest that even moderate amounts of noise correlation can dramatically affect the neural code when larger populations are considered (Schneidman et al. 2006). The large differences between the structures of raw and noise correlations observed during prey and conspecific stimulation imply that electric fish use different strategies for encoding both stimulus categories. Our results furthermore show that noise correlations can be differentially modulated by behaviorally relevant sensory input and theoretical studies of population coding are just incorporating the effects of these stimulus-modulated correlations (Pola et al. 2003; Shamir and Sompolinsky 2004).

Burst firing and sensory processing

ELL pyramidal cells have an intrinsic burst mechanism that has been well characterized in vitro (Doiron et al. 2001; Fernandez et al. 2005; Lemon and Turner 2000; Oswald et al. 2004), and a recent study has confirmed its existence in vivo (Oswald et al. 2004). Oswald et al. (2004) have also shown that bursts within a single pyramidal cell’s spike train selectively encoded the low temporal frequency components of sensory stimuli. As such, they proposed that bursts would encode prey stimuli that mostly contain low temporal frequencies (Nelson and MacIver 1999). Our results showing increased bursting under prey-like stimulation with respect to baseline levels are consistent with this. Moreover, we have shown that the number of synchronous bursts from pyramidal cell pairs could be used by downstream neurons to distinguish between prey and communication stimuli. Interestingly, the discriminability d′ was still high for time windows corresponding to the behavioral time scale (~150 ms) over which these animals detect prey (Nelson and MacIver 1999).

Our hypothesis that synchronous bursts within a given time window could be used to distinguish between prey and conspecific stimuli in downstream neurons appears to be justified as neurons in torus semicircularis (TS) receiving direct input from pyramidal cells have been shown to selectively respond with synaptic facilitation to simulated pyramidal cell burst firing (Fortune and Rose 1997, 2001). Furthermore, TS neurons also possess subthreshold voltage-gated sodium conductances that lead to nonlinear amplification of coincident synaptic input (Fortune and Rose 1997, 2003). It thus appears that TS neurons possess all the relevant neural mechanisms to optimally respond to synchronous bursts from pyramidal cells. Further studies are needed to understand the mechanisms by which TS neurons decode information from ELL pyramidal cell populations.

Feedback regulation of burst firing and correlated activity

It is well known that pyramidal cells receive massive amounts of feedback synaptic input from higher centers (Berman and Maler 1999; Sas and Maler 1983, 1987). As in other systems, feedback input to ELL pyramidal cells have been shown to mediate gain control as well as selective attenuation of redundant stimulus patterns (Bastian 1986, 1999; Bastian et al. 2004). In particular, it has been shown that conspecific stimuli activate parallel fiber feedback input to pyramidal cells from the caudal lobe of the cerebellum to a much greater extent than prey stimuli (Bastian et al. 2004; Chacron 2006; Chacron et al. 2005a). Previous studies have also shown that lesions of the indirect feedback pathway caused reduced baseline firing in pyramidal cells but dramatically increased pyramidal cell firing during conspecific-like stimulation (Bastian 1986). This suggests that the indirect feedback pathway has a net inhibitory effect when a conspecific-related stimulus is present and pyramidal cell bursting is antagonized by inhibitory input (Bastian and Nguyenkim 2001; Noonan et al. 2003). Therefore we hypothesize that activation of parallel fiber feedback input by conspecific stimuli leads to decreased bursting and therefore decreased correlated activity.

There is tremendous interest in understanding the role of correlated activity in neural coding, and it has been known for some time that certain stimuli can cause altered correlated firing among groups of neurons (Ahissar and Vaadia 1992; Destexhe et al. 1998; Doiron et al. 2003; Friedrich and Laurent 2001; Gray and Singer 1989; Kashiwadani et al. 1999; Macleod and Laurent 1996; Sillito et al. 1994; Stopfer et al. 1997). Our results add to these by showing that correlated activity can be differentially modulated by two behaviorally relevant classes of stimulation. Furthermore, our results have shown a mechanism by which this could occur: the regulation of burst firing through activation of feedback inputs from higher centers. Finally, these results suggest mechanisms by which neurons within the torus semicircularis, postsynaptic to the pyramidal cells, could differentiate between each stimulus class. Properties of certain classes of torus cells have properties well suited to decoding these differential pyramidal responses.

Neural circuitry devoted to controlling correlated activity is also likely to be found in other systems. Results in visual cortical area V1 have shown that stimulation of the nonclassical receptive field leads to decorrelation and increased information transmission (Vinje and Gallant 2000, 2002). We have previously shown that pyramidal cells also possessed a non-classical receptive field and that the indirect feedback input was its anatomical correlate (Chacron et al. 2003, 2005a). As the nonclassical receptive field of V1 neurons also depends on feedback input (Angelucci et al. 2002), it is likely that mechanisms similar to those described here also operate in V1. Like ELL pyramidal cells, lateral geniculate nucleus (LGN) relay cells also have a well-characterized intrinsic burst mechanism that can be modulated through synaptic input from cortical layer 6 and from the parabrachial brain stem region (Colbert et al. 1997; Ersir et al. 1997; Fanselow et al. 2001; Sherman 2001; Sherman and Guillery 1996, 2002). A recent review has in fact highlighted the anatomical similarities between the ELL and the mammalian thalamus (Krahe and Gabbiani 2004) and mechanisms similar to the ones described here may also function in LGN. Finally, we note that control of correlated activity through burst firing may not always require feedback. Previous results in the mammalian retina have shown that correlated activity and burst firing among retinal ganglion cells decreased as a function of increasing illumination level (Mastronarde 1983). As such, control of burst firing and correlated activity could also be achieved through lateral inhibition in the mammalian retina.