Skip to main content
PMC home page
Nature Communications logoLink to Nature Communications
. 2016 Apr 21;7:11403. doi: 10.1038/ncomms11403

Nonadditivity of critical Casimir forces

Sathyanarayana Paladugu 1,*, Agnese Callegari 1,*, Yazgan Tuna 1,2,*, Lukas Barth 1, Siegfried Dietrich 3,4, Andrea Gambassi 5, Giovanni Volpe 1,2,a
PMCID: PMC4844688  PMID: 27097797

Abstract

In soft condensed matter physics, effective interactions often emerge due to the spatial confinement of fluctuating fields. For instance, microscopic particles dissolved in a binary liquid mixture are subject to critical Casimir forces whenever their surfaces confine the thermal fluctuations of the order parameter of the solvent close to its critical demixing point. These forces are theoretically predicted to be nonadditive on the scale set by the bulk correlation length of the fluctuations. Here we provide direct experimental evidence of this fact by reporting the measurement of the associated many-body forces. We consider three colloidal particles in optical traps and observe that the critical Casimir force exerted on one of them by the other two differs from the sum of the forces they exert separately. This three-body effect depends sensitively on the distance from the critical point and on the chemical functionalisation of the colloid surfaces.

Inline graphicThe critical Casimir force, rising from fluctuating field confined between surfaces, is predicted to be nonadditive, but there is no experimental verification to date. Here the authors provide data support by quantifying the forces between three interacting colloidal particles using holographic traps.

From gravitation to electromagnetism, the fundamental physical interactions are additive: for instance, the force exerted on a probe electric charge in a homogeneous medium by two other charges equals the sum of the forces exerted by each of them separately. In more complex situations, however, effective interactions take hold—and these forces are not necessarily additive1. Accordingly, a crucial issue is whether, and if so to what extent, genuine many-body effects are present, such as those which have been experimentally reported for the effective electrostatic interaction among charged particles immersed in a liquid medium2,3.

Effective long-ranged forces acting on mesoscopic objects emerge at the micrometre scale when these objects spatially confine a surrounding fluctuating field. Casimir forces in quantum electrodynamics (QED) are a notable example due to the confinement of vacuum electromagnetic fluctuations between two conductors4; these forces are typically attractive and, thus, cause undesired stiction of the metallic parts of nanodevices5. The thermodynamic analogues of QED Casimir forces are critical Casimir forces, which were theoretically predicted by Fisher and de Gennes in 1978 (ref. 6): the confinement of thermal fluctuations in a binary liquid mixture may result in attractive or repulsive interactions with universal features7. These thermal fluctuations typically occur on the molecular scale; however, on approaching a critical point of a second-order phase transition, they become relevant and correlated across a much larger (up to several microns) length scale characterized by a correlation length ξ. The first direct experimental evidence for critical Casimir forces was provided only in 2008 (refs 8, 9): using total internal reflection microscopy (TIRM), femtonewton effective forces were experimentally measured between a single colloid and a planar surface immersed in a critical mixture; remarkably, both attractive and repulsive forces were found, in excellent agreement with theoretical predictions. Since then, these forces have been investigated under various conditions, for example, by varying the properties of the involved surfaces10,11,12,13,14 or with moving boundaries15. In addition, a number of studies of the phase behaviour of colloidal dispersions in a critical mixture16,17,18,19,20,21 indicate critical Casimir forces as candidates for tuning the self-assembly of nanostructures22 and quantum dots23, while analogous fluctuation-induced effects have been investigated, for example, at the percolation transition of a chemical sol24, in the presence of temperature gradients25, and even in granular fluids26 and active matter27,28,29,30. To gain full control and possibly harness critical Casimir interactions, it is pivotal to understand to what degree the many-body effects play a role. In fact, these fluctuation-induced forces and, in particular, the critical Casimir forces are theoretically expected to be nonadditive, but experimental evidence for the corresponding many-body effects is still lacking.

Here we report a set of experiments that demonstrates and quantifies the three-body effects present in critical Casimir forces acting on colloidal microspheres immersed in a near-critical binary liquid mixture. Corresponding theoretical studies31,32,33 reveal that these effects can either increase or decrease the critical Casimir forces depending on the temperature T of the mixture, on the spatial dimensionality, on the geometrical arrangement, on the shape and on the distance between the involved surfaces, in a way that is difficult to rationalize but with an overall contribution that can be up to 20% of the pairwise additive interaction. Due to this rather complex dependence on a large number of geometrical and physical variables, it is a priori unclear whether this effect can be experimentally detected in colloidal suspensions. Using holographic optical tweezers (HOTs)34 and digital video microscopy (DVM)35,36 to probe in situ the forces acting on spherical colloids immersed in a critical mixture of water and 2,6-lutidine in various geometrical configurations, we observe that the critical Casimir force exerted on a probe colloid by two other colloids differs from the sum of the forces exerted by them separately. These many-body effects are controlled by adjusting the criticality of the mixture, for example, by tuning its temperature or by changing the surface properties of the particles. Since interactions among micro- and nanoscopic particles in fluids are central to a wide spectrum of physical, chemical and biological phenomena, the insight provided here might prove useful for a diverse range of applications, including control of microscopic self-assembly of colloids, formation and stabilization of nanoparticle suspensions, aggregates, colloidal molecules and photonic crystals, as well as phase and biomimetic behaviours of micro- and nanoparticles—considering in particular that the many-body effects are expected to become even more important on the nanoscale37,38.

Results

Outline of the experimental approach

Before getting into the experimental details, we briefly outline the strategy of the experiment. We employ a set-up in which three colloidal microspheres are held by HOTs at the corners of an almost equilateral triangle. First, we measure the two-body critical Casimir forces arising, on approaching criticality, on each of the three pairs of particles in the absence of the remaining colloid, which is temporarily moved into an auxiliary trap. Then, assuming additivity of critical Casimir forces, these measurements are used to predict the forces acting on a pair of particles in the presence of the third one, which is eventually brought closer. Finally, we compare this additive prediction with the actually measured three-body potential: the significant discrepancies that appear clearly demonstrate the nonadditivity of critical Casimir forces.

Critical mixture and theoretical potentials

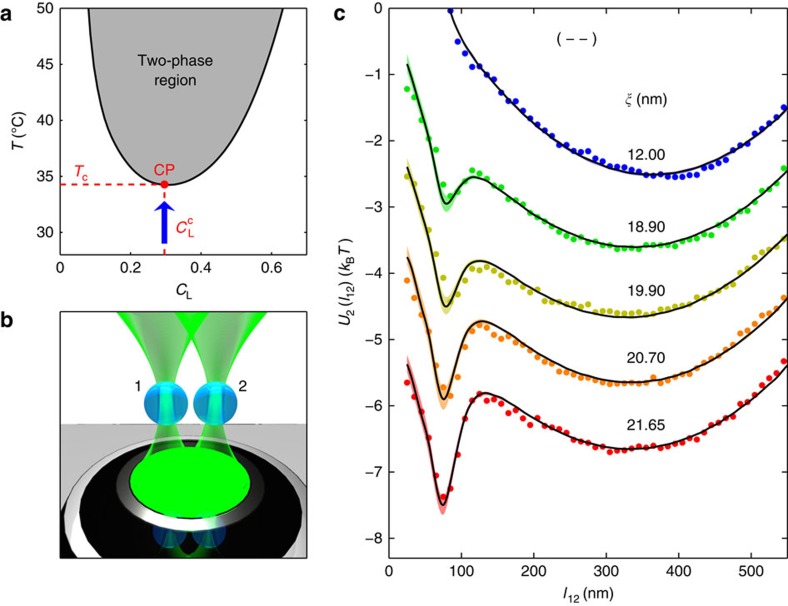
As solvent, we employ a mixture of water and 2,6-lutidine at the critical lutidine mass fraction 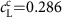Inline graphic (see the phase diagram in Fig. 1a describing a lower critical point at the temperature Tc≃307 K (refs 8, 9, 39)). A few degrees below Tc, the mixture is homogeneous and critical Casimir forces are negligible. However, as T approaches Tc (arrow in Fig. 1a), critical concentration fluctuations emerge, which generate critical Casimir forces7. These forces depend strongly on the adsorption preferences of the surface of the particles, that is, on whether they preferentially adsorb water or lutidine, realizing (−) and (+) boundary conditions, respectively8,9. In particular, critical Casimir forces are attractive between two particles carrying the same boundary conditions, that is, (++) and (−−), while repulsive for (+−) and (−+). In the experiment, we employ both hydrophilic (−) pristine silica spheres (diameter 2R=2.06±0.05 μm) and hydrophobic (+) silica spheres obtained by treating their surfaces with octyltriethoxysilane.

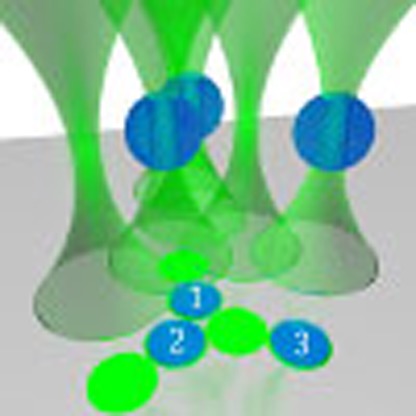
Figure 1. Two-body effective potentials in a critical mixture.

Figure 1

Open in a new tab

(a) Phase diagram of the water–2,6-lutidine mixture featuring a lower critical point (CP) at the bottom of the coexistence line (thick solid line39). Measurements are performed at the critical lutidine mass fraction 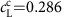Inline graphic, while the temperature T is gradually increased towards its critical value Tc≃307 K, as indicated by the arrow. (b) Cartoon of the experimental set-up for the measurement of effective pair interactions: two spherical silica colloids (blue spheres, diameter 2R=2.06±0.05 μm) are held in the bulk of the binary mixture (not shown) by two optical tweezers (green conoids) obtained by focusing a laser beam via the objective indicated directly below (black and silver against a grey background). While the size of the particles is to scale with their relative distance, the objective and its distance from the particle are not. (c) Effective pair potential U2(l12) between two hydrophilic colloids labelled 1 and 2 (with boundary conditions (−−), that is, attractive critical Casimir forces) as a function of the in-plane surface-to-surface distance l12: the symbols represent the experimental data and the solid lines the theoretical fits with the associated uncertainty (shading). From top to bottom, T increases towards Tc, which is accompanied by an increase of the fitted correlation length ξ and by the formation of an increasingly deep dip due to an attractive critical Casimir force, in agreement with the theoretical predictions. For clarity, symbols and curves corresponding to different temperatures have been separated vertically by a shift of 1 × kBT.

We start by considering the configuration schematically shown in Fig. 1b, with two particles, labelled by 1 and 2. These particles are subject to a one-body potential Uot due to optical traps, and a two-body contribution due to both a screened electrostatic pair repulsion Ues and a critical Casimir pair potential UC, while no evidence of van der Waals interactions was found; the total potential U2 of this configuration is therefore

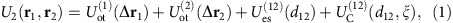graphic file with name ncomms11403-m2.jpg

where ri is the position of the centre of particle i, Δri=ri−Ri, and Ri is the position of the centre of the ith trap, while dij=|ri−rj|−2R is the distance between the surfaces of particles i and j. The optical traps are harmonic40, that is,

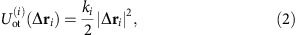graphic file with name ncomms11403-m3.jpg

where the stiffness ki (≃0.4 pN μm−1 for the data in Figs 1 and 4, and ≃0.8 pN μm−1 for those in Fig. 5) is nearly the same for all traps, as discussed below. The Derjaguin-Landau-Verwey-Overbeek (DLVO) electrostatic potential1 can be parameterised as

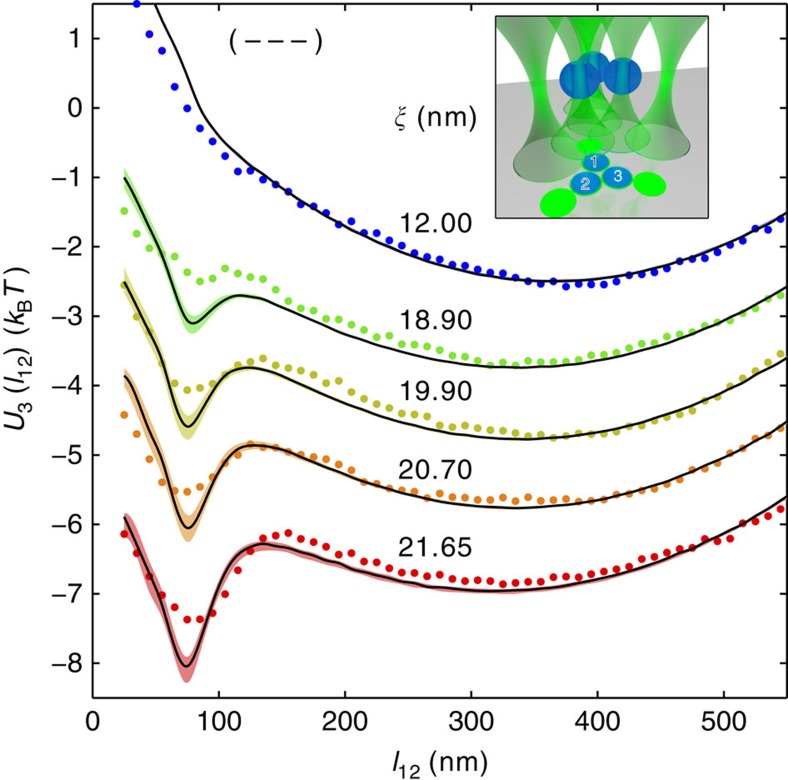
Figure 4. Many-body critical Casimir forces with symmetric boundary conditions.

Figure 4

Open in a new tab

The symbols represent the measured effective potential U3(l12) between the particles 1 and 2 (labelled in black in the inset) in the presence of particle 3 (labelled in white in the inset) as a function of the in-plane surface-to-surface distance l12 on increasing (from top to bottom) the correlation length ξ. All particles are hydrophilic (−−−), resulting in attractive critical Casimir forces. The solid lines represent the corresponding theoretical predictions obtained by assuming additivity of the measured pair potentials between particles 1–2, 1–3 and 2–3 with the associated uncertainty indicated by the shading. The observed discrepancy increases as ξ increases, providing quantitative evidence of the nonadditive nature of the critical Casimir interactions. The colour code of the data points is the same as in Fig. 1, and symbols and lines are vertically separated by 1 × kBT for reasons of clarity. Inset: cartoon of the trap and colloid configuration during the measurement (see Fig. 2 for details).

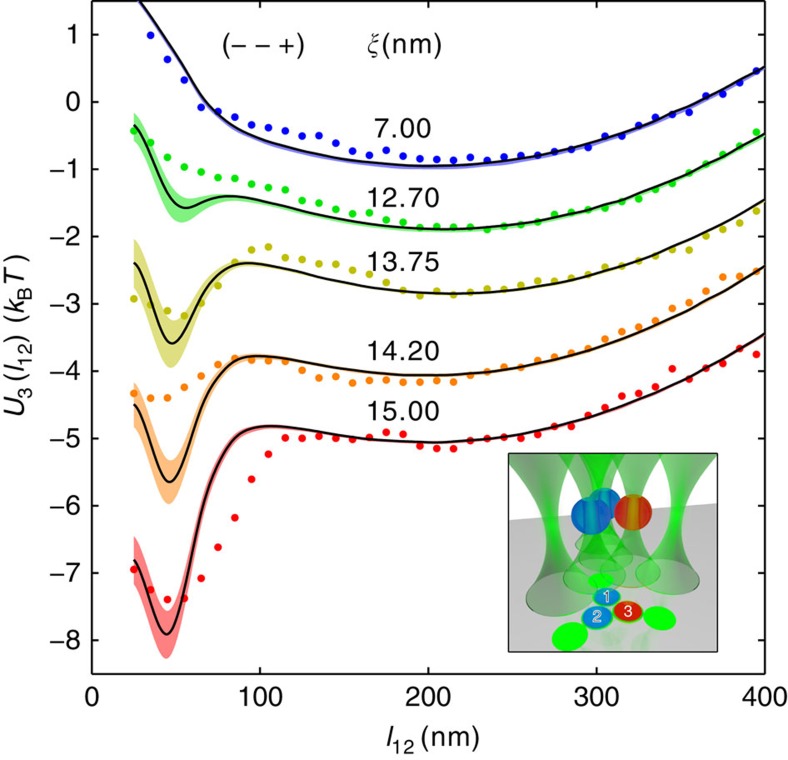
Figure 5. Many-body critical Casimir forces with asymmetric boundary conditions.

Figure 5

Open in a new tab

The symbols represent the measured effective potentials U3(l12) between particles 1 and 2 (blue, labelled in black in the inset) in the presence of particle 3 (red, labelled in white in the inset) as a function of the in-plane surface-to-surface distance l12 on increasing (from top to bottom) the correlation length ξ. Particles 1 and 2 (blue spheres in the inset) are hydrophilic (−), while particle 3 (red sphere in the inset) is hydrophobic (+), so that the two-body critical Casimir forces cause attraction between 1 and 2 and repulsion between 2 and 3, and between 3 and 1. The solid lines represent the corresponding theoretical prediction obtained by assuming additivity of the measured pair potentials between particles 1–2, 1–3 and 2–3, with the associated uncertainty indicated by the shading. The observed discrepancy between the lines and the symbols increases as ξ increases, providing quantitative evidence of the nonadditive nature of critical Casimir interactions also in the presence of opposing boundary conditions. Symbols and lines corresponding to different temperatures are vertically separated by 1 × kBT for reasons of clarity. Inset: cartoon of the trap and colloid configuration during the measurement (see Fig. 2 for details).

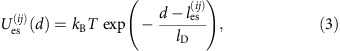graphic file with name ncomms11403-m4.jpg

where kB is the Boltzmann constant, lD (≃10 nm) is the Debye length for the solvent and 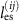Inline graphic (≃90 nm) is a measure of the strength of the interaction between the two colloidal particles i and j, which depends, inter alia, on their surface charges. The mild dependence of both Uot and Ues on the temperature T can be neglected, as here T is varied by at most 1%. Finally, the critical Casimir pair potential 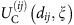Inline graphic depends on the correlation length ξ of the critical mixture and, within the Derjaguin approximation 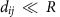Inline graphic (with dij≲0.3R in the present experiment), is given by8,9

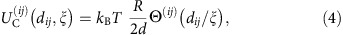graphic file with name ncomms11403-m8.jpg

where Θ(ij)(x) is the universal scaling function characterized by the boundary conditions involved, but otherwise independent of the material properties of the mixture and of the particles; it can be inferred from available numerical data8,9,41,42. The correlation length ξ varies as ξ(T)=ξ0(1−T/Tc)−ν, where the mixture-specific quantity ξ0=0.20±0.02 nm (s.e.m.) has been determined by light-scattering experiments43, while ν=0.63 is a universal critical exponent of the three-dimensional Ising universality class, holding for classical binary mixtures9. In the presence of three particles, their total potential U3 can be decomposed into the sum of individual one-body, pairwise two-body and remaining three-body contributions:

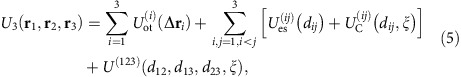graphic file with name ncomms11403-m9.jpg

where 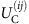Inline graphic depends on the boundary conditions at the surfaces of the particles i and j, while U(123) is the nonadditive three-body potential, which includes the contribution 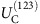Inline graphic of the three-body critical Casimir potential, the existence and magnitude of which we want to assess. Note that 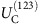Inline graphic can be distinguished from other possible contributions (such as those due to electrostatics2,3) because of its sensitive dependence on temperature, which effectively controls also its spatial range.

Measurement of two-body and three-body potentials

Until now direct measurements of critical Casimir forces have been performed only on single particles above planar surfaces using TIRM8,10; TIRM, however, necessarily involves a planar surface and therefore does not allow the measurement of forces arising between identical spherical particles, as they occur in colloidal suspensions. We have therefore developed an experimental set-up capable of manipulating and observing multiple particles in the bulk of a critical mixture. Our set-up is based on a combination of HOTs34,40 and DVM35,36,40; its schematic is shown in Supplementary Fig. 1. The HOTs are realised by shaping a laser beam using a spatial light modulator; in this way, we generate multiple reconfigurable optical traps within the sample, which allow us to gently hold the colloids with nanometric accuracy in the bulk of the critical mixture, that is, 50 μm above the lower surface of the sample cell; this distance is large enough to ensure that the critical Casimir forces between this surface and the particles are negligible. The laser power at each trapping site is kept low enough (≃2 mW) to avoid significant heating (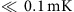Inline graphic (ref. 40)). The DVM uses a monochromatic camera acquiring videos at 200 fps; these frames are analysed using standard DVM algorithms to determine the projected positions of the particles with nanometric accuracy35,36 (see Methods for details). The crucial temperature control of the binary mixture is achieved in two stages as described in the Methods section and is able to maintain a set temperature with an accuracy of ±2 mK.

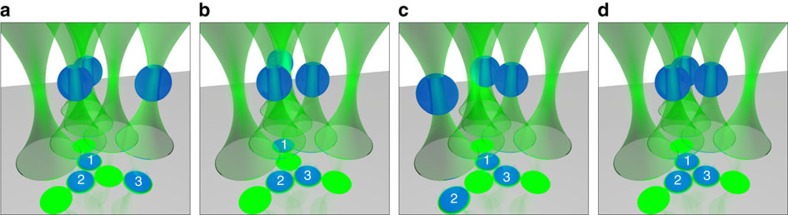
We perform all measurements using the same configuration of six traps, all obtained by means of the same hologram on the spatial light modulator, which produces spatially displaced but otherwise almost identical optical potentials. Three of these traps, referred to as internal ones, have their centres located at the vertices of an approximately equilateral triangle with edges of ≃2.3 μm; the centres of the remaining three traps, referred to as external ones, are instead located at a distance ≃2.3 μm from each vertex, along the bisector of the corresponding external angle (Fig. 2). The six traps are sufficiently far apart to guarantee the independence of the optical potentials40. The internal traps are used to hold either two (Fig. 2a–c) or three particles (Fig. 2d) for measuring the pair interaction or three-body potentials, respectively. The particles that are not needed in a certain measurement are temporarily moved from the internal to the closest of the external traps, where they have negligible interactions with the other particles. There, their surface-to-surface distance is >100 times larger than both the largest value of the range ξ of the critical Casimir forces and the typical range lD of the electrostatic repulsion involved in the experiment. In this way, the three colloids—labelled 1, 2 and 3—are selected at the beginning of the experiment and employed for the whole set of measurements; this eliminates possible systematic errors due to differences in the properties of the colloids of the batch we use. We start at a temperature T a few degrees below Tc, for which no critical fluctuations are present and the mixture is homogenous. First, we characterise the optical potential in equation (2) by measuring ki of each internal trap employing the configurations in Supplementary Fig. 2a: the particle under measurement (for example, particle 1 in configuration a1) is held in an internal trap, while the other two particles (for example, particles 2 and 3 in configuration a1) are moved into the nearest external traps. Then, by holding each pair (that is, 1–2, 1–3 and 2–3) of particles in the respective internal traps while keeping the third particle (that is, 3, 2 and 1, respectively) in the corresponding external trap, we measure and characterise the electrostatic interaction in equation (3) between each possible pair of particles, using the configurations shown in Fig. 2a–c, respectively. Finally, we measure the three-body interactions by having all three colloids in the internal traps as shown in Fig. 2d. At temperatures much lower than Tc, we obtain additivity of the interactions (in particular, of the electrostatic one), as expected. We then increase T in small steps towards Tc and repeat the measurement of the pair and three-body interactions at each step. The details of the measurement cycle are shown in Supplementary Fig. 2b.

Figure 2. Experimental configurations.

Figure 2

Open in a new tab

Cartoon of the geometrical arrangement of the six optical tweezers (green conoids) and the colloids (blue spheres) during the experiment. The resulting harmonic optical traps are arranged as indicated beneath by the schematic orthogonal projection on the coverslip, with colloids and traps represented by numbered blue and dark green circles, respectively. The sizes of the particles are to scale with their distance, but not with the distance from the coverslip. At each temperature T, the interactions between the pairs 1–2, 1–3 and 2–3 of colloids are measured in the configurations a,b and c, respectively. The effective potential between colloids 1 and 2 in the presence of colloid 3 is then measured in the configuration d. While measuring the pair interactions in a–c, the remaining colloid is optically moved into the nearest external trap. All six optical traps are always switched on during the measurements in order not to alter the hologram on the spatial light modulator and the corresponding optical potentials.

For each value of T, we acquire the histogram of the probability distribution P2(l12) of the in-plane surface-to-surface distance l12 between the particles 1 and 2 (see Methods for the definition of l12), from which we infer the effective potential U2(l12)≡−kBT ln P2(l12) shown by the symbols in Fig. 1c for various values of the correlation length ξ determined as described below. The solid lines in Fig. 1c represent, instead, the theoretical predictions based on equation (1) obtained via a Monte Carlo integration of the Boltzmann factor exp(−U2(r1, r2)/(kBT)) (see Methods for additional details), where the only fitting parameter is ξ because the optical and the electrostatic potentials have already been characterized at low T (see above). Note that the indicated values of ξ have been determined by a best fit to a part of the experimental data (highlighted by darker colours in the histograms in Supplementary Fig. 3) and are the same for the three pairs of particles as ξ only depends on the temperature of the mixture; the relationship between the sample temperature T and the correlation length is shown in Fig. 3. We obtain a very good agreement between the measured and the theoretical effective potentials for all three pairs of particles (Supplementary Fig. 3a–c). This demonstrates that equation (4) properly describes the two-body critical Casimir interaction 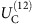Inline graphic, which is responsible for the formation of the dip in U2(l12) at l12≃80 nm and which appears as ξ increases. In addition, this agreement provides the direct experimental evidence of the occurrence of critical Casimir forces between two spherical colloidal particles, which is a geometrical configuration that had not been previously explored. Note that U2(l12) at separations l12≳250 nm is essentially determined by Uot, while for l12≲50 nm it is strongly influenced by the short-distance behaviour of Ues, which might not be accurately captured by equation (3). Accordingly, the range of l12 relevant for assessing the comparison between theory and experiment, and the emergence of (possibly many-body) critical Casimir forces, extends from the bottom of the dip to its right.

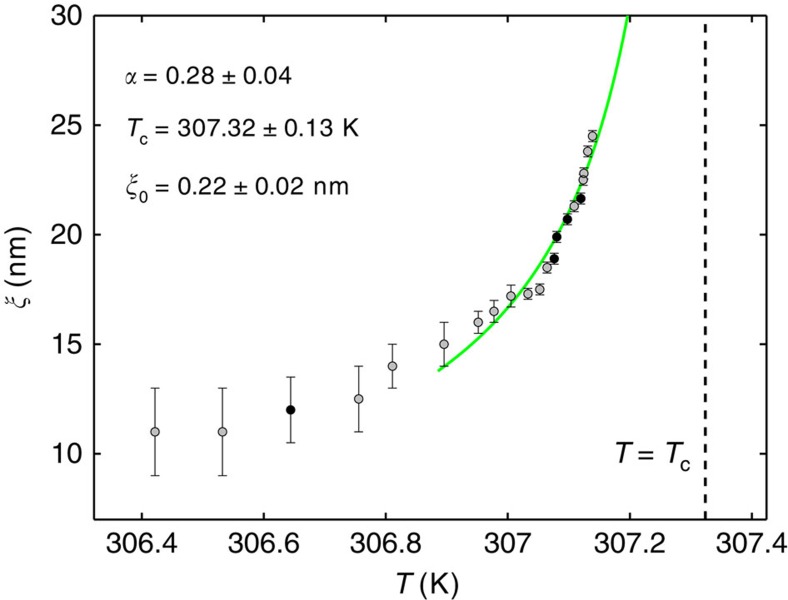
Figure 3. Temperature dependence of the correlation length.

Figure 3

Open in a new tab

The symbols indicate the values of the bulk correlation length ξ obtained from the best fit to the experimental data for the effective pair potential U2(l12); the error bars represent 2 s.d.'s. The black symbols correspond to the data displayed in Fig. 1c. To compare with the theoretical prediction given by equation (4), we take into account that the actual temperature T of the mixture is expected to be a linear combination of the temperature To set at the microscope objective, which is varied during the experiment, and the fixed temperature Tb=306.15 K of the thermal bath, that is., T=(1−α)Tb+αTo with 0<α<1. The green solid line corresponds to the best fit of the expected algebraic law ξ=ξ0(1−T/Tc)−ν with ν=0.63 for the data with ξ≳15 nm, which yields α=0.28±0.04, Tc=307.32±0.13 K and ξ0=0.22±0.02 nm. This estimate of ξ0 is compatible with the results of light-scattering experiments (see, for example, Table III in ref. 9). The estimate of Tc (indicated by the vertical dashed line) agrees with the known value for water and 2,6-lutidine. The overall agreement between the experimental data and the expected behaviour is quite good.

At this point, we can predict the effective potential U3(l12) associated with the distribution P3(l12) of the in-plane distance between particles 1 and 2 in the presence of particle 3 (Fig. 2d) using the measured two-body interactions and assuming additivity, that is, U(123)≡0 in equation (5). Again, these theoretical predictions are computed numerically via a Monte Carlo integration of the Boltzmann factor exp(−U3(r1, r2, r3)/(kBT)) (see Methods for additional details). The resulting effective potential U3(l12) between particles 1 and 2 is indicated by the solid lines in Fig. 4, while the symbols are the corresponding experimental data: the clear discrepancy between the two provides evidence for the presence of nonadditive (many-body) effects. The data with the smallest ξ depart appreciably from additivity at short distances (l12≲70 nm) due to a short-ranged electrostatic three-body effect that reduces repulsion3 and therefore amplifies the effects of the two-body critical Casimir attraction. On the contrary, as ξ increases, the effective potential is less attractive than expected, indicating that such a reduction is due to the many-body critical Casimir interaction 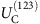Inline graphic, especially for l12 between 70 and 250 nm, where the two- and three-body electrostatics effects are negligible.

As pointed out above, one of the most distinguished features of the two-body critical Casimir forces is that their attractive or repulsive character depends on the surface properties of the particles. While the experiment described above involves three hydrophilic particles (−−−), we repeated the experiment with one hydrophobic (3) and two hydrophilic (1, 2) particles (−−+); the corresponding results are shown in Fig. 5 and Supplementary Fig. 4. In this experimental setting, the distance between the internal traps is slightly decreased by ≈0.1 μm; consequently, the electrostatic repulsion between the trapped particles increases and thus a trap twice as stiff is required to keep the colloids sufficiently close to experience critical Casimir forces at correlation lengths similar to those explored in the (−−−) configuration. Also in this case, we observe good agreement between theory and experiment for the pair-interaction effective potentials U2(lij) that can be inferred from the histograms of the corresponding distribution P2(lij) (Supplementary Fig. 4a–c), while sizeable discrepancies emerge in the three-body potential U3(l12) (Fig. 5; Supplementary Fig. 4d). In contrast to the previous case, the experimental data demonstrate that, depending on the distance and the correlation length, the many-body effects may also deepen the critical Casimir potential between particles 1 and 2.

The experiments described above typically correspond to values of the scaling variables R/ξ≃100 and lij/R≃0.1 that are outside the ranges of the available theoretical predictions for the many-body effects32: their highly nontrivial dependence on temperature and geometrical features renders questionable any attempt to extrapolate and therefore to compare these predictions with the present experimental data. Interestingly enough, assuming for 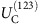Inline graphic the simple functional form of the Axilrod-Teller three-atom potential that describes three-body corrections to the van der Waals interaction (see, for example, ref. 32), with a suitable choice of the overall amplitude, reduces the discrepancy between the experimental and the corresponding theoretical predictions.

Discussion

Our results provide direct experimental evidence of the emergence of critical Casimir forces between two colloids and demonstrate the presence of pronounced three-body effects. These many-body critical Casimir forces strongly depend on the proximity to criticality of the fluid solvent, and can therefore be tuned, for example, by changing the temperature of the system or by altering the surface properties of the involved colloids. While we have focused on configurations with three particles, the experimental set-up and protocol discussed here are versatile enough to allow the investigation of the many-body potentials associated with a larger number of particles, possibly of non-spherical shape and dissolved in a variety of different solvents. In particular, in salty near-critical mixtures, one can expect a subtle interplay between the many-body effects of electrostatic and critical Casimir forces similar to those observed in the case of the two-body interaction between charged colloids44,45. Anisotropic solvents such as nematic liquid crystals, instead, may lead to effective many-body interactions with a complex dependence on the direction of the nematic director46 and on the shape of the involved colloids47, which could be investigated by extending the present approach. Criticality amounts to the occurrence of order parameter fluctuations on the spatial scale of the correlation length, which in principle can diverge and, thus, lead to the emergence of complex and nonadditive interactions at very large scales. They may find natural applications in various disciplines, such as in the realization of colloidal molecules or reversible self-assembly, as well as in the organization of cellular membranes48 and possibly even in the patterns of brain activation49. Furthermore, in view of their similarity, these effects can also shine light on certain aspects of the many-body effects in QED Casimir forces, while the experimental approach described here can be naturally extended to the recent attempt to measure these forces with optical tweezers50.

Methods

Experimental set-up

The experimental set-up combines HOTs and DVM (Supplementary Fig. 1), and is build around a home-made microscope. A laser beam (wavelength λ=532 nm, power 500 mW) is expanded by a telescope and projected onto a phase-only spatial light modulator (Holoeye, PLUTO-VIS). The hologram on the spatial light modulator imposes a phase modulation onto the beam, allowing the generation of multiple trapping spots. The resulting beam is then projected onto the entrance pupil of a high-numerical-aperture oil-immersion objective (magnification × 100, numerical aperture 1.30) by a series of lenses and mirrors arranged in a 4f configuration40. The objective focuses the beam in the sample plane and creates a series of reconfigurable traps. As the mixture approaches criticality, the induced fluctuations of the refractive index may in principle interfere with HOT and alter the features of the resulting optical potentials. However, the correlation length ξ≲22 nm explored in our experiments (Fig. 3) remains always sufficiently small in comparison with λ, and thus does not significantly influence the optical beam propagation and, therefore, the generated optical potentials. In particular, the values of the trap stiffnesses ki, which we infer from the best fits to the experimental data, show no systematic dependence on T. Since the configuration on the phase mask imposed on the spatial light modulator is always the same during each data acquisition (Supplementary Fig. 2), the resulting optical trapping potentials are also always the same. In addition, during the calibration of the set-up, we have tested the stability of all internal and external traps with particles in the configurations used later while acquiring the data; this allowed us to confirm the harmonicity of the traps and to exclude the presence of ghost traps in the region of space explored by the particles. The DVM is realised using a standard configuration with white light illumination and a monochromatic CMOS camera (200 f.p.s.). Since, near Tc, critical fluctuations depend very sensitively on small temperature changes, the microscope is enclosed within a thermally stabilised box to avoid any air flow, which may cause instability of the sample temperature. The sample holder is thermally isolated from the underneath translation stage with a teflon film. The necessary fine control of the temperature of the sample is achieved in two stages: first, the temperature of the microscope box is controlled to within ±50 mK; second, a closed-loop controller (realized with a Pt100 temperature sensor and a Peltier heating/cooling element) keeps the temperature of the sample cell to within ±2 mK. We remark that within each set of experiments the temperature T is gradually increased towards Tc.

Sample preparation

The binary liquid mixture used in all experiments is composed of water and 2,6-lutidine at the critical lutidine mass fraction 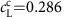Inline graphic. The mixture undergoes a second-order phase transition at a lower critical point with temperature Tc≃307 K (refs 8, 9, 39). The corresponding phase diagram is shown in Fig. 1a (ref. 39): it consists of two regions, corresponding to the mixed (white) and the demixed (grey) phases with a lower critical point. In all experiments, we use silica colloids with diameter 2R=2.06±0.05 μm (Microparticles GmbH). In the measurements involving hydrophobic particles, these silica colloids are treated chemically to make them hydrophobic, that is, we silanized their surfaces with octyltriethoxysilane. The sample cell containing the critical mixture and a small amount of colloids is a 200-μm-thick silica cuvette, which is sealed with teflon plugs to avoid evaporation of the mixture and to allow its usage for the whole duration of the experiment (≈1 day).

Data analysis

The raw data obtained from the various measurements are videos showing the orthogonal projection on a plane of the Brownian motion of the particles in three spatial dimensions and consisting of ≈60,000 frames acquired at 200 f.p.s. From these videos, we extract the in-plane position (xi and yi) of the centre of each colloid i as a function of time using standard DVM algorithms35,40. During the measurements of two- and three-body potentials, the surface-to-surface distance between the involved colloids is typically smaller than their common radius R; accordingly, to obtain the actual value rphys of the distance between their centres, it is necessary to correct36 the measured optical distance rmeas by adding a distance-dependent correction δr(rmeas). We have determined the function δr(rmeas), which approximately ranges between −60 and −10 nm in our experiments, on the basis of the optical images of single colloids, as explained in ref. 36. On the basis of these trajectories, we calculate the in-plane surface-to-surface distance 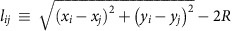Inline graphic between particles i and j, which allows us to construct the histograms Pn(lij), corresponding to the acquired frames with n=2 or 3 particles being close, and from them to determine the effective potentials Un(lij)=−kBT ln Pn(lij). Since lij is obtained from a differential measurement, all common-mode noise (for example, due to slow mechanical drifts over the duration of the experiment) is automatically removed.

Monte Carlo integration

For each set of parameters, we compute the theoretical in-plane surface-to-surface separation histograms Pn(lij) and the associated effective potentials Un(lij) via a suitable Monte Carlo integration of the Boltzmann factors exp(−U2(r1, r2)/(kBT)) and exp(−U3(r1, r2, r3)/(kBT)) with the theoretical potentials given by equations (1), (4) and (5) with U(123)=0 for the configurations with two and three close particles, respectively, based on the measured parameters of the optical traps and of the electrostatic interaction (equation (3)). 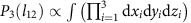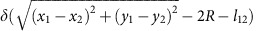For instance, in the presence of three close particles, one has 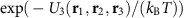Inline graphic Inline graphicInline graphic, where ri≡(xi, yi, zi) is the position of particle i in a Cartesian coordinate system. To account for a (small) anisotropy of the generated optical traps, the data analysis and the fit are carried out by assuming 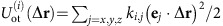Inline graphic, where ex,y,z are the unit vectors along the principle orthogonal axes of the ellipsoidal trap, instead of equation (2). For all traps, ex,y turn out to lie almost within the x−y plane, with ki,x≃ki,y and ki,z≃0.3ki,x. In particular, we verified that the actual values of ki,z do not significantly affect the comparison between the theoretical predictions and the experimental data. The Monte Carlo integration discussed here is necessary because of the large number of variables (6 and 9 for P2 and P3, respectively) over which the Boltzmann factor has to be integrated. The presence of the harmonic optical traps is exploited to introduce an importance sampling based on the corresponding Gaussian distributions, assumed to have variances ≃kBT/ki,x, kBT/ki,y and kBT/ki,z along the three spatial axes. We have checked that the eventual theoretical predictions for both the two- and three-body potentials are not affected by this assumption or by the number of sampled points in space, which was set to a sufficiently large value, of the order of 107−108.

Additional information

How to cite this article: Paladugu, S. et al. Nonadditivity of critical Casimir forces. Nat. Commun. 7:11403 doi: 10.1038/ncomms11403 (2016).

Supplementary Material

Supplementary Information

Supplementary Figures 1-4

ncomms11403-s1.pdf (3.2MB, pdf)

Acknowledgments

G.V. was partially funded by a Marie Curie Career Integration Grant (PCIG11GA-2012-321726) and a Distinguished Young Scientist award of the Turkish Academy of Sciences (TÜBA). This work was partially supported by Tubitak grant no. 111T758. L.B. was supported by an internship awarded by DAAD Rise.

Footnotes

Author contributions P.S. improved the set-up, performed the measurements and extracted the experimental trajectories. A.C. performed the analysis, the simulations and the comparison of the experimental data with theory. Y.T. implemented the initial set-up and performed the initial measurements. L.B. contributed to the implementation of the initial set-up. S.D. provided guidance for the theory and the interpretation of the data. A.G. developed the theory and contributed the comparison of the experimental data with theory. G.V. conceived and supervised the experiment and the data analysis. All authors participated in analysing the results and in writing the article.

References

  1. Israelachvili J. Intermolecular and Surface Forces 2nd edn Academic Press (1992) . [Google Scholar]
  2. Merrill J. W., Sainis S. K. & Dufresne E. R. Many-body electrostatic forces between colloidal particles at vanishing ionic strength. Phys. Rev. Lett. 103, 138301 (2009) . [DOI] [PubMed] [Google Scholar]
  3. Brunner M., Dobnikar J., von Grünberg H.-H. & Bechinger C. Direct measurement of three-body interactions amongst charged colloids. Phys. Rev. Lett. 92, 078301 (2004) . [DOI] [PubMed] [Google Scholar]
  4. Casimir H. B. G. On the attraction between two perfectly conducting plates. Proc. K. Ned. Akad. Wet B51, 793–795 (1948) . [Google Scholar]
  5. Capasso F., Munday J. N., Iannuzzi D. & Chan H. B. Casimir forces and quantum electrodynamical torques: Physics and nanomechanics. IEEE J. Sel. Topics Quantam Electron 13, 400–414 (2007) . [Google Scholar]
  6. Fisher M. E. & de Gennes P. G. Phenomena at the walls in a critical binary mixture. C. R. Acad. Sci. Paris B 287, 207–209 (1978) . [Google Scholar]
  7. Gambassi A. The Casimir effect: from quantum to critical fluctuations. J. Phys. Conf. Ser. 161, 012037 (2009) . [Google Scholar]
  8. Hertlein C., Helden L., Gambassi A., Dietrich S. & Bechinger C. Direct measurement of critical Casimir forces. Nature 451, 172–175 (2008) . [DOI] [PubMed] [Google Scholar]
  9. Gambassi A. et al. Critical Casimir effect in classical binary liquid mixtures. Phys. Rev. E 80, 061143 (2009) . [DOI] [PubMed] [Google Scholar]
  10. Nellen U., Helden L. & Bechinger C. Tunability of critical Casimir interactions by boundary conditions. Europhys. Lett. 88, 26001 (2009) . [Google Scholar]
  11. Tröndle M., Kondrat S., Gambassi A., Harnau L. & Dietrich S. Normal and lateral critical Casimir forces between colloids and patterned substrates. Europhys. Lett. 88, 40004 (2009) . [Google Scholar]
  12. Tröndle M., Kondrat S., Gambassi A., Harnau L. & Dietrich S. Critical Casimir effect for colloids close to chemically patterned substrates. J. Chem. Phys. 133, 074702 (2010) . [DOI] [PubMed] [Google Scholar]
  13. Tröndle M. et al. Trapping colloids near chemical stripes via critical Casimir forces. Mol. Phys. 109, 1169–1185 (2011) . [Google Scholar]
  14. Gambassi A. & Dietrich S. Critical Casimir forces steered by patterned substrates. Soft Matter 7, 1247 (2011) . [Google Scholar]
  15. Furukawa A., Gambassi A., Dietrich S. & Tanaka H. Nonequilibrium critical Casimir effect in binary fluids. Phys. Rev. Lett. 111, 055701 (2013) . [DOI] [PubMed] [Google Scholar]
  16. Soyka F., Zvyagolskaya O., Hertlein C., Helden L. & Bechinger C. Critical Casimir forces in colloidal suspensions on chemically patterned surfaces. Phys. Rev. Lett. 101, 208301 (2008) . [DOI] [PubMed] [Google Scholar]
  17. Bonn D. et al. Direct observation of colloidal aggregation by critical Casimir forces. Phys. Rev. Lett. 103, 156101 (2009) . [DOI] [PubMed] [Google Scholar]
  18. Gambassi A. & Dietrich S. Colloidal aggregation and critical Casimir forces. Phys. Rev. Lett. 105, 059601 (2010) . [DOI] [PubMed] [Google Scholar]
  19. Zvyagolskaya O., Archer A. J. & Bechinger C. Criticality and phase separation in a two-dimensional binary colloidal fluid induced by the solvent critical behavior. Europhys. Lett. 96, 28005 (2011) . [Google Scholar]
  20. Mohry T. F., Maciołek A. & Dietrich S. Phase behavior of colloidal suspensions with critical solvents in terms of effective interactions. J. Chem. Phys. 136, 224902 (2012) . [DOI] [PubMed] [Google Scholar]
  21. Edison J. R. et al. Critical Casimir forces and colloidal phase transitions in a near-critical solvent: A simple model reveals a rich phase diagram. Phys. Rev. Lett. 114, 038301 (2015) . [DOI] [PubMed] [Google Scholar]
  22. Faber S., Hu Z., Wegdam G. H. & Schall P. Controlling colloidal phase transitions with critical Casimir forces. Nat. Commun. 4, 1584 (2013) . [DOI] [PubMed] [Google Scholar]
  23. Marino E., Kodger T. E., ten Hove J. B., Velders A. H. & Schall P. Assembling quantum dots via critical Casimir forces. Sol. Energy Mater. Sol. Cells (in the press) . [Google Scholar]
  24. Gnan N., Zaccarelli N. & Sciortino F. Casimir-like forces at the percolation transition. Nat. Commun. 5, 3267 (2014) . [DOI] [PubMed] [Google Scholar]
  25. Kirkpatrick T. R., Ortiz de Zárate J. M. & Sengers J. V. Nonequilibrium Casimir-like forces in liquid mixtures. Phys. Rev. Lett. 115, 035901 (2015) . [DOI] [PubMed] [Google Scholar]
  26. Cattuto C., Brito R., Marconi U. M. B., Nori F. & Soto R. Fluctuation-induced Casimir forces in granular fluids. Phys. Rev. Lett. 96, 178001 (2006) . [DOI] [PubMed] [Google Scholar]
  27. Ray D., Reichhardt C. & Reichhardt C. J. O. Casimir effect in active matter systems. Phys. Rev. E 90, 013019 (2014) . [DOI] [PubMed] [Google Scholar]
  28. Parra-Rojas C. & Soto R. Casimir effect in swimmer suspensions. Phys. Rev. E 90, 013024 (2014) . [DOI] [PubMed] [Google Scholar]
  29. Harder J., Mallory S. A., Tung C., Valeriani C. & Cacciuto A. The role of particle shape in active depletion. J. Chem. Phys. 141, 194901 (2014) . [DOI] [PubMed] [Google Scholar]
  30. Ni R., Cohen Stuart M. A. & Bolhuis P. G. Tunable long range forces mediated by self-propelled colloidal hard spheres. Phys. Rev. Lett. 114, 018302 (2015) . [DOI] [PubMed] [Google Scholar]
  31. Mattos T. G., Harnau L. & Dietrich S. Many-body effects for critical Casimir forces. J. Chem. Phys. 138, 074704 (2013) . [DOI] [PubMed] [Google Scholar]
  32. Mattos T. G., Harnau L. & Dietrich S. Three-body critical Casimir forces. Phys. Rev. E 91, 042304 (2015) . [DOI] [PubMed] [Google Scholar]
  33. Hobrecht H. & Hucht A. Many-body critical Casimir interactions in colloidal suspensions. Phys. Rev. E 92, 042315 (2015) . [DOI] [PubMed] [Google Scholar]
  34. Grier D. G. A revolution in optical manipulation. Nature 424, 810–816 (2003) . [DOI] [PubMed] [Google Scholar]
  35. Crocker J. C. & Grier D. G. Methods of digital video microscopy for colloidal studies. J. Colloid Interface Sci. 179, 298–310 (1996) . [Google Scholar]
  36. Baumgartl J. & Bechinger C. On the limits of digital video microscopy. Europhys. Lett. 71, 487–493 (2005) . [Google Scholar]
  37. Sacanna S., Irvine W. T. M., Chaikin P. M. & Pine D. J. Lock and key colloids. Nature 464, 575–578 (2010) . [DOI] [PubMed] [Google Scholar]
  38. Batista C. A. S., Larson R. G. & Kotov N. A. Nonadditivity of nanoparticle interactions. Science 350, 1242477 (2015) . [DOI] [PubMed] [Google Scholar]
  39. Grattoni C. A., Dawe R. A., Seah C. Y. & Gray J. D. Lower critical solution coexistence curve and physical properties (density, viscosity, surface tension, and interfacial tension) of 2, 6-lutidine+water. J. Chem. Eng. Data 38, 516–519 (1993) . [Google Scholar]
  40. Jones P. H., Maragò O. M. & Volpe G. Optical Tweezers: Principles and Applications Cambridge Univ. Press (2015) . [Google Scholar]
  41. Vasilyev O., Gambassi A., Maciołek A. & Dietrich S. Monte Carlo simulation results for critical Casimir forces. Europhys. Lett. 80, 60009 (2007) . [Google Scholar]
  42. Hasenbusch M. Thermodynamic Casimir effect: universality and corrections to scaling. Phys. Rev. B 85, 174421 (2012) . [Google Scholar]
  43. Gülari E., Collings A. F., Schmidt R. L. & Pings C. J. Light scattering and shear viscosity studies of the binary system 2,6-lutidine-water in the critical region. J. Chem. Phys. 56, 6169–6179 (1972) . [Google Scholar]
  44. Nellen U. et al. Salt-induced changes of colloidal interactions in critical mixtures. Soft Matter 7, 5360 (2011) . [Google Scholar]
  45. Bier M., Gambassi A., Oettel M. & Dietrich S. Electrostatic interactions in critical solvents. Europhys. Lett. 95, 60001 (2011) . [Google Scholar]
  46. Poulin P., Stark H., Lubensky T. C. & Weitz D. A. Novel colloidal interactions in anisotropic fluids. Science 275, 1770 (1997) . [DOI] [PubMed] [Google Scholar]
  47. Lapointe C. P., Mason T. G. & Smalyukh I. I. Shape-controlled colloidal interactions in nematic liquid crystals. Science 326, 1083 (2009) . [DOI] [PubMed] [Google Scholar]
  48. Machta B. B., Veatch S. L. & Sethna J. P. Critical Casimir forces in cellular membranes. Phys. Rev. Lett. 109, 138101 (2012) . [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Haimovici A., Tagliazucchi E., Balenzuela P. & Chialvo D. R. Brain organization into resting state networks emerges at criticality on a model of the human connectome. Phys. Rev. Lett. 110, 178101 (2013) . [DOI] [PubMed] [Google Scholar]
  50. Ether D. S. jr et al. Probing the Casimir force with optical tweezers. Europhys. Lett. 112, 44001 (2015) . [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Figures 1-4

ncomms11403-s1.pdf (3.2MB, pdf)

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES