Abstract
Predicting the pharmacokinetics of highly protein-bound drugs is difficult. Also, since historical plasma protein binding data was often collected using unbuffered plasma, the resulting inaccurate binding data could contribute to incorrect predictions. This study uses a generic physiologically based pharmacokinetic (PBPK) model to predict human plasma concentration-time profiles for 22 highly protein-bound drugs. Tissue distribution was estimated from in vitro drug lipophilicity data, plasma protein binding, and blood: plasma ratio. Clearance was predicted with a well-stirred liver model. Underestimated hepatic clearance for acidic and neutral compounds was corrected by an empirical scaling factor. Predicted values (pharmacokinetic parameters, plasma concentration-time profile) were compared with observed data to evaluate model accuracy. Of the 22 drugs, less than a 2-fold error was obtained for terminal elimination half-life (t1/2, 100% of drugs), peak plasma concentration (Cmax, 100%), area under the plasma concentration-time curve (AUC0–t, 95.4%), clearance (CLh, 95.4%), mean retention time (MRT, 95.4%), and steady state volume (Vss, 90.9%). The impact of fup errors on CLh and Vss prediction was evaluated. Errors in fup resulted in proportional errors in clearance prediction for low-clearance compounds, and in Vss prediction for high-volume neutral drugs. For high-volume basic drugs, errors in fup did not propagate to errors in Vss prediction. This is due to the cancellation of errors in the calculations for tissue partitioning of basic drugs. Overall, plasma profiles were well simulated with the present PBPK model.
Keywords: Physiologically based pharmacokinetic (PBPK) modeling, Protein binding, Distribution volume, hepatic metabolism
INTRODUCTION
The two primary parameters that define the systemic disposition of a drug are its volume of distribution and clearance. One factor that greatly impacts both volume of distribution and clearance is plasma protein binding, represented by the fraction unbound in plasma (fup). Although drugs highly bound to albumin tend to be restricted to the plasma, hydrophobic bases that bind to α -acid glycoprotein can be highly partitioned into tissues. For highly protein-bound drugs, estimation of volume of distribution is particularly sensitive to values of fup. For clearance, the extent of plasma protein binding is important for renally cleared drugs as well as drugs cleared predominantly by the liver with a low extraction ratio [1]. Although there are well established methods to predict human PK from preclinical data, retrospective analyses indicate that the accuracy of quantitative predictions decreases with lower intrinsic metabolic clearance and higher plasma protein binding. Obach et al found that for highly bound compounds (free fraction in plasma below 0.1), clearance was severely under-predicted using a standard well-stirred model for the liver [2]. Baker et al [3] also suggested that hepatic clearance was usually under-estimated using scaled data obtained from hepatocytes and microsomes. This under-prediction of clearance was most common when the compound was highly bound and/or a sinusoidal transporter substrate. Consideration of transporter effects in vitro was not sufficient to provide a direct, quantitative estimate of hepatic clearance in vivo. Given the importance of protein binding for PK prediction, accurate experimental fup values are critical. It has been shown previously that fup is very sensitive to changes in plasma pH in vitro [4]. Since plasma is buffered by the CO2-carbonic anhydrase system, in vitro plasma pH will rise over time in the absence of CO2 or an alternate buffer. This increase in pH generally results in an over prediction of plasma protein binding (average fup,CO2/fup,air = 2.3 for 55 compounds). Although conducting equilibrium dialysis experiments in the presence of CO2 is becoming more common, much of the historic fup data has been collected with unbuffered plasma.
Over the past few years, physiological-based pharmacokinetic (PBPK) models, which integrate physiological information (tissue blood flows, size and composition) and compound specific data (clearance, tissue and blood affinities), have been developed to predict the temporal profiles of xenobiotics and their metabolites in vivo. Recent advances in the prediction of tissue distribution and hepatic metabolism have made this approach more attractive. For instance, in vitro data can, in theory, predict tissue partitioning [5–7], apparent volume of distribution at steady state[8] and hepatic plasma clearance [9, 10]. In reality, these methods are rarely used to ab initio predict ADME properties, but are integrated into the drug metabolism-pharmacokinetic (DMPK) experimental and modeling process. Several PBPK modeling studies have aimed at evaluating the utility of integrated PBPK methods. Generic PBPK models incorporate compound independent physiological parameters along with measured or predicted drug-specific properties and have been used for a diverse set of drug molecules. However, in many studies, accurate prediction was not observed, or required incorporation of information from preclinical species. A PhRMA initiative predicted human PK profiles for 14 drugs after intravenous administration [11]. In this study, between 50% and 71% of the primary human PK parameters were predicted with medium to high accuracy (< 2-fold error). A retrospective analysis which predicted human PK parameters for 26 clinical drugs using PBPK models concluded that the accurate prediction required two conditions: steady state distribution volume (Vss) had to be corrected with rat in vivo data, and protein binding was ignored during clearance prediction for acidic and neutral compounds[12]. Jones et al estimated a PBPK model for the prediction of human plasma concentration profile for 21 compounds [13]. For 11 compounds that were cleared by cytochrome P450 (CYPs), clearance was predicted using a well-stirred model which included a physiological scaling factor, blood binding data, and liver blood flow. For the other 10 compounds which were cleared by other pathways such as phase II metabolism, renal elimination, and extra hepatic metabolism, clearance was estimated by using a single-species-based allometric method with a fixed exponent. To predict human distribution volume (Vss), an initial verification step in pre-clinical species was required to determine suitable tissue composition equations. The distribution equations used were determined by the ability of the models to accurately reproduce rat Vss upon intravenous single-dose administration. The distribution methods for 5 compounds among the 21 were estimated by using Arundel’s model [11], and the others were estimated by either the Poulin [5] or Rodgers [6, 7] models. These analyses highlight that drug distribution and elimination are generally poorly predicted using only in vitro data and that it is critical to fully understand the assumptions in the methodology.
Since the PK profiles of highly-protein-bound compounds are poorly predicted, in the present study, 22 highly protein bound compounds were modeled using only in vitro data and a single generic PBPK model. Also, given the questionable nature of historic fup data and the importance of this data for PBPK models, it is possible that errors in experimental fup values may contribute to inaccuracies in PBPK models. Therefore, we have investigated the impact of errors in fup on the PK predictions for these compounds. In this report, we show that a single model with an empirical scaling factor for acidic and neutral drugs can accurately predict the PK parameters of these compounds. We also show that inaccuracies in fup result in errors in clearance and/or volume prediction, depending on the ionic character and PK properties of the drug.
MATERIALS and METHODS
Compounds and sources of in Vitro and in Vivo Parameters
A set of highly protein-bound compounds (n=22) was studied in this analysis. Drugs were selected based on the availability of intravenous administration data in human clinical studies (see Appendix), as well as the following experimentally determined biochemical and physicochemical parameters [2, 7, 14–17]: unbound fraction in plasma (fup), unbound fraction in microsomal/hepatocytic incubation (fuinc), basic and acidic dissociation constants (pKa), n-octanol: water partition coefficient of the non-ionized species (Pow), calculated vegetable oil: water partition coefficient at pH 7.4 (Dvo,7.4), in vitro intrinsic clearance (CLint,in vitro) determined in hepatic microsomes or hepatocyte suspension cultures, and the blood-to-plasma concentration ratio (BP). Drugs with predominately hepatic elimination were selected and drugs that are known transporter substrates were excluded. Compounds were divided into acidic (n=7), neutral/very weak bases (n=8) and basic drugs (n=7). When an experimental value for microsomal binding was not available, the fraction unbound in microsomal/hepatic incubation was predicted according to a published model [18]. All drugs exhibited linear pharmacokinetics under the presented dose range. Plasma protein binding of the drugs was assumed to be reversible and unsaturated. For the drugs in this study, the observed values of fup range from 0.0038 to 0.08, human hepatic clearance (CLh) from 0.123 to 108.3 L/h, and reported Vss from 7.64 to 962.8 L covering a large range of PK properties for highly bound compounds. The available physicochemical, and in vitro and in vivo PK data are summarized in Table 1.
Table 1.
Drug specific input parameters for the calculation of tissue-to-plasma partitioning parameter (Ptp) and hepatic extraction in the human PBPK generic model.
| Name | fup | pKa | Class | LogPOW | LogD7.4 | fuinc | CLint,in vivo (ml/min kg) | BP | CLh (L/h) | Vss (L) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Obs | Pre | Obs | Pre | |||||||||
|
|
|
|
||||||||||
| Diclofenac | 0.0038 | 4.15 | acid | 4.51 | 0.95 | 0.99 | 189 | 0.55 | 17.7 | 11.4 | 8.92 | 9.27 |
| Fenoprofen | 0.010 | 4.50 | acid | 3.10 | 0.75 | 0.99 | 10.8 | 0.56 | 1.96 | 2.03 | 7.64 | 8.75 |
| Ibuprofen | 0.015 | 4.85 | acid | 3.97 | 1.07 | 0.84 | 8.66 | 0.55 | 3.34 | 2.88 | 8.23 | 9.31 |
| Glipizide | 0.020 | 5.90 | acid | 1.64 | 0.13 | 0.95 | 2.57 | 0.56 | 1.70 | 1.03 | 12.0 | 8.28 |
| Isoxicam | 0.020 | 4.36 | acid | 1.38 | −1.97 | 0.99 | 1.00 | 0.56 | 0.29 | 0.39 | 12.9 | 8.71 |
| ketoprofen | 0.017 | 4.45 | acid | 3.12 | 0.00 | 0.96 | 10.3 | 0.56 | 5.19 | 3.34 | 8.95 | 8.96 |
| Tenoxicam | 0.007 | 4.78 | acid | 1.90 | 0.81 | 0.91 | 1.03 | 0.67 | 0.123 | 0.154 | 12.8 | 9.21 |
| Felodipine | 0.0048 | 5.39 | neutral | 3.86 | 2.95 | 0.32 | 98.0 | 1.00 | 43.6 | 45.1 | 231 | 131 |
| Nifedipine | 0.068 | 5.30 | neutral | 2.20 | 1.10 | 0.90 | 13.0 | 0.67 | 20.5 | 29.9 | 49.5 | 43.5 |
| Prazosin | 0.030 | 6.50 | neutral | 1.30 | 1.88 | 0.99 | 7.65 | 0.70 | 13.6 | 9.94 | 47.5 | 36.8 |
| Lorazepam | 0.058 | 11.0 | neutral | 2.34 | −2.28 | 0.94 | 2.40 | 0.60 | 1.70 | 2.03 | 35.3 | 27.3 |
| Omeprazole | 0.050 | 9.29 | neutral | 2.23 | −0.76 | 0.98 | 98.1 | 0.57 | 31.9 | 51.8 | 18.0 | 32.7 |
| Diazepam | 0.020 | 3.40 | weak base | 2.99 | 2.07 | 0.57 | 2.30 | 0.58 | 4.27 | 3.72 | 122 | 61.7 |
| Midazolem | 0.050 | 6.00 | weak base | 2.95 | 1.93 | 0.88 | 160 | 0.56 | 29.5 | 51.3 | 55.1 | 142 |
| Oxazepam | 0.033 | 2.35 | weak base | 2.90 | 1.88 | 0.90 | 8.06 | 1.00 | 8.53 | 12.6 | 82.3 | 77.2 |
| Clozapine | 0.055 | 7.50 | base | 2.90 | 3.13 | 0.13 | 4.60 | 0.86 | 28.2 | 19.8 | 183 | 283 |
| Fluphenazine | 0.012 | 7.90 | base | 4.36 | 2.89 | 0.12 | 302 | 1.00 | 24.2 | 50.0 | 80.7 | 178 |
| Propafenone | 0.040 | 9.86 | base | 3.20 | −0.054 | 0.26 | 166 | 0.96 | 49.6 | 75.0 | 194 | 293 |
| Haloperidol | 0.080 | 8.66 | base | 4.30 | 3.44 | 0.34 | 50.0 | 0.34 | 35.7 | 58.2 | 401 | 335 |
| Chlorpromazin e |
0.050 | 9.30 | base | 5.40 | 2.53 | 0.11 | 24.9 | 1.56 | 72.9 | 70.3 | 602 | 796 |
| Promethazine | 0.023 | 9.10 | base | 4.38 | 2.30 | 0.11 | 76.3 | 1.88 | 108 | 96.8 | 963 | 968 |
| Verapamil (+) | 0.064 | 8.50 | base | 3.80 | 2.88 | 0.43 | 122 | 0.85 | 58.4 | 63.3 | 242 | 280 |
fup: unbound fraction in plasma; fuinc: unbound fraction in microsomal/hepatocytic incubation; Pow: n-octanol: water partition coefficient of the non-ionized species; Dvo,7.4: vegetable oil: water partition coefficient at pH 7.4; CLint,PB: physiologically based in vivo intrinsic clearance; BP: the blood-to-plasma concentration ratio; CLh: plasma clearance; Vss: distribution volume; Obs: reported value; Pre: predicted value.
Generic PBPK model
The major structural elements of PBPK models are derived from the anatomical structure of the organism. The generic PBPK model used in this study (equations 1 – 7) is composed of 12 compartments, namely blood, adipose, bone, brain, gut, heart, liver, lung, kidney, muscle, skin and spleen. The individual organs relevant to the various pharmacokinetic processes are all interconnected by the systemic circulation, which is divided into arterial and venous blood flows. It is assumed that the uptake of drug is limited by blood perfusion, and drug distribution is achieved instantaneously and homogenously within the tissue (perfusion limited). The liver is considered to be the only site of clearance and no other elimination routes are considered. The anatomical framework contains species-specific physiological parameters (independent of the drug) and can therefore be applied to any compound. Massbalance differential equations were written to describe the change in drug amount over time for each tissue compartment. All simulations were performed with the same model structure using Mathematica (Wolfram Mathematica 9.0, Wolfram Research).
For most non-eliminating tissues (adipose, bone, brain, gut, heart, kidney, muscle, skin, and spleen):
| (1) |
Where, C is concentration (mg/L), Q represents blood flow (L/min), and V refers to volume (L). The subscripts t, ab and vb represent tissue, arterial blood and venous blood, respectively. Cvbt is calculated from the following two equations:
| (2) |
Where, Ptp is the tissue to plasma concentration ratio, defined as
| (3) |
Kpu is the ratio of total tissue concentration to unbound plasma concentration. For the eliminating tissue (liver):
| (4) |
Where, the subscripts h, g and sp represent liver, gut and spleen respectively. Eh is the hepatic extraction ratio. For lung:
| (5) |
Where, the subscript l refers to lung and Qc is the total cardiac output. For arterial blood:
| (6) |
For mixed venous blood:
| (7) |
The mean physiological data for a human male with standard bodyweight of 70 kg were taken from literature [19–21] and are summarized in Table 2. The total cardiac output (L/min) used in the present model was assumed to be 5.69 L/min.
Table 2.
Tissue composition data used for the evaluation of tissue partition coefficient
| Blood flow rate (L/min) |
Volume (L) |
Fractional tissue volume | Tissue Conc. Of Acidic phospholipids (mg/g) | Tissue-to-Plasma | |||||
|---|---|---|---|---|---|---|---|---|---|
| Neutral Lipids | Neutral Phospholipids | Intracellular water | Extracellular water | Albumin Ratio | Lipoprotein Ratio | ||||
| Adipose | 0.296 | 12.46 | 0.853 | 0.00160 | 0.135 | 0.0170 | 0.400 | 0.0490 | 0.0680 |
| Bone+Rest | 0.563 | 15.52 | 0.0170 | 0.00170 | 0.100 | 0.346 | 0.670 | 0.100 | 0.0500 |
| Brain | 0.683 | 1.40 | 0.0390 | 0.00150 | 0.162 | 0.620 | 0.400 | 0.0480 | 0.0410 |
| Gut | 0.967 | 1.20 | 0.0380 | 0.0125 | 0.282 | 0.475 | 2.41 | 0.158 | 0.141 |
| Heart | 0.228 | 0.330 | 0.0140 | 0.0111 | 0.320 | 0.456 | 2.25 | 0.157 | 0.160 |
| Kidney | 1.08 | 0.310 | 0.0120 | 0.0242 | 0.273 | 0.483 | 5.03 | 0.130 | 0.137 |
| Liver | 1.42 | 1.82 | 0.0140 | 0.0240 | 0.161 | 0.573 | 4.56 | 0.0860 | 0.161 |
| Lung | 5.69 | 0.530 | 0.0220 | 0.0128 | 0.336 | 0.446 | 3.91 | 0.212 | 0.168 |
| Muscle | 1.08 | 28.0 | 0.0100 | 0.00720 | 0.118 | 0.630 | 1.53 | 0.0640 | 0.0590 |
| Skin | 0.330 | 2.59 | 0.0600 | 0.00440 | 0.382 | 0.291 | 1.32 | 0.277 | 0.0960 |
| Spleen | 0.114 | 0.168 | 0.00770 | 0.0113 | 0.207 | 0.579 | 3.18 | 0.097 | 0.207 |
| Blood cell | 0.00170 | 0.00290 | – | 0.603 | 0.500 | ||||
Distribution
The in vivo concentration ratio of tissue to plasma (Ptp) was estimated with equation 3. Kpu is obtained from the relationship between physiological data (composition of lipoprotein, water, neutral and acidic phosphate lipids) and compound specific determinants (lipophicility, pKa and plasma protein binding). Kpu was predicted with mechanistic tissue composition equations 8 and 9 developed by Rodgers et al [6, 7]. The equation for acids, very weak bases and neutrals is as follows:
| (8) |
Where, or monoprotic acids X = 1 + 10pHiw−pKa, and Y 1 +10pHp−pKa, or very weak monoprotic bases X = 1+ 10pKa−pHiw and Y = 1+ 10pKa−pHp; or neutral drugs X and Y equal 1 due to the lack of ionization. pHp and pHiw refer to the pH in plasma and intracellular water, which are assumed to be 7.4 and 7.0 respectively. The notation f represents the fractional tissue volume, with the subscripts iw, ew, nl, np and p representing intracellular water, extracellular water, neutral lipid, neutral phospholipid and plasma, respectively. For all tissue except adipose, Pow is the n-octanol: water partition coefficient. For adipose, Pow is replaced by the calculated vegetable oil: water partition coefficient (Dvo, 7.4). [PR] refers to the concentration ratio of serum binding protein in tissue to plasma. For the present model, the albumin ratio is used for acids and the lipoprotein ratio is used for neutral drugs (Table 2). The equation for moderate-to-strong bases is as follows:
| (9) |
For moderate-to-strong bases, X = 1+ 10pKa −pHiw, and Y = 1+ 10pKa−pHp. [AP−]T is the concentration of acidic phospholipids in the tissue, and KaAP is the association constant of compound for acidic phospholipids. As Rodgers indicated previously, KaAP is predicted by rearranging equation 9 to equation 10, and applying it to blood cell. Since there is no extracellular space for blood cells, then that KpuBC (the blood cell to plasma water concentration ratio) can be determined in vitro from the blood-to-plasma concentration ratio, fraction unbound in plasma, and the hematocrit (equation 11) [22].
| (10) |
| (11) |
Where, subscript BC represents blood cell and H is the human hematocrit, which is 0.45.
Elimination
The liver was considered to be the sole elimination site, with no renal elimination of the unchanged drug. The in vitro hepatic intrinsic clearance (CLint,in vitro) values were determined from standard substrate depletion assays, and were scaled up to the physiologically based in vivo intrinsic clearance (CLint,PB). For this purpose, physiologically based scaling factor (SFPB) for hepatic microsomes or hepatocytes were used for the conversion of in vitro parameters to in vivo clearance.
| (12) |
Where, the SFPB (856 mg protein/kg) is the average recovery of microsomal protein per gram of liver (40 mg protein/g liver) multiplied by the average liver weight in human (21.4 g liver/kg or 1500 g liver/70kg). The scaling factor for hepatocytes is (120 × 106 cells/g liver) × (1500 g liver/70 kg bodyweight) [23]. The in vitro clearance of fenoprofen [14], glipizide [14], ketoprofen [23], nifedipine [23], oxazepam [14] and lorazepam [23] were evaluated from hepatocyte data, since either the principal metabolic pathway involves conjugation to glucuronic acid or data from microsomal incubation was unavailable. Hepatic clearance was estimated with the well-stirred model, by integrating Clint,PB,, fup, fuinc and BP into the prediction of the liver extraction ratio (Eh). As proposed by Berezhkovskiy et al [24], a correction for pH partitioning between intracellular and extracellular water was included as follows:
| (13) |
Where, Fic/ec is the ratio of the unbound drug concentrations in tissue intracellular water to extracellular water/plasma at equilibrium. For a neutral drug, Fic/ec is unity. For strong monoprotic basic compounds, the limiting values is when pKa ≥ pHp +2 (strong ionization). This indicates the unbound drug concentration is 2.5-fold greater in intracellular tissue water than plasma. Inversely, the unbound monoprotic acid compounds may be up to 2.5 times smaller in intracellular water than in plasma. Although successful prediction for basic compounds was accomplished based on the SFPB and Fic/ec corrections, the approach tended to systemically underestimate hepatic clearance for acidic and neutral compounds. To address this issue, an empirical scaling factor (SFEmpirical) was introduced to predict Eh for both acidic and neutral drugs.
SFEmpirical was defined as the ratio of observed- to physiological- based intrinsic clearance (CLint,Empirical vs CLint,PB). The former was derived from published plasma clearance (CLh,obs) using a rearrangement of the well stirred liver model with equation 15. The latter (CLint,PB) is calculated with equation 12. Since drug concentration is likely measured in plasma during clinical pharmacokinetic studies, most reported clearance values are referenced to plasma rather than blood. Therefore, the relationship between CLh,obs and CLint,Empirical was described by equation (14):
| (14) |
CLint,Empirical is calculated after rearrangement of equation 14:
| (15) |
The SFEmpirical was determined by the average fold difference between CLint,Empirical and CLint,PB using equation (16) for both acidic and neutral drugs (n=15).
| (16) |
The Eh was predicted for acidic and neutral compounds with equation (17):
| (17) |
Furthermore, two additional compounds, naproxen for acid and zolpidem for neutral, were chosen to estimate the ability of SFEmpirical to predict plasma-time profiles in human. The published human plasma profiles [25, 26] at the clinical doses were compared to the simulated plasma profiles.
Assessment of predictive accuracy
The concentration-time profiles of each drug were simulated with the described PBPK model using physiological parameters, in vitro data, and SFEmpirical. Non-compartmental analyses were performed to estimate the PK parameters at the given dose when comparing the predicted and observed profiles (Kinetica 5.0, Adept Scientific, United Kingdom). Areas under the plasma concentration-time curve (AUC0–t and AUC0−∞) were calculated with the linear trapezoidal rule and standard equations. Cmax represents the maximum observed concentration at the first time point. The half-life (t1/2) was calculated as 0.693/kel (kel is elimination rate constant), clearance (CLh) was calculated as Dose/AUC0−∞, Vss was calculated by the product of CLh and the mean residence time (MRT).
The predicted and observed PK parameters of each drug were compared and an overall degree of accuracy and precision was assessed. Briefly, the prediction accuracy was assessed by comparing predicted versus observed value of Cmax, AUC0–t, MRT, t1/2, CLh and Vss. The average fold error (AFE) is the log average of the fold errors of the parameters, and provides a measure of under- or over-prediction. AFE was calculated to give a measure of predictive ability:
| (18) |
Where n is sample size. Further, absolute average fold error (AAFE) was assessed:
| (19) |
AAFE combines the under- and over-prediction of the parameter, and can be applied to quantities of different orders of magnitude.
The concordance correlation coefficient (CCC) evaluates the degree to which pairs of predicted and observed data fall on the line of unity passing through the origin, and provides a measurement of precision and accuracy [8].
| (20) |
Where, x and y are predicted and observed values, respectively, x and y are the mean values, and the other parameters are detailed as follows:
| (21) |
| (22) |
| (23) |
Impact of altered fup values on Vss and CLh prediction
Inaccurate fup values under non-physiological conditions may result in misleading pharmacokinetic in vitroin vivo predictions, particularly for highly bound drugs. In order to evaluate the impact of inaccurate fup data on PK parameter prediction, we performed identical simulations with altered fup values. Since errors in fup due to unbuffered experimental conditions generally result in decreased fup values, all the reported fup values (see Table 1) were multiplied by 2 [4], and the 22 PBPK models were re-parameterized. This goal of this exercise was not to better predict the pharmacokinetic parameters but to evaluate the impact of errors in fup.
RESULTS
Prediction of SFEmpirical
Prediction accuracy was highly dependent on the properties of the compounds investigated. The drugs in the present study have a large range of pKa values, resulting in Fic/ec values from 0.04 to 2.51. Although combining the parameter Fic/ec with fup, as suggested by Berezhkovskiy[24], predicted CLh accurately for basic drugs, clearance of acidic and neutral drugs was under-predicted and this correction exacerbated the error. In the current study, we combined Fic/ec with a SFEmpirical for acidic and neutral compounds. The SFEmpirical was the average fold difference between observed and predicted intrinsic clearance, which was determined to be 12.1 for all acidic/neutral compounds in current study and was used to correct the under-prediction of CLh for these compounds. The determination of SFEmpirical is given in the Appendix.
Prediction of human plasma concentration-time curves for 22 drugs
Simulated and observed plasma concentration-time curves for each drug are depicted in Figure 1. Visual inspection of plasma concentration-time profiles indicate a general agreement between predicted and observed profiles. The graphs of predicted CLh and Vss compared with observed values were also provided in Figure 2. A comparative assessment of the observed and predicted PK parameters for 22 compounds is given in Table 3. Although there are significant deviations in the predicted and observed plasma profiles, the non-compartmental kinetic parameters obtained with the simulated PBPK model profile were similar to those for the clinical data. Based on the AFEs and AAFEs of all 22 drugs, there is no systematic underestimation or overestimation of the in vivo PK parameters. The more accurately predicted parameters were t1/2 and Cmax, for which 100% (22/22) of compounds fell within twofold error. The predictions of AUC0–t, MRT and CLh are within twofold error for 21 of 22 compounds and one compound within threefold error. Vss was predicted within twofold error for 20 of 22 drugs and the others within threefold error.
Figure 1.
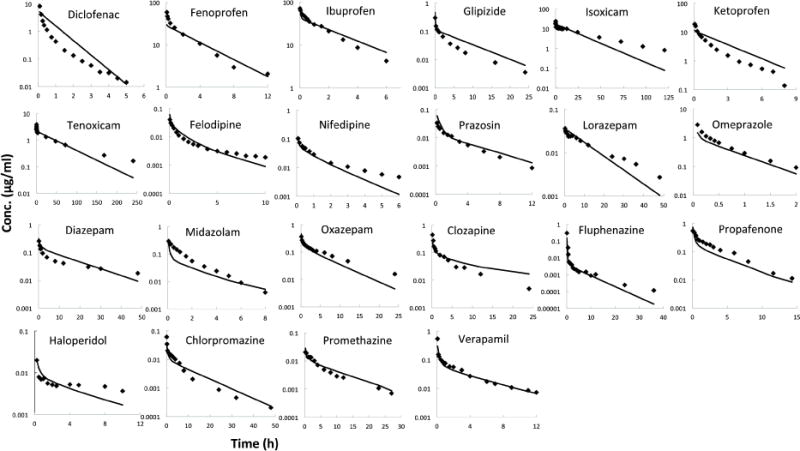
Comparison of PBPK model predicted and observed plasma concentration-time profiles after intravenous administration in human. (The in vivo data were taken from literature as detailed in Methods. Lines are predicted concentration-time curves and plotted data points are observed concentration of drug.)
Figure 2.
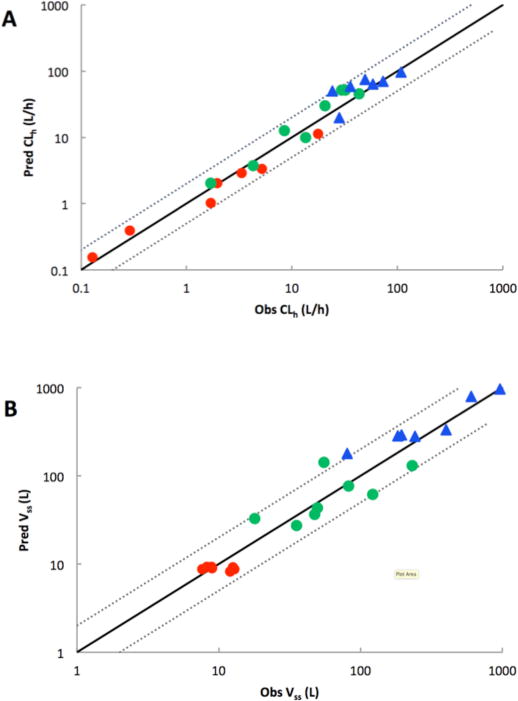
Plot of predicted versus observed CLh and Vss for generic PBPK models. The solid line represents the line of unity and the dotted line represents a twofold error. (The in vivo data were taken from literature and CLh and Vss were determined by a non-compartmental model as detailed in Methods. Acids: red circles; Neutrals: green circles; Bases: blue triangles)
Table 3.
Predictive performance of PBPK model
| PK | n | < 2-folda | 2–3 folda | AFE | AAFE | CCC |
|---|---|---|---|---|---|---|
| Total | ||||||
| Cmax | 22 | 22 | 0 | 0.867 | 1.46 | 0.933 |
| AUC0–t | 22 | 21 | 1 | 0.951 | 1.31 | 0.976 |
| t1/2 | 22 | 22 | 0 | 0.869 | 1.39 | 0.851 |
| MRT | 22 | 21 | 1 | 0.953 | 1.42 | 0.835 |
| CLh | 22 | 21 | 1 | 1.08 | 1.36 | 0.919 |
| Vss | 22 | 20 | 2 | 1.03 | 1.38 | 0.963 |
| Acid | ||||||
| Cmax | 7 | 7 | 0 | 0.771 | 1.49 | 0.896 |
| AUC0–t | 7 | 7 | 0 | 1.17 | 1.29 | 0.964 |
| t1/2 | 7 | 7 | 0 | 0.828 | 1.39 | 0.843 |
| MRT | 7 | 7 | 0 | 1.04 | 1.45 | 0.826 |
| CLh | 7 | 7 | 0 | 0.865 | 1.34 | 0.866 |
| Vss | 7 | 7 | 0 | 0.895 | 1.22 | −0.091 |
| Neutral and Weak Base | ||||||
| Cmax | 8 | 8 | 0 | 1.07 | 1.36 | 0.787 |
| AUC0–t | 8 | 8 | 0 | 0.871 | 1.37 | 0.899 |
| t1/2 | 8 | 8 | 0 | 0.822 | 1.47 | 0.823 |
| MRT | 8 | 8 | 0 | 0.780 | 1.47 | 0.793 |
| CLh | 8 | 8 | 0 | 1.22 | 1.36 | 0.805 |
| Vss | 8 | 7 | 1 | 0.950 | 1.55 | 0.549 |
| Strong Base | ||||||
| Cmax | 7 | 7 | 0 | 0.769 | 1.54 | 0.790 |
| AUC0–t | 7 | 6 | 1 | 0.857 | 1.27 | 0.920 |
| t1/2 | 7 | 7 | 0 | 0.972 | 1.30 | 0.500 |
| MRT | 7 | 6 | 1 | 1.10 | 1.33 | 0.400 |
| CLh | 7 | 6 | 1 | 1.19 | 1.37 | 0.770 |
| Vss | 7 | 6 | 1 | 1.31 | 1.38 | 0.940 |
a: number of drugs who have an AFE of less than 2 and 2–3, respectively.
n: number of drug; AFE: average fold-error; AAFE: absolute average fold-error; CCC: concordance correlation coefficient.
An additional acidic and neutral compound was modeled in order to evaluate the utility of the empirical scaling factor. The present PBPK model with SFEmpirical was able to accurately simulate the plasma profile and predict PK parameters of naproxen and zolpidem (Figure 3). With the exception of Cmax of naproxen, which varied around threefold from the observed value, all other PK parameters were within twofold error (Table 4).
Figure 3.
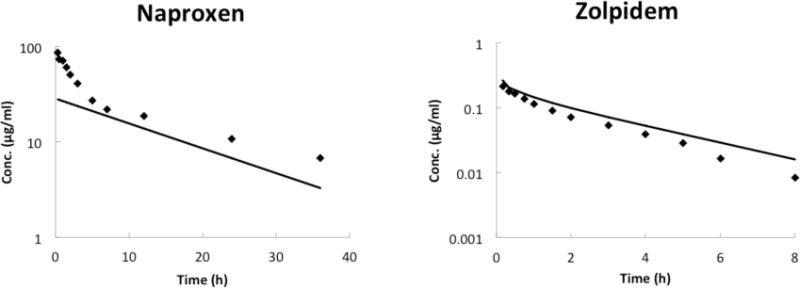
Observed and predicted plasma concentration-time profiles of naproxen and zolpidem after intravenous administration in human. The SFEmpirical predicted in this study was evaluated with one acid and one neutral drug, naproxen and zolpidem respectively. (The in vivo data were taken from literature as detailed in Methods. Lines are predicted concentration-time curves and plotted data points are observed concentration of drug.)
Table 4.
Observed and predicted pharmacokinetic parameters analyzed by non-compartmental model for naproxen and zolpidem after intravenous administration.
| Name | Class | Observed
|
Predicted
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cmax μg/ml |
AUC0–t μg/ml*h |
t1/2 h |
MRT h |
CLh L/h |
Vss L |
Cmax μg/ml |
AUC0–t μg/ml*h |
t1/2 h |
MRT h |
CLh L/h |
Vss L |
||
| Naproxen | Acid | 85.8 | 677 | 17.0 | 21.2 | 0.296 | 6.27 | 28.0 | 448 | 12.7 | 18.4 | 0.480 | 8.78 |
| Zolpidem | Neutral | 0.211 | 0.444 | 1.88 | 2.55 | 21.4 | 54.6 | 0.262 | 0.581 | 2.33 | 3.12 | 15.8 | 49.3 |
Impact of fup assay error on simulated clearance and distribution volume
Since historically reported fup values may be inaccurate due to use of un-buffered plasma, the impact of altered fup values on PK predictions was evaluated. Clearance predictions for low extraction compounds are affected proportionally by increases in fup, whereas predictions for high clearance compounds are not impacted (See figure 4). For neutral and acidic drugs, Vss predictions for low-volume acidic drugs are minimally affected, while Vss for highvolume neutral drugs is proportionally increased. For basic drugs, Vss is relatively insensitive to the fup value used (See figure 5). This is a result of the method used to parameterize tissue binding for basic drugs. The distribution of basic drugs is predominantly modeled by their partitioning into acidic phospholipids. This component in the PBPK model is parameterized with an experimental BP. Since Kpu is derived from a relationship between BP and fup, any error in fup measurements will result in an inversely proportional change in Kpu of basic drugs. Since Ptp is a product of Kpu and fup, the errors will cancel and the Vss prediction will be insensitive to errors in fup. Although the data in Figure 4 were generated with a scaling factor of 12.1, if a new scaling factor were calculated for the data with twofold higher fup, the scaling factor would be decreased from 12.1 to 5.95.
Figure 4.
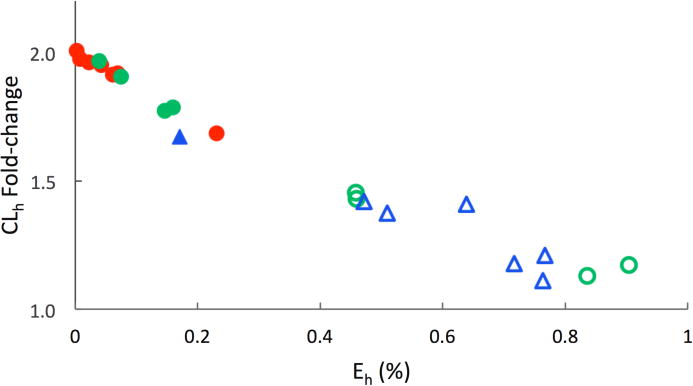
Effect of increased fup (2-fold) on CLh prediction for low to high extraction ratio (Eh) drugs. (Acids: red circle; Neutral: green circles; Bases: blue triangles; poorly cleared compounds with Eh < 0.25: closed symbols; highly cleared compounds with Eh > 0.25: open symbols). The fold-change in CLh was calculated with 2-fold increased fup. This fold-change in CLh is plotted against the Eh of the drug. The fold-change in CLh for low Eh compounds is proportional to increase in fup, whereas CLh for high Eh compounds is unaffected.
Figure 5.
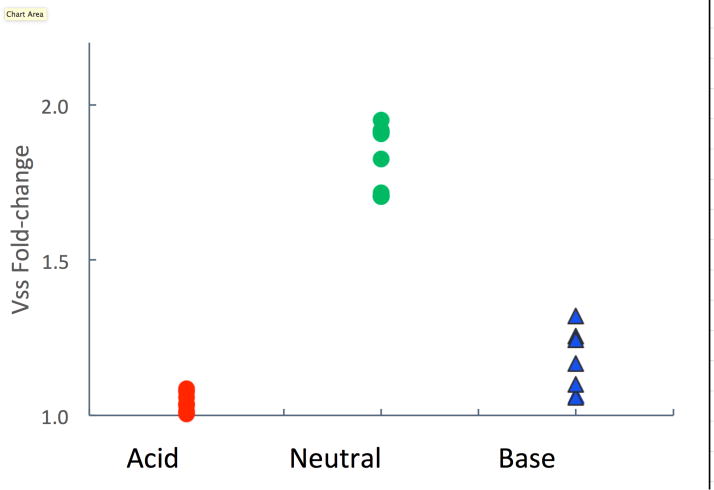
Effect of increased fup (2-fold) on distribution volume prediction for acidic, neutral, and basic compounds. (Acids: red circles; Neutral: green circles; Bases: blue triangles). The fold-change in Vss was calculated with 2-fold increased fup. Vss predictions for low-volume acidic drugs are minimally affected, while Vss for high-volume neutral drugs is proportionally increased. For basic drugs, Vss is relatively insensitive to the fup value used.
DISCUSSION
The observed discrepancy of intrinsic clearance between in vitro and in vivo studies is a major issue that currently prevents the use of PBPK methodology in lieu of animal studies early in discovery. Predicting in vivo intrinsic clearance requires both accurate in vitro measurements and a sufficient understanding of the relationships between in vitro data and in vivo pharmacokinetics. Since intrinsic clearance is determined by the product of fup and the unbound intrinsic clearance, systematic deficiencies in the measurement and interpretation of both of these properties can result in inaccurate predictions. There is evidence that hepatic clearance is usually under-predicted for highly protein-bound compounds such as those in this study [2, 27]. For perfusion-limited PBPK models, it is assumed that equilibrium between blood and liver concentration is instantaneous. Due to different pH of extracellular and intracellular water for hepatocytes (pH partitioning), Berezhkovskiy proposed an ionization correction for hepatic clearance prediction [24, 28]. Including the ionization correction in the current study leads to a relatively unbiased average prediction for basic compounds (AFE=1.19). However, prediction accuracy for acids and neutrals with ionization resulted in an increased under-prediction of clearance (data not shown). Since pH partitioning is a mechanistic expectation, other unknown factors are likely responsible for the under-prediction of acids and neutrals. Therefore, this study applied an empirical scaling factor (SFEmpirical) to correct the systemic under-prediction of hepatic clearance. Ito and Houston[29] evaluated five different methods to predict human in vivo intrinsic clearance: 1) in vitro data with a physiologic scaling factor (SF), 2) an empirical SF, 3) physiologic and drug-specific SFs (the ratio of in vivo and in vitro CLint in rats), 4) using rat CLint,in vivo directly and 5) using rat data with allometric scaling. The authors reported an approximately 9-fold underestimation with the well-stirred model with the physiologic SF to predict in vivo CLint. This was confirmed with a larger data set of 52 drugs. Later, Poulin et al [30] proposed a method based on the hypothesis that the ionic interaction of albumin-drugs complex would supply more unbound drugs to hepatocyte surface and promote distribution in the liver. The correction factor proposed by Poulin is 13.3, which is employed for albumin bound compounds only (including acidic and neutral compounds), and leads to a slight over-prediction for acidic drugs, but within 2-fold AFE. More recently, Halifax and Houston [27] assessed Poulin’s method to predict the CLint,in vivo for 107 drugs, and demonstrated superior precision and lower bias in the majority of cases, but questioned the mechanistic basis for the required scaling factors. Mechanistically, providing a higher concentration of drug at the plasma membrane will not affect the equilibrium of free drug concentrations, since the free energy of the intracellular and extracellular unbound drug are the same. Any process that can alter the equilibrium concentrations, albumin mediated or not, must be energetically driven, either directly or by another concentration gradient. Until such a process is identified, all reported scaling factors are effectively empirical.
The reason that a physiologically-based direct scaling approach leads to a systematic underestimation of clearance for acidic and neutral compounds is still unclear. Although established uptake transporter substrates were excluded from this study, some of the drugs in this study could still be substrates for uptake, and/or efflux transporters. For example, Lagas et al [31] found that diclofenac was efficiently transported by murine Bcrp1 and moderately by human BCRP. Kindla et al [32] demonstrated that diclofenac was significantly transported by OATP1B3. Morita et al [33] investigated the role of rat organic anion transporter 2 (rOat2) in the hepatic uptake of ketoprofen and found this uptake was significantly inhibited by rOat2 inhibitors and probenecid. The involvement of uptake transporters may be one factor contributing to poor prediction of drug clearance.
The relationship between fup and clearance is well understood. The CL of a low extraction drug will be affected to a great extent by the drug’s plasma protein binding. On the other hand, the CL of highly extracted drugs is unlikely to be affected by plasma protein binding [34]. This trend is clearly indicated in the 22 drugs evaluated. As shown in Figure 4, inaccurate fup values can have a profound effect on the clearance prediction for low clearance drugs. Since most of the acidic and neutral compounds in the present dataset are low clearance drugs, errors in predicted clearance will be approximately proportional to any errors in fup. Our thorough understanding of the relationship between fup and clearance[1] clearly underscores the importance of accurate fup determination. This also highlights the potential impact of inaccurate historical fup data (generated with unbuffered plasma) on PK predictions.
We used available IV dosing PK data for this study, and the impact of first pass metabolism is outside the scope of this study. Extra-hepatic metabolism is nevertheless an important factor contributing to drug clearance. Among the drugs we studied, for example, there is evidence for intestinal metabolism of diclofenac, felodipine, nifedipine, midazolam and fenoprofen [35–40]. Our generic PBPK model (Figure A1) assumes only hepatic clearance, and the gut is modeled as a non-eliminating organ. Clearance estimates might be significantly improved by modeling intestinal clearance if this organ clearance contributes significantly to overall drug clearance. In the absence of in vitro intestinal metabolism data and relative contribution of the intestine to overall clearance, it is challenging to model intestinal clearance with enough confidence to obtain meaningful estimates.
The most common method to predict human Vss is to scale animal data. For PBPK models, the methodology proposed by Poulin and Theil [20] uses physicochemical data and physiological data such as tissue composition to define tissue distribution. This method accounts for non-specific binding to lipids and the reversible binding to plasma/tissue protein. With the exception of strong bases, this approach provided reasonable prediction of tissue distribution. Rodgers et al extended the model for tissue distribution by incorporating the high affinity of ionized bases to the acidic phospholipids [6]. In this approach, the binding capacity between the basic drug and acidic phospholipid was parameterized by using red blood cell partitioning in vitro. Several studies have been performed to evaluate these two methodologies. De Buck et al [12] investigated the prediction of human Vss for 26 strong bases and found Rodgers methodology is superior to Poulin and Theil (84% vs 32% within 2-fold errors). Jones et al [41] reported some in-house data from Pfizer and showed similar results (75% vs 45% within 2-fold error).
The present study applied the Rodgers model to predict the drug distribution, and high prediction accuracy was obtained for the 22 compounds evaluated, with 90% of Vss values predicted within 2-fold error and 100% within 3-fold error. The Vss prediction error in the current and previous studies may be a result of model deficits. Errors could be due to poor membrane permeability (these models are not permeability limited) or transporter activity. Other possibilities include inadequate parameterization of the models used to predict Kpu. For example, the vegetable oil to water partition constant, used to parameterize adipose partitioning, is calculated from one of two relationships derived originally for very small molecules and solvents [42]. Since these parameters were used to predict Kpu values ab initio, significant errors could be expected. Many of the predicted concentration-time profiles are log linear whereas most of the experimental profiles show more dramatic distribution phases. Perfusion-limited drug distribution was assumed in this model, i.e., drug concentrations are treated as reaching an instantaneous equilibrium between blood and tissue. Mathematically, the tissues are described as well-stirred compartments where the drug concentration is immediately at the same level throughout the whole tissue. The assumption of perfusion-limitation may be justified for rapidly permeability compounds in highly perfused tissues like heart, liver or kidney. However, the rate-limiting step for distribution will not be captured for tissues with a permeability barrier or compounds with poor permeability [43].
Protein binding can significantly influence the clearance and volume distribution prediction of a compound. Lombardo et al [44] developed the prediction of Vss for 64 neutral and basic compounds and validated this approach with a test group including 14 compounds. It is noted that five of six outliers have fup value below 0.1. Obach et al found the clearance of basic compounds, especially those highly bound to blood proteins were markedly under-predicted [2]. Recently, a PhRMA initiative that predicted human CLh using traditional IVIVE calculation methods, also observed that highly bound drugs were more likely to be outliers [45]. Underestimation of fup values could result in an under-prediction of clearance for drugs with a low unbound intrinsic clearance. The impact of fup on clearance decreases as the organ clearance approaches organ blood flow. Also, plasma protein binding decreases volume of distribution, but low volume drugs will be less sensitive to changes in fup than high volume drugs. Given the importance fup for both primary PK parameters (CLh and Vss), fup data quality and usage should be considered carefully. Historical fup data was not always generated with buffered plasma, resulting in a possible underestimation of fup. We therefore investigated the impact of twofold higher fup on our PBPK predictions. As shown in Figure 4, keeping the scaling factor constant at ~12 for acidic and neutral drugs, predicted CLh was impacted by a twofold increase in fup as expected, with low clearance compounds showing an ~twofold increase in CLh. Alternatively, a new scaling factor of 5.95 could be calculated for the data set with two-fold higher fup.
With the exception of basic compounds, the impact of fup on Vss was as anticipated, with predicted Vss increasing for high volume compounds. For basic compounds, a weaker correlation between an increase in fup and Vss prediction was observed. This can be understood by considering equations 10 and 11, which are used to calculate the tissue binding constant Kpu for basic compounds. These equations use the experimental BP value to calculate binding to acidic phospholipids. As part of this calculation, fup is used to determine the affinity constant (KaAP) for the acidic phospholipids. When binding to acidic phospholipids dominates, Kpu value will decrease twofold with a twofold increase in fup. Kpu will be multiplied by fup to determine Ptp (Eq. 3). Thus, when incorporating the new Kpu and fup values in the PBPK model for basic compounds, errors in fup will largely cancel, resulting in a minimal change in Vss prediction.
For most of the 22 compounds in the present study, the predicted parameters (CLh and Vss) fell within twofold error (Figure 2). This is especially noteworthy, considering that the simulation was based on an ideal 70 kg male human, while the plasma profiles used are from subjects with diverse demographic data and metabolic profiles. Nevertheless, there are several reasons that could explain the discrepancy between observed vs predicted plasma profiles. An obvious cause for inaccurate concentration-time profiles shown in Figure 1 is the assumption that distribution is prefusion-rate-limited. For diclofenac, ketoprofen, glipizide and diazepam, the distribution phase is not well simulated by the model. For the poor parameter predictions in Table 1, inadequacy of fup value could cause poor CLh prediction for compounds with low hepatic extraction, such as glipizide and ketoprofen. Inaccurate intrinsic clearance estimation could cause poor prediction for haloperidol since the compound is metabolized by multiple cytochrome P450 isoform(s) (CYP3A4 and 2D6) and large inter-individual variability in the activity was observed in vitro [46]. The average scaling factor may be inappropriate for isoxicam and lorazepam, and saturation of hepatic metabolism might be considered for propafenone [47]. As indicated previously, consideration of transporters could improve the prediction of distribution and clearance for compounds such as midazolam (Pgp substrate) [48] and diclofenac (BCRP substrate) [31]. Any of the stated reasons or their combination could explain less than optimal prediction for specific drugs.
CONCLUSION
In conclusion, the present PBPK model provides reasonable predictions of human pharmacokinetics for the investigated compounds. These successful predictions were achieved for 22 highly protein bound compounds cleared mainly by hepatic elimination, when an empirical clearance scaling factor was used for neutral and acidic compounds. The present model was built with a dataset including a limited number of drugs. Therefore, additional studies using a larger database are required to evaluate whether the reported scaling factor will translate to a broader chemical space. Significant errors may occur if the underlying assumptions of the model are inaccurate, or in vitro scaling methods are deficient. For instance, active transport processes, extra-hepatic clearance, or permeability rate limited distribution are not captured in the present model. Some of these limitations could be addressed by the addition of permeability barriers with transport. However, this would require the availability of additional input data for quantification of the various processes involved, as well as validation of the in vitro to in vivo scaling approaches [49]. Therefore, it is necessary to update any PBPK model as additional data becomes available.
Acknowledgments
KK and SN acknowledge funding support from NIH grant R01 GM104178-02.
Appendix
Pharmacokinetic references
A set of highly protein-bound compounds (n=22) was studied in this analysis. Drugs were selected based on the availability of intravenous administration data in human clinical studies [A1–22].
Fig A1. Schematic diagram of the generic PBPK model framework.
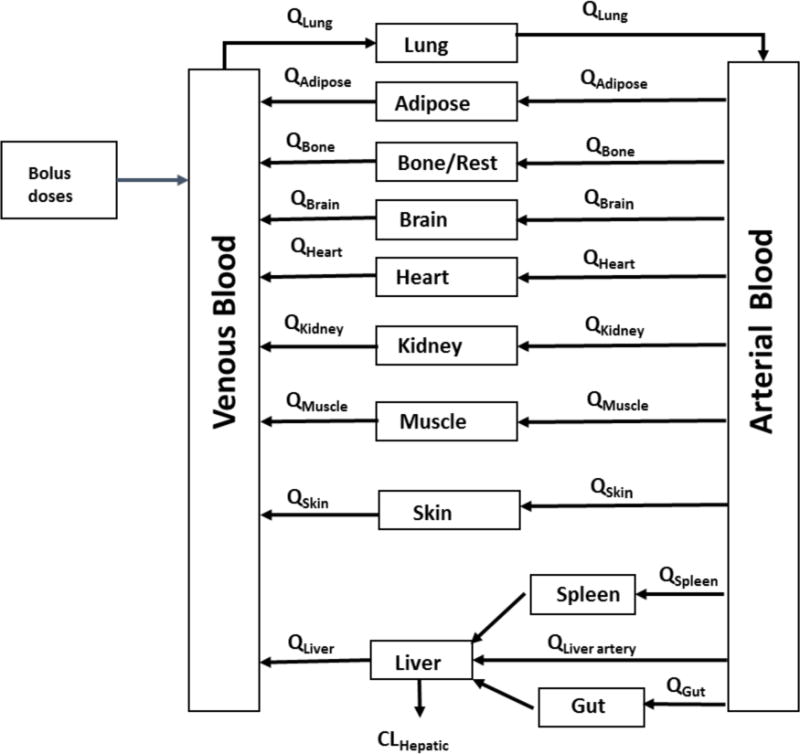
The differential equations are listed in the methods section.
Table A1.
The determination of SFEmpirical for all acidic and neutral drugs
| Name | fup | CLint,PB ml/min kg |
CLint,Empirical ml/min kg |
Fold of (CLint,Empirical/CLint,PB) | |
|---|---|---|---|---|---|
| Acid | Diclofenac | 0.0038 | 189 | 4463 | 23.61 |
| Fenoprofen | 0.01 | 10.8 | 121 | 11.18 | |
| Ibuprofen | 0.015 | 8.66 | 120 | 13.63 | |
| Glipizide | 0.02 | 2.57 | 48 | 18.60 | |
| Isoxicam | 0.02 | 1 | 8.6 | 8.60 | |
| Ketoprofen | 0.017 | 10.29 | 196 | 19.08 | |
| Tenoxicam | 0.007 | 1.03 | 9.6 | 9.31 | |
| Neutral | Felodipine | 0.0048 | 98 | 1413.7 | 14.43 |
| Nifedipine | 0.068 | 13 | 101.0 | 7.77 | |
| Prazosin | 0.03 | 7.65 | 138.4 | 18.09 | |
| Lorazepam | 0.058 | 0.69 | 6.8 | 9.80 | |
| Omeprazole | 0.05 | 98.1 | 432.6 | 4.41 | |
| Diazepam | 0.02 | 2.3 | 31.7 | 13.79 | |
| Midazolam | 0.05 | 160 | 322.3 | 2.01 | |
| Oxazepam | 0.033 | 8.06 | 61.5 | 7.64 | |
| Mean | 12.1 |
- A1.Martin W, Koselowske G, Toberich H, Kerkmann T, Mangold B, Augustin J. Pharmacokinetics and absolute bioavailability of ibuprofen after oral administration of ibuprofen lysine in man. Biopharm Drug Dispos. 1990;11:265–78. doi: 10.1002/bdd.2510110311. [DOI] [PubMed] [Google Scholar]
- A2.Rubin A, Rodda BE, Warrick P, Ridolfo AS, Gruber CM., Jr Physiological disposition of fenoprofen in man. II. Plasma and urine pharmacokinetics after oral and intravenous administration. J Pharm Sci. 1972;61:739–45. doi: 10.1002/jps.2600610514. [DOI] [PubMed] [Google Scholar]
- A3.Willis JV, Kendall MJ, Jack DB. A study of the effect of aspirin on the pharmacokinetics of oral and intravenous diclofenac sodium. Eur J Clin Pharmacol. 1980;18:415–8. doi: 10.1007/BF00636795. [DOI] [PubMed] [Google Scholar]
- A4.Debruyne D, Hurault de Ligny B, Ryckelynck JP, Albessard F, Moulin M. Clinical pharmacokinetics of ketoprofen after single intravenous administration as a bolus or infusion. Clin Pharmacokinet. 1987;12:214–21. doi: 10.2165/00003088-198712030-00003. [DOI] [PubMed] [Google Scholar]
- A5.Kolle EU, Vollmer KO. Pharmacokinetics of isoxicam following intravenous, intramuscular, oral and rectal administration in healthy volunteers. Br J Clin Pharmacol. 1986;22(Suppl 2):135S–141S. doi: 10.1111/j.1365-2125.1986.tb02995.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- A6.Schmidt HA, Schoog M, Schweer KH, Winkler E. Pharmacokinetics and pharmacodynamics as well as metabolism following orally and intravenously administered C14-glipizide, a new antidiabetic. Diabetologia. 1973:320–30. doi: 10.1007/BF01218442. [DOI] [PubMed] [Google Scholar]
- A7.Edgar B, Regardh CG, Lundborg P, Romare S, Nyberg G, Ronn O. Pharmacokinetic and pharmacodynamic studies of felodipine in healthy subjects after various single, oral and intravenous doses. Biopharm Drug Dispos. 1987;8:235–48. doi: 10.1002/bdd.2510080305. [DOI] [PubMed] [Google Scholar]
- A8.Robertson DR, Waller DG, Renwick AG, George CF. Age-related changes in the pharmacokinetics and pharmacodynamics of nifedipine. Br J Clin Pharmacol. 1988;25:297–305. doi: 10.1111/j.1365-2125.1988.tb03307.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- A9.Stebler T, Guentert TW. Bioavailability of intramuscularly administered tenoxicam. Biopharm Drug Dispos. 1993;14:483–90. doi: 10.1002/bdd.2510140604. [DOI] [PubMed] [Google Scholar]
- A10.Bateman DN, Hobbs DC, Twomey TM, Stevens EA, Rawlins MD. Prazosin, pharmacokinetics and concentration effect. Eur J Clin Pharmacol. 1979;16:177–81. doi: 10.1007/BF00562058. [DOI] [PubMed] [Google Scholar]
- A11.Kaplan SA, Jack ML, Alexander K, Weinfeld RE. Pharmacokinetic profile of diazepam in man following single intravenous and oral and chronic oral administrations. J Pharm Sci. 1973;62:1789–96. doi: 10.1002/jps.2600621111. [DOI] [PubMed] [Google Scholar]
- A12.Heizmann P, Eckert M, Ziegler WH. Pharmacokinetics and bioavailability of midazolam in man. Br J Clin Pharmacol. 1983;16(Suppl 1):43S–49S. doi: 10.1111/j.1365-2125.1983.tb02270.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- A13.Sonne J, Loft S, Dossing M, Vollmer-Larsen A, Olesen KL, Victor M, Andreasen F, Andreasen PB. Bioavailability and pharmacokinetics of oxazepam. Eur J Clin Pharmacol. 1988;35:385–9. doi: 10.1007/BF00561369. [DOI] [PubMed] [Google Scholar]
- A14.Cheng YF, Lundberg T, Bondesson U, Lindstrom L, Gabrielsson J. Clinical pharmacokinetics of clozapine in chronic schizophrenic patients. Eur J Clin Pharmacol. 1988;34:445–9. doi: 10.1007/BF01046700. [DOI] [PubMed] [Google Scholar]
- A15.Connolly S, Lebsack C, Winkle RA, Harrison DC, Kates RE. Propafenone disposition kinetics in cardiac arrhythmia. Clin Pharmacol Ther. 1984;36:163–8. doi: 10.1038/clpt.1984.157. [DOI] [PubMed] [Google Scholar]
- A16.Koytchev R, Alken RG, McKay G, Katzarov T. Absolute bioavailability of oral immediate and slow release fluphenazine in healthy volunteers. Eur J Clin Pharmacol. 1996;51:183–7. doi: 10.1007/s002280050182. [DOI] [PubMed] [Google Scholar]
- A17.Andersson T, Cederberg C, Regardh CG, Skanberg I. Pharmacokinetics of various single intravenous and oral doses of omeprazole. Eur J Clin Pharmacol. 1990;39:195–7. doi: 10.1007/BF00280061. [DOI] [PubMed] [Google Scholar]
- A18.Greenblatt DJ, Divoll M, Harmatz JS, Shader RI. Pharmacokinetic comparison of sublingual lorazepam with intravenous, intramuscular, and oral lorazepam. J Pharm Sci. 1982;71:248–52. doi: 10.1002/jps.2600710227. [DOI] [PubMed] [Google Scholar]
- A19.Yeung PK, Hubbard JW, Korchinski ED, Midha KK. Pharmacokinetics of chlorpromazine and key metabolites. Eur J Clin Pharmacol. 1993;45:563–9. doi: 10.1007/BF00315316. [DOI] [PubMed] [Google Scholar]
- A20.Cheng YF, Paalzow LK, Bondesson U, Ekblom B, Eriksson K, Eriksson SO, Lindberg A, Lindstrom L. Pharmacokinetics of haloperidol in psychotic patients. Psychopharmacology (Berl) 1987;91:410–4. doi: 10.1007/BF00216005. [DOI] [PubMed] [Google Scholar]
- A21.Eichelbaum M, Mikus G, Vogelgesang B. Pharmacokinetics of (+)−, (−)− and (+/−)− verapamil after intravenous administration. Br J Clin Pharmacol. 1984;17:453–8. doi: 10.1111/j.1365-2125.1984.tb02371.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- A22.Taylor G, Houston JB, Shaffer J, Mawer G. Pharmacokinetics of promethazine and its sulphoxide metabolite after intravenous and oral administration to man. Br J Clin Pharmacol. 1983;15:287–93. doi: 10.1111/j.1365-2125.1983.tb01501.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
References
- 1.Wilkinson GR, Shand DG. Commentary: a physiological approach to hepatic drug clearance. Clin Pharmacol Ther. 1975;18:377–90. doi: 10.1002/cpt1975184377. [DOI] [PubMed] [Google Scholar]
- 2.Obach RS. Prediction of human clearance of twenty-nine drugs from hepatic microsomal intrinsic clearance data: An examination of in vitro half-life approach and nonspecific binding to microsomes. Drug Metab Dispos. 1999;27:1350–9. [PubMed] [Google Scholar]
- 3.Baker M, Parton T. Kinetic determinants of hepatic clearance: plasma protein binding and hepatic uptake. Xenobiotica. 2007;37:1110–34. doi: 10.1080/00498250701658296. [DOI] [PubMed] [Google Scholar]
- 4.Kochansky CJ, McMasters DR, Lu P, Koeplinger KA, Kerr HH, Shou M, Korzekwa KR. Impact of pH on plasma protein binding in equilibrium dialysis. Mol Pharm. 2008;5:438–48. doi: 10.1021/mp800004s. [DOI] [PubMed] [Google Scholar]
- 5.Poulin P, Theil FP. A priori prediction of tissue:plasma partition coefficients of drugs to facilitate the use of physiologically-based pharmacokinetic models in drug discovery. J Pharm Sci. 2000;89:16–35. doi: 10.1002/(SICI)1520-6017(200001)89:1<16::AID-JPS3>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- 6.Rodgers T, Leahy D, Rowland M. Physiologically based pharmacokinetic modeling 1: predicting the tissue distribution of moderate-to-strong bases. J Pharm Sci. 2005;94:1259–76. doi: 10.1002/jps.20322. [DOI] [PubMed] [Google Scholar]
- 7.Rodgers T, Rowland M. Physiologically based pharmacokinetic modelling 2: predicting the tissue distribution of acids, very weak bases, neutrals and zwitterions. J Pharm Sci. 2006;95:1238–57. doi: 10.1002/jps.20502. [DOI] [PubMed] [Google Scholar]
- 8.Poulin P, Theil FP. Development of a novel method for predicting human volume of distribution at steady-state of basic drugs and comparative assessment with existing methods. J Pharm Sci. 2009;98:4941–61. doi: 10.1002/jps.21759. [DOI] [PubMed] [Google Scholar]
- 9.Austin RP, Barton P, Cockroft SL, Wenlock MC, Riley RJ. The influence of nonspecific microsomal binding on apparent intrinsic clearance, and its prediction from physicochemical properties. Drug Metab Dispos. 2002;30:1497–503. doi: 10.1124/dmd.30.12.1497. [DOI] [PubMed] [Google Scholar]
- 10.Ito K, Houston JB. Comparison of the use of liver models for predicting drug clearance using in vitro kinetic data from hepatic microsomes and isolated hepatocytes. Pharm Res. 2004;21:785–92. doi: 10.1023/b:pham.0000026429.12114.7d. [DOI] [PubMed] [Google Scholar]
- 11.Poulin P, Jones RD, Jones HM, Gibson CR, Rowland M, Chien JY, Ring BJ, Adkison KK, Ku MS, He H, Vuppugalla R, Marathe P, Fischer V, Dutta S, Sinha VK, Bjornsson T, Lave T, Yates JW. PHRMA CPCDC initiative on predictive models of human pharmacokinetics, part 5: Prediction of plasma concentration-time profiles in human by using the physiologically-based pharmacokinetic modeling approach. J Pharm Sci. 2011;100:4125–57. doi: 10.1002/jps.22550. [DOI] [PubMed] [Google Scholar]
- 12.De Buck SS, Sinha VK, Fenu LA, Nijsen MJ, Mackie CE, Gilissen RA. Prediction of human pharmacokinetics using physiologically based modeling: a retrospective analysis of 26 clinically tested drugs. Drug Metab Dispos. 2007;35:1766–80. doi: 10.1124/dmd.107.015644. [DOI] [PubMed] [Google Scholar]
- 13.Jones HM, Gardner IB, Collard WT, Stanley PJ, Oxley P, Hosea NA, Plowchalk D, Gernhardt S, Lin J, Dickins M, Rahavendran SR, Jones BC, Watson KJ, Pertinez H, Kumar V, Cole S. Simulation of human intravenous and oral pharmacokinetics of 21 diverse compounds using physiologically based pharmacokinetic modelling. Clin Pharmacokinet. 2011;50:331–47. doi: 10.2165/11539680-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 14.Sohlenius-Sternbeck AK, Afzelius L, Prusis P, Neelissen J, Hoogstraate J, Johansson J, Floby E, Bengtsson A, Gissberg O, Sternbeck J, Petersson C. Evaluation of the human prediction of clearance from hepatocyte and microsome intrinsic clearance for 52 drug compounds. Xenobiotica. 2010;40:637–49. doi: 10.3109/00498254.2010.500407. [DOI] [PubMed] [Google Scholar]
- 15.Hallifax D, Foster JA, Houston JB. Prediction of human metabolic clearance from in vitro systems: retrospective analysis and prospective view. Pharm Res. 2010;27:2150–61. doi: 10.1007/s11095-010-0218-3. [DOI] [PubMed] [Google Scholar]
- 16.Lau YY, Sapidou E, Cui X, White RE, Cheng KC. Development of a novel in vitro model to predict hepatic clearance using fresh, cryopreserved, and sandwich-cultured hepatocytes. Drug Metab Dispos. 2002;30:1446–54. doi: 10.1124/dmd.30.12.1446. [DOI] [PubMed] [Google Scholar]
- 17.Naritomi Y, Terashita S, Kimura S, Suzuki A, Kagayama A, Sugiyama Y. Prediction of human hepatic clearance from in vivo animal experiments and in vitro metabolic studies with liver microsomes from animals and humans. Drug Metab Dispos. 2001;29:1316–24. [PubMed] [Google Scholar]
- 18.Poulin P, Haddad S. Microsome composition-based model as a mechanistic tool to predict nonspecific binding of drugs in liver microsomes. J Pharm Sci. 2011;100:4501–17. doi: 10.1002/jps.22619. [DOI] [PubMed] [Google Scholar]
- 19.Brown RP, Delp MD, Lindstedt SL, Rhomberg LR, Beliles RP. Physiological parameter values for physiologically based pharmacokinetic models. Toxicol Ind Health. 1997;13:407–84. doi: 10.1177/074823379701300401. [DOI] [PubMed] [Google Scholar]
- 20.Poulin P, Theil FP. Prediction of pharmacokinetics prior to in vivo studies. 1. Mechanism-based prediction of volume of distribution. J Pharm Sci. 2002;91:129–56. doi: 10.1002/jps.10005. [DOI] [PubMed] [Google Scholar]
- 21.Fenneteau F, Poulin P, Nekka F. Physiologically based predictions of the impact of inhibition of intestinal and hepatic metabolism on human pharmacokinetics of CYP3A substrates. J Pharm Sci. 2010;99:486–514. doi: 10.1002/jps.21802. [DOI] [PubMed] [Google Scholar]
- 22.Rowland M, Tozer T. Clinical pharmacokinitics: Concepts and applications. Williams and Wilkins; City: 1995. pp. 502–503. [Google Scholar]
- 23.McGinnity DF, Soars MG, Urbanowicz RA, Riley RJ. Evaluation of fresh and cryopreserved hepatocytes as in vitro drug metabolism tools for the prediction of metabolic clearance. Drug Metab Dispos. 2004;32:1247–53. doi: 10.1124/dmd.104.000026. [DOI] [PubMed] [Google Scholar]
- 24.Berezhkovskiy LM. The corrected traditional equations for calculation of hepatic clearance that account for the difference in drug ionization in extracellular and intracellular tissue water and the corresponding corrected PBPK equation. J Pharm Sci. 2011;100:1167–83. doi: 10.1002/jps.22324. [DOI] [PubMed] [Google Scholar]
- 25.Calvo MV, Lanao JM, Dominguezgil A. Bioavailability of Rectally Administered Naproxen. International Journal of Pharmaceutics. 1987;38:117–122. doi: 10.1016/0378-5173(87)90106-2. [DOI] [Google Scholar]
- 26.Patat A, Trocherie S, Thebault JJ, Rosenzweig P, Dubruc C, Bianchetti G, Court LA, Morselli PL. Eeg Profile of Intravenous Zolpidem in Healthy-Volunteers. Psychopharmacology. 1994;114:138–146. doi: 10.1007/Bf02245455. [DOI] [PubMed] [Google Scholar]
- 27.Hallifax D, Houston JB. Evaluation of hepatic clearance prediction using in vitro data: emphasis on fraction unbound in plasma and drug ionisation using a database of 107 drugs. J Pharm Sci. 2012;101:2645–52. doi: 10.1002/jps.23202. [DOI] [PubMed] [Google Scholar]
- 28.Berezhkovskiy LM, Liu N, Halladay JS. Consistency of the novel equations for determination of hepatic clearance and drug time course in liver that account for the difference in drug ionization in extracellular and intracellular tissue water. J Pharm Sci. 2012;101:516–8. doi: 10.1002/jps.23000. [DOI] [PubMed] [Google Scholar]
- 29.Ito K, Houston JB. Prediction of human drug clearance from in vitro and preclinical data using physiologically based and empirical approaches. Pharm Res. 2005;22:103–12. doi: 10.1007/s11095-004-9015-1. [DOI] [PubMed] [Google Scholar]
- 30.Poulin P, Kenny JR, Hop CE, Haddad S. In vitro-in vivo extrapolation of clearance: modeling hepatic metabolic clearance of highly bound drugs and comparative assessment with existing calculation methods. J Pharm Sci. 2012;101:838–51. doi: 10.1002/jps.22792. [DOI] [PubMed] [Google Scholar]
- 31.Lagas JS, van der Kruijssen CM, van de Wetering K, Beijnen JH, Schinkel AH. Transport of diclofenac by breast cancer resistance protein (ABCG2) and stimulation of multidrug resistance protein 2 (ABCC2)-mediated drug transport by diclofenac and benzbromarone. Drug Metab Dispos. 2009;37:129–36. doi: 10.1124/dmd.108.023200. [DOI] [PubMed] [Google Scholar]
- 32.Kindla J, Muller F, Mieth M, Fromm MF, Konig J. Influence of non-steroidal anti-inflammatory drugs on organic anion transporting polypeptide (OATP) 1B1- and OATP1B3-mediated drug transport. Drug Metab Dispos. 2011;39:1047–53. doi: 10.1124/dmd.110.037622. [DOI] [PubMed] [Google Scholar]
- 33.Morita N, Kusuhara H, Nozaki Y, Endou H, Sugiyama Y. Functional involvement of rat organic anion transporter 2 (Slc22a7) in the hepatic uptake of the nonsteroidal anti-inflammatory drug ketoprofen. Drug Metab Dispos. 2005;33:1151–7. doi: 10.1124/dmd.104.001552. [DOI] [PubMed] [Google Scholar]
- 34.Pang KS, Rowland M. Hepatic clearance of drugs. I. Theoretical considerations of a “well-stirred” model and a “parallel tube” model. Influence of hepatic blood flow, plasma and blood cell binding, and the hepatocellular enzymatic activity on hepatic drug clearance. J Pharmacokinet Biopharm. 1977;5:625–53. doi: 10.1007/BF01059688. [DOI] [PubMed] [Google Scholar]
- 35.Gill KL, Houston JB, Galetin A. Characterization of in vitro glucuronidation clearance of a range of drugs in human kidney microsomes: comparison with liver and intestinal glucuronidation and impact of albumin. Drug Metab Dispos. 2012;40:825–35. doi: 10.1124/dmd.111.043984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Grundy JS, Eliot LA, Foster RT. Extrahepatic first-pass metabolism of nifedipine in the rat. Biopharm Drug Dispos. 1997;18:509–22. doi: 10.1002/(sici)1099-081x(199708)18:6<509::aid-bdd38>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
- 37.Regardh CG, Edgar B, Olsson R, Kendall M, Collste P, Shansky C. Pharmacokinetics of felodipine in patients with liver disease. Eur J Clin Pharmacol. 1989;36:473–9. doi: 10.1007/BF00558072. [DOI] [PubMed] [Google Scholar]
- 38.Rubin A, Warrick P, Wolen RL, Chernish SM, Ridolfo AS, Gruber CM., Jr Physiological disposition offenoprofen in man. 3. Metabolism and protein binding of fenoprofen. J Pharmacol Exp Ther. 1972;183:449–57. [PubMed] [Google Scholar]
- 39.Sattari S, Jamali F. Involvement of the rat gut epithelial and muscular layer, and microflora in chiral inversion and acyl-glucuronidation of R-fenoprofen. Eur J Drug Metab Pharmacokinet. 1997;22:97–101. doi: 10.1007/BF03189791. [DOI] [PubMed] [Google Scholar]
- 40.Thummel KE, O’Shea D, Paine MF, Shen DD, Kunze KL, Perkins JD, Wilkinson GR. Oral first-pass elimination of midazolam involves both gastrointestinal and hepatic CYP3A-mediated metabolism. Clin Pharmacol Ther. 1996;59:491–502. doi: 10.1016/S0009-9236(96)90177-0. [DOI] [PubMed] [Google Scholar]
- 41.Jones HM, Gardner IB, Watson KJ. Modelling and PBPK simulation in drug discovery. AAPSJ. 2009;11:155–66. doi: 10.1208/s12248-009-9088-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Leo A, Hansch C, Elkins D. Partition Coefficients and Their Uses. Chemical Reviews. 1971;71:525–616. doi: 10.1021/Cr60274a001. [DOI] [Google Scholar]
- 43.Blakey GE, Nestorov IA, Arundel PA, Aarons LJ, Rowland M. Quantitative structure-pharmacokinetics relationships: I. Development of a whole-body physiologically based model to characterize changes in pharmacokinetics across a homologous series of barbiturates in the rat. J Pharmacokinet Biopharm. 1997;25:277–312. doi: 10.1023/a:1025771608474. [DOI] [PubMed] [Google Scholar]
- 44.Lombardo F, Obach RS, Shalaeva MY, Gao F. Prediction of volume of distribution values in humans for neutral and basic drugs using physicochemical measurements and plasma protein binding data. J Med Chem. 2002;45:2867–76. doi: 10.1021/jm0200409. [DOI] [PubMed] [Google Scholar]
- 45.Ring BJ, Chien JY, Adkison KK, Jones HM, Rowland M, Jones RD, Yates JW, Ku MS, Gibson CR, He H, Vuppugalla R, Marathe P, Fischer V, Dutta S, Sinha VK, Bjornsson T, Lave T, Poulin P. PhRMA CPCDC initiative on predictive models of human pharmacokinetics, part 3: Comparative assessement of prediction methods of human clearance. J Pharm Sci. 2011;100:4090–110. doi: 10.1002/jps.22552. [DOI] [PubMed] [Google Scholar]
- 46.Kudo S, Ishizaki T. Pharmacokinetics of haloperidol: an update. Clin Pharmacokinet. 1999;37:435–56. doi: 10.2165/00003088-199937060-00001. [DOI] [PubMed] [Google Scholar]
- 47.Komura H, Iwaki M. Nonlinear pharmacokinetics of propafenone in rats and humans: application of a substrate depletion assay using hepatocytes for assessment of nonlinearity. Drug Metab Dispos. 2005;33:726–32. doi: 10.1124/dmd.104.002550. [DOI] [PubMed] [Google Scholar]
- 48.Tolle-Sander S, Rautio J, Wring S, Polli JW, Polli JE. Midazolam exhibits characteristics of a highly permeable P-glycoprotein substrate. Pharm Res. 2003;20:757–64. doi: 10.1023/a:1023433502647. [DOI] [PubMed] [Google Scholar]
- 49.Rowland M, Peck C, Tucker G. Physiologically-based pharmacokinetics in drug development and regulatory science. Annu Rev Pharmacol Toxicol. 2011;51:45–73. doi: 10.1146/annurev-pharmtox-010510-100540. [DOI] [PubMed] [Google Scholar]


