Abstract
Objective
The purpose of this study was to compare the relative fit of two alternative factor models of allostatic load (AL) and physiological systems, and to test factor invariance across age and sex.
Methods
Data were from the Midlife in the United States (MIDUS) II study Biomarker Project, a large (N = 1,255) multisite study of adults aged 34–84 (56.8% women). Specifically, 23 biomarkers were included, representing seven physiological systems: metabolic lipids, metabolic glucose, blood pressure, parasympathetic nervous system, sympathetic nervous system, hypothalamic-pituitary-adrenal axis, and inflammation. For factor invariance tests, age was categorized into three groups (≤ 45, 45 to 60, and > 60 years).
Results
A bi-factor model where biomarkers simultaneously load onto a common allostatic load factor and seven unique system-specific factors provided the best fit to the biomarker data (CFI = .967, RMSEA = .043, SRMR = .028). Results from the bi-factor model were consistent with invariance across age groups and sex.
Conclusions
These results support the theory that represents and operationalizes AL as multi-system physiological dysregulation and operationalizing AL as the shared variance across biomarkers. Results also demonstrate that in addition to the variance in biomarkers accounted for by AL, individual physiological systems account for unique variance in system-specific biomarkers. A bi-factor model allows researchers greater precision to examine both AL and the unique effects of specific systems.
Keywords: physiological dysregulation, allostatic load, biomarkers, MIDUS
INTRODUCTION
Psychosomatic research has characterized the relations of psychological variables and indicators of major physiological regulatory systems in humans such as the parasympathetic nervous system (PNS) and the hypothalamic-pituitary-adrenal (HPA) axis (for examples of reviews, see 1, 2, 3). Measures of physiological systems are frequently operationalized via the use of biomarkers. As the field of psychosomatic medicine has advanced, it is increasingly common for multiple biomarkers to be assessed. Although many biomarkers exist for each physiological system, there is little consensus on how to integrate these biomarkers to assess the state and functioning of physiological systems and multi-system physiological dysregulation. Despite the lack of consensus on how to integrate multiple biomarkers, it does appear that employing combinations of biomarkers is valuable. For example, in one study, a composite risk score of biomarkers predicted all-cause mortality over and above age and sex (4), and in another study the number of high risk biomarkers combined demonstrated a gradient relationship with mortality (5).
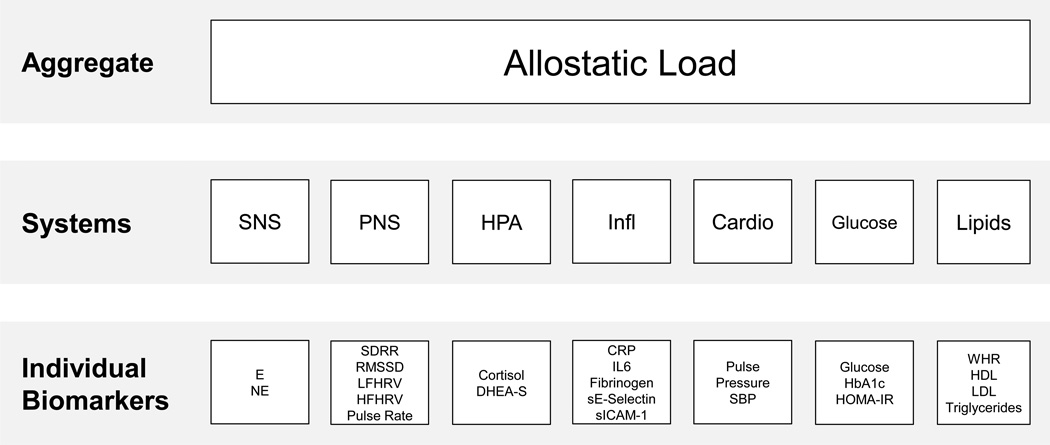
One conceptual approach to integrating biomarkers of multiple systems is allostatic load (AL), which posits that the body’s adaptation to challenge and demands of the environment (allostasis; 6) over time takes a physiological toll and results in cumulative wear-and-tear or dysregulation across multiple physiological systems (7). Thus, the dysregulation is hypothesized to be a multi-systems phenomenon that occurs across multiple regulatory systems rather than in particular systems only (for a review, see 8). Figure 1 shows a diagram of three potential levels of analysis for biomarkers, from using specific biomarkers as outcomes (bottom), to combining multiple biomarkers to assess specific physiological systems (middle), and the highest aggregate combining multiple physiological systems (AL; top). The primary goal of this paper is to test two plausible measurement models of biomarkers hypothesized to represent both overall AL and individual physiological systems.
Figure 1.
Continuum of specificity of biomarker outcomes, from the level of individual biomarkers, to individual physiological systems, to composites across multiple systems.
An individual with allostatic overload and system-wide dysregulation will demonstrate some degree of dysregulation in multiple physiological regulatory system involved in allostasis, and this physiological dysregulation may be assessed using a composite index from multiple systems. To date, such Indices of AL have typically been created by assuming equal influence of individual biomarkers, dichotomizing them into high and low health risk based on quartiles or clinical risk points, averaging within a particular physiological system (e.g., cardiovascular), and then summing (e.g., 4, 9). Similar indices have been created by first standardizing individual biomarkers and then summing (e.g., 10). Although less commonly applied to biological data, scale development and testing methods such as factor analysis have been used for years to develop and validate measures of latent constructs (e.g., depressive symptoms) from multiple observed indicators (e.g., feeling sad or blue, loss of interest). For an introduction to factor analysis in psychosomatic research, see (11).
The few studies that have examined the psychometric properties and tested the factor structure of biomarkers in relation to AL found that a second-order AL factor (i.e., biomarkers load onto individual system factors which in turn load onto AL) provided adequate fit to the data (12–14). Related work in metabolic syndrome has shown a similar hierarchical factor structure (e.g., 15, 16). In addition, a second-order AL factor model of biomarkers was found to be invariant across sex and ethnicity (13), and provided good fit when controlling for sex and age (12); it did, however, differ between participants on and off of medications in an elderly sample (14).
Limitations are apparent in the existing literature on AL. First, previous research has had relatively few biomarkers per system, leaving open the question whether the same factor structure will emerge when systems are more comprehensively assessed. Second, although AL is hypothesized to be prominent in the aging process (17), to our knowledge, no previous study has tested whether the measurement of AL is invariant across adulthood or whether the relations among biomarkers differ as a function of age. Finally, although a second-order factor model provided adequate fit in previous studies, there was room for improvement of model fit. Given the complex relations among biomarkers, examining alternative models may be valuable.
In the present study, we used data from the Midlife in the United States (MIDUS) II Biomarker Project, to address the following aims.
Aim 1
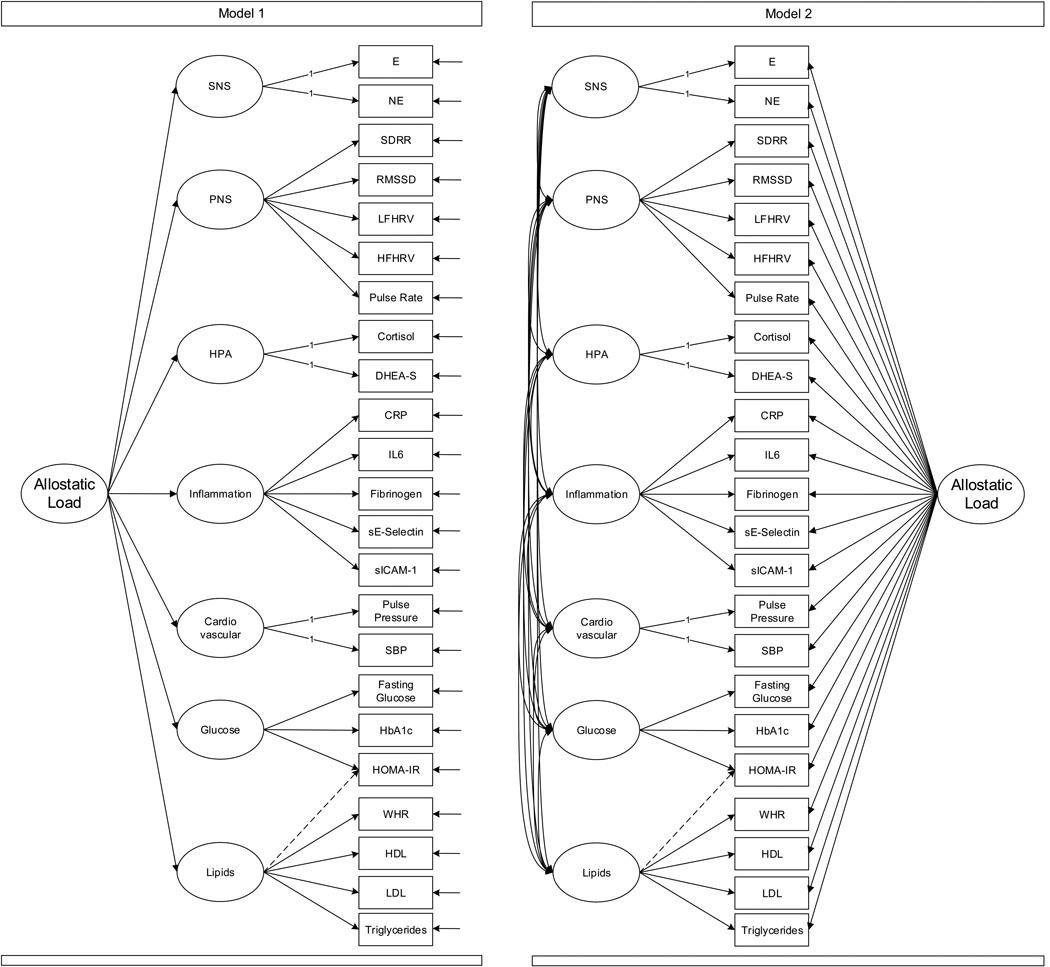
To test and compare two theoretically-derived factor models that reflect the following hypotheses: (1) biomarkers within a physiological system are associated, and (2) based on AL theory that there is system-wide dysregulation, biomarkers or systems should load onto a common factor. The structure of the two models is diagrammed in Figure 2.
Figure 2.
Sample diagrams of the two plausible factor models tested and compared. Adapted from http://score-project.org and reprinted with permission.
Model 1
Biomarkers load onto their respective physiological system, and the seven systems, in turn, load onto a second-order factor. This model tests whether relations among biomarkers are explained by each physiological subsystem, and the relations among the physiological subsystems are explained by a single, common second-order factor (allostatic load).
Model 2
Biomarkers load onto their respective physiological system, and the seven systems are allowed to freely covary; in addition, each biomarker loads directly onto a common factor (AL). This bi-factor model tests whether the relations among biomarkers are explained by two processes: 1) a common factor, capturing the notion that there is an underlying process influencing multiple physiological systems and 2) system-specific factors, capturing the notion that beyond the common portion shared across biomarkers, there are unique effects of particular physiological systems that are independent of other systems. Model 1 is nested within Model 2 allowing for a direct test of fit.
Specifically, we hypothesize that Model 1 will demonstrate acceptable fit and represent a parsimonious version of a correlated-systems model. Finally, if system-wide effects drive the individual systems, then Model 2 will demonstrate no better fit than Model 1, and be less parsimonious. However, if the system-wide and system-specific effects have unique and non-overlapping elements, Model 2 should demonstrate better fit. Because we expect important, unique system-wide and system-specific effects, we hypothesize that Model 2 will demonstrate the best fit.
Aim 2
To test whether the optimal factor structure underlying biomarkers of AL (Aim 1) is invariant across adulthood from 34 to 84 years of age and sex.
Methods
Sample
The sample came from the larger MIDUS study. The first wave of data, MIDUS I, included phone interviews and mailed questionnaires to a national sample of adults, aged 25 to 74 and was designed to assess factors related to physical and psychological health and well-being in early adulthood, middle adulthood, and older age. Data for MIDUS I were collected in 1994-1995 in four parts: a large, national probability sample (the core sample; N = 3,487), siblings of the core sample (N = 950), twins (N = 957 pairs), and an over-sampling in metropolitan areas (N = 757). Participants from MIDUS I, as well as an additional sample of urban African-Americans living in Milwaukee, WI (N = 592, to increase diversity) were assessed in 2005 for MIDUS II (18). MIDUS II included follow up questionnaires, and a subset of participants who were eligible and consented (N = 1,054 from the original sample and N = 201 from the Milwaukee sample) participated in the MIDUS II Biomarker Project, where extensive biological data were collected (19). Thus, a total of 1,255 participants were included coming from 1,098 families (944 families contributing one participant, 152 families contributing two participants, one family contributing three participants, and one family contributing four participants).
Procedure
As part of the MIDUS II Biomarker project, participants went to one of three (University of California Los Angeles, University of Wisconsin, and Georgetown University) General Clinical Research Centers for a medical exam, comprehensive biomarker assessment (e.g., fasting blood draw, 12-hour urine, electrocardiography), and reported on medication history. Details on MIDUS are available online at http://www.midus.wisc.edu and for the biomarker project, see (19). The MIDUS II Biomarker Project was approved by the Institutional Review Boards of the University of Wisconsin, Madison, the University of California, Los Angeles, and Georgetown University.
Demographics and Health Outcomes
Demographic data including age, sex, and ethnicity were collected via self-report. Self-reported medication use, including antihypertensive medications, heart rate reducing (e.g., beta blockers), diabetes medications, cholesterol-lowering mediations, and fibrates, was collected and used to identify medication free participants.
Biological Measures
Seven physiological systems were measured using 23 biomarkers. Details on collection and assay of biomarkers are reported in Supplementary data file 1 in (20).
Sympathetic Nervous System
The sympathetic nervous system (SNS) was measured using 12-hour, overnight urinary epinephrine (E) in μg/g creatinine and norepinephrine (NE) in μg/g creatinine.
Parasympathetic Nervous System
The parasympathetic nervous system (PNS) was measured using heart rate variability and resting pulse rate (in beats per minute). Heart rate variability was assessed via electrocardiography and was operationalized as the standard deviation of beat to beat intervals (R―R interval; SDRR), root mean square of successive differences (RMSSD), low frequency spectral power (LFHRV) and high frequency spectral power (HFHRV).
Hypothalamic Pituitary Adrenal Axis
The hypothalamic pituitary adrenal (HPA) axis was measured using 12-hour, overnight urinary cortisol mg/g creatinine and blood serum dihydroepiandrosterone sulfate (DHEA-S) in μg/dL.
Inflammation
Inflammation was measured using plasma levels of C-reactive protein (CRP) in mg/L, interleukin-6 (IL6), fibrinogen in mg/dL, sE-Selectin in ng/mL, and soluble intracellular adhesion molecule 1 (sICAM-1) in ng/mL.
Cardiovascular
The cardiovascular system was measured with resting systolic blood pressure (SBP) in mmHg and diastolic blood pressure (DBP) in mmHg. For the model, these were converted into pulse pressure (SBP – DBP) and SBP.
Glucose
The metabolic glucose system was measured using the homeostatic model assessment of insulin resistance (HOMA-IR), fasting glucose in mg/dL, and glycosylated hemoglobin (HbA1c) in percent.
Lipids
The metabolic lipid system was measured using waist-to-hip ratio (WHR), high density lipoprotein (HDL) cholesterol in mg/dL, low density lipoprotein (LDL) cholesterol in mg/dL, and triglycerides in mg/dL.
Data Analysis
Structural equation modelling (SEM) was used to compare the two alternative models of the relations among biomarkers, with age and sex included as covariates for each biomarker.
Model fit indices were used to find the best fitting of the two hypothesized factor structures. In addition, Model 1 is nested within Model 2. A chi-square difference test adjusted for the scaling factor (21) was conducted between Models 1 and 2. Multiple group SEM was used to test whether the best-fitting model (1 or 2) was the same (invariant) or varied across different groups. Specifically, model invariance was tested for age group (≤ 45, 45 to 60, >60 years) to establish whether the structure is consistent or differs for younger and older participants and sex (Female vs. Male). To compare factor means across groups (a common objective in research on allostatic load), it is generally considered necessary (22) that the models at least demonstrate: configural invariance (i.e., the same number of factors, and indicators loading on the same factors), metric invariance (i.e., the factor loadings are identical across groups), and scalar invariance (i.e., the intercepts of the indicators are identical across groups). Sequentially more constrained models (i.e., configural only, configural + metric, and configural + metric + scalar) across groups were tested. Chi-square tests are reported, but results are considered consistent with model invariance only if the most restrictive configural + metric + scalar invariance was met as demonstrated both by adequate model fit and by minimal change in model fit (CFI, RMSEA, SRMR) from less constrained models, with ΔCFI < .01 being suggested as one indicator of an invariant model (23). Residual variances were not constrained to be equal across groups, as it is expected that variability may differ between groups (e.g., participants in the youngest age group may not have the same range on biomarkers as older adults may have).
Finally, if the bi-factor model is correct, it should exhibit item parameter invariance (24), that is, the same general and system-specific factor loadings should result regardless of the specific subset of biomarkers or systems assessed. This follows from the logic that if the items are indicators of the latent factors specified, we should be measuring the same latent factor regardless of which specific indicators are used, and so when some items are dropped, the factor loadings of the remaining items should not change (i.e., be invariant). To examine item parameter invariance, seven additional models were fit. Each of the seven models started with the overall bi-factor model on all participants, and systematically dropped one of the seven systems by removing all the biomarkers of a particular system as well as the system-specific factor. For example, one model was the bi-factor model without the inflammation system, and dropped CRP, IL6, fibrinogen, sE-Selectin, and sICAM-1, leaving 18 biomarkers, one common AL factor, and six system-specific factors.
Statistical Methods
Biomarkers were assessed for univariate normality and log transformations were applied to E, NE, SDRR, RMSSD, LFHRV, HFHRV, cortisol, DHEA-S, CRP, IL6, sE-Selectin, HbA1c, fasting glucose, HOMA-IR, and triglycerides. Outliers were addressed by Winsorizing the lower and upper 0.5%. Because multivariate non-normality remained despite these transformations, a robust estimator and standard errors were used. To address the small amount (< 3%) of missing data, full information maximum likelihood (FIML) estimation was used (25). Standard errors and model tests were adjusted for non-independence within families using clustered standard errors based on the Huber-White “sandwich” estimator implemented in Mplus, thus independence is assumed among cluster units, not individual units
Good model fit was chosen as the combination of the Comparative Fit Index (CFI) > 0.95, standardized root mean squared residual (SRMR) < .08, and root mean squared error of approximation (RMSEA) < .06 (26). Example Mplus input scripts are available from the Standardizing Physiological Composite Risk Endpoints Project website: http://score-project.org. Data management, descriptive statistics, and transformations were conducted using R v. 3.1.1 (27) and Mplus v. 7.3 (Los Angeles, CA: Muthén & Muthén) via MplusAutomation v. 0.6-3 (28) for the structural equation models.
Results
Participant age ranged from 34 to 84 with approximately equal numbers of females and males. Sample characteristics and descriptive statistics for the biomarkers (untransformed) are presented in Table 1. Based on preliminary analyses, three modifications were made to all hypothesized models. First, HOMA-IR was allowed to cross load on both the lipid metabolism and glucose metabolism factors. Second, heart rate was used as an indicator of the PNS rather than the cardiovascular factor. Third, a residual correlation between HFHRV and RMSSD was allowed. No other modifications to the hypothesized models were made.
Table 1.
Descriptive statistics for sample demographics and raw biomarker values
| Median (IQR)/N (%) | |
|---|---|
| Demographics | |
| Age (years) | 54 (45, 62) |
| Sex: Female | 713 (56.8%) |
| Ethnicity: White | 967 (77.2%) |
| African American | 222 (17.7%) |
| Other | 64 (5.1%) |
| Medications: None | 486 (38.7%) |
| Sympathetic nervous system | |
| Urine epinephrine (mg/g of creatinine) | 1.67 (1.13, 2.46) |
| Urine norepinephrine (mg/g of creatinine) | 24.80 (18.14, 32.94) |
| Parasympathetic nervous system | |
| R-R interval standard deviation (ms) | 32.53 (23.72, 44.62) |
| Root mean square of successive differences (ms) | 18.38 (12.13, 27.57) |
| Low-frequency power (ms2) | 245.95 (114.95, 514.50) |
| High-frequency power (ms2) | 140.45 (58.80, 304.75) |
| Resting heart rate (beats per minute) | 70.00 (64.00, 79.00) |
| Hypothalamic-pituitary-adrenal axis | |
| Urine cortisol (mg/g of creatinine) | 12.00 (6.75, 19.00) |
| Serum dehydroepiandrosterone sulfate (µg/dL) | 87.00 (52.00, 145.00) |
| Inflammation | |
| Serum C-reactive protein (mg/L) | 1.44 (0.69, 3.64) |
| Serum interleuken-6 (ng/L) | 2.17 (1.37, 3.52) |
| Fibrinogen (mg/dL) | 344.00 (291.00, 403.00) |
| Soluble E-selectin (ng/mL) | 39.16 (28.17, 52.41) |
| Soluble Intracellular adhesion molecule-1 (mg/L) | 273.85 (220.03, 338.08) |
| Cardiovascular | |
| Pulse Pressure (mmHg) | 54.00 (45.00, 64.00) |
| Systolic blood pressure (mmHg) | 130.00 (119.00, 143.00) |
| Glucose | |
| Fasting blood glucose (mg/dL) | 96.00 (90.00, 105.00) |
| Blood glycosylated hemoglobin (%) | 5.86 (5.60, 6.24) |
| Homeostasis model assessed insulin resistance | 2.40 (1.43, 4.35) |
| Lipids | |
| Waist-to-hip circumference ratio | 0.89 (0.82, 0.97) |
| High-density lipoprotein cholesterol (mg/dL) | 52.79 (42.50, 66.25) |
| Low-density lipoprotein cholesterol (mg/dL) | 102.00 (80.23, 128.32) |
| Serum triglycerides (mg/dL) | 106.00 (77.00, 155.00) |
Aim 1: Model Comparisons
Model fit indices comparing the two alternative models (Figure 2) are shown in Table 2. The second-order model (Model 1) demonstrated acceptable fit, with two of three indices meeting the criteria for good fit, although the CFI did not (CFI = .928, RMSEA = .058, SRMR = .056). As expected, the bi-factor model (Model 2) demonstrated the best fit to the data, and met all criteria for good model fit (CFI = .967, RMSEA = .043, SRMR = .028). The bi-factor model also fit significantly better than the second-order factor model (Δχ2df = 36 = 508.68, p < .001). These results suggest that a common factor does underlie the individual biomarkers, but that there are also unique, system-specific effects.
Table 2.
Model Fit Statistics
| Bi-factor Invariance Testing |
||||
|---|---|---|---|---|
| Second Order | Bi-factor | Age | Sex | |
| Parameters | 120 | 156 | 364 | 214 |
| χ2 | 1174.1 | 623.6 | 1215.4 | 1004.6 |
| DF | 225 | 189 | 671 | 430 |
| P value | <.001 | <.001 | <.001 | <.001 |
| CFI | .928 | .967 | .957 | .953 |
| TLI | .904 | .948 | .942 | .940 |
| RMSEA | .058 | .043 | .044 | .046 |
| LL | .055 | .039 | .040 | .042 |
| UL | .061 | .047 | .048 | .050 |
| SRMR | .056 | .028 | .051 | .042 |
| AIC | 66297.9 | 65750.2 | 65704.4 | 65726.6 |
| BIC | 66914.0 | 66551.1 | 67573.2 | 66825.3 |
Note. CFI = Comparative Fit Index, TLI = Tucker Lewis Index, RMSEA = root mean square error of approximation, LL = 90% CI lower limit for RMSEA, UL = 90% CI upper limit for RMSEA, SRMR = standardized root mean square residual, AIC = Akaike Information Criterion, BIC = Bayesian Information Criterion. Age groups were ≤ 45 (n = 324), 45 to 60 (n = 557), and >60 years (n = 373) and sex groups were female (n = 712) and male (n = 542). Invariance was tested for the best fitting, bi-factor model. Continuous age and sex were included as covariates in all models, except sex was omitted as a covariate in the sex invariance model. N ranged from 1,252 – 1,254 due to missing data.
Aim 2: Model Invariance
The fit of the bi-factor model was tested across age (≤ 45, 45 to 60, > 60 years) and sex (female, male) groups using a multiple group model. Results from the configural, configural + metric, and configural + metric + scalar invariance tests are shown in Table S1 and sex-specific loadings are shown in Figure S1, in Supplemental Digital Content 1. The configural + metric + scalar invariant models were tested against the configural only model for sex. The configural only model for age did not converge, so for age, the configural + metric invariant model was used as the comparison. For this reason, age group-specific loadings also could not be shown as only the constrained models converged, which by definition have identical loading. Although the configural + metric + scalar invariant model fit statistically significantly worse for both age and sex (all ps < .05), the change in fit indices was small for age (ΔCFI = .003, ΔRMSEA = .001, ΔSRMR = .002) and sex (ΔCFI = .007, ΔRMSEA = .001, ΔSRMR = .008). In addition, the configural + metric + scalar invariant models demonstrated good fit (all CFIs > .95, all RMSEAs < .06, all SRMRs < .08). Thus, overall the results were consistent with model invariance by age and sex. The final configural + metric + scalar invariant model fit indices are shown in Table 2.
Final Model Estimates
The standardized loadings of each biomarker on the system-specific and common AL factor for the final overall bi-factor model are shown in Table 3. With the exception of LDL, E, and DHEA-S, all biomarkers loaded significantly and in the direction such that higher AL scores indicate more physiological dysregulation. LDL and DHEA-S were not statistically significant, and E loaded negatively on AL, indicating that the higher the AL score, the lower E. Although biomarkers from the PNS and cardiovascular (blood pressure) systems loaded in the expected directions and were statistically significant, loadings were small or modest. In the bi-factor model, most correlations among biomarkers across systems will be captured by the common AL factor, so as expected the estimated correlations among the latent system-specific factors were generally small, with the largest two between the HPA and SNS (r = .34) and cardiovascular system (r = .23), with all other factor correlations ≤ .20 (see Table 4 for details).
Table 3.
Standardized Factor Loadings from the Final Bi-factor Model
| Overall Bi-Factor Model | Medication Free Bi-Factor Model | |||
|---|---|---|---|---|
| System Loadings | AL Loadings | System Loadings | AL Loadings | |
| SNS | Loading [95% CI] | Loading [95% CI] | Loading [95% CI] | Loading [95% CI] |
| E | 0.70*** [0.67, 0.74] | −0.27*** [−0.35, −0.18] | 0.70*** [0.64, 0.77] | −0.33*** [−0.47, −0.18] |
| NE | 0.70*** [0.66, 0.73] | 0.14** [0.05, 0.22] | 0.71*** [0.65, 0.76] | 0.10 [−0.04, 0.25] |
| PNS | ||||
| SDRR | −0.93*** [−0.96, −0.91] | −0.20*** [−0.28, −0.12] | −0.94*** [−0.98, −0.91] | −0.12 [−0.27, 0.03] |
| RMSSD | −0.81*** [−0.84, −0.79] | −0.11* [−0.19, −0.02] | −0.81*** [−0.85, −0.78] | −0.08 [−0.22, 0.05] |
| LFHRV | −0.76*** [−0.79, −0.73] | −0.23*** [−0.31, −0.15] | −0.77*** [−0.82, −0.72] | −0.15* [−0.27, −0.02] |
| HFHRV | −0.76*** [−0.79, −0.73] | −0.11** [−0.19, −0.03] | −0.76*** [−0.80, −0.71] | −0.05 [−0.18, 0.08] |
| Pulse Rate | 0.32*** [0.26, 0.37] | 0.36*** [0.29, 0.43] | 0.36*** [0.27, 0.45] | 0.40*** [0.28, 0.52] |
| HPA | ||||
| Cortisol | 0.31*** [0.21, 0.40] | −0.31*** [−0.39, −0.23] | 0.21 [−0.02, 0.44] | −0.22*** [−0.35, −0.08] |
| DHEA-S | 0.30*** [0.21, 0.39] | −0.06 [−0.13, 0.01] | 0.22 [−0.01, 0.45] | −0.00 [−0.11, 0.11] |
| Inflammation | ||||
| CRP | 0.55*** [0.45, 0.65] | 0.55*** [0.48, 0.62] | 0.55*** [0.32, 0.77] | 0.59*** [0.46, 0.73] |
| IL6 | 0.39*** [0.30, 0.48] | 0.53*** [0.45, 0.60] | 0.32*** [0.17, 0.47] | 0.59*** [0.48, 0.71] |
| Fibrinogen | 0.56*** [0.46, 0.66] | 0.37*** [0.29, 0.45] | 0.59*** [0.42, 0.76] | 0.36*** [0.23, 0.49] |
| sE-Selectin | −0.01 [−0.10, 0.09] | 0.37*** [0.30, 0.44] | −0.08 [−0.23, 0.06] | 0.33*** [0.21, 0.44] |
| sICAM-1 | 0.09 [−0.01, 0.20] | 0.24*** [0.16, 0.32] | 0.16 [−0.00, 0.32] | 0.23*** [0.10, 0.37] |
| Cardiovascular | ||||
| Pulse Pressure | 0.83*** [0.80, 0.86] | 0.09* [0.02, 0.16] | 0.86*** [0.80, 0.91] | 0.23*** [0.11, 0.35] |
| SBP | 0.83*** [0.80, 0.85] | 0.12** [0.04, 0.20] | 0.75*** [0.70, 0.79] | 0.30*** [0.18, 0.41] |
| Glucose | ||||
| Glucose | 0.90*** [0.86, 0.94] | 0.41*** [0.32, 0.50] | 0.90*** [0.84, 0.95] | 0.39*** [0.26, 0.52] |
| HbA1c | 0.60*** [0.52, 0.68] | 0.38*** [0.30, 0.46] | 0.50*** [0.37, 0.63] | 0.31*** [0.19, 0.42] |
| HOMA-IR | 0.28*** [0.20, 0.35] | 0.65*** [0.57, 0.73] | 0.25*** [0.16, 0.33] | 0.65*** [0.51, 0.79] |
| Lipids | ||||
| HOMA-IR† | 0.27*** [0.14, 0.39] | 0.37*** [0.21, 0.53] | ||
| WHR | 0.14* [0.03, 0.24] | 0.43*** [0.37, 0.49] | 0.20* [0.04, 0.35] | 0.38*** [0.27, 0.49] |
| HDL | −0.45*** [−0.58, −0.32] | −0.32*** [−0.42, −0.22] | −0.56*** [−0.72, −0.40] | −0.26** [−0.45, −0.06] |
| LDL | 0.26*** [0.19, 0.34] | 0.01 [−0.08, 0.11] | 0.39*** [0.27, 0.50] | 0.09 [−0.06, 0.25] |
| Triglycerides | 0.73*** [0.60, 0.86] | 0.37*** [0.25, 0.49] | 0.67*** [0.54, 0.80] | 0.31*** [0.13, 0.49] |
Note. System and AL denote the loadings of each biomarker on the specific system factor or on the common allostatic load factor. Standardized loadings are presented for all models. N = 1,254 for the overall bi-factor models, and N = 486 for the medication free bi-factor model.
cross-loading of HOMA-IR on Lipids system.
p < .001,
p < .01,
p < .05
Table 4.
Estimated Latent Factor Correlations from the Final Bi-Factor Model
| 1. | 2. | 3. | 4. | 5. | 6. | 7. | |
|---|---|---|---|---|---|---|---|
| 1. SNS | - | ||||||
| 2. PNS | .08 | - | |||||
| 3. HPA | .34 | .07 | - | ||||
| 4. Inflammation | .16 | .09 | .20 | - | |||
| 5. Cardiovascular | .10 | −.08 | .23 | .11 | - | ||
| 6. Glucose | .06 | .01 | .15 | −.14 | .06 | - | |
| 7. Lipids | −.05 | .13 | −.09 | −.05 | .13 | .11 | - |
| 8. AL | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Note. N = 1,254 from the bi-factor model
As a sensitivity analysis, the factor loadings from the final bi-factor model on only those 486 participants who were medication free are also presented in Table 3. In general, the results are quite similar, with some additional non-significant parameters due to the reduced sample size.
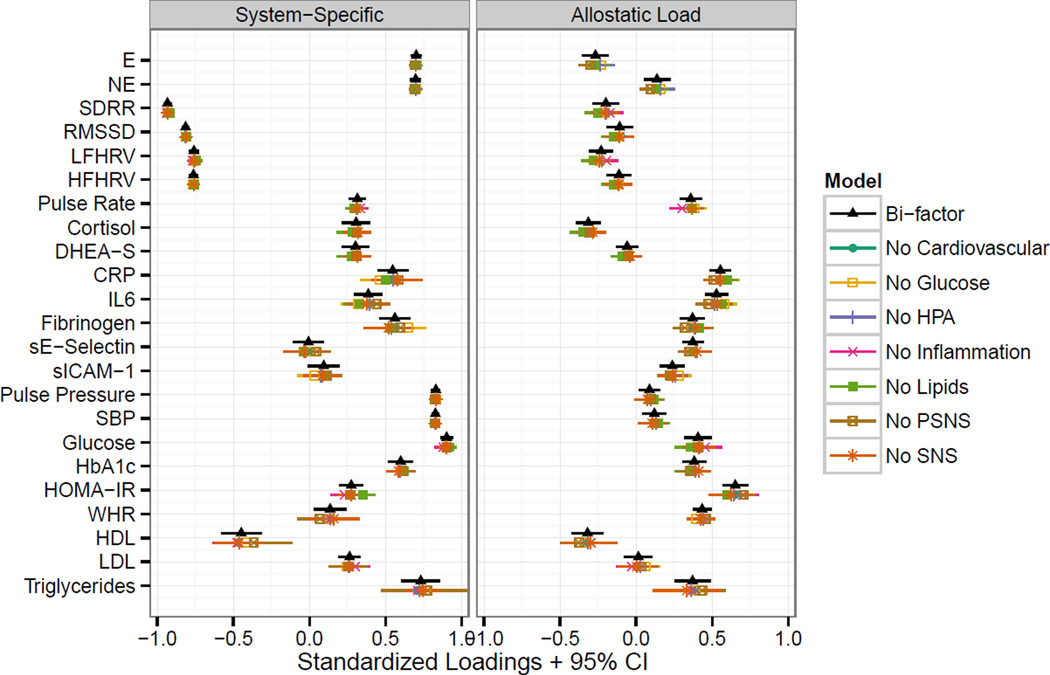
Finally, item parameter invariance was examined by comparing the standardized loadings from the seven reduced models (each now with only six systems assessed) to the full bi-factor model. None of the loadings from the reduced models fell outside the confidence interval for the overall bi-factor model, and most exhibited minimal differences (Figure 3). These results are consistent with what would be expected if the model had item parameter invariance.
Figure 3.
Item Parameter Invariance Plot. Standardized loadings with 95% confidence intervals for the overall bi-factor model are shown in black triangles. Results from seven “reduced” models where each system was systematically dropped are shown slightly below the results from the overall bi-factor model. The overlap in points and confidence intervals shows that the standardized loadings for the remaining biomarkers do not change substantially when biomarkers for any one system are dropped.
Discussion
Across 23 biomarkers in a large sample of adults, a bi-factor model of AL provided both good fit and was the best fitting model. This result has two important implications. First, it confirms what previous studies have demonstrated that consistent with AL theory, a common factor underlies biomarkers of multi-system physiological functioning (12–14). Second, it is the first study, to our knowledge, that demonstrates that in addition to the common underlying AL factor, individual physiological systems account for unique variance in biomarkers not accounted for by the common factor. Composites of biomarkers within a system or factor scores from the second-order factor (Model 1) model will conflate system-specific effects and effects of the common factor. Using a bi-factor model (Model 2) provides an alternative and novel method that allows the examination of either the common allostatic load factor, the system-specific factors unconflated from allostatic load, or both.
Most loadings were in the expected directions, but there were exceptions. Contrary to AL theory, epinephrine loaded negatively on the common AL factor, although it correlated positively with norepinephrine (r = .50), which did load positively on the AL factor. To our knowledge of the three other studies that examined the factor structure of AL, only one assessed epinephrine and found that it was not significantly associated with AL (9). Cortisol also loaded negative onto the common AL factor, but it is less clear whether high or low values of basal cortisol are desirable (e.g., Seeman and colleagues found that higher AL was associated with a lower cortisol awakening response and flatter change over the day; 13). Alternatively, this may be unique to the MIDUS study as participants had to travel to one of three clinical research centers for the overnight stay when their biomarkers were assessed, which may have affected their overnight urinary cortisol.
Overall, the largest factor loadings for the common AL factor were from biomarkers from the inflammation, glucose, and lipid systems. Biomarkers in the SNS, PNS, and cardiovascular (blood pressure) systems did not load strongly on the common AL factor, but did load onto their system-specific factors. These systems also had the strongest correlations among the system-specific factors. Although AL theory does not hypothesize stronger associations among these systems than other systems, these results make sense in that the biomarkers from these systems only load modestly on the common AL factor, with more of their variance accounted for by the system-specific factors, leading to higher correlations among the system factors (although none of these correlations are large). These results suggest that for the SNS, PNS, and cardiovascular (blood pressure) systems, it may be particularly important to examine their unique effects beyond overall AL. By examining shared and system-specific effects, we believe this bi-factor model can facilitate greater precision in the next generation of research. For example, different types of stressors (e.g., low grade chronic stress versus traumatic stress) may be associated with higher allostatic, but show differential effects on specific systems, such as SNS or PNS.
In a recent editorial, Gallo, Fortmann, and Mattei (29) argued for a need to standardize the measurement of AL and for researchers to report on the specific components of AL. We agree that the specific components of AL are important; indeed the bi-factor structure suggests that specific physiological systems account for additional variance in biomarkers over and above AL. Using a method that allows both AL and specific physiological systems to be used as independent predictors or outcomes facilitates examining both system-wide (AL) and system-specific effects. We believe that using a bi-factor model represents an important advance in psychosomatic research for untangling the relations between psychological factors and system-specific and system-wide physiological dysregulation.
The results were consistent with item parameter invariance for the bi-factor model. The property of item parameter invariance means that the system-specific and allostatic load factor loadings would not change regardless of the specific biomarkers measured. Item parameter invariance is an important property that underlies methods such as computer adaptive testing where not all participants are given the same questions and yet they receive comparable scores on the same underlying construct. If this result is replicated and shown reliable, it has the potential to provide a pathway to resolve discrepancies across studies due to different biomarkers being measured by deriving scores on the same underlying allostatic load and individual system factors, even if the exact subset of biomarkers assessed varies. Another implication is that research that does not measure all 23 biomarkers can still derive a comparable allostatic load score, opening the possibility of a “short” version of allostatic load where fewer biomarkers are assessed to save cost or participant burden. However, one disadvantage of measuring fewer biomarkers is that it may no longer be possible to obtain a score on a particular system-specific factor. Furthermore, reducing the number of biomarkers by leaving off specific biomarkers or whole systems will reduce the reliability of both the common AL factor score and system-specific scores. To recommend which biomarkers should be measured to optimally measure AL, future research is needed to examine the relationships between AL scored from different biomarkers and other constructs it should be related to such as stress, physical functioning, morbidity, and mortality.
We found that for the bi-factor model, results were consistent with what would be expected if it was invariant between males and females, which is consistent with prior research on AL comparing females and males (13), as well as across age groups.
Limitations of the current study should be noted. The sample was predominantly White, with fewer African-Americans and small numbers of other ethnicities represented. In addition, only basal levels of biomarkers were assessed; future research is needed to examine relations among functional measures of biomarkers (e.g., inflammatory response to antigens). Finally, when testing measurement invariance where the model fit is compared across subgroups of the sample, many subgroups were small and in these multiple group models, the overall sample size was small compared to the number of parameters and complexity of our measurement model. However, with 1,254 participants, this is one of the largest studies with extensive biomarker data available.
The study also has several important strengths. The current study comprehensively assessed seven physiological systems using 23 biomarkers. The use of many biomarkers ensures that each of the seven systems are measured by more than one biomarker, allowing us to differentiate effects shared across systems and effects unique to systems. Another strength is the broad age range from 34- to 84-years old. Finally, the current study used careful statistical analyses including: accounting for clustering in twins and siblings in the MIDUS data, non-normality of the biomarkers, missing data, and investigating alternative theoretical models.
In conclusion, across 23 biomarkers in MIDUS, we found evidence for a common AL factor, as well as for seven system-specific factors, and this model held across age groups and sex. Although our findings were consistent with a model where AL was invariant across subpopulations and invariant to dropping biomarkers from any one system, these results do not preclude the possibility that the measurement of AL may differ importantly by the sample or population being studied. Nevertheless, they do point to the robustness of allostatic load, and perhaps suggest that apparently disparate sets of biomarkers used in many studies may actually be more comparable than expected. Future research is needed to examine the predictive effects of AL and specific systems on health. Future research could also explore whether for specific outcomes, such as particular diseases, or for different predictors, such as chronic or acute stress, different profiles emerge across the common AL factor and system-specific factors. In order to standardize the measurement of AL as Gallo, Fortmann, and Mattei (29) suggest, further work is needed to reach consensus on how to define “optimal” measures of AL and specific physiological systems (e.g., predict disease incidence or mortality, predict functioning), and then to develop and validate sets of biomarkers for each system and for AL overall—work that is challenging given the great diversity of samples and populations studied. Nevertheless, findings that the bi-factor model was consistent with item parameter invariance, if replicated, open the intriguing possibility that just as in computer adaptive testing where not all participants complete the same questions, yet can be given comparable scores, it may be possible to obtain comparable AL scores from different sets of biomarkers and perhaps begin to resolve concerns about the challenge interpreting the AL literature when measurement is inconsistent.
Supplementary Material
Acknowledgments
Sources of Funding
MIDUS I was supported by the John D. and Catherine T. MacArthur Foundation Research Network on Successful Midlife Development. MIDUS II was supported by a grant from the National Institute on Aging (P01-AG020166). MIDUS II was further supported by the following grants: M01-RR023942 (Georgetown), M01-RR00865 (UCLA) from the General Clinical Research Centers Program and UL1TR000427 (UW) from the National Center for Advancing Translational Sciences (NCATS), National Institutes of Health. Wiley was supported by a training grant from NIGMS T32GM084903.
Acronyms
- AL
allostatic load
- SNS
sympathetic nervous system
- PNS
parasympathetic nervous system
- HPA
hypothalamic-pituitary-adrenal axis
- WHR
waist-to-hip ratio
- HDL
high density lipoprotein
- LDL
low density lipoprotein
- HOMA-IR
homeostatic model assessment of insulin resistance
- HbA1c
glycosylated hemoglobin
- SBP
systolic blood pressure
- DBP
diastolic blood pressure
- SDRR
standard deviation of beat to beat intervals
- RMSSD
root mean square of successive differences (RMSSD) of beat to beat intervals
- LFHRV
low frequency spectral power
- HFHRV
high frequency spectral power
- E
epinephrine
- NE
norepinephrine
- Cort
cortisol
- DHEA-S
dihydroepiandrosterone sulfate
- CRP
C-reactive protein
- IL6
interleukin-6
- sE-Selectin
soluble E-selectin
- sICAM-1
soluble intracellular adhesion molecule 1
- MIDUS
Midlife in the United States
- CFI
comparative fit index
- RMSEA
root mean square error of approximation
- SRMR
standardized root mean square residual
- TLI
Tucker Lewis Index
- AIC
Akaike Information Criterion
- BIC
Bayesian Information Criterion
Footnotes
Conflicts of Interest
The authors declare no conflicts of interest.
References
- 1.Cohen S, Herbert TB. Health psychology: Psychological factors and physical disease from the perspective of human psychoneuroimmunology. Annu Rev Psychol. 1996;47:113–142. doi: 10.1146/annurev.psych.47.1.113. [DOI] [PubMed] [Google Scholar]
- 2.Uchino BN, Cacioppo JT, Kiecolt-Glaser JK. The relationship between social support and physiological processes: A review with emphasis on underlying mechanisms and implications for health. Psychological Bulletin. 1996;119:488–531. doi: 10.1037/0033-2909.119.3.488. [DOI] [PubMed] [Google Scholar]
- 3.Krantz DS, Manuck SB. Acute psychophysiologic reactivity and risk of cardiovascular disease: A review and methodologic critique. Psychological Bulletin. 1984;96:435. [PubMed] [Google Scholar]
- 4.Karlamangla AS, Singer BH, Seeman TE. Reduction in allostatic load in older adults is associated with lower all-cause mortality risk: MacArthur studies of successful aging. Psychosomatic Medicine. 2006;68:500–507. doi: 10.1097/01.psy.0000221270.93985.82. [DOI] [PubMed] [Google Scholar]
- 5.Gruenewald TL, Seeman TE, Ryff CD, Karlamangla AS, Singer BH. Combinations of biomarkers predictive of later life mortality. Proceedings of the National Academy of Sciences. 2006;103:14158–14163. doi: 10.1073/pnas.0606215103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sterling P, Eyer J. Allostasis: A new paradigm to explain arousal pathology. In: Fisher S, Reason J, editors. Handbook of life stress, cognition and health. Oxford, England: John Wiley & Sons; 1988. pp. 629–649. [Google Scholar]
- 7.McEwen BS, Stellar E. Stress and the individual: mechanisms leading to disease. Arch Intern Med. 1993;153:2093–2101. [PubMed] [Google Scholar]
- 8.Juster R-P, McEwen BS, Lupien SJ. Allostatic load biomarkers of chronic stress and impact on health and cognition. Neuroscience & Biobehavioral Reviews. 2010;35:2–16. doi: 10.1016/j.neubiorev.2009.10.002. [DOI] [PubMed] [Google Scholar]
- 9.Seeman TE, Glei D, Goldman N, Weinstein M, Singer B, Lin Y-H. Social relationships and allostatic load in Taiwanese elderly and near elderly. Social Science & Medicine. 2004;59:2245–2257. doi: 10.1016/j.socscimed.2004.03.027. [DOI] [PubMed] [Google Scholar]
- 10.Brody GH, Yu T, Chen Y-f, Kogan SM, Evans GW, Windle M, Gerrard M, Gibbons FX, Simons RL, Philibert RA. Supportive family environments, genes that confer sensitivity, and allostatic load among rural african american emerging adults: A prospective analysis. J Fam Psychol. 2013;27:22. doi: 10.1037/a0027829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Babyak MA, Green SB. Confirmatory Factor Analysis: An Introduction for Psychosomatic Medicine Researchers. Psychosomatic Medicine. 2010;72:587–597. doi: 10.1097/PSY.0b013e3181de3f8a. 10.1097/PSY.0b013e3181de3f8a. [DOI] [PubMed] [Google Scholar]
- 12.McCaffery JM, Marsland AL, Strohacker K, Muldoon MF, Manuck SB. Factor structure underlying components of allostatic load. PLoS One. 2012;7:e47246. doi: 10.1371/journal.pone.0047246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Seeman TE, Gruenewald TL, Karlamangla AS, Sidney S, Liu K, McEwen BS, Schwartz J. Modeling multisystem biological risk in young adults: The Coronary Artery Risk Development in Young Adults Study. Am J Hum Biol. 2010;22:463–472. doi: 10.1002/ajhb.21018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Booth T, Starr JM, Deary I. Modeling multisystem biological risk in later life: Allostatic load in the lothian birth cohort study 1936. Am J Hum Biol. 2013;25:538–543. doi: 10.1002/ajhb.22406. [DOI] [PubMed] [Google Scholar]
- 15.Marsland AL, McCaffery JM, Muldoon MF, Manuck SB. Systemic inflammation and the metabolic syndrome among middle-aged community volunteers. Metabolism. 2010;59:1801–1808. doi: 10.1016/j.metabol.2010.05.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.McCaffery JM, Shen B-J, Muldoon MF, Manuck SB. Ambulatory blood pressure and the metabolic syndrome in normotensive and untreated hypertensive men. Metabolic Syndrome and Related Disorders. 2007;5:34–44. doi: 10.1089/met.2006.0014. [DOI] [PubMed] [Google Scholar]
- 17.McEwen BS. Interacting mediators of allostasis and allostatic load: towards an understanding of resilience in aging. Metabolism. 2003;52(Supplement 2):10–16. doi: 10.1016/s0026-0495(03)00295-6. [DOI] [PubMed] [Google Scholar]
- 18.Radler BT, Ryff CD. Who participates? Accounting for longitudinal retention in the MIDUS national study of health and well-being. Journal of Aging and Health. 2010;22:307–331. doi: 10.1177/0898264309358617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Love GD, Seeman TE, Weinstein M, Ryff CD. Bioindicators in the MIDUS national study: Protocol, measures, sample, and comparative context. Journal of Aging and Health. 2010;22:1059–1080. doi: 10.1177/0898264310374355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gruenewald TL, Karlamangla AS, Hu P, Stein-Merkin S, Crandall C, Koretz B, Seeman TE. History of socioeconomic disadvantage and allostatic load in later life. Social Science & Medicine. 2012;74:75–83. doi: 10.1016/j.socscimed.2011.09.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Satorra A, Bentler PM. A scaled difference chi-square test statistic for moment structure analysis. Psychometrika. 2001;66:507–514. doi: 10.1007/s11336-009-9135-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Meredith W. Measurement invariance, factor analysis and factorial invariance. Psychometrika. 1993;58:525–543. [Google Scholar]
- 23.Cheung GW, Rensvold RB. Evaluating goodness-of-fit indexes for testing measurement invariance. Structural equation modeling. 2002;9:233–255. [Google Scholar]
- 24.Reise SP. The rediscovery of bifactor measurement models. Multivariate Behavioral Research. 2012;47:667–696. doi: 10.1080/00273171.2012.715555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Enders CK, Bandalos DL. The relative performance of full information maximum likelihood estimation for missing data in structural equation models. Structural Equation Modeling. 2001;8:430–457. [PubMed] [Google Scholar]
- 26.Hu L, Bentler PM. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling. 1999;6:1–55. [Google Scholar]
- 27.R Core Team. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; 2015. [Google Scholar]
- 28.Hallquist M, Wiley JF. MplusAutomation: Automating Mplus model estimation and interpretation. 2014. 0.6-3 ed. [Google Scholar]
- 29.Gallo LC, Fortmann AL, Mattei J. Allostatic load and the assessment of cumulative biological risk in biobehavioral medicine: Challenges and opportunities. Psychosomatic Medicine. 2014;76:478–480. doi: 10.1097/PSY.0000000000000095. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.