Abstract
Coronary heart disease is a leading cause of death among Americans for which coronary artery bypass graft (CABG) surgery is a standard surgical treatment. The success of CABG surgery is impaired by a compliance mismatch between vascular grafts and native vessels. Tissue engineered vascular grafts (TEVGs) have the potential to be compliance matched and thereby reduce the risk of graft failure. Glutaraldehyde (GLUT) vapor-crosslinked gelatin/fibrinogen constructs were fabricated and mechanically tested in a previous study by our research group at 2, 8, and 24 hrs of GLUT vapor exposure. The current study details a computational method that was developed to predict the material properties of our constructs for crosslinking times between 2 and 24 hrs by interpolating the 2, 8, and 24 hrs crosslinking time data. matlab and abaqus were used to determine the optimal combination of fabrication parameters to produce a compliance matched construct. The validity of the method was tested by creating a 16-hr crosslinked construct of 130 μm thickness and comparing its compliance to that predicted by the optimization algorithm. The predicted compliance of the 16-hr construct was 0.00059 mm Hg−1 while the experimentally determined compliance was 0.00065 mm Hg−1, a relative difference of 9.2%. Prior data in our laboratory has shown the compliance of the left anterior descending porcine coronary (LADC) artery to be 0.00071 0.0003 mm Hg−1. Our optimization algorithm predicts that a 258-μm-thick construct that is GLUT vapor crosslinked for 8.1 hrs would match LADC compliance. This result is consistent with our previous work demonstrating that an 8-hr GLUT vapor crosslinked construct produces a compliance that is not significantly different from a porcine coronary LADC.
Keywords: biopolymer, tissue engineered vascular graft, small diameter vascular graft, compliance matched, optimization, electrospinning, glutaraldehyde
Introduction
In 2010, cardiovascular disease (CVD) was present in more than one third of the U.S. population over the age of 20, and accounted for 787,650 American deaths [1]. Of these deaths, nearly half of all cases point to coronary heart disease as the underlying cause. CABG surgery is a common treatment for coronary heart disease and is the process in which autologous vessels or vascular grafts are used to bypass diseased vessels [2]. Current CABG methods are inadequate as many grafts suffer from an increased risk of thrombosis and graft failure due to intimal hyperplasia caused by a compliance mismatch between the artery and graft [2,3].
TEVGs are a potential solution to the aforementioned issues associated with bypass graft surgery as they can be engineered to have a compliance that matches that of the native vessel and also to be nonthrombogenic, biocompatible, nonimmunogenic, and infection resistant [4]. In order to design a compliance-matched TEVG, it is a logical first step to try to mimic the material and microstructure of a native vessel. Coronary arteries consist primarily of smooth muscle cells (SMCs) embedded in an extracellular matrix of collagen and elastin fibers [3]. Previous research has suggested that electrospinning layers of collagen and elastin tissue to create vascular constructs are the viable option to replicate the biomechanical properties of vascular tissue [5–7]. Our research group has successfully electrospun and characterized nonsynthetic biopolymer vascular grafts using gelatin and fibrinogen. The effect of crosslinking time via exposure to GLUT vapor on their mechanical behavior was also characterized [4]. Because compliance matching with the host artery is of critical importance in graft design [2,3,8], a computational technique has been developed to predict the compliance of our constructs based on the thickness of the construct and the duration of crosslinking time. Predictability of material properties is useful for compliance matching and improving viability of implanted grafts, while also being cost and time effective. The purpose of this technical brief is to detail the method behind the computational optimization of thickness and crosslinking time to achieve a vascular graft compliance matched to porcine LADC artery.
Methods
Electrospun Construct Fabrication.
Our research group has previously fabricated tubular constructs using gelatin extracted from porcine skin (Sigma-Aldrich, St. Louis, MO) and fraction I bovine fibrinogen (Sigma-Aldrich) at a ratio of 80:20 gelatin:fibrinogen dissolved in 1,1,1,3,3,3-Hexafluoro-2-propanol (HFP) (Sigma-Aldrich) at 10% w/v. This solution was dispensed through a 23 gauge stainless steel dispensing needle on a 5 ml BD syringe loaded into a NE-100 single syringe pump (New era pump systems Inc., USA). A 15 kV voltage difference was applied between the dispensing tip and a 1.6 mm OD mandrel rotating at 25 RPM and translating at 10 mm/s. The voltage difference caused the biopolymer solution to be deposited onto the mandrel, forming a tubular construct. This electrospinning setup can be seen in Fig. 1 [4].
Fig. 1.

Electrospinning setup
These constructs were then removed from the stainless steel rod and suspended in the air in a chamber containing 25% (v/v) liquid GLUT. Three experimental groups with three replicates each were created and allowed to crosslink for 2, 8, and 24 hrs before mechanical testing [4]. These constructs were used as the basis for the present study.
Mechanical Testing.
A microbiaxial optomechanical device (MOD) has been used by our laboratory to characterize the mechanical properties of various soft tissues [9–14]. This device, shown in Fig. 2, is capable of stretching tubular samples longitudinally while also applying an intraluminal pressure and recording the axial load, intraluminal pressure, circumferential strain, and axial strain. Six different protocols were performed on each specimen. After preconditioning, the intraluminal pressure was increased from 0 to 120 mm Hg with constant axial loads of 0, 10, and 30 g. The axial load was then increased from 0 to 30 g with constant intraluminal pressures of 0, 70, and 120 mm Hg [4,15,16].
Fig. 2.

MOD being used to test a gelatin/fibrinogen tubular construct
Material Properties.
The compliance of the constructs was defined according to Eq. (1) [4]
| (1) |
where and are the diameters of the construct at an intraluminal pressure of 120 mm Hg and 70 mm Hg, respectively.
Data from the mechanical testing were fit to a four-parameter Fung-type strain energy model [4,15]
| (2) |
| (3) |
where represents the strain energy density and (kPa), , , and are material constants, is the circumferential Green strain, and is the axial Green strain. The second Piola-Kirchhoff stresses for the above constitutive relationship are
| (4) |
| (5) |
where is the circumferential second Piola-Kirchhoff stress and represents the axial second Piola-Kirchhoff stress. The 2-, 8-, and 24-hr crosslinked constructs were found, on average, to have the constants shown in Table 1 for the Fung-type constitutive model [4].
Table 1.
Constants for constitutive model at 2, 8, and 24 hrs of crosslinking time, as seen in Ref. [4]
| Crosslinking time | C (kPa) | A1 | A2 | A3 | R2 |
|---|---|---|---|---|---|
| 2 hrs | 31.0 | 24.0 | 7.3 | 2.6 | 0.90 |
| 8 hrs | 49.1 | 16.7 | 7.9 | 3.0 | 0.88 |
| 24 hrs | 83.6 | 22.6 | 12.1 | 4.1 | 0.96 |
Prediction of Material Properties.
A method was developed to predict the mechanical behavior of constructs for any crosslinking time between 2 and 24 hrs without building and testing new constructs. This was achieved by interpolating the existing data for 2, 8, and 24 hrs of crosslinking. Interpolation of stress–strain response surfaces was performed using the following equations:
| (6) |
| (7) |
In these expressions, is crosslinking time while , , , and are constants determined by fitting all of the data for the 2-, 8-, and 24-hr crosslinked constructs separately for and . This exponential form was chosen because the exponential Fung-type constitutive model was successfully used with these constructs previously [4]. Note that Eqs. (6) and (7) do not form a constitutive model for use in finite element simulation. The purpose of these response functions is to approximate what experimental stress–strain data would be for any arbitrary level of GLUT vapor crosslinking time, , between 2 and 24 hrs. Examples of these surfaces for crosslinking times of 2, 4, 8, 12, 16, and 24 hrs are shown in Fig. 3. It is apparent from the figure that as crosslinking time increases, the constructs become stiffer both circumferentially and axially, as expected [4]. Note that this model is valid for any value of crosslinking time between 2 and 24 hrs. After these response surfaces are generated, the constants for the Fung-type constitutive model are determined by simultaneously fitting the data from the response surfaces to Eqs. (4) and (5). Finally, these constants are then used to define the material properties for a finite-element simulation.
Fig. 3.
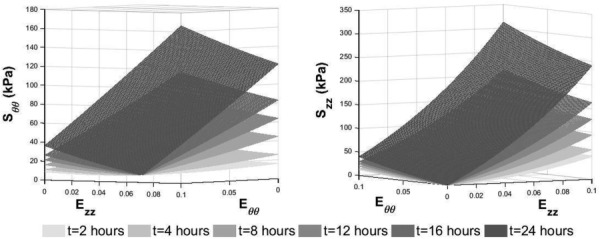
Time dependent response surfaces used to determine constants for constitutive model in order to predict material behavior for crosslinking times for which experimental data has not been collected
Finite Element Simulation.
matlab was used in conjunction with finite element analysis software abaqus to generate and mesh the geometries used in the optimization. An axisymmetric model with four-noded, reduced-integration, axisymmetric, solid elements with hybrid formulation was used. Figure 4 shows the boundary value problem that was solved (iteratively) by abaqus.
Fig. 4.
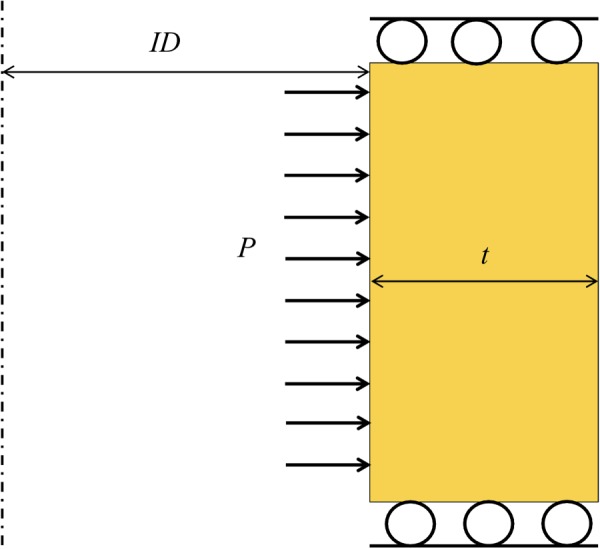
Example of an axisymmetric tube with fixed boundary conditions at the top and bottom and an applied pressure, P, on the inner surface. The tube has inside diameter (ID) and thickness t. The dotted line is the line of axisymmetry.
Optimization.
Our laboratory has previously written custom matlab code to interact with abaqus without opening the graphical user interface [17,18]. A matlab–abaqus optimization routine was developed that simulates pressurized constructs as seen in Fig. 4 and extracts the diameter at 70 and 120 mm Hg to calculate the compliance. With each iteration, a different combination of thickness and material properties are sent to abaqus. The gradient based bounded optimization function fminsearchbnd is used in matlab to push the objective function (the difference between the compliance predicted by the current iteration and the desired compliance) to zero by updating the values of thickness and crosslinking time for the next iteration. A bounded optimization function is used to limit the thickness to a physiologically reasonable range and to allow only crosslinking times between 2 and 24 hrs. The simulation continues to update until the predicted compliance is sufficiently close to the desired compliance (see Fig. 5).
Fig. 5.
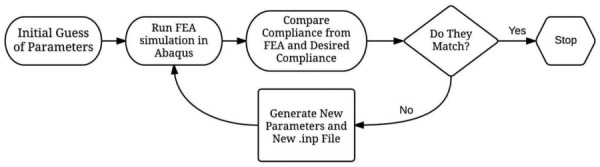
Optimization program schematic
Results
Both coefficient of determination (R2) values and visual assessment were used to determine the validity of the surface model fit to the experimental data. Tables 2 and 3 show the constants that were found to best fit the data and Fig. 6 shows visually how well the response surfaces match the experimental data.
Table 2.
Constants and R2 for Eq. (6)
| A (kPa) | B1 | B2 | B3 | B4 (s−1) | B5 (s−1) | R2 |
|---|---|---|---|---|---|---|
| 45,355.8 | 0.013 | 0.015 | 0.0097 | 0.00014 | 0.00053 | 0.84 |
Table 3.
Constants and R2 for Eq. (7)
| C (kPa) | D1 | D2 | D3 | D4 (s−1) | D5 (s−1) | R2 |
|---|---|---|---|---|---|---|
| 407.1 | 7.92 | 2.33 | 0.58 | 0.08 | 0.015 | 0.94 |
Fig. 6.
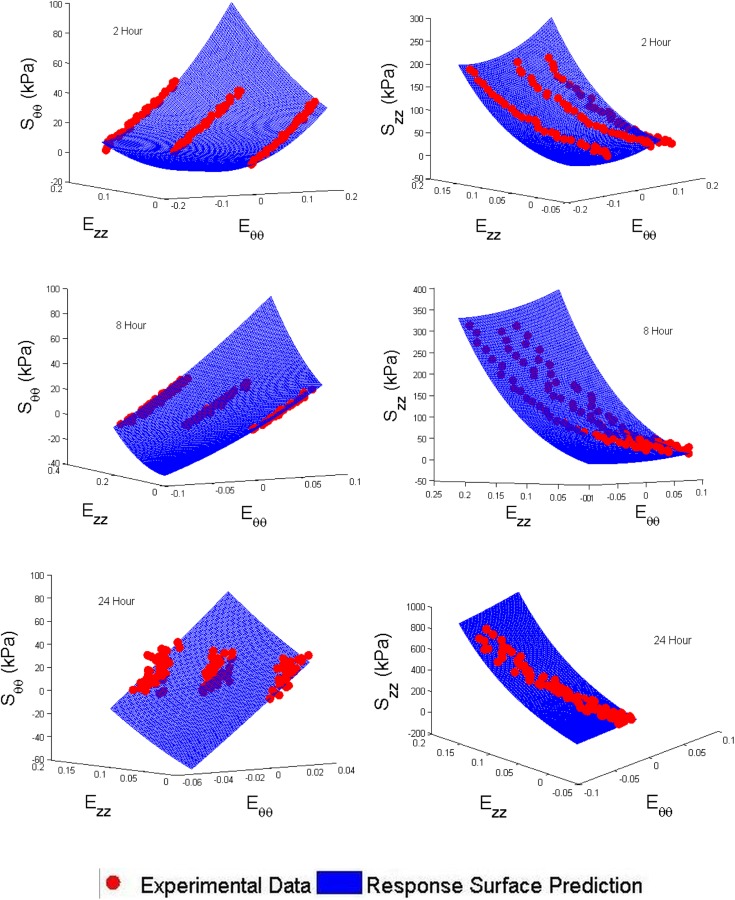
Response surface and experimental data comparison
Verification of Material Property Prediction.
To verify the accuracy of the material properties predicted using the response surface model, a 16-hr crosslinked construct was fabricated and mechanically tested using the MOD. This construct had an outside diameter of 1.12 mm and thickness of 130 m. A simulation in abaqus performed using the material properties generated by the response surfaces predicted that such a construct would have a compliance of 0.00059 mm Hg−1. The actual compliance of the construct tested was 0.00065 mm Hg−1, giving a percent relative error of 9.2%.
Compliance Matched Construct.
In a previous study by our research group, porcine coronary artery data was collected and used for comparison with our TEVGs [4,15]. Porcine LADC artery was found to have a compliance of 0.00071 0.0003 mm Hg−1 [4]. A simulation was run to predict what thickness and crosslinking time one of our gelatin/fibrinogen constructs should have in order to compliance match the LADC. The simulation result indicated that a construct 258 μm thick with 8.1 hrs of crosslinking would match the compliance of a LADC. Figure 7 shows a plot of the objective function with each iteration and the final parameters that are predicted to produce a compliance matched construct. An animated version of this figure is available in the online supplementary material.
Fig. 7.
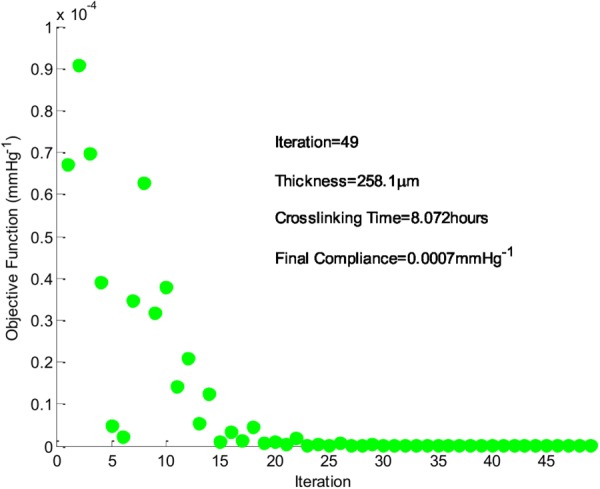
Objective function (current compliance–desired compliance) and simulation results. The desired compliance was 0.0007 mm Hg−1.
Discussion
In summary, a method has been developed for predicting the mechanical behavior, specifically the compliance, of our electrospun constructs for any thickness and for crosslinking times between 2 and 24 hrs. It was predicted that a 258 μm thick construct with 8.1 hrs of crosslinking would match the compliance of porcine LADC.
This corroborates the previous finding by our laboratory that an 8-hr crosslinked construct and LADC exhibit no statistical difference in compliance [4]. Previous compliance matching work has been done by altering the chemistry of segmented polyurethanes and the microarchitecture of the electrospun mesh in synthetic grafts [3]. Additionally, Dargaville et al. modified the mechanical properties of gamma radiation crosslinked small diameter electrospun synthetic scaffolds spun with L-lactide-co-trimethylene carbonate (LLA-TMC) fibers by using different percentages of TMC [19]. The present study is unique in the use of a computational approach to predict the compliance of nonsynthetic grafts by altering the thickness of the graft as well as the length of crosslinking time via exposure to GLUT vapor.
The accuracy of the compliance matching is limited somewhat by the difficulty in electrospinning constructs of the exact desired thickness. The electrospinning process can produce constructs within 20 μm from the goal thickness, which can lead to slightly different material behavior than predicted. Furthermore, our laboratory has shown that SMCs can be grown on gelatin/fibrinogen fibers as used in the present study [20]. Seeded SMCs are likely to have a significant impact on the mechanical properties of the gelatin/fibrinogen constructs [4]. In the future, it will be important to quantify this effect in order to more accurately predict the compliance of a construct in vivo.
In this study, the compliance matching program was used to predict the compliance of 80% gelatin-20% fibrinogen constructs. However, native vasculature contains alternating layers of elastin and collagen, providing a combination of strength and compliance. Our research group is currently working on improving the durability and deformability of our constructs by electrospinning alternating layers of gelatin/fibrinogen and tropoelastin into the same construct. The necessary parameters in these layered constructs will eventually be optimized to match the compliance of native artery using an approach similar to that presented here. Being able to control the individual thickness of each alternating layer of gelatin/fibrinogen and tropoelastin will allow for a more precise control over the compliance of the construct while also providing a more biomimetic microstructural matrix organization. It should be noted that although the present study optimizes the thickness and crosslinking time for gelatin/fibrinogen constructs, the flexibility of the computational approach presented here is broadly applicable to the optimization of a variety of fabrication challenges in tissue engineering. Computational prediction of compliance is a cost effective way to determine the ideal geometry and crosslinking time for constructs that will be used in animal trials. During preclinical in vivo trials, this method can be used to aid in the fabrication of constructs that match the compliance of native vessel in the current specimen, and could eventually be applied to make patient specific compliance matched grafts based on information derived from imaging of the patient's vessel.
Supplementary Material
Acknowledgment
This research was funded by the NIH Grant No. NHLBI-1R21HL111990 to JPVG. We would also like to acknowledge Avinash Ayyalasomayajula for his help in implementing the computational optimization algorithm and Stephen Howerton for his assistance with editing.
Contributor Information
Scott Harrison, Department of Aerospace and Mechanical Engineering, , The University of Arizona, , Tucson, AZ 85721 , e-mail: scottharrison@email.arizona.edu.
Ehab Tamimi, Graduate Interdisciplinary Program in , Biomedical Engineering, , The University of Arizona, , Tucson, AZ 85721 , e-mail: ehab@email.arizona.edu.
Josh Uhlorn, Department of Biomedical Engineering, , The University of Arizona, , Tucson, AZ 85721 , e-mail: juhlorn@email.arizona.edu.
Tim Leach, Department of Biomedical Engineering, , The University of Arizona, , Tucson, AZ 85721 , e-mail: tsleach@email.arizona.edu.
Jonathan P. Vande Geest, Department of Aerospace and Mechanical Engineering, , The University of Arizona, , Tucson, AZ 85721;; Department of Biomedical Engineering, , The University of Arizona, , Tucson, AZ 85721; Graduate Interdisciplinary Program in , Biomedical Engineering, , The University of Arizona, , Tucson, AZ 85721; BIO5 Institute for Biocollaborative Research, , The University of Arizona, , Tucson, AZ 85721; Soft Tissue Biomechanics Laboratory, , The University of Arizona, , Tucson, AZ 85721 , e-mail: jpv1@email.arizona.edu
References
- [1]. Go, A. S. , Mozaffarian, D. , Roger, V. L. , Benjamin, E. J. , Berry, J. D. , Blaha, M. J. , Dai, S. , Ford, E. S. , Fox, C. S. , Franco, S. , Fullerton, H. J. , Gillespie, C. , Hailpern, S. M. , Heit, J. A. , Howard, V. J. , Huffman, M. D. , Judd, S. E. , Kissela, B. M. , Kittner, S. J. , Lackland, D. T. , Lichtman, J. H. , Lisabeth, L. D. , Mackey, R. H. , Magid, D. J. , Marcus, G. M. , Marelli, A. , Matchar, D. B. , McGuire, D. K. , Mohler, E. R., 3rd , Moy, C. S. , Mussolino, M. E. , Neumar, R. W. , Nichol, G. , Pandey, D. K. , Paynter, N. P. , Reeves, M. J. , Sorlie, P. D. , Stein, J. , Towfighi, A. , Turan, T. N. , Virani, S. S. , Wong, N. D. , Woo, D. , and Turner, M. B. , 2014, “ Heart Disease and Stroke Statistics–2014 Update: A Report From the American Heart Association,” Circulation, 129(3), pp. e28–e292. 10.1161/01.cir.0000441139.02102.80 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2]. Liu, T. , Liu, S. , Zhang, K. , Chen, J. , and Huang, N. , 2014, “ Endothelialization of Implanted Cardiovascular Biomaterial Surfaces: The Development From In Vitro to In Vivo,” J. Biomed. Mater. Res. Part A, 102(10), pp. 3754–3772. 10.1002/jbm.a.35025 [DOI] [PubMed] [Google Scholar]
- [3]. Nezarati, R. M. , Eifert, M. B. , Dempsey, D. K. , and Cosgriff-Hernandez, E. , 2015, “ Electrospun Vascular Grafts With Improved Compliance Matching to Native Vessels,” J. Biomed. Mater. Res. Part B, Appl. Biomater., 103(2), pp. 313–323. 10.1002/jbm.b.33201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4]. Tamimi, E. , Ardila, D. C. , Haskett, D. G. , Doetschman, T. , Slepian, M. J. , Kellar, R. S. , and Vande Geest, J. P. , 2015, “ Biomechanical Comparison of Glutaraldehyde-Crosslinked Gelatin Fibrinogen Electrospun Scaffolds to Porcine Coronary Arteries,” ASME J. Biomech. Eng., 138(1), p. 011001. 10.1115/1.4031847 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5]. Boland, E. D. , Matthews, J. A. , Pawlowski, K. J. , Simpson, D. G. , Wnek, G. E. , and Bowlin, G. L. , 2004, “ Electrospinning Collagen and Elastin: Preliminary Vascular Tissue Engineering,” Front. Biosci., 9(2), pp. 1422–1432. 10.2741/1313 [DOI] [PubMed] [Google Scholar]
- [6]. MCClure, M. J. , Sell, S. , Simpson, D. , and Bowlin, G. , 2009, “ Electrospun Polydioxanone, Elastin, and Collagen Vascular Scaffolds: Uniaxial Cyclic Distension,” J. Eng. Fibers Fabr., 4(2), pp. 18–25. [Google Scholar]
- [7]. Wong, C. S. , Liu, X. , Xu, Z. , Lin, T. , and Wang, X. , 2013, “ Elastin and Collagen Enhances Electrospun Aligned Polyurethane as Scaffolds for Vascular Graft,” J. Mater. Sci.: Mater. Med., 24(8), pp. 1865–1874. 10.1007/s10856-013-4937-y [DOI] [PubMed] [Google Scholar]
- [8]. Chung, J. , and Li, J. K. , 2004, “ Hemodynamic Simulation of Vascular Prosthesis Altering Pulse Wave Propagation,” 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (IEMBS '04), San Francisco, CA, Sept. 1–5, pp. 3678–3680. 10.1109/IEMBS.2004.1404033 [DOI] [PubMed] [Google Scholar]
- [9]. Haskett, D. S. E. , Fouts, M. , Larson, D. , Azhar, M. , Utzinger, U. , and Vande Geest, J. P. , 2012, “ The Effects of Angiotensin II on the Coupled Microstructural and Biomechanical Response of C57BL/6 Mouse Aorta,” J. Biomech., 45(5), pp. 722–729. 10.1016/j.jbiomech.2011.11.017 [DOI] [PubMed] [Google Scholar]
- [10]. Haskett, D. G. , Azhar, M. , Utzinger, U. , and Vande Geest, J. P. , 2013, “ Progressive Alterations in Microstructural Organization and Biomechanical Response in the apoE Mouse Model of Aneurysm,” Biomatter, 3(2), pp. e24648-24641–e24648-24610. 10.4161/biom.24648 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11]. Haskett, D. G. , Doyle, J. , Gard, C. , Chen, H. , Ball, C. , Estabrook, M. A. , Encinas, A. C. , Dietz, H. C. , Utzinger, U. , Vande Geest, J. P. , and Azhar, M. , 2012, “ Altered Tissue Behavior of Non-Aneurysmal Descending Thoracic Aorta in the Mouse Model of Marfan Syndrome,” Cell Tissue Res., 347(1), pp. 267–277. 10.1007/s00441-011-1270-y [DOI] [PubMed] [Google Scholar]
- [12]. Keyes, J. T. , Borowicz, S. M. , Rader, J. H. , Utzinger, U. , Azhar, M. , and Vande Geest, J. P. , “ Design and Demonstration of a Microbiaxial Optomechanical Device for Multiscale Characterization of Soft Biological Tissues With Two-Photon Microscopy,” Microsc. Microanal., 17(2), pp. 167–175. 10.1017/S1431927610094341 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13]. Keyes, J. T. , Lockwood, D. R. , Utzinger, U. , Montilla, L. G. , Witte, R. S. , and Vande Geest, J. P. , 2013, “ Comparisons of Planar and Tubular Biaxial Tensile Testing Protocols of the Same Porcine Coronary Arteries,” Ann. Biomed. Eng., 41(7), pp. 1579–1591. 10.1007/s10439-012-0679-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14]. Keyes, J. T. , Utzinger, U. , and Vande Geest, J. P. , 2011, “ Adaptation of a Two-Photon-Microscope-Interfacing Planar Biaxial Testing Device for the Microstructural and Macroscopic Characterization of Small Tubular Tissue Specimens,” ASME J. Biomech. Eng., 133(7), p. 075001. 10.1115/1.4004495 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15]. Keyes, J. T. , Lockwood, D. R. , Simon, B. R. , and Vande Geest, J. P. , 2013, “ Deformationally Dependent Fluid Transport Properties of Porcine Coronary Arteries Based on Location in the Coronary Vasculature,” J. Mech. Behav. Biomed. Mater., 17(1), pp. 296–306. 10.1016/j.jmbbm.2012.10.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16]. Keyes, J. T. , Haskett, D. G. , Utzinger, U. , Azhar, M. , and Vande Geest, J. P. , 2011, “ Adaptation of a Planar Microbiaxial Optomechanical Device for the Tubular Biaxial Microstructural and Macroscopic Characterization of Small Vascular Tissues,” ASME J. Biomech. Eng., 133(7), p. 075001. 10.1115/1.4004495 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17]. Williams, M. J. , Utzinger, U. , Barkmeier-Kraemer, J. M. , and Vande Geest, J. P. , 2014, “ Differences in the Microstructure and Biomechanical Properties of the Recurrent Laryngeal Nerve as a Function of Age and Location,” ASME J. Biomech. Eng., 136(8), p. 081008. 10.1115/1.4027682 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18]. Keyes, J. T. , Simon, B. R. , and Vande Geest, J. P. , 2013, “ Location - Dependent Coronary Artery Diffusive and Convective Mass Transport Properties of a Lipophilic Drug Surrogate Measured Using Nonlinear Microscopy,” Pharm. Res., 30(4), pp.1147–1160. 10.1007/s11095-012-0950-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19]. Dargaville, B. L. , Vaquette, C. , Rasoul, F. , Cooper-White, J. J. , Campbell, J. H. , and Whittaker, A. K. , 2013, “ Electrospinning and Crosslinking of Low-Molecular-Weight Poly(Trimethylene Carbonate-co-l-Lactide) as an Elastomeric Scaffold for Vascular Engineering,” Acta Biomater., 9(6), pp. 6885–6897. 10.1016/j.actbio.2013.02.009 [DOI] [PubMed] [Google Scholar]
- [20]. Ardila, D. C. , Tamimi, E. , Danford, F. L. , Haskett, D. G. , Kellar, R. S. , Doetschman, T. , and Vande Geest, J. P. , 2014, “ TGFβ2 Differentially Modulates Smooth Muscle Cell Proliferation and Migration in Electrospun Gelatin-Fibrinogen Constructs,” Biomaterials, 37(1), pp. 164–173. 10.1016/j.biomaterials.2014.10.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


