Cancer Patients’ Survival: Standard Calculation Methods And Some Considerations Regarding Their Interpretation

Abstract

Background

Cancer patients’ survival is an extremely important but complex indicator for assessing regional or global inequalities in diagnosis practices and clinical management of cancer patients. The population-based cancer survival comparisons are available through international projects (i.e. CONCORD, EUROCARE, OECD Health Reports) and online systems (SEER, NORDCAN, SLORA). In our research we aimed to show that noticeable differences in cancer patients’ survival may not always reflect the real inequalities in cancer care, but can also appear due to variations in the applied methodology for relative survival calculation.

Methods

Four different approaches for relative survival calculation (cohort, complete, period and hybrid) have been implemented on the data set of Slovenian breast cancer patients diagnosed between 2000 and 2009, and the differences in survival estimates have been quantified. The major cancer survival comparison studies have been reviewed according to the selected relative survival calculation approach.

Results

The gap between four survival curves widens with time; after ten years of follow up the difference increases to more than 10 percent points between the highest (hybrid) and the lowest (cohort) estimates. In population-based comparison studies, the choice of the calculation approach is not uniformed; we noticed a tendency of simply using the approach which yields numerically better survival estimates.

Conclusion

The population-based cancer relative survival, which is continually reported by recognised research groups, could not be compared directly as the methodology is different, and, consequently, final country scores differ. A uniform survival measure would be of great benefit in the cancer care surveillance.

1. Introduction

Cancer patients’ survival is, together with the incidence, prevalence and mortality, one of the basic cancer burden indicators. Population-based survival of cancer patients, as shown by cancer registries for more than 60 years (1), is a valuable indicator, which reflects patients’ characteristics as well as the organisation, accessibility, quality and efficiency of the healthcare system. Generally, it greatly differs from the survival of patient groups with a particular disease treated in individual hospitals, as commonly presented by clinicians (2).

Because of the extreme importance of survival indicator for assessing regional, international or global inequalities in the diagnosis practices and clinical management of cancer patients, several comparisons between and within countries are available today: the CONCORD study provides relative survival estimates for 31 countries on five continents (3, 4), the EUROCARE study offers the relative survival data for 23 European countries (5, 6), the OECD health reports present relative survival data for OECD countries (7, 8), the SEER estimates the relative survival for 98% of the U.S. population (9), the NORDCAN provides the relative survival data for 5 North European countries (10), and the SLORA calculates the relative survival measures for Slovenia (11).

The data on cancer patients are collected in cancer registries according to the internationally agreed and comparable procedures. Despite the exemplary quality and comparability of the data, the applied relative survival methods are not consistent between and within the releases of above studies, and, consequently, the published results on the population-based survival for the comparable calendar years and populations vary considerably.

In groups of patients, survival represents the proportion of patients still alive after a certain period of time since the diagnosis. In population-based survival analyses, we tend to estimate only the dying probability of patients with a disease investigated (i.e. the probability of dying from cancer) and thus tend to avoid all non-cancer causes of death. Such survival is called net cancer survival, and it is methodologically most correctly estimated using PoharPerme method, but traditionally one of the relative survival methods is used as an approximation (12, 13).

The basic and, at the same time, the most simple measure of survival is the so-called observed survival, where causes of death are not considered and survival of the patients is not compared to the population survival. Among various methods available for calculating the observed survival, currently, the most frequently used is the Kaplan-Meier’s method (14). The observed survival rate accounts for all deaths, and it is a true reflection of the actual mortality in a patient group. When considering a particular cause of death (i.e. cancer), typically all deaths due to other causes could simply be censored (the so-called cause-specific survival) (15). Such a technique for estimating net survival would seem reasonable also in population studies, however, in practice, it turns out that the number of patients entered into such studies is too large to allow the exact cause of death to be established for each individual patient; the data on the official causes of death, which are usually collected by national mortality registries, are often insufficiently accurate for these purposes (16, 17). Therefore, and because of the incomparability of the observed survival between different populations, in population studies net cancer survival is estimated by relative survival methods, rather than by the cause-specific survival (18).

Relative survival is calculated as a ratio between the observed and the expected survival, i.e. the survival expected with respect to gender and age in a certain time period in the entire population from which the patients come (19). The expected survival is calculated from general mortality data, published routinely in the form of mortality tables within the framework of countries’ vital statistics (20). Relative survival of cancer patients is generally reported for one, three, five and ten years after the diagnosis. The study designs in the relative survival analysis can be distinguished according to the definition of persons at risk who contribute to each conditional survival probability and according to the use of follow-up time. Four different study designs are described and implemented in our research – all applied in several recognised relative survival comparison studies or online reports (3-11). We have adopted the same terminology for various study designs (cohort, complete, period and hybrid approach) as suggested by Brenner and Rachet (21), even though this terminology has not been used consistently in the literature (22). The four approaches do not differ in the mathematical point of view, since the calculation procedures for the estimation of relative survival and its confidence intervals are the same in all four study designs. The major difference in four approaches is in the case selection (Figure 1): from the same patients’ pool, distinctive individuals are selected for each particular approach, which certainly leads to the difference in end results. All diagnosed patients were included in relative survival estimates with complete approach only. With cohort approach the patients from the earliest incidence year were selected, but with period and hybrid approaches only most recently diagnosed patients are picked up (21, 23).

Figure 1.

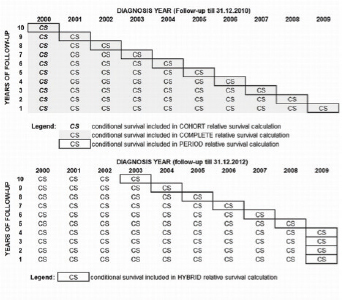
The illustration of the choice of patients diagnosed between the years 2000 and 2009 that contribute to a relative survival calculation with cohort, complete and period approaches (top: a follow up untill the end of 2010) and those that contribute to the hybrid approach (bottom: a follow up untill the end of 2012).

In our paper, we aim to highlight some important methodological issues regarding the design and interpretation of population-based survival comparison studies, and to draw specific attention to the possibility that noticeable differences in cancer patients’ survival may not always reflect the real inequalities in the access to cancer care, but can also appear due to variations in the methodology applied in the calculation of survival.

2. Methods

To demonstrate the quantitative differences in results between cohorts, complete, period and hybrid relative survival, the relative survival estimates for Slovenian female breast cancer patients diagnosed between 2000 and 2009 have been calculated using each of four study designs (Table 1). The sample was derived from the population-based Cancer Registry of the Republic of Slovenia. All cases registered on the basis of a death certificate or autopsy only were excluded prior to analyses, since survival in these cases is equal to zero. The administrative censoring date was December 31, 2010, except for the hybrid relative survival analysis, where the follow-up was extended until December 31, 2012. For the expected survival calculation, the Slovenian life tables (20) and the Ederer II method (24) were used in all examples. The Pohar-Perme estimator (PPE) (25) is added in Table 1 for comparison, since it is the only unbiased estimator for net survival.The analysis was performed with the STATA software package, using publicly available macros (26).

Table 1.

The one- to ten-year relative survivals with 95% confidence intervals and Pohar Perme relative survival estimators for Slovenian female breast cancer patients diagnosed between 2000 and 2009* derived by cohort, complete, period and hybrid approaches.

Follow-up time	COHORT all patients diagnosed in 2000		COMPLETE all patients diagnosed from 2000 to 2009		PERIOD some patients diagnosed from 2000 to 2009*		HYBRID some patients diagnosed from 2003 to 2009*
	Relative survival (95% confidence interval)	Pohar Perme estimator	Relative survival (95% confidence interval)	Pohar Perme estimator	Relative survival (95% confidence interval)	Pohar Perme estimator	Relative survival (95% confidence interval)	Pohar Perme estimator
1-year	96 (94-97)	96	95 (95-96)	96	96 (92-99)	97	96 (92-99)	97
2-year	90 (87-92)	91	92 (91-92)	92	93 (89-96)	93	93 (89-96)	93
3-year	85 (82-87)	85	88 (87-89)	88	89 (85-92)	90	89 (86-92)	90
4-year	80 (77-83)	81	85 (84-86)	86	87 (83-91)	88	87 (84-90)	88
5-year	77 (74-80)	77	83 (82-84)	83	85 (81-89)	85	85 (82-88)	86
6-year	73 (70-77)	75	80 (79-81)	81	83 (79-86)	83	84 (80-87)	83
7-year	72 (68-75)	72	79 (77-80)	80	80 (76-84)	82	82 (78-85)	82
8-year	71 (67-74)	72	77 (75-78)	78	78 (74-82)	78	80 (76-83)	79
9-year	70 (66-74)	72	76 (74-77)	77	76 (72-80)	76	79 (75-82)	78
10-year	69 (65-73)	73	75 (73-76)	77	75 (71-79)	75	78 (74-81)	77

^*With period and hybrid approaches, only the most recently diagnosed survivors are included (the included incidence years are specified in Figure 1).

^*With period and hybrid approaches, only the most recently diagnosed survivors are included (the included incidence years are specified in Figure 1).

Distinctive patients sampling has been applied as explained below and summarized in Figure 1: With the cohort approach, the entire group of patients must be followed-up for a certain period of time, in our case for ten years. Thus, every person included in the analysis should have the possibility to survive these ten years. In Slovenian breast cancer patients, where the patients diagnosed from 2000 to 2009 and followed-up until the end of 2010 are available (Figure 1, top), only the patients diagnosed in 2000 can be followed-up for ten years, and thus, only they are included in the cohort analysis of ten-year relative survival. With the complete approach, the patients diagnosed at a later date and followed up for less than ten years are also included (Figure 1, top). The patients followed-up for a shorter period of time are considered in the calculation of complete relative survival only for the time when they were actually followed-up. Thus, the group diagnosed three years before the study was completed (in 2007 in our example case), contributes to one- and three-year complete relative survival, but not to five- or ten-year survival. The period survival approach includes only the patients diagnosed in the most recent calendar year (the year 2009 in Figure 1) in the calculation of one-year survival, while the calculation of two-year survival includes only those patients who were diagnosed two years before (2008) and who have survived the first year; accordingly, the calculation of five-year survival includes only those patients who were diagnosed five years before (2005) and who are still alive at least four years after the diagnosis. The approach that combines the features of the period and cohort relative survival analyses is called hybrid relative survival (21). With hybrid approach, the follow up time is available for a more recent period than records on cancer patients (at the bottom part of Figure 1, patients were diagnosed until 2009, but in the case of the hybrid approach, the follow-up was performed until the end of 2012). For the calculation of conditional survival after one, two and three years, the cohort approach on 2009 patients was applied, as all 2009 patients were followed-up for three years. Moreover, for the calculation of conditional survival after four to ten years, the period analysis of patients diagnosed in the most recent years available (2008–2002) is used.

3. Results

3.1. An Empirical Example

The sample data set included 11,060 females with a median follow-up time of 4.2 years. The up-to-ten-year relative survival curves derived by the cohort, complete, period and hybrid relative survival analyses are plotted in Figure 2 and 95% confidence intervals are presented in Table 1.

Figure 2.

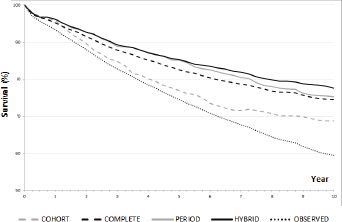
The relative survival curves derived by cohort, complete, period and hybrid approaches, and Kaplan-Meier observed survival for Slovenian female breast cancer patients diagnosed between 2000 and 2009.

The observed survival curve resulting from Kaplan-Meier analysis of the complete data set is added to Figure 2, showing that the ten-year survival of breast cancer patients is higher by 10 to 20 percentage points (or relatively from 15% to 30%) if non-cancer causes of death are analysed properly. Comparing the effect of such elimination of non-cancer causes of death already after five years after diagnosis, relative survival is higher by 2 to 10 percentage points.

The four compared relative survival approaches give similar results only for the first year after diagnosis (Table 1). The gap among the curves widens with time, proving to be the largest after ten years of a follow-up: the difference in ten-year survival between the approach giving the highest results (the hybrid analysis) and the approach giving the lowest results (the cohort analysis) is 9 percentage points (11%). Complete and period approaches’ results are between cohorts an hybrid approach, but the gap between them narrows with time after a diagnosis. In the first six years after a diagnosis, there is practically no difference between the results of period and hybrid approaches, as only after several years the difference inpatients’ selection results in better hybrid survival estimates. The estimates are expectably the most precise in complete approach, where all available patients are included in the calculation, but with all other approaches the precision of the estimates is similar.

Within the pool of the same patients, the highest survival is reported with the hybrid approach. The results slightly differ only with period and complete approaches, but they are significantly lower with cohort approach.

3.2. The Selection of the Relative Survival Approach in Practice

Currently, comparable population-based survival statistics are provided by three prominent research groups: CONCORD, EUROCARE and OECD Health Care Quality Indicators (HCQI) Project (3-8). They all report relative survival for selected countries in successive time periods. Table 2 gives an overview of the included data and relative survival calculation approach. The final findings are published in the most prominent science journals, and they have a major impact on the understanding of the inequalities in cancer control between countries, meanwhile also influencing regional health policies and health systems.

Table 2.

The differences in the relative survival calculation approaches between and within major population-based cancer survival studies, aiming to compare cancer care in several countries.

Population-based relative survival follow-up	Diagnosis year of included patients	End of follow-up year	Relative survival approach
CONCORD-1 (3)	1990-1994	1999	cohort
CONCORD-2 (4)	1995-2004	2009	cohort
CONCORD-2 (4)	2005-2009	2009	period
EUROCARE-4 (5)	1995-1999	2003	cohort
EUROCARE-4 (5)	1996-2002	2003	period
EUROCARE-5 (6)	2000-2007	2008	complete
EUROCARE-5 (6)	1999-2007	2008	period
OECD HCQI 2011 (7)	1995-2004	2009	not specified
OECD HCQI 2013 (8)	1995-2009	2012	period or cohort

The data for these studiesare gathered from population-based cancer registries; in many cases, the same registries provide data for all three studies. The CONCORD and EUROCARE studies collect individual data and perform all data quality checks and calculations, while the OECD HCQI Project collects only the end results on relative survival. What causes certain confusion in the evaluation of all these results is that the relative survival calculation approach is inconsistent between and within studies.

In the studies designed before the empirical evaluation of the period relative survival approach in 2002 (23), the method of choice was always the cohort approach. Currently, it appears that the researchers tend to choose, if the data are sufficient, the period approach for more recently diagnosed patients. The cohort approach remains the method of choice only for the relative survival calculations when patients are followed-up for longer periods. In EUROCARE-5, the classical cohort approach is replaced by the complete approach (6).

Considering the choice of relative survival approach, the OECD results are rather unclear. In their report in 2011, the choice of the approach was completely left to the cancer registries, and for the 2014 report, the OECD recommends using the period approach as a priority. Alternatively, the cohort analysis can also be used. Bearing in mind that different approaches give different results with the same data, such comparisons of relative survival would not be very efficient.

From the relative survival data, which are available through online systems, the SEER system offers the most flexibility in choosing different approaches with respect to the year of diagnosis and follow-up time. The SEERStat software (27) allows the user to select from the cohort, complete and period analyses, but the pre-prepared tables for Cancer Statistics Review (9) provide only the conditional survival probabilities for a specific diagnosis year and survival time, and thus the reader is left with the choice of selecting the research study design. In the NORDCAN project, the cohort survival approach is generally used, but for the later periods, the hybrid approach is applied (10). SLORA provides its users only with the relative survival calculated by the cohort approach (11).

4. Discussion

In our research, we point out the discrepancy in the end results when the relative survival is estimated by four different study designs: cohort approach, complete approach, period approach and hybrid approach. The approaches differ according to the selection of patients that contribute to the calculation of survival and by the definition of the follow-up date. The extent of difference in the end results depends on the type of cancer and patients’ age, but generally, when used on the same population, the relative survival is the highest with the hybrid approach and the lowest with the cohort one. As a rule, the final measure calculated by means of any of the presented approaches is entitled only as “relative survival” and it is compared and interpreted in the common perspective. The biostatisticians and epidemiologists might be aware of differences and incomparability of the different approaches, however, when the results are disseminated, the journalists, public officials and general public can neither understand their complexity nor correctly interpret the results.

A tendency to use the approach which yields numerically better survival of cancer patients was noticed in most reports reviewed in this paper, and can be observed also in survival studies performed directly on cancer registry data (28). The period approach to relative survival calculation was developed in order to enable the use of information from the most recently diagnosed patients contributing to survival calculation. Namely, the continuous advances in medicine are associated with a better prognosis in patients diagnosed in recent years. However, the period approach has been often criticised, as, by definition, it selectively includes the most recently diagnosed patients and hence predicts the survival of patients whose follow-up was too short. On the other hand, the cohort and complete approaches consider only the existing data, and the results represent the real situation. The results of period relative survival should be presented and interpreted with a certain degree of caution. As evident from the procedure described in Figure 1, by means of the period relative survival approach we are including only the best (i.e. the most recent) available conditional survival probabilities. By performing such selection we are ignoring the fact that the patients contributing to the calculation of the one- to four-year conditional survival probability might not even survive five years. Thus we can only predict what their five-year survival would be like.

There are also other methodological issues that, besides the selection of a study design, distort the end results of survival analysis. Among the most important are: age-adjustment procedures, the expected survival calculation method, and the quality assurance of the input data. Data quality is carefully monitored by the CONCORD (3, 4) and EUROCARE (5, 6) studies, but the OECD studies relies only on the internal quality controls performed by individual cancer registries. The scientific discussion on the appropriate life-table method for the calculation of the expected survival has been long-lasting and is not finished yet. The Ederer II method (24), recognised as the least biased, was chosen by the recent EUROCARE studies (5, 6), while in the OECD Project, the Hakulinen method (29) is accepted as well. Age adjustment should be performed in all international comparisons, as this appears to be the best procedure to avoid the variation in survival due to differences in the age profile of cancer patients between the populations (30). The International Cancer Survival Standard weights (31) have become a golden standard for age standardisation of relative survival in the CONCORD, EUROCARE and OECD HCQI. Identical weights promise the comparability of end results of different studies. However, the procedure of age standardisation itself irregularly affects the relative survival results; the study of Slovenian cancer patients’ survival empirically showed that the downward deviation of survival results after agestandardisation is greater in cancer sites with a small number of cancer patients in particular age groups (2).

Recently, Pohar-Perme et al. (25) showed mathematically that all classical methods of relative survival calculation provide biased estimates of net survival, since the results are not independent of the national general population mortality. Therefore, they are particularly unsuitable for comparison between countries. Pohar-Perme et al. proposed a new estimator (the Pohar-Perme estimator – PPE) that enables the desired unbiased comparability. Roche et al. compared the PPE with the classical estimators commonly used in population-based survival studies on the actual data from FRANCIM cancer registries network. They concluded that, in estimating net survival, cancer registries should abandon all classical (relative and cause-specific) methods for calculating population based survival, and adopt the new PPE (13). Despite the fact that Roche’s assessment has been criticised (22), it seems that PPE is currently recognised as the most appropriate estimator of net survival. Moreover, it has been applied in the CONCORD-2 study (4). However, even if not biased theoretically, the researcher must decide on one of the patient selection approaches (cohort, complete, period or hybrid) also in the PPE calculation. The values of oneto ten-year relative survival estimated by the PPE using the cohort, complete, period and hybrid approaches were calculated for our empirical example and added to Table 1. The results are only slightly different from our basic calculation performed using the Ederer II method, but the difference between the four approaches is again evident.

5. Conclusions

In conclusion, population-based cancer relative survival, which is continually reported by recognised research groups, could not be compared directly. Even though the studies are performed with the same statistical methods, on the matching patients’ pool and identical time periods, the sample of patients included in the calculation and, consequently, the final scores of countries differ. As relative survival is the basic cancer care indicator, the results of the survival analysis should not be misleading. Conclusions based on biased comparisons could lead to unnecessary public health interventions as well as unfavourable clinical decisions. The epidemiological and biostatistical scientific communities should standardise the relative survival methodology, providing the policy-makers and the clinicians with a uniform survival measure. In any case, results should always be properly commented and the approach used in the analysis should be clearly described.