Abstract
Background and Aims Floral development is remarkably robust in terms of the identity and number of floral organs in each whorl, whereas vegetative development can be quite plastic. This canalization of flower development prevents the phenotypic expression of cryptic genetic variation, even in fluctuating environments. A cruciform perianth with four petals is a hallmark of the Brassicaceae family, typified in the model species Arabidopsis thaliana. However, variable petal loss is found in Cardamine hirsuta, a genetically tractable relative of A. thaliana. Cardamine hirsuta petal number varies in response to stochastic, genetic and environmental perturbations, which makes it an interesting model to study mechanisms of decanalization and the expression of cryptic variation.
Methods Multitrait quantitative trait locus (QTL) analysis in recombinant inbred lines (RILs) was used to identify whether the stochastic variation found in C. hirsuta petal number had a genetic basis.
Key Results Stochastic variation (standard error of the average petal number) was found to be a heritable phenotype, and four QTL that influenced this trait were identified. The sensitivity to detect these QTL effects was increased by accounting for the effect of ageing on petal number variation. All QTL had significant effects on both average petal number and its standard error, indicating that these two traits share a common genetic basis. However, for some QTL, a degree of independence was found between the age of the flowers where allelic effects were significant for each trait.
Conclusions Stochastic variation in C. hirsuta petal number has a genetic basis, and common QTL influence both average petal number and its standard error. Allelic variation at these QTL can, therefore, modify petal number in an age-specific manner via effects on the phenotypic mean and stochastic variation. These results are discussed in the context of trait evolution via a loss of robustness.
Keywords: Cardamine hirsuta, Arabidopsis thaliana, floral development, petal number, stochastic variation, quantitative trait locus, species diversity, developmental robustness.
INTRODUCTION
Flowering plants evolved around 125–145 million years ago and quickly expanded to become the dominant plant group on land. Today there are an estimated 532 000 species of angiosperms while all other land plants are represented by only an estimated 34 000 species (The Plant List version 1.1, http://www.theplantlist.org/). One reason for this evolutionary success is believed to reside in the efficiency of the flower as a reproductive system. A perianth, consisting of sepals and petals, was one of several important innovations in the flower (Endress, 2001; Baum and Hileman, 2007). Petals play a key role in flower opening and pollinator attraction, encouraging outcrossing and the evolution of pollination syndromes, which describe a set of floral traits associated with specific pollinators (Glover, 2007). These processes favour speciation via reproductive isolation, and contributed to the high number of angiosperm species (Fenster et al., 2004).
Floral development is particularly robust to changing conditions, especially floral organ identity and number. For example, the number of floral organs is not influenced by environmental perturbation, while the numbers of leaves or branches are strongly affected (Givnish, 2002). Floral pattern is determined early in development by the precise spatial and temporal activation of floral organ identity genes, as summarized by the ABC model (Coen and Meyerowitz, 1991). Basal angiosperms, such as Amborellaceae or Nymphaeaceae, display a more plastic flower organization, with floral organ number varying between individuals and frequent fusions or mosaics occurring between different organ types (Buzgo et al., 2004). This observation led to the ‘fading borders model’ for the determination of floral organ identity in basal angiosperms, where borders of ABC gene expression are not strictly defined (Buzgo et al., 2004; Soltis et al., 2007). Major trends in angiosperm evolution include the acquisition of flowers with a stable number of organs per whorl (merism), whorled phyllotaxy and synorganization, which describes interactions between individual floral organs to form a higher complexity functional unit, such as the gynostemium of orchids (Specht and Bartlett, 2009). These trends reflect the canalization of floral development that took place during angiosperm evolution, to produce floral phenotypes that are buffered to environmental, genetic or stochastic perturbations in nature (Waddington, 1959). For example, the canalization of corolla lobe number in the Asterid Linanthus is a floral phenotype that has been examined in detail (Huether, 1968). Since pollinators recognize rather specific floral morphologies, one can easily imagine why canalization of flower development could have been under positive selection during evolution.
Canalization is the process by which phenotypic variation under a given perturbation is reduced, for example due to suppression of the expression of genetic variation (Gibson and Dworkin, 2004). As such, cryptic genetic variation can accumulate in developmental pathways without a deleterious effect since the phenotypic output is buffered (Flatt, 2005; Felix and Wagner, 2008). Robustness-conferring genes are hypothesized to buffer the output of developmental pathways by affecting the variance of a trait but not its phenotypic mean (Felix and Barkoulas 2012). Cryptic genetic variation can be revealed by strong perturbations, such as inhibition of Hsp90 (heat shock protein 90) chaperone function, or high environmental stresses such as heat shocks (Rutherford and Lindquist, 1998; Queitsch et al., 2002; Cowen and Lindquist, 2005). The phenotypic expression of this genetic variation is then exposed to natural selection, and advantageous mutations can be fixed in natural populations (Rohner et al., 2013), which provides a molecular framework for the paradox of having robust and evolvable morphological traits (Waddington, 1959; Flatt, 2005; Felix and Wagner, 2008). There are different degrees of robustness; the Caenorhabditis elegans vulva cell patterning is strongly robust to perturbations with an error frequency of around 10–3 in isogenic lines (Felix and Wagner, 2008), whereas constancy of a pentamerous corolla in Linanthus had an error rate of 2 % in natural populations (Huether, 1968). In contrast to this, some developmental processes are considered plastic (i.e. uncanalized) and vary considerably in response to environmental, genetic or stochastic variation [e.g. the number of flowers produced by A. thaliana plants, or wing pigmentation in some butterflies (Brakefield et al., 1996; Pigliucci, 1998; Hall et al., 2007)].
Petal number variation is a derived feature of Cardamine hirsuta flowers, and evolved from a robust petal number of four in the Brassicaceae (Endress, 1992; Hay et al., 2014). Therefore, understanding the genetic basis for petal number variation in C. hirsuta may provide evidence for trait evolution via a loss of robustness. In this work, we addressed whether we could identify a genetic basis for the stochastic variation in petal number found in recombinant inbred lines (RILs) generated from a cross between two C. hirsuta accessions that differed in average petal number. We used multitrait quantitative trait locus (QTL) analysis to identify genomic regions affecting the average petal number and its standard error, either for the whole plant or for groups of four consecutive flowers. We found a considerable heritability for stochastic variation and identified four QTL that influenced both average petal number and its standard error. Our results suggest that evolutionary change has shifted C. hirsuta petal number outside of a buffered zone such that allelic variation at these QTL affects both the phenotypic mean and stochastic variation.
MATERIALS AND METHODS
Plant material and growth conditions
The Cardamine hirsuta Ox × Wa RIL population and the founding accessions Oxford (Ox) and Washington (Wa) have been described previously (Hay et al., 2014). Plants were grown in a controlled environment room under 16/8 h photoperiod (day/night) at 22 °C/20 °C, respectively. Seeds were sown on a moist peat:vermiculite mixture (2:1) in 7 × 7 cm pots and subsequently stratified at 4 °C in the dark for 10 d before transferring the pots to the growth room.
Petal number quantification
Three replicates of each RIL were quantified for petal number in each of the first 24 flowers to develop on the main inflorescence or on all flowers when <24 flowers were produced. Flowers were removed from the plant when they opened, and petal number was counted using a dissecting microscope. The average petal number per plant was calculated, and both the mean petal number per RIL and the standard error of this mean were used as phenotypes for QTL analysis. Additionally, average petal number was calculated in non-overlapping bins of four flowers per plant, and the mean petal number for each bin per RIL, as well as the standard error of this mean, were used as phenotypes for QTL analysis. The standard error was chosen as a measure of stochastic variation rather than the more traditional coefficient of variance (CV) because the average petal numbers per plant were often close to 0, and at these values the CV is particularly sensitive to small changes in average and tends to approach infinity. We used the Levene’s statistic as an additional measure of stochastic variation (Hall et al., 2007). We calculated the Levene’s statistic per plant as the absolute difference between the average petal number and the mean per RIL, divided by the mean per RIL.
Multitrait QTL analysis on recombinant inbred lines
Statistical analysis was done using R version 3.1 except phenotypic analysis and multitrait QTL analysis, which were performed using Genstat 16th edition (VSN International, 2013). Broad-sense heritabilities (H2) were calculated according to the implementation in Genstat: 1 – [(non-genetic (within RIL) variance/number of plants per RIL)/genetic (between RILs) variance component], where the variance components are estimated by fitting a mixed model with RIL as a random term. Multitrait QTL analysis is based on fitting a mixed model where the QTL are fixed effects and the genotypes are random effects. Genetic predictors were calculated with no more than 2 cM between them from the C. hirsuta genetic map (Hay et al., 2014). The mean per RIL of the average petal number over 24 flowers per plant was analysed together with (a) the standard error of this mean, and (b) the mean Levene’s statistic per RIL. Additionally, the mean average petal numbers of non-overlapping bins of four flowers, and the accompanying standard errors, were analysed together as 12 traits. For this analysis, the standard errors of bins covering flowers 17–20 and 21–24 were eventually excluded because no significant QTL effects were detected. A simple interval mapping scan was followed by several composite interval mapping scans during which cofactors were either added or removed until no further improvement could be made. The resulting set of co-factors was used to fit a final multitrait QTL model to determine the allelic effects and the variance explained by these effects.
RESULTS
Cardamine hirsuta petal number variation
Petal number in C. hirsuta varies (1) at different scales and (2) in response to different perturbations. (1) As a derived character, C. hirsuta petal number varies at the between-species scale from related species in the Brassicaceae with four petals (Hay et al., 2014). At the within-species scale, we find natural variation in C. hirsuta petal number in different accessions (Pieper et al., 2015). At the scale of the individual plant, petal number varies between isogenic individuals and between the different flowers produced by a single plant (Fig. 1A, B). However, the extent to which the genetic basis for this trait variation is shared across scales is unknown. (2) Cardamine hirsuta petal number is responsive to different types of genetic, environmental and stochastic variation. First, both natural and induced genetic variation causes petal number to vary in C. hirsuta (Pieper et al., 2015). For example, allelic variation between the Ox and Wa accessions causes a difference in average petal number (Fig. 1B). Secondly, environmental variation, such as changing ambient temperature, causes petal number to vary between isogenic individuals (Pieper et al., 2015). Thirdly, stochastic variation causes variation in petal number between isogenic individuals in a constant environment (Fig. 1B). Ageing is an important factor that contributes to variation around the mean petal number for an individual plant, such that early-emerging flowers generally have a higher petal number than late-emerging ones along the main stem (Fig. 1B). However, petal number also varies between isogenic individuals at the same flower position (within the Ox or Wa accessions for instance, Fig. 1B), and this stochastic variation is considerable [e.g. the average standard error of the mean (s.e.m.) petal number for Ox is 0.34, where average petal number is 1.52].
Fig. 1.
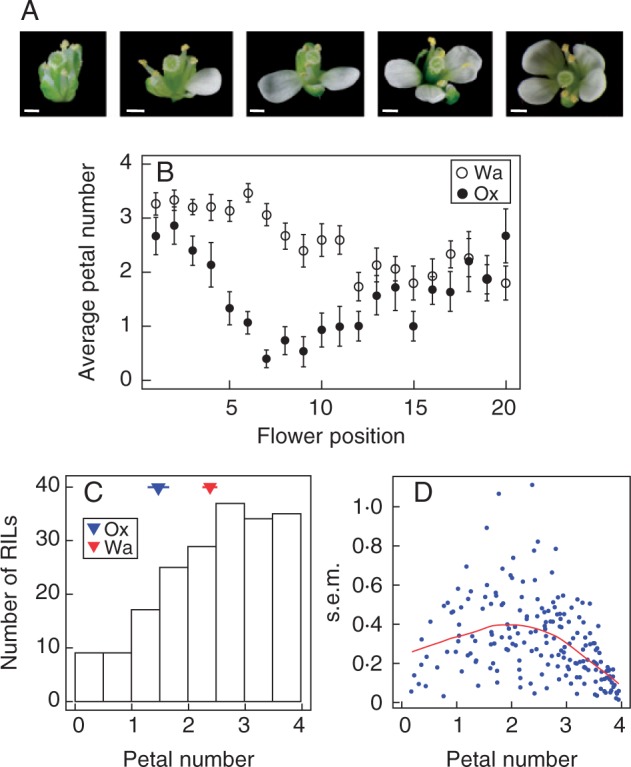
Cardamine hirsuta petal number variation. (A) Representative C. hirsuta flowers showing petal number variation from zero to four. (B) Average petal number of the Ox and Wa (as indicated in the key) accessions plotted according to flower position along the main inflorescence. Error bars show s.e.m. (n = 15 plants). (C) Distribution of average petal number in the Ox × Wa RIL population. Average petal numbers for the founder accessions are displayed as blue (Ox) and red (Wa) triangles. (D) Distribution of the s.e.m. for average petal number in the Ox × Wa RIL population plotted according to average petal number. The Loess regression curve is shown in red.
Multitrait QTL analysis for average petal number and its stochastic variation
The phenotypic distribution for average petal number in the Ox × Wa RIL population covered the entire range of possible values from zero to four, thereby showing considerable transgression beyond the petal numbers of the founding strains (Fig. 1C). The broad-sense heritability (H2) of the average petal number was very high at 0.86 (Table 1). Taken together, this indicates that average petal number is a quantitative trait with a strong genetic basis in C. hirsuta. The stochastic variation in petal number, as determined by the s.e.m. of three replicates of each RIL, showed a non-linear relationship with average petal number. The stochastic variation was largest and showed the greatest variation for plants having an average petal number around two while it diminished when petal number approached both zero and four (Fig. 1D). This reflects two constraints: the obvious constraint of zero petals and a developmental constraint such that petal number does not exceed four petals. The H2 of the stochastic variation in petal number was estimated using an alternative measure of stochastic variation: the Levene’s statistic, because the s.e.m. was not suited for this purpose (see Table 1). The H2 of the stochastic variation was considerable at 0.58, indicating that this trait also has a genetic basis in C. hirsuta. These findings indicated that both traits, average petal number and stochastic variation, are likely to be influenced by QTL.
Table 1.
Summary of QTL analysis for mean petal number, standard error and Levene’s statistic over 24 flowers
| Trait | Population mean | H2 | Chr2, 4·7 cM | Chr4, 93·9 cM | Chr5, 11·15 cM | Chr5, 61·0 cM | Chr8, 0·0 cM |
|---|---|---|---|---|---|---|---|
| muPN | 2·48 | 0·86 | 0·76 (14·5) | −0·52 (6·8) | 0·40 (4·1) | 0·55 (7·7) | −0·94 (22·1) |
| s.e.m. | 0·25 | * | −0·33 (2·7) | – | – | −0·41 (4·2) | – |
| LS | 0·39 | 0·58 | −0·29 (2·1) | – | – | −0·34 (2·8) | – |
QTL effects are shown for homozygous substitution of Ox alleles with Wa alleles.
The percentage of variance explained by the respective QTL effect is provided in parentheses.
Non-significant effects are indicated by ‘–’.
muPN, average petal number of up to 24 flowers per plant; s.e.m., standard error of the mean muPN per RIL; LS, Levene’s statistic.
Broad-sense heritability (H2) is estimated as the ratio of genetic variance to total phenotypic variance.
*H2 is not calculated for the trait s.e.m. because it is problematic to estimate the genetic variance component.
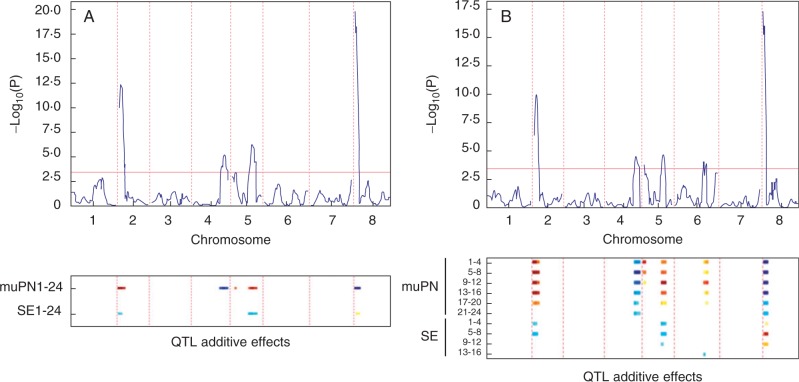
To investigate whether common or independent QTL affected each trait, we performed multitrait QTL analysis of average petal number and s.e.m. per RIL (Fig. 2A). We identified five QTL; each QTL affected average petal number and two of them also affected stochastic variation (Fig. 2A; Table 1), indicating that both traits share a common genetic basis. We obtained similar results when we used the Levene’s statistic as an alternative measure of stochastic variation, suggesting that this trait is reliably phenotyped by either statistical measure (Table 1; Supplementary Data Fig. S1). A QTL on the top of chromosome 8 had the largest effect on average petal number (–0.94 petals for a homozygous substitution of Ox alleles with Wa alleles) and explained most of the variance for this trait (22·1 %), but this QTL did not affect stochastic variation (Table 1). Two QTL with the second and third largest effects on average petal number also affected stochastic variation (QTL on chromosomes 2 and 5, Table 1). The effects of both QTL were of opposite sign for both traits: the Wa allele increased average petal number and decreased stochastic variation.
Fig. 2.
Multitrait QTL scans for mean average petal number and the s.e.m. (A, B) The upper panel shows the log-transformed test statistic [–log10(P)] plotted against genetic position. Chromosomes 1–8 are labelled on the x-axis and the significance threshold (α = 0·05) is indicated by the horizontal red line. The lower panel represents significant allelic effects of the QTL, as a heat-map scale, on multiple traits indicated on the y-axis. QTL effects where the Wa allele reduces the trait are shown in blue and those where the Wa allele increases the trait in yellow-red. Darker shades represent stronger effects. Analysis of the mean per RIL of petal number averaged over up to 24 flowers per plant and the s.e.m. are shown in (A). Analysis of means per RIL of petal number averaged in non-overlapping bins of four consecutive flowers per plant and the respective s.e.m. are shown in (B). The numbers in the trait names show the range of flower positions covered by the respective bins, where 1 is the first flower to develop on a plant.
We considered that QTL effects on stochastic variation might also depend on flower position based on the relationships between petal number and flower position (Fig. 1B), and between stochastic variation and petal number (Fig. 1D). To test this hypothesis, multitrait QTL analysis was performed on average petal numbers of non-overlapping bins of four flowers and the respective s.e.m. We found the five QTL detected previously plus one additional QTL on chromosome 6 (Fig. 2B). Each QTL affected average petal number over at least three consecutive bins (12 flowers). The strength of the effects and the variance explained by them varied slightly during inflorescence development and tended to be largest for flowers 5–8 or 9–12 (Table 2).
Table 2.
Summary of QTL analysis for mean petal number and standard error in non-overlapping bins of four flowers
| Trait | Population mean | Chr2, 8·1 cM | Chr4, 93·9 cM | Chr5, 7·8 cM | Chr5, 61·0 cM | Chr6, 87·7 cM | Chr8, 0·0 cM |
|---|---|---|---|---|---|---|---|
| muPN 1–4 | 2·78 | 0·68 (11·7) | −0·42 (4·3) | 0·48 (5·8) | 0·46 (5·2) | 0·30 (2·2) | −0·84 (18·0) |
| muPN 5–8 | 2·52 | 0·74 (13·9) | −0·56 (7·8) | 0·42 (4·2) | 0·48 (5·5) | 0·24 (1·3) | −0·92 (21·6) |
| muPN 9–12 | 2·24 | 0·70 (12·4) | −0·48 (6·0) | 0·32 (2·7) | 0·62 (9·5) | 0·48 (5·7) | −0·84 (18·0) |
| muPN 13–16 | 2·28 | 0·82 (17·2) | −0·44 (5·0) | 0·24 (1·6) | 0·58 (8·3) | – | −0·78 (15·5) |
| muPN 17–20 | 2·25 | 0·64 (10·4) | −0·42 (4·3) | – | 0·44 (4·8) | – | −0·50 (6·1) |
| muPN 21–24 | 2·00 | – | −0·58 (8·1) | 0·46 (5·1) | – | – | −0·78 (14·9) |
| s.e.m. 1–4 | 0·31 | −0·32 (2·5) | – | – | −0·40 (3·9) | – | – |
| s.e.m. 5–8 | 0·40 | −0·42 (4·6) | – | – | −0·46 (5·1) | – | 0·56 (8·0) |
| s.e.m. 9–12 | 0·40 | – | – | – | – | – | 0·36 (3·4) |
| s.e.m. 13–16 | 0·47 | – | – | – | – | −0·36 (3·4) | – |
QTL effects are shown for homozygous substitution of Ox alleles with Wa alleles.
The percentage of variance explained by the respective QTL effect is provided in parentheses.
Non-significant effects are indicated by ‘–’.
muPN, mean petal number of four flowers in the range indicated, where 1 is the first flower to develop on a plant; s.e.m., standard error of the respective mean petal number.
Four of the detected QTL were also found to affect stochastic variation using this phenotyping approach, including the two QTL found previously. The effects on stochastic variation were only significant for a maximum of two consecutive bins (eight flowers), and no significant effects on stochastic variation were observed for flowers at positions higher than 16; therefore, these flowers were excluded from the analysis. For the QTL on chromosomes 2 and 8, we observed the largest effect on both stochastic variation and average petal number for flower bin 5–8. However, this association was uncoupled for the QTL on chromosomes 5 and 6. On chromosome 5, we found QTL effects on stochastic variation for flower bins 1–8, while the strongest effects of this QTL on petal number were for flower bins 9–16. Similarly, the QTL on chromosome 6 had significant effects on stochastic variation for flower bin 13–16 while its effects on average petal number were only significant for flower bins 1–12. These results indicate that although there is a strong genetic correlation between average petal number and stochastic variation, the effects on both traits are independent to some degree.
DISCUSSION
The genetic basis of stochastic variation in petal number
Here, we show that both average petal number and its stochastic variation vary in C. hirsuta RILs, and that both types of phenotypic expression are under genetic control. We found that a considerable proportion of the stochastic variation associated with average petal number has a genetic basis in the RIL population (H2 = 0·58), but only a fraction of this could be attributed to detected QTL effects. We identified four QTL that affected both average petal number and its standard error, indicating that the mean and uniformity of this trait share a common genetic basis. However, the allelic effects of some QTL indicated that the uniformity of petal number could be modified independently of the average trait value. Thus, our genetic analysis of petal number variation in C. hirsuta provides evidence for a less well-explored type of genetic control that leads to differences in not only the phenotypic mean but also its stochastic variation between genotypes.
Our estimation that at least half of the stochastic variation associated with average petal number in C. hirsuta can be attributed to genetic control is higher than previous studies of stochastic trait variation (Hall et al., 2007). However, the amount of variance explained by our QTL model is more similar to the trait heritabilities reported previously (Hall et al., 2007). An overestimation of the broad-sense heritability for stochastic variation in our study, and/or the contribution of non-additive genetic effects and small effect QTL that were below our power to detect, are likely to explain this result. However, the most significant factor contributing to the missing heritability in our study probably comes from the developmental constraints imposed on the observable variation in stochastic noise for petal number. We found that the distribution of standard error was dependent on average petal number, with a maximum around two petals and minima at zero and four petals (Fig. 1D). Therefore, in contrast to continuous traits, the variation in stochastic noise was highly constrained as average petal number moved towards four or zero.
Developmental constraints on C. hirsuta petal number
Arabidopsis thaliana floral development produces a robust phenotype of four petals, which reflects the ancestral state in the Brassicaceae. For illustrative purposes, we can characterize this robustness in relation to activity of a petal development pathway such as microRNA regulation of the CUP-SHAPED COTYLEDONS 1 and 2 (CUC) transcription factors (Rhoades et al., 2002). Inducing very high pathway activity by the introduction of mir164-resistant CUC1 transgenes increases petal number beyond four, while inhibiting pathway activity by mir164 overexpression decreases petal number below four, but in wild-type plants petal number is buffered against normal pathway variation (Fig. 3A; Laufs et al. 2004; Mallory et al., 2004). These induced variants shift mean petal number outside of the buffered zone, resulting in increased variance.
Fig. 3.
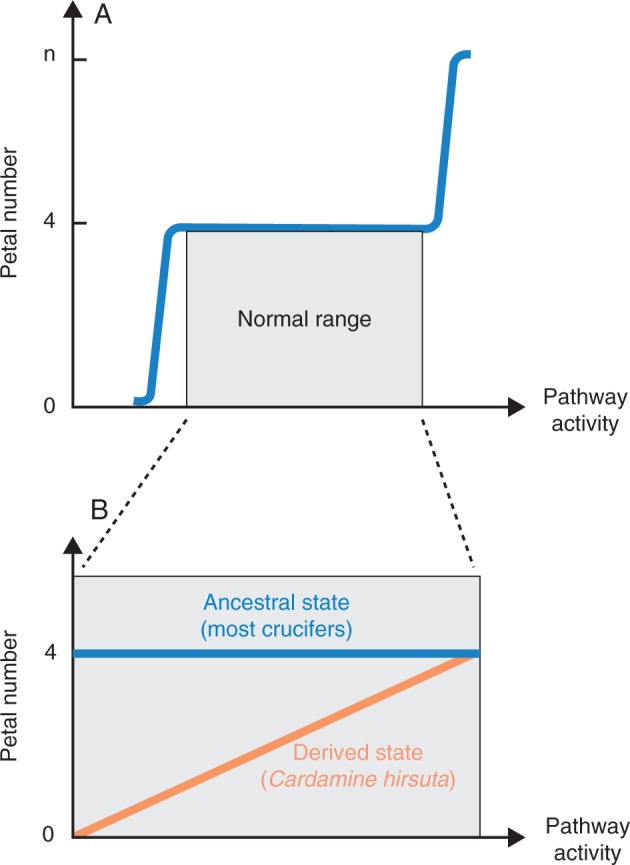
Schematic representation of trait evolution from a robust to non-robust state. (A) A stable petal number of four that is robust to a given perturbation is the ancestral character state in the Brassicaceae. Petal number is buffered within the normal range of developmental pathway activity, such that only very high or very low activity shifts the mean trait value outside the buffering zone and increases variance. (B) In comparison with most crucifers, C. hirsuta petal number is not buffered against the normal variation of developmental pathway activity in response to a given perturbation. As such, C. hirsuta shows a derived character state of petal number variation between zero and four. This could reflect an abbreviated buffering zone in C. hirsuta or a reduction in the normal range of C. hirsuta pathway activity such that it falls below the buffering zone found in most crucifers.
Evolutionary change in C. hirsuta floral development has produced a non-robust phenotype where petal number is no longer buffered against the normal variation of developmental pathways to a given perturbation (Fig. 3B). This natural variation in C. hirsuta petal number is one-sided with respect to the buffered trait value of four petals that exists in most crucifers, and petal numbers above four are only found in induced variants, similar to A. thaliana (A. Hay unpublished data). The four QTL that we identified in this study that influence stochastic variation in C. hirsuta petal number each had significant effects on the average trait value. Therefore, we do not suggest that these loci represent robustness genes, but rather that they comprise genetic variation that is available in C. hirsuta to alter the mean and variance of petal number. Therefore, these loci could also exist as cryptic genetic variation that is phenotypically suppressed in species such as A. thaliana with robust petal number.
The production of four petals in A. thaliana is regulated by the activity of a larger genetic network than the microRNA-regulated CUC pathway. In brief, the genetic control of petal identity and establishment of the boundaries that demarcate petal position must also interface with pathways that control the size of the floral meristem, the outgrowth of lateral organs and the patterning of their polarity (Irish, 2008, and references therein; Eshed et al., 2001; Benková et al., 2003; Huang et al., 2012; Lampugnani et al., 2012). Identifying the genes underlying the QTL detected here will help us to understand which aspects of petal development were modified during evolution to produce petal number variation in C. hirsuta.
Evolutionary significance of petal number variation in C. hirsuta
Cardamine hirsuta is a predominantly selfing species (Hay et al., 2014) and we can view petal number variation in the context of this evolutionary transition to self-compatibility. Petals help to open the floral bud, expose the receptive pistil to outcrossing and attract potential pollinators, and a reduction in petal size is frequently seen following the evolutionary loss of self-incompatibility mechanisms (Sicard and Lenhard, 2011). This trend may reflect a relaxation on the selective pressure to maintain conspicuous petals in selfing species, and loss of robustness in petal number could reflect a similar relaxation and evolve by neutral drift. Alternatively, petal number variation may be a selected particularity of the selfing syndrome in C. hirsuta whereby four petals assist bud opening and provide an opportunity to outcross, while petal loss delays bud opening and provides reproductive assuredness by efficient selfing. In conclusion, we showed that QTL effects on variance and mean cannot be uncoupled in the species-specific trait of petal number variation in C. hirsuta. Our findings will inform future studies on the contribution of cryptic genetic variation to species diversity.
SUPPLEMENTARY DATA
Supplementary data are available online at www.aob.oxfordjournals.org and consist of Figure S1: genome-wide multitrait QTL mapping scan for mean average petal number and Levene’s statistic on flowers 1–24.
ACKNOWLEDGEMENTS
We thank R. Melzer and G. Theissen for inviting us to contribute to this special issue, and J. Lempe for critical reading of the manuscript. This work was supported by the Biotechnology and Biological Sciences Research Council [grant no. BB/H01313X/1]; a Max Planck Society W2 Minerva Research Fellowship and a Royal Society University Research Fellowship to A.H.; and a European Molecular Biology Organization Long Term Fellowship to M.M.
LITERATURE CITED
- Baum DA, Hileman LC. 2007. A developmental genetic model for the origin of the flower. In: Ainsworth C, ed. Annual Plant Reviews Volume 20: Flowering and its Manipulation. Oxford: Blackwell Publishing Ltd, 1–27. [Google Scholar]
- Benková E, Michniewicz M, et al. 2003. Local, efflux-dependent auxin gradients as a common module for plant organ formation. Cell 115: 591–602. [DOI] [PubMed] [Google Scholar]
- Brakefield PM, Gates J, Keys D, et al. 1996. Development, plasticity and evolution of butterfly eyespot patterns. Nature 384: 236–242. [DOI] [PubMed] [Google Scholar]
- Buzgo M, Soltis PS, Soltis DE. 2004. Floral developmental morphology of Amborella trichopoda (Amborellaceae). International Journal of Plant Sciences 165: 925–947. [Google Scholar]
- Coen ES, Meyerowitz EM. 1991. The war of the whorls: genetic interactions controlling flower development. Nature 353: 31–37. [DOI] [PubMed] [Google Scholar]
- Cowen LE, Lindquist S. 2005. Hsp90 potentiates the rapid evolution of new traits: drug resistance in diverse fungi. Science 309: 2185–2189. [DOI] [PubMed] [Google Scholar]
- Endress PK. 1992. Evolution and floral diversity: the phylogenetic surroundings of arabidopsis and antirrhinum. International Journal of Plant Sciences 153: S106–S122. [Google Scholar]
- Endress PK. 2001. Origins of flower morphology. Journal of Experimental Zoology 291: 105–115. [DOI] [PubMed] [Google Scholar]
- Eshed Y, Baum SF, Perea JV, Bowman JL. 2001. Establishment of polarity in lateral organs of plants. Current Biology 11: 1251–1260. [DOI] [PubMed] [Google Scholar]
- Felix M-A, Barkoulas M. 2012. Robustness and flexibility in nematode vulva development. Trends in Genetics 28: 185–195. [DOI] [PubMed] [Google Scholar]
- Felix M-A, Wagner A. 2008. Robustness and evolution: concepts, insights and challenges from a developmental model system. Heredity 100: 132–140. [DOI] [PubMed] [Google Scholar]
- Flatt T. 2005. The evolutionary genetics of canalization. Quarterly Review of Biology 80; 287–316 [DOI] [PubMed] [Google Scholar]
- Fenster CB, Armbruster WS, Wilson P, Dudash MR, Thomson JD. 2004. Pollination syndromes and floral specialization. Annual Review of Ecology, Evolution, and Systematics 35: 375–403. [Google Scholar]
- Gibson G, Dworkin I. 2004. Uncovering cryptic genetic variation. Nature Reviews Genetics 5: 681–690. [DOI] [PubMed] [Google Scholar]
- Givnish T. 2002. Ecological constraints on the evolution of plasticity in plants. Evolutionary Ecology 16: 213–242. [Google Scholar]
- Glover BJ. 2007. Understanding flowers and flowering. Oxford: Oxford University Press. [Google Scholar]
- Hall MC, Dworkin I, Ungerer MC, Purugganan M. 2007. Genetics of microenvironmental canalization in Arabidopsis thaliana. Proceedings of the National Academy of Sciences, USA 104: 13717–13722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hay AS, Pieper B, Cooke E, et al. 2014. Cardamine hirsuta: a versatile genetic system for comparative studies. The Plant Journal 78: 1–15. [DOI] [PubMed] [Google Scholar]
- Huang T, Lopez-Giraldez F, Townsend JP, Irish VF. 2012. RBE controls microRNA164 expression to effect floral organogenesis. Development 139: 2161–2169. [DOI] [PubMed] [Google Scholar]
- Huether CAJ. 1968. Exposure of natural genetic variability underlying the pentamerous corolla constancy in Linanthus androsaceus ssp. androsaceus. Genetics 60: 123–146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irish VF. 2008. The Arabidopsis petal: a model for plant organogenesis. Trends in Plant Science 13: 430–436. [DOI] [PubMed] [Google Scholar]
- Lampugnani ER, Kilinc A, Smyth DR. 2012. PETAL LOSS is a boundary gene that inhibits growth between developing sepals in Arabidopsis thaliana. The Plant Journal 71: 724–735. [DOI] [PubMed] [Google Scholar]
- Laufs P, Peaucelle A, Morin H, Traas J. 2004. MicroRNA regulation of the CUC genes is required for boundary size control in Arabidopsis meristems. Development 131: 4311–4322. [DOI] [PubMed] [Google Scholar]
- Mallory AC, Dugas DV, Bartel DP, Bartel B. 2004. MicroRNA regulation of NAC-domain targets is required for proper formation and separation of adjacent embryonic, vegetative, and floral organs. Current Biology 14: 1035–1046. [DOI] [PubMed] [Google Scholar]
- Pieper B, Monniaux M, Hay A. 2015. The genetic architecture of petal number in Cardamine hirsuta. New Phytologist , doi:10.1111/nph.13586. [DOI] [PubMed] [Google Scholar]
- Pigliucci M. 1998. Developmental phenotypic plasticity: where internal programming meets the external environment. Current Opinion in Plant Biology 1: 87–91. [DOI] [PubMed] [Google Scholar]
- Queitsch C, Sangster TA, Lindquist S. 2002. Hsp90 as a capacitor of phenotypic variation. Nature 417: 618–624. [DOI] [PubMed] [Google Scholar]
- Rhoades MW, Reinhart BJ, Lim LP, Burge CB, Bartel B, Bartel DP. 2002. Prediction of plant microRNA targets. Cell 110: 513–520. [DOI] [PubMed] [Google Scholar]
- Rohner N, Jarosz DF, Kowalko JE, et al. 2013. Cryptic variation in morphological evolution: HSP90 as a capacitor for loss of eyes in cavefish. Science 342: 1372–1375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rutherford SL, Lindquist S. 1998. Hsp90 as a capacitor for morphological evolution. Nature 396: 336–342. [DOI] [PubMed] [Google Scholar]
- Sicard A, Lenhard M. 2011. The selfing syndrome: a model for studying the genetic and evolutionary basis of morphological adaptation in plants. Annals of Botany 107: 1433–1443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soltis DE, Chanderbali AS, Kim S, Buzgo M, Soltis PS. 2007. The ABC model and its applicability to basal angiosperms. Annals of Botany 100: 155–163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Specht CD, Bartlett ME. 2009. Flower evolution: the origin and subsequent diversification of the angiosperm flower. Annual Review of Ecology, Evolution, and Systematics 40: 217–243. [Google Scholar]
- VSN International. 2013. Genstat for Windows 16th edition. Hemel Hempstead, UK: VSN International; GenStat.co.uk. [Google Scholar]
- Waddington CH. 1959. Canalization of development and genetic assimilation of acquired characters. Nature 183: 1654–1655. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.