Relationship between the species-representative phenotype and intraspecific variation in Ranunculaceae floral organ and Asteraceae flower numbers

Abstract

Background and Aims Phenotypic variation in floral morphologies contributes to speciation by testing various morphologies that might have higher adaptivity, leading eventually to phylogenetic diversity. Species diversity has been recognized, however, by modal morphologies where the variation is averaged out, so little is known about the relationship between the variation and the diversity.

Methods We analysed quantitatively the intraspecific variation of the organ numbers within flowers of Ranunculaceae, a family which branched near the monocot–eudicot separation, and the numbers of flowers within the capitula of Asteraceae, one of the most diverse families of eudicots. We used four elementary statistical quantities: mean, standard deviation (s.d.), degree of symmetry (skewness) and steepness (kurtosis).

Key Results While these four quantities vary among populations, we found a common relationship between s.d. and the mean number of petals and sepals in Ranunculaceae and number of flowers per capitulum in Asteraceae. The s.d. is equal to the square root of the difference between the mean and specific number, showing robustness: for example, 3 in Ficaria sepals, 5 in Ranunculus petals and Anemone tepals, and 13 in Farfugium ray florets. This square-root relationship was not applicable to Eranthis petals which show little correlation between the s.d. and mean, and the stamens and carpels of Ranunculaceae whose s.d. is proportional to the mean. The specific values found in the square-root relationship provide a novel way to find the species-representative phenotype among varied morphologies.

Conclusions The representative phenotype is, in most cases, unique to the species or genus level, despite intraspecific differences of average phenotype among populations. The type of variation shown by the statistical quantities indicates not only the robustness of the morphologies but also how flowering plants changed during evolution among representative phenotypes that eventually led to phylogenetic diversification.

INTRODUCTION

Variation in floral organ numbers, as well as flower numbers, is found within populations of single species and even within individual plants (Herrera, 2009; Ronse De Craene, 2015; Fig. 1A). This variation can originate from genetic or epigenetic regulation, environmental perturbation, and/or stochastic error during gene expression resulting in variation in the numbers of protein molecules within single cells, which has been extensively analysed in species ranging from bacteria to mammals (McAdams and Arkin, 1997; Elowitz et al., 2002; Sanchez and Golding, 2013). This molecular stochasticity is transmitted via spatio-temporal gene expression (Houchmandzadeh et al., 2002; Gregor et al., 2007; Bergmann et al., 2007; Tkačik et al., 2008; Manu et al., 2009) and tissue growth (Alim et al., 2012) to the macroscopic characteristics of organs, such as the number of animal body segments (Kettle et al., 2003; Vedel et al., 2010) and plant floral organs (Kitazawa and Fujimoto, 2014). Despite such variation, only the modal morphologies have been regarded as the typical or representative phenotype of a species.

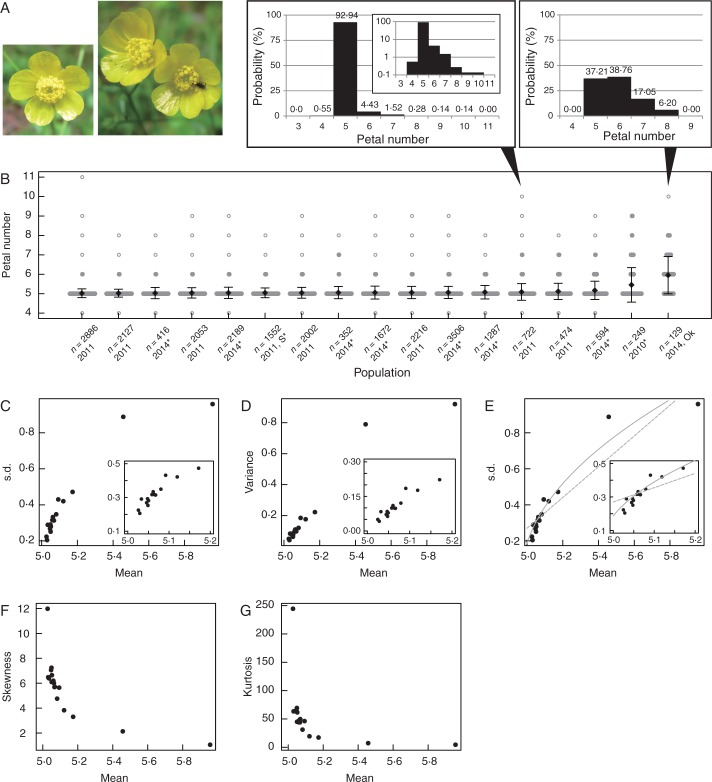
Fig. 1.

Intraspecific variation of petal number in Ranunculus japonicus (Ranunculaceae). (A) Typical flower of R. japonicus with five petals (left) and two flowers of an individual plant with six and seven petals, respectively (right). The histograms indicate the probability of each petal number in the two populations. (B) The variation in petal numbers of R. japonicus measured in different years and locations in Japan, including nine published measurements marked by asterisks (*; Kitazawa and Fujimoto, 2014). The populations are ordered by the means denoted by solid diamonds. The sample size and year for each measurement are represented as the x-axis label. All populations were distributed in Osaka prefecture except for two populations measured in Shiga (S) and Okayama (Ok) prefectures. The width of the grey bars indicates the probability of each petal number in each population. Open circles indicate non-zero probabilities of less than 1 %. (C, D) The relationship between the mean and s.d. (C) or variance (D). (E) The NLS fitting of linear (dashed line) and square-root (solid line) functions. (F, G) The relationship between the mean and skewness (F) or kurtosis (G).

Around the end of the 19th century, the variation in floral organ numbers, and floret number variation in the Asteraceae, was widely discussed by statisticians. This variation was quantified based on the frequency distributions of floral organ numbers in wild and cultivated populations (de Vries, 1894; Ludwig, 1895). de Vries (1894, 1895, 1899) found three types of curve describing this variation: the symmetric curve (Galton Kurve), the negatively or positively skewed curve (halbe Galton-Kurve; de Vries, 1894; Fig. 1A) and the bimodal curve (zweigipflige Variationskurve; de Vries, 1895). He performed field experiments with repeated selection of plants with larger numbers of petals or ray florets for several generations and found that a change between the curve types emerged within single lineages of Ranunculaceae and Asteraceae species (de Vries, 1894, 1899). Ludwig (1895) described multimodal variation curves in Asteraceae floret numbers showing more than one peak within a population. He stated that those modal numbers were related to Fibonacci numbers, namely 8, 13, 21, 34, etc., or to the sums (e.g. 8 + 21 = 29) or the multiples (e.g. 8 × 2 = 16) of Fibonacci numbers (Ludwig’s law), and concluded that therefore the representative phenotype is common among species. The variation in daisy floret numbers in Europe measured by de Vries (1899) agreed with Ludwig’s law, but an exception with a mode of 22 was soon found by Lucas (1898) in a North American daisy population, which was later supported by Shull (1902) and Tower (1902), suggesting that the mode can change depending on the location and/or the season. Their findings indicate two possibilities: the representative phenotype is polymorphic among populations, or is unique to the species but does not correspond to the mode. An alternative method to find the representative in such highly varied phenotypes is required to examine these possibilities.

At the beginning of the 20th century, the periodical Biometrika was founded to promote the study of biometrics and in which natural variation in plants and animals was discussed from a statistical point of view. In the journal, researchers described many forms of variation in flower-related numbers, such as petal and sepal numbers in Adoxaceae and Ranunculaceae and flower (floret) numbers in Asteraceae and Apiaceae inflorescences (e.g. Ludwig, 1901; Weldon, 1901). Karl Pearson, one of the founders and a major editor of Biometrika, introduced not only the mean and standard deviation (s.d.) but also the skewness to analyse quantitatively the variation in data submitted to the journal (e.g. Pearson, 1909). The utility of these statistical quantities has been exemplified recently: the relationship between the mean and s.d. quantifies numerical variation in protein molecules within a cell (Paulsson, 2004; Shibata and Fujimoto, 2005; Bar-Even et al., 2006). Both theoretical (Thattai and van Oudenaarden, 2001) and experimental (Ozbudak et al., 2002) studies have shown that the functional relationship between the s.d. and the mean differs depending on the underlying source of variation, either transcription or translation. Therefore, focusing on the relationship between s.d. and mean will allow us to characterize the varied phenotype not only by the mean and modal phenotype.

In this study, we examined two questions. Can the statistical quantities recognize any universality of any clade-specific or organ-specific floral organ number variation? Is there any number, such as any ‘Fibonacci-related number’, that is particularly preferred? To answer these, we combined statistical analyses, mainly the relationship between the mean and s.d., and field observations of variation in Ranunculaceae floral organs and Asteraceae ray floret numbers. Our approach revealed that the relationship between mean and higher order measures of variation, i.e. skewness (asymmetry) and kurtosis (steepness), show how the variation changes among populations of the same or related species.

MATERIALS AND METHODS

Five basic statistical quantities

To describe the floral organ number variation comprehensively, we calculated five basic statistical quantities: mode, mean, s.d., skewness and kurtosis (Joanes and Gill, 1998); for each variation curve data were measured in a wild population with sample size n.

The mode, M, is the state (in this case, the specific organ number) that was found at the highest frequency in the population.

The mean, μ, is the primary moment around zero given by

$$\mu ={\sum }_{i=1}^n{x}_i/n,$$

where x_i denotes the organ number of the ith flower.

The s.d. describes the degree of variation as the secondary moment around the mean. The unbiased estimation of the s.d., σ_u, applied to data sets sampled from a fraction of a population, is

$${\sigma }_{\text{u}}^2={\sum }_{i=1}^n{(x_i-\mu )}^{\text{2}}/(n-\text{1}).$$

The skewness, γ_u, is the tertiary moment about the mean divided by σ_u³ and gives the degree of asymmetry of the curve. The skewness is zero in symmetric variation such as that described by the standard Gaussian distribution. Positive skewness indicates a heavier tail on the side larger than the mean, which we call the right side, compared with the tail on the side smaller than the mean, which we call the left side. Negative skewness indicates a heavier tail on the left side compared with the tail on the right side. The unbiased form is

$${\gamma }_{\text{u}}=n{\sum }_{i=1}^n{(x_i-\mu )}^{\text{3}}/\{(n-\text{1})(n-\text{2}){\sigma }_{\text{u}}^3\}.$$

Kurtosis, κ_u, is the quaternary moment around the mean divided by σ_u⁴ and represents the steepness (peakedness) of the curve. Greater kurtosis appears when the variation curve has both an extraordinarily high frequency on its mode and a wide tail around the mode. The unbiased form is

$${\kappa }_{\text{u}}=n(n+\text{1}){\sum }_{i=1}^n{(x_i-\mu )}^{\text{4}}/\{(n-\text{1})(n-\text{2})(n-\text{3}){\sigma }_{\text{u}}^4\}-\text{3}{(n-\text{1})}^{\text{2}}/\{(n-\text{2})(n-\text{3})\}.$$

The second term is introduced to set the kurtosis of the standard Gaussian distribution to zero.

Plant samples

We calculated the five statistical quantities for two plant families belonging to the basal eudicots (Ranunculaceae) and the core eudicots (Asteraceae), respectively. The variation measured was taken from published data or our own study as indicated in Figs 1–5 and Supplementary Figs S1–S5 and discussed below. Our data sets were collected in natural and cultivated environments in Japan. In addition to the data sets published previously (Kitazawa and Fujimoto, 2014), we collected new data for the floral organs of the Ranunculaceae and Asteraceae flowers. The sampling of each floral population was limited both temporally (1–8 d) and spatially (diameter up to 100 m), because seasonal (Weldon, 1901) as well as geographical effects (Ludwig, 1901) on floral organ numbers can be significant.

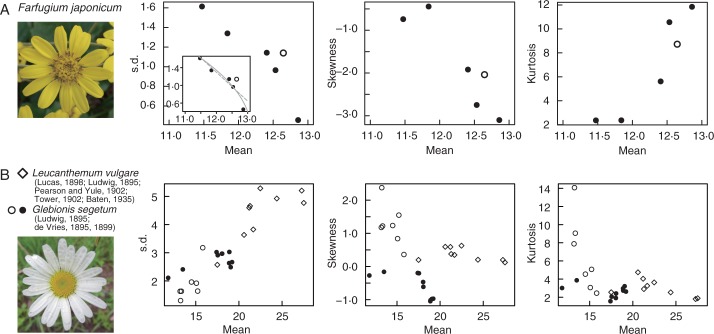
Fig. 2.

Intraspesific variation of ray floret numbers in Asteraceae. (A) Statistical quantities of Farfugium japonicum (tribe Senecioneae). Each closed circle corresponds to an individual plant in Osaka University campus (all heads found in 1 d were counted for each individual; 18 ≤ n ≤ 30), whereas the open circle denotes a population at a different location (n = 108). Small window shows the result of NLS fitting of linear (grey dashed line) and square-root (grey solid line) models. (B) Tribe Anthemideae including Glebionis segetum (open and closed circles; Ludwig, 1895; de Vries, 1895, 1899; 97 ≤ n ≤ 1000) and Leucanthemum vulgare (diamonds; Lucas, 1898; Ludwig, 1895; Pearson and Yule, 1902; Tower, 1902; Baten, 1935; 168 ≤ n ≤ 10006) were analysed. Closed circles indicate measurements with negative skewness.

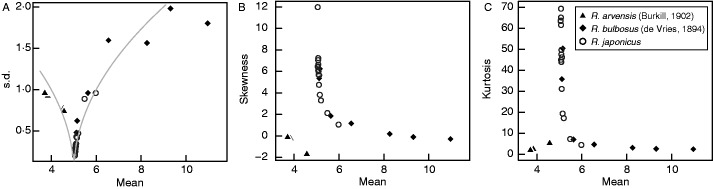
Fig. 3.

Petal-number variation is unimodal in the genus Ranunculus. Comparison between our data sets for R. japonicus (Fig. 1) and two species published previously by other authors: R. arvensis (Burkill, 1902; 1203 ≤ n ≤ 2298) and R. bulbosus (de Vries, 1894; 29 ≤ n ≤ 1130). (A) Standard deviation fitted with the function σ_u = √|μ − 5| (grey solid line). (B) Skewness. (C) Kurtosis. One of the R. japonicus measurements with (μ, κ_u) = (5·02, 242) is not plotted to avoid scale-down.

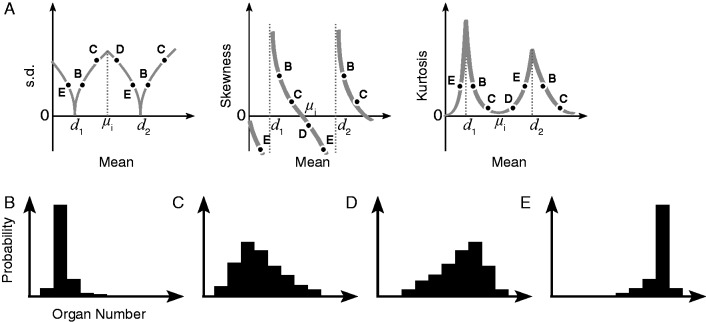
Fig. 4.

Schematic diagram of the changes of statistical quantities between stable modes. (A) In Ranunculus perianth-type variations, the s.d. is close to zero, and the skewness and kurtosis are nearly diverged around the stable modes d₁ and d₂. Some species have more than one stable mode, and the correlation between the mean and s.d. changes its sign at µ_i, the x-intersect of skewness. Kurtosis has peaks at the stable modes, reflecting the high stability of these numbers. The letters correspond to the variation curves in B–E. (B–E) The representative shape of variation curves. (B) The curve is steep and right-tailed when the mean of a given population is slightly larger than the stable mode (either d₁ or d₂). As the mean increases from the stable mode, the curve becomes flattened (lower kurtosis; C) and left-tailed (negative skewness; D). (E) When the mean is slightly smaller than the stable mode, the curve is steep and left-tailed.

Fig. 5.

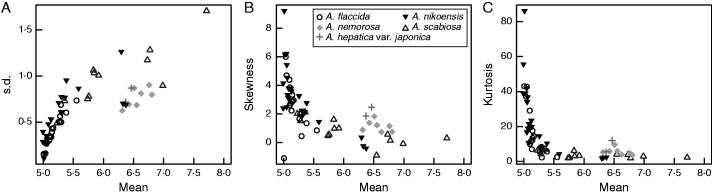
Tepal-number variation is bimodal in the genus Anemone (Ranunculaceae). Comparison between the data sets for A. flaccida, A. scabiosa, A. nikoensis and A. hepatica, which were collected by ourselves except for one from Ohno (1991; see Fig. S1A), and the data sets for A. nemorosa by Yule (1902; n = 1000).

Because the Ranunculaceae has diverse floral morphologies (e.g. the perianth parts are differentiated into sepals and petals in some species but undifferentiated in others), we divided the data sets into several groups according to their phylogenetic relationships. Ranunculaceae species have been classified previously based on karyomorphology, embryogeny, morphology (Tamura, 1962) and several molecular phylogenies based on, for example, chloroplast DNA (Johansson and Jansen, 1993) and nuclear 26S ribosomal DNA (Ro et al., 1997). The Ranunculaceae is divided into five subfamilies: Glaucidioideae, Hydrastidoideae, Coptidoideae, Thalictroideae and Ranunculoideae (Wang et al., 2009). All of the species that we examined are members of subfamily Ranunculoideae and are subdivided among three tribes: Ranunculeae (Ranunculus and Ficaria; Hörandl et al., 2005), Anemoneae (Anemone) and Helleboreae (Eranthis).

We measured natural variation in two species of the Ranunculeae, namely R. japonicus and Ficaria verna (syn. R. ficaria), and we examined published data collected by other authors for R. arvensis (Burkill, 1902), R. bulbosus (de Vries, 1894), R. hederaceus (Salisbury, 1934), R. omiophyllus (Salisbury, 1934), R. parviflorus (Salisbury, 1931), R. repens (Pledge, 1898; Salisbury, 1973) and F. verna (Babington, 1834; Ludwig, 1901; Weldon, 1901; Macdonell, 1903; Salisbury, 1919). The perianths of Ranunculeae species consist of two whorls with distinct morphologies. The outer sepals are green, whereas the inner petals are lustrous yellow or white in the species mentioned here. The floral organ number of the two whorls is usually five in Ranunculus (K5C5 in floral formulae indicating five sepals, K5, and five petals, C5), whereas the modal number of petals and sepals of F. verna was reported as K3C8 in German populations and K5C8 in a Swiss population (Ludwig, 1901).

Anemoneae is an attractive target for the study of floral organ numbers, because it includes species with dimerous, trimerous and pentamerous flowers (Ren et al., 2010). The perianth of Anemoneae flowers is undifferentiated and has no distinction between the petals and sepals. The number of perianth lobes, or tepals, is five (P5) and/or six (P6), which can differ within a species as in A. ranunculoides, whose terminal flower is trimerous (P6) and the lateral flowers are pentamerous (P5; Schöffel, 1932). We measured variation in the tepal numbers of four East Asian species of Anemone, namely A. flaccida, A. scabiosa [the accepted name in The Plant List (http://www.theplantlist.org/); syn. A. hupehensis var. japonica], A. nikoensis and A. hepatica var. japonica (syn. Hepatica nobilis var. japonica). Anemone hepatica was previously regarded as a separate genus Hepatica, based largely on morphology (Tamura, 1991; Ziman et al., 2008), but recent molecular phylogenetic analysis places it in Anemone (Hoot et al., 2012). In addition, we analysed several other published data sets for A. flaccida (Ohno, 1991) and A. nemorosa (Yule, 1902). These species are classified into two subgenera of the genus Anemone: A. hepatica and A. flaccida are classified in subgenus Anemonidium, whereas A. nemorosa, A. hupehensis and A. nikoensis are in subgenus Anemone (Hoot et al., 2012), while a molecular analysis for A. nikoensis is lacking (Ziman et al., 2008).

Eranthis pinnatifida (tribe Helleboreae) shows number variation in sepals and nectariferous petals, which are narrow tubular organs with forked tips. As E. pinnatifida has a white (rarely bluish), pentamerous calyx (K5C8), Nakai (1937) distinguished several species distributed in Central Asia and eastward, including E. pinnatifida, from European and West Asian Eranthis species, which have a yellow, trimerous calyx (K6C6). He treated the former as an independent genus, Shibateranthis, based mainly on colour and sepal texture. Although that classification was supported by a molecular phylogeny showing that Shibateranthis Nakai forms a monophyly that is a sister to E. hyemalis (Lee et al., 2012), we employed the name E. pinnatifida according to The Plant List.

We also observed variation in floret numbers in Asteraceae capitulum inflorescences. Although all Asteraceae flowers are borne in a capitulum, the composition of the florets differs between the Asteraceae subfamilies. All capitula in the subfamily Asteroideae have both ligulate and tubular florets, whereas all the florets in subfamily Cichorioideae are ligulate. We examined the variation in ray floret numbers in two tribes within subfamily Asteroideae: Senecioneae (Farfugium japonicum) and Anthemideae [Glebionis segetum (syn. Chrysanthemum segetum; Ludwig, 1895; de Vries, 1895, 1899) and Leucanthemum vulgare (syn. Chrysanthemum leucanthemum; Ludwig, 1895; Lucas, 1898; Pearson and Yule, 1902; Tower, 1902; Baten, 1935)].

Correlation coefficient and least squares fitting

The Pearson product-moment correlation coefficient (PCC) between a set of two variables x and y is (Sokal and Rohlf, 2012):

$$\text{PCC}={\sum }_{i=1}^m(x_i-\overline{x})(y_i-\overline{y})/{({\sum }_{i=1}^m{(x_i-\overline{x})}^{\text{2}}{\sum }_{i=1}^m{(y_i-\overline{y})}^{\text{2}})}^{\text{1}/\text{2}},$$

where x_i and y_i denote mean and s.d., respectively, of each population in the present paper, and $\overline{x}$ and $\overline{y}$ denote mean of mean and mean of s.d., respectively, of m populations. The least squares fitting of s.d. as a function of the mean was done by non-linear least squares (NLS) fitting using the R statistical software interface, and we compared a linear model with a non-linear model introduced later by the residual sum of squares (RSS). When the number of fitting parameters is identical among the models, the evidence ratio, representing how many times the non-linear model is supported better by the data than the linear model, is given by (the first equation of page 26 by substituting RSS in the last two equations of page 25 in Burnham et al., 2011)

$$\text{Evidence\hspace{0.17em}ratio}={({\text{RSS}}_{\text{L}}/{\text{RSS}}_{\text{NL}})}^m{}^{/\text{2}},$$

where RSS_L, RSS_NL and m are RSS of the linear and non-linear model, and number of data sets (populations), respectively.

RESULTS

Perianth organ number variation in two Ranunculaceae species

The 17 measurements of petal number variations of Ranunculus japonicus showed a right-tailed distribution (Fig. 1A, B), consistently to ‘halbe Galton’ curve (de Vries, 1894) whose tail on one side is heavier than on the other side (e.g. Fig. 1A middle). Modes were found at five, except for one measurement in Okayama. Among the measurements, although the means and modes were variable between five and six, indicating these values were not species-specific, the s.d. (σ_u) seemed to increase with increasing mean (Fig. 1B error bars). Hence, we examined the dependency of the s.d. on the mean (Fig. 1C). The s.d. correlated highly with the mean (PCC = 0·93, P = 6·5 × 10⁻⁸) and aligned on a single line increasing monotonically, indicating it can be expressed as either a linear (σ_u = aμ − b) or non-linear (concave downward) function. As the relationship between the mean and variance (σ_u²) seemed linear (Fig. 1D), we fitted the s.d.–mean relationship by σ_u = c√(μ − d) as well as σ_u = aμ − b using the NLS method and compared by RSS. For the linear model, the parameters were selected as σ_u = 0·854μ − 4·00 and RSS was 0·101, whereas the non-linear model became σ_u = 1·08√(μ − 4·97) with RSS = 0·0417 (Evidence ratio 1·84 × 10³ times; see Materials and Methods for definition), indicating that the square-root (non-linear) model was better than the linear model (Fig. 1E). Therefore, the s.d. of petal number variation of R. japonicus was likely to be proportional to the square root of the difference between the mean and specific number, where the proportional coefficient was almost unity (c = 1·08) and s.d. converged to zero at the mean of five (d = 4·97), i.e. the most frequent modal number of petals. As the measurements in different years at the same location (2011 and 2014, in Osaka) as well as those in the same year at different locations (2011, the distance between Shiga and Osaka is about 100 km) followed the same s.d.–mean relationship, it was likely that the properties in both environmentally and genetically induced variation can be taken together in a view of statistical quantities. As the mean increased from five, the degree of right-tailed asymmetry became lower, as indicated by the monotonic decrease of the skewness to zero (Fig. 1F). While the range of petal numbers was four to eight or nine in most populations (Fig. 1B), the probability of the modal number decreased from 97·5 to 39 %, as indicated by the monotonic decrease in kurtosis (Fig. 1G). Taken together, as the mean increased, s.d. increased following σ_u = c√(μ − d), and both skewness and kurtosis monotonically decreased.

To examine whether this square-root relationship between the mean and s.d. and monotonic decrease of skewness and kurtosis are applicable to other species, we analysed tepal number variation in Anemone flaccida (Supplementary Information, Fig. S1). Similarly to R. japonicus, the s.d. correlated positively with the mean (Fig. S1A–C; PCC = 0·97, P = 1·1 × 10⁻⁹). NLS fitting for the s.d.–mean relationship of these 16 data sets supported the square-root relationship (σ_u = 0·959√(μ − 4·97); Evidence ratio 1·52 × 10³ times) whose parameter values were almost equal to those of R. japonicus petals as well (Fig. S1D). All measurements showed a right-tailed distribution, as indicated by the positive skewness, except for one measurement with negative skewness (Fig. S1E). Skewness and kurtosis (Fig. S1F) were highest when the mean was close to five, and monotonically decreased with increasing mean, consistent with data for R. japonicus.

Applicability of the square-root s.d.–mean relationship in floral organ number variation of Ranunculaceae

We investigated whether the square-root relationship found in Ranunculus japonicus petal numbers and Anemone flaccida tepal numbers also occurs in other species and organs in Ranunculaceae. Tepal number variation of two species of Anemone, A. nikoensis and A. scabiosa (syn. A. hupehensis var. japonica), consistently showed strong correlations between mean and s.d. (Supplementary Information, Fig. S2). Although it was hard to say that the square-root model was better for A. nikoensis and A. scabiosa than the linear model by RSS, the parameters for the linear model were less accurate compared with the square-root model in terms of statistical testing (Fig. S2). Commonly in all four species analysed above, the parameters for the square-root model σ_u = c√(μ − d) took similar values (c ∼ 1 and d ∼ 5).

As the genus Eranthis branched earlier than Anemoneae–Ranunculeae branching (Wang et al., 2009), it is worth comparing Eranthis sepals and petals with Anemone tepals and Ranunculus petals to test the applicability of the square-root relationship. The correlation was weak in the sepals (PCC = 0·58, P = 0·082) and did not occur in the petals (PCC = 0·13, P = 0·73), and the relationship σ_u = c√(μ − d) was hardly found in either organ in Eranthis pinnatifida (Supplementary Information, Fig. S3).

The inconsistency between the petals in Eranthis and Ranunculus may be due to the limitation of the square-root relationship to the two genera (Anemone and Ranunculus), or because of the increase in the mean. To examine the latter possibility, we compared the model with petal (7 < μ < 10) and sepal number (3 < μ < 5) variation in Ficaria verna (Ranunculeae) mainly from the literature (Supplementary Information, Fig. S4). The correlation between mean and s.d. was weak in F. verana (Fig. S4A). Both skewness and kurtosis peaked around the mean of eight, and monotonically decreased as the mean increased (Fig. S4B, C). By contrast, with sepal number variation, the s.d. correlated more strongly with the mean (PCC = 0·63, P = 0·011), and the s.d. reached zero when the mean was close to three, indicating the robustness of this number (Fig. S4D). NLS fitting showed that the square-root relationship was rather better than the linear relationship (Fig. S4D, small window). In addition to the monotonic decreases of skewness and kurtosis that are consistent with R. japonicus petal numbers, we also found changes in the symmetry of the variation curve (Fig. S4E–G). The variation curve was right-tailed as the mean increased up to four, while two data sets with means larger than four showed left-tailed curves, as indicated by the negative values of skewness (Fig. S4E, G). Thus, the square-root s.d.–mean relationship is unclear in F. verana petals but likely in sepals, while the monotonic decreases of skewness and kurtosis in both sepals and petals are consistent with the variation of Ranunculus japonicus petal numbers (Fig. 1F, G) and Anemone flaccida tepal numbers (Supplementary Information, Fig. S1E, F).

Ranunculeae flowers have multiple stamens and carpels in apocarpous gynoecia, and both the mean and s.d. were remarkably larger than those of the sepals and petals. The s.d. values of the stamen and carpel numbers seemed to increase with increasing means, but the correlation was not statistically significant (Supplementary Information, Fig. S5). Although a lack of data prevents further analysis, the downward-convex curve in the variance–mean relationship in carpel numbers (Fig. S5D) suggests a linear relationship between the s.d. and mean.

We found three types of variation curve distinguished by statistical quantities in the four genera of Ranunculaceae. The square-root mean–s.d. relationship σ_u = c√(μ − d) was found in Ranunculus petals, Ficaria sepals and Anemone tepals (Fig. 1E, and Supplementary Information, Figs S1D and S4D). In this Ranunculus-perianth type of variation, the s.d. reached zero when the mean was near certain numbers d = 3 or 5 specific to the genus or species, and the absolute values of the skewness and the kurtosis monotonically decreased to zero as the mean increased from the certain numbers (Fig. 1F, G, and Supplementary Information, Figs. S1E, F and S4E, F). In the Eranthis-petal type of variation, the s.d. exhibited no clear dependence on the mean (Fig. S3B). In the large-mean (μ > 10) type of variation found in carpels and stamens, the s.d. was likely to be a linear function of the mean (Fig. S5). In the Ficaria petals, a functional relationship could not be identified in the present measurements, while the correlation between s.d. and mean was higher than Eranthis petals and a preference to a particular organ number was found by the kurtosis and skewness (μ = 8; Supplementary Information, Fig. S4A–C).

Flower-number variation in the capitula of Asteraceae (Asterales)

To see if the square-root relationship between the mean and s.d. is restricted to the perianth organs of Ranunculaceae, we also examined ray floret number variation among individuals of Farfugium japonicum (Asteraceae). Unlike most of the Ranunculaceae perianth data analysed above, the s.d. was negatively correlated with the mean (PCC = −0·88, P = 0·019; Fig. 2A, left graph). By contrast, the s.d.–mean curve was similar to the square-root function in Ranunculeae by reflection through a vertical line, as suggested by slightly low RSS in the square-root model with an opposite sign inside the square root function [σ_u = 1·28√(13·1 − μ), RSS = 0·122, whereas σ_u = 0·652μ + 9·12, RSS = 0·165; Evidence ratio 2·13 times]. In addition, the skewness took negative values, as seen in Ficaria sepals (μ > 4 in Supplementary Information, Fig. S4D–F), and kurtosis increased as the mean increased (Fig. 2A, centre and right graphs). Therefore, the s.d.–mean relationship with opposite sign associated with the negative skewness and reflection of the kurtosis in Farganium japonicum.

To examine the extent of the negative correlation between s.d. and mean in Asteraceae ray florets, we analysed two species in another tribe, Anthemideae [Glebionis segetum (de Vries, 1895, 1899; Ludwig, 1895) and Leucanthemum vulgare (Ludwig, 1895; Lucas, 1898; Pearson and Yule, 1902; Tower, 1902; Baten, 1935)], which has been a central subject of the statistics of number variation (Supplementary Information, Fig. S6). While s.d. was positively correlated with the mean on the whole (PCC = 0·73, P = 9·6 × 10⁻⁴ in G. segetum; PCC = 0·75, P = 0·019 in L. vulgare; Fig. 2B), s.d. was negatively correlated with the mean at μ > 17 in G. segetum (PCC = −0·67, P = 0·061), where the skewness was negative and the kurtosis increased as the mean increased (closed circles in Fig. 2B). Therefore, we found two relationships between the mean and other quantities in G. segetum: the first was increasing s.d., decreasing positive skewness and decreasing kurtosis (Fig. 2B, open circles), and the second was decreasing s.d., decreasing negative skewness and increasing kurtosis (Fig. 2B, closed circles). The first relationship agreed with Ranunculus petals and Anemone tepals, whereas the second was found in Farganium japonicum. The fact that the statistical quantities changed continuously from the first to the second in G. segeum suggests that the s.d. decreases as the mean gets closer to specific number(s), both in Ranunculaceae perianth organs and in Asteraceae ray florets.

DISCUSSION

Although the stochasticity in floral organ number was observed in various species, we found the variation follows a rule that is unique to species and organs in most cases. Especially in species of the Ranunculaceae, variation in perianth organ numbers followed a common functional relationship between the mean and s.d. Here we discuss the significance of the rule in species evolution.

The meaning of the parameter d in square-root s.d.–mean relationship: ‘stable mode’

The relationship between the s.d. and the mean followed σ_u = c√(μ − d) in the Ranunculus-perianth type of variation, such as that in R. japonicus petals, Anemone flaccida tepals and Ficaria verna sepals. In these species, c ≈ 1 (c = 1·08 in R. japonicus, 0·959 in A. flaccida, 1·19 in A. nikoensis, 0·889 in A. scabiosa and 0·746 in F. verna), and d agreed with a specific integer where the kurtosis had its peak (d ≈ 5 in the Anemone tepals and R. japonicus petals, and d ≈ 3 in F. verna sepals). In ray-floret numbers in Farfugium japonicum (Asteraceae), a similar s.d.–mean relationship σ_u = c√(d − μ) was found with similar parameters, namely, c ≈ 1 and d ≈ 13, and the kurtosis consistently took the highest value around the mean of 13 (Fig. 2A).

As d represents the x-intercept where s.d. is zero, the robustness of organ number is highest at d. Therefore, we named this specific number found at the peak of kurtosis as ‘stable’ mode and thus the Ranunculus-perianth type of variation follows σ_u = √(μ − stable mode) or σ_u = √(stable mode − μ). Here, we propose a relationship taking the absolute difference between the mean and the stable mode, σ_u = √|μ − stable mode|, for Ranunculus and Anemone perianth organs and Asteraceae ray florets.

We have support from the Asteraceae and Ranunculus, respectively, for the relationship σ_u = √|μ − stable mode|. First, although the s.d.–mean relationship of Glebionis segetum did not clearly follow σ_u = √|μ − d|, kurtosis of the species had small peaks at means of 13 and 20 (Fig. 2B), which supported existence of the stable modes at d₁ ≈ 13 and d₂ ≈ 20. As the s.d. increased until the mean reached a number around 17 and decreased thereafter, the expression inside the square root function should be able to be set independent of the sign of μ − d₁ or μ − d₂. Secondly, the relationship σ_u = √|d − μ| was supported in the genus Ranunculus when plotting statistical quantities for petal number variation in R. arvensis (Burkill, 1902) and R. bulbosus (de Vries, 1894), in addition to R. japonicus with a function σ_u = √|μ − 5| (Fig. 3). As expected, the s.d. correlated with the mean either negatively (μ < 5; R. arvensis) or positively (μ > 5; R. bulbosus and R. japonicus).

The skewness and kurtosis are also explained in a common model (Fig. 4). When the mean is larger than a stable mode, the variation curve is left-tailed (Fig. 4B and C), whereas when the mean is smaller than the stable mode, the variation curve is right-tailed (Fig. 4D and E). The variation curve is steep when the mean is close to the stable mode (Fig. 4B and E), and broadened when the mean is distant from the stable mode (Fig. 4C and D). Multiple stable modes can exist, and at a point μ_i around the median of the two stable modes, the s.d. and kurtosis reach a local maximum and a local minimum, respectively, and the skewness changes its sign (Fig. 4A). This model is consistent with all four quantities in Ranunculus (Figs 1 and 3) and Anemone (Supplementary Information, Fig. S1) perianth organs, and Asteraceae ray florets (Fig. 2), and also explains two populations of Ficaria verna sepals (μ > 4 in Supplementary Information, Fig. S4D–G) with lower s.d. than three other populations (μ ≈ 3·5) and negative skewness, suggesting another stable mode around five.

The meaning of the ‘outliers’ in Anemone

In our calculation of the statistical quantities for tepal numbers of three Anemone species (Supplementary Information, Figs S1 and S2), the s.d. approached zero when the mean was five, similar to that in Ranunculus (Fig. 1). By contrast, two measurements of A. nikoensis around the mean of 6·4 and one of A. scabiosa around the mean of 7 had relatively low s.d. compared with other measurements (Fig. S2). Interestingly, these values were close to those found in trimerous (six-lobed) Anemone species A. nemorosa (Yule, 1902) and A. hepatica (syn. Hepatica nobilis; Fig. 5). As the kurtosis of these two species was larger than that found in Ranunculus [e.g. the average kurtosis of the seven populations of A. nemorosa (6·3 < μ < 6·9; Fig. 5C) is 1·5 times larger than an R. bulbosus population (μ = 6·55; Fig. 3C)], they probably have another stable mode at a number between 5 and 6·5. This value would be six if the stable mode is an integer as in Ranunculus petals and Ficaria sepals, suggesting that those two groups probably indicate the separation between pentamerous and trimerous Anemone flowers, respectively. Therefore, the intraspecific polymorphism between trimerous and pentamerous might have appeared as different statistical quantities in A. nikoensis and A. scabiosa.

Evolutionary robustness and diversification of stable modal numbers

How have the stable modes changed among angiosperm species? In the Ranunculaceae perianth organs, while three, five and eight (and perhaps six in Anemone) were found to be stable modes, their robustness varied depending on the clade.

In tribe Ranunculeae, the Ficaria verna sepals exhibited an intraspecific change between two stable modes (Supplementary Information, Fig. S4D–F). In genus Ranunculus, by contrast, the stable mode of petal numbers was five for all species covering different subclades (R. arvensis in section Echinella, R. bulbosus in sect. Polyanthemos and R. japonicus in sect. Ranunculus in subgenus Ranunculus, a temperate to subtropical clade; Hörandl and Emadzade, 2012). Even in the R. bulbosus generations that de Vries (1894) selected for larger numbers of petals, the stable mode stayed at five (Fig. 3), as shown by the monotonic increase of the s.d. and the convergence of the skewness and kurtosis to zero as the mean increased from five to ten, without showing any stability on the mean of eight, which was the stable mode for F. verna petals (Supplementary Information, Fig. S4A–C). Hence, R. bulbosus does not hold a stable mode at eight, and the stable modes may have been separated between those two genera Ranunculus and Ficaria in Ranunculeae. Examination of the genera Ficaria and Coptidium, which is the closest clade to Ficaria (Hörandl and Emadzade, 2012) and whose petal number is often greater than five, could clarify the phylogenetic robustness of the stable modes of five and eight in Ranunculeae.

In the genus Anemone (Anemoneae), these measurements showed the possibility of mixed merosity (P5/P6) in A. nikoensis and A. scabiosa, which is of particular interest because it resembles the transition between the eudicots and the monocots, while A. flaccida (P5), A. nemorosa (P6) and A. hepatica (P6) exhibited no such intermingling (Fig. 5A). The polymorphism of P5 and P6 may have been gained or lost during evolution of the genus Anemone at various clade-levels: the subgenus Anemonidium includes A. flaccida (P5) and A. hepatica (P6) while the subgenus Anemone contains A. nemorosa (P6), A. nikoensis (P5/P6) and A. scabiosa (P5/P6). Anemone nemorosa and A. nikoensis are located even in subsection Anemonanthea in section Anemone (Ziman et al., 2008; Hoot et al., 2012), whereas A. scabiosa is located in subsection Vitifoliae in section Rivularidium (Zhang et al., 2015), indicating that interspecific and intraspecific polymorphisms (P5/P6) occur repeatedly at the section-level in the subgenera. In addition, while the s.d. continuously changed during the transitions among the stable modes in the Ficaria sepals (Supplementary Information, Fig. S4D), the transition between the stable modes at five and six in Anemone tepals occurred rather discontinuously (Fig. 5A). These continuous and discontinuous changes might indicate different mechanisms of evolutionary diversification of organ numbers. Further studies of these polymorphisms (P5/P6) in A. nikoensis and A. scabiosa as well as related species within these subsections, sections and subgenera will clarify their phylogenetic diversification.

Possible developmental basis for the square-root relationship

Two models have been suggested as the developmental basis for floral organ number variation. Bachmann and Chambers (1978) proposed that the variation is caused by the occasional fusion or split of floral organ primordia, whose variation curve follows a Poisson distribution. We previously suggested a model that assumed stochastic shifts of the expression boundaries of homeotic (organ fate determination) genes and a semi-concentric (whorled-type) organ arrangement (Kitazawa and Fujimoto, 2014). Although the square root relationship between s.d. and mean is satisfied with the Poisson distribution from a statistical point of view, the Poisson was not the best-fitting model for most Ranunculaceae perianth organs data sets (Ranunculus japonicus petals and Anemone flaccida tepals). Interestingly, the latter model fitted best most data sets of the Asteraceae ray florets. Moreover, this model accounted not only for the decrease of s.d. around the stable mode but also the sign change of skewness and maximum kurtosis at the stable mode. As three parameters in the latter model correspond to the stochastic shift of expression boundary and the organ arrangement, finding parameter(s) that satisfy the square-root relationship would clarify the underlying source of variation in the developmental process. By examining such statistical models, the three types of s.d.–mean relationships, i.e. Ranunculus-perianth, Eranthis-petal and large-mean types, could be indicators of different sources of stochasticity during floral development, as seen in the stochastic gene expression where variation originates from transcription and translation, respectively (Thattai and van Oudenaarden, 2001; Ozbudak et al., 2002; Kærn et al., 2005).

Coexistence of the Ranunculus-perianth and large-mean types of variation

The Ranunculus-perianth and large-mean types may be interrelated evolutionarily, as the intermediate properties relative to these two types of variation appeared around means of 10–20, such as the Ficaria verna petals and ray florets in tribe Anthemideae (Asteraceae). In these organ/flowers, although the monotonic decrease of skewness and the maximum of kurtosis at the stable mode are common properties of Ranunculus petals, the s.d.–mean relationship was much more scattered. Thus, the Ranunculus-perianth type of variation becomes obscured as the mean increases. Flowers of some species of Ficaria and Anemone (Ranunculaceae) have more than ten perianth organs: F. fascicularis (syn. Ranunculus kochii), A. keiskeana in the subgenus Anemonidium that includes A. flaccida, and A. apennina and A. blanda in another subgenus Anemone (Hoot et al., 2012). Study of the variation of these Ranunculaceae species and Asteraceae species with floret modal numbers below ten (e.g. genera Cosmos and Ixeris) might elucidate the full evolutionary spectrum of the variation types.

Stable modes resolve a long-standing controversy regarding flower number and floral organ number variation

Ludwig (1895) strongly advocated specific numbers in Asteraceae florets. Shull (1902), who was sceptical of Ludwig’s law, referred to Lucas’s result showing 22 as the mode (Lucas, 1898) and stated that their finding implies modal number changes depending on location and not on Fibonacci-related numbers (Shull, 1902). Although Ludwig (1895) tried to extend the Fibonacci-related numbers to include proximal numbers (e.g. 9, the number between 8 and 5 × 2 = 10), Shull (1902) criticised the extended Fibonacci-related numbers because they include a large proportion of natural numbers. We defined statistically specific numbers, whether or not they were Fibonacci numbers, as stable modes by focusing on multiple populations at the species or genus level and not on a single population as done by Ludwig and Shull. Even when the modal numbers differ among populations, as in the tepals of Anemone and the ray florets of Leucanthemum (Ludwig, 1895; Lucas, 1898), the stable mode can be a powerful tool to find species-specific modes. In the Ranunculeae perianth-organ variation, the s.d. converged to zero, and the skewness and kurtosis diverged when the mean of the population was near three (Ficaria sepals; Supplementary Information, Fig. S4A–C), five (Ranunculus petals; Fig. 1) or eight (Ficaria petals; Fig. S4D–F), indicating a strong preference for those Fibonacci numbers (Fig. S1). In the Asteraceae ray floret-number variation, although the s.d. does not fall to zero, the local maxima of the skewness and kurtosis indicate stable modes around the Fibonacci numbers 13 and 21 (Fig. 2). Thus, the stable modes support Ludwig’s law while absorbing Shull’s criticisms.

In conclusion, using statistical quantities, we found three types of s.d.–mean relationships in floral organ numbers, depending on the floral organ type and phylogenetic clade. The Ranunculus-perianth type was found in the Ranunculus, Ficaria and Anemone perianth segments (tepals, sepals and petals; Ranunculaceae), and ray florets of Farfugium (Asteraceae). In this type of variation, the s.d. followed σ_u = √|μ − d|, where d corresponds to the stable mode specific to the genus or species (e.g. five in Ranunculus; Fig. 1B). The absolute values of the skewness and the kurtosis increased sharply when the mean was immediately below the stable modes, indicating the existence of local maxima at those numbers, and they decreased as the mean increased (e.g. Fig. 1F and G). In the Eranthis-petal type of variation, the s.d. exhibited no clear dependence on the mean (Supplementary Information, Fig. S3B). The s.d.–mean relationship in number variations with large means was likely to be linear (e.g. Ranunculeae stamens and carpels; Fig. S5), where the Ficaria petals and Asteraceae ray florets exhibited intermediate properties of these types. The skewness-mean and kurtosis-mean relationships further show how the variation changes between populations of the same or related species and gives a novel way of finding a stable mode as the representative phenotype for a species or genus. What developmental processes determine the stable-mode phenotype (Kitazawa and Fujimoto, 2015) and how the variation is developmentally or environmentally generated (Kitazawa and Fujimoto 2014) are future problems to understand the evolutionary development of flowers.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. Fig. S1: statistical quantities of petal numbers of Anemone flaccida. Fig. S2: the s.d.–mean relationship in tepal numbers of Anemone nikoensis (A) and A. scabiosa (B). Fig. S3: s.d.–mean relationship of the Eranthis pinnatifida sepal (A) and petal (B) numbers. Fig. S4: statistical quantities for Ficaria verna petal and sepal numbers. Fig. S5: s.d. and variance of Ranunculeae stamen and carpel numbers. Fig. S6: the flower number variation in the two Anthemideae species.