Multitasking vs. multiplexing: Toward a normative account of limitations in the simultaneous execution of control-demanding behaviors

Abstract

Why is it that behaviors that rely on control, so striking in their diversity and flexibility, are also subject to such striking limitations? Typically, people cannot engage in more than a few — and usually only a single — control-demanding task at a time. This limitation was a defining element in the earliest conceptualizations of controlled processing, it remains one of the most widely accepted axioms of cognitive psychology, and is even the basis for some laws (e.g., against the use of mobile devices while driving). Remarkably, however, the source of this limitation is still not understood. Here, we examine one potential source of this limitation, in terms of a tradeoff between the flexibility and efficiency of representation (“multiplexing”) and the simultaneous engagement of different processing pathways (“multitasking”). We show that even a modest amount of multiplexing rapidly introduces cross-talk among processing pathways, thereby constraining the number that can be productively engaged at once. We propose that, given the large number of advantages of efficient coding, the human brain has favored this over the capacity for multitasking of control-demanding processes.

Introduction

The human ability for controlled processing is striking in its power and flexibility, and yet equally so in its limitations. People are famously poor at multitasking control-demanding behaviors, often able to execute only a few, and sometimes no more than one at a time, and these limitations are central to debates that have broad social significance (e.g., the use cell phones while driving). Nevertheless, there is still little agreement about the source of these limitations.

Limits in our ability to multitask control-demanding behaviors have sometimes been taken to suggest that the capacity for control itself is limited. Indeed, limited capacity was a defining feature in the earliest conceptualizations of controlled processing (e.g., Posner & Snyder, 1975; Shiffrin & Schneider, 1977), which asserted that that controlled processing relies on a single, centralized, and capacity-limited centralized resource. Although early theories failed to specify the nature of this resource, subsequent theories have been more explicit about the mechanisms involved (e.g., Anderson, 1983; Baddeley, 1986; Engle, 2002; Just & Carpenter, 1992), for example linking the constraints on control to the long recognized capacity limits of working memory (e.g., Miller, 1956; Sternberg, 1966; Oberauer & Kliegl, 2006), and/or the constraints on centralized procedural resources needed to execute task-related processes (e.g., Salvucci & Taatgen, 2008). However, these risk stipulating rather than explaining the limitation. Furthermore, the notion of a resource limitation is startling if one considers that control processes are known to rely on the function of the prefrontal cortex, a structure that occupies a major fraction of the human neocortex and comprises about three billion neurons (Williams & Herrup, 1988; Pakkenberg & Gundersen, 1997; Thune, Uvlings, & Pakkenberg, 2001; Herculano-Houzel 2009). Thus, is seems unlikely that a structural limitation alone can explain the constraints on multitasking. Though some have proposed it reflects metabolic limitations (Muraven, Tice, & Baumeister, 1998) this too seems unlikely. Other functions, such as vision, routinely engage widespread regions of neocortex in an intense and sustained manner.

Multitasking vs. multiplexing

An alternative approach to understanding limitations in control-dependent multitasking is to consider that these may arise from functional (computational) rather than, or perhaps in addition to, structural constraints. One important functional constraint may be the problem presented by multiplexing of representations — that is, the use of the same representations for different purposes by multiple processes.¹ This idea has its roots in early “multiple resources” theories of attention (Navon & Gopher, 1979; also see Allport, 1980; Logan, 1985; Wickens, 1984). These argued that the degradation in behavior observed when people try to multitask may be due to cross-talk within local processing resources specific to the particular tasks involved, rather than the constrained resource of a single, centralized general purpose control mechanism (Baddeley 1970; Posner & Snyder, 1975). Cross-talk arises when two (or more) tasks make simultaneous demands on the same processing or representational apparatus. Insofar as each is capable of supporting only a single process or representation at a given time, then these can be thought of as a limited capacity “resources,” though there are assumed to be multiple different resources to support the various types of processes and representations of which the system is capable. Accordingly, cross-talk can arise anywhere in the system where two tasks make competing use of the same local resource(s). This, in turn, will interfere with multitasking.²

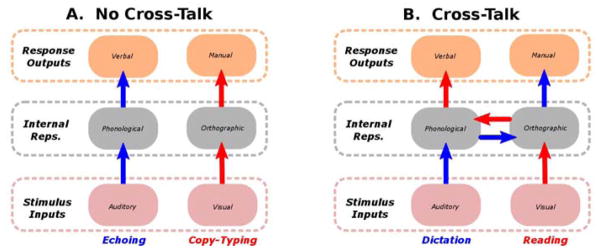
A classic example contrasts two dual-task conditions: echoing an auditory stream while simultaneously typing visually presented text (copy-typing), versus simultaneously reading aloud and taking dictation. The former pair is relatively easy to learn, while the latter is considerably more difficult (Shaffer, 1975). The multiple resources explanation suggests that echoing and copy-typing involve non-overlapping representations and processing pathways (one auditory-phonological-verbal, and the other visual-orthographic-manual). Because they make use of distinct resources there is no risk of cross-talk, and so it is possible to do both at once (see Figure 1a). In contrast, reading out loud and dictation make shared use of both phonological and orthographic representations (see Figure 1b), and thus are subject to the problem of cross-talk: The two tasks demand that different representations of a given type be activated at the same time (e.g., the one to be read and the one to be transcribed). Insofar as this is not possible (e.g., to simultaneously activate phonological representations corresponding to different stimuli), then competition will arise which, if not properly managed, will lead to interference and degradation of performance. Allport et al., (1972) summarized this clearly in one of the earliest articulations of the multiple resources (or “channels”) hypothesis:

Figure 1. Multitasking and cross-talk.

Schematic diagrams of the processing pathways involved in two dual-task situations. Panel A shows the pathways engaged by verbally repeating auditorily presented words (echoing) and transcribing visually presented text (copy-typing). Since the pathways carrying the information relevant to each task from input to output do not overlap, there is no cross-talk, making it possible to carry out both simultaneously (i.e., to multitask). Panel B shows the pathways engaged by typing auditorily presented words (dictation; blue arrows) and reading text aloud (red arrows). In this case, the pathways for the two tasks overlap; that is, they make common use of the same sets of representations (e.g., phonological representations are need for both encoding the words for dictation, and generating the responses for reading). Insofar as each task may involves representing different specific information of the same type, then the pathway overlap will produce cross-talk and interference, making it difficult if not impossible to multitask.

“In general, we suggest, any complex task will depend on the operation of a number of independent, specialized processors, many of which may be common to other tasks. To the extent to which the same processors are involved in any two particular tasks, truly simultaneous performance of these two tasks will be impossible. On the other hand, the same tasks paired respectively with another task requiring none of the same basic processors can in principle be performed in parallel with the latter without mutual interference” (p. 233).

The problem of mutual interference, or cross-talk, arises due to the multiplexing of representations; that is, the use of the same representations for different purposes — for example, the use of phonological representations for both encoding auditorily presented words, and for reading words out loud. Presumably, multiplexing occurs in the brain because it is efficient and affords flexibility. For example, we would not want to have two sets of phonological representations, one for listening and another for speaking, no less additional ones for echoing, singing, etc. Furthermore, it allows that representations that arise for one purpose can be put to use for others. Multiplexing can also support powerful forms computation, such as similarity-based inference (Hinton, McClelland, & Rumelhart, 1986; Forbus, Gentner, & Law, 1995). Theories of “embodied” or “grounded” cognition (e.g., Barsalou, 2008) have made similar arguments, proposing that the same neural apparatus used for sensory-motor processes is also used for more abstract forms of thought. In support of this, neuroimaging studies have documented use of the specific parts of the visual system for both perception and imagery (Kosslyn, Thompson, & Alpert, 1997), and the motor system for action execution, planning and even interpretation (Di Pellegrino, Fadiga, Fogassi, Gallese, & Rizzolatti, 1992; Jeannerod, 1994; Goebel, Khorram-Sefat, Muckli, Hacker, & Singer, 1998; Gallese & Goldman, 1998; Iacoboni, Dubeau., Mazziotta, & Lenzi, 2003).

As noted above, however, multiplexing carries with it the problem of cross-talk. Furthermore, this problem is not limited to competition between instructed processes. It extends more generally to situations in which interference can arise from competing habitual (or “automatic”) processes. In general, it has been argued that a primary purpose of control is the management of such crosstalk (e.g., Berlyne, 1957; Botvinick et al., 2001; Meyer & Kieras, 1997), by restricting the number of competing processes that are executed at once. Note that, however, that on this account limitations arise from cross-talk within local, task-specific “resources” (e.g., phonological or visual representations), rather than from the capacity constraint on a single centralized control resource (such as working memory). Indeed, from this perspective, control helps solve the problem of cross-talk. However, its consistent engagement under circumstances that involve cross-talk (and therefore its close association with them) could engender the misinterpretation that control itself is fundamentally subject to (rather than a solution for) capacity constraints on performance.

There is still ongoing debate about whether limits in the ability to multitask are due to the capacity constraints of a centralized control mechanism (perhaps even for the very same reasons they arise in more specialized mechanisms) or they can be accounted for entirely in terms of the cross-talk among task-specific mechanisms, and this debate has fueled considerable computational modeling work (e.g., Meyer & Kieras, 1997, 2000; Salvucci & Taatgen, 2008). However, both types of account would seem to concur on two fundamental points regarding the importance of cross-talk: 1) it represents a critical factor in limiting multitasking (wherever it may occur); and 2) the need to limit it drives the need for control in the first place. Thus, achieving a deeper understanding of the relationship between cross-talk, control and multitasking is an important goal, especially if general properties can be identified. The work we present here is an attempt to address this goal.

We conducted a quantitative examination of the influence that multiplexing (and associated cross-talk) has on control and multitasking. In striving for generality, we did this under a simple and generic set of conditions: each task involved a direct set of mappings from input to output; cross-talk occurred when tasks involved the same inputs or outputs; control acted only to select tasks for execution; and there were no intrinsic capacity constraints on control. The last of these conditions was meant to isolate the influence that multiplexing had on multitasking, independent of any additional influence that constraints on the capacity for control might have. We used two different formalisms to implement these conditions, and in each instance optimized processing parameters (including control) to maximize aggregate performance over all tasks. We then examined the extent to which the introduction of multiplexing impacted the number of tasks that could be executed at once. Not surprisingly, we found that the optimal number of tasks to carry out decreased as multiplexing increased. Critically, however, this decrease was precipitous and extreme, and was virtually unaffected by the size of the system. This suggests the intriguing idea that the presence of multiplexing — and the potential for cross-talk that it introduces — not only poses a demand for control, but at the same time imposes limits on the amount of control that should be allocated. This, in turn, suggests that the extensive use of multiplexed representations in the brain may provide at least one normative source of constraints on multitasking of control-dependent processes.

In the sections that follow we provide a brief review of previous modeling work addressing the relationship between cross-talk and control, that formed the basis for the current work. We then describe extensions of this work, using two models to quantify the relationship between multiplexing, cross-talk and limits in the multitasking of control-dependent processes. Finally, we conclude with a discussion of how our findings relate to other accounts of constraints on the capacity for control-dependent processing, as well as promising directions for future work on this topic.

A simple model of controlled processing and cross-talk

We start with a model of the Stroop task (Stroop, 1935; MacLeod, 1991). While this task is not typically thought of in the context of multitasking, it provides perhaps the simplest example of the problem that multiplexing and cross-talk present to multitasking, and one of the most intensively studied examples of controlled processing. In this task, participants are presented with a written word displayed in color (e.g., GREEN), and asked to name the color in which it is displayed (i.e., say “red”). This invariably takes longer (and is more prone to error) than if they are simply asked to read the word, or to name the color of a word written in the same color (e.g., RED). The traditional interpretation of these findings — which are among the most robust in all of behavioral science — is that color naming is a control-demanding process (slower, effortful, and subject to interference), whereas word reading is automatic (faster, effortless, and performed even in the absence of control; Posner & Snyder, 1975). A more recent, and nuanced interpretation is that the demands for control are context dependent and, in particular, dependent on the nature of any competing tasks (e.g., Kahneman & Treisman, 1984; Cohen, Dunbar, & McClelland, 1990; Engle, 2002). By all accounts, however, when a task involves behavior that must compete with other more reflexive, habitual or otherwise prepotent responses, then performance on the task will demand the allocation of control, in order to avert the cross-talk induced by the more automatic process. Color naming in the Stroop task provides a clear of example of this.

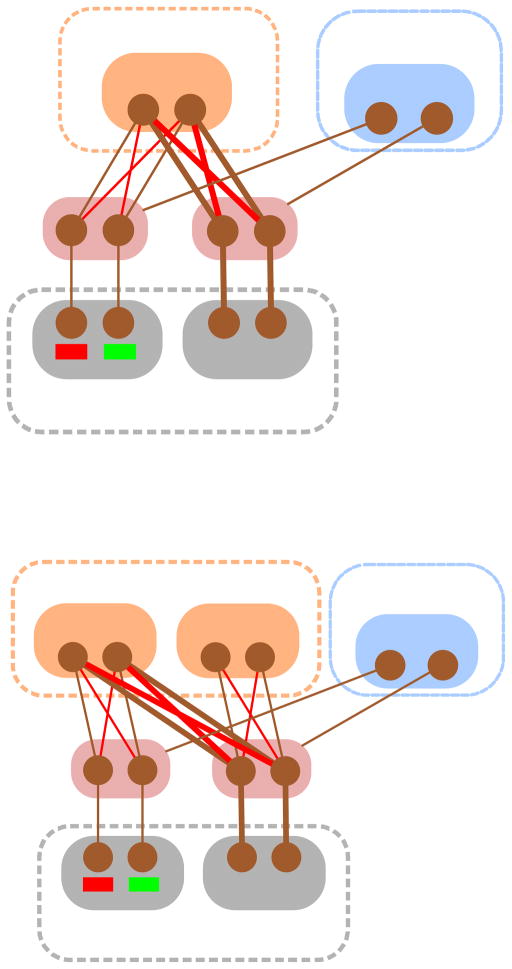
Cohen et al. (1990) described a neural network model that provided a mechanistic account for many of the findings observed in the Stroop task. In that model (Figure 2a), task performance was simulated as the flow of activity between sets of processing units that comprised pathways from stimuli to responses. The model was made up of two sets of input units, one representing the orthographic form of the stimulus and the other its color. Each of these projected to a corresponding set of associative (“hidden”) units that, in turn, converged on a set of response units representing the verbal (phonological form of the) response. Thus, there were two pathways: one for word reading, comprised of connections from the orthographic input units to their associative units and from them to the verbal response layer; and one for color naming (from the color inputs units, by way of their associative units, to the response layer). Note that the response units served two purposes, reading the word or naming the color of the stimulus. In this respect, the representations in response layer were multiplexed, and thus constituted a limited “resource” for which the two pathways competed.

Figure 2. Stroop model.

Panel A: Original model of the Stroop task [Cohen et al 1990]. The bottom units (pink background) are used to represent stimuli along the two dimensions (color and orthographic form). These pass activity to intermediate (associative) units (grey background) which, in turn, pass activity to output units (orange background) that represent the possible verbal responses. The activities of the intermediate units are modulated by task demand (control) units (upper-right, blue background) that represent each of the two possible tasks (color naming and word reading). Brown links between units represent excitatory connections (positive weights); red links represent inhibitory connections (negative weights); and thicker lines represent stronger connections. The word reading pathway has stronger connections than the color naming pathway (presumably due to greater practice and/or more consistent mapping), implementing the greater automaticity of this task. As a result, in order to perform the color naming task, and respond correctly to an incongruent stimulus (e.g., GREEN), the color naming control unit must be activated (see text for explanation). In this respect, color naming is a control-demanding task, relying on the corresponding control unit to manage potential interference from cross-talk produced by the word reading pathway. Panel B: Extended model, that includes a pathway for the word-action task described in the text. Note that there is now multiplexing in both the verbal response layer, as well as the intermediate word processing layer. As a consequence of the latter, color naming and word-action tasks cannot be performed simultaneously without the risk of cross-talk.

To simulate the greater automaticity of word reading, the connections along that pathway were stronger than along the color naming pathway. As a consequence, when a conflict stimulus was presented (e.g., GREEN), the model responded to the word rather than the color, much as participants do when they are presented with such stimuli and provided only with the instruction to “respond” (i.e., without specifying which specific task to perform). However, when instructed to name the color, people can do so. This is a clear example of the capacity for control; that is, the ability to respond to a weaker dimension of a stimulus, in the face of competition from a stronger, prepotent response. The model explained this in terms of the “top-down” influence of a set of control units used to represent the task to be performed. Activating the color naming task unit sent additional biasing activity to the associative units in the color pathway, so that they were more responsive to their inputs. In this way, the model was able to respond to the color of the stimulus, even in the face of competition from the otherwise stronger word reading pathway. This illustrated a fundamental function of control: the management of cross-talk in the service of task performance.

This model and similar ones have been used to account for performance in a wide range of cognitive tasks that rely on control (e.g., Cohen et al., 1990; Servan-Schreiber et al., 1998; Braver & Cohen, 2000; O’Reilly et al., 2002; Rougier et al., 2005; Liu, Holmes, & Cohen, 2008; Yu, Dayan, & Cohen, 2009, Botvinick & Cohen, in press) and the role of neural structures in supporting this function (such as the prefrontal cortex, basal ganglia, and dopamine systems — Braver & Cohen, 2000; Miller & Cohen, 2001; O’Reilly & Frank, 2006). More specifically, they have also directly addressed the role that control plays in managing cross-talk (e.g., Botvinick et al. 2001; Yeung, Botvinick, & Cohen, 2004; Shenhav, Botvinick, & Cohen, 2013). However, their focus has been on situations in which control is needed to manage cross-talk from unintended processes, and not situations in which this arises from multitasking (that is, cross-talk from other intended processes). Accordingly, they have not directly addressed limitations in multitasking of control-dependent processes. However, an important source of such limitations is implicit in these models.

Cross-talk and limits on multitasking

Imagine an extension of the Stroop task, in which a person is asked not only to name the color of the word, but also to respond to the word itself with some other action (e.g., pressing a different button for each word). Figure 2b shows an elaboration of the Stroop model corresponding to this set of tasks, in which the word units are now mapped to a set of manual actions, in addition to verbal responses. Carrying out both tasks simultaneously requires activating both the color and word reading units. While in principle this is possible — there are no intrinsic constraints in the model on how many control units can be activated — the consequence is that color naming will once again be subject to cross-talk from the word. Attempting to perform these two tasks makes it clear that it is almost (if not entirely) impossible to do so at the same time, much like reading and dictation.³ The original Stroop model shows how multiplexing presents a risk of cross-talk, and thus poses the need for control. This extension shows that multiplexing can also impose a limit on the amount of control that should be allocated at once.

In these examples, cross-talk occurred due to multiplexing at the response layer, where the same verbal responses are afforded to two potentially competing process — color naming and word reading. More generally, however, such cross-talk can arise anywhere that there are multiplexed representations (as in the example of reading and dictation described above), To the extent that multiplexing is widespread, the potential for crosstalk and the corresponding need for control will be high. At the same time, this may bring with it constraints on the amount of control that should be allocated. As an analogy, consider the problem faced in designing a network of train tracks and then scheduling the trains: Increasing the directness of connections between sources and destinations necessarily increases the density of tracks, and therefore the number of crossing points. Managing these, in turn, requires limiting the number of trains that are running at the same time, or carefully scheduling their transit (e.g., by restricting the number of green lights that can be simultaneously lit at crossing points). By analogy, dense overlap of representations in the brain (multiplexing) may be an efficient way of encoding information (and serving concomitant functions, such as constraint satisfaction and inference); however, this brings with it the potential for interference due to crosstalk, and thus may restrict the number of control-dependent processes that can safely be licensed at once and thereby limit multitasking.

The foregoing provides a qualitative account for why multiplexing of representations introduces the need for control, and the concomitant constraints that it places on multitasking. However, it does not provide a quantitative account. For example, how severely does the presence of multiplexing constrain multitasking, and to what extent are these effects scale invariant — that is, to what extent do they depend on the size of the system? To address these questions, we constructed variants of the Stroop model that allowed us to amplify the number of pathways, manipulate the amount of multiplexing, and normatively evaluate the number of pathways that could be simultaneously engaged — that is, the limits of multitasking. We hypothesized that introducing even modest amounts of multiplexing into a network would dramatically constrain its ability to multitask, and that this effect would be largely insensitive to the size of the network — that is, there would be limited improvements in multitasking ability even with large increases in network size. The latter case is important, given the striking disparity between the large number of potential processing pathways in the human brain yet the severely restricted number of control-demanding tasks that people can simultaneously perform.

Methods

We constructed two variants of the Stroop model that extended it to simulate more than two pathways. These used the same basic architecture, but different processing functions and objective functions (to evaluate the influence of cross-talk and control on performance). The first model (I/O Matching) used a simple linear mapping from inputs to outputs for each pathway, and the match between the output and a specified target value as the objective function. The second model (DD) used a drift diffusion process to simulate the dynamics of processing in each pathway, and reward rate as the objective function. We present both models to establish the generality of our findings, and extrapolate the anticipated influence of critical factors (such as non-linearity of the processing function) to a broader class of models.

In the section that follows, we describe the overall network architecture that was common to both models, followed by the processing characteristics and objective functions that were specific to each. We then describe the procedures used to optimize processing and control in each network, and to evaluate the corresponding limits of multitasking. Finally, we describe the three factors that we manipulated to determine the influence of multiplexing on the limits of multitasking.

Network architecture

Pathways

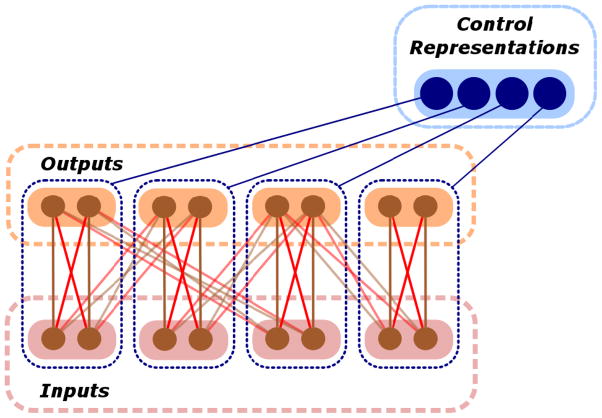
Figure 3 shows the overall network architecture used for both models. For simplicity (and analytic tractability in the case of the DD model), we restricted these pathways to simulating simple two-alternative forced choice tasks. All of the units in the models used linear processing functions (relating their input to their output), and the models were comprised of only input and output layers. We refer to the projections from each pair of input units to a pair of output units as a pathway P, with each pathway implementing the input-output mapping corresponding to a different task. Within each pathway, each input unit of the pair was connected to one of the output units in the corresponding pair with a weight of 0.5, and the other output unit with a weight of −0.5 ( see Figure 3 inset; these specific values, and those for the activity of the input units as described below, were used to simplify mathematical analysis — see SOM A for details). Thus, all weights were symmetric within a pathway, and their magnitudes were equal across all pathways. The weights of connections between input units and output units that did not form a pathway were set to 0.

Figure 3. Network Architecture.

The example shows a network with four pairs of input and output units (N = 4), with overlapping pathways (F = 1), and the level of incongruence used in most simulations (φ = 0.75). Pairs of input units connected to directly overlying pairs of output units (i.e., those contained within the same dotted-blue box) constitute relevant pathways; that is those to be multitasked. Connections between pairs of input and output units in different boxes (shown in slightly lighter colors) represent irrelevant pathways. As in Figure 2, brown connections have positive weights and red ones have negative weights. Connections between pairs of input and output units that have weights of the same signs are congruent, and those having opposite signs are incongruent (see Note 7 for explanation). Control units are shown in blue. Their connections to the corresponding pathways are also shown in blue, indicating that they have a multiplicative effect on the activity of the input and output units in those pathways (see text for explanation).

For the purposes of analysis, we focused on a subset of pathways relevant to the tasks to be performed (P_relevant) — that is, the tasks desired to be multitasked. We denote the number of relevant pathways by N. In Figure 3 these are illustrated as the pathways that connect a pair of input units to the immediately overlying pair of output units. The remaining pathways (P_irrelevant; shown as crossed pathways in Figure 3) implemented multiplexing in the model — that is, the assumption that other, overlapping input-output mappings subserve tasks that are useful in other contexts but are irrelevant in the present one, and therefore introduced the potential for cross-talk. Two factors determined the extent of this cross-talk: the prevalence of pathway overlap (multiplexing), and whether inputs to overlapping pathways were likely to generate the same or different (and therefore interfering) responses. We discuss these factors further below, under Network Configuration.

Control

Each pathway in the network was subject to control. As in the Stroop model, this was implemented by a dedicated unit that modulated the flow of activity from the input to output units. Thus, there were N control units, the activities of which were defined by a vector κ = (k₁, k₂, . . . , k_N). In the Stroop model, control signals were implemented as a bias added to the input of the associative units in the corresponding pathway. Because units in that model used non-linear (sigmoidal) processing functions, the bias had the effect of modulating the gain of those units (Cohen et al., 1990). However, units in the present model used linear processing functions, so we implemented modulation as a direct multiplicative effect. Specifically, the control signal k_i for a given pathway multiplied the activity of the units in that pathway. The values of k were bounded by 1 (k_i ∈ [0, 1]), paralleling the bounded effects of control in the case of non-linear units (i.e., bounds on the derivative of the sigmoidal function). Furthermore, control was applied to both the input and output units in each relevant pathway, in accord with the idea that these implemented the input-output mapping corresponding to the task to be controlled.⁴ Finally, it should be noted that there were no intrinsic constraints on the number of control units that could be activated at a given time. This was determined exclusively by procedures that optimized overall performance of the network, as described below.

Processing

I/O Matching model

This model implemented a simple, single pass feed forward network composed of linear output units. On each trial, one unit for each pair of input units in a pathway was assigned an activity value i of 0.5, and the other a value of −0.5 (these can be thought of as corresponding to the net input to the intermediate units in the Stroop model in Figure 2a; Cohen et al., 1990). For simplicity in evaluating the effects of cross-talk (discussed under Network Configuration below), and without loss of generality, the leftmost input unit was always assigned a value of 0.5 and the rightmost unit −0.5. The activity of each output unit was then computed as the sum of all the inputs connected to it, scaled by both connection weight and each pathway’s control value. For example, the activity of the q^th relevant pathway’s left output unit (indexed as “1”, where the right unit is indexed as “2”) was :

$$Y_{q1}=\sum _{p\in P_q}{k}_p(w_{p1}{i}_{p1}+w_{p2}{i}_{p2})$$ Eq. 1

where the sum is over all connected pathways to the q^th pair of output units, [i_p1, i_p2] is the activity of left and right input units of the pathway p, [w_p1, w_p2] are the weights of the corresponding connections (as described above), and k_p is the value of control for the pathway that includes these units. For the purposes of the objective function (see below), we constrained the activity of all output units to remain in the range [−1,+1]. We did this by further multiplying all weights w_j by 1/R, where R was the total number of projections received by each output unit (R = F+1, where F was the parameter that determined the degree of pathway overlap — see Pathway Overlap below).

The “task” to be performed by each pathway in the P_relevant set was simply for the output units in that pathway to match the activity of the corresponding input units. Accordingly, the performance criterion (i.e., objective function) used for this model was the sum of the squared differences between each input-output pair, divided by the number of pathways in the P_relevant set; that is, the mean-squared error (MSE) of the output vector compared to the input vector. However, in order to account for control on the output units, a subtle but important consideration also had to be taken into account: the influence of pathways assigned low control values. As discussed below, optimization procedures reduced control to pathways that were subject to cross-talk, in order to diminish their deleterious contribution to network performance. However, if left unchecked, the outputs of a fully inactivated pathway might still be heavily influenced by cross-talk from irrelevant pathways. To properly account for this, as noted above, we scaled the values of the output units (as well as the input units) by the corresponding control value, so that the scaled activity modifying Eq. 1 above is Ȳ_q1 = k_qY_q1. These scaled outputs are what were matched to the inputs in the objective function (see SOM A for details). In this way, control influences both the outputs and inputs in a relevant pathway. Note that as constructed, the objective function favors allocating control to (i.e., activating) as many pathways as possible (i.e., maximizing multitasking), while weighing this against the costs to performance of any interference introduced by crosstalk.

DD model

This model used the same network architecture as the I/O Matching model. However, the activity of the output units was determined by simulating the dynamics of information accumulation using a drift diffusion process (Ratcliff, 1978; Ratcliff, Van Zandt, & McKoon, 1999) for each pathway. Drift diffusion processes have been used widely to simulate performance in two alternative forced choice decision tasks (Ratcliff & Rouder, 1998; Simen et al., 2009; Balci et al., 2011), and have been shown to provide a good approximation of underlying neural processes (Shadlen & Newsome, 2001; Usher & McClelland, 2001; Schall, 2001; Gold & Shadlen, 2007). Furthermore, they have the advantage of being tractable to analysis, and thus can be parameterized for optimal performance (Bogacz et al., 2006; we will return to this below). Here, we extended the standard implementation of a DD model to include multiple overlapping processes. Thus, the activity of each output unit was linear combination of its inputs, as in Eq. 1. However, in this case, the difference in activity between the two output units in a pathway then served as the drift rate for a DD process, and a response was made when this crossed a specified threshold.⁵ The drift rate was modulated not only by activity of the input units and the value of the control parameter k_p for that pathway (i.e., for pathways in the P_relevant set), but also by the input received from, and control parameters for, overlapping pathways (i.e., in the P_irrelevant set; see Figure 3 and SOM A for details).

To insure that performance was sampled over as representative a range of input conditions as possible, the activity of each input unit on each trial was drawn from a uniform distribution of values between 0 and 1. This contrasted with the I/O Matching model, in which inputs were either 0.5 or −0.5. For the DD model, it was important to sample inputs of varying strengths since the performance criterion used for this model (reward rate — see below) depended non-linearly on drift rate (and therefore input activity; see Bogacz et al., 2006). For completeness, in addition to the uniform distribution, we also examined other distributions of input values and obtained similar results (see SOM B). As in the I/O Matching model, greater activity was always assigned to the left versus right input unit in each pair.

In accord with prior optimality analyses of DD processes (e.g., Bogacz et al., 2006), we used reward rate as the objective function for this model (see SOM A). Specifically, we optimized the response threshold for the DD process implemented by each pathway for the conditions of each trial (see Optimization, below), so as to maximize its reward rate on that trial. Then, paralleling the I/O Matching Model, we scaled the reward rate for each pathway by its corresponding level of control. Finally we summed the scaled reward rates for each pathway to obtain a reward rate for the entire network:

$$RR=\sum _{p=1}^N{k}_p{RR}_p$$ Eq. 2

Here, RR_p denotes the reward rate for each pathway. Thus, each term in the sum of Eq. 2 represents the p^th pathway's reward rate, scaled by its control policy κ, and the sum is taken over all pathways. As with the I/O Matching model, the objective function favored allocating control to as many pathways as possible (maximizing multitasking), but subject to the constraint that doing so did not degrade performance (and thereby decrease reward rate).

Optimization of performance and control policy

For each of the two models described above, we sought to identify the optimal allocation of control over the pathways in the P_relevant set (that is, how much multitasking could be supported). We examined how this was influenced by pathway overlap (that is, the degree of multiplexing in the network). As described above, the objective function for both models favored allocation of control to as many pathways as possible (while remaining sensitive to any degradation in performance introduced by cross-talk). This insured that our analyses favored multitasking as much as possible, and therefore that estimates of the limitations in this ability were as conservative as possible.

In order to further insure that optimization of control policy favored multitasking as much as possible, we needed to be sure that processing in each pathway in the P_relevant set was optimized for each trial, given the inputs and allocation of control on that trial. This was not a problem for the I/O Matching model, since the outputs were a simple linear sum of the inputs modulated by control. However, insuring optimal performance for the DD model required an additional step, since its performance depended not only on the inputs and control for each pathway, but also on the response thresholds. As described in Bogacz et al. (2006), in the DD model there is a single response threshold that optimizes performance for a given drift rate (determined, in our model, by the inputs and control in a pathway). Thus, to insure that performance was optimized for the current control policy, it was necessary to optimize the threshold in each pathway for the inputs and amount of control allocated to it. We did this using the analyses reported in Bogacz et al. (2006).

Accordingly, we used the following iterative procedure to identify the optimal control policy for a given network architecture. First, we sampled a set of inputs and arbitrarily chose a level of control for each pathway in the P_relevant set. For the I/O Matching model, we then computed the outputs and evaluated the objective function (see Eq. S1 in SOM A). For the DD model, we identified the optimal response threshold for each pathway based on its inputs and allocation of control, and then analytically computed the resulting reward rates for each output unit’s DD process using equations in Bogacz et al. (2006). For both models, we then used parallelized optimization software to iteratively sample control policies, and identify the one that corresponded to a global maximum of the corresponding objective functions (see SOM C for details). In the results presented below, each point was obtained by solving the relevant optimization problem 10,000 times.

Evaluation of limits on multitasking

The purpose of the procedures described above were to determine, for a given network configuration, the optimal control policy for that configuration. We then identified the degree of multitasking that this afforded. That is, our primary goal was to determine, under the optimal control policy for a given network configuration, how many pathways were allocated sufficient control to support task performance. Toward this end, we considered all pathways as active that were assigned a level of control of k_p >= 0.5 for a given control policy, and denoted the number of such pathways as K. We selected 0.5 as the threshold for considering a pathway as active based on simulations using a wide range of parameter values and network configurations. For the I/O matching model, this threshold corresponded to ~75% match of its output to its input. For the DD model, it corresponded to harvesting ~72% of maximal possible reward rate along a pathway. The number of active pathways K, defined in this way, provided an index of the limits on multitasking, with a smaller number indicating more severe limitation.

Network configuration

Using the procedures described above, we conducted simulations to examine how three factors determining network configuration impacted the limits on multitasking (as defined above): degree of pathway overlap (multiplexing), the extent to which this produced cross-talk (interference), and network size.

Pathway overlap (F)

As described under Network Architecture, each pair of input units projected to at least one pair of output units that comprised its pathway in the P_relevant set. In addition, it could also project to other pairs of output units, constituting pathways in the P_irrelevant set. The number of such pathways was determined by a parameter F (for “fan-out”). This specified the number of output unit pairs to which pairs of input units projected (beyond the one in the P_relevant set), and could range from 0 (no “fan-out” connections) to N – 1 (connected to all output unit pairs). Thus, F determined the amount of pathway overlap in the network, and consequently the amount of multiplexing. It is intuitively obvious that for F = 0 full multitasking is optimal, as there is no opportunity for cross-talk. What was of interest was how increasing F interacted with other network factors to influence the limits on multitasking. In determining irrelevant pathways, we simply assigned each input unit pair F random output unit pairs, making sure not to doubly connect input units to output units. We also tried various other schemes for connecting inputs to outputs (such as nearest neighbor connections), all of which did not produce noticeably different results (see SOM B for details). In the analyses below, we considered the effects of pathway overlap both with respect to its absolute value (as described above), and with respect to its value as a proportion of network size, F/N.

Incongruence (φ)

Increasing pathway overlap increased multiplexing, and therefore the potential for cross-talk in the network. In principle, such cross-talk could either enhance or degrade multitasking performance, depending upon whether information arriving at a pair of output units from the irrelevant pathway(s) was congruent with information arriving along the relevant pathway, and therefore facilitated processing, or was incongruent and therefore interfered with processing. This was determined by a parameter φ that specified the frequency with which processing along irrelevant pathways was congruent vs. incongruent with processing along the relevant pathways.⁶ This ranged from 0 (full congruency; i.e., activated inputs units in irrelevant pathways all had connection weights to the output units with the same sign as the activated unit in the relevant one) to 1 (full incongruency). Intuitively it is clear that for φ = 0 full multitasking will be optimal, whereas as for φ = 1 multitasking will be deleterious. What was of interest was how intermediate values of φ interacted with other network factors to influence the limits on multitasking.

Network size (N)

While it is clear that increasing pathway overlap together with incongruence in our models would limit multitasking, what was not clear was how restrictive this effect would be, nor how it would scale with network size (i.e., the number of relevant pathways). The latter is particularly important, given the large number of potential pathways in the human brain. For example, if the effects of pathway overlap and/or interference scaled linearly with network size (enforcing a limit of some fixed percentage of available pathways), this would provide a poor explanation for the remarkably constrained ability that is observed in humans for multitasking involving controlled-processing (i.e., even a small percentage of a very large number is also a large number). Rather, these effects would need to exhibit dramatically sub-linear scaling to explain the striking disparity between the size of the human brain and its limited ability to multitask using controlled processing. To test for this, we simulated networks ranging in size from N = 10 to 1,000 pathways, evaluating the influence of pathway overlap and interference on the limits of multitasking at each scale.

Results

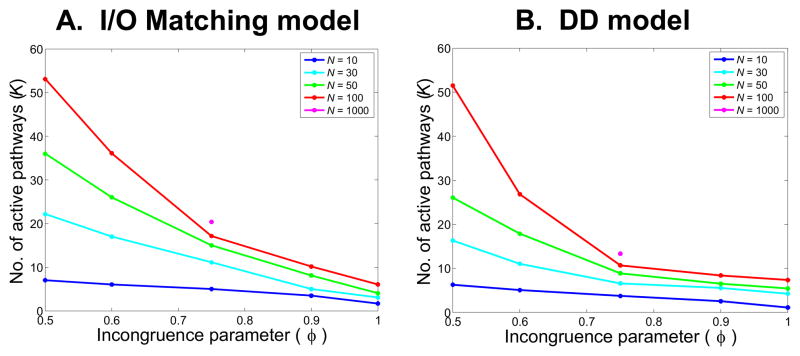
Figure 4 shows performance of the I/O Matching and DD models for different levels of interference φ, and for a value of pathway overlap of F=20% (i.e. F = N/5). We only consider cases in which φ > 0.5, as this is the range in which the irrelevant pathways cause interference.

Figure 4. Capacity constraints as a function of incongruence for networks of different sizes.

Plots show the number of pathways active (k>0.5; see text for explanation) under the optimal control policy for different levels of incongruence (φ; along the X-axis) and networks of different sizes (N; different colored lines). All results are for pathway overlap of F = 20% (i.e., F = N/5). Due to the computational demands of our model, we were only able to simulate networks of size 1000 for φ = 0.75, F = 20%). Panel A: I/O Matching model. Note the steeper slope of decline for larger networks, with convergence (at the highest levels of incongruence) to a value of about 10 active pathways, irrespective of network size. Even at φ = 0.75 (the value used for most simulations), the number of pathways that can be simultaneously engaged increases by three for an increase in network size of about 100 (K = 7 for N = 10; K = 23 for N = 1000). Panel B: DD model: These effects are substantially accentuated for the DD model, with near convergence for networks of all sizes at φ = 0.75.

As expected, increasing incongruence increased the limits on multitasking, as evidenced by a reduction in the number of active pathways K. Under maximal interference φ = 1, even as network size increased well beyond 10 pathways, K converged to a value of around 10 in both models. In the DD model, asymptotic convergence seems to occur around a value of 0.75. At that level of incongruence, even in the I/O Matching model the number of active control representations grew very slowly with network size, with only 17 active control representations in a network of size 100, and only 3 more with a tenfold increase in network size (to N = 1000). Based on these observations, we use a fixed value of interference of φ = 0.75 in subsequent simulations examining the effects of pathway overlap.

Interpreting the empirical significance of this parameter value is, of course, difficult. However, it does not seem unreasonable to assume, for performance of a task focused on a particular dimension of information, that information from other, irrelevant dimensions is distracting 75% of the time. Indeed, it seems possible that this is an underestimate, given that our models focus on tasks involving only two choices; that is, in which the probability of incongruence by chance is 50%. As the number of choices increases, the likelihood of incongruence by chance increases quickly. These considerations, coupled with the observation that this is the lowest value at which the effects of performance approach asymptote, suggest that φ = 0.75 is a reasonable (and perhaps conservative) point of reference.

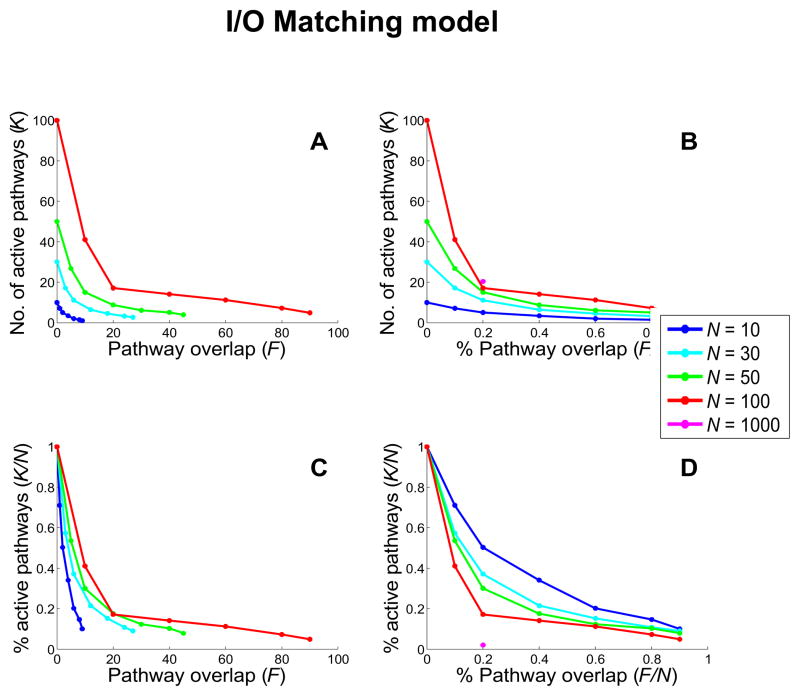
Figure 5 shows how multitasking in the I/O Matching model is affected by pathway overlap (F) in networks of various sizes. The effects are shown both in terms of absolute values of F and K, and when these are expressed as fractions of network size N. As anticipated, increasing F quickly reduces K; that is, it increased the limits on multitasking. However, there are two important features of this effect. First, it is highly nonlinear, with even modest amounts of pathway overlap (e.g., a value of F = 20%, upper-right panel) producing a considerable reduction in the number of tasks that can be supported. Furthermore, this effect accelerates with network size. That is, there is substantial sub-linearity, with a strong constraint on the degree of multitasking — in terms of the absolute number of tasks that can be performed — that is only minimally influenced by network size. For example, as mentioned above, even for a network with 1,000 pathways, pathway overlap of 20% limits the amount of multitasking to below 30 pathways.

Figure 5. Capacity constraints in the I/O Matching model as a function of pathway overlap for networks of different sizes.

Results are for incongruence φ = 0.75. Top panels (A and B) show capacity constraints under the optimal control policy in terms of the absolute number of active pathways (K), and the bottom panels (C and D) show results in terms of the percentage of active pathways (K/N). Left panels (A and C) show results in terms of the absolute amount of pathway overlap (F), and the right panels (B and D) in terms of the percentage of pathway overlap (F/N). Note that when there is no overlap (F = 0), all relevant pathways are active (K = N), indicating full multitasking. Increasing F quickly drives this down, limiting multitasking. This effect is substantially greater for larger network sizes, with networks of all sizes converging to a similar limit in multitasking at around F = 20%.

As with φ, it is difficult to relate F directly to a comparable quantity in the brain. However, a value of 20% seems reasonable, if not modest, given the high degree of convergence for pathways in the brain. For example, using two publicly available large scale cortical connectivity data sets (Rubinov & Sporns, 2010), compiled from tract-tracing studies in the macaque brain (in which nodes represent cortical areas and links represent large corticocortical tracts), yield convergence estimates of 15% (using data from Young, 1993) and 23% (using data from Sporns, Honey, & Kötter, 2007). It is also worth noting, again, that our analyses using the I/O Matching model provide what is likely to be a lower bound on the effect of pathway overlap and interference on multitasking. The results for the DD model support this conjecture.

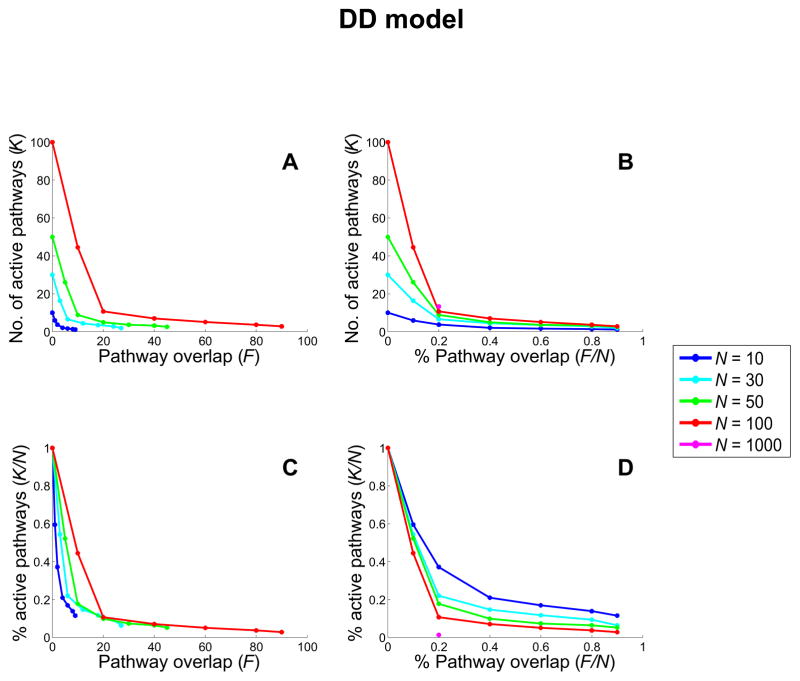
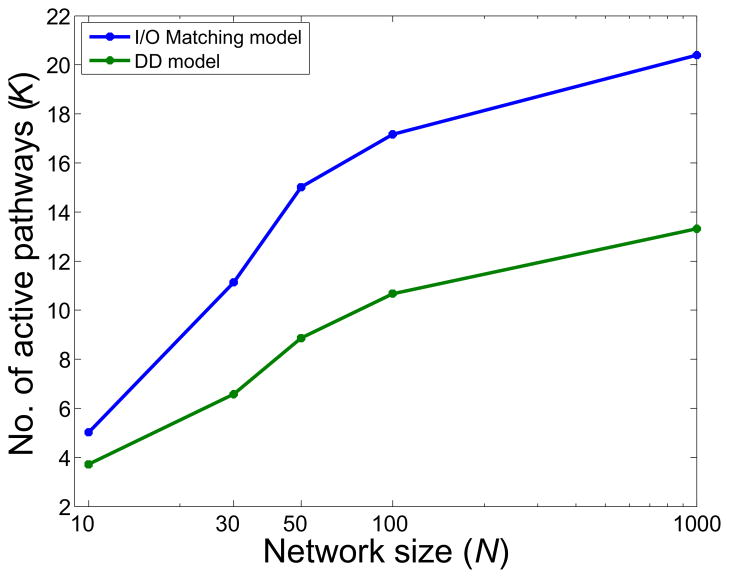
Figure 6 shows results for the DD model analogous to those shown in Figure 5 for the I/O Matching model. As a comparison of these results makes clear, the DD model exhibits similar effects to those of the I/O Matching model, only in accentuated form. For example, for network size N = 1000 and F = 20%, multitasking was limited to less than 14 active pathways, considerably below the level for the comparable network in the I/O Matching model. Figure 7 summarizes these effects, showing how the ability for multitasking changes with network size (for F = 20%), with the DD model exhibiting a lower slope and approaching a substantially lower asymptotic value than the I/O Matching model. In the General Discussion, we consider factors that may explain these differences, and others that may further accentuate the effects of multiplexing on multitasking.

Figure 6. Capacity constraints in the DD model as a function of pathway overlap for networks of different sizes.

See Figure 5 caption for details. Again, the effects are substantially more pronounced as compared to the I/O Matching model, with a striking convergence in the limit on multitasking to less than 14 active pathways for a level of pathway overlap of F = 20%, irrespective of network size.

Figure 7. Capacity constraints as a function of network size.

The optimal control policy is plotted for networks of varying size (N = 10 to 1,000) for the I/O Matching (blue) and DD (green) models. Results are for pathway overlap of F = 20% and incongruence of φ = 0.75. Note that the slope of both lines reduces considerably as network size increases, with the slope for the DD model decreasing more quickly and reaching a lower value than the I/O Matching model. See text for discussion. (Note: the change in slope from N = 10 to 30 is due to a disproportionately high number of active connections for small networks — about 50% of the units in the smallest network are active — a small effect that vanishes as N exceeds 30.)

Several important questions could be asked about these results. A first question is: how sensitive was performance to the optimal value of K? For example, increasing the number of active control units beyond this value could be associated with only small costs to performance, calling into question the importance of this limit for multitasking. To examine this, we tested performance using values of K above and below the optimal value in both the I/O Matching and DD models. The results (shown in SOM D, Figure S5) confirmed that, in both cases, maximum performance was achieved for the value of K identified as optimal (validating the optimization procedures), and that even small deviations from this value were associated with considerable decrements in performance. We also observed that increasing the number of active control units was more detrimental than decreasing the number, indicating that a conservative policy should favor limiting rather than licensing multitasking.

A second question is how sensitive these effects are to the objective function used to determine the optimal control policy? This is perhaps less relevant to the DD model, for which the objective function — reward rate — has both face validity, and has been used extensively in other theoretical work on the DD model (Bogacz et al., 2006; Simen et al., 2006; Balci et al., 2011). Thus, we focused our attention on the I/O Matching model. In the SOM D, we report results using a simpler objective function (sum of absolute error; see SOM D, Figure S5 panel C), and show that these do not differ qualitatively from those reported above.

Finally, it is reasonable to ask why the limits in multitasking we observed were “hard;” that is, why scaling of the optimal value of K with network size was so severely sublinear. It is difficult to give a precise answer to this question, since the high dimensionality of the system coupled with the nonlinearities of the objective function made it intractable to closed-form analysis (hence the need for simulations). However, in SOM E, we report additional simulations using the I/O Matching model, that provide some insight into the source of these effects. They suggest that while modulation of the entire pathway (i.e., both input and output layers) produces optimal performance, the sublinear scaling of optimal K with network size relies heavily on control at the output layer (see SOM E, Figures S6–S9). Some intuition for this effect can be gained by considering the extended version of the Stroop task described in the introduction. Presented with the options of performing both the color naming and word-action tasks or just one of these, it would almost certainly be preferable to choose the latter. Assume, for the purposes of illustration, that the word-action task is chosen. In this case, the full model would modulate the activity of both the intermediate and response (output) units of the color naming pathway, leaving only the word-action pathway activated (see Figure 2b). However, now suppose it were not possible to modulate the output units in a pathway. This would fail to suppress the effect of the intermediate units in the word pathway on the verbal response units, which (for incongruent stimuli) would produce an error in the color naming task (since the input to those units from the intermediate units in the color pathway were suppressed). Therefore, under these conditions, it would be preferable to allocate control to the color naming pathway, allowing its input and intermediate units to influence the response, and at least partially counteract the effects of the cross-talk at the output layer. In other words, in the absence of the ability to control the output, activating pathways that are subject to some (but perhaps not too much) cross-talk can contribute beneficially to their own outputs, and in some cases outweigh the cost of any additional cross-talk they introduce into the network. However, when output can be controlled this is not necessary, and the optimal policy is to limit processing to only the best performing pathways.

General Discussion

The simulations reported above provide a quantitative examination of the effects of pathway overlap on the number of tasks that can be simultaneously performed by networks with the capability of performing multiple two-alternative forced choice decision tasks. The results reveal that increasing overlap rapidly constrains the number of tasks that can be performed at once, and that this reaches a maximum in a manner that is only weakly influenced by network size. These findings support the idea that multiplexing of representations in the brain may be an important source of limits in the ability for multitasking of control-dependent tasks. That said, the upper limits on multitasking observed in the models (10–30 tasks for a wide range of parameters) are noticeably higher than those typically observed for humans (certainly under 10). This may be due to a number of factors.

One factor is suggested by the difference in results observed for the I/O Matching and DD models. The limits on multitasking were less severe in the simpler, fully linear I/O Matching model than for the DD model. Two primary differences in the latter were the addition of an integration process, and the added non-linearity that this introduced in the relationship between processing and performance. Presumably, the integration process afforded an additional opportunity for cross-talk from irrelevant pathways to interfere with processing in the relevant ones. The non-linearity may have also contributed to this effect. The inclusion of additional non-linearities commonly used in neural network models (e.g., in the processing function itself) could be expected to further accentuate it (e.g., by amplifying the influence of activation in irrelevant pathways on relevant ones). Other factors that are likely to have a similar effect are multiple choices (increasing the likelihood of incongruence among processes), recurrent connectivity (increasing interaction among processes), more complex processes involving multiple levels of representation (increasing the opportunities for pathway overlap — such as the reading/dictation example in the introduction), asymmetric pathway strengths (possibly increasing reliance on control, as in the Stroop task), and distributed representations (contributing directly to multiplexing). None of these were implemented in the current models, but all of them are common features of real world tasks and neural systems. The combined effect of these factors is likely to substantially potentiate the constraining effects of pathway overlap on the ability to carry out multiple simultaneous processes. Of course, additional work is needed to determine whether and how these add to the constraints on multitasking. It is important to emphasize, however, that none of these factors alone would constrain multitasking in the absence of pathway overlap — that is, in the absence of multiplexing. In this respect, multiplexing can be viewed as a primary causal factor, with which these others may interact.

Our models suggest that multiplexing can impose strict limits on multitasking of control-dependent processes, without any recourse to limitations in the control system itself. That is, there was no intrinsic limitation to the number of control units that could be activated at once, nor did their engagement carry any direct costs or penalties — only those that associated with the consequences on performance. Of course, introspection, traditional dogma (e.g. Posner & Snyder, 1975), and recent experimental findings (Kool et al., 2010; Kool & Botvinick, 2012; Dixon & Christoff, 2012; Westbrook et al., 2013) all suggest that the exertion of control does carry an intrinsic cost, in the form of “mental effort.” An intriguing explanation for this may be that such costs, experienced as subjective disutility, reflect intrinsic biases limiting the engagement of control signals in order to minimize the risk of cross-task.

Although our work focused on the role of multiplexing in limiting multitasking, it does not preclude — and may complement — models that address potential constraints on the capacity of control mechanisms themselves. The existence of such constraints have consistently been suggested by one remarkably robust phenomenon — the psychological refractory period (PRP; Welford, 1952). This refers to the observation of a seemingly immutable cost associated with performing more than one control-demanding task at once, as compared to performing them each individually. The PRP has been offered as evidence that the capacity constraints of a centralized control mechanism impose a “central-bottleneck” that prohibits truly concurrent multitasking, requiring instead that control-demanding tasks be carried out in sequence (e.g., Pashler, 1984). However, more recent accounts suggest that these effects may reflect the influence of task instructions rather than a central-bottleneck (e.g., Schumacher et al., 2001; Howes, Lewis & Vera, 2009). Nevertheless, several theories continue to propose that multitasking and control may rely on a centralized mechanism, and neuroscientiifc has been martialed in support of this claim (Tombu et al., 2011; Duncan & Owen, 2000; Roca et al., 2011).

One influential class of theories has used production system architectures to develop computationally explicit models of multitasking performance. Traditionally, these have exploited a fundamental feature of this architecture — reliance on goal representations in declarative memory for the execution of control-demanding behavior — to explain constraints on multitasking (e.g. Byrne & Anderson, 2001). Using this framework, more recent threaded cognition models have proposed that bottlenecks can exist both in central mechanisms responsible for control (such as declarative memory) as well as in peripheral modules responsible for task-specific processes, and that constraints on multitasking can arise from either or both, depending on the specific characteristics of the tasks involved (e.g., Salvucci & Taatgen, 2008). However, even these models assume that the execution of all tasks relies on coordination by a common, serial procedural resource. Thus, while these models have produced remarkably detailed accounts of human multitasking performance in a variety of tasks, they risk stipulating (in the form of constraints on centralized mechansims) the effects to be explained. At least one production system model, EPIC (Meyer & Keiras, 1997), occupies the far extreme of parallelism, accounting for constraints on multitasking performance under a variety of conditions entirely in terms of (i.e., as a response to) the conflicts that arise among shared peripheral processors.

Our models share obvious similarity with the threaded cognition model and, even more so, the EPIC model, as well as the early multiple resource theories discussed in the introduction, in emphasizing the importance of cross-talk among interacting task-specific pathways as a constraint on multitasking. However, the focus of the production system models has been largely on the challenges posed by prioritizing and/or scheduling processes that are in potential conflict, and using these to account for the details of human multitasking behavior. Our work might be viewed as complementary to such work, addressing in a more general way a more proximal issue: the quantitative relationship between multiplexing, the demands for control that it poses, and the simultaneous limits it seems to impose on the licensing of control. The simple, and generic nature of our models suggests that our observations may represent general properties of systems involving interacting processes, that may be relevant to a broad class of models.

In a separate line of work, neurally-inspired models of a very different flavor than the ones presented here have been proposed to explain capacity limits in working memory systems — that is, in the number of representations that can be actively maintained (e.g., Haarmann & Usher, 2001; Todd, Niv, & Cohen, 2008; Ma and Huang, 2009; also see Oberauer & Kliegl, 2006). These may be relevant to limits in the capacity for control-dependent processing, insofar as most models of controlled processing (whether neurally inspired or more abstract) assume that this relies on the active maintenance of control signals, and therefore relies on some component of the working memory system (e.g., of task rules, intentions and/or goals; e.g., Anderson, 1983; Miller & Cohen, 2001; Engel, 2002; Cowan, 2001). Thus, constraints on the capacity for active maintenance may also contribute to limits in the capacity for control-dependent processing, and integrating such models with the work presented here (e.g. introducing attractor dynamics into the control representations in our model) represents an interesting and potentially valuable direction for future research.

Even allowing for the possibility that there are capacity constraints imposed by characteristics of the control system itself, the present work provides support for the longstanding idea, suggested by multiple resource theories, that the architecture of the rest of the processing system — over which the control system must preside — represents an important source of such constraints. Importantly, it brings this idea into contact with the growing efforts to consider control from a normative perspective (Todd, Niv & Cohen, 2008; Dayan, 2007; Shenhav, Botvinick, & Cohen, 2013; Botvinick & Cohen, in press). A normative approach to theory may be particularly relevant to an understanding of controlled processing, which can usefully be defined as the set of mechanisms responsible for optimizing processing in the service of maximizing cumulative reward. One recent theory proposes that, from this perspective, a critical function of the control system is to estimate the expected value of candidate control-demanding processes (EVC), and specify control signals in a way that maximizes this quantity (Shenhav, Botvinick, & Cohen, 2013). This must take into account not only the expected benefits from controlled processes, but also the potential costs associated with their execution. Such costs include the potential for interference from cross-talk that arises from simultaneously engaging multiple processes. The work we have presented here examines how such costs can figure into the choice of an optimal control policy, and in particular how it may favor a policy that restricts the allocation of control to a limited number of processes. Put simply, it makes “sense” not to try to do more things than can be done, since the expected returns for doing so will be low. From this perspective, our findings are consistent with the EVC theory, providing a normative account of why the control system may actively choose to limit multitasking.

An important assumption of this account is that multiplexing is either a predetermined feature of the processing architecture in the brain, or that its benefits outweigh the costs they impose on multitasking. Multiplexing would seem to be a fixed characteristic of at least some parts of the processing system, for example the motor system. That is, it seems reasonable to think that the limited dimensionality of the motor system, relative to the large space of potential stimuli to which me can respond, is one factor that imposes multiplexing (e.g., we don’t have two mouths, one to respond to the color and the other to the word in the Stroop task). However, this cannot account for the capacity constraints on control more generally. Internal processes (such as memory retrieval, mental imagery, planning and problem solving) are not constrained by the dimensionality of the motor system, and yet clearly exhibit the same strict limitations on multitasking (i.e., a “single line of thought) as do more overt control-demanding behaviors. This suggests that if limitations of “internal multitasking” — like those of overt behaviors — reflect constraints imposed by multiplexing, then there must be some intrinsic benefits to the multiplexing of internal representations that support such processes. We suggested some of these in the introduction, such as efficiency of coding and inference (Hinton et al., 1986; Forbus et al., 1995). This may also include learning (for example, the use of distributed, similarity-based representations to reduce the state space for reinforcement learning mechanisms).⁷ It will be important, in future work, to explore the relationship between multiplexing and multitasking, by identifying meaningful objective functions that can be used to evaluate the worth of multiplexing representations, and integrating these with the ones for processing (used to evaluate multitasking) that we have explored here.

While more comprehensive normative analysis is clearly an important goal, the findings reported here provide a strong hint concerning their likely outcome. The interaction between multiplexing and multitasking that we observed was heavily asymmetric: Even modest degrees of multiplexing quickly and strongly diminished the value of multitasking. This suggests that, in a tradeoff between the two, there needs to be only modest benefits to multiplexing to normatively justify constraints on multitasking.

Finally, it is important to consider whether and how the work we have presented here aligns with work addressing related questions in other fields. Concerns about crosstalk and process scheduling are fundamental to many areas of engineering (such as computer operating system design, network communications, and transit systems) and other areas of the life sciences (e.g., genetic expression and cell migration during development). Accordingly, these issues have prompted the development of mathematical tools in control theory, network topology, and graph theoretical analysis. However, these tools and their application have focused either on optimizing the scheduling of sequential processes, or increasing and maintaining robustness of a complex system (Carlson & Doyle, 2002). To our knowledge, there has not been any theoretical or applied work that specifically addresses the intersection of factors relevant to the problem we have outlined in this article: the constraints on parallel processing introduced by cross-talk from the multiplexing of representations upon which those processes depend. Because of the non-linearity and high dimensionality of the optimization problem, we were forced to resort to numerical computations. Ideally, we would like more rigorous, analytic tools for quantifying the constraints that multiplexing imposes on multitasking within the processing architecture of neural systems. In this respect, the problem we have posed represents a novel and potentially interesting future challenge for mathematical analysis.

In summary, we have presented simulations that outline the constraints on multitasking imposed by the multiplexing of representations. The latter demands the engagement of control mechanisms, to prevent cross-talk. From this perspective, the very feature of the system that demands control, and yet contributes to its flexibility — multiplexing — appears at the same time to limit the number of control-demanding tasks that can be executed at once. As discussed above, this is likely to interact with other features of controlled processing that together may explain the remarkable limits observed in the human ability for multitasking. To date, research efforts in this area reflect a level of multitasking that appears unbound by any constraints on control. Hopefully this has begun to produce insights that, with more interactive efforts in the future, will lead to a more complete and coherent understanding of limitations in the performance of control-demanding behaviors in humans — behaviors that are otherwise some of the most flexible, powerful and characteristic of those exhibited by humans.

Relevance of this article to the commemoration of Ed Smith.

The span of Ed Smith’s work, and its influence on cognitive science and cognitive neuroscience, was both deep and broad, embracing both experimental work and formal theory. Some of his earliest and most influential work focused on the nature of similarity relationships and conceptual representations. Later, in his collaboration with John Jonides, he shifted his interest to cognitive control and, in particular, how it is implemented in the brain. It seems fitting, therefore, that the work we present in this special issue bridges these two themes, relating a fundamental functional characteristic of controlled processing — its limited ability for multitasking — to the nature of representations and processing in the brain. Although our contribution focuses on capacity constraints in cognition, the breadth and force of Ed’s work are evidence of the truly awe inspiring achievements possible even within the bounds of those limitations.