Improving Cerebellar Segmentation with Statistical Fusion

Abstract

The cerebellum is a somatotopically organized central component of the central nervous system well known to be involved with motor coordination and increasingly recognized roles in cognition and planning. Recent work in multi-atlas labeling has created methods that offer the potential for fully automated 3-D parcellation of the cerebellar lobules and vermis (which are organizationally equivalent to cortical gray matter areas). This work explores the trade offs of using different statistical fusion techniques and post hoc optimizations in two datasets with distinct imaging protocols. We offer a novel fusion technique by extending the ideas of the Selective and Iterative Method for Performance Level Estimation (SIMPLE) to a patch-based performance model. We demonstrate the effectiveness of our algorithm, Non-Local SIMPLE, for segmentation of a mixed population of healthy subjects and patients with severe cerebellar anatomy. Under the first imaging protocol, we show that Non-Local SIMPLE outperforms previous gold-standard segmentation techniques. In the second imaging protocol, we show that Non-Local SIMPLE outperforms previous gold standard techniques but is outperformed by a non-locally weighted vote with the deeper population of atlases available. This work advances the state of the art in open source cerebellar segmentation algorithms and offers the opportunity for routinely including cerebellar segmentation in magnetic resonance imaging studies that acquire whole brain T1-weighted volumes with approximately 1 mm isotropic resolution.

1. INTRODUCTION

The cerebellum is an anatomic region of the central nervous system located in the posterior fossa, inferior to the cerebrum and posterior to the brain stem. As with the cerebrum, the cerebellum consists of two hemispheres (left and right), but also contains midline gray matter structure known as the vermis [1-3]. The cerebellum consists of a layer of tightly folded gray matter surrounding densely packed white matter beneath. The white matter contains four gray matter nuclei: the dentate, globose, emboliform, and fastigial, which receive input fibers from the cerebellar cortex and output to the cerebrum; these cerebellar nuclei account for most of the fibers leaving the cerebellum. The somatotopically organized cerebellum plays an important role in motor function and secondary roles in higher order cognition and decision making. Segmentation of the cerebellum provides a unique challenge in that the cerebellar lobules are not easily differentiated in healthy subjects due to the resolution of the imaging whereas subjects with cerebellar atrophy have more easily differentiable structures (Figure 1).

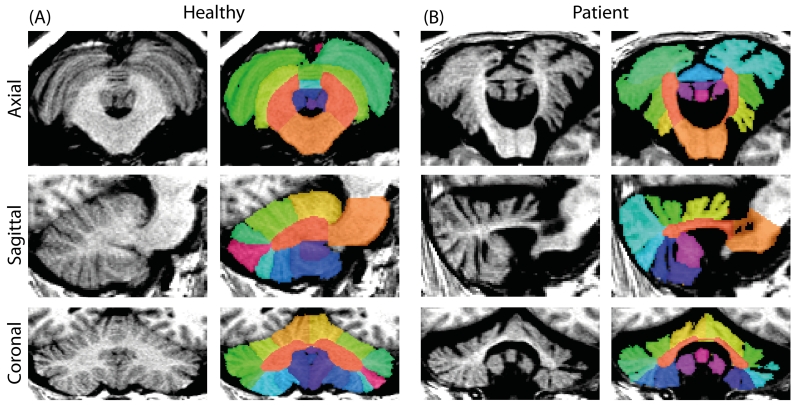
Figure 1.

Axial, coronal, and sagittal segmentation results for a healthy (A) subject and a patient with severe cerebellar ataxia (B). Note the easily differentiable lobules in the patient whereas the differentiation of the lobules is lost to the resolution of the imaging in the healthy subject.

Automated segmentation of the cerebellum has been deeply discussed and characterized in the literature. Van der Lijn used atlas registration and local feature descriptors to segment the left and right hemispheres of the cerebellum but did not segment any of the individual lobules or the vermis [4]. Saeed and Puri developed a semi-automated procedure using template selection and local texture to segment the whole cerebellum [5]. Powell et al use machine learning with probabilistic atlases to segment the cerebellum into upper, middle, and lower lobules but do not explore deeper characterization of regions and only apply their method to healthy subjects [6]. Diedrichsen et al present a probabilistic atlas for segmentation characterizing all of the cerebellar lobules but the single probabilistic atlas does not individually provide robust segmentations across diverse subject populations [7]. Lastly, Yang et al propose performing multi-atlas segmentation of the cerebellar lobules and vermis followed by a post-hoc graph cut to model the boundaries [8].

Herein we propose new segmentation algorithms which combines the ideas of patch-based correspondence of Coupe et al and strong internal atlas selection of Langerak and SIMPLE [9, 10]. The first algorithms, Local SIMPLE and Local Spatial SIMPLE, incorporate intensity information into the generative model of SIMPLE similar to the models of locally-weighted vote and we extend the model to allow spatially varying performance parameters [11, 12]. The third algorithm we propose, Non-Local SIMPLE, combines the ideas of patch-based fusion with the strong semi-parametric atlas selection of SIMPLE, but instead of treating atlases independently, Non-Local SIMPLE assumes an independence between local patches and develops a performance model around them. We evaluate the effectiveness of these models on two distinct populations of cerebellum atlases and compare these algorithms to previous segmentation techniques.

2. METHODS

We begin be defining the data and the standard pipeline used for multi-atlas segmentation. We then define the generative models underlying Local SIMPLE and Non-Local SIMPLE. For these models, we define: T_i is the true label at voxel i, s is an arbitrary label, I_i is the intensity observed at voxel i by the target image, D_i is a 1 × R vector of labels observed at i, R is the number of available raters, L is number of observed labels, N is the number of observed voxels, b is an integer pooling region, A_i is a 1 × R vector of the intensity values observed at i, c is a 1 × R binary vector indicating the current atlas selection state for each atlas, ϵ is a 1 × R rater error vector, σ is the standard deviation used in intensity weighting, k is the current iteration during expectation maximization, j is a particular rater, θ is a R × 2 × L × L matrix where θ_jnss′ is the likelihood rater j observes s given that the true label is s′ and their atlas selection status is n. For brevity the definitions of θ are left to Xu et al [12].

Data

Two datasets were considered in this study. The first dataset, herein Anura, consisted of 25 subjects, 13 with cerebellar ataxia and 12 healthy, ranging in age from 36 to 73, 23 female and 2 male, scanned with a 1.5T three dimensional SPGR sequence and cerebellum manually traced by a trained expert. The second dataset, herein AT, consisted of 45 subjects, 15 healthy controls and 30 patients with various cerebellar diseases, ranging in age from 29 to 90, 21 female 24 male, scanned with a 3T three dimensional MPRAGE sequence. Each subject was labeled by two intermediate experts and gold-standard segmentations were generated by fusing the manual labelings together.

Multi-Atlas Pipeline

All data from both populations followed the same protocol for registration. The data were first bias corrected with N4 bias correction. For each dataset, each pair of scans was non-rigidly registered using the Advanced Normalization Tools (ANTs) SyN algorithm and the default parameters for brain registration [13]. Labels volumes were then deformed to the subject space using the ANTs warping tool and nearest neighbor interpolation.

We compare our new algorithms with several previous algorithms. The first algorithms we compare against are majority vote and non-locally weighted [9, 11]. Second, we compare against the SIMPLE algorithm from Langerak and a spatially varying extension, herein Spatial SIMPLE [10, 12, 14]. Lastly we compare our results to previous work on the same dataset by Yang et al where a multi-atlas segmentation was used as an initialization and a post-hoc graph cut was used to correct the image boundaries [15].

Local and Local Spatial SIMPLE

Following the generative model definition of SIMPLE from Xu et al [12] we incorporate local intensity into the model as

$$f(T_i=s,I_i\mid D_i,A_i,c,ϵ,\sigma ,\theta )$$ (1)

which we can solve through expectation-maximization. We define the E-Step as

$$\begin{array}{cc}\hfill W_{si}^k& =\frac{f(T_i=s)\prod _{j\in R}f(A_{ij}\mid I_i,\sigma )f(D_{ij}\mid T_i=s,c_j^k,{ϵ}_j^k)}{{\Sigma }_{s^{″}}f(T_i=s^{″})\prod _{j\in R}f(A_{ij}\mid I_i,\sigma )f(D_{ij}\mid T_i=s^{″},c_j^k,{ϵ}_j^k)}\hfill \\ \hfill & =\frac{f(T_i=s)\prod _{j\in R}p(A_{ij}\mid I_i,\sigma ){\theta }_{j{c}_j^{k}s{s}^{\prime }}}{{\Sigma }_{s^{″}}f(T_i=s^{″})\prod _{j\in R}f(A_{ij}\mid I_i,\sigma ){\theta }_{j{c}_j^k{s}^{″}{s}^{\prime }}}\hfill \end{array}$$ (2)

assuming conditional independence between the raters and the rater’s intensity and where $p(A_{ij}\mid I_i)=\exp \frac{{(A_{ij}-I_i)}^2}{\sigma }$ [11]. The M-Step directly follows Xu et al so it is excluded from this work. Briefly, the maximization of ${ϵ}_j^{k+1}$ is total weight of the observed label for rater j across the image and $c_j^{k+1}$ is defined based on a semi-parametric atlas selection method from the original SIMPLE definition [10]. To extend the model to be spatially varying we redefine θ as an R × 2 × L × L × N matrix defined identically as before, c as an N × R matrix corresponding to the atlas selection decision for each rater at each voxel, and ϵ as an N × R error vector for each rater at each voxel. The E-Step becomes

$$W_{si}^k=\frac{f(T_i=s)\prod _{j\in R}p(A_{ij}\mid I_i,\sigma ){\theta }_{j{c}_{ji}^{k}s{s}^{\prime }i}}{{\Sigma }_{s^{″}}f(T_i=s^{″})\prod _{j\in R}f(A_{ij}\mid I_i,\sigma ){\theta }_{j{c}_{ji}^k{s}^{″}{s}^{\prime }i}}$$ (3)

and the M-Step once again follows Xu except the values of ϵ are calculated over the pooling are b and thus c is calculated per-voxel based on the estimates of ϵ.

Non-Local SIMPLE

Patch-based label fusion has been incorporated into many label fusion techniques such as Non-Local STAPLE and Non-Locally Weighted Vote [9, 16]. In these techniques, the correspondence model smooths the labels over the nearby region based on the intensity differences. We define the generative model of Non-Local SIMPLE as

$$f(T_i=s,I\mid D,A,c,ϵ,\sigma ,{א}_s,{א}_p,\theta ,b)$$ (4)

where א_s are the parameters of non-local search, א_p are the parameters of non-local distance calculation, c as an N × R × א_s matrix corresponding to the patch selection decision for each rater at each voxel over their non-local search space, ϵ as an N × R × א_s error matrix for each rater at each voxel over their non-local search area, and θ is a confusion R × 2 × L × L × N × א_s defined both spatially and over the non-local correspondence search region. We estimate the solution of this model through expectation maximization. We define the E-Step as

$$W_{si}^k=\frac{f(T_i=s)\prod _{j\in R}\prod _{i^{\prime }\in {א}_s}p(A_{i^{\prime }}\mid I_i,{א}_p,\sigma ){\theta }_{j{c}_{ji{i}^{\prime }}^{k}s{s}^{\prime }i{i}^{\prime }}}{{\Sigma }_{s^{″}}f(T_i=s^{″})\prod _{j\in R}\prod _{i^{″}\in {א}_s}p(A_{i^{″}}\mid I_i,{א}_p,\sigma ){\theta }_{j{c}_{ji{i}^{″}}^k{s}^{″}{s}^{\prime }i{i}^{″}}}$$ (5)

where

$$p(A_{i^{\prime }}\mid I_i,{א}_p,\sigma )=\exp \left(-\frac{{\mid \mid {א}_p\left(A_{i^{\prime }}\right)-{א}_p\left(I_i\right)\mid \mid }^2}{\sigma }\right)$$ (6)

which is the standard definition of non-local correspondence of Euclidean distance between the atlas and target patches in an exponential distribution [9, 16]. This E-Step expansion assumes a conditional independence between patches and the non-local intensity probability model. The M-Step follows as with Local Spatial STAPLE where the confidence is calculated over the pooling region b between the patch in the atlas and the target voxel in the atlas. For instance

$${ϵ}_{ij{i}^{\prime }}^{k+1}={\arg }_{{ϵ}_{{\mathrm{iji}}^{\prime }}}\max \sum _{s^{\prime }}\sum _{a\in -b:b}\sum _s{W}_{s(i+a)}^k\ln {\theta }_{j{c}_{ji{i}^{\prime }}^{k}s{s}^{\prime }i{i}^{\prime }}\delta \left(D_{(i^{\prime }+a)j},s^{\prime }\right)$$ (7)

following from the derivation of Xu et al, where δ is the dirac delta function. Thus, Non-Local SIMPLE performs patch-based performance modeling with strong atlas selection following from the works of Langerak, Xu, and Coupe [10, 12].

Statistical Analysis

To assess the performance of each statistical fusion technique, each atlas was segmented in a leave-one-out study with each algorithm (i.e., 24 atlases per target in the Anura set and 44 atlases per target in the AT set). Since the registration and label propagation steps were identical between algorithms, we treat the segmentation results as paired between label fusion algorithms. We calculate the Dice coefficient between each set of true atlas labels and each label fusion approach. Since we cannot assume these Dice results fit any distribution, we perform a Wilcoxon signed-rank test between each algorithm. All significant results reported are at a p<0.05.

3. RESULTS

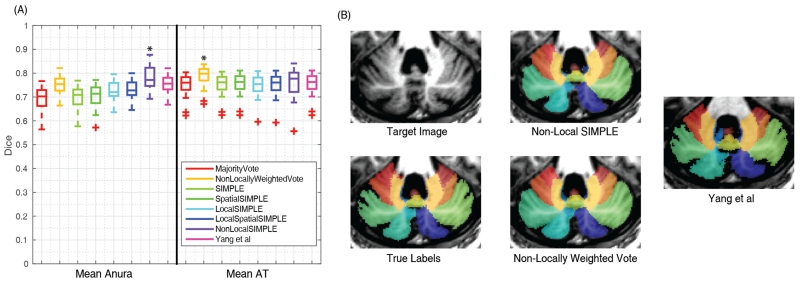
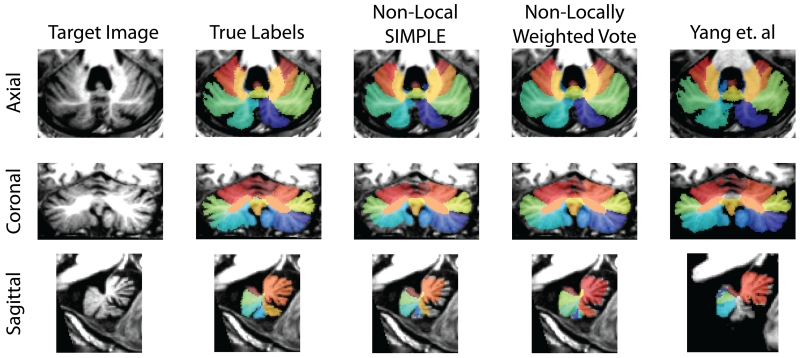
In the leave-one-out segmentation of the Anura dataset, Non-Local SIMPLE produced statistically significant improvements in mean Dice compared to all other algorithms. Non-Local SIMPLE had an improvement in mean Dice of 0.03 on average compared with Non-Locally Weighted Vote and the approach of Yang et al. On the AT dataset, Non-Locally Weighted Vote significantly outperformed all other techniques by at least 0.04 mean Dice. Non-Local SIMPLE significantly outperformed the results of Yang et al on the AT data by 0.01 Dice (Figure 2). Qualitatively Non-Locally Weighted Vote tends to slightly over-segment the cerebellar lobules whereas Non-Local SIMPLE under-segments. The results of Yang et al appear to produce segmentations more consistent with the true anatomic boundaries but have greater issues with labels shifting between regions (Figure 2). The full Dice scores for all regions of interest are available in Figures 3 and 4 and more qualitative results are available in Figure 5.

Figure 2.

Summarized segmentation results for the Anura and AT datasets. Non-Local SIMPLE outperformed all other techniques on the Anura dataset (A). On the AT dataset Non-Locally Weighted Vote significantly outperformed all other techniques, but Non-Local SIMPLE still outperformed the previously gold-standard technique of Yang et al (A).Qualitatively, Non-Locally Weighted Vote seemed to oversegment the lobules whereas Non-Local SIMPLE tended to undersegment. The results of Yang et al visually produced results more consistent with the anatomic boundaries but had more internal boundary shifts than either Non-Locally Weighted Vote or Non-Local SIMPLE.

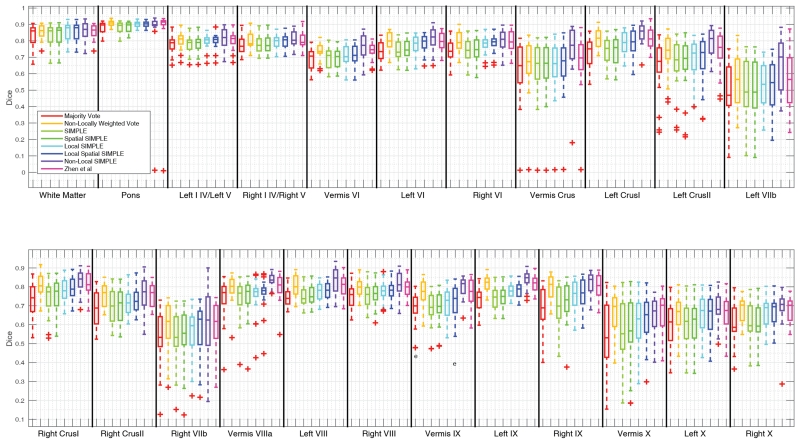
Figure 3.

Quantitative segmentation results for the Anura dataset. Non-Local SIMPLE shows either significant improvements over other algorithms or comparable results to other algorithms for all labels.

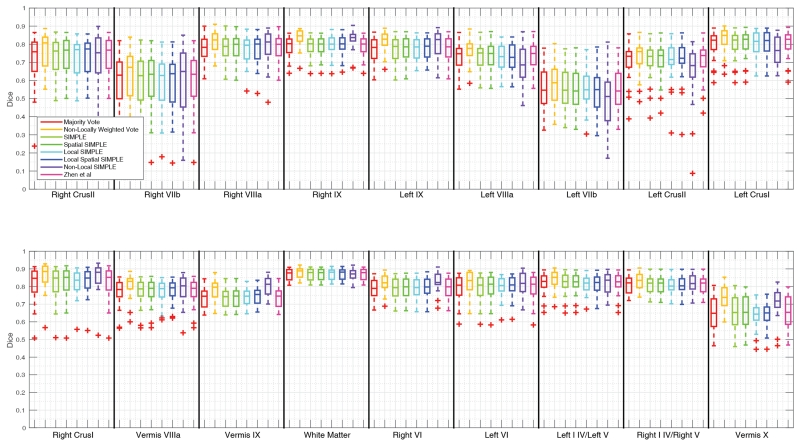
Figure 4.

Quantitative segmentation results for the Ataxia dataset. No algorithm shows significant improvement across all labels but Non-Locally Weighted Vote provides both consistent and accurate results across most labels.

Figure 5.

Qualitative segmentation results from the median Ataxia subject. Non-Locally Weighted Vote tends to slightly over-segment regions of interest while Non-Local SIMPLE tends to under-segment regions. The adaptation of Yang et. al appears to generate a segmentation more consistent with anatomic boundaries but can produce severe missegmentations as seen in the sagittal view. Other algorithms are not shown since they infrequently outperformed the algorithms shown here.

4. DISCUSSION

In this work, we investigated new algorithms for fully-automated multi-atlas segmentation of the cerebellum. We proposed three approaches for segmentation deriving from the work of Langerak and Xu on the SIMPLE atlas selection and performance model [10, 12]. The first two algorithms, Local SIMPLE and Local Spatial SIMPLE, incorporated local image similarity into the generative model definition of SIMPLE and extended the base algorithm to consider only the local region in performance model calculation. The third algorithm, Non-Local SIMPLE, extends the SIMPLE model to patches in the area around the registered atlas images, incorporating the work of Coupe and patch-based segmentation into SIMPLE [9]. We then evaluated these algorithms against several previous algorithms, including the previous gold-standard cerebellar segmentation algorithm, on two sets of cerebellar atlases [15]. On the first set, Non-Local SIMPLE beat all other techniques with a p < 0.05. On the second set, Non-Locally Weighted Vote produced the best segmentation results, but Non-Local SIMPLE still outperformed the previous gold-standard technique. In conclusion, we have shown that cerebellar segmentation is a challenging task and no current technique produces significant improvements over other techniques so application specific considerations and trade-offs should be considered. Future work will investigate secondary processing techniques [17] to address systematic over/under-segmentation concerns with the currently leading methods. We note that the proposed techniques are targeted at cases where a large number of atlases are available (i.e., greater than 30).