Abstract
Objective:
The aim of this study was to determine which physical delivery parameter changes are most suitable for multiple-level dose-painting treatment plans with helical tomotherapy (HT).
Methods:
A total of 96 treatment plans were generated for 12 patients who had undergone fluorine-18 fludeoxyglucose positron emission tomography/CT (18F-FDG-PET/CT) scan to plan head and neck cancer treatment. Based on these PET-CT images, the dose was escalated to 96 Gy in 32 fractions as a function of PET intensity values. The intensity-based prescription was converted into seven discrete dose levels. For the same patient, different HT plans were optimized by varying parameters such as field width (FW), pitch (PF) and modulation factor (MF). Dose conformity was evaluated using quality–volume histograms, quality factors (QFs), weighted index of achievement (IOAw), coldness (IOCw) and hotness (IOHw). Moreover, doses to organs at risk (OARs), target volumes and execution time were analyzed.
Results:
Median QFs were the best for FW = 1.05 cm (QF = 2.10) and the worst for FW = 2.5 cm (QF = 3.04). The same trend was observed for IOAw, IOCw and IOHw. Combination of FW = 1.05 cm and MF = 5 leads to the longest beam-on time (above 25 min), whereas FW = 2.5 cm and MF = 3 lead to the shortest time (below 8 min). Data analyzed based on dose–volume histogram showed that changes in FW had the strongest impact on plan quality, whereas the effect of MF and PF changes was moderate.
Conclusion:
HT is suitable for multiple-level dose-painting treatment plans.
Advances in knowledge:
Changes in FW and MF had the greatest impact on dose distribution quality and beam-on time. Changes in PF only influenced doses to the OARs.
INTRODUCTION
The state of the art treatment planning is to ensure that the dose delivered to the planning target volume (PTV) is as homogeneous as possible while simultaneously sparing nearby organs at risk (OARs).1 Many indices are available to measure dose conformity and uniformity.2,3 However, because of variations within the tumour structure, some regions respond differently to radiation. A prime example of this involves hypoxic regions within the tumour, which have been found to have a negative impact on the response to radiotherapy4–7 and have been associated with radioresistance. Similarly, other regions within the tumour may need dose escalation, which must be carefully tailored to avoid acute and late toxicity. This variable structure within tumours has led Ling et al8 to suggest that biological imaging should be incorporated in the treatment planning process to replace physical conformity with biological conformity.
In response to the notion of non-homogeneous tumour regions, dose painting by numbers (DPBNs) was created. The aim of this technique is to prescribe a heterogeneous dose inside the tumour based on the tumour-specific characteristics, which can be assessed with functional imaging, such as positron emission tomography (PET). Depending on the tracer, it is possible to measure various biological processes. Increased fluorine-18 fludeoxyglucose (18F-FDG) uptake is associated with cellular metabolism, fluorine-18-labelled 3ʹ-deoxy-3ʹ-fluorothymidine uptake with proliferation and 18F-fluoromisonidazole uptake with hypoxia while carbon-11-labelled choline uptake is associated with lipid metabolism.9 Thus, by assessing biological information and incorporating this into the treatment planning process, it becomes possible to identify subvolumes (which may be more or less radioresistant than the surrounding areas) and to target these, as appropriate, with a higher or lower radiation dose. Modern technology is now sufficiently advanced to allow for generating very sophisticated dose distribution,10,11 such as that contoured in DPBN, to fully target and modulate the dose as suitable to each region of the tumour, thereby increasing cell killing and tumour control.
Although some published studies12–14 have investigated dose painting based on systems developed in-house, few have evaluated commercially available systems such as the TomoTherapy® Hi-Art® (Accuray, Madison, WI) treatment planning system (TPS).15 Given this context, we carried out the study presented here, in which we sought to determine which treatment planning parameters used in the TomoTherapy Hi-Art TPS are most suitable for dose-painting plans. We specifically focused on beam-on time, conformity to the target volumes and OAR sparing.
METHODS AND MATERIALS
Patients
12 patients previously treated for locally advanced head and neck tumours (hypopharynx, oropharynx and oral cavity) were included in this retrospective study. Patients were immobilized in the supine position with an individualized thermoplastic mask (CIVCO Medical Solutions, Kalona, IA). Planning 18F-FDG-PET/CT (Philips Medical Systems, Amsterdam, Netherlands) scans were acquired for each patient in the treatment position before therapy. Next, the OARs were contoured on planning CT using Eclipse™ TPS v. 10.0 (Varian® Medical Systems, Palo Alto, CA). The following OARs were included: the parotid glands, spinal cord (SC), planning OAR volume (PRV) SC, brain stem (BS), mandible and target volumes. All clinical target volumes (CTVs) and gross tumour volumes were contoured manually by the same physician based on the available images and medical history. Lymph node contouring was performed in accordance with the guidelines described by Gregoire et al.16 The CTV was expanded by 3 mm to create the PTV. In order to generate a PRV SC, a margin of 3 mm was added to the SC.
The study was approved by the ethics committee of the Pozan University of Medical Sciences and registered under the number 364/15.
Treatment plans
Since commercially available TPS does not permit dose prescription for each voxel, DPBN was carried out by using a structure-based treatment planning method, which is a reasonable alternate to voxel-based dose prescription when a sufficient number of subcontours are used within the region of interest.17 For this reason, uptake data from PET images were segmented into seven subcontours according to the method proposed by Vanderstraeten et al14 and Deveau et al.15 The lowest PET voxel intensity Ilow utilized for dose escalation was calculated as: Ilow = 0.25 I95%, where I95% is 95% of PET voxel intensity within the dose-painted region. The highest voxel intensity (Ihigh) used for dose escalation was Ihigh = I95%. This range of voxel intensities was chosen to minimize the noise of the PET signal.18 Next, the range of PET voxel intensities from Ilow to Ihigh was divided into seven equal parts corresponding to seven dose escalation subcontours. The dose-painting contours were corrected by the same physician to assure that they remained within the CTV. Because the radiobiological significance of the PET voxel intensity values is not known, we assumed a linear relationship between voxel intensity and dose, following the example of Das et al,18 Vanderstraeten et al14 and Deveau et al.15 As a result, seven dose-painted contours with intensities between Ilow and Ihigh were treated with seven equally spaced prescribed doses from Dlow to Dhigh. The equation for structure-based prescription dose of i-th contour with intensity Ii is:14
| (1) |
Finally, CT scans and contours were exported in the digital imaging and communications in medicine format to the TomoTherapy Hi-Art TPS (v. 4.2), where treatment plans were created using a 6-MV photon beam in helical mode using a superposition/convolution algorithm. A simultaneous integrated boost technique with fine calculation grid size (0.2 × 0.2 cm) was used. For each patient, eight different HT treatment plans were created, each optimized by varying the treatment parameters as follows: field width (FW) = 1.05 or 2.5 cm; pitch (PF) = 0.287 or 0.43; and modulation factor (MF) = 3 or 5. Table 1 shows the summary of planning parameters used for each treatment plan. Treatment plans were optimized using simultaneous integrated boost. The dose was administered in 32 fractions (fxs) using multiple dose levels (Table 2).12,13
Table 1.
Values of planning parameters used to create eight different treatment plans
| Plan number | FW | PF | MF |
|---|---|---|---|
| 1 | 1.05 | 0.287 | 3 |
| 2 | 1.05 | 0.287 | 5 |
| 3 | 1.05 | 0.43 | 3 |
| 4 | 1.05 | 0.43 | 5 |
| 5 | 2.5 | 0.287 | 3 |
| 6 | 2.5 | 0.287 | 5 |
| 7 | 2.5 | 0.43 | 3 |
| 8 | 2.5 | 0.43 | 5 |
FW, field width; MF, modulation factor; PF, pitch.
Table 2.
Dose prescription for dose-painting plans
| Description | Dfx (Gy) | Dtotal (Gy) | NID2Gy (Gy) |
|---|---|---|---|
| Elective LNRs—PTV56.00Gy | 1.75 | 56.00 | 51.57 |
| High risk LNRs—PTV62.08Gy | 1.94 | 62.08 | 61.33 |
| Primary CTV—PTV67.20Gy | 2.10 | 67.20 | 70.00 |
| PET primary | 2.16–3.00 | 69.12–96.00 | 73.00–120.71 |
CTV, clinical target volume; Dfx, dose per fraction; Dtotal, total dose; LNRs, lymph node regions; NID2Gy, normalized isoeffective dose; PET, positron emission tomography; PTV, planning target volume.
In order to reduce user bias, each plan was optimized with the same goals. This process was always divided into two parts. First, 100 iterations were used to reduce doses to the OARs (according to constraints shown in Table 3). Then, in the next 100 iterations, conformal and homogeneous dose distribution in the target volumes was obtained according to International Commission on Radiation Units and Measurements report number 83.19
Table 3.
Dose constraints used for optimization of each treatment plan
| OAR | Dose constraints |
|---|---|
| Spinal cord | Dmax < 45 Gy |
| PRV spinal cord | Dmax < 50 Gy |
| Brain stem | Dmax < 54 Gy |
| Mandible | Dmax < 70 Gy |
| Parotid glands | Dmean < 26 Gy |
Dmax, maximum dose; Dmean, mean dose; OAR, organ at risk; PRV, planning OAR volume.
Analysis
The plans were analyzed based on dose–volume histogram (DVH) data. We investigated the mean dose for both the parotid glands and the maximum doses for the SC, PRV SC, BS and mandible. Maximum doses are reported as D1%, where Dx% is a dose in x% of the volume. Additionally, the volumes covered by the isodose 50 Gy (V50Gy) and 60 Gy (V60Gy) were analyzed for the PRV SC and mandible, respectively. Minimum and maximum doses were compared for the PTV of the elective lymph node regions (LNRs) (PTV56.00Gy), high-risk LNRs (PTV62.08Gy) and the primary PTV (PTV67.20Gy) covered by the 95% isodose. Minimum doses were reported as dose in 99% of the volume (D99%). Dose to a minimum significant volume, rather than point dose, was used to avoid very small peaks of point doses (i.e. based on a single voxel), a common occurrence in intensity-modulated radiation therapy techniques.
To simplify the evaluation and comparison of PET primary volumes for each plan, a concept of quality–volume histogram (QVH) and quality factor (QF) was used:14
| (2) |
where Qp is the dose obtained during treatment planning at voxel p (n voxels in total) divided by the prescribed dose at that voxel. Typical size of the voxel in this study was 0.2 × 0.2 × 0.2 cm. QF can be interpreted as an average absolute deviation of Q to 1 for the PET primary volume. The QVH is obtained by plotting the volume of the dose-painted region as a function of Q values. In an ideal dose-painting plan, the QVH for the PET primary volume would be a step line at Q = 1 and QF would be equal to 0.
The drawback of QF is that each target voxel has the same impact. As a result, lower dose-painting volumes (DPVs) have larger impact on QF since they contain much more voxels than regions with higher dose-painting doses (e.g. DPV69.12Gy includes more voxels than DPV96.00Gy). To overcome this, three new plan quality indexes were used according to Park et al.20 To measure the level of achievement of a prescription goal, weighted index of achievement (IOAw) was used; to measure the hot and cold spots, weighted indices of hotness (IOHw) and coldness (IOCw) were measured:
| (3) |
| (4) |
| (5) |
| (6) |
where V is the total target volume, vi is the volume of the i-th voxel in the target volume, Dmean,Rx is mean prescribed dose for the target volume, Di,Rx and Di,Plan are prescribed and obtained during treatment planning dose of the i-th voxel, respectively.
In an ideal dose-painting plan, all indices would be equal to 1. The higher the discrepancy from 1, the greater the dissimilarity between prescribed and obtained dose distribution. One needs to remember that the value of IOCw is always equal to or less than 1, whereas IOAw and IOHw have values equal to or greater than 1.
To speed up the process of QF, QVH, IOAw, IOHw and IOCw calculation, an in-house software program was developed using the MATLAB® environment v. R2009b (MathWorks® Inc., Natick, MA).
All treatment plans were also analyzed for the beam-on time. The data were statistically analyzed using XLSTAT software (Addinsoft SARL, New York, NY). To compare different plans stratified by a single parameter (e.g. FW 2.5 vs 1.0 cm), a Wilcoxon (double-sided) test was used. Additionally, we used an agglomerative hierarchical clustering discriminant analysis (AHCDA) to verify which treatment planning parameter (FW, PF or MF) had the strongest impact on the final dose distribution and beam-on time. The idea of cluster analysis is to classify the data according to their similarity values. The analyzed data set is divided into several discrete groups that have the highest similarity value. All statistics were performed for α = 0.05.
RESULTS
Data from 96 treatment plans were analyzed, and the summary of results for the DVH-based parameters, beam-on time and QF is presented in Table 4. Median doses in the table were calculated for plans that contained the tested parameter (four plans for each patient). The mean volume of the dose-painting volume (DPV69.12Gy) was 43.4 cm3 [standard deviation (SD), 29.1 cm3]. The volume of next subcontours (DPV73.60Gy, DPV78.08Gy, DPV82.56Gy, DPV87.04Gy, DPV91.52Gy and DPV96.00Gy) was: 24.4 cm3 (SD = 16.6 cm3), 14.8 cm3 (SD = 10.5 cm3), 8.5 cm3 (SD = 6.6 cm3), 3.8 cm3 (SD = 3.4 cm3), 1.0 cm3 (SD = 1.5 cm3), 0.2 cm3 (SD = 0.5 cm3), respectively.
Table 4.
Dose–volume statistics (median dose with range) for all patients according to the treatment plans
| Parameter | FW=1.05 | FW=2.5 | PF=0.287 | PF=0.43 | MF=3 | MF=5 |
|---|---|---|---|---|---|---|
| QF | 2.10 (1.54–5.94) | 3.04 (1.75–6.86) | 2.65 (1.55–6.86) | 2.72 (1.66–6.75) | 2.71 (1.60–6.90) | 2.72 (1.55–6.75) |
| IOAW | 1.0263 (1.0195–1.0725) | 1.0394 (1.0220–1.0839) | 1.0344 (1.0195–1.0839) | 1.0358 (1.0211–1.0839) | 1.0351 (1.0198–1.0839) | 1.0357 (1.0195–1.0839) |
| IOCW | 0.9827 (0.9679–0.9858) | 0.9775 (0.9670–0.9826) | 0.9794 (0.9669–0.9854) | 0.9786 (0.9676–0.9858) | 0.9788 (0.9670–0.9854) | 0.9790 (0.9683–0.9858) |
| IOHW | 1.0289 (1.0216–1.0765) | 1.0435 (1.0227–1.0890) | 1.0383 (1.0216–1.0875) | 1.0397 (1.0227–1.0890) | 1.0389 (1.0221–1.0875) | 1.0395 (1.0216–1.0890) |
| Beam-on time (s) | 1389.3 (907.7–2064.6) | 577.5 (383.2–864.1) | 885.9 (383.2–2061.0) | 884.8 (383.3–2064.6) | 711.4 (383.2–1255.0) | 1193.8 (640.0–2064.6) |
|
D1% (Gy) | ||||||
| PTV56.00Gy | 58.0 (57.2–59.9) | 58.9 (57.9–60.0) | 58.5 (57.2–60.0) | 58.6 (57.2–59.8) | 58.5 (57.2–60.0) | 58.5 (57.2–59.3) |
| PTV62.08Gy | 63.8 (63.0–66.0) | 64.0 (63.2–66.0) | 63.9 (63.1–66.0) | 63.9 (63.0–66.0) | 63.9 (63.1–66.0) | 63.9 (63.0–66.0) |
| PTV67.20Gy | 69.4 (67.2–70.4) | 70.1 (67.8–71.3) | 69.7 (67.4–71.3) | 69.8 (67.2–71.3) | 69.8 (67.2–71.3) | 69.8 (67.4–71.3) |
|
D99% (Gy) | ||||||
| PTV56.00Gy | 53.3 (51.8–54.4) | 52.9 (51.0–54.9) | 53.1 (51.0–54.9) | 53.3 (51.0–54.4) | 53.1 (51.0–54.9) | 53.3 (51.0–54.3) |
| PTV62.08Gy | 59.5 (56.7–61.0) | 58.9 (54.7–60.8) | 59.4 (54.7–60.8) | 59.3 (56.7–61.0) | 59.0 (54.7–60.8) | 59.6 (56.5–61.0) |
| PTV67.20Gy | 64.3 (61.0–65.3) | 63.3 (61.0–63.0) | 63.7 (61.0–65.3) | 63.7 (61.0–65.3) | 63.7 (61.0–65.3) | 63.7 (61.6–65.3) |
|
V95% (%) | ||||||
| PTV56.00Gy | 99.1 (98.3–99.9) | 98.8 (98.0–99.7) | 99.0 (98.2–99.7) | 99.1 (98.0–99.9) | 99.0 (98.2–99.7) | 99.1 (98.0–99.9) |
| PTV62.08Gy | 99.2 (98.4–100.0) | 99.0 (96.0–99.9) | 99.2 (96.0–100.0) | 99.2 (98.1–100.0) | 99.0 (96.0–100.0) | 99.2 (98.0–100.0) |
| PTV67.20Gy | 99.6 (96.0–100.0) | 98.8 (97.2–99.9) | 99.2 (96.00–100.0) | 99.3 (97.2–100.0) | 99.2 (96.0–100.0) | 99.3 (97.6–100.0) |
|
D1% (Gy) | ||||||
| Brain stem | 36.3 (28.9–45.7) | 32.7 (27.8–43.8) | 33.9 (27.8–45.2) | 34.4 (28.8–45.7) | 34.2 (28.6–45.7) | 33.8 (27.8–45.4) |
| Spinal cord | 39.7 (38.8–41.6) | 39.8 (38.3–42.4) | 39.6 (38.3–42.3) | 39.9 (38.6–42.4) | 39.8 (38.3–42.4) | 39.8 (38.3–42.1) |
| PRV spinal cord | 43.8 (42.6–45.1) | 43.9 (42.3–46.4) | 43.6 (42.3–46.2) | 44.0 (42.5–46.4) | 43.9 (42.4–46.4) | 43.8 (42.3–45.4) |
| Mandible | 67.9 (54.9–75.2) | 68.7 (57.4–79.5) | 68.1 (54.9–79.3) | 68.4 (54.9–79.5) | 68.1 (54.9–79.3) | 68.4 (54.9–79.5) |
| V60Gy mandible (%) | 27.3 (0.2–41.3) | 28.8 (0.3–44.7) | 28.4 (0.2–44.7) | 28.6 (0.3–44.7) | 28.6 (0.2–44.7) | 28.5 (0.2–44.3) |
| Dmean contralateral parotid (Gy) | 24.0 (18.6–28.2) | 24.1 (17.9–29.8) | 24.0 (17.9–29.6) | 24.1 (18.0–29.8) | 24.0 (17.9–29.8) | 24.0 (18.3–29.4) |
| Dmean ipsilateral parotid (Gy) | 28.6 (24.7–35.6) | 29.5 (25.0–39.3) | 29.1 (24.7–38.0) | 29.3 (24.9–39.3) | 29.3 (25.0–38.0) | 29.3 (24.7–39.3) |
Dmean, mean dose; DX%, dose in X% volume; FW, field width; IOAW, weighted index of achievement; IOCW, weighted index of coldness; IOHW, weighted index of hotness; MF, modulation factor; PF, pitch; PRV, planning organ at risk volume; PTV, planning target volume; QF, quality factor; VXGy, volume of the structure that is covered by the isodose X Gy.
Median doses were calculated for plans that contained the exact parameter in the column header (four plans for each patient).
PTVYGy excludes PTVXGy for X > Y.
Beam-on time
Plans with FW = 2.5 cm and MF = 3 yielded the lowest beam-on time, a statistically significant difference compared with plans with FW = 1.05 cm and MF = 5, respectively. Statistical analysis showed that PF = 0.287 and PF = 0.43 do not influence the beam-on time (p = 0.338).
Target volume coverage
The lowest value of maximum dose in PTVs (PTV56.00Gy, PTV62.08Gy and PTV67.20Gy) was obtained for FW = 1.05 cm and the highest for FW = 2.5 cm. MF did not have any impact on D1% in any PTV, similar to PF for PTV62.08Gy. However, significant difference could be observed between plans with PF = 0.287 and PF = 0.43 for PTV56.00Gy and PTV67.20Gy, with slightly better results for PF = 0.287.
In terms of minimum doses and V95%, the trend was similar to the maximum dose: FW has the most significant impact on D99% and V95%. The results for FW = 2.5 cm were always the poorest of all the parameters. For PTV56.00Gy, MF and PF did not influence the minimum dose. However, for PTV62.08Gy and PTV67.20Gy, MF turned out to be significant: a higher MF lead to better coverage of the PTV.
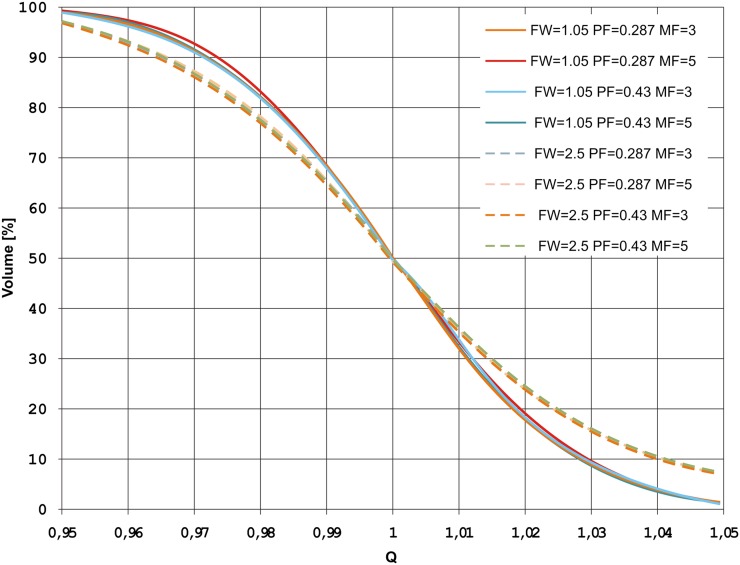
The best QF was obtained for FW = 1.05 cm (2.10), whereas the worst QF was found for FW = 2.5 cm (3.04). No significant differences were observed for the MF and PF. This can be also seen on a QVH for one of the patients in Figure 1.
Figure 1.
Quality (Q)–volume histogram for different treatment planning parameters for one of the patients. FW, field width; MF, modulation factor; PF, pitch.
More reliable index of dose distribution assessment in DPV—IOAw was found to be analogical to QF. It showed that the best IOAw was obtained for FW = 1.05 cm (1.0263) and the worst for FW = 2.5 cm (1.0394). The same was observed for IOCw and IOHw. From Table 5, one may notice that statistically significant difference was observed also for MF—the higher the MF, the better the IOAw, IOCw and IOHw, and as a result dose distribution in DP region. Changes in PF did not have an impact on the indexes.
Table 5.
Comparison of p-values for the various treatment plans
| Parameter | FW 1.05 vs 2.5 | PF 0.287 vs 0.43 | MF 3 vs 5 |
|---|---|---|---|
| QF | p < 0.001 | p = 0.253 | p = 0.310 |
| IOAW | p < 0.001 | p = 0.354 | p = 0.034 |
| IOCW | p < 0.001 | p = 0.225 | p = 0.041 |
| IOHW | p < 0.001 | p = 0.411 | p = 0.028 |
| Beam-on time (s) | p < 0.001 | p = 0.338 | p < 0.001 |
|
D1% (Gy) | |||
| PTV56.00Gy | p < 0.001 | p = 0.003 | p = 0.791 |
| PTV62.08Gy | p < 0.001 | p = 0.344 | p = 0.281 |
| PTV67.20Gy | p < 0.001 | p = 0.002 | p = 0.336 |
|
D99% (Gy) | |||
| PTV56.00Gy | p < 0.001 | p = 0.315 | p = 0.111 |
| PTV62.08Gy | p < 0.001 | p = 0.317 | p < 0.001 |
| PTV67.20Gy | p < 0.001 | p = 0.104 | p = 0.004 |
|
V95% (%) | |||
| PTV56.00Gy | p = 0.001 | p = 0.292 | p = 0.150 |
| PTV62.08Gy | p < 0.001 | p = 0.247 | p < 0.001 |
| PTV67.20Gy | p < 0.001 | p = 0.201 | p = 0.049 |
|
D1% (Gy) | |||
| Brain stem | p < 0.001 | p = 0.003 | p < 0.001 |
| Spinal cord | p = 0.397 | p < 0.001 | p = 0.007 |
| PRV spinal cord | p = 0.011 | p < 0.001 | p = 0.010 |
| Mandible | p < 0.001 | p = 0.012 | p = 0.006 |
| V60Gy mandible (%) | p < 0.001 | p = 0.416 | p = 0.926 |
| Dmean contralateral parotid (Gy) | p = 0.277 | p = 0.010 | p = 0.255 |
| Dmean ipsilateral parotid (Gy) | p < 0.001 | p = 0.005 | p = 0.363 |
Dmean, mean dose; DX%, dose in X% volume; FW, field width; IOAW, weighted index of achievement; IOCW, weighted index of coldness; IOHW, weighted index of hotness; MF, modulation factor; PF, pitch; PRV, planning organ at risk volume; PTV, planning target volume; QF, quality factor; VXGy, volume of the structure that is covered by the isodose X Gy.
Statistically significant results (confidence level α = 0.05) are in bold.
PTVYGy excludes PTVXGy for X > Y.
Normal tissue sparing
Doses in the PRV SC were <50 Gy in all cases. Therefore, no statistical analysis was needed to further evaluate this parameter. The DVH comparison for the rest of the OARs showed that each treatment planning parameter (FW, PF and MF) has a statistically significant impact on maximum dose for critical organs.
The highest maximum dose for the SC and PRV SC was observed for PF = 0.43, with the lowest observed for PF = 0.287. However, the difference between the median doses for all the patients was small (0.4 Gy). Differences between PF (0.287 vs 0.43) and FW (1.05 vs 2.5) were even smaller—only 0.1 Gy.
Larger differences in the maximum dose were observed for the BS. The lowest dose (32.7 Gy) was observed for plans with FW = 2.5 cm and the highest (36.3 Gy) for FW = 1.05 cm. Differences between PF (0.287 vs 0.43) and MF (3 vs 5), although statistically significant, were not clinically significant since the median dose changed only by 0.5 and 0.4 Gy, respectively.
For D1% in the mandible, the lowest median dose (67.9 Gy) was observed for plans with FW = 1.05 and the highest (68.7 Gy) for FW = 2.5. Plans with a PF of 0.287 had significantly lower maximum doses than plans with PF = 0.43); the same was true (i.e. lower maximum doses) for MF = 3 vs MF = 5. However, in both cases, the difference was only 0.3 Gy. The volume covering the mandible with the 60-Gy isodose (V60Gy) was the smallest (27.3%) for plans with FW = 1.05 cm and the highest (28.8%) for FW = 2.5 cm; this difference was statistically significant (p < 0.001). By contrast, the difference between the remaining parameters (PF and MF) was not significant.
Sparing of the contralateral parotid gland was not possible in only one patient. By contrast, both the parotid glands could be spared in two patients. The lowest mean dose (28.6 Gy) in the ipsilateral parotid gland was observed for plans with FW = 1.05 cm and the highest (29.5 Gy) for FW = 2.5 cm, a statistically significant difference (p < 0.001). The significant difference was also found for plans with different PF values (p = 0.005), although they only varied by 0.2 Gy. For the contralateral parotid gland, median doses were similar for all plans with the exception of a significant difference (p = 0.010) for plans with different PF values: plan with PF = 0.287 resulted in slightly lower doses compared with PF = 0.43.
Regarding doses to the OARs, it should be noted that statistical significance was very often shown (Table 5) for different parameters (FW, PF and MF), but it was not always clinically relevant—e.g. 1.5% reduction in V60Gy for the mandible when changing FW from 2.5 to 1.05 cm (Table 4) probably does not decrease the risk of osteoradionecrosis.
The AHCDA, which took into account beam-on time, QF and DVH parameters for PTVs and OARs, divided the plans twice. The first classification was for FW (1.05 vs 2.5 cm) and the second one for MF (3 vs 5). This means that among all the data, the highest degree of dissimilarity between treatment plans was observed for FW. Whereas, plans with MF = 3 differed by smaller amount to plans with MF = 5.
DISCUSSION
In this study, we compared various combinations of treatment planning parameters (FW, PF and MF) to determine which combination produces the best results in terms of target coverage and sparing of key OARs. Our analysis of treatment plans showed that FW and MF are crucial parameters for dose-painting plans, regarding both quality of the dose distribution and beam-on time. The remaining parameter—PF, usually had an impact only on the dose to OARs.
Our study is an extension of the feasibility study (only one patient and no analysis of the OARs or beam on-time) carried out by Deveau et al.15 Since both of these factors are important, we included them in our analysis, as well as the fact that the volume that was treated enclosed not only the dose-painted region but also LNRs and primary PTV.
The shape of the dose-painted area was not challenging—it was always a regular shape where dose-painted volumes were more or less aligned to each other. Such situation leads to a gradual increase of the dose inside a PET primary, which is quite natural for the optimization system. However, the volumes of the highest doses (DPV87.04Gy − DPV96.00Gy) were also the smallest, which pushes the optimization to create a high dose gradient in craniocaudal (C-C) direction. For this reason, median QFs for all plans were similar approximately 2.7, except for FW = 1.05 cm and FW = 2.5 cm (Table 4). It means that FW = 1.05 cm would be the most suitable for generation of optimal dose distribution in the PET primary area. This hypothesis is also advocated by the results obtained for IOAw, IOCw and IOHw—index number was always closest to 1 in plans with FW = 1.05 cm.
While analyzing QVH curves, usually VQ=0.95 and VQ=1.05 should be ≥95% and ≤5%, respectively.14 It means that 95% of the dose-painted volume should receive at least 95% of the prescribed dose, and hot spots above 105% should be in <5% of the volume. In our study, most of the QVHs were similar. For this reason, we have included a QVH only for one randomly selected patient (Figure 1). One may notice, that the shape of the QVH is different for FW = 1.05 cm vs FW = 2.5 cm. It can be seen that for all plans, the above-mentioned criteria were fulfilled for VQ=0.95 (VQ=0.95 ≈ 99.4% for FW = 1.05 and VQ=0.95 ≈ 97.4% for FW = 2.5). However, VQ=1.05 was met only for plans with FW = 1.05 (VQ=1.05 ≈ 1.5% for FW = 1.05 cm and VQ=1.05 ≈ 7.8% for FW = 2.5 cm). This, once again, shows the need for FW = 1.05 in the dose-painting region.
We found that the shortest median beam-on time (approximately 10 min) was achieved for two groups of plans: FW = 2.5 cm and MF = 3 (Table 4). This seems to be an acceptable time for sophisticated head and neck treatments. However, plans that used FW = 2.5 cm also had the highest QF, IOAw and IOHw and the lowest IOCw, meaning that the dose distribution in the dose-painting region was the worst of all plans. Moreover, parameters such as V95%, and the minimum and maximum doses in PTVs for LNRs and primary CTV, were significantly better for smaller FW values, which leads to a better resolution in the C-C direction. For this reason, it would be reasonable to use FW = 1.05 cm for DPBN plans, especially when the DPV is sophisticated.
The PF and MF parameters were found to impact the dose to the OARs. The lower PF value did not lead to an increase in beam-on time, but it did lower the maximum dose to the SC, PRV SC, BS and mandible and the mean dose to the parotid glands. This result contradicts the findings of Deveau et al15 who concluded that PF changes are not sensitive to dose-painted plans. We believe that this discrepancy can be attributed to the fact that those authors did not consider the dose to the OARs, whereas we did.
Our study also showed that changes in the MF value will always influence beam-on time. In most cases, MF = 5 resulted in lower doses to the OARs but longer treatment time. Changing the FW value (i.e. FW = 1.05 cm and FW = 2.5 cm) lead to more dramatic improvements, whereas changing between MF = 3 and MF = 5 had less of an impact on the doses to the OARs. Moreover, MF does not influence the dose beamlets and can be changed during the optimization process. These findings indicate that dose-painting optimization should start with MF = 5, which can be systematically decreased until satisfactory beam-on time is achieved.
Our findings are in good agreement with previous studies regarding MF, PF combinations for optimal treatment plans without dose painting.21–23 This means that these HT parameters could be kept the same as used in routine clinical practice, except for FW, which should be changed from typical 2.5–1.05 cm for DPBN plans.
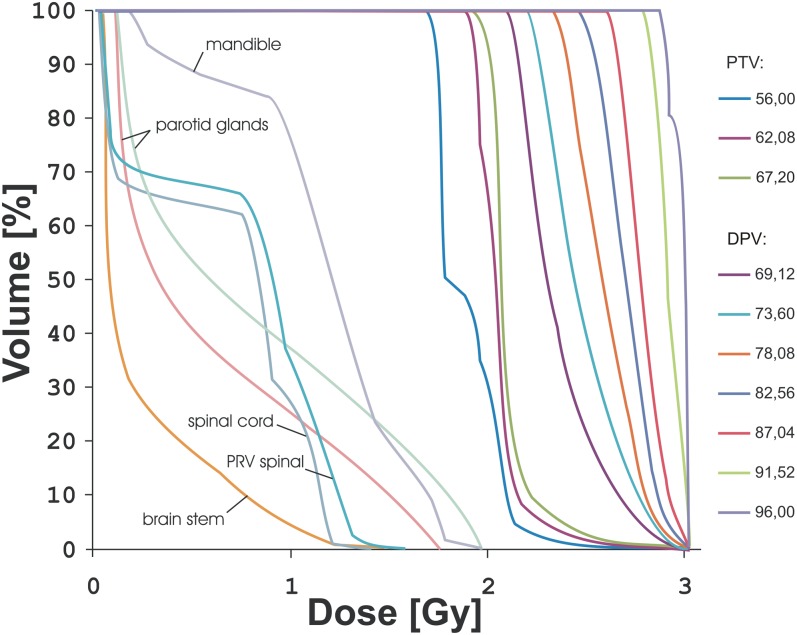
Figure 2 presents the DVH for a single fx for one patient using these parameter settings: FW = 1.05 cm, PF = 0.287 and MF = 3. As the figure shows, dose per fx for all OARs is below the standard fractionation dose (2 Gy), so there was no need to calculate an equivalent dose in 2-Gy fxs. Beam-on time for this plan was 434.8 s (approximately 7 min), and all constraints from Table 3 were fulfilled. This plan could have been used in this patient, although the dose escalation is very high and perhaps questionable. This planning study was performed for an extreme situation, with maximum escalation to normalized isoeffective dose (NID2Gy) = 120.71 Gy [the volume was 0.2 cm3 (SD = 0.5 cm3)], such a high dose would not be used clinically; however, this proves that multiple-level dose escalation using HT is possible to very high doses without violating the OAR doses.
Figure 2.
Dose–volume histogram (single fraction) for treatment plan with field width = 1.05 cm, pitch = 0.287 and modulation factor = 3 for one of the patients. The planning target volumes (PTVs) from 69.12 to 96.00 Gy are positron emission tomography primary regions that were dose painted. DPV, dose-painting volume.
It is important to stress that beam-on time and plan quality depends on the delivery mode of the tomotherapy machine: the next generation HT is equipped with dynamic jaw and dynamic couch movements, which can reduce treatment time by 66%.24 In addition, the latest HT machines reduce dose penumbra and thus the integral dose and dose to the OARs may be lower.21 However, the option of dynamic jaws is favourable only at the beginning and the end of the PTV in C-C direction. Since, in our study the dose-painted region was never placed at the edge of the PTV in the C-C direction, the next generation HT would probably not improve substantially the dose distribution. Nevertheless, even with the older tomotherapy machines used in the present study, we have demonstrated that HT is capable of generating a discrete dose-painting plan.
Based on the AHCDA, the FW parameter had the strongest impact on the quality of the plan, followed by the MF. Since AHCDA did not classify PF into a separate group, it means that treatment plans with PF = 0.287 and PF = 0.43 are very similar.
DPBN suffers from some limitations and should be used with caution. One of them is sensitivity to motion and geometric errors during external beam radiation therapy. Korreman et al25 demonstrated that a systematic error of 2 mm in any direction results in a significant decrease of dose conformality for DPBN plans. However, recently, Witte et al26 and Sterpin et al17 presented a solution to this problem. Although the first method (robust optimization technique) could not be implemented in this study because of technical issues (this optimization technique is not available in HT TPS), the second one (modifying the dose prescription by dilation and deconvolution) could be a useful tool.
CONCLUSION
The present study shows that the Hi-Art TomoTherapy system is capable of generating discrete dose-painting plans. The limitations of voxel-based prescription in HT TPS can be overcome by using a sufficient number of subcontours with equally spaced discrete prescribed doses. The two most important parameters of the dose-painting plans to minimize beam on-time while delivering a high-quality dose distribution are FW and the MF. PF is less important, and has moderate impact on the dose to the OARs.
DPBN planning is a very sophisticated and challenging process. Selection of appropriate FW and MF is crucial since both of these parameters influence beam-on time and dose distribution quality. It is advisable to make this decision individually for each patient (based on the patient's condition and the complexity of DPV), keeping in mind that longer treatment time may increase intra-fx errors and machine workload.
Acknowledgments
ACKNOWLEDGMENTS
The authors thank Professor Vincent Grégoire for his thoughtful comments and discussion.
Contributor Information
Malgorzata Skórska, Email: malgorzata.skorska@wco.pl.
Tomasz Piotrowski, Email: tomasz.piotrowsk@wco.pl.
Adam Ryczkowski, Email: adam.ryczkowski@wco.pl.
Joanna Kaźmierska, Email: joanna.kazmerska@wco.pl.
REFERENCES
- 1.Peszynska-Piorun M, Malicki J, Golusinski W. Doses in organs at risk during head and neck radiotherapy using IMRT and 3D-CRT. Radiol Oncol 2012; 46: 328–36. doi: 10.2478/v10019-012-0050-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Feuvret L, Noël G, Mazeron JJ, Bey P. Conformity index: a review. Int J Rad Oncol Biol Phys 2006; 64: 333–42. doi: 10.1016/j.ijrobp.2005.09.028 [DOI] [PubMed] [Google Scholar]
- 3.Piotrowski T, Martenka P, de Patoul N, Jodda A, Coevoet M, Malicki J, et al. The new two-component conformity index formula (TCCI) and dose-volume comparisons of the pituitary gland and tonsil cancer IMRT plans using a linear accelerator and helical tomotherapy. Rep Pract Oncol Radiother 2009; 14: 133–45. doi: 10.1016/S1507-1367(10)60028-4 [DOI] [Google Scholar]
- 4.Hockel M, Knoop C, Schlenger K, Vorndran B, Knapstein PG, Vaupel P. Intratumoral pO2 histography as predictive assay in advanced cancer of the uterine cervix. Adv Exp Med Biol 1994; 345: 445–50. doi: 10.1007/978-1-4615-2468-7_59 [DOI] [PubMed] [Google Scholar]
- 5.Hockel M, Schlenger K, Aral B, Mitze M, Schaffer U, Vaupel P. Association between tumor hypoxia and malignant progression in advanced cancer of the uterine cervix. Cancer Res 1996; 56: 4509–15. [PubMed] [Google Scholar]
- 6.Brizel DM, Sibley GS, Prosnitz LR, Scher RL, Dewhirst MW. Tumor hypoxia adversely affects the prognosis of carcinoma of the head and neck. Int J Radiat Oncol Biol Phys 1997; 38: 285–9. doi: 10.1016/S0360-3016(97)00101-6 [DOI] [PubMed] [Google Scholar]
- 7.Nordsmark M, Overgaard M, Overgaard J. Pretreatment oxygenation predicts radiation response in advanced squamous cell carcinoma of the head and neck. Radiother Oncol 1996; 41: 31–9. doi: 10.1016/S0167-8140(96)91811-3 [DOI] [PubMed] [Google Scholar]
- 8.Ling CC, Humm J, Larson S, Amols H, Fuks Z, Leibel S, et al. Towards multidimensional radiotherapy (MD-CRT): biological imaging and biological conformality. Int J Radiat Oncol Biol Phys 2000; 47: 551–60. doi: 10.1016/S0360-3016(00)00467-3 [DOI] [PubMed] [Google Scholar]
- 9.Bandurska-Luque A, Piotrowski T, Skrobała A, Ryczkowski A, Adamska K, Kaźmierska J. Prospective study on dosimetric comparison of helical tomotherapy and 3DCRT for craniospinal irradiation—A single institution experience. Rep Pract Oncol Radiother 2015; 20: 145–52. doi: 10.1016/j.rpor.2014.12.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ślosarek K, Osewski W, Grządziel A, Radwan M, Dolla Ł, Szlag M, et al. Integral dose: comparison between four techniques for prostate radiotherapy. Rep Pract Oncol Radiother 2014; 20: 99–103. doi: 10.1016/j.rpor.2014.10.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.López E, Lazo A, Gutiérrez A, Arregui G, Núñez I, Sacchetti A. Influence of 11C-choline PET/CT on radiotherapy planning in prostate cancer. Rep Pract Oncol Radiother 2015; 20: 104–12. doi: 10.1016/j.rpor.2014.11.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Duprez F, De Neve W, De Gersem W, Coghe M, Madani I. Adaptive dose painting by numbers for head-and-neck cancer. Int J Radiat Oncol Biol Phys 2011; 80: 1045–55. doi: 10.1016/j.ijrobp.2010.03.028 [DOI] [PubMed] [Google Scholar]
- 13.Madani I, Duthoy W, Derie C, De Gersem W, Boterberg T, Saerens M, et al. Positron emission tomography-guided, focal-dose escalation using intensity-modulated radiotherapy for head and neck cancer. Int J Radiat Oncol Biol Phys 2007; 68: 126–35. doi: 10.1016/j.ijrobp.2006.12.070 [DOI] [PubMed] [Google Scholar]
- 14.Vanderstraeten B, Duthoy W, De Gersem W, De Neve W, Thierens H. [18F]fluoro-deoxy-glucose positron emission tomography ([18F]FDG-PET) voxel intensity-based intensity-modulated radiation therapy (IMRT) for head and neck cancer. Radiother Oncol 2006; 79: 249–58. doi: 10.1016/j.radonc.2006.03.003 [DOI] [PubMed] [Google Scholar]
- 15.Deveau MA, Bowen SR, Westerly DC, Jeraj R. Feasibility and sensitivity study of helical tomotherapy for dose painting plans. Acta Oncol 2010; 49: 991–6. doi: 10.3109/0284186X.2010.500302 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gregoire V, Coche E, Cosnard G, Hamoir M, Reychler H. Selection and delineation of lymph node target volumes in head and neck conformal radiotherapy. Proposal for standardizing terminology and procedure based on the surgical experience. Radiother Oncol 2000; 56: 135–50. doi: 10.1016/S0167-8140(00)00202-4 [DOI] [PubMed] [Google Scholar]
- 17.Sterpin E, Differding S, Janssens G, Geets X, Grégoire V, Lee JA. Generation of prescriptions robust against geometric uncertainties in dose painting by numbers. Acta Oncol 2015; 54: 253–60. doi: 10.3109/0284186X.2014.930171 [DOI] [PubMed] [Google Scholar]
- 18.Das SK, Miften MM, Zhou S, Bell M, Munley MT, Whiddon CS, et al. Feasibility of optimizing the dose distribution in lung tumours using fluorine-18-fluorodeoxyglucose positron emission tomography and single photon emission computed tomography guided dose prescriptions. Med Phys 2004; 31: 1452–61. doi: 10.1118/1.1750991 [DOI] [PubMed] [Google Scholar]
- 19.ICRU. Report 83: prescribing, recording, and reporting photon-beam intensity-modulated aadiation therapy (IMRT). J ICRU 2010; 10. doi: 10.1093/jicru/ndq002 [DOI] [PubMed] [Google Scholar]
- 20.Park YK, Park S, Wu HG, Kim S. A new plan quality index for dose painting radiotherapy. J Appl Clin Med Phys 2014; 15: 4941. doi: 10.1120/jacmp.v15i4.4941 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.De Kerf G, Van Gestel D, Mommaerts L, Van den Weyngaert D, Verellen D. Evaluation of the optimal combinations of modulation factor and pitch for Helical TomoTherapy plans made with TomoEdge using Pareto optimal fronts. Radiat Oncol 2015; 10: 191. doi: 10.1186/s13014-015-0497-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ryczkowski A, Piotrowski T. Influence of the modulation factor on the treatment plan quality and execution time in Tomotherapy in head and neck cancer: in-phantom study. J Can Res Ther 2013; 9: 618–23. doi: 10.4103/0973-1482.126458 [DOI] [PubMed] [Google Scholar]
- 23.Moldovan M, Fontenot JD, Gibbons JP, Lee TK, Rosen II, Fields RS, et al. Investigation of pitch and jaw width to decrease delivery time of helical tomotherapy treatments for head and neck cancer. Med Dosim 2011; 36: 397–403. doi: 10.1016/j.meddos.2010.10.001 [DOI] [PubMed] [Google Scholar]
- 24.Sterzing F, Uhl M, Hauswald H, Schubert K, Sroka-Perez G, Chen Y, et al. Dynamic jaws and dynamic couch in helical tomotherapy. Int J Radiat Oncol Biol Phys 2010; 76: 1266–73. doi: 10.1016/j.ijrobp.2009.07.1686 [DOI] [PubMed] [Google Scholar]
- 25.Korreman SS, Ulrich S, Bowen S, Deveau M, Bentzen SM, Jeraj R. Feasibility of dose painting using volumetric modulated arc optimization and delivery. Acta Oncol 2010; 49: 964–71. doi: 10.3109/0284186X.2010.498440 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Witte M, Shakirin G, Houweling A, Peulen H, van Herk M. Dealing with geometric uncertainties in dose painting by numbers: introducing the ΔVH. Radiother Oncol 2011; 100: 402–6. doi: 10.1016/j.radonc.2011.08.028 [DOI] [PubMed] [Google Scholar]