Background Gene Expression Networks Significantly Enhance Drug Response Prediction by Transcriptional Profiling

Abstract

A central goal of gene expression studies coupled with drug response screens is to identify predictive profiles that can be exploited to stratify patients. Numerous methods have been proposed towards this end, most focusing on novel statistical methods and model selection techniques which attempt to uncover groups of genes whose expression profiles are directly and robustly correlated with drug response. However, biological systems process information through the crosstalk of multiple signaling networks, whose ultimate phenotypic consequences may only be determined by the combined input of relevant interacting systems. By restricting predictive signatures to direct gene-drug correlations, biologically meaningful interactions that may serve as superior predictors are ignored. Here we demonstrate that predictive signatures which incorporate the interaction between background gene expression patterns and individual predictive probes can provide superior models than those that directly relate gene expression levels to pharmacological response, and thus should be more widely utilized in pharmacogenetic studies.

INTRODUCTION

The NCI60 panel of cancer cell lines was developed in the late 1980s to facilitate in vitro assay-based drug discovery. As genomic and drug response data has accumulated on the individual NCI60 cell lines, they have been used in pharmacogenetic, mechanism of action, and pharmacological response prediction studies [1]. The vast majority of pharmacological response prediction studies have relied upon the correlation of a single or groups of gene expression microarray probes with drug response, with a focus on novel methods for feature selection and/or the development of novel statistical models for the generation of predictions e.g. [2–5 reviewed in 6]. These methods substantially improve prediction accuracy and robustness through statistical sophistication; however, they do not take into account a central biological concept, which is that no gene, or gene product, acts in isolation [7]. While it is probably true that a reductionist approach to many biological problems is likely to identify the major genetic determinants of the expression of most phenotypes, it has long been known that these major determinants receive and integrate input from a vast network of other actors, whose combined contributions influence the ultimate activity of the major determinants, or, more importantly, modify the outcome driven by the major determinants [8]. Some important signaling examples include the numerous signaling pathways which converge on p53 in determination of cell cycling and apoptosis [9], the integration of insulin, growth factor, and mitogen signaling as well as redox status and cellular energy state on mTOR and its control of translation, protein synthesis and cellular growth and proliferation [10], or the interactions between cell cycle proteins which only produce transitions from state-to-state when certain combinations of agents exist at once.

In general, the first step of model generation for the prediction of drug response from large gene expression datasets is prioritization of genes with some minimum level of correlation with the response in question. However, interacting networks cannot be expected to correlate strongly with drug response since their influence may only be observed when the major determinant of drug response and the interacting network complement one another or are both at a synergistic state. A major problem with identifying these interaction partners without a priori knowledge of the partners is the extremely large number of combinations of possible partners in the human genome, and the fact that individual genes are unlikely to accurately represent the overall state of a biological network.

Multidimensional scaling and general eigendecomposition methods have been previously used to reveal the modular organization of genetic networks [11–13]. These statistical techniques have been shown to accurately summarize the gene expression state of large networks of functionally related genes. Therefore, eigendecomposition methods should capture the overall state of the major genetic networks that may act as modifying actors for drug response. In other contexts, eigendecomposition methods have been applied to genome-wide association studies (GWAS) to reveal genetic background and population substructure among study participants that could either reflect important genetic influences on phenotypic variation or inherent genetic differences that could lead to false associations between specific genes and phenotypes [14–16]. In the case of GWAS, false positive associations are removed by identifying associations that can be explained by subtle background allele frequency differences across populations contributing to the study. For drug response prediction, our interest lies in identifying situations where the influence of a particular gene on drug response is amplified and/or dependent on the state of modifying networks extracted by principal component analysis, not confounded by them.

Toward this end, we have compared how well drug response can be predicted by simple statistical models which either directly relate probe and background networks to drug response or consider probe-by-background network interactions. Throughout this manuscript we refer to ‘probes’ as individual probes on our example Affymetrix dataset. To generalize this approach, the term ‘probe’ could be replaced by individual transcript expression levels measured through other gene expression methods. Similarly, ‘background networks’ and principal components are used interchangeably. Generally, ‘background networks’ could be represented by any data reduction method that summarizes the expression of a gene network. We demonstrate that probe-by-background network interactions significantly enhance drug response predictions, over-and-above the predictive power garnered through utilizing individual probes and background networks alone. It should be noted upfront that we do not claim the specific approach taken herein is the optimal method for these data, or any other dataset. Rather, we aim to demonstrate, through simple models, that consideration of the broader genetic context within which a drug targets a particular gene or protein is important for making accurate predictions about the response to that drug.

METHODS

MAS5 normalized Affymetrix U133A+B gene expression data (39,115 probes) for the NCI60 was downloaded from http://discover.nci.nih.gov/ [17]. Drug response data (gi50) for 99 FDA approved oncology drugs was downloaded from the Developmental Therapeutics Program website (http://dtp.nci.nih.gov/). Drug response data was filtered for the NCI60 parental cell lines, and averaged across multiple replicates. Drugs displaying little or no variation (based on standard deviation of drug response across the cell lines) in response were filtered, resulting in a total of 85 final drugs. All statistical analyses were performed with the R statistical package. Heatmaps were generated using the NeatMap package [18]. For detailed explanations regarding the data analysis approach, see Supplemental Methods.

RESULTS

Background Gene Expression

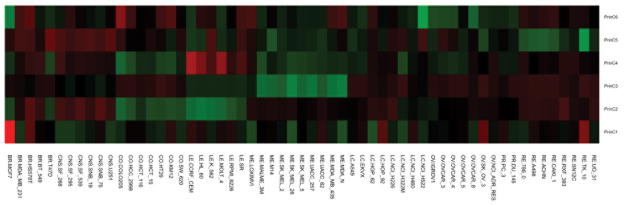
To generate the background gene expression states we performed exploratory principal component analysis (PCA) on the correlation matrix of all 39,115 probes present in the Affymetrix U133A+B data downloaded from the NCI [17]. We chose principal component analysis because it optimally captures the largest amount of variance, minimizing the number of networks (components), and thus the number of statistical comparisons, required to explore the underlying structure of the dataset. It should be noted that the assumptions made by PCA may not be optimal for this or other datasets, however we ultimately chose PCA because of its variance maximizing character, and its use in other gene expression analysis contexts appears to produce satisfactory results even when the assumption of normality is violated. Other data reduction approaches, such as independent component analysis could be readily substitute for PCA if deemed more appropriate for the underlying data structure [19]. In our case, the first component alone accounted for 81.27% of the variance; however, it is clear that this component only explains the difference between the estrogen receptor positive breast cancer cell line, MCF7, and the rest of the NCI60 cell lines (Figure 1). Most methods for determining the number of significant components (including parallel analysis, scree test, acceleration factor, and Horn’s test) suggest that only the first component is significant, yet we know this is not the case since biological significance can be assigned to the other components (see Discussion). Therefore, in order to capture further background gene expression networks, while keeping the total number of retained components (and the total number of statistical tests performed) at a minimum, we chose to retain all components explaining at least 0.5% of the variance. 6 background networks, accounting for 85.86% of the variance, were retained in this manner. Figure 1 depicts the state of each cell line with respect to each of the retained principle components. With the exception of the first principal component, the retained components appear to capture expression states that differ between the major cancer types represented in the NCI60.

Figure 1. Relationship of Background Networks to NCI60 Cell Lines.

The relationship between the background networks and each of the NCI60 cell lines is displayed as a heatmap. Each prinicipal component was normalized to a mean of zero for display purposes. For each component, cell lines with similar colors within the heatmap are associated with similar expression states of that background network. Note that principal component one strongly separates the ER+ MCF7 cell line from the rest of the cell lines, and other components tend to group cancer types together with some similarities across cancer types or for specific cell lines.

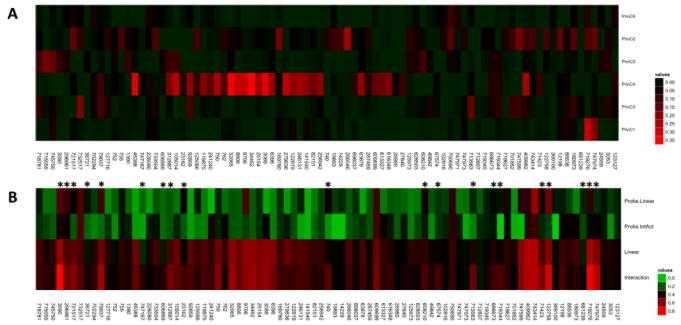
Each of the background networks captured by the 6 principal components was used as a predictor of drug response in a linear regression. Figure 2A displays the adjusted R-square value of these regressions. Drugs in figure 2 are clustered based on the correlation of their gi50 values across the NCI60 cell lines. With the exception of the 4th principal component, few strong correlations existed between the background networks and drug response. Notable correlations between background networks and drug response include: 1) background network 1 with fulvestrant (NSC 719276) and raloxifene (NSC 747974), both of which are anti-estrogen agents, consistent with the relationship of background network 1 with the MCF7 cell line; 2) background component 2 with oxaliplatin (NSC 266046) and nilotinib (NSC 747599), consistent with the separation of colorectal cancers and leukemias by background network 2; and 3) background network 4 with a range of nitrogen mustard alkylating agents (clustered mostly at the mid-left side of Figure 2A).

Figure 2. Background Networks and Drug Response Models.

A) The correlation of drug response values with the background gene expression networks is displayed as a heatmap or Adjusted R-squared values. The maximum observed correlation is 0.36 between background network 4 and uracil nitrogen mustard (NSC 34462). Other strong correlations are observed between background network 4 and other alkylating agents. Weaker correlations are observed between the other components and a single agent, whereas most agents are not strongly correlated with any background network. B) The highest adjusted R-square value attained for the directly linear (Linear) and interaction model (Interaction) is displayed. Additionally, the R-square value for the probe, in isolation, from each of the most predictive models is displayed for the directly linear (Probe.Linear) and interaction (Probe.IntAct) model is show. Drugs showing at least a 10% improvement in adjusted R-square value in the interaction models are marked with an asterisk. Comparison of rows 3 and 4 reveals an increase in predictive power when background networks are utilized. Comparison of rows 1 and 2 reveals that the probes from the interaction models showing an improvement over the directly linear models are less predictive in isolation than the most predictive probe from the directly linear models (more and brighter green cells). Note that the significance of each color differs in Figure 2A vs. Figure 2B, as depicted by the different color bars.

Probe by Background Predictions

To test whether probe-by-background network interactions significantly improve drug response predictions, we first compared the predictive power of linear regression models relating drug gi50 values to probes and background networks to models relating drug gi50 values to probes, background networks, and probe-by-background interaction terms. We accounted for overfitting effects due to the consideration of many potential models during model selection and the resulting inflation of R-squared in multiple ways: 1) we ensured the degrees of freedom of the compared models were equal by generating models with equal numbers of predictors; 2) comparison of models with differing numbers of predictors are facilitated by only considered appropriately adjusted R-squared values; and 3) ultimately the significance of each probe-by-background network interaction model was confirmed by label-shuffling permutations. Overfitting of the models themselves is not expected given the use of linear models with far fewer predictors than datapoints (3 vs. 59).

We performed fifteen linear regressions with different combinations of probes and background networks for each drug, such that three terms, one probe and two background networks, were tested (i.e., all 15 combinations of 6 background networks were tested). The model with the greatest predictive power for each drug was chosen. To identify the most predictive interaction terms in models involving each probe and background combination, models with three predictive terms, the probe alone, the background network alone, and an interaction term between the probe and background network were fit to the gi50 values of each drug. Note that in this manner, 15 tests per probe (586,725 total tests) are performed to choose the best models that do not contain and interaction term for each drug, whereas 6 tests per probe (234,690 total tests) were performed to choose the best models that include interaction terms, biasing us against identifying superior interaction models by chance, which is appropriate given that we wanted to be conservative with respect to claiming the existence of probe-by-background network interaction effects for any drug.

The results of these models are displayed in Figure 2B and Supplemental Table 1. The third row in Figure 2B contains the highest adjusted R-square value obtained per drug when a directly linear model is utilized while the fourth row contains the highest adjusted R-square value obtained when interaction models are utilized. Comparison of these two rows reveals a few standout cases of very strong predictive power involving models with probe-by-background network interaction terms vs. those without interaction terms, including citrovorum factor (NSC 3590), 13-cis-retinoic acid (NSC 122758) and fulvestrant (NSC 719276). An overall trend for greater predictive power would not necessarily be expected since many of the analyzed drugs are not “targeted” therapies; however, despite the fact that we tested 2.5-fold more models without probe-by-background network interactions, the average adjusted R-square was significantly higher for the best models that included an interaction term (paired T-test p-value = 0.001, paired Mann-Whitney test p-value = 0.02). This observation suggests that probe-by-background network interactions are more strongly predictive than probes in isolation.

If the probe-by-background network interaction is fundamentally important to driving the improvement in predictive power, rather than marginally more powerful than background networks alone, we suspect that the probe selected in the interaction models, when considered in isolation, may be less predictive than the probe selected among models without interaction terms. That is, the probe that interacts with a background network may express much of its predictive power only in the context of the background network’s expression state. Thus, we compared the predictive power of the probe selected among models that did not include an interaction terms vs. those that included an interaction term (Figure 2B first and second rows respectively). Overall, this comparison revealed no significant difference between the predictive power of the probes in the models without the interaction terms vs. the models with the interaction models (paired T-test p-value = 0.12, paired Mann-Whitney test p-value = 0.14). However, there is a clear trend towards less predictive power for the probes identified in models that included interaction terms, most likely masked by the untargeted, generally cytotoxic, agents. When only drugs with improved predictive performance under the interaction model are considered, as defined by a 10% increase in the adjusted R-squared value of the interaction vs. no interaction term models (marked by asterisks in Figure 2B), it is clear that the improvement in performance is derived from the interaction term (paired T-test p-value = 7.5·10⁻⁵, paired Mann-Whitney test p-value = 5.2·10⁻⁵). Finally, to confirm the significance of the probe-by-background interaction, we determined the significance of the interaction term by comparing the probe-by-background model to its corresponding model with the interaction term removed. ANOVA revealed that 27 of the 85 models tested had significant interaction terms at a Bonferroni corrected threshold of 0.0006 and 51 of 85 models were significant at a threshold of p-value<0.05 (Supplemental Table 1). Therefore, we conclude that it is precisely the interaction term that contributes to the improved predictability in a subset of drugs.

Significance of Interaction Models

Although we have presented a number of steps to control for overfitting, a remaining concern is that inclusion of an interaction term increases the total number of independent features considered for model selection as compared model selection performed without interaction terms. Therefore, to demonstrate that these probe-by-background network models are truly significant predictors of drug response, rather than models that happened to perform well by chance alone, we determined the empirical significance of these models through label-shuffling permutations. We shuffled the cell line identifiers for the gene expression data and background networks 1,000 times, where labels were shuffled identically in the gene expression data and background networks, and performed the same model selection procedure as described above, selecting the highest adjusted R-square value achieved per drug for each of the 1,000 permutations of data. These results were used to calculate an empirical p-value for the adjusted R-square values obtained from our analysis of the actual data. The corresponding empirical p-values for each drug are presented in Supplemental Table 1 and Figure 3. The Q-Q plot in figure 3 clearly shows the significance of these interaction models. While the models for the drugs at the lower left hand corner of the plot in Figure 3 would not be considered significant, there is a clear and large deviation from the expected distribution of p-values across all 85 drugs. Again, we would not expect all drug response predictions to improve when taking into account the state of background networks, as some drugs are non-selectively cytotoxic no matter what the state of the target cell. Regardless, over half the drugs analyzed were associated with empirical p-values less than 0.05. These results demonstrate the remarkable gains in drug response predictability achieved by accounting for the interaction between background genetic networks and individual drivers of drug response.

Figure 3. Empirical Significance of Combined Models.

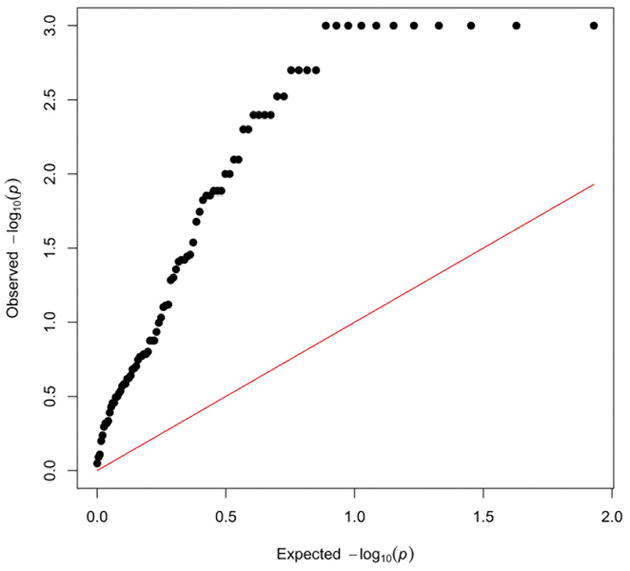
Empirical significance of the interaction models is displayed as a Q-Q plot. The maximum negative log p-value is 3.0 due to a maximum of 1,000 permutations performed. There is a clear deviation from the expected distribution of p-values (line of identity) across most of the interaction models.

DISCUSSION

The genome is composed of numerous elements which interact in complex systems to propagate exogenous and endogenous signals into a biological response. Systems biology approaches to genomic analysis attempt to reconstruct this framework of genetic elements in order to derive accurate biological conclusions, rather than attempting to derive insights on the basis of isolated parts [20]. While the ultimate goal of systems biology is to completely understand this framework in order to model biological processes, systems biology concepts can be applied without knowing the structure of the framework a priori. Rather, by simply recognizing and accepting the fact that genes act within a network, we can attempt to uncover these interactions and utilize them to enhance biological predictions.

In our review of the various approaches used to predict drug response from the NCI60 gene expression data e.g. [2–5 reviewed in: 6], all methods, as far as we could tell, relied upon weighting, or pre-selecting, genes directly correlated with drug response in some manner. While these approaches produce interesting and important results, we believe they can be much improved by taking into account indirect relationships between genes and drugs. Understandably, most genome-wide analysis strategies, of any type of genomic data, tend to ignore interactions simply due to the fact that the enormous number of combinations of possible interactions leads to a statistically intractable multiple testing problems. However, data summarization approaches, such as multidimensional scaling or the eigendecomposition/principal components approach presented here, can reduce the number of tests into a more manageable amount. Clearly, the summarization approach taken here is missing an enormous number of biologically relevant background networks. We do not claim that the six principal components used here to represent background networks reflect anywhere near the number of relevant background networks operating within the human genome, nor do we claim that the approach taken herein is the optimal for this dataset, or any other dataset, rather we simply wanted to demonstrate that even a relatively simple approach to taking into account the interaction between major background components and single gene expression levels is capable of significantly improving predictive power. One important caveat is that our approach may demonstrate gains in predictive power due to the use of an example dataset containing tumor samples of various types. That is, the PCA approach may extract fundamental differences between tumor types that drive or act as surrogates for differences in drug response, whereas global signatures predictive of drug response may not be present within a single tumor type. Although we believe our method is generally applicable, this is an important caveat to consider when applying the method to other datasets. Generally, this approach can be adapted to more sophisticated data summarization, feature selection, and model construction approaches, depending on the underlying structure of the data, in order to fully realize the gain in predictive power.

Another concern is the biological interpretation of the predictive models produced by our approach. Clearly, a list of probes correlated with drug response, and their corresponding genes, provide an easy foothold for biological interpretation. In our background network approach, we suggest that enrichment analysis can provide biological meaning to the background networks. For example, background networks 2 and 3 produced some models where the majority of the predictive power came from the probe-by-background network interaction term. If we take all probes correlated with background network 2 or 3, at an R-squared threshold > 0.6, and subject those corresponding genes to biological process enrichment analysis, we find that background network 2 is strongly correlated with genes involved in cellular adhesion and motility, while background network 3 is strongly correlated with genes involved in pigmentation and melanocyte differentiation (results not shown). These direct relationships between gene expression values and network component values are lost as the relationship between the principal components of lesser significance and the gene expression data becomes more complicated, but they can be reconstructed by considering component loadings.

A few interesting cases arose in which very large gains in predictive power were observed through consideration of gene-by-background network interactions. Nelfinavir (NSC 747167), a protease inhibitor used to treat HIV, and more recently under investigation as an anti-neoplastic agent [21], is predicted (best model: probe 222308_x_at x principal component 2) to inhibit growth of cancer cells exhibiting non-adherent growth (principal component 2) and over-expressing THOC1 (222308_x_at). THOC1, involved in splicing and nuclear export, has been shown to be important for cancer growth, especially in RAS dependent cells, though the exact mechanism remains unclear [22–23]. These observations suggest that nonadherent cells expressing THOC1 are susceptible to ER stress induced by nelfinavir. Additionally, our data lends some credence to the hypothesis that some melanomas may be susceptible to anti-estrogen treatments [24]. Our modeling predicts that anastrazole (NSC 719344), an aromatase inhibitor (best model: probe 219460_s_at x principal component 3), inhibits the growth of pigmented cancer cells (principal component 3) with lower levels of TMEM127. Melanoma cells with low TMEM127 levels display low anastrazole gi50 levels as compared to all other cell lines, including melanoma cell lines with high TMEM127 levels. TMEM127 is a negative regulator of mTOR signaling [25] suggesting a subset of melanoma cells activate mTOR signaling at least partially through estrogen signaling and may be susceptible to anti-estrogen therapy, or combined inhibition of estrogen and mTOR signaling as seen in breast cancer [26].

In conclusion, we have demonstrated the value of including genetic background effects into drug response prediction, rather than relying upon one-to-one relationships between individual probes or genes and drug response in order to identify predictive signatures of response. This approach would surely benefit from more sophisticated feature and model selection techniques, and should be explored further in order to discover even more powerful and robust signatures of response.