Potential for measurement of the distribution of DNA folds in complex environments using Correlated X-ray Scattering

Abstract

In vivo chromosomal behavior is dictated by the organization of genomic DNA at length scales ranging from nanometers to microns. At these disparate scales, the DNA conformation is influenced by a range of proteins that package, twist and disentangle the DNA double helix, leading to a complex hierarchical structure that remains undetermined. Thus, there is a critical need for methods of structural characterization of DNA that can accommodate complex environmental conditions over biologically relevant length scales. Based on multiscale molecular simulations, we report on the possibility of measuring supercoiling in complex environments using angular correlations of scattered X-rays resulting from X-ray free electron laser (xFEL) experiments. We recently demonstrated the observation of structural detail for solutions of randomly oriented metallic nanoparticles [D. Mendez et al., Philos. Trans. R. Soc. B 360 (2014) 20130315]. Here, we argue, based on simulations, that correlated X-ray scattering (CXS) has the potential for measuring the distribution of DNA folds in complex environments, on the scale of a few persistence lengths.

Correlated X-ray scattering (CXS) represents a new methodology for determining the internal atomic level structure of a monodisperse ensemble of randomly oriented molecules. An X-ray shot of a solution of randomly oriented molecules is axially symmetric about the incoming X-ray direction. In CXS, angular correlations between detector pixels with a radius of given scattering vector q contain information about the internal structure of the randomly oriented molecules.² Previous observations of local symmetries in colloidal glasses³ successfully applied the CXS technique. Recent work on metallic nanoparticles¹ shows the feasability to extract three-dimensional structural detail beyond the low resolution data of small-angle X-ray scattering. Here, we report on simulations of the expected correlations for a solution containing short lengths of DNA of order of a couple of persistence lengths which show characteristic features associated with the double-helical structure of DNA.

For a given q, the scattering signal n(q, ϕ) arriving on pixel (q, ϕ) of an area detector is made up of two components: a component n_u(q, ϕ) due to scattering events from individual molecules in the ensemble and a component n_c(q, ϕ) due to events where more than one photon scatters from the same individual molecule in the ensemble.

The determination of the internal structure of the molecule is attained by computing the angular correlator C(q, δϕ) around a given q-ring on the detector. The correlator of scattering intensities n(q, ϕ), n(q, ϕ − δϕ) is defined by

$$C(q,\delta \varphi )=n(q,\varphi )\otimes n(q,\varphi -\delta \varphi )\equiv \frac{1}{N_{\varphi }(q)}\sum _{\varphi }^{N_{\varphi }(q)}(n(q,\varphi -\delta \varphi )-\overline{n}(q))(n(q,\varphi )-\overline{n}(q)),$$ (1)

where n̄(q) denotes the angular average of n(q, ϕ) around the ring of wave vector q. The average of the correlator over the illuminated ensemble 〈(n_u + n_c) ⊗ (n_u + n_c)〉 then contains a term (n_u ⊗ n_u + n_u ⊗ n_c + n_c ⊗ n_u) from the uncorrelated scattering events, superposed on the correlator (n_c ⊗ n_c) from the multiphoton scattering events.

The computed correlator for the uncorrelated events generates Gaussian random noise at each pixel around the ring. As shown by Kirian et al.,⁴ the sum of this term over many snapshots of the ensemble in which each shot contains a different set of the molecular orientations, will have magnitude of order $\sqrt{N}$ where N is the number of shots. This is to be considered relative to the sum over the correlators for the multiphoton scattering events, which scales as N. Hence for large N, the sum over the correlators for N X-ray shots converges toward the correlator of the constituent molecules. In Ref. 1, we showed that we could experimentally verify this convergence for around 10,000 shots of randomly oriented samples of silver nanoparticles. For the case of the silver nanoparticles, we were able to show that the average correlator may be represented by a model of the silver nanoparticles as an FCC lattice contained within a sphere of nanoparticle size (20 nm).

For the case of DNA, we have computed the expected correlated scattering for various lengths of DNA up to around of order 2 persistence lengths (50 nm) by computing the scattering function S = | Σ _i f_i exp(iq · r_i)|² (where r₁ and f_i are the atomic positions and scattering structure factors), averaged over 30,000 random orientations for the three Euler angles of the molecule. (For an overview of the q-dependence of the correlated scattering, see Fig. 1.) These calculations reveal the pronounced effect of thermal fluctuations on the correlated scattering. Near q = 0, where the length scale probed in the scattering experiment is much larger than the length of the DNA, all systems exhibit correlated scattering that is independent of the angle between the scattering wave vectors, reflective of the fact that at length scales much larger than the size of the molecule, all molecules scatter as isotropic point particles. As q increases, the anisotropic configurations of the DNA molecules is revealed by the gradual evolution of peaks centered at 0 and π radians. Such a signature can be expected for a rod-like structure with longitudinally correlated density fluctuations. The q at which the rod-like scattering emerges is characteristic of the thermodynamic persistence length of the ensemble with the stiffest molecules exhibiting orientational order at the lowest values of q. The effect of thermal fluctuations is further captured in the dependence of the correlation function on the persistence length, l_p, at fixed q shown in Fig. 2. As the DNA stiffness is softened, the amplitude of the peak at π radians relative to the value at π/2 is progressively dampened, presumably due to enhanced transverse fluctuations of the polymer away from the principal longitudinal axis. The correlator thus contains both the thermodynamic persistence length of the ensemble, as well as quantitative details of the spatial density distribution that arises due to thermal fluctuations. At low to intermediate q, the correlated scattering thus has a characteristic peak around π radians which is characteristic of a rod-like scattering.

Fig. 1.

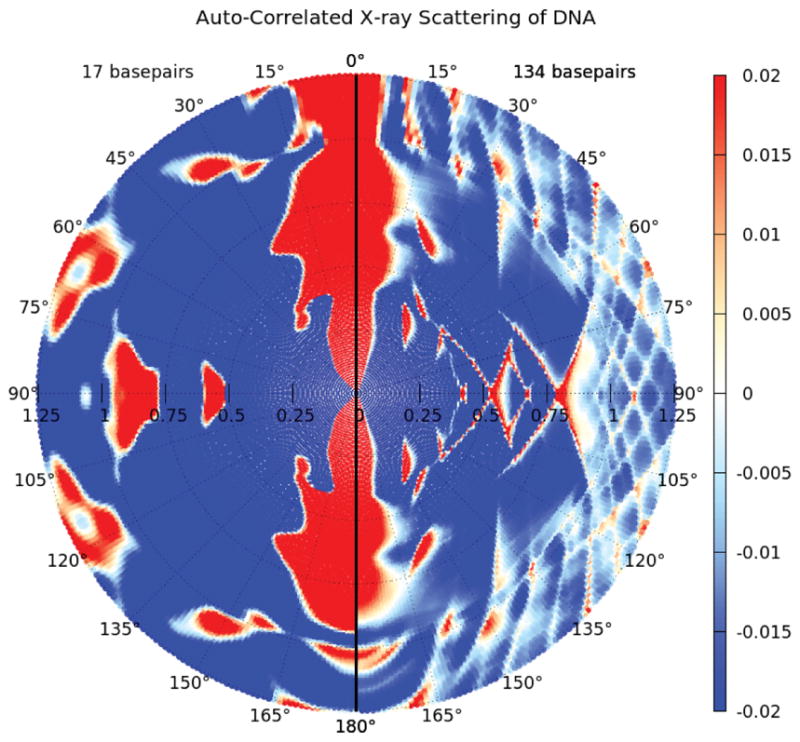
(Color online) Dependence of the correlated X-ray scattering (CXS) on the DNA double-helix length. The CXS is averaged over intensities of 30,000 simulated orientations of two rigid B-form molecules (left: 17 bp and right: 134 bp), respectively.

Fig. 2.

(Color online) Small angle CXS: Effect of thermal flexibility on angular correlated X-ray scattering around the Bragg ring at q = 0.05 nm⁻¹ in 294 bp long (L = 100 nm) DNA molecules modeled as worm-like chains with persistence lengths, l_p. Scattering calculations are averaged over 30,000 molecular fluctuations generated by equilibrium Monte Carlo simulations. The correlator is normalized to its value at 0 radians to show the relative prominence of the peak. A soft X-ray beam energy of 124 eV was assumed for projection onto the two-dimensional detector.

To a good approximation, at low to intermediate q, a linear DNA molecule subject to thermal fluctuations can be described by the Kratky–Porod worm-like chain (WLC) model.⁵ In the spirit of linear elasticity theory, the spatial configuration of the double-helical axis is modeled by a bending free energy, H, that is quadratic in the local curvature. That is

$$\frac{H}{k_{B}T}=\frac{l_p}{2}\int ds{\left(\frac{\partial \mathbf{u}}{\partial s}\right)}^2,$$ (2)

where u denotes the local orientation of the double-helical axis and s is a contour length parameter that spans the length of the double-helical axis. The conformation statistics of an ensemble of DNA molecules modeled as a WLC are completely determined by the thermodynamic value of l_p, which defines the characteristic length scale over which correlations in polymer orientation along the chain decay due to thermal fluctuations. Under physiological salt conditions and temperature, double-stranded DNA is quite stiff with a persistence length of about 50 nm (150 base pairs). However, the persistence length of double-stranded DNA is rather sensitive to its electrostatic environment with persistence lengths that can range from about 30 nm to 350 nm, depending on the concentration of monovalent salt and the presence of multivalent ions.

With this in view, in order to estimate the influence of flexibility on the correlated scattering, we have performed Monte Carlo simulations of the dependence of the correlated scattering on the momentum transfer q. We show in Fig. 2 the dependence of the correlated scattering on the thermodynamic persistence length of an ensemble (30,000 molecules) of 300 bp DNA fragments in the low to intermediate q regime. These simulations give a measure of the persistence length dependence of the correlated scattering from simulated WLC DNA ensembles with persistence lengths ranging from 20 nm to 170 nm. These results in turn suggest that for a sample with a distribution p(l) of persistence lengths, a fit to the measured correlated scattering can allow for a determination of the probability distribution p for the persistence length in the sample.

Because we are measuring correlations, we have been able to show that the presence of uncorrelated scattering from other molecules which are not bound to the DNA tends to be canceled out in an ensemble average. We have done a very simple test by looking at simulations of expected correlated scattering from DNA in the presence of two lysozyme molecules randomly placed in the vicinity of the DNA. We were able to identify the length of the DNA molecule used in the simulations by calculating Pearson’s correlation coefficient of the correlated scatterings (see Table 1). As shown by these results, the uncorrelated scattering from the additional molecule did indeed cancel out and did not show up in the simulated correlation scattering. We are not claiming our simple test reflects the very complicated crowding effects found inside a living cell. But it should be noted that even for very small DNA pieces (large relative component from lysozyme), the remaining correlated scattering signal of the weighted mixture components⁶ comprises the dominant DNA signature.

Table 1.

Pearson’s correlation coefficient for correlated scattering from DNA in the presence of lysozyme.

Pearson	17 bp + Lys	32 bp + Lys	124 bp + Lys
17 bp	0.945	0.935	0.732
32 bp	0.974	0.989	0.854
124 bp	0.819	0.851	0.998

These considerations lead us to consider the possibility of making measurements of DNA scattering in bacteria in vivo. One of the major determinants of in vivo chromosomal behavior is the function of topoisomerases that twist and disentangle the DNA double helix, leading to supercoiling of the DNA strand. The disruption of topoisomerase activity results in altered gene expression and cell death. Thus, the supercoiling of DNA under biological conditions is an important feature for the machinery regulating transcription. Considerations by Hong et al.⁷ suggest that the conformations of bacterial chromosomes are strongly modified by supercoiling. Use of correlated scattering on intact bacteria could be a way to study supercoiling in vivo. (This would need a compact sample with many bacteria in order to get adequate signal.) Such measurements could provide a significant contribution toward the understanding of the mechanisms of gene expression in bacteria.

All these considerations are subject to the availability of X-ray lasers as a source for X-ray scattering. As discussed above, the important component in an X-ray scattering experiment to look for correlations is that the probability of finding pairs of correlated scattering events from the same molecule within the ensemble of orientations is sufficiently large. In that limit, the relative background suppression by averaging over many shots of differently disordered samples is greatly increased by using an X-ray laser since the fluence of the X-rays on the individual molecule can be big enough for the probability for multiphoton scattering events to be considerably enhanced relative to the probability for single scattering events which form the uncorrelated background.