Two-photon quantum walk in a multimode fiber

Control of a two-photon quantum walk in a complex multimode system by wavefront shaping.

Abstract

Multiphoton propagation in connected structures—a quantum walk—offers the potential of simulating complex physical systems and provides a route to universal quantum computation. Increasing the complexity of quantum photonic networks where the walk occurs is essential for many applications. We implement a quantum walk of indistinguishable photon pairs in a multimode fiber supporting 380 modes. Using wavefront shaping, we control the propagation of the two-photon state through the fiber in which all modes are coupled. Excitation of arbitrary output modes of the system is realized by controlling classical and quantum interferences. This report demonstrates a highly multimode platform for multiphoton interference experiments and provides a powerful method to program a general high-dimensional multiport optical circuit. This work paves the way for the next generation of photonic devices for quantum simulation, computing, and communication.

INTRODUCTION

In a random walk process, the walker chooses which path to take on the basis of the toss of a coin. Quantum walkers also randomly choose which path to follow but maintain coherence over the paths taken. This simple phenomenon lies at the core of simulating condensed matter systems, quantum-enhanced search algorithms, and universal models of quantum computation (1, 2). Single walker quantum dynamics, which can be understood in terms of classical wave evolution, have been explored by using several physical platforms including atomic systems (3, 4) and photonics (5–10). Quantum walks and their applications become more complex with additional walkers and cannot be understood using only classical wave propagation. For example, quantum walks with entangled photons (11) have led to simulation of Anderson localization and Fano resonances mimicking fermionic-like systems (12). Further attention has been devoted to the computational complexity of multiphoton quantum walks, which has the potential to demonstrate an undisputed quantum advantage through the boson-sampling algorithm (13–19). Integrated optical circuits permitting nearest-neighbor coupling between a few tens of modes have been the key technology used in the nascent field of multiphoton quantum walks (20–22). Here, we explore an alternative route to high-dimensional mode coupling by harnessing the multimode nature of random media. Coherent wave propagation through a disordered medium results in a speckle pattern arising from the highly complex multiple scattering process. Propagation in such a complex environment represents a quantum walk because each scattering event redistributes the photons in different optical modes. Whereas the propagation of nonclassical states of light through such media has been explored theoretically and experimentally (23–27), these investigations have yet to realize the full potential of quantum walks, which require the ability to prepare arbitrary input states of the walkers. A paradigm shift has occurred in the last few years in which digital wavefront shaping has emerged as a powerful approach to manipulate light propagation through complex media (28). This has had a significant impact on a wide range of research including biomedical imaging, optical sensing, and telecommunications (29–31).

Whereas controlled propagation of single-photon states through random media has been recently demonstrated (32–34), scaling this approach to multiphoton states is challenging because of the exceptionally high number of spatial and spectral modes of a diffusive medium. Multimode fiber (MMF) provides a platform that delivers a sufficiently large number of coupled modes (35) to demonstrate a new regime of modal capacity for quantum light, yet the number of modes is small enough to enable controllable propagation using techniques developed with classical light. Strong and complex multimode coupling in the fiber arises from interference between a well-defined number of spatial modes supported by the fiber. Moreover, the use of MMF for quantum applications is enhanced by the near-lossless optical propagation along the fiber. In this system, photons are continuously redirected during their propagation through coupling between modes, thus undergoing a continuous-time quantum walk (11). Here, we marry the highly multimode coupling power of MMF with wavefront shaping techniques to realize a programmable linear-optical network for quantum optical technologies. As an initial demonstration of this approach, we show that two-photon propagation through this highly multimode device can be controlled by shaping the wavefront of each photon on the input of the MMF.

RESULTS

Here, we report the results of a two-photon quantum walk experiment using an 11-cm graded-index MMF with a 50-μm core diameter supporting approximately 380 transverse spatial and polarization modes at 810 nm. For our investigation, we use the experimental setup depicted in Fig. 1. Two orthogonally polarized degenerate narrowband photons derived from a spontaneous parametric down conversion (SPDC) source (see Methods) are launched into an MMF. Before entering the MMF, each photon is individually shaped by spatial light modulators (SLM V and SLM H) to control its transverse spatial profile. Varying the path length difference δ between the individual photon paths by means of a translation stage adjusts their relative arrival time to the MMF. This enables partial control over the distinguishability of the two photons (see the Supplementary Materials). While light propagates through the fiber, polarization and spatial modes mix and an unpolarized speckle pattern is observed at the output. The emerging light from the MMF is polarized by means of a polarizing beam splitter (PBS) and then analyzed by either an imaging electron-multiplied charged-coupled device (EMCCD) or a pair of avalanche photodiodes (APDs) coupled to polarization-maintaining single-mode fibers (PMSMFs), mounted on translation stages.

Fig. 1. Apparatus to control the propagation of photon pairs through an MMF.

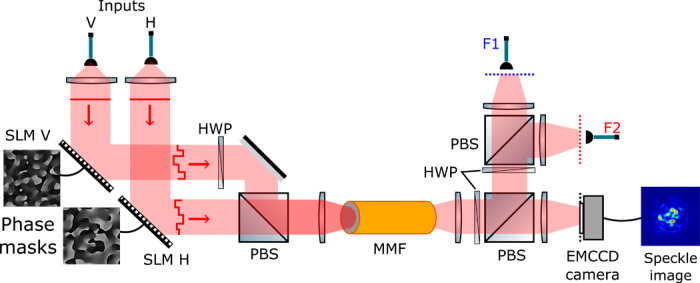
Photon pairs from a SPDC source (not shown) are injected in a graded-index MMF (50-μm core diameter) with orthogonal polarizations. Two SLMs (SLM H and SLM V) are used to shape the transverse spatial waveform of each photon. Output light is monitored by an EMCCD camera and two PMSMFs, F1 and F2, connected to APDs all imaging the output plane of the MMF. A half-wave plate and a PBS positioned just after the MMF permit selection of one specific polarization of the output field.

Reconstruction of a two-photon transmission matrix

To demonstrate the capacity of an MMF for multimode, multiphoton quantum optics, we first characterize the propagation of photon pairs by recording the two-photon transmission matrix (TTM) of the system. Different two-photon input states are prepared by programming the SLMs to excite different transverse input modes of the MMF (Fig. 2A). Direct measurements made using the EMCCD camera presented in Fig. 2B show how each photon is delocalized over approximately 50 independent output speckle grains. The overall intensity distribution is the incoherent sum of each individual photon intensity profile and is independent of the indistinguishability of the photons. Intensity correlations are measured by coincidence detection events between the two output SMFs, which can be positioned at two different locations in the output image plane denoted by {|X₁〉, |X₂〉} and {|Y₁〉, |Y₂〉} for fiber 1 (F1) and fiber 2 (F2), respectively. We measure a 16 × 4 coincidence matrix in Fig. 2B by scanning four orthogonal input transverse spatial states for each photon, set by the SLMs, and measure the corresponding coincidence rates at four pairs of output fiber positions. The so-called TTM reconstructed here characterizes the propagation of photon pairs through the MMF between the selected states taking into account the classical and quantum interferences occurring in the fiber.

Fig. 2. Experimental measurement of the TTM.

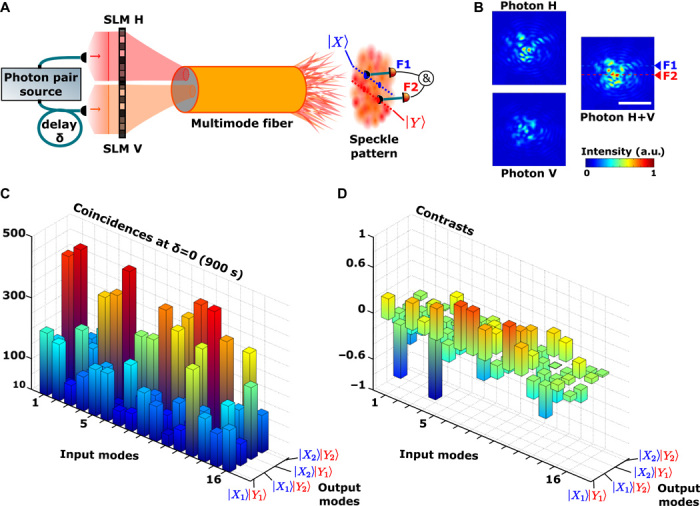
(A) Schematic of the experimental setup using a two-photon state injected into two different transverse spatial modes. (B) Recorded intensity images of the corresponding output speckle patterns for photon H only, photon V only, and H+V simultaneously, containing about 50 independent speckle grains. The scale bar represents 25 μm in the output plane of the MMF. The H+V speckle pattern corresponds to the incoherent sum of each individual case. (C) Coincidence detection patterns between F1 and F2 reconstructed for 16 two-photon input states programmed by the SLMs. F1 and F2 scan four output coincidence positions denoted |X₁Y₂〉, |X₁Y₂〉, |X₁Y₂〉, |X₁Y₂〉. The 16 × 4 coincidence matrix measured here represents a subset of the complete TTM that consists of approximately (380 × 380)² elements. (D) For the same 16 × 4 elements, the differences observed in coincidence patterns measured with distinguishable (δ = 0.4 mm) or indistinguishable (δ = 0) photons are quantified by reconstructing the nonclassical contrast matrix. A contrast is given by the formula C = (R_δ=0 − R_{δ=0.4 mm})/R_{δ=0.4 mm}, where R_δ is the coincidence rate of a two-photon output state at a path length difference of δ. This matrix is a clear signature of quantum interference effects occurring in the MMF. Coincidences are monitored for 900 s with a coincidence window of 2.5 ns.

The measured intensity correlations are modified when the distinguishability of the two photons is adjusted from indistinguishable (δ = 0) to distinguishable (δ = 0.4 mm), while each individual intensity profile remains unchanged. This signature of two-photon quantum interference is analogous to the Hong-Ou-Mandel effect (36). Quantitative analysis of this two-photon inference is conducted by calculating the nonclassical contrast for each input-output configuration (Fig. 2D). The nonclassical contrast is defined as C = (R_δ=0 − R_{δ=0.4 mm})/R_{δ=0.4 mm}, where R_δ=0 (R_{δ=0.4 mm}) is the two-photon coincidence rate at zero (0.4 mm) path length difference between input photons; the classical bound on the magnitude contrast is 0.5. These results demonstrate that the quantum coherence between the photons is robust under propagation through the MMF, which acts as a high-dimensional multimode platform for quantum interference.

Control of photon-pair propagation

To control the multiphoton interference in the MMF, we adopt the wavefront shaping technique used for imaging through opaque systems that utilizes phase-only SLMs (28–31, 37). This technique exploits the strong and complex mode mixing that occurs inside the disordered system to manipulate the classical field at the output. The approach used by Popoff et al. (37) to control the propagation of classical light through a multimode scattering medium can be generalized to control the propagation of two photons through the TTM associated with a random medium. The coincidence matrix reported in Fig. 2 represents direct estimates of a small subset of 64 elements of the TTM. However, given the large number of modes (approximately 380) supported by the MMF, a more convenient approach is to calculate the TTM from the transmission matrix (TM) of the MMF, which can be measured with greater precision using classical light (see Methods). Following this approach using the calculated TTM, two SLM configurations are found to optimize the coincidence rate of the targeted state ${\widehat{\mathit{a}}}_{|{\mathit{X}}_2\rangle }^{+}{\widehat{\mathit{a}}}_{|{\mathit{Y}}_3\rangle }^{+}|0\rangle$, where |X₂〉 and |Y₃〉 are two arbitrarily chosen positions in the output plane.

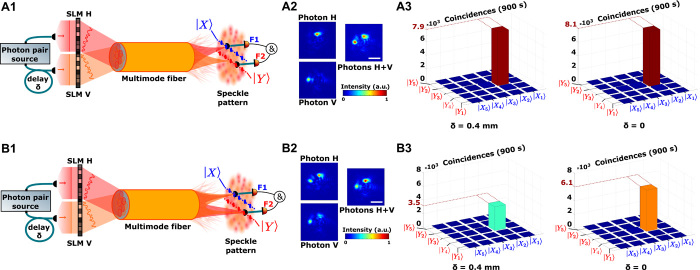
In the first configuration, the SLMs are programmed to focus photon H at output position |X₂〉 and, independently, photon V at output position |Y₃〉. The EMCCD camera images (Fig. 3A2) show strong localization of the photons at the two targeted positions. The focusing process is confirmed with the intensity correlations measured by the APDs coupled to SMFs, where the coincidence pattern shows a pronounced spike in the coincidence count rate when the collection fibers are set at these positions (Fig. 3, A2 and A3). Because each photon is directed independently to a different output, we do not observe significant changes in the coincidence rate when moving from the distinguishable (δ = 0.4 mm) to the indistinguishable case (δ = 0).

Fig. 3. Focusing photon pairs in a targeted two-photon output state of the MMF.

(A1 to A3) The first configuration (A1) directs photon H to output position |X₂〉 of F1 and photon V to output position |Y₃〉 of F2. This is visible in the direct images measured using the EMCCD camera (A2). Coincidence profiles (A3) are measured for 25 coincidence output fiber position pairs. Coincidence rates in the targeted two-photon state ${\widehat{\mathit{a}}}_{|{\mathit{X}}_2\rangle }^{+}{\widehat{\mathit{a}}}_{|{\mathit{Y}}_3\rangle }^{+}|0\rangle$ are about 100 times higher than the background, for both distinguishable and indistinguishable photons. (B1 to B3) The second configuration (B1) corresponds to photon H being prepared in a superposition of output states |X₂〉 and |Y₃〉 with a relative phase ϕ_H = 0 and photon V directed to a superposition of the same output states with a relative phase ϕ_V = 0. Direct images measured with the EMCCD confirm that both photons are directed to the two output states (B2). The effect of nonclassical interference is shown on the output coincidence speckle patterns (B3), where we observe an increase of 72% in the coincidences rate in the state ${\widehat{\mathit{a}}}_{|{\mathit{X}}_2\rangle }^{+}{\widehat{\mathit{a}}}_{|{\mathit{Y}}_3\rangle }^{+}|0\rangle$ in the indistinguishable case (δ = 0) compared to the distinguishable case (δ = 0.4 mm). Coincidence measurements are acquired for 900 s with a coincidence window of 2.5 ns. The white scale bars represent 25 μm in the output plane of the MMF.

In the second case, each photon is prepared in a superposition of these two output positions (Fig. 3B1). SLM H (SLM V) is programmed to direct photon H (V) in a superposition of output states |X₂〉 and |Y₃〉 with a controlled relative phase ϕ_H (ϕ_V), that is, $|{\mathit{X}}_2\rangle +{\mathit{e}}^{\mathit{i}{\mathrm{\varphi }}_{\text{H}}}|{\mathit{Y}}_3\rangle$ ($|{\mathit{X}}_2\rangle +{\mathit{e}}^{\mathit{i}{\mathrm{\varphi }}_{\text{V}}}|{\mathit{Y}}_3\rangle$). The EMCCD camera images (Fig. 3B2) confirm that each photon is delocalized on the two targeted output spatial regions. In this configuration, multiple paths can lead to coincidence detection of a photon at output positions |X₂〉 and |Y₃〉, in which photon H arrives at |X₂〉 and photon V at |Y₃〉 or vice versa. If these outcomes are indistinguishable, then quantum interference between the multiple paths occurs. When the SLM sets the phase condition ϕ_H = ϕ_V, the multiple paths will interfere constructively. As shown in Fig. 3B3, we observe an increase in the coincidence rate of 72% for indistinguishable photons (δ = 0) compared to distinguishable photons (δ = 0.4 mm), whereas single counts remain unaffected. Our method enables the output two-photon state to be prepared in a well-controlled superposition of the two targeted output spatial states by exploiting both classical and quantum interferences.

Complete control over quantum interference between the two photons is presented in Fig. 4. Nonclassical contrast measurements performed for 64 different relative phases settings (ϕ_H, ϕ_V) are presented in Fig. 4A. Photon pairs interfere constructively, leading to a photon bunching effect, when ϕ_H = ϕ_V, and destructively when ϕ_H = ϕ_V ± π. By scanning the path length difference between the two photons for three specific phase settings, (ϕ_H, ϕ_V) ∈ {(0, 0), (0, π), (0, π/2)}, we retrieve three HOM-like plots (Fig. 4B) displaying a peak (green), a dip (red), and flat line (blue). We thus demonstrate the possibility to distribute both photons into two arbitrary output states of the system with complete control over the coupling parameters.

Fig. 4. Deterministic control of quantum interferences.

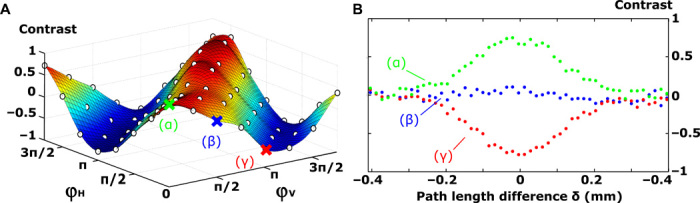
(A) Nonclassical interference contrast measured for two photons mapped onto a superposition of two output states with different phase settings (ϕ_H, ϕ_V). The nonclassical contrast is defined as C = (R_δ=0 − R_{δ=0.4 mm})/R_{δ=0.4 mm}, where R_δ is the two-photon coincidence rate of the targeted output state ${\widehat{\mathit{a}}}_{|{\mathit{X}}_2\rangle }^{+}{\widehat{\mathit{a}}}_{|{\mathit{Y}}_3\rangle }^{+}|0\rangle$ at a path length difference of δ. Contrast values are measured with 8 × 8 = 64 phase settings. (B) Contrast values for three phase settings [(α), (ϕ_H = 0, ϕ_V = 0); (β), (ϕ_H = 0, ϕ_V = π/2)_; (γ), (ϕ_H = 0, ϕ_V = π)] as a function of the path length difference between input photons δ. The observed effects are consistent with the initial indistinguishability of the photons evaluated with a HOM experiment (see the Supplementary Materials). Data are acquired for 290 s with a coincidence window of 2.5 ns.

DISCUSSION

Platforms for multimode interference of multiphoton states hold promise for a variety of quantum applications. A key experimental challenge with this approach lies in scaling up the number of modes and photons involved in such experiments. Here, we present a technique that uses knowledge of the TM of an MMF combined with wavefront shaping methods to demonstrate control of two-photon interference in a set of selected output spatial states. Our results show that this system has the potential for a programmable multimode optical network (38), establishing MMFs as a reconfigurable, high-dimensional platform for multiphoton quantum walks. The low loss, stability, and scalability of this device indicate its potential for realization of quantum walks in regimes where classical verification is challenging. Moreover, photonic lanterns (39) could permit simple and efficient interfacing of the MMF with a large array of detectors. The use of broadband nonclassical sources combined with recently developed spatiotemporal wavefront shaping techniques (40, 41) provides additional degrees of freedom to increase the number of modes that can be addressed and extend the possibilities for quantum information processing. During the publishing process, a new work relative to photon pairs propagation and control in disordered media has been reported by Wolterink et al. (42).

METHODS

Experimental details

Photon pairs were generated by a type II SPDC process. A 10-mm periodically poled potassium titanyl phosphate (PPKTP) crystal pumped with a 25-mW continuous-wave laser diode at 405 nm produced pairs of frequency-degenerate photons at 810 nm. Both photons were spectrally filtered using narrowband interference filters centered at 810 nm [full width at half maximum bandwidth (FWHM), 1 nm]. A two-photon interference contrast of 86% was measured by performing a Hong-Ou-Mandel interference experiment using a balanced beam splitter (see the Supplementary Materials).

The classical source used to record the TM was a superluminescent diode (SLED) with a 20-nm bandwidth spectrum centered at 810 nm. The source was filtered with the same narrowband filter (FWHM, 1 nm) used with the SPDC source. Both sources were coupled to the wavefront shaping apparatus using PMSFMs and could be easily swapped.

A phase-only liquid-crystal SLM was subdivided in two independent parts, denoted SLM H and SLM V. Each part had an active area of 8 × 9 mm² and a resolution of 960 × 1080 pixels.

A graded-index MMF with a 50-μm core diameter and an 11-cm length (reference number: GIF50C, from Thorlabs) was used in the experiments. This MMF carried about 380 optical modes. Its properties had been chosen to neglect temporal dispersion effects, and light propagation could be considered quasi-monochromatic (see the Supplementary Materials).

TM measurement

The input face of the MMF and the SLM plane were Fourier-conjugated by a lens of focal length f = 20 mm (Fig. 1). When a phase ramp was programmed on the SLM, a diffraction-limited spot of light was focused at a specific position on the MMF input face. At the output of the MMF, intensity speckle patterns were acquired using both an EMCCD camera and two PMSMFs coupled to APDs. The TM was reconstructed by recording output fields with a phase-stepping holographic method for different positions of the focused spot. Each input mode corresponds to a certain position of the focused spot—or, in an equivalent way, a certain phase ramp pattern on the SLM—and an output mode was defined either as the spatial mode of one of the PMSMFs or as an EMCCD camera pixel. In this experiment, the TM was measured for both input polarizations by programming 180 spatial modes on SLM H and 190 spatial modes on SLM V, leading to a total of N = 370 modes. At the end of the process, the TM was projected onto the SLM on a pixel basis using matrix multiplication.

Controlling photon-pair propagation using the TTM

The TTM matrix was calculated from the measured TM. By analogy to the method described by Popoff et al. (37), the transpose conjugate of the TTM was used as an inverse operator to determine the two-photon input field that allowed focusing photon pairs into output state ${\widehat{\mathit{a}}}_{|{\mathit{X}}_2\rangle }^{+}{\widehat{\mathit{a}}}_{|{\mathit{Y}}_3\rangle }^{+}|0\rangle$. The two SLM configurations presented in Fig. 3 are equivalent solutions of the inverse process maximizing the coincidence rate in ${\widehat{\mathit{a}}}_{|{\mathit{X}}_2\rangle }^{+}{\widehat{\mathit{a}}}_{|{\mathit{Y}}_3\rangle }^{+}|0\rangle$ under our experimental constraints (see the Supplementary Materials).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/1/e1501054/DC1

Experimental details

Controlling the two-photon field using the two-photon transmission matrix.

Validation of the experimental data

Table S1. Statistical analysis of experimental data presented in Fig. 3.

Fig. S1. Characterization of the photon-pair indistinguishability by the Hong-Ou-Mandel experiment.

Fig. S2. Dispersion characterization through the MMF.

Fig. S3. Statistical analysis of experimental data represented in Fig. 2.

Fig. S4. Statistical analysis of experimental data presented in Fig. 4.

References (43, 44)