Transient lattice contraction in the solid-to-plasma transition

Ultrafast x-ray heating of clusters leads to bond contraction in the solid-to-plasma transition.

Abstract

In condensed matter systems, strong optical excitations can induce phonon-driven processes that alter their mechanical properties. We report on a new phenomenon where a massive electronic excitation induces a collective change in the bond character that leads to transient lattice contraction. Single large van der Waals clusters were isochorically heated to a nanoplasma state with an intense 10-fs x-ray (pump) pulse. The structural evolution of the nanoplasma was probed with a second intense x-ray (probe) pulse, showing systematic contraction stemming from electron delocalization during the solid-to-plasma transition. These findings are relevant for any material in extreme conditions ranging from the time evolution of warm or hot dense matter to ultrafast imaging with intense x-ray pulses or, more generally, any situation that involves a condensed matter-to-plasma transition.

INTRODUCTION

In condensed matter systems, electronic configurations determine structural geometries. For the general, static case, electrons form bonds and the atoms arrange themselves in positions to minimize the potential energy of the system. In the classical melting process, the vibrational motion of atoms becomes significant compared to their interatomic distance, resulting in continuous electronic reconfiguration (1, 2).

In recent years, new phenomena have been reported where a strong optical excitation of the bulk crystal leads to opposite extremes of nonthermal melting (3, 4) or bond hardening (5). In both cases, the valence electrons are promoted to the conduction band, modifying the interatomic potential energy landscape. Subsequently, the excitation energy is transferred to phonon modes. The optical excitation drives the mechanical properties of the system, but on the femtosecond time scale, the overall geometrical properties remain unchanged. The phenomenon we present is an intrinsically different case of collective change in the bond character, which is induced through electron delocalization during a solid-to-plasma transition. This leads to a transient lattice contraction on time scales comparable to charge transfer processes.

RESULTS

The experimental concept is summarized in Fig. 1A and is described in more detail in the Supplementary Materials. First, an intense 10-fs x-ray pulse isochorically heats a 70-nm xenon cluster (<N> ~3 × 10⁶ atoms) to a nanoplasma state. Only the initial few percent of the photoelectrons and Auger electrons can leave the cluster, whereas the remaining electrons are trapped in the increasingly deep Coulomb potential, forming a quasineutral solid-density nanoplasma (6). The trapped photoelectrons and Auger electrons thermalize within femtoseconds, with electron temperatures of a few hundred electron volts (see the Supplementary Materials), but the energy transfer from the hot electron gas to the ions is orders of magnitude slower (7). The transition from a solid, neutral cluster to a nanoplasma is depicted in Fig. 1, B to C. In the neutral cluster, electrons are localized at the atoms in the van der Waals system. Upon heating, the electrons are promoted to highly excited states in the deep nanoplasma Coulomb potential. Although these electrons are hot, they are quasi-free and share characteristics with a free-electron gas. The structural evolution of the nanoplasma is probed with Bragg scattering from a second x-ray pulse delayed by 15 to 80 fs (8) as described in the Supplementary Materials.

Fig. 1. Experimental scheme for the solid-to-plasma transition in xenon nanoclusters.

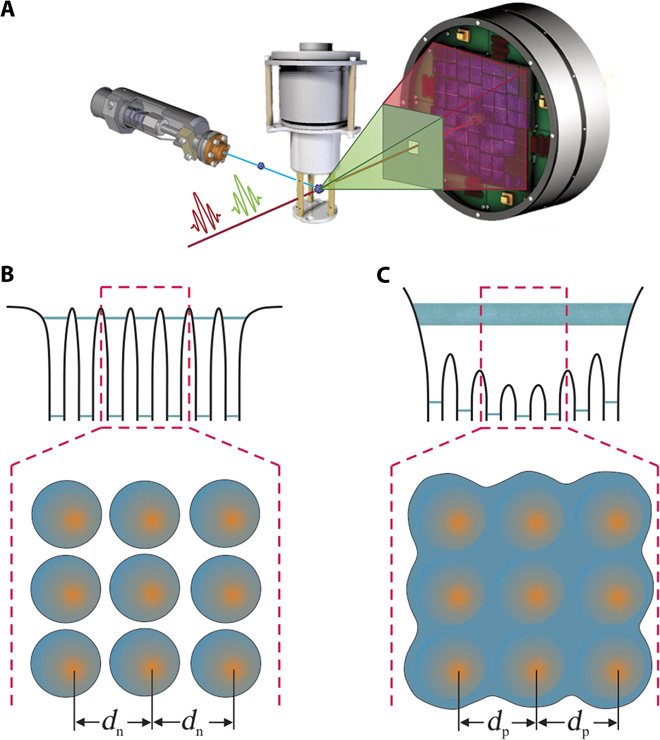
(A) An initial 10-fs hard x-ray pulse ionizes the Xe cluster and forms a nanoplasma. A second 10-fs x-ray pulse at slightly lower photon energy measures geometrical and electronic properties of the plasma. Bragg peaks are recorded on an x-ray detector placed behind a nickel filter that absorbs photons from the initial x-ray pulse but is transparent to photons from the probe pulse. Coincident ion spectra are recorded with a TOF spectrometer. (B) Electrons are highly localized in the initial van der Waals cluster, forming an ordered crystal lattice with a well-defined neutral atomic spacing (d_n). (C) During the nanoplasma transition, the highly excited electrons become delocalized in the deep Coulomb potential, affecting the overall lattice geometry with a new plasma spacing (d_p).

The lattice geometry in the nanoplasma can be inferred from the positions of the Bragg peaks on the detector. Neutral xenon clusters can form simple face-centered cubic (fcc) and hexagonal close-packed (hcp) lattices (9), and our analysis focuses strictly on single-grain fcc particles (see the Supplementary Materials). The femtosecond time-resolved data indicate a lattice contraction during the solid-to-plasma transition. In Fig. 2A, the (220) fcc Bragg peaks are shown as a function of pump-probe delay (0-, 60-, and 80-fs delays) for single particles. For the control data set, with no delay, the (220) Bragg peak has a momentum transfer q of 2.928 Å⁻¹. With this q value, the average length of the fcc unit cell is determined by $\mathit{a}=\frac{2\mathrm{\pi }}{\mathit{q}}\sqrt{{\mathit{h}}^2+{\mathit{k}}^2+{\mathit{l}}^2}$, where h, k, and l are the Miller indices, here given by 2, 2, and 0. Thus, the (220) Bragg reflection from the 0-fs delay data set corresponds to a Xe nanocluster with a unit cell length of 6.07 Å, which agrees well with the previously measured xenon fcc lattice constant (10). As the delay is increased between the x-ray–x-ray pump–probe pulses, the (220) Bragg peak systematically shifts to higher q (higher scattering angle). This shift is indicative of a collective x-ray–induced lattice contraction (see Fig. 2B). Within 80 fs, the (220) Bragg peaks shifts to a q value of 3.010 Å⁻¹, indicative of a unit cell length of 5.90 Å or lattice compression of ~0.17 Å (~3%). A very similar trend is observed while tracking the (111) fcc peak. The average lattice compression measured from the (111) and (220) fcc peaks is ~0.2 Å in 80 fs.

Fig. 2. Evidence for atomic motion on the few-femtosecond time scale.

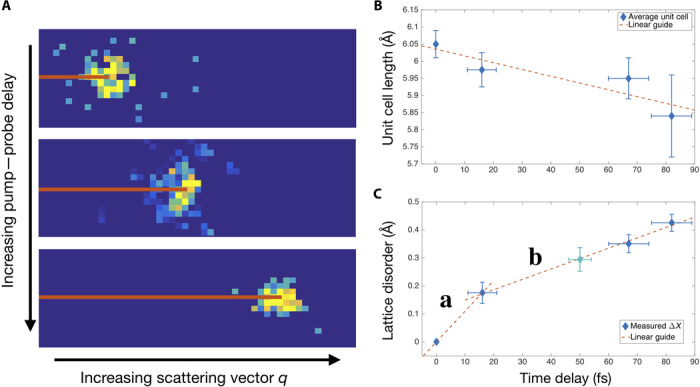
(A) Bragg peaks from the (220) fcc reflection plane shift to higher scattering vector q with increasing pump-probe delay (0-, 60-, and 80-fs delays pictured here). (B) The average unit cell lengths measured from the q value for the (111) and (220) fcc reflection planes show a consistent decrease with increasing delay. (C) Apparent lattice disorder is calculated from the DWF. Two distinct regimes show a fast disorder (region a) on the same time scale as electronic responses, and a slower change (region b) indicative of lattice distortion. The teal marker is for the 50-fs delay average data set where single-shot data could not be filtered on single-grain clusters.

In competition with lattice compression, the strongly excited cluster also undergoes ultrafast electronic and structural damage. Both effects lead to attenuation of the Bragg intensities, and for simplicity, both are expressed here with the Debye-Waller factor (DWF), even though the DWF only describes average lattice disorder. The DWF is given by D = exp(−q²ΔX²/3), where D = I/I₀ is the ratio of intensity in the Bragg peaks, q is the scattering vector, and ΔX is the average displacement of nodes in the crystal. The apparent lattice disorder from the DWF is plotted as a function of pump-probe delay in Fig. 2C. The data show two distinct time constants, one with a fast rise time between the 0- and 15-fs delay points (region a) and a slower regime between 15 and 80 fs (region b). The rapid decrease in region a is on a time scale comparable to the x-ray pulse length and major Auger relaxation times. It is therefore interpreted to be dominated by electronic damage. An upper bound for the signal attenuation from electron damage can be estimated from cluster ionization; that is, a reduction in the number of electrons participating in the scattering process will decrease the peak intensity. Data from the time-of-flight (TOF) spectrometer show a most probable Xe charge state of Xe⁹⁺ (see inset of Fig. 3), leaving a total electron fraction of 45/54 per atom. Elastic scattering at high-momentum transfer q is dominated by tightly bound inner shell electrons (11); thus, the attenuation in signal from electronic damage is bounded by a maximum of 1 − (45/54)² ~30%. This intensity decrease would result in a DWF of 0.7 for the (220) reflection and an apparent lattice disorder of 0.34 Å slightly larger than the 0.2 Å apparent disorder we observed. In region b of Fig. 2C, the DWF evolves much more slowly and indicates an increasing disorder in the nanoplasma lattice compared to the cold van der Waals cluster.

Fig. 3. TOF spectra from Xe clusters and atomic Xe.

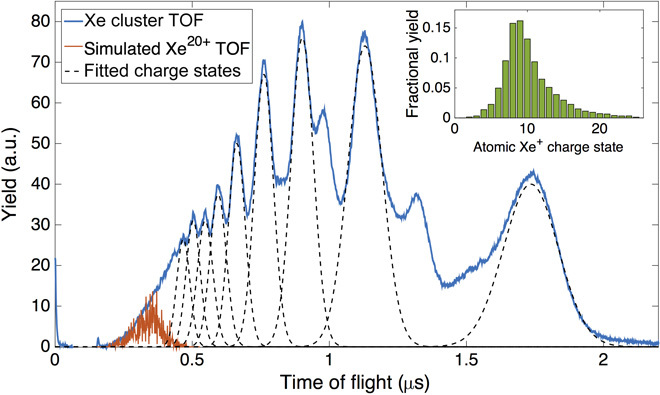
The TOF spectrum from Xe clusters shows high charge state ions with high kinetic energies, indicative of a hot nanoplasma. Kinetic energy distributions are simulated and fit with an ion optics Monte-Carlo software package. The Xe²⁰⁺ peak corresponds to a maximum kinetic energy of 45 keV and an average kinetic energy of 10 keV. (Inset) Atomic Xe reference data show a most probable charge state of Q = 9+. A maximum charge state of Q = 25+ is observed, with more than 98% of collected ions having a charge state of 20+ or less.

The simultaneously recorded ion TOF spectra displayed in Fig. 3 yield information about the nanoplasma long-time dynamics (12–14). The cluster is initially highly charged, and the nanoplasma subsequently disintegrates through surface explosion of highly charged ions followed by rapid hydrodynamic expansion. X-ray ionization processes in the cluster are similar to those in pure atoms (15), which means that under similar conditions, a relevant maximum charge state in Xe clusters of ~Xe²⁰⁺ should be expected. Ion kinetic energy distributions from Xe²⁰⁺ are simulated and fit to the cluster TOF data shown in Fig. 3, indicating a maximum and average kinetic energy of 45 and 10 keV, respectively (see the Supplementary Materials). This ion charge state and kinetic energy distribution specify an electron temperature of ~600 eV and an electron density of ~10²⁸ e⁻/m³, which is consistent with experiments on Xe clusters (7) and simulations on Xe ions (16).

DISCUSSION

We are now in the paradoxical situation in which the femtosecond structural information shows a lattice contraction, whereas data from the TOF spectrometer indicate a rapid cluster expansion with a violent surface explosion. While the expansion is in line with previous knowledge (13, 14), lattice compression has neither been observed experimentally nor described by any theoretical models. In principle, Coulomb explosion of surface ions can impart a momentum transfer to the static cluster core, akin to a compression wave, but such dynamics are phonon-driven and occur on a longer time scale than we observed. Even in highly ionized plasmas, which have a speed of sound of ~1 nm per 10 fs, a compression wave would move across the cluster on the picosecond time scale. Furthermore, we observed clear Bragg spots that are indicative of a collective contraction, whereas a compression wave would nonuniformly squeeze the nanoplasma lattice.

In an alternative explanation, the observed and unanticipated lattice compression during the solid-to-plasma transition is attributed to transient bond contraction stemming from the strongly enhanced electron mobility in the xenon nanoplasma. The delocalized valence electrons in the nanoplasma core are quasi-free, converting the weakly bound van der Waals cluster into a more “metallic-like” state and leading to a transient bond length decrease resulting in an overall contraction of the lattice. Such a drastic change in the potential energy landscape of the whole particle extends well beyond nearest-neighbor interactions and could account for a collective lattice adjustment, giving rise to shifting Bragg peaks as observed in the experimental data (see Fig. 2A). In a more formal description of the “nanoplasma metallization,” we used the Debye length, which describes the length scale where an electric charge is shielded in a plasma. It is the plasma equivalent to the Thomas-Fermi length in metals and can be estimated from the ion TOF data to approximately 1 Å (see the Supplementary Materials). This is close to the Thomas-Fermi lengths for common metals such as copper (λ_TF = 0.75 Å) and gold (λ_TF = 0.6 Å). With a Debye length of λ_D = 1 Å, the minimum size of the unit cell anticipated for a Xe nanoplasma with metallic bonding is 4.8 Å (see the Supplementary Materials), which is much smaller than the minimum value expected from the Xe Lennard-Jones potential of 6.2 Å (17) and still smaller than the average 5.84 Å we observed after 80 fs.

In general, a system undergoing massive electronic excitations will force cold ions to experience a new energy landscape, which will then force a structural bond readjustment. However, the directionality of the bond change may depend on the initial bonding character and structural arrangement of the system. Previous studies of large samples subjected to electronic stress show both an expansive and a contractive character (18, 19). Further, we note that the observed transient lattice contraction may be specific to finite systems. In an infinite system, the net force on any atom is zero. In the nanoplasma, a stress gradient exists from the center atom to the surface. The well-defined Bragg peaks in Fig. 2A indicate that a large fraction of the atoms must have adjusted to a new lattice constant. In the present experiment, the outer third of the atomic shells contain 70% of the atoms. Along these lines, the observed lattice contraction is not completely homogeneous, even though it is based on a collective change in bond character, as we observed increasing disorder in the time evolution of the system as described by the DWF in Fig. 2C.

The present investigation reveals that in condensed matter systems, a strong electronic excitation can lead to an ultrafast change in overall bond character, inducing collective structural changes. We observed lattice contraction on time scales comparable to chemical reactions in small molecules such as electron dissociation dynamics and bond restructuring. These results carry significance for any phenomena involving a solid-to-plasma transition. An electronically driven transient structural change in warm dense matter may influence possible ignition methods (20). In ultrafast x-ray scattering experiments, lattice deformations will lead to smearing of Bragg peaks in series femtosecond crystallography (21) and may ultimately limit the attainable resolution in coherent diffractive imaging (22).

MATERIALS AND METHODS

The experiment was performed in the 100-nm focus chamber of the Coherent X-ray Imaging (CXI) instrument at the Linac Coherent Light Source (LCLS) (23, 24). To measure time-dependent x-ray–induced dynamics, two 10-fs x-ray pulses were produced using the recently developed double-pulse operating mode at the LCLS (8). Twin electron bunches radiating at slightly different energies in the LCLS undulator produced two high-intensity x-ray pulses in the experimental end station. The x-ray pulses were separated by up to 80 fs, with a photon energy separation of ~70 eV straddling the nickel K-edge at 8.33 keV. The first x-ray pulse, with photon energy above the nickel K-edge and a pulse energy of ~300 μJ, diffracts off the Xe cluster and begins to induce dynamics in the system. The second x-ray pulse, with photon energy just below the nickel K-edge and a pulse energy of 700 μJ, Bragg scatters off the disintegrating Xe cluster and passes through the nickel filter. Bragg peaks from the second x-ray pulse are recorded on the Cornell-SLAC Pixel Array Detector (CSPAD) located 70 mm downstream of the interaction region. A TOF spectrometer is used to measure ions in coincidence with Bragg scattering. Structural and electronic information is obtained with coincident detection of x-ray photons and ions. Clusters with a diameter of 70 nm were produced with a pulsed valve by supersonic expansion of Xe through a 200-μm nozzle with a half-opening angle of 4°. The clusters were sent through two differentially pumped skimmer stages and a set of movable slits to produce a defined, localized target and ensure less than one Xe cluster in the interaction region per free-electron laser (FEL) pulse. Further information is provided in the Supplementary Materials.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/1/e1500837/DC1

Materials and Methods

Fig. S1. Transmission of the 30-μm nickel filter around the nickel K-edge.

References (25–30)