Ice-nucleating bacteria control the order and dynamics of interfacial water

Specialized bacteria trigger ice formation by controlling the molecular structure and energy transfer in interfacial water.

Abstract

Ice-nucleating organisms play important roles in the environment. With their ability to induce ice formation at temperatures just below the ice melting point, bacteria such as Pseudomonas syringae attack plants through frost damage using specialized ice-nucleating proteins. Besides the impact on agriculture and microbial ecology, airborne P. syringae can affect atmospheric glaciation processes, with consequences for cloud evolution, precipitation, and climate. Biogenic ice nucleation is also relevant for artificial snow production and for biomimetic materials for controlled interfacial freezing. We use interface-specific sum frequency generation (SFG) spectroscopy to show that hydrogen bonding at the water-bacteria contact imposes structural ordering on the adjacent water network. Experimental SFG data and molecular dynamics simulations demonstrate that ice-active sites within P. syringae feature unique hydrophilic-hydrophobic patterns to enhance ice nucleation. The freezing transition is further facilitated by the highly effective removal of latent heat from the nucleation site, as apparent from time-resolved SFG spectroscopy.

INTRODUCTION

Ice-nucleating proteins (INPs) anchored to the outer cell membrane of ice-active bacteria can induce the formation of ice crystals close to the ice melting point (1). Ice-active bacteria such as Pseudomonas syringae are thus frequently used to facilitate artificial snow production in winter sports areas around the world, and they play an important role in frost damage on crops and other types of vegetation (1, 2). Moreover, airborne ice-active microorganisms are involved in the interaction of atmospheric aerosols, clouds, and precipitation, and they may influence the hydrological cycle and the coevolution of life and climate through feedback mechanisms that receive increasing attention in Earth system and climate research (bioprecipitation cycle) (3–8).

Despite extensive literature that attests to the importance of interactions of ice-active bacteria in biology and environmental science (1, 4, 8–13), remarkably little is known about the structure of the water-bacteria interface and the molecular mechanism by which the INPs used by these organisms interact with water to increase its freezing point. Although the ice-active sequences of several INPs are known, x-ray diffraction or nuclear magnetic resonance–based structural data of these large proteins consisting of 1200 amino acids are not available. Over the past 15 years, the interactions of INPs with water molecules have mostly been studied with molecular dynamics (MD) simulation methods. Kajava and Lindow (11), Garnham et al. (14), and others (15–17) have modeled INPs in contact with water and proposed that INPs are anchored to the cell surface by membrane-active sequences at the protein termini and folded to present ice nucleation sites to the surrounding water. This work suggests that these sites consist of threonine (Thr)– and serine (Ser)–rich repeat units that mimic the basal plane of ice through their hydroxyl groups in combination with captured, clathrate waters incorporated into the protein surface. The ice mimicry of the ice nucleation sites serves as a template for orienting water into a lattice, which effectively nucleates the formation of ice crystals (11, 14, 18, 19).

The idea of ice templating by INPs is striking, but the model has not been experimentally tested—likely because of the difficulties in experimentally studying protein structure and hydration at interfaces. Here, we used sum frequency generation (SFG) spectroscopy (20) to examine the hypothesis that INPs are able to induce structural order and drive phase transitions in their hydration shell. SFG spectroscopy is a nonlinear optical spectroscopy that provides surface-specific vibrational spectra and has been successfully applied to elucidate interfacial water organization at a variety of interfaces (20–22), including antifreeze proteins (AFPs) (23). Briefly, in an SFG experiment, infrared (IR) laser pulses are overlapped with visible laser pulses at the interface (see Materials and Methods for more information about the experiment). Molecular resonances excited by the IR pulse enhance the signal and yield a vibrational spectrum of the interface. The selection rules of SFG dictate that only ordered, interfacial molecules generate a detectable signal. This allows one to specifically probe ordered interfacial water molecules without spectral interference with randomly oriented bulk water.

The bacterium P. syringae uses the ice nucleation protein inaZ to promote ice nucleation (1). inaZ is a membrane protein located at the outer cell membrane of P. syringae, where it can interact with surrounding water layers. It is the most efficient and most widely studied model system of all biogenic ice nucleators and is therefore a promising model system to investigate biologically driven ice nucleation. In our study, we used inactivated P. syringae bacteria, which are commercially available under the product name Snomax. This cell product has become a very important model and reference system in the quickly growing atmospheric science and ice nucleation (IN) community (24, 25). The IN activity of our specific sample was verified by a droplet-freezing assay (see the Supplementary Materials). To determine the interaction of P. syringae with water, we probed a P. syringae solution (0.1 mg/ml) in heavy water (D₂O) in a temperature-controlled trough. Surface tension measurements showed that the IN material partitioned to the air-water interface, which was probed with SFG (see the Supplementary Materials). To account for the fact that the samples contain a variety of biomolecules besides the inaZ proteins, we have included a range of control substances in our study, representative of different classes of surface active molecules found within cells.

RESULTS

Figure 1A shows SFG spectra in the O–D and C–H stretching regions at temperatures ranging from room temperature (RT, 22°C) down to 5°C, that is, 1°C above the melting point of D₂O ice (freezing of this sample occurred at 4°C). The RT SFG spectrum for P. syringae at the air-water interface contains C–H resonances between 2800 and 3000 cm⁻¹, related to a variety of aliphatic carbon species such as lipid tails, amino acid side chains, and hydrocarbons. Interfacial deuterated water gives rise to a broad band between 2300 and 2600 cm⁻¹, which is assigned to a continuum of O–D stretching vibrational states going from weakly (near 2500 cm⁻¹) to more strongly (near 2390 cm⁻¹) hydrogen-bonded water molecules (26, 27). As the temperature of the water decreased, we observed a progressive increase of the SFG intensity, which implies a significant increase of interfacial water order and alignment. Although the general features observed in the P. syringae spectra, such as hydrocarbon and water modes, are also typically observed in the spectra of monolayers of lipids and proteins in contact with water (28, 29), we did not observe such temperature dependence for any of the ice-inactive interfaces that we studied. Figure 1 (B to E) shows the spectra of monolayers of different control substances representing various types of ice-inactive biological molecules. To test the role of intact inaZ protein sites for their water-structuring and ice-forming abilities, we used a misfolded synthetic 15–amino acid fragment of the inaZ IN domain and a protein extract of the P. syringae sample that contains, inter alia, denatured inaZ proteins as negative controls. Because lipids can be expected at the water interface, we included a model DPPG lipid monolayer (1,2-dipalmitoyl-sn-glycero-3-phosphoglycerol) in the list of controls. As a well-studied and stable model protein for interfacial studies, we also collected water spectra at the lysozyme-water interface. The DPPG sample showed an increase of the CH modes with decreasing temperature, likely explained by increased ordering of the lipid alkyl chains. Because lipids are also present in the bacteria sample, this likely also explains the increased CH intensity in the P. syringae spectra (also see fig. S1). Within the detection limit of our experiment, we did not observe changes in the water SFG intensity or resonance position for any of the control substances.

Fig. 1. SFG spectra of P. syringae.

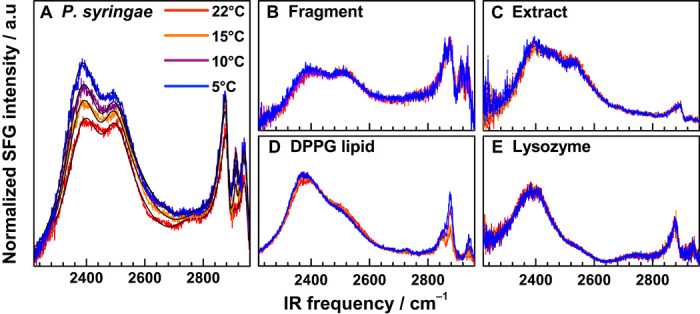
(A to E) SFG spectra of P. syringae bacteria lysate, which contain ice-active inaZ proteins (A) and control substances (B to E) in contact with water at different temperatures. INPs increase the water signal with decreasing temperatures, whereas control substances leave the water signal unchanged. a.u., arbitrary units.

Figure 2 displays the analysis of the SFG amplitude for water bands observed for the P. syringae sample. To quantify the changes of the water structure when cooling from RT to 5°C, we show in Fig. 2A SFG spectra and fits for the weakly and strongly hydrogen-bonded water bands for the respective temperatures. The results of the analysis—SFG amplitude changes for all four temperatures—are summarized in Fig. 2B. The data show that the increase of the water signal is mostly related to an increase of the strongly bound water mode; the weakly bound water mode remains almost unchanged.

Fig. 2. Analysis of temperature-dependent SFG spectra for P. syringae at a water surface.

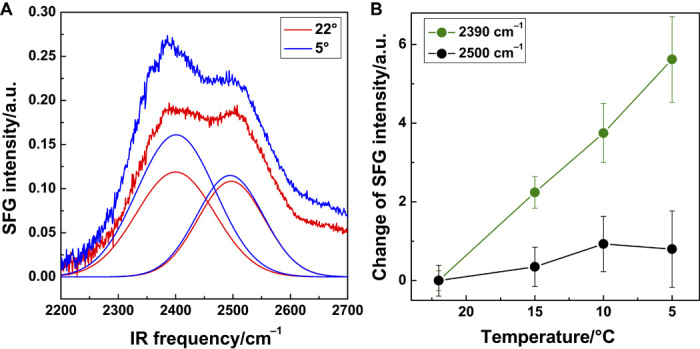
(A) Spectra for RT and 5°C along with two fitting components related to more weakly and strongly hydrogen-bonded water within the broad water spectrum. CH and nonresonant fitting components are not included here. (B) Plots of the amplitudes obtained from fits to the SFG spectra from RT to 5°C. The mode related to more strongly hydrogen-bonded water increases strongly, whereas the weakly hydrogen-bonded water mode remains almost unchanged.

Temperature changes can also induce refolding of proteins at interfaces and cause changes in the composition of interfacial layers. The amide I SFG spectra of the P. syringae sample (Supplementary Materials) showed no measurable changes in the configuration of interfacial proteins. The surface tension of the samples was recorded during the cooling process (summarized in the Supplementary Materials), and the results agree with the assumption that the surface coverage of the surface was largely unaffected by the temperature change (see the Supplementary Materials). This view was supported by x-ray photoelectron spectroscopy (XPS) data, which showed that the surface composition remained unchanged when the sample was cooled from RT to 5°C (see the Supplementary Materials).

When relating water alignment to specific components or sites within P. syringae, it is important to take into account the complexity of this multicomponent system. However, our analysis is facilitated by the fact that, among ice nucleators, inaZ proteins exhibit the highest freezing point observed. Other insoluble materials present in the solution, including the control substances shown and discussed in Fig. 1, could possibly act as IN but are not active at these high temperatures (30), and thus will not structure water at the reported temperatures. On the basis of these considerations, it can be concluded that the interaction of an IN material with water close to the freezing temperature will be dominated by the ice-active agent within the IN material—that is, inaZ proteins in P. syringae. The presence of significant amounts of soluble material within the P. syringae lysate can be expected to lead to the common freezing point depression (25, 31, 32). This effect would inhibit ice nucleation and diminish water structuring for the investigated temperatures. This view is also supported by the droplet freeze assay performed with our P. syringae samples (see the Supplementary Materials), which demonstrates the presence of a single, effective ice nucleus acting on the water near the ice melting temperature.

Using MD methods, the Yasuoka and Davies laboratories have predicted that INPs can order water more effectively at their “operating” temperatures—close to the ice melting point (14, 17). Our data now support this hypothesis. P. syringae shows higher water SFG signals, that is, stronger water interaction, under low-temperature conditions.

Two conditions will promote interfacial ice nucleation: (i) the alignment of water into a regular structure and (ii) effective removal of latent heat due to the phase transition. The first condition of water ordering is met by the IN bacteria, as can be seen in the significant increase of the SFG signal. To test the correlation of SFG intensity increase with water ordering and to identify which water species are involved in the ordering process in the P. syringae sample, we performed MD simulations of an inaZ ice nucleation site in contact with water at 26.85° and 1.85°C and calculated the O–D stretch SFG intensity (see Fig. 3 and the Supplementary Materials for details). Water SFG spectrum calculations at interfaces have been successfully used at various surfaces such as lipid layers (33) and the air-water interface (34).

Fig. 3. MD simulation of the inaZ ice-active site.

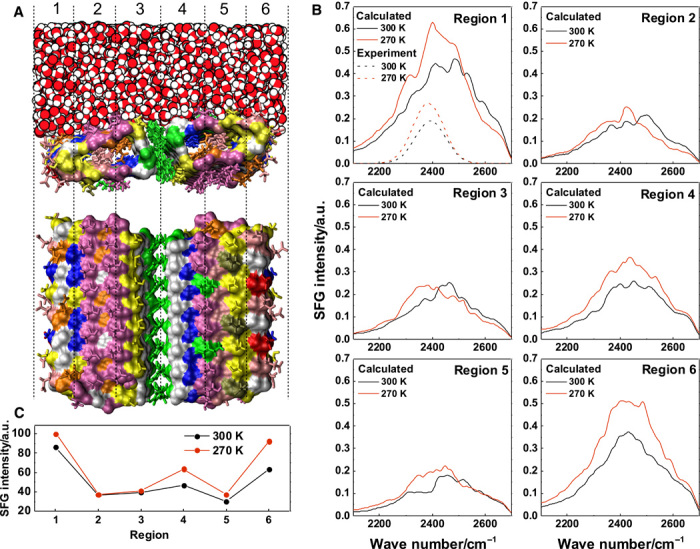
(A) The top view illustrates the ladder-type regions of groups of amino acids on the IN dimer. The side view shows an MD snapshot of the water structure at the IN site. Together, side chains and clathrate water form a template for ice nucleation. Threonine, purple; serine, yellow; alanine, blue; tyrosine, green; glutamic acid, orange; glycine, white. (B) Calculated SFG spectra for regions with different amino acids present. Thr- and Ser-rich areas leave the water signal intensity unchanged, whereas there is a clear trend toward a stronger water signal near glutamic acid– and serine-rich regions. (C) Integrated SFG intensity for the IN site regions at 270 and 300 K. The increased intensity at regions 1 and 6 indicates more ordered water near the perimeter of the IN site.

To trace the origin of this temperature-dependent effect, we decomposed the simulation cell into the six regions schematically depicted in Fig. 3A, to examine the contribution to the SFG spectra from the water molecules contained in each region. These are shown in Fig. 3B. A comparison of the lower-frequency fitting component (near 2390 cm⁻¹) of the experimental spectra with the calculated bands is shown in the first panel of Fig. 3B. The experimental SFG spectra are representative of the entire bacteria in contact with water and are likely not reproduced by spectrum calculations for the inaZ protein alone. In addition, because we are investigating a single active site, that is, an infinitely diluted system, any lateral interactions or higher-order assemblies of the INPs would be visible in the simulations. However, the calculation should be able to capture temperature-induced changes in the experimental spectra if those changes are a result of inaZ-water interactions. The simulated SFG spectra reproduce the remarkable enhancement of the SFG intensity for low-frequency O–D SFG modes with decreasing temperature.

The spectra also reveal significant variations in the contributions to the SFG intensity from different parts of the IN site due to the different composition and structure of the amino acids contained in these regions. The variation of the SFG intensities calculated for the different regions is summarized in Fig. 3C. Regions 1 and 6 provide very strong SFG intensity as well as a striking intensity increase at lower temperatures, whereas both effects are less pronounced in the inner, more hydrophobic regions 2 to 5. This implies that the marked change of the water ordering at lower temperatures is mainly driven by the hydrophilic outer regions. For the Thr “ladder” motif in regions 2 and 3—which has been hypothesized to play a major role in templating ice growths by binding clathrate water to the IN site—the SFG signal remains unchanged by temperature but shows a significant red shift of the SFG band. Such a decoupling of Thr sites and water molecules has also been observed for strongly ice-binding insect AFPs (35, 36), although other AFPs showed a strong coupling to adjacent water layers (23). For P. syringae, although water order near Thr sites appears to be less affected by temperature than in the outer regions, stronger binding of water in the Thr region might affect water order in neighboring regions by long-range interactions within the water network or improved rigidity throughout the side-chain lattice.

However, because the Thr ladder motif does not impose ordering of water superior to other protein sites, in contrast to previous explanations for the excellent ice nucleation activity of this inaZ protein (11, 14), the question arises of which other effects could explain its formidable IN potential. The water structure across regions 1 to 6 indicates that hydrophilic surfaces bond to the adjacent water molecules, whereas the clathrate water molecules at the Thr sites are decoupled from the bulk water molecules. Instead of binding water, the Thr ladder motif acts as an extended hydrophobic domain, which can maintain contact with water (see fig. S10).

It is known that the water structure at a water-hydrophobic interface is similar to the water structure at a water-vapor interface (37). The inaZ protein uniquely features a hydrophilic-hydrophobic-hydrophilic pattern (regions 1 to 6), imposing corresponding structural changes in the adjacent water alternating between liquid- and vapor-like water interfaces. Previous theoretical and experimental studies demonstrated that ice nucleation can be enhanced at the triple line, that is, when the IN substrate is in the vicinity of the water-vapor interface (38–44). Scale analysis of the triple-line tensions (ice-liquid-substrate, ice-air-substrate, and liquid-air-substrate) suggests that this effect is important for surface features on the nanometer scale (39). The inaZ protein may provide such a favorable environment for ice nucleation, even when immersed in liquid water, thereby extending this symmetric configuration over significant length. The unique feature of providing three phase contact points may result in generally observed enhanced freezing. Thus, clathrate water matching alone may not explain the exceptional IN ability of inaZ, but its alternating water structuring by the repeated hydrophilic-hydrophobic pattern may contribute significantly. This may also explain why flat hydrophilic surfaces act as good IN substrates, potentially via chemical bonds, lattice match, or active sites (45, 46), but do not exhibit the exceptional IN capability of inaZ. In addition to these very unique features, the observed promotion of water order near the hydrophilic sites also has a direct impact on the second requirement for effective ice formation—removal of latent heat.

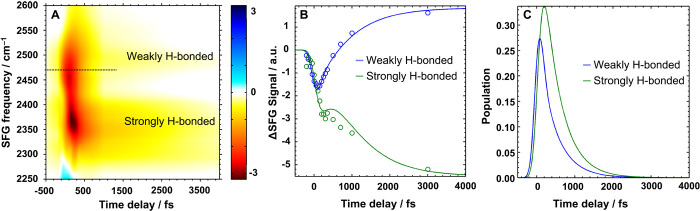
Molecular alignment within the H-bonding network of water can promote long-range energetic coupling and therefore, by effectively funneling heat away from the interface, promote the formation of critical ice embryos necessary for nucleation. When water molecules are coaligned, their mutual dipole-dipole interaction is strongly increased, so that vibrational energy transfer can more readily occur between water molecules. The strength of the intermolecular interaction between water molecules at the P. syringae–water interface can be estimated through the vibrational energy transfer dynamics of interacting O–D groups. At surfaces, time-resolved IR pump/SFG probe spectroscopy (47, 48) enables the efficiency of energy transfer to be measured. Here, an IR excitation (pump) pulse excites O–D groups at a specific vibrational frequency. The effect of the excitation is followed in time with the SFG probe pulses (see the Supplementary Materials for more details). The excitation of O–D groups leads to a depleted SFG intensity at the excitation frequency; when vibrational energy transfer occurs, the vibrational frequency can change because of the slightly different H-bonding environments of the donor and the acceptor. The rate at which the vibrational quantum moves from one spectral band to another is a direct measure for the rate of energy transfer.

Figure 4A shows a time-resolved difference–SFG spectrum for P. syringae at 5°C after excitation with a 2470-cm⁻¹ pump pulse (the excitation frequency is marked with a dashed black line). It can be seen that, for the P. syringae film, the bleach is strongest not at the excitation energy but at 2370 cm⁻¹, demonstrating very efficient energy transfer within the water network to lower energies. Figure 4B displays the time-resolved bleach integrated over two spectral regions: the strongly H-bonded part near 2330 to 2430 cm⁻¹ and the weakly H-bonded part near 2480 to 2580 cm⁻¹. The offset visible at long delay times is due to thermal effects. The energy transfer from the weakly H-bonded to the strongly H-bonded molecules is significantly more efficient compared with that of the ice-inactive lysozyme-water interface and the bare air-water interface, which is directly visible in the reduced intensity in the signal at low frequency after excitation around 2500 cm⁻¹ (see fig. S11). To estimate the efficiency, the data have been fitted using a coupled differential equation model (see the Supplementary Materials). This model splits the water ensemble with a continuous broad distribution of hydrogen bond strength into two spectral regions of water molecules (strongly and weakly H-bonded molecules) that can exchange population and decay to the ground state. The coupling time extracted from this model is a measure of how efficiently energy transfer occurs between more strongly and more weakly H-bonded water molecules. Modeling the time-resolved data in this way gives a coupling time between the more strongly and the more weakly H-bonded water molecules of only 80 ± 50 fs for the P. syringae and 190 ± 80 and 670 ± 250 fs for the lysozyme-water interface and the bare air-water interface, respectively. This shows that P. syringae has more efficient energy transfer than the control samples.

Fig. 4. Energy transfer processes at the water-INP interface.

(A) Time-resolved difference sum frequency spectrum for the water–P. syringae interface after excitation with a 2470-cm⁻¹ pump pulse near the weakly H-bonded water resonances (dashed line). The signal bleach is very intense in the low-frequency water peak related to strongly H-bonded water. This shows that energy transfer is very rapid and efficient. For clarity, any spectral changes due to thermal effects have been removed. (B) Time-dependent bleach integrated over two spectral regions, 2330 to 2430 cm⁻¹ (strongly H-bonded) and 2480 to 2580 cm⁻¹ (weakly H-bonded). Fits of the data using a coupled differential equation model reveal extremely efficient (80 ± 50 fs) energy transfer between more weakly and more strongly H-bonded water molecules. (C) Time-resolved populations of the more weakly and more strongly H-bonded water molecules extracted from the coupled differential equations. The states become populated from the excitation pulse, energy transfer, and decay to the ground states (not plotted). For the water–P. syringae interface, the more strongly H-bonded state’s population is higher than that of the initially excited peak, which proves extremely efficient energy transfer.

Figure 4C shows the time-resolved populations of the two spectral regions (more strongly and more weakly H-bonded water) extracted from the coupled differential equation model. The states become populated from the excitation pulse, over the 300-fs pump pulse duration, from energy transfer, and depopulate by decay to the ground states. The initially excited state (blue, weakly H-bonded water) has the greatest population at zero pump-probe delay time. Some of this population is transferred to the strongly H-bonded state (green). For the water–P. syringae interface, the strongly H-bonded state’s population is very high, even higher than that of the initially excited weakly H-bonded feature. This is not the case for other water interfaces (lysozyme-water and water-air; see fig. S11) and shows that P. syringae can drive the energy transfer process particularly efficiently.

DISCUSSION

We demonstrate that P. syringae bacteria can effectively order water molecules in their vicinity, which supports the hypothesis that they carry IN active sites, which can promote the nucleation of ice. In addition, vibrational energy is very rapidly exchanged through the surrounding water near the bacterial surface. Ordering and thermal energy removal through effective energetic coupling within the water network are advantageous for ice nucleation by inaZ sites at the bacterial surface. The water order is significantly enhanced with decreasing temperatures, which indicates that the molecular mechanisms involved in biogenic ice nucleation have been evolutionarily optimized for temperatures close to the freezing point of water. Heterogeneous ice nucleation initiated by substrates is little understood and contributes to large uncertainties in the prediction of climate change (49). Close analysis of the interaction of inaZ proteins with water exemplifies the fact that surface sites matching ice templates and the presence of hydrophilic sites (by matching bonds) commonly assumed to promote ice nucleation (50) are not sufficient to explain the IN properties of P. syringae but that on a nanometer scale, a symmetric hydrophobic-hydrophilic pattern can play an important role in water structuring and thus ice nucleation, an effect testable in future experimental studies. The model discussed here is valid for bacteria similar to P. syringae. Other species involved in biogenic ice nucleation, for example fungi and pollen (9), may use variations or entirely different mechanisms.

Lipids, proteins, and surfactants did not show any detectable increase of water ordering at lower temperatures. AFPs are another substance found to be capable of ordering water more effectively at low temperatures (23); AFPs can protect organisms from ice crystal formation at extremely low temperatures and can very effectively track down and bind to ice crystallites and block their growth using specific ice-binding sites. On the basis of the time-resolved SFG spectra (see the Supplementary Materials), we found that the energy transfer within the interfacial water layer was also very efficient—again similar to P. syringae. However, the underlying molecular processes are still under discussion (23, 51). Despite the structural adaptation to low temperatures in both AFPs and IN bacteria, ice-active bacteria, acting as superb ice nucleators, have additional molecular features that drastically alter their role in the environment compared to AFPs, including their participation in precipitation processes and thus in the global hydrological cycle and climate.

MATERIALS AND METHODS

The SFG setup was based on a Ti:sapphire femtosecond laser oscillator (Mai Tai, Spectra-Physics). A regenerative amplifier (Spitfire Ace, Spectra-Physics) pumped by a Nd:YLF (neodymium-doped yttrium lithium fluoride) laser (Empower, Spectra-Physics) was used to generate a 5-mJ pulse at 800 nm with a 40-fs duration at a repetition rate of 1 kHz. An output energy of 1.7 mJ was used to pump a commercial optical parametric amplifier (TOPAS-C, Spectra-Physics). The signal and idler pulses of the parametric amplifier were mixed in a silver gallium disulfide (AgGaS₂) difference frequency generation crystal, resulting in 4-μJ IR pulses centered at 2500 cm⁻¹ with a full width at half maximum (FWHM) of ~450 cm⁻¹. The narrowband visible upconversion pulses (25 μJ; FWHM, ~15 cm⁻¹) were obtained by passing 800-nm pulses (1-mJ pulse energy) through a Fabry-Perot etalon (SLS Optics Ltd.). The visible and IR beams were spatially and temporally overlapped on the sample surface with incident angles of 36° and 41°, respectively, with respect to the surface normal. The desired ssp (s-polarized SFG, s-polarized visible, p-polarized IR) polarization was obtained using a polarizer and half-wave plates. The visible and IR beams were focused on the sample. The sum frequency signal was collected in reflection geometry and collimated by a lens before passing through a short-wave pass filter to remove the residual visible light. The polarization of the SFG light was controlled by polarization optics before the SFG light was guided to a spectrograph (Acton Instruments) and detected with an electron-multiplied charge-coupled device camera (Newton, Andor Technologies). All SFG spectra were recorded under ssp polarization conditions. Here, spectra were recorded in the O–D stretching region between 2400 and 2800 cm⁻¹ and the C–H stretching region between 2800 and 3100 cm⁻¹ simultaneously. The SFG sample area and the IR beam path were flushed with nitrogen to avoid spectral artifacts from water vapor. All the SFG spectra were normalized using reference spectra obtained from z-cut quartz. The measured SFG intensity was proportional to the square of the second-order nonlinear susceptibility χ⁽²⁾ of the sample and the intensities of the visible and IR beams

$${\mathit{I}}_{\text{SFG}}\propto {|{\chi }^{(2)}|}^2{\mathit{I}}_{\text{VIS}}{\mathit{I}}_{\text{IR}}$$ (1)

When the frequency of the incident IR field is resonant with the vibrational mode n, the SFG field can be strongly enhanced. Then, the susceptibility χ⁽²⁾ consists of a nonresonant (NR) and a resonant (RES) term

$${\mathrm{\chi }}^{(2)}={\mathrm{\chi }}_{\text{NR}}^{(2)}+{\mathrm{\chi }}_{\text{RES}}^{(2)}={\mathit{A}}_{\text{NR}}{\mathit{e}}^{\mathit{i}{\mathrm{\phi }}_{\text{NR}}}+{\displaystyle {\sum }_{\mathit{n}}}\frac{{\mathit{A}}_{\mathit{n}}}{{\mathrm{\omega }}_{\mathit{n}}-{\mathrm{\omega }}_{\text{IR}}-\mathit{i}{\mathrm{\Gamma }}_{\mathit{n}}}$$ (2)

where A_NR represents the amplitude of the nonresonant susceptibility, φ_NR is its phase relative to the resonant contributions, and A_n is the amplitude of the nth vibrational mode with resonant frequency ω_n. Γ_n is the linewidth of the peak at ω_n. Equation 2 was used to fit the measured SFG spectra. We note that this established procedure uses the phase φ_NR as a fitting parameter while keeping the relative phases between resonant contributions constant (52, 53). The P. syringae and all protein and peptide solutions had bulk concentrations of 0.1 mg/ml. P. syringae had a pH of 6.24 and a conductivity of 192.3 μS/cm. The control protein and peptide experiments were performed at pH 7.4 in phosphate-buffered saline solution.

For the time-resolved SFG spectroscopy, a spectrally narrow (~100 cm⁻¹) p-polarized pump pulse was added to the static SFG spectroscopy. The pump pulses were tuned across the absorption band of water. For the detection process, broadband mid-IR and narrowband visible upconversion pulses were mixed at the interface to generate a conventional SFG signal, as described in the previous paragraph. The high-intensity and narrowband pump pulses were generated in an independent parametric conversion process in which we used the residual 800 nm and idler pulses from the TOPAS. The idler pulses were doubled in a β-barium borate (BaB₂O₄) crystal, resulting in pulses with a central wavelength of ~1000 nm. Afterward, the doubled idler and 800 nm pulses were combined in a parametric amplification process in a lithium niobate (LiNbO₃) crystal. This resulted in ~50 μJ pulses with a width of 120 cm⁻¹, with a tunable central wavelength between 2100 and 2900 cm⁻¹. At the sample, the pump energy was 42 μJ for P. syringae and D₂O, 38 μJ for lysozyme, and 35 μJ for AFPs. At the pump-probe SFG setup, the angles of incident with respect to the surface normal were 55°, 40°, and 70° for the pump, probe IR, and visible probe, respectively. For each excitation frequency (2530 and 2370 cm⁻¹), the time delay between the pump and probe pulses was varied using an electronically controlled delay line, and a series of sum frequency spectra at different delay times was recorded. The trough was rotated to ensure that the sample was continuously refreshed, and the water level was kept stable through the use of a reservoir.

Inactivated P. syringae bacteria (Snomax) were purchased from Snomax International. DPPG lipid monolayers (Avanti Polar Lipids) were prepared by dissolving the lipid in chloroform and spreading the solution on a trough filled with heavy water to a final surface pressure of 14 mN/m. The protein extract was prepared using 100 mg of P. syringae (Snomax) and the commercially available ReadyPrep Protein Extraction Kit obtained from Bio-Rad. The ice-inactive fragment of the inaZ protein (GYGSTGT-AGADSSLI) was obtained from GenScript. The protein extract and the inaZ fragment were used in concentrations of 0.1 mg/ml in heavy water. AFP type III was purchased from A/F Protein Inc.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/4/e1501630/DC1

Supplementary Text

fig. S1. Fitting results for SFG spectra.

fig. S2. SFG spectra recorded in the amide I region for P. syringae at the air-water interface at RT and 5°C.

fig. S3. Time traces of surface tension changes recorded while the temperature was changed in the trough for D₂O and Snomax at the air-water interface.

fig. S4. Surface tension changes relative to the tension at 22°C for pure D₂O and the Snomax sample for sample temperatures studied with SFG.

fig. S5. XPS spectra of P. syringae films adsorbed at the water-air interface at 22° and 5°C and transferred to gold-coated silicon chips following the Langmuir-Schaefer (54) method.

fig. S6. XPS survey spectrum of the Snomax sample.

fig. S7. Droplet freeze assay for the P. syringae sample used in this study.

fig. S8. Illustration of the simulation box.

fig. S9. Calculated SFG intensity ${|{\mathrm{\chi }}_{\mathit{x}\mathit{x}\mathit{z}}^{(2)}(\mathrm{\omega })|}^2$ for the O–D stretch chromophores within 15 Å of the center of mass of the IN dimer in the z direction.

fig. S10. Snapshot of the MD simulation near the Thr-rich region (Fig. 3, region 2, main text) of an IN site.

fig. S11. Time-resolved difference sum frequency spectra for control substances.

fig. S12. Energy transfer processes at the water-AFP interface.

table S1. Elemental compositions (atom %) determined by XPS of protein monolayers deposited onto gold-coated silicon chips with the Langmuir-Schaefer technique.

table S2. Time scales (in femtoseconds) extracted from the coupled differential equation fits (only ${\mathrm{\tau }}_{\mathsf{down}}$ was allowed to float; the others were fixed).

References (55–68)