Climate-driven polar motion: 2003–2015

Ice sheets and continental hydrology changes on decadal time scales are the dominant drivers of decadal scale polar motion.

Abstract

Earth’s spin axis has been wandering along the Greenwich meridian since about 2000, representing a 75° eastward shift from its long-term drift direction. The past 115 years have seen unequivocal evidence for a quasi-decadal periodicity, and these motions persist throughout the recent record of pole position, in spite of the new drift direction. We analyze space geodetic and satellite gravimetric data for the period 2003–2015 to show that all of the main features of polar motion are explained by global-scale continent-ocean mass transport. The changes in terrestrial water storage (TWS) and global cryosphere together explain nearly the entire amplitude (83 ± 23%) and mean directional shift (within 5.9° ± 7.6°) of the observed motion. We also find that the TWS variability fully explains the decadal-like changes in polar motion observed during the study period, thus offering a clue to resolving the long-standing quest for determining the origins of decadal oscillations. This newly discovered link between polar motion and global-scale TWS variability has broad implications for the study of past and future climate.

INTRODUCTION

Polar motion is the movement of Earth’s spin axis as it wanders through the crust. Observations have tracked this motion for more than 100 years. Astrometric data, when combined with space methods, form a continuous time series since 1899 (1–4) and have sufficient signal-to-noise ratio to accurately determine the pole position to a level much less than 1 millisecond of arc (mas; 1 mas ≈ 3.09 cm). The time variations in pole position are described by the Cartesian orthogonal vector positions $\mathit{X}(\mathit{t})\widehat{\mathit{x}}$ and Y(t) ŷ, with vector dyads $\widehat{\mathit{x}}$ and ŷ pointing along the longitudes of mean Greenwich and 90° East, respectively. When this time series is filtered to remove the 433-day Chandler and annual wobbles and shorter time-scale variability, a clear linear drift in X(t) and Y(t) is revealed (1, 2, 4, 5), with interannual variability dominated by a 25- to 35-year periodicity (called the Markowitz wobble) and 6- to 14-year decadal periodicities (4, 6). The origins of linear drift (1, 2, 5, 7) are far better understood than are interannual variability seen in the data (8, 9). Here, we identify the mechanisms that largely explain all of the observed polar motions during a 13-year time span, from April 2002 to March 2015, by analyzing monthly data from the Gravity Recovery and Climate Experiment (GRACE) mission (10).

We develop our analysis from observed pole positions, or Earth Orientation Parameters (EOP), that are provided by the International Earth Rotation and Reference Systems Service (IERS) and compute corresponding polar motion excitations, with components χ₁(t) and χ₂(t), from EOP 08 C04 solutions (https://hpiers.obspm.fr/eop-pc/analysis/excitactive.html) by setting the Chandler period to 433 days and its quality factor to 179 (4). Because we are interested in frequencies below that of the Chandler wobble, it is reasonable to approximate [X(t) Y(t)]^T ≈ [χ₁(t) χ₂(t)]^T (see Materials and Methods). Figure 1 shows observed polar motion excitations χ₁(t) and χ₂(t) since 1976, when satellite measurements were first available. The 20th century linear drift is generally explained by the glacial isostatic adjustment (GIA) processes (1, 2, 5) associated with 100,000 years of waxing and waning of the Pleistocene great ice sheets that periodically covered northern hemispheric landmasses (7). Strong deviation in linear drift since about 2000 is likely related to climate-induced mass redistribution (5), including the melting of polar ice sheets (11). Both Markowitz and decadal variabilities are thought to have excitation mechanisms that originate either from the subtle dynamics of Earth’s fluid core or from large-scale global mass transport at Earth’s surface. However, core mechanisms fail to explain the amplitudes of the observed decadal motions by more than an order of magnitude (9), and a comprehensive search for decadal-scale atmosphere-ocean mass transport and angular momentum exchange demonstrated that these fail to explain the decadal amplitudes by more than a factor of 3 (8, 12).

Fig. 1. Observed pole position data.

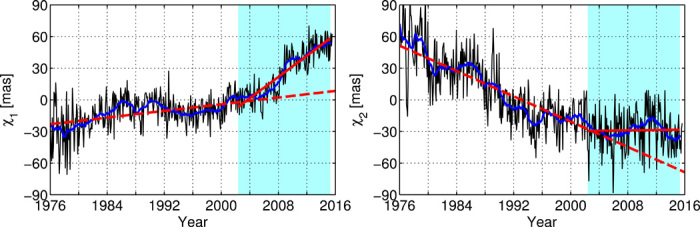
Mean monthly polar motion excitations (black lines) derived from the observed daily values after removing semiannual, annual, and Chandler wobbles. Smoothed solutions (blue lines) reveal quasi-decadal variability in the corresponding component of the 20th-century linear trend (dashed red lines). Cyan shadows in the background cover our study period, over which the drift direction deviates (solid red lines) from the long-term linear trend.

Here, we demonstrate for the first time that both the strong deviation in linear drift since about 2000 (5, 11) and the decadal-like variability are explained by global-scale continent-ocean mass transport, with robust changes in terrestrial water storage (TWS) playing an unexpectedly large role. Rigorous incorporation of TWS changes reduces the variance of a fit to the polar drift data by about 66% for χ₁(t) and by about 92% for χ₂(t), a great reduction over those incorporating only cryospheric changes (11). The variability in TWS excitation signal fully explains the ~20-mas amplitude of the observed change in χ₂(t) during the study period, offering a clue as to the origins of decadal-scale oscillations that are so ubiquitous in the 115-year polar motion record (3, 4, 6).

RESULTS

We compute the variations in polar motion from the changes in Earth’s inertia tensor caused by the climate-driven surface mass redistribution (see Materials and Methods). It is therefore important to understand the spatiotemporal variability in the transport of water mass between the continents and the oceans. For convenience, we define a mass-conserving loading function, L(θ, λ, t), with dimensions of water equivalent height (WEH) as follows

$$\mathit{L}(\mathrm{\theta },\mathrm{\lambda },\mathit{t})=\mathit{H}(\mathrm{\theta },\mathrm{\lambda },\mathit{t})\mathcal{C}(\mathrm{\theta },\mathrm{\lambda })+\mathit{S}(\mathrm{\theta },\mathrm{\lambda },\mathit{t})\mathcal{O}(\mathrm{\theta },\mathrm{\lambda })$$ (1)

Here, H(θ, λ, t) is the change in WEH on the continents with mask $\mathcal{C}(\mathrm{\theta },\mathrm{\lambda })$, S(θ, λ, t) is the associated change in sea level with ocean mask $\mathcal{O}(\mathrm{\theta },\mathrm{\lambda })$, and (θ, λ) represents the geographic coordinates on Earth’s surface. We compute H(θ, λ, t) by analyzing the GRACE Release-05 Level-2 monthly GSM data products provided by the Center for Space Research (available at http://www.csr.utexas.edu/grace/RL05.html). We use the standard processing of GRACE data, which are distributed in the form of monthly varying Stokes coefficients, as described in Materials and Methods. Briefly, we replace the degree 1 and degree 2 Stokes coefficients with more accurate values (13, 14), including those derived from satellite laser ranging (SLR) observations. We then calculate the total WEH gravity signal from Stokes coefficient anomalies, using a Gaussian filter with a 300-km radius. Finally, we remove the GIA signal (15) and scale the remaining WEH. This procedure forms our climate-driven surface loading H(θ, λ, t). Following Schrama et al. (16), we individually scale H(θ, λ, t) for the entire Greenland Ice Sheet (GIS), three nonoverlapping subdomains of the Antarctic Ice Sheet (AIS), and 15 regions of global glaciers and ice caps (GICs), with corresponding uncertainties arising from a suite of GIA computations and the choice of degree 1 and degree 2 Stokes coefficients. We scale H(θ, λ, t) for TWS over the noncryospheric continental domain using the so-called gain factors (17) to account for leakage errors and to restore the attenuated signals. The budget of continental mass directly contributes to the sea-level change. Continental mass variability, along with this ocean loading, induces perturbations in the gravitational and rotational potentials of the planet, causing the further redistribution of S(θ, λ, t), which is gravitationally self-consistent. Here, we compute S(θ, λ, t) by solving the perturbation theory of relative sea level on an elastically compressible rotating Earth (18).

Figure 2 shows the least-squares retrieval of linear trend in L(θ, λ, t) during the study period, using the monthly GRACE solutions and associated sea-level computations. The GIS has lost ice mass at a pace of about −278 ± 19 Gt/year. Much of this loss comes from southern Greenland, where pervasive thinning occurs as a result of collective surface mass balance changes and increased outflux (19). The AIS has also lost mass, but at a more modest rate of −92 ± 26 Gt/year. However, there is great contrast in regional patterns, and coastal East AIS has mainly gained mass, especially in and adjacent to Dronning Maud Land and Enderby Land, as a result of increased precipitation (19). The AIS is losing mass from the Amundsen Sea Sector and the Antarctic Peninsula at a rapid rate. These two loss areas involve changing ice dynamics and, to a lesser degree, surface mass balance (19, 20). Other continental signals in Fig. 2A are composed of those associated with TWS and global GICs. Among the features that stand out are the negative TWS signals around Eurasia (the Indian subcontinent and the Caspian Sea). Relatively large negative signals appear around the Canadian Arctic (−61 ± 5.2 Gt/year), Alaska (−42.1 ± 6.8 Gt/year), and Patagonia (−22.1 ± 6.6 Gt/year), reflecting the large mass loss from these glaciated regions (16, 20, 21). All of these features are consistent with numerous reports of cryospheric and hydrographic mass changes that are comparable to the time span of our study (19–23). A total mass loss from the continents of about −530 Gt/year raises the global mean sea level at a rate of about 1.46 mm/year. The linear trend in S(θ, λ, t) of Fig. 2D shows a large drop in local sea level around the GIS and along the Amundsen Sea Sector, and an enhanced sea-level rise in the corridor between South Africa and Dronning Maud Land. The pattern of $\stackrel{.}{\mathit{S}}(\mathrm{\theta },\mathrm{\lambda },\mathit{t})$ in the corridor is caused, in nearly equal measure, by changes in gravitational attraction between the oceans and the continents [as induced by $\stackrel{.}{\mathit{H}}(\mathrm{\theta },\mathrm{\lambda },\mathit{t})$] and by rotational feedback (see Materials and Methods). Although the values of S(θ, λ, t) are generally one order of magnitude smaller than the values of global H(θ, λ, t), they have a very long wavelength character and form an important component of polar motion excitations (24).

Fig. 2. Climate-induced mass redistribution on Earth’s surface.

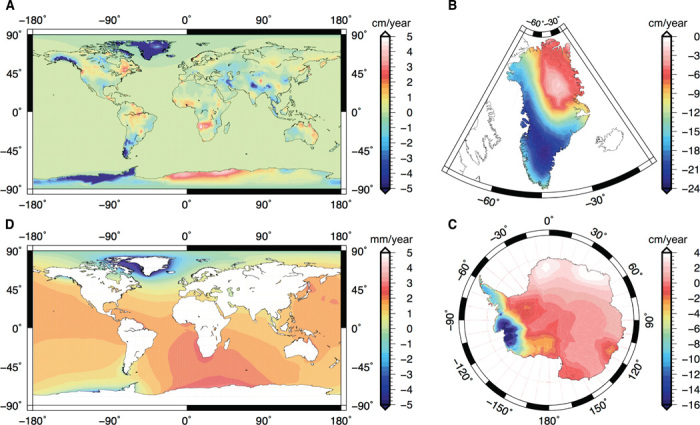
(A) Linear rate of change in mass (in WEH per year) during April 2002 to March 2015, derived from monthly GRACE observations and associated sea-level computations. Solutions are reproduced with different color scales for (B) the GIS, (C) the AIS, and (D) the oceans.

The variations in polar motion induced by polar ice sheets, global GICs, and TWS are shown in Fig. 3A. Because the pole excitations are related to the degree 2 order 1 spherical harmonic (SH) coefficients of L(θ, λ, t), χ₁(t) and χ₂(t) are greatly sensitive to mass changes occurring around ±45° latitudes (fig. S1). Despite the proximity to the poles, the mass of ice sheets is changing so rapidly that they contribute greatly to drift in the pole position. Mass loss from the GIS yields positive ${\stackrel{.}{\mathrm{\chi }}}_1(\mathit{t})$ and negative ${\stackrel{.}{\mathrm{\chi }}}_2(\mathit{t})$ values of similar magnitudes. Positive trends for the AIS-associated χ₁(t) and χ₂(t) are driven by the combination of mass loss from the Amundsen Sea Sector and mass gain in Dronning Maud Land and Enderby Land. Mass loss from the Antarctic Peninsula acts to diminish ${\stackrel{.}{\mathrm{\chi }}}_1(\mathit{t})$ while enhancing ${\stackrel{.}{\mathrm{\chi }}}_2(\mathit{t})$, contributing to a muted rate of χ₁(t) compared to χ₂(t) for the whole of the AIS. A similar interpretation can be made for TWS and global GICs. A large-scale water mass loss from Eurasia, as well as losses from southern South America, produce a large positive TWS-induced ${\stackrel{.}{\mathrm{\chi }}}_2(\mathit{t})$. Glacial mass loss signals of Alaska and Patagonia collectively drive a negative ${\stackrel{.}{\mathrm{\chi }}}_1(\mathit{t})$. In contrast, ${\stackrel{.}{\mathrm{\chi }}}_2(\mathit{t})$ driven by GICs in Alaska, the Canadian Arctic, High Mountain Asia, and Patagonia tend to operate with differing signs and, consequently, yield a muted negative excitation.

Fig. 3. Climate-induced polar motion.

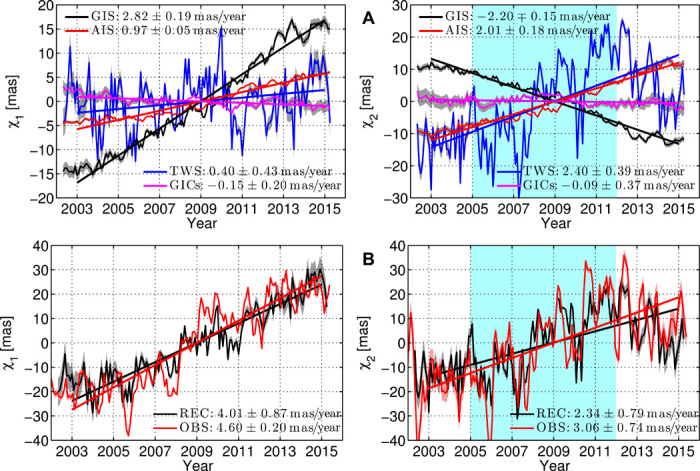
(A) Polar motion excitations caused by four climate-related sources. (B) Total reconstructed (REC) and observed (OBS) excitations. We add global (nontidal) AOM-associated excitations (${\stackrel{.}{\mathrm{\chi }}}_1=-0.03$ and ${\stackrel{.}{\mathrm{\chi }}}_2=0.22$ mas/year) to the reconstructed solutions and remove the 20th century linear trends from the observations (see Materials and Methods). (For ease of comparison, minor smoothing is applied to the observed data.) Large positive gradients during 2005–2012 (cyan shadow), followed by negative trends, are apparent for χ₂(t), and it may be explained by analogous trends associated with TWS [see (A)].

As the space gravimetry time series lengthens, it might be possible to use observations of changes in the spin rate of the pole, proportional to the change in length of day ΔLOD(t), as additional constraints on continent-ocean mass transport. However, the interannual variability of this component of rotation is more strongly influenced by axial angular momentum transfer. Models of this angular momentum transfer currently lack the sophistication required for isolating surface mass transport from these ΔLOD(t) data (25). A separation would allow isolation of the change in Earth’s oblateness ΔJ₂(t), which is fully independent of the SLR-based ΔJ₂(t) used in our analysis. We elaborate on this issue in Materials and Methods.

To model the more complete picture of climate-driven surface mass redistribution, we also consider (nontidal) atmospheric and oceanic mass (AOM) contributions that were removed from the GRACE GSM data products. We use complementary GRACE Release-05 Level-2 GAC solutions to compute the AOM-associated polar motion and to find that its contributions, particularly to χ₂(t), provide some nonnegligible excitations (see Materials and Methods). We now combine the individual contributions of polar ice sheets, global GICs, TWS, and AOM to reconstruct the total climate-driven polar motion. Figure 3B compares our reconstructions with the corresponding components of observed data that are obtained after removing long-term linear trends. Henceforth, we deal only with these detrended time series, unless otherwise specified. The solutions provide an excellent reconciliation of the data: The TWS and the three cryospheric components together explain 88 ± 18% and 70 ± 34% of observed ${\stackrel{.}{\mathrm{\chi }}}_1(\mathit{t})$ and ${\stackrel{.}{\mathrm{\chi }}}_2(\mathit{t})$, respectively. Adding global AOM contribution further improves the fit to ${\stackrel{.}{\mathrm{\chi }}}_2(\mathit{t})$ by an additional 7%. We are also able to reconstruct the sharp changes in direction for χ₂(t) at around 2005 and 2012; although the onset of eastward motion (positive ${\stackrel{.}{\mathrm{\chi }}}_2$) at around 2005 is well documented (11), this reversal of polar motion toward the west after 2012 is a new observation with a causal origin that we can clearly isolate in this analysis. The large amplitude (~20 mas) of the reversal in χ₂(t) in 2012 is comparable to those associated with observed decadal variabilities of polar motion over the past 115 years (3, 4, 6), thus suggesting that it is an emergent decadal-like oscillation. The complete picture of the redirected polar motion is more complicated than can be derived solely from changes in the ice sheets, and the large-amplitude swings must include noncryospheric mechanisms. Comparing polar motion excitations of Fig. 3 (A and B) reveals that TWS is the most plausible causal mechanism for the decadal-like oscillation during the study period (see also table S1); it has previously been identified as the dominant mechanism for annual and semiannual wobbles (26).

This discovery requires a detailed analysis of the spatiotemporal variability of TWS: The trend in the global mass budget of TWS during the study period is small, and there is no anomalous variability in it at around 2012 (see Materials and Methods). However, we find that the spatial patterns of mass redistribution are strikingly different before and after 2012. As seen in Fig. 4, there is almost a complete reversal in wet (excess water mass) and dry (water mass deficit) patterns, and the intensity of wetness and drought has strengthened during 2012–2015. Mass gain in Asia and southern South America, accompanied by enhanced mass loss from western North America and Australia, is collectively consistent with the observed westward drift in polar motion since 2012.

Fig. 4. Spatiotemporal variability in TWS.

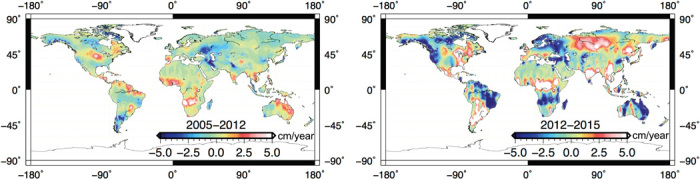
Linear trends in TWS mass redistribution (in WEH per year) during two periods (from January 2005 to December 2011 and from January 2012 to December 2014) derived from monthly GRACE observations.

SUMMARY AND DISCUSSION

Figure 5 summarizes our key discoveries about the changes in polar motion. Mean rates of change in the polar motion vector during 2003–2015, after removing the long-term linear drift signals, are shown in Fig. 5A. The total reconstructed signal has been partitioned to highlight the relative excitation strength of five major climatological components. The global cryospheric excitations alone explain 66 ± 7% of the observed magnitude of the polar motion vector, but the associated drift direction deviates by 38° ± 11°. Combining TWS excitations with cryospheric signals greatly reduces the variance of a fit to the amplitude and direction of polar motion: The reconstructed motion has 83 ± 23% magnitude and is within 5.9° ± 7.6° of the observed (detrended) polar motion (5.52 mas/year along 33.6° East longitude). The data fit to the magnitude is slightly improved (by 1.5%) when we add global AOM contributions, and the direction is better aligned toward the observations by 2.6°. The discrepancies between the observed motion and the reconstructed motion may be partially explained by the uncertainty in the assumed long-term linear trend (see Materials and Methods) or by the net effect of other smaller (motion) excitation mechanisms, including wind stress and ocean current variability. Figure 5B shows a comparison between the total observed mean annual pole position (including the long-term linear trend) and the total reconstructed mean annual pole position. The observed east-west wander of the pole during 2003–2015 is reproduced—owing to the excitation strength of variability in the spatial distribution of TWS—about the mean drift direction that is roughly along the Greenwich meridian.

Fig. 5. Origins of observed polar motion.

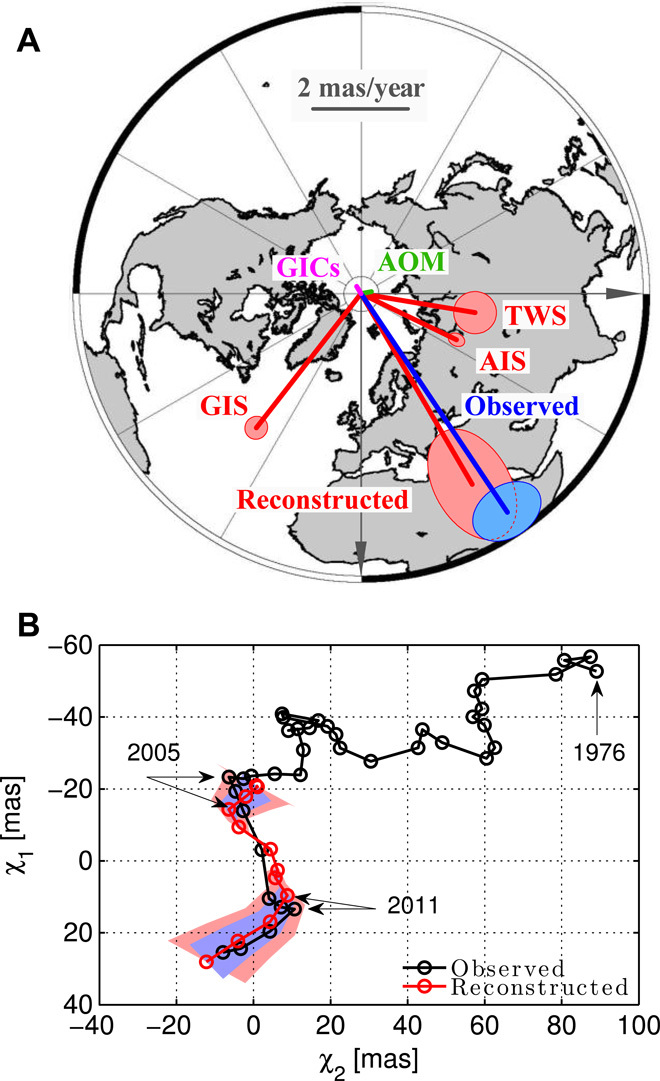
(A) Reconstruction and partition of polar motion during 2003–2015. Observed data have the 20th-century linear trends removed. Semimajor and semiminor axes of error ellipses are defined by the uncertainties in the magnitude and direction of the corresponding polar motion vector. For clarity, we do not show error ellipses for GICs, which have large uncertainties but very small amplitudes (see Materials and Methods) and AOM. (B) Observed (including the long-term linear trend) and reconstructed mean annual pole positions, in the excitation domain, with respect to the 2003–2015 mean position. Blue error band is associated with the reconstructed solution; red signifies additional errors that are related to uncertainty in the long-term linear trend.

Near-decadal shifts in large-scale global wet and dry patterns (Fig. 4), which fully explain an emergent decadal-like oscillation of polar motion, are quite similar to those mapped as a drought index during 1900–1995 based on monthly air temperature and precipitation records (27). We propose that these form the causal mechanism for the long-sought origins of 10- to 20-mas decadal oscillations seen throughout the 115-year polar motion record (3, 4, 6). These are consistent with our current notional understanding of near-decadal shifts in patterns of ocean storage of thermal energy which characterize the current paradigm of decadal changes in continental rainfall and drought (28). The polar motion record may therefore offer yet unexploited information about the intensities, duration, and globality of wet and dry periods, providing possible data constraints on models of past changes in horizontal water vapor transport (29). Such model quantification will have important ramifications for climate change during the 21st century, as we now face an increased intensity of the global water cycle (30, 31).

MATERIALS AND METHODS

Polar motion: Theory and methods

Euler’s equations of classical mechanics that conserve angular momentum form the fundamental equations of motion for a rotating body. Consider body-fixed right-handed Cartesian coordinates with the origin located at the center of mass of the planet. In the present context, where the external torque is absent, we may express Euler’s equations as (32, 33)

$$\frac{\mathit{d}}{\mathit{d}\mathit{t}}[\mathit{h}(\mathit{t})+\mathbf{\omega }(\mathit{t})·\mathit{I}(\mathit{t})]+\mathbf{\omega }(\mathit{t})\times [\mathit{h}(\mathit{t})+\mathbf{\omega }(\mathit{t})·\mathit{I}(\mathit{t})]=0$$ (2)

Here, ω(t) is the angular velocity vector, I(t) is the inertia tensor that changes as a result of the redistribution of Earth’s (surface and interior) mass, and h(t) is the change in angular momentum attributable to motion relative to the rotating reference frame. Because the polar motion is minimally affected by the motion-induced change in angular momentum in the lower-frequency domains (lower than the Chandler wobble frequency) that we are interested in, the following discussion is based on the assumption that h(t) ≅ 0.

In the chosen body-fixed coordinates and assumed initial equilibrium state, the products of inertia tensor vanish (that is, I_ij = 0 for i ≠ j = 1, 2, 3) and the moments of inertia tensor for (assumed) rotationally symmetric Earth are given by I_ii = A (for i = 1, 2) and I₃₃ = C, where A is the mean equatorial and C is the polar moment of inertia. Similarly, components of angular velocity vector are given by ω_i = δ_i3Ω (for i = 1, 2, 3), where δ_i3 is the Kronecker delta and Ω is the mean rotational velocity of Earth. Following the mass redistribution on Earth’s surface, both I(t) and ω(t) are perturbed from their initial equilibrium states. Let ${\mathcal{J}}_{\mathit{i}\mathit{j}}$ and Ωm_i be the respective perturbation terms, where m_i are nondimensional and typically on the order of ≤ 10⁻⁶. Inserting these perturbation terms into Eq. 2 and dropping second- or higher-order terms give the following coupled equation to be solved for m₁(t) and m₂(t) characterizing the rotational pole (32, 33)

$$\left\{\begin{array}{c}{\mathit{m}}_1(\mathit{t})\\ {\mathit{m}}_2(\mathit{t})\end{array}\right\}+\frac{1}{{\mathrm{\sigma }}_{\mathit{r}}}\frac{\mathit{d}}{\mathit{d}\mathit{t}}\left\{\begin{array}{c}-{\mathit{m}}_2(\mathit{t})\\ {\mathit{m}}_1(\mathit{t})\end{array}\right\}={\mathit{k}}_{\mathrm{e}}\left\{\begin{array}{c}{\mathrm{\chi }}_1(\mathit{t})\\ {\mathrm{\chi }}_2(\mathit{t})\end{array}\right\}$$ (3)

Here, σ_r is the Chandler wobble frequency for an elastic Earth (with 433-day periodicity) and k_e is an effective degree 2 Love number that accounts for rotation-induced perturbations in gravitational and rotational potentials (18, 32, 33). The excitation functions are given by

$$\left\{\begin{array}{c}{\mathrm{\chi }}_1(\mathit{t})\\ {\mathrm{\chi }}_2(\mathit{t})\end{array}\right\}=\frac{1}{\mathit{C}-\mathit{A}}\left\{\begin{array}{c}{\mathcal{J}}_{13}(\mathit{t})\\ {\mathcal{J}}_{23}(\mathit{t})\end{array}\right\}+\frac{1}{\mathrm{\Omega }(\mathit{C}-\mathit{A})}\frac{\mathit{d}}{\mathit{d}\mathit{t}}\left\{\begin{array}{c}{\mathcal{J}}_{23}(\mathit{t})\\ -{\mathcal{J}}_{13}(\mathit{t})\end{array}\right\}$$ (4)

Here, the first terms on the right-hand side are directly induced by mass redistribution and, hence, are often called “mass excitation functions” (33).

The IERS reports the pole position vector, with components [X(t) Y(t)]^T, in the celestial reference frame, whereas rotational pole [m₁(t) m₂(t)]^T and excitation pole [χ₁(t) χ₂(t)]^T are computed in the body-fixed terrestrial reference frame. However, for frequencies much lower than the Chandler wobble frequency that we are interested in, the celestial intermediate pole, the rotational pole, and the excitation pole all have virtually the same motion (4, 33), that is

$${[\mathit{X}(\mathit{t})\mathit{Y}(\mathit{t})]}^{\mathrm{T}}\approx {[{\mathit{m}}_1(\mathit{t}){\mathit{m}}_2(\mathit{t})]}^{\mathrm{T}}\approx {[{\mathrm{\chi }}_1(\mathit{t}){\mathrm{\chi }}_2(\mathit{t})]}^{\mathrm{T}}$$ (5)

The low-frequency polar motion estimates provided in this study are essentially those computed from Eq. 4.

To evaluate perturbations in the product of inertia (particularly ${\mathcal{J}}_{13}$ and ${\mathcal{J}}_{23}$ appearing in Eq. 4) induced by climate-driven surface mass redistribution, we defined a mass-conserving loading function, L(θ, λ, t), as in Eq. 1. The loading function and the relevant components of inertia tensor are related as (18)

$${\mathcal{J}}_{\mathit{n}3}(\mathit{t})=-\frac{4\mathrm{\pi }{\mathit{a}}^4}{\sqrt{15}}{\mathrm{\rho }}_{\mathrm{w}}{\mathit{L}}_{21\mathit{n}}(\mathit{t}) \text{for} \mathit{n}=1,2$$ (6)

Here, a is the mean radius of Earth, ρ_w is the water density, and L_21n(t) represents degree 2 order 1 SH coefficients of L(θ, λ, t), which follows from the following orthogonal relationship

$${\mathit{L}}_{21\mathit{n}}(\mathit{t})=\frac{1}{4\mathrm{\pi }}{\displaystyle \int }\mathit{L}(\mathrm{\theta },\mathrm{\lambda },\mathit{t}){\mathcal{𝒴}}_{21\mathit{n}}(\mathrm{\theta },\mathrm{\lambda })\mathit{d}\mathbb{S}$$ (7)

Here, 𝒴_21n(θ, λ) represents the 4π-normalized degree 2 order 1 SHs, with cosine and sine components denoted by n = 1 and n = 2, respectively (18, 34). As shown in fig. S1, the inertia tensor, and hence polar motion, are greatly sensitive to mass changes occurring around ±45° latitudes. The integral appearing in Eq. 7 is applied over the surface domain of a unit sphere $\mathbb{S}$.

Computation of H(θ, λ, t)

To fully define the global loading function (Eq. 1), we computed H(θ, λ, t) by analyzing the GRACE Release-05 Level-2 monthly GSM data products provided by the Center for Space Research at the University of Texas at Austin. The monthly time series of these data were distributed in the form of Stokes coefficients up to SH degree and order 60 (10, 34). Here, we covered a 13-year period, from April 2002 to March 2015. There were only partial or no data available for a few months during the study period, and we filled these data gaps through linear scaling or interpolation between adjacent monthly data, as appropriate. Because GRACE cannot measure the degree 1 Stokes coefficients as a result of its sensitivity only to the center of mass frame, we used those obtained from the analysis of SLR observations (35) or those inferred from the GRACE solutions and ocean model outputs (13). We also replaced degree 2 Stokes coefficients with more accurate SLR-based estimates (14, 36). We did not apply the pole tide correction (37) because its effects on the continental WEH were minimal (on the order of 1%) and our estimates of oceanic mass variations [S(θ, λ, t)] follow from the solutions of the sea-level equation [see Computation of S(θ, λ, t)] that are independent of GRACE-inferred ocean mass redistribution. Nonetheless, the pole tide–associated errors should be within our uncertainty estimates, which were constrained by, among other factors, the plausible range of degree 1 and degree 2 Stokes coefficients (see Polar Motion: Results).

After filling the data gaps and inserting more accurate degree 1 and degree 2 Stokes coefficients as summarized above, we followed the standard procedure to retrieve climate-driven monthly WEH signals, as discussed elsewhere (34, 38). We first obtained the Stokes coefficient anomalies by removing the corresponding mean values during the study period. We calculated the total WEH caused by both the surface mass redistribution and the GIA processes embedded in GRACE data, using a Gaussian filter with a 300-km radius. We isolated the climate-driven WEH by removing the GIA signals provided by A et al. (15) and finally applied appropriate (regional) scaling to account for the so-called leakage effects and attenuated signals. A detailed description of solution scaling and uncertainties thereof is provided in Polar Motion: Results.

Computation of S(θ, λ, t)

The budget of continental mass directly contributes to the sea-level change, via mass conservation. The variability in H(θ, λ, t) on the continents, along with this ocean loading, induces perturbations in the gravitational and rotational potentials of the planet, causing the further redistribution of S(θ, λ, t), which is gravitationally self-consistent. For an elastically compressible rotating Earth, the gravitationally consistent S(θ, λ, t) is given by (18)

$$\mathit{S}(\mathrm{\theta },\mathrm{\lambda },\mathit{t})=\frac{\mathit{a}}{\mathit{M}}[\mathcal{G}(\mathrm{\theta },\mathrm{\lambda })\otimes \mathit{L}(\mathrm{\theta },\mathrm{\lambda },\mathit{t})]+\frac{1}{\mathsf{g}}{\displaystyle \sum _{\mathit{m}=0}^2}{\displaystyle \sum _{\mathit{n}=1}^2}{\mathrm{\Lambda }}_{2\mathit{m}\mathit{n}}(\mathit{t}){\mathcal{𝒴}}_{2\mathit{m}\mathit{n}}(\mathrm{\theta },\mathrm{\lambda })+\mathit{E}(\mathit{t})$$ (8)

Here, M is the total mass of Earth, $\mathsf{g}$ is the acceleration resulting from gravity, $\mathcal{G}(\mathrm{\theta },\mathrm{\lambda })$ is the Green’s function for an elastically compressible Earth that parameterizes the perturbations in gravitational potential and associated solid-Earth deformation, Λ_2mn(t) represents the degree 2 SH coefficients related to perturbations in rotational potential and associated solid-Earth deformation, and E(t) is the eustatic term that follows from the mass conservation constraint. The operator ⊗ appearing in Eq. 8 signifies the spatial convolution over the surface of a unit sphere $\mathbb{S}$.

Computation of S(θ, λ, t) requires a priori knowledge of L(θ, λ, t), which in turn depends on S(θ, λ, t) itself (cf. Eq. 1). We therefore solved the coupled system of Eqs. 1 and 8 using a recursive scheme. All of our calculations were based on a novel mesh-based approach (18), which, unlike contemporary pseudo-spectral methods, remained numerically accurate and computationally efficient as the resolution requirements approached those of contemporary ice sheets or ocean models (on the order of a few kilometers).

Polar motion: Results

Accurate estimates of polar motion induced by the climate-driven global change in L(θ, λ, t) require careful retrieval of H(θ, λ, t) from the GRACE observations. A common practice is to directly compare H(θ, λ, t) obtained from the standard GRACE processing (hereafter termed “original” signal) with more accurate field- and model-based estimates and to scale it accordingly. In this section, we summarize our scaling approach and present estimates of polar motion (Eq. 4). To understand the origins of observed polar motion during the study period (Fig. 1), we partitioned the continental domain $\mathcal{C}(\mathrm{\theta },\mathrm{\lambda })$ into the following four nonoverlapping subdomains that represent unique components of Earth’s climate system: the GIS, the AIS, GICs, and the continental hydrosphere. Although the first three components together characterized the global cryospheric changes, the fourth component accounted for the variability in TWS.

Cryospheric changes

The largest uncertainty in the original H(θ, λ, t) is perhaps related to the GIA correction (15, 38, 39), especially for the AIS (19, 40). The choice of degree 1 and degree 2 Stokes coefficients is also shown to have a considerable impact on WEH estimates for polar ice sheets (16, 38). Using a suite of GIA models and various choices of low-degree Stokes coefficients, Schrama et al. (16) provided a rigorous estimate of mass evolution and uncertainties thereof for the entire GIS, three nonoverlapping subdomains of the AIS, and 15 glaciated regions that cover the global GICs. Their estimates are generally consistent with other published results (19–23, 38, 40), and we scaled our estimates such that the trend in total mass and uncertainties thereof were reproduced during the common time span. The corresponding solutions and uncertainties of χ₁(t) and χ₂(t) presented below account for the lump-sum effects of GIA, degree 1 and degree 2 Stokes coefficients, leakage errors, and signal attenuation.

Our domain of the GIS covered the ice sheet and peripheral GICs. We scaled the original H(θ, λ, t) for the entire domain by a factor of 1.64 (16, 19) so that the total mass loss during the study period is about −278 ± 19 Gt/year (fig. S2). Pervasive and sustained thinning of the southern GIS, as seen in the figure, was consistent with other published results (19, 22, 40) and was attributed to the combination of negative surface mass balance and enhanced outflux (19). The associated loss in gravity anomaly was reflected in the “sea-level fingerprint” (fig. S2A) that shows the drop in local sea level and the rise elsewhere, particularly around East Asia and the Drake Passage between the Antarctic Peninsula and southern South America. Our estimates of GIS-driven polar motion are shown in fig. S2B. We found that the GIS promoted a positive ${\stackrel{.}{\mathrm{\chi }}}_1$ (2.82 ± 0.19 mas/year) and a negative ${\stackrel{.}{\mathrm{\chi }}}_2$ (−2.20 ∓ 0.15 mas/year), consistent with the signatures of relevant SHs (cf. fig. S1). Because our error estimates were based on the basic assumption that the spatial pattern of H(θ, λ, t) is relatively stable, these could not fully quantify the uncertainties in drift direction. However, here, we considered the maximum uncertainty obtained from four possible combinations of limiting values of ${\stackrel{.}{\mathrm{\chi }}}_1(\mathit{t})$ and ${\stackrel{.}{\mathrm{\chi }}}_2(\mathit{t})$. Consequently, the GIS causes the pole position vector to drift along 37.96° ± 3.82° West longitude at a rate of 3.58 ± 0.24 mas/year during the study period.

Our AIS domain comprised the continental ice sheet and the relatively small peripheral GICs. We applied scaling factors of 1.16, 1.43, and 2.08 for the West AIS, the East AIS, and the Antarctic Peninsula, respectively (16, 19, 38). Although the net budget of the entire AIS is negative (−92 ± 26 Gt/year), the East AIS has gained mass at a rate of about 80 ± 16 Gt/year as a result of increased precipitation (19). Large losses are recorded for the West AIS (−137 ± 7 Gt/year) and the Antarctic Peninsula (−35 ± 3 Gt/year) as a consequence of accelerated ice dynamics and, to a lesser degree, increasingly negative surface mass balance (19, 20). The spatial distribution of $\stackrel{.}{\mathit{H}}(\mathrm{\theta },\mathrm{\lambda },\mathit{t})$ for the entire AIS is shown in fig. S3. High rates of ice loss along the Amundsen Sea Sector and the moderate rates of loss in the Antarctic Peninsula and gain in Dronning Maud Land and Enderby Land, as seen in the figure, are consistent with numerous reports of mass changes that are comparable to the time span of our study (19, 20, 22, 40). The associated $\stackrel{.}{\mathit{S}}(\mathrm{\theta },\mathrm{\lambda },\mathit{t})$ shown also suggests a large drop in local sea level around the Amundsen Sea Sector and a rise around Dronning Maud Land and Enderby Land. We computed the corresponding polar motion and found that ${\stackrel{.}{\mathrm{\chi }}}_1(\mathit{t})=0.97\pm 0.05$ mas/year and ${\stackrel{.}{\mathrm{\chi }}}_2(\mathit{t})=2.01\pm 0.18$ mas/year (fig. S3C). The positive rates for both χ₁(t) and χ₂(t) were consistent with mass loss from the Amundsen Sea Sector and mass gain in Dronning Maud Land and Enderby Land. Mass loss from the Antarctic Peninsula acted to diminish ${\stackrel{.}{\mathrm{\chi }}}_1(\mathit{t})$ while enhancing ${\stackrel{.}{\mathrm{\chi }}}_2(\mathit{t})$, contributing to a muted rate of χ₁(t) that was causally related to the entire AIS (cf. fig. S1). Following the same approach as for the GIS, we sourced the AIS-driven components of the polar motion vector to a direction along 64.24° ± 3.37° East longitude of amplitude 2.23 ± 0.18 mas/year during the study period.

We formed a global GIC domain by creating 15 nonoverlapping regions (fig. S4). Our regional masks for mass change determination were based on the fraction of 0.5° × 0.5° global grids covered by regional GICs (21). We mapped this gridded information onto our computational mesh (18) by using an anisotropic mesh refinement algorithm so that the finer mesh, with a characteristic element size on the order of 10 km, is used in the glaciated regions. We then assumed that any element with ≥ 1% ice coverage has a GRACE signal dominated by GIC changes, and we defined the regional mask accordingly. Some of these regions have lost mass at a great pace, whereas others did not exhibit significant long-term trends during the span of our study (fig. S5). Alaska (−42.1 ± 6.8 Gt/year), the North Canadian Arctic (−33.9 ± 3.3 Gt/year), the South Canadian Arctic (−28.4 ± 1.9 Gt/year), Patagonia (−19.5 ± 4.8 Gt/year), and High Mountain Asia (−8.6 ± 0.6 Gt/year) are the areas with the greatest loss. We individually scaled all of these 15 regions to derive H(θ, λ, t) for global GICs. (See fig. S4A for $\stackrel{.}{\mathit{H}}(\mathrm{\theta },\mathrm{\lambda },\mathit{t})$ during the study period.) The associated computation of $\stackrel{.}{\mathit{S}}(\mathrm{\theta },\mathrm{\lambda },\mathit{t})$ suggests a considerable sea-level drop in the region north of ≈ 45° latitude. Figure S4B summarizes our estimates of polar motion excitations. By combining polar motions driven by individual regions, we found minimal overall contributions of global GICs with relatively large uncertainties: ${\stackrel{.}{\mathrm{\chi }}}_1(\mathit{t})=-0.15\pm 0.20$ mas/year and ${\stackrel{.}{\mathrm{\chi }}}_2(\mathit{t})=-0.09\pm 0.37$ mas/year. Figure S1 shows that glacial mass loss in Alaska and Patagonia collectively drives a negative ${\stackrel{.}{\mathrm{\chi }}}_1(\mathit{t})$. Similarly, χ₂(t) caused by GICs in Alaska, the Canadian Arctic, High Mountain Asia, and Patagonia tends to operate with differing signs, and hence yields a rather muted (negative) ${\stackrel{.}{\mathrm{\chi }}}_2(\mathit{t})$.

TWS changes

Excluding the cryospheric domains, the mass redistribution in the continents may be interpreted as the TWS changes. By definition, we may express the TWS, W(θ, λ, t), as follows (41)

$$\mathit{W}(\mathrm{\theta },\mathrm{\lambda },\mathit{t})=-[\mathit{V}(\mathrm{\theta },\mathrm{\lambda },\mathit{t})+{\displaystyle \int }\nabla \mathit{Q}(\mathrm{\theta },\mathrm{\lambda },\mathit{t})\mathit{d}\mathit{t}]-{\displaystyle \int }\mathit{R}(\mathrm{\theta },\mathrm{\lambda },\mathit{t})\mathit{d}\mathit{t}$$ (9)

Here, V(θ, λ, t) is the vertically integrated water vapor anomaly, ∇Q(θ, λ, t) is the divergence of the horizontal water transport, and R(θ, λ, t) is the runoff. The first term on the right-hand side is equivalent to the difference between precipitation and evapotranspiration. If we evaluate Eq. 9 on a monthly time interval during the study period, the TWS signal would essentially be the same as the monthly WEH signal derived from the GRACE observations, or W(θ, λ, t) ≡ H(θ, λ, t).

Figure S6A shows the linear trend in the original H(θ, λ, t) that needs to be scaled appropriately. Landerer and Swenson (17) analyzed monthly TWS signals obtained from the GRACE observations and the Noah land surface model, simulated within the Global Land Data Assimilation System (GLDAS-Noah), and derived global gridded gain factors (fig. S6B). These scaling factors, when applied to the original H(θ, λ, t), helped to correct for the leakage errors and to restore the attenuated signals. Relatively large gain factors along the coasts, as seen in the figure, implied that a large signal loss prevails between the oceans and the continents. Figure S6C shows the corrected $\stackrel{.}{\mathit{H}}(\mathrm{\theta },\mathrm{\lambda },\mathit{t})$ and associated variations in $\stackrel{.}{\mathit{S}}(\mathrm{\theta },\mathrm{\lambda },\mathit{t})$ during the study period. The feature that stands out in the present context of polar motion is a strong and large-scale, negative TWS signal around Eurasia (the Indian subcontinent and the Caspian Sea). This and the global signals are consistent with the general picture that has emerged from the GRACE monthly variability on continental land masses (23, 42, 43). Such variability in global TWS induces changes in sea level such that it rises in the Atlantic Ocean and falls around the Drake Passage and the Asia Pacific.

The total TWS mass evolution and our estimates of polar motion are plotted in fig. S6D. The trends in global mass budget are small for both the original and the corrected TWS signals, implying that the net contribution of TWS to the global mean sea level is minimal. The patterns of polar motion are generally unaffected by the gain factors: The reversal in χ₂(t) since about 2012, for example, is apparent for both the original and the corrected TWS changes. However, we found some sensitivity of gain factors on the solved-for linear trend in polar motion, particularly for χ₁(t), and this forms the basis of our uncertainty estimates. There is no physically or statistically rigorous basis for defining the uncertainties for TWS-driven polar motion, and we simply considered the solutions associated with the original TWS signals as the limiting values. Consequently, the respective contributions of TWS variability and uncertainties to ${\stackrel{.}{\mathrm{\chi }}}_1(\mathit{t})$ and ${\stackrel{.}{\mathrm{\chi }}}_2(\mathit{t})$ are 0.40 ± 0.43 and 2.40 ± 0.39 mas/year. This suggests that the robust changes in TWS cause the polar motion vector to drift along 80.5° ± 8.7° East longitude at a rate of about 2.43 ± 0.45 mas/year during the study period.

Nontidal AOM variability

There is nontidal AOM contribution to Earth’s surface mass redistribution that is not included in the GRACE GSM solutions. The AOM-associated Stokes coefficients, which are provided as complementary GRACE GAC solutions, are computed from the European Centre for Medium-Range Weather Forecast (ECMWF) operational atmospheric model and the baroclinic Ocean Model for Circulation and Tides (OMCT) driven by the same atmospheric model. We estimated corresponding polar excitations using the following linear relationship (11)

$$\left\{\begin{array}{c}{\mathrm{\chi }}_1(\mathit{t})\\ {\mathrm{\chi }}_2(\mathit{t})\end{array}\right\}=\frac{-\sqrt{5}}{\sqrt{3}(1+{\mathit{k}}_2^{\prime })}\frac{1.098{\mathit{a}}^2\mathit{M}}{\mathit{C}-\mathit{A}}\left\{\begin{array}{c}\mathrm{\Delta }{\mathit{C}}_{21}(\mathit{t})\\ \mathrm{\Delta }{\mathit{S}}_{21}(\mathit{t})\end{array}\right\}$$ (10)

Here, ΔC₂₁(t) and ΔS₂₁(t) are the Stokes coefficients and ${\mathit{k}}_2^{\prime }$ is the degree 2 load Love number. Results are shown in fig. S7. The figure shows, as expected, that the global AOM variability induces high (seasonal) amplitude excitations. We found that the AOM had negligible contribution to ${\stackrel{.}{\mathrm{\chi }}}_1$ (−0.03 mas/year), but it had sizable effects on ${\stackrel{.}{\mathrm{\chi }}}_2$ (0.22 mas/year) during the study period.

Observed and reconstructed polar motion

To compare our estimates of polar motion with the observed data (Fig. 1), it is first necessary to remove the long-term trends from the observations. Here, we considered the GIA-driven true polar wander along 75° West longitude at a rate of 0.85° (great-circle distance) per million years (5) as the long-term trend of the pole position vector. Other estimates that are mostly inferred from ~100 years of polar motion record are generally within the 25% uncertainties (1, 2, 44, 45). Therefore, we used ${\stackrel{.}{\mathrm{\chi }}}_1(\mathit{t})=0.79\pm 0.20$ mas/year and ${\stackrel{.}{\mathrm{\chi }}}_2(\mathit{t})=-2.95\pm 0.74$ mas/year as the long-term trends. Subtracting these from the observed rates of ${\stackrel{.}{\mathrm{\chi }}}_1(\mathit{t})=5.39$ mas/year and ${\stackrel{.}{\mathrm{\chi }}}_2(\mathit{t})=0.11$ mas/year (during 2003–2015) gave ${\stackrel{.}{\mathrm{\chi }}}_1(\mathit{t})=4.60\pm 0.20$ mas/year and ${\stackrel{.}{\mathrm{\chi }}}_2(\mathit{t})=3.06\pm 0.74$ mas/year. In what follows, we quantify how much of these detrended motions are explained by the cryospheric mass changes alone (11) and how many improvements we make to a data fit through rigorous incorporation of TWS and global AOM signals.

Table S1 summarizes ${\stackrel{.}{\mathrm{\chi }}}_1(\mathit{t})$ and ${\stackrel{.}{\mathrm{\chi }}}_2(\mathit{t})$ during the study period. By combining the AIS, the GIS, and global GIC signals, we found that the total cryospheric changes accounted for ${\stackrel{.}{\mathrm{\chi }}}_1(\mathit{t})=3.64\pm 0.44$ mas/year and ${\stackrel{.}{\mathrm{\chi }}}_2(\mathit{t})=-0.28\pm 0.70$ mas/year, and caused the pole position vector to drift along 4.4° ± 11.4° West longitude at a rate of 3.65 ± 0.38 mas/year. This suggests that the global cryospheric changes explain only about 66.0 ± 6.8% of the observed (detrended) polar motion and predict the mean drift direction within 38.0° ± 11.4°. By adding TWS signals, we obtained ${\stackrel{.}{\mathrm{\chi }}}_1(\mathit{t})=4.04\pm 0.87$ mas/year and ${\stackrel{.}{\mathrm{\chi }}}_2(\mathit{t})=2.12\pm 1.09$ mas/year, which is a great reduction in the variance of a fit to the data (by about 66% for χ₁ and by about 92% for χ₂). As a consequence, our total reconstruction of the pole position vector predicted a drift along 27.7° ± 7.6° East longitude at a rate of 4.56 ± 1.26 mas/year. This means that the TWS excitations, when combined with cryospheric signals, reduce the variance of a fit to the magnitude of the pole position vector by 74% and to the direction of the pole position vector by 97%, and explain nearly the entire amplitude (82.6 ± 22.8%) and mean directional shift (within 5.9° ± 7.6°) of the observed (detrended) polar motion. The data fit to the magnitude was slightly improved (by 1.5%) as we added the global AOM contributions, and the direction was further aligned toward the observations by 2.6°.

Use of ΔLOD(t) as an additional constraint on ΔJ₂(t)

Lunar Laser Ranging (LLR) has been operating since 1970 and has provided accurate determination of the rate of slowing of the axial rotation by the transfer of angular momentum from Earth to the lunar orbit by tidal dissipation (46). The slowing may, for example, be expressed as ω₃(t) = Ω[1 + m₃(t)]. The rate of deceleration ${\stackrel{.}{\mathit{m}}}_3(\mathit{t})$ is effectively secular on a time scale of 10 million years. Although the rate of slowing is roughly consistent with ancient eclipse observations that constrain the secular ΔLOD(t) (33), there is a systematic offset in the time of recorded eclipses (47). The offset in the LLR-determined m₃(t) (from that observed in eclipse data) is, in fact, consistent with an additional slight secular increase in the rotation rate caused by a change in the polar moment of inertia C due to GIA (48). GIA processes are uncomplicated by angular momentum transfer, and a linear relation exists between the change in Earth’s gravitational bulge [that is, $\mathrm{\Delta }{\mathit{J}}_2^{\mathrm{G}\mathrm{I}\mathrm{A}}(\mathit{t})$] and the associated secular nontidal ΔLOD^GIA(t).

A natural question to ask concerning our focus on the period of space geodetic observations is whether a ΔLOD(t) time series might contain additional information that constrains cryospheric and hydrological mass variability on interannual time scales. However, the motion terms in the excitation function associated with zonal winds and ocean currents have a relatively strong influence on the ΔLOD(t) time series (4). On centennial time scales, these angular momentum exchanges have comparatively short periods, and ΔLOD(t) can be adequately described by the mass terms in the excitation function. However, for data taken since the mid-1970s, when SLR data first became available for directly constraining $\mathrm{\Delta }{\mathit{J}}_2(=-\sqrt{5}\mathrm{\Delta }{\mathit{C}}_{20})$, angular momentum (motion) terms have a non-negligible contribution to ΔLOD(t) observations, and the physical models that drive such motions must be carefully considered. A recent analysis (49) of the IERS time series for ΔLOD(t) has attempted to isolate the motion excitations and thus deduce a ΔLOD(t) proxy for ΔJ₂(t), potentially providing a consistency check on SLR-based ΔJ₂(t) observations (36, 49, 50). However, in addition to the angular momentum transfer within Earth’s surface fluid envelope, a relatively poorly modeled angular momentum coupling between the mantle and the core must also be considered. This fact necessitates using a filter to remove 7-year and longer periodicities (49) from ΔLOD(t) and suggests that useful inferences of large-scale surface mass transport from axial changes in rotation during the 13-year GRACE time series considered in our analysis will be quite difficult to obtain.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/4/e1501693/DC1

Fig. S1. SHs of degree 2 order 1.

Fig. S2. GIS and polar motion excitations.

Fig. S3. AIS and polar motion excitations.

Fig. S4. Global GICs and polar motion excitations.

Fig. S5. Mass evolution of regional GICs.

Fig. S6. TWS and polar motion excitations.

Fig. S7. Polar motion excitations due to nontidal AOM variability.

Table S1. Polar motion excitation rates for different time periods.