Computational modeling of cardiac fibroblasts and fibrosis

Abstract

Altered fibroblast behavior can lead to pathologic changes in the heart such as arrhythmia, diastolic dysfunction, and systolic dysfunction. Computational models are increasingly used as a tool to identify potential mechanisms driving a phenotype or potential therapeutic targets against an unwanted phenotype. Here we review how computational models incorporating cardiac fibroblasts have clarified the role for these cells in electrical conduction and tissue remodeling in the heart. Models of fibroblast signaling networks have primarily focused on fibroblast cell lines or fibroblasts from other tissues rather than cardiac fibroblasts, specifically, but they are useful for understanding how fundamental signaling pathways control fibroblast phenotype. In the future, modeling cardiac fibroblast signaling, incorporating -omics and drug-interaction data into signaling network models, and utilizing multi-scale models will improve the ability of in silico studies to predict potential therapeutic targets against adverse cardiac fibroblast activity.

Introduction

Fibroblasts are integral to the normal structure and function of the heart. During development, fibroblasts deposit extracellular matrix (ECM) to provide structural integrity of the myocardium [1,2]. Throughout life, fibroblasts maintain and remodel the ECM in response to the environment and act as sentinel cells, integrating the tissue’s response to various mechanical, chemical, and electrical cues [2,3]. For example, fibroblasts play a role in initiating and resolving the inflammatory response following myocardial injury such as infarction [4]. Finally, it is increasingly clear that fibroblasts are electrically coupled to myocytes and contribute to the electrical properties of the myocardium [2,3,5].

Cardiac injury, such as an infarct, prompts changes in fibroblast activity that can be helpful or pathologic. Following an infarct, inflammatory cytokines induce migration of fibroblasts into the tissue that are, at later stages of healing, induced to deposit collagen and differentiate into pro-fibrotic myofibroblasts. A balance of ECM production and degradation is necessary to prevent excessive loss of matrix proteins which can increase risk of wall rupture and infarct expansion [6], or excessive matrix production which can lead to increased interstitial fibrosis even in areas distant from the infarct [7]. Activated myofibroblasts have been observed in human cardiac tissue many years after an infarct, indicating the potential for long-term tissue remodeling by fibroblasts [8]. Fibroblast activation can be triggered by many other forms of cardiac injury including pressure overload [1], diabetes [9], and infectious diseases such as Chagas disease[10] or Coxsackie B3 infection [11].

Not only does fibroblast activity change in response to injury and disease, but altered fibroblast matrix production can also provoke disease. For example, myxomatous valve disorders are associated with an increase in matrix metalloproteinase (MMP) production by myofibroblasts without an increase in collagen expression leading to a loss of structural integrity in the valve [12]. Increased ventricular fibrosis is associated with a worse prognosis and worsened diastolic dysfunction [13,14]. Fibrosis is also implicated in conduction abnormalities that increase risk for arrhythmia [3,15]. Restoring the balance of fibroblast activity could be a valuable therapeutic approach, which would rely on a more complete understanding of fibroblast regulation and function.

Yet the complexity of cardiac fibroblasts and fibrotic tissue hinders such an understanding. Teasing apart the competing roles of fibroblasts in response to mechanical, chemical, and electrical cues is difficult to do experimentally. When closely integrated with experimental studies, computational models can provide a powerful framework for developing a quantitative understanding of complex biological systems. Indeed, computational models of cardiomyocytes have long been employed to make substantial insights into cardiac electrophysiology, mechanics, and signaling networks, as recently reviewed elsewhere [16,17]. Increasingly, computational models have also begun to provide important insights into cardiac fibroblasts and cardiac fibrosis. Here, we review the contributions of computational modeling to the field’s understanding of how fibroblasts modulate electrical conduction, coordinate tissue remodeling, and integrate signals. We then outline future directions for improving modeling of cardiac fibroblasts toward a better understanding of the role of fibroblasts in heart disease and targeted design of therapeutic strategies.

Section 1: Electrophysiological Modeling

Fibroblasts play a role in electrical conduction through the heart both indirectly through regulation of extracellular matrix proteins and directly by connecting to cardiac myocytes [18,19]. Fibroblasts have been shown to conduct electrical activity through direct connection to myocytes via gap junctions composed of Cx43 and Cx45 [3,20]. Their resting membrane potential in vitro is primarily determined by K+ currents and was measured around at −60mV [5]. Fibroblasts alter myocyte electrical behavior in vitro by raising their resting membrane potential and by slowing conduction velocity [21]. Here we review how computational modeling has been used to better understand how electrical coupling to fibroblasts modulates both cardiac myocyte and tissue electrophysiology.

1.1 Linking Fibroblasts to Cardiac Myocytes

Kohl et al. developed the first computational model linking fibroblasts and cardiac myocytes, applying it to test the hypothesis that mechanosensitive fibroblasts modulate the spontaneous firing rate of the sinoatrial node (SAN) [22]. They modeled fibroblasts as electrically passive (lacking voltage-dependent ion currents) but responsive to mechanical stretch. When coupled to a single myocyte, this model predicted that fibroblasts increased the rate of SAN firing in response to stretch, consistent with previous studies. Further, the model was able to predict how variations in the coupling between fibroblasts and myocytes would affect these responses [22]. The Oxsoft model was later expanded by linking it with the Kurata rabbit SAN model and was used to examine how fibroblasts affect SA node activity [23]. The model predicted that fibroblasts act as electrical sinks and slow conduction from SAN to atrium. This could provide a mechanistic link between age-associated increases atrial conduction times and atrial fibroblast numbers.

While early models represented fibroblasts as electrically passive, the MacCannell model was the first to incorporate active, voltage-dependent ion currents based on patch clamp measurements from isolated cardiac fibroblasts [24]. This electrically active fibroblast model was coupled to the ten Tusscher model of cardiac myocyte electrophysiology, which has experimentally-based parameters for ion current densities and gating kinetics from human ventricular myocytes and in vivo data [25]. The MacCannell model described the fibroblast’s electrical activity based on four currents: a delayed-rectifier K+ current, an inward-rectifying K+ current, a Na+-K+ pump, and a “leak” Na+ current. The parameters for the delayed-rectifier K+ current were derived experimentally, while the parameters for the inward-rectifying K+ current were estimated from the ten Tusscher model. This “active” model was more accurate than a comparable “passive” model of fibroblast activity, which lacked voltage-dependent ion currents. This model predicted that fibroblasts would partially depolarize the resting membrane potential for myocytes and shorten the action potential duration (Figure 1A), which agrees with experimental studies[3]. This model was subsequently adapted for use in several models of tissue-level conduction as described below.

Figure 1. Electrical Behavior of Fibroblasts.

(A) The MacCannell model predicts myocyte action potential duration and fibroblast potential elevation are shortened as the number of fibroblasts connected to myocytes is increased. Figure adapted with permission by Biophysical Journal from MacCannell et al 2007 [24]. (B) Predictions from the Ashihara model show that increased numbers of fibroblasts connected to a myocyte can slow conduction (dashed arrow) or even cause conduction block (double lines). Figure adapted with permission by Circulation Research from Ashihara et al 2012 [37].

Around the same time, Jacquemet et al. published a more phenomenological model that described the voltage-dependence of fibroblast ion currents as a polynomial fit to in vitro data[26]. They coupled the fibroblast to a model of a mouse myocyte[27] as a single fibroblast-myocyte pair or a strand of myocytes covered with a layer of fibroblasts. Increasing myocyte-fibroblast coupling and increasing fibroblast activity decreased the conduction velocity and prolonged action potential duration. Importantly, they predicted that the fibroblast’s resting membrane potential was an important determinant of the effect on the myocyte. When the myocyte membrane potential was more negative than the fibroblast, the fibroblast acted as a source of current, but the fibroblast acted a current sink when the myocyte potential was less negative. A later modification of this model retained the same fibroblast-myocyte organization but used a model of a canine atrial myocyte[28] coupled to the MacCannell model[29].This model predicted the myocyte resting membrane potential would be higher with increased fibroblast-myocyte coupling, in agreement with the MacCannell model. They determined that a lower fibroblast resting membrane potential shortens the action potential duration (APD), while a higher resting membrane potential prolongs the APD. This reconciles the apparent contradiction between the findings in their previous study and those in the MacCannell study using the same conclusion that the relative difference between the myocyte and fibroblast membrane potentials determines the effect on electrical conduction.

Others have used a more detailed Markov model of the fibroblast time- and voltage-dependent outward K+ current and reached the same conclusion that the relative membrane potentials of the two cells is important for determining the effect of fibroblasts on electrical activity[30]. Additionally, the model predicted that increased heterocellular coupling (through decreased myocyte-fibroblast resistance) intensified the effect of fibroblasts on electrical activity. Overall, these studies and others[31–33], provide quantitative support for hypothesis that fibroblasts affect the electrical activity of cardiomyocytes by acting as a current source or sink depending on the context. The Sachse model used four arrangements of myoctes and fibroblasts that are simplifications of organizations that could be observed in vivo. For example, fibroblasts forming a bridge between chains of myocytes, as would be found in focal fibrosis, were predicted to lead to conduction block, which was consistent with in vitro studies[20]. Together these studies provide a basis for understanding how coupling to a fibroblast affects myocyte resting potential and action potential, and applying these simplified models to more complex heterocellular arrangements allows for an increased understanding of tissue-level electrical conduction and arrhythmia.

1.2 Modeling Fibroblast Contribution to Ventricular Arrhythmia

A number of studies have built upon these models of conduction velocity to examine the impact of fibroblasts on ventricular arrhythmia. In a highly influential study, Zlochiver et al. combined experimental and computational approaches to examine the role of myofibroblast-myocyte coupling on reentrant arrhythmias[34]. Their model coupled an active myofibroblast model to the Viswanathan model of a ventricular myocyte[34,35] to simulate electrical propagation in a co-culture of myofibroblasts and myocytes. The arrangement of the cells was designed to match the experimental arrangements measured in vitro. Their model predicted that increased myofibroblasts would decrease reentry of a spiral wave but would increase the complexity of the electrical propagation (increased phase singularities). Further, an increase in myofibroblast-myocyte and myofibroblast-myofibroblast coupling decreased phase singularities but had a biphasic relationship with conduction velocity, with the lowest conduction velocity occurring at intermediate myofibroblast density. These findings were remarkably consistent with data from their co-culture experiments[34]. The biphasic relationship between conduction velocity and myofibroblast coupling highlights the potential for fibroblasts either to contribute to or protect against conduction abnormalities.

Other models have expanded on the detailed MacCannell fibroblast model to explore how fibroblasts contribute to arrhythmia development. The Zlochiver group later developed a model based on the MacCannell model linked to the ten Tusscher model with fibroblasts arranged as a layer on top of a sheet of myocytes (bilayer model) or interspersed between the myocytes as a monolayer[36]. This model predicted a biphasic relationship between spontaneous depolarization frequency that peaks at intermediate fibroblast/myocyte ratios. However, they found that stability of the reentrant wave decreases with increased fibroblast density and increased fibroblast-myocyte coupling, which is in contrast to the Zlochiver model. The most likely reason they cited for the discrepancy was that the previous model assumed that fibroblasts and myocytes were the same size. While this assumption may be appropriate in vitro, this newer model represented the in vivo case where fibroblasts are much smaller than myocytes.

There are also other factors regarding fibroblasts and extracellular matrix that differ between in vitro and in vivo experiments. Ashihara et al. adapted the MacCannell model to model fibroblasts or myofibroblasts and coupled it to the Courtmanche human atrial model[37]. Myofibroblasts were represented as fibroblasts with increased capacitance. They found that both fibroblasts and myofibroblasts shortened action potential duration and that areas of high fibroblast or myofibroblast density slow conduction (Fig. 1B) and are arrhythmogenic, but that fewer myofibroblasts than fibroblasts are sufficient to induce conduction block. Simulation of ablation in those areas prevented reentry, providing a rationale for the treatment of arrhythmia with ablation.

Myocardial infarction is a risk factor for the development of arrhythmia. McDowell et al. integrated the MacCannell model into a finite element model (FEM) based on an MRI of a rabbit heart to investigate how fibroblasts in the infarct zone and peri-infarct zone affect electrical conduction throughout the heart [38]. As predicted by the Jacquemet model [29], this model predicted that the fibroblasts act as a current sink during the action potential to shorten APD, but during rest the fibroblasts act as a current source and raise the resting membrane potential. Furthermore, the resting membrane potential was higher with increased myofibroblast-myofibroblast coupling within the scar and was further increased with a higher density of myofibroblasts in the infarct zone. Their model also predicted that intermediate levels of myofibroblasts in the peri-infarct zone are arrythmogenic because there is a dispersal of the APD, but at higher densities the myofibroblasts act as a current sink to limit reentry. Together these studies indicate that fibroblasts can support arrhythmia by increasing the heterogeneity of electrical conduction, but they can limit arrhythmia by slowing conduction or facilitating conduction depending on the strength of fibroblastmyocyte or fibroblast-fibroblast connection. As the electrical properties of fibroblasts in vivo are clarified (recently reviewed by Kohl et al. [39]), updates on these models can incorporate more accurate parameters and improve our understanding of the role of fibroblasts in modulating electrical activity in the heart.

Section 2: Fibroblasts and Tissue Remodeling

The extracellular matrix is a critical determinant of cardiac mechanics, and abnormal quantity or organization of matrix can lead to both systolic and diastolic dysfunction. Many past studies have used computational modeling to demonstrate the acute mechanical effects of cardiac matrix structure and organization [40–44]. Herein, we focus our review on models that predict fibroblast-mediated, long-term changes in scar structure, i.e. growth and remodeling during wound healing and/or fibrosis. Cardiac fibroblasts drive matrix turnover through an orchestrated balance of matrix protein secretion and processing (e.g., collagen I, collagen III, fibronectin, elastin, etc.), proteinase secretion and activation (e.g., MMP 1, 2, 3, 7, 8, 9, 12, 13, 14, etc.), and proteinase inhibitor secretion and activation (e.g., tissue inhibitor of metalloproteinases (TIMP) 1, 2, 3, 4) (see reviews by Creemers [45], Lindsey [46], and Vanhoutte [47]). Fibroblasts can also organize matrix structure by exerting acto-myosin generated contractile forces on matrix fibers via focal adhesions [48,49], and by directing the deposition of matrix fibers with preferred orientations parallel to the cells’ own orientations [50–52]. Fibroblast-mediated turnover and fibroblast-mediated remodeling are both sensitive to chemical and mechanical environmental cues that can dramatically change during disease conditions [53,54]. The relationships between local signals and long-term matrix remodeling have therefore been the focus of a number of computational studies, which have varied in modeling framework and biological complexity. Here we divide the studies by the biological components explicitly included in their simulations: matrix only, matrix plus fibroblasts, or matrix plus multiple cell types.

2.1 Matrix-Only Models

Extracellular matrix growth and remodeling across diverse tissues has been predicted using a variety of computational frameworks including simple ODE (ordinary differential equation) models, FEMs, constrained mixture models, agent-based models, and others. To our knowledge, the first simulations focusing specifically on cardiac matrix remodeling were performed by Driessen and colleagues to test the effects of mechanical loading on collagen fiber orientations in the aortic valve. In a series of studies [55–57], they used an FEM of the aortic valve geometry and loading to calculate strain and stress distributions throughout the valve. Assuming that steady-state fiber content increases linearly with stretch² and that fibers tend to align according to positive principal strain directions, matrix remodeling simulations were conducted stepwise with new matrix structure (and corresponding new material parameters) calculated in remodeling steps, then new tissue strains calculated in FEM steps. Over time, these straight-forward assumptions proved to be sufficient to successfully generate the distinctive, fiber architecture experimentally observed in mature valves with fibers running from commissure to commissure.

2.2 Matrix & Fibroblast Models

Some of the earliest models explicitly combining fibroblasts with matrix remodeling were formulated by Dallon and colleagues, who simulated fibroblast-mediated dermal wound healing by simulating matrix properties as a continuous 2D-vector field and fibroblasts as discrete elements migrating in that field [58,59]. In these simulations, fibroblasts oriented themselves by averaging their previous orientation direction with the local collagen fiber direction, then migrated, reoriented existing collagen, and laid down new collagen according to prescribed rate parameters. Not surprisingly, the long-term matrix alignment and content was highly dependent on a variety of parameters including initial cell positions, cell speed, cell persistence, fiber reorientation rate, initial fiber alignment, fiber production rate and others. In two later studies, Dallon et al. [60] and McDougall et al. [61] improved upon their basic model to include the effects of chemical signals in the wound territory. Specifically, the concentrations of tissue growth factor beta (TGFβ) and a generic chemoattractant were included in the simulations as functions of position and time in order to modulate a variety of rate parameters according to experimental observations (e.g., TGFβ increases collagen deposition, and chemotactic gradients enhance wound infiltration rates). These important model additions improved the match between model and experimental data, and also enabled more explicit testing of specific therapeutic interventions.

In the first model of cardiac infarct wound healing, Rouillard and Holmes adapted Dallon and McDougall’s agent-based model (ABM) to simulate cardiac fibroblast infiltration and collagen remodeling in infarct tissue (Figure 2) [62]. A critical extension of Rouillard was the addition of a mechanical cue to combine with local chemical and structural cues to guide fibroblast proliferation, orientation, migration, apoptosis, collagen production, collagen degradation, and collagen reorientation. An additional advance was that nearly every parameter value was determined directly from independent experimental data in the literature. With this framework, Rouillard found that a uniaxial strain environment lead to an anisotropic collagen matrix with both cells and fibers aligned in parallel to the strain direction, while a biaxial strain environment lead to an isotropic collagen matrix with cells and fibers more randomly oriented. Importantly, both these predictions matched experimental data from rat infarcts subjected to either uniaxial or biaxial loading environments for 3 weeks [63,64]. Moreover, the model also correctly recapitulated a transmural variation in infarct collagen alignment experimentally observed in pig infarcts [65]: collagen alignment is highest at the midwall where the mechanical cue and pre-existing fiber cue are parallel, and alignment is lowest at the endocardial and epicardial surfaces where mechanical cue and pre-existing fiber cue are competing. These findings demonstrate the ability of these types of models to integrate information about multiple different mechanisms of matrix remodeling to predict their combined effects in vivo, which is vital to the ability to develop effective therapeutic interventions to control matrix structure and thereby improve cardiac function in disease conditions.

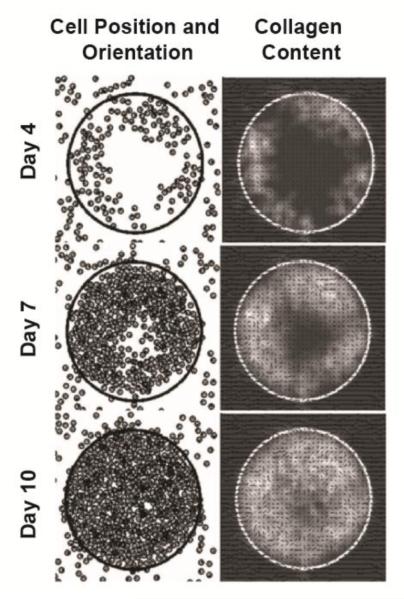
Figure 2. Agent-based modeling of infarct wound healing.

Rouillard and Holmes used an agent-based framework to capture fibroblast proliferation, orientation, migration, and collagen remodeling in response to mechanical, chemical, and structural cues. During the healing time course, high chemokine levels in the wound lead to fibroblast infiltration and collagen accumulation, and the strainpattern (biaxial vs. uniaxial) determined fibroblast and collagen orientations (random vs. aligned, respectively). Figure is adapted with permission by the Journal of Physiology from Rouillard and Holmes 2012 [62].

Rouillard and Holmes have recently updated their original framework by coupling ABM predictions to an FEM of infarct mechanics [66]. Those simulations used the previously developed ABM to predict changes in scar structure, which is passed as fiber-based constitutive material properties to an FEM of a 2D infarct section. New strains are then calculated by the FEM and passed back to ABM to provide updated mechanical cues for the next remodeling time step, and so forth. This coupled ABM-FEM allowed Rouillard to correctly predict not only scar fiber structure but also regional deformations seen following coronary ligation in rats [64]. It also suggested that fibroblast alignment parallel to a strain cue actually provides negative feedback to drastic changes in local fiber orientations: as fiber orientation deviates from an aligned direction, the tissue becomes stiffer parallel to the new orientation and strain becomes greater perpendicular to the new orientation, driving fibroblasts and subsequent fiber orientations away from the deviation direction and back toward the original alignment direction. We should note one limitation to their approach is that fibroblast-mediated reorientation of collagen was represented by phenomenologically modifying local fiber orientation distributions. As an alternative, several groups have simulated cell compaction of collagen gels by explicitly calculating the mechanical equilibrium between each cell’s contractile forces and nearby collagen fibers’ mechanical properties [67,68].

2.3 Multiple Cell Type Models

While the addition of fibroblasts to matrix remodeling simulations offers many benefits, fibroblasts are of course not the only cell type contributing to changes in cardiac matrix structure, and several groups have included a variety of other cells in efforts to more faithfully capture important cell-cell interactions. For example, Neagu and colleagues developed a lattice-based ABM of endothelial-mesenchymal transformation (EMT) during cardiac morphogenesis based on the interactions of endothelial cells, mesenchymal cells, and local matrix [69]. Each component interacts with neighboring components by cohesion and adhesion, and migration. Proliferation, or EMT occur according to a decision-tree of component interactions and remodeling probabilities. With the assumed behavior rules and cohesion/adhesion interaction parameters, simulations predicted not just the occurrence of EMT but also the morphological formation of cushion tissue. Additionally, simulations predicted that cell-matrix adhesion is more critical than cell-cell adhesion for promoting EMT – a finding with potential therapeutic implications.

Jin and colleagues also investigated the role of interacting cell types as well as fibrosis-related cytokines by developing an ODE model of fibroblast, macrophage, collagen, TGFβ, and MMP9 mass action kinetics in post-infarction myocardium [70]. The basic interactions included the following: macrophages secrete TGFβ and MMP9, TGFβ stimulates fibroblasts to secrete collagen, TGFβ stimulates macrophage infiltration, TGFβ inhibits MMP9, and MMP9 degrades collagen. Interaction parameters were set to experimentally-estimated values, and myocardial remodeling was simulated for 30 days, which correctly predicted biphasic macrophage, TGFβ, and MMP levels, and monotonically increasing fibroblast and collagen levels. Perhaps surprisingly, simulating reduced TGFβ actually raised collagen levels while elevated TGFb reduced collagen levels. This finding was due to TGFβ-induced macrophage infiltration leading to 1) high MMP9 levels and collagen degradation, and 2) lower early fibroblast levels because of macrophage crowding. Experimentally, there is in fact evidence that elevating TGFβ delays wound healing after cardiac injury (Nakajima 2000).

Galvao and colleagues have developed 2D and 3D ABMs of Chaga’s cardiomyopathy by including not just fibroblasts and fibrosis but also the Trypanosoma cruzi parasites, inflammatory cells, cardiomyocytes, bone marrow stem cells (BMSC), and tumor necrosis factor-α [10,71]. In their lattice-based simulations, each grid location is designated as one of these component types or left empty, and successive time steps updates each location designation according to simple, experimentally-motivated rules based on which component types are nearby. For example, a cardiomyocyte location near a fibroblast will transition to a fibrotic location to simulate fibroblast deposition of matrix, or an empty location near a parasite will transition to a parasite to simulate T. cruzi replication. Using just a handful of these transition rules was sufficient for the model to reproduce experimentally-observed, biphasic temporal dynamics of fibrotic area, inflammatory cell fraction, and parasite nest numbers over 7 months of disease progression in infected mice, and subsequent 6 months of BMSC injection therapy [72,73]. The simulations also found that the spatial pattern of fibrosis was the most critical determinant of the kinetics of BMSC-induced regeneration in the Chagastic heart and should therefore be an important therapeutic consideration.

The above studies highlight the utility of computational approaches to investigate cardiac fibroblast behavior and matrix remodeling in a variety conditions, and it is clear that modeling approaches can range in system complexity by including not just matrix but also fibroblasts, not just fibroblasts but also other cell types, and not just cell types but also specific signaling molecules. Additional levels of complexity, while requiring more experimental data for model generation and validation, offer new layers of therapeutic relevance by enabling simulations to both elucidate mechanisms and screen novel treatment approaches. Not surprisingly, similar modeling frameworks have been applied to fibroblasts and fibrosis in non-cardiac tissues as well including pulmonary fibrosis [74], cystic fibrosis [75], liver fibrosis [76], and kidney fibrosis [77].

Section 3: Signaling Networks and Fibroblast Phenotype

Fibroblasts are a plastic cell type – able to respond to chemical, mechanical, and electrical cues with large alterations in cell behavior. For example, fibroblasts break down the extracellular matrix by producing MMPs in response to inflammatory cytokines. However, growth factors prompt fibroblasts to increase their expression of collagens and fibronectin, leading to tissue-level fibrosis. Fibroblasts migrate in response to inflammatory cues in order to infiltrate an infarct. Phenotypic alterations also occur such as endothelial to mesenchymal transitions, which increase the number of fibroblasts or differentiation into the contractile, pro-fibrotic myofibroblast phenotype. Ultimately, these changes lead to tissue-level remodeling and altered electrical conduction as described above. To our knowledge, there are no published models of cardiac fibroblast-specific signaling. However, such models are useful for investigating how external cues are translated into changes in cell behavior and for predicting which signaling players are necessary for a specific cellular response. Here we review models of fundamental signaling pathways, migration, and phenotype switching in non-cardiac fibroblasts as they are likely useful for understanding cardiac fibroblast physiology.

Several kinetic models based on data in other cell types have been built of signaling pathways that are relevant to fibroblast physiology. For example, a large-scale model of epidermal growth factor (EGF) signaling with 94 different signaling isoforms was used to examine how EGF receptor dynamics affect MAPK activation in HeLa cells. This model predicted that increasing the concentration of EGF or the EGF receptor was translated in the signaling network as an increase in the rate or duration of ERK activation rather than an increase in peak ERK activation [78]. Extracellular signaling models have also been developed such as Vempati et al.’s model of a network of 17 MMPs and TIMPs that predicted active MMP9 can deactivate other active MMP9 molecules[79]. Previously it had been assumed that only TIMPs deactivated MMP9, but that mechanism was insufficient to quantitatively explain the experimental dynamics of MMP9 activity. Both of these studies point to the benefit of large-scale models of signaling networks as a method for hypothesizing key determinants of phenotypes.

3.1 Models of Signaling Networks Regulating Migration

Migration is important for recruitment of fibroblasts into the cardiac tissue. Importantly, inhibiting migration of fibroblasts affects wound healing after an infarct [80]. The Lauffenberger group used decision-tree modeling to investigate how EGF and fibronectin signaling integrate to affect cell migration speed. This data-driven modeling approach was based on a 3T3 lineage cell line expressing human EGF-receptor. The initial model was based on one time point and found that ERK phosphorylation level was sufficient to predict whether a fibroblast was moving slowly or not, but determining whether migration was at medium or high speed required information on MLC (myosin light chains), PKC (protein kinase C), and PLC (phospholipase C) phosphorylation levels [81]. A later model from this group incorporated data from two time points. This model predicted a biphasic relationship between migration speed and MLC levels, so that at low levels of MLC, migration speed is paradoxically increased. This new model also predicted ERK was necessary for medium or high-speed migration [82].

Rangamani et al. built a stochastic cell-spreading model regulated by a curated kinetic model of integrin signaling based on data from MEFs (mouse embryonic fibroblasts) [83]. This model was used to make predictions about mechanical determinants of migration kinetics. In this study, they concluded that initiation of migration depends on the signaling environment, but, once triggered, migration depends on membrane mechanics and is robust to changes in integrin-mediated signaling. These models demonstrate how in silico studies of signaling can provide potential mechanisms for how dynamic signals are translated into cell behavior.

3.2 Models of Signaling Networks Regulating Phenotype Switching

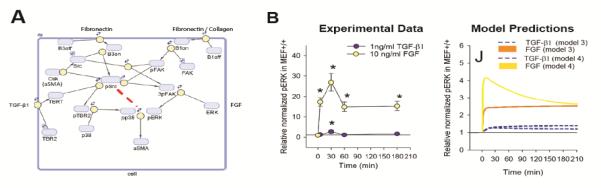
Cardiac injury triggers EMT and differentiation of fibroblasts into myofibroblasts to increase the number and activity of fibroblasts. Myofibroblasts express high levels of collagen and fibronectin as well as contractile proteins such as αSMA (alpha smooth muscle actin). Schroer et al. used a kinetic model based on experimental data from wild type and FAK−/− (focal adhesion kinase knock out) MEFs to explore how TGFβ, FGF(fibroblast growth factor), and integrin signaling pathways combine to influence expression of alpha smooth muscle actin. In this study they compared different mechanistic models and found that including a time-dependent negative regulation of ERK in the model was important for explaining the adaptive kinetics observed experimentally (Figure 3). The model also predicted that FAK KO increases the sensitivity of αSMA to substrate stiffness [84]. This study highlights how signaling network models can be used to test potential signaling interactions and identify likely mechanisms that can be validated experimentally.

Figure 3. Fibroblast Signaling Network.

(A) Schematic of signaling network incorporating integrin, TGFβ, and FGF pathways. The red line indicates the time-dependent ERK regulation included in model 4 (B) Comparison of the experimental levels of ERK phosphorylation with TGFβ or FGF treatment with the model prediction demonstrates that including ERK regulation improved the model prediction. Figures adapted with permission by Cellular and Molecular Bioengineering from Schroer et al 2014 [84].

Similarly, data-driven models can be used to hypothesize how signaling is changing in different phenotypic contexts. Desai et al. used phosphorylation data from an airway epithelial cell line to build a mixed-effects model to study the signaling differences after epithelial-mesenchymal transition (EpMT) when the cells have become fibroblast-like. Epithelial-mesenchymal transition is analogous to the endothelial-mesenchymal transition that occurs in the heart during development or cardiac injury to increase the density of fibroblasts in the tissue [85]. Interestingly, they found that following EpMT there is a rewiring of the phosphorylation network [86]. For example, they identified a novel loss of connection between IL6 and pSTAT3 and an increased correlation between pSMAD2 and GSK3α in cells that had undergone EpMT, which could be the basis for differential signaling in this phenotype.

Together these models indicate that context-specific signaling is important in determining phenotype. The role of the fibroblast in integrating mechanical, chemical, and electrical cues makes understanding context-dependent signaling important for identifying useful therapeutic targets against fibrosis. As there are significant differences between cardiac fibroblasts and other fibroblasts [87] it would be important to apply a computational modeling approach to cardiac fibroblasts, specifically, to identify which key signaling components determine fibroblast behavior in the heart.

Future Directions

Here we have reviewed a wide variety of modeling approaches applied to aspects of cardiac fibroblast physiology. Different types of modeling are appropriate for answering different biological questions (see Table 1). While there are pros and cons to individual modeling approaches, in general models can be improved by incorporating more biological detail to increase relevance, or by simplifying the model to improve computational efficiency and biological interpretation. Incorporating new data into computational models increases their predictive capability so that model interpretation can generate more plausible hypotheses. One way to incorporate data in an unbiased way is by developing models using high-throughput datasets as described in the next section. Additionally, model reduction approaches as described by Holland et al. can simplify highly detailed models without sacrificing predictive power, which can simplify interpretation of model predictions [89]. Here, we identify three major areas of significant potential for future computational models of cardiac fibroblasts: incorporation of high-throughput data, multi-scale modeling of tissue physiology, and a focus on using models to identify potential therapeutic targets.

Table 1.

Summary of approaches used to model fibroblasts and fibrosis.

Physiology	Model Type	Description	Model Size	Spatial Scale	Time Scale	Reference s
Electrical	Ordinary Differential Equations (ODEs)	Based on conservation of charge and ion channel biophysics	~10-100 parameters; 2-10 ODEs	10 μm−1 cm	msec - minutes	[22– 24,30,34,3 6,37]
	Finite Element Method (FEM)	Tissue modeled as continuum of elements, constrained by conservation of mass and charge.	~106 elements	10 cm	msec - minutes	[38]
Remodeling	FEM	Tissue modeled as continuum of elements, constrained by conservation of mass and momentum	100-500 elements	10 μm −1 cm	hours - weeks	[55–57,88]
	Agent Based Model (ABM)	Treats cells as agents responding to a set of rules.	1-5 agents, 10- 50 parameters	10 μm − 1 cm	hours -weeks	[10,58– 62,69,71]
	ODEs	Predicts changes in cells and proteins over time.	15 parameters; 4 ODEs	1 cm	weeks	[70]
Signaling	ODEs	Predicts changes in proteins, constrained by mass-action kinetics	10-200 parameters; 4- 100 ODEs	10 μm	seconds - hours	[78,79,83,8 4]
	Decision tree model	Predicts outcome based on a sequence of branching decisions	5 nodes	10 μm	NA	[81,82]
	Mixed-effects model	Statistical model calibrated to experimental data	13 parameters; one equation	10 μm	minutes	[86]

Inference from High-Throughput Data Sets

As high-throughput sequencing and proteomic methods become more common, integrating these datasets into computational models will be an important tool for understanding the functional consequences of the many simultaneous changes revealed by these data. There are available datasets of gene expression in cardiac fibroblasts and myofibroblasts [42,43], and there are algorithms for combining high-throughput datasets with some manual curation to increase biological relevance of the predicted hits [44,45]. Using gene expression data to generate predictive models allows an unbiased method for determining context-dependent effects on phenotype.

Proteomics datasets can also be used to infer networks, which can be adapted into predictive computational models. For example, statistical modeling has been applied to a proteomics dataset to generate hypotheses about crosstalk in coxsackievirus B3 infection in cardiomyocytes[93]. Kupfer et al. used the NetGenerator algorithm to infer an ODE signaling model of gene expression from synovial fibroblasts from rheumatoid arthritis patients^[47,48]. These types of approaches could be applied to cardiac fibroblasts in order to generate testable hypotheses linking gene expression to phenotype. Ultimately, this could lead to an understanding of the genetic predisposition for cardiac fibrosis and heart failure.

Multi-Scale Modeling

This review highlights the breadth of cardiac fibroblast-related computational studies extending across length scales from subcellular signaling, to local cell-cell and cell-matrix interactions, to tissue remodeling, and to organ level conduction properties. Of course, processes across these scales do not occur in isolation but operate as an interconnected system with every level passing information to other levels. In fact, many phenomena emerge specifically out of these multi-scale interactions. For a more complete understanding of fibroblast functions within such a system, researchers are now developing multi-scale modeling frameworks. Such approaches have shown benefit in many contexts including morphogenesis, wound healing, blood flow, arterial growth and remodeling, bone mechanics, cardiac mechanics, and many others [96–103], but multi-scale models involving cardiac fibroblasts and fibrosis are still rare.

As described above, Rouillard and Holmes extended their multi-cell ABM of myocardial infarct growth and remodeling by coupling it with an FEM of infarct mechanics to iteratively update both local scar structures and tissue-level deformations [66]. It is easy to imagine how to extend such a model to an even larger scale by replacing the prescribed tissue loading with a whole-ventricle FEM for computing new boundary loads. Additionally, the ABM framework is well-suited for extending to a smaller scale as well by replacing prescribed turnover rate constants with an intracellular signaling model to calculate collagen and MMP synthesis rates based on each cell’s local chemical and/or mechanical signals. Such an approach could be useful for modeling other tissue-level behaviors as well. For example, a multi-scale model linking intracellular signaling to a tissue-level ABM could be useful for modeling fibroblast reprogramming to myocytes and the effect on tissue function (see review on reprogramming in this issue by Czubryt et al. [104]). While multi-scale modeling brings computational challenges, it offers enormous potential for integrating biological processes within the context of a broader system to determine functional responses to diseases and therapies.

Prioritizing Therapeutic Targets Against Fibrosis

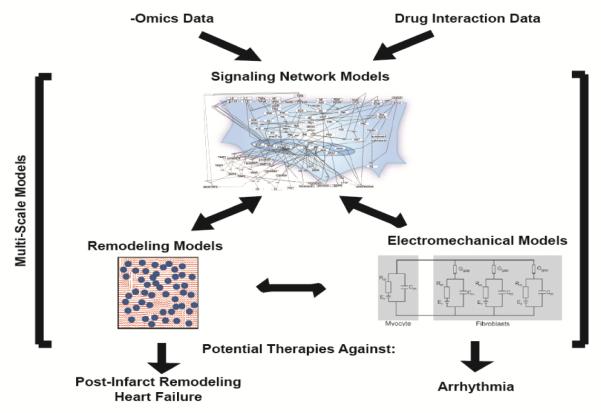
Current heart failure therapies such as ACE inhibitors and aldosterone antagonists can affect cardiac fibrosis, and promising drugs such as nintedanib and pirfinedone have been approved to reverse lung fibrosis. However, the mechanisms by which these drugs limit fibrosis is not clearly understood. Computational models can help identify the mechanisms by which these drugs suppress fibrosis and can identify therapeutic strategies that could be more targeted and efficacious against cardiac fibrosis. Computational models of cardiomyocyte signaling have successfully been used to predict which signaling nodes are most important for cardiomyocyte hypertrophy in vitro[105,106] or how phenomena such as compartmentalization affect hypertrophy[107,108]. Markov models are also useful for determining the effect of ion channel mutations on electrical conduction[109]. Integrating molecular level models into tissue level models can help clarify how mutations develop into tissue-level phenotype changes (Figure 4). A well-designed model can save money by testing all potential therapeutic targets in silico and identifying the most likely hits. Pharmaceutical companies are already using modeling to direct research focus in an effort to increase the likelihood of success and lower costs[110]. It is likely this approach will benefit academic research in the same manner.

Figure 4. Summary of Future Directions.

Currently used models of electrical conduction, cardiac tissue remodeling, and signaling networks could be integrated with -omics data and drug interaction data and combined into multi-scale models to identify potential therapeutics against heart disease.

Conclusions

Computational models have been useful for clarifying the role of cardiac fibroblasts in electrical conduction and tissue remodeling in the heart. Although cardiac-specific models of fibroblast signaling have not yet been developed, models of general fibroblast signaling have generated hypotheses about how fibroblasts integrate signaling cues. Future work will benefit from incorporating large -omics datasets into computational models. Multi-scale models allow researchers to explore how molecular- and cellular-level changes affect tissue function. This can be useful for identifying potential therapeutic targets against cardiac fibrosis.

Highlights.

• Computational models have been used to define the functions of cardiac fibroblasts in ventricular electrical conduction and tissue remodeling.

• Models of signaling networks have helped identify key determinants of fibroblast phenotype, but such models have not yet focused specifically on cardiac fibroblasts.

• Future work using models that integrate large -omics datasets and multi-scale biological functions will provide a framework for identifying potential therapeutic targets against cardiac fibrosis.

Abbreviations

ECM

extracellular matrix

MMP

metalloproteinase

SAN

sinoatrial node

APD

action potential duration

FEM

finite element model

TIMP

tissue inhibitor of metalloproteinases

ABM

agent-based model

TGFβ

tissue growth factor beta

EMT

endothelial-mesenchymal transition

BMSC

bone marrow stem cells

EGF

epidermal growth factor

MLC

myosin light chains

PKC

protein kinase C

PLC

phospholipase C

MEF

mouse embryonic fibroblast

αSMA

alpha smooth muscle actin

FAK

focal adhesion kinase

FGF

fibroblast growth factor

EpMT

epithelial-mesenchymal transition

IL6

interleukin 6

pSTAT3

phosphorylated signal transducer and activator of transcription 3

pSMAD2

phosphorylated mothers against decapentaplegic homolog 2

GSK3α

glycogen synthase kinase-3 alpha

ODE

ordinary differential equation