Alignment Algorithms and Per-Particle CTF Correction for Single Particle Cryo-Electron Tomography

Abstract

Single particle cryo-electron tomography (cryoSPT) extracts features from cryo-electron tomograms, followed by 3D classification, alignment and averaging to generate improved 3D density maps of such features. Robust methods to correct for the contrast transfer function (CTF) of the electron microscope are necessary for cryoSPT to reach its resolution potential. Many factors can make CTF correction for cryoSPT challenging, such as lack of eucentricity of the specimen stage, inherent low dose per image, specimen charging, beam-induced specimen motions, and defocus gradients resulting both from specimen tilting and from unpredictable ice thickness variations. Current CTF correction methods for cryoET make at least one of the following assumptions: that the defocus at the center of the image is the same across the images of a tiltseries, that the particles all lie at the same Z-height in the embedding ice, and/or that the specimen grid and carbon support are flat. These experimental conditions are not always met. We have developed a CTF correction algorithm for cryoSPT without making any of the aforementioned assumptions. We also introduce speed and accuracy improvements and a higher degree of automation to the subtomogram averaging algorithms available in EMAN2. Using motion-corrected images of isolated virus particles as a benchmark specimen, recorded with a DE20 direct detection camera, we show that our CTF correction and subtomogram alignment routines can yield subtomogram averages close to 4/5 Nyquist frequency of the detector under our experimental conditions.

1. Introduction

Cryo-electron tomography (cryoET) allows direct visualization of macromolecular complexes in vitro and in cells at nanometer resolution, without stains or fluorescent tags (Baumeister et al 1999; Gan, & Jensen 2012). CryoET can also be used to structurally characterize pleomorphic (Harris et al 2006) and disordered specimens, such as amyloid aggregates (Darrow et al 2015; Shahmoradian & Galaz-Montoya et al 2013), as well as complexes exhibiting conformational and compositional heterogeneity (Dai et al 2013). Due to mechanical limitations of the electron microscope and the slab geometry of frozen-hydrated specimens, imaging is typically limited to a maximum useful tilt of ±60°, leaving a region of angular space from which micrographs of the specimen cannot be recorded. The lack of micrographs from this region, called “the missing wedge”, causes anisotropic resolution in reconstructed tomograms (Radermacher 1988), making their interpretation more difficult.

The resolution of a single tomogram is rarely better than 40–50 Å. However, single particle cryo-electron tomography (cryoSPT, also known as “subtomogram averaging”) (Walz et al 1997) can yield 3D maps with improved resolution by averaging near-identical subtomograms extracted from tomograms.

CryoSPT has been used to characterize a myriad of biological assemblies (Harapin et al 2013) in vitro and ex vivo, especially those not amenable to traditional single particle cryoEM, such as pleomorphic viruses (Dai et al 2013; Harris et al 2006; Harris et al 2013; Huiskonen et al 2010; Schmid et al 2012), flagellae (Carbajal-González et al 2013; Koyfman et al 2011; Zhao et al 2013), membrane-bound ribosomes (Pfeffer et al 2012; Pfeffer et al 2015), nuclear pore complexes (Maimon et al 2012; Stoffler et al 2003) and other membrane proteins (Dalm et al 2015; Davies et al 2011; Eibauer et al 2012). Such studies, as well as tools developed for subtomogram averaging (Castaño-Diez et al 2012; Forster et al 2007; Hrabe et al 2012; Nicastro et al 2006), have been comprehensively reviewed (Fernandez 2012; Kudryashev et al 2012; Schmid 2011).

CryoSPT can now routinely yield 20–40 Å resolution, with a few recent studies achieving subnanometer resolution (Bharat et al 2015; Schur et al 2013; Schur et al 2015). However, resolving the structure of macromolecular complexes to better than 20 Å resolution under typical cryoSPT conditions is far from routine and requires correction of the contrast transfer function (CTF), which in turn requires knowledge of the defocus for every image in a tiltseries. The low signal to noise ratio (SNR) due to radiation damage constraints (dose fractionation) (McEwen et al 1995) and ice thickness, the defocus gradient in images of tilted specimens, as well as specimen-stage instability, can make CTF correction for cryoET particularly challenging. Nonetheless, the emergence of direct detection devices (DDD cameras) (Bammes et al 2012; Faruqi et al 2003; Jin et al 2008) allows aligning successive frames from a given specimen area to produce a final summed image with optimal data preservation across a broad range of spatial frequencies (Brilot et al 2012; Shigematsu, & Sigworth 2013). Consequently, averages from aligned DDD frames might facilitate measuring one or more CTF ripples, directly from low-dose cryoET images.

Most existing methods for CTF correction in cryoET consider a “flat” and linear defocus gradient across tilted specimen images, assuming that the ice-embedded particles are coplanar within the ice layer. Yet, the geometry of the ice can differ from that of a rectangular slab (Wright et al 2006), yielding ice thickness gradients (Stoffler et al 2003; Zhang et al 2008) and non-planar particle distributions. Therefore, we previously made a theoretical analysis on the feasibility of performing CTF correction for cryoSPT, taking ice thickness into account. We did this by computing the distribution of particles in the embedding ice and calculating their defocus variations with respect to the mean defocus (Galaz-Montoya et al 2015). The defocus shift was calculated along Z, which is defined here as the axis perpendicular to the plane of the cryoEM grid. In that study, we confirmed with simulated data that ignoring the distribution of particles along Z during CTF correction could limit resolution for cryoSPT. Of note, this correction becomes more relevant with thicker ice (i.e., the larger the spread of particles distribution in Z) and at higher target resolutions. We also showed that, in theory, one could correct the CTF for each particle in each tilted specimen image instead of correcting entire micrographs.

Here we demonstrate our recent per-particle CTF correction method (Galaz-Montoya et al 2015) using real data - cryoET tiltseries acquired with a direct electron detector (DE20). The imaged specimen was Venezuelan Equine Encephalitis Virus (VEEV, ~700 Å in diameter), which we used as a benchmark since its structure has been solved at near-atomic resolution by single particle cryoEM (Zhang et al 2011). We measured the defocus directly from the imaging area, making none of the aforementioned common assumptions in the field (i.e., thin slab geometry, flat grids, defocus trends, eucentric specimen stage or accurate defocusing). Because the primary goals of the current study are to investigate movie-mode drift correction for cryoSPT using a DDD, as well as our proposed per-particle CTF correction method, using an icosahedrally symmetric test particle is appropriate. The high level of symmetry reduces the impact of various potential issues during subtomogram alignment, such as the missing wedge, conformational heterogeneity or preferred particle orientation, making interpretation of the results less ambiguous.

We have also improved upon our recent computational tools for SPT (Galaz et al 2012; Murray et al 2014; Galaz-Montoya et al 2015) distributed through EMAN2 (Tang et al 2007) by increasing their level of automation and implementing alternative missing wedge compensation and subtomogram alignment strategies. Benchmark tests with simulated data, for which the ground truth is known, indicate that our new alignment tools are much faster as well as more accurate. The tools for SPT in EMAN2 previously required the user to specify initial processing parameters to normalize, filter, mask and shrink subtomograms before alignment. Knowing the size of the particles was also required to automatically optimize alignment parameters (angular range and angular step). We have now developed a fully automated alignment algorithm, which uses internally generated parameters. This method can align large subtomogram volumes faster than the previous algorithm by orders of magnitude, with equal or better accuracy.

2. Materials and Methods

2.1 Cryo electron tomography data collection

VEEV was cultured and purified as described previously (Zhang et al 2011). CryoEM grids were prepared by depositing 5 μL of VEEV mixed with 100 Å gold fiducials on 200 mesh Quantifoil copper grids with a holey carbon support. An additional thin carbon film was overlaid on the grids before specimen deposition. We collected 13 tiltseries of frozen-hydrated VEEV manually, using a JEM3200FSC electron microscope equipped with a 3K × 4K DE20 camera (Direct Electron, LP, San Diego, CA) and an in-column energy filter set to a width of 25 eV. The magnification was 10,000x, yielding an image sampling of 5 Å/pixel. This magnification was selected so that the entire hole in the holey-carbon support was visible in every image of a tiltseries, since the carbon flanking the hole provides a strong signal for CTF estimation, and the sharp edge of the hole facilitates drift correction. We collected six unidirectional tiltseries from −50° to +50° and seven bidirectional tiltseries from 0 to +50° and −5° to −50°, with a tilt step of 5°. Empirically, we found that tiltseries present less charging when collected bidirectionally (starting at low tilt angle, or 0°) opposed to unidirectionally. However, unidirectional tiltseries data collection and processing are more straightforward, particularly when the tiltseries are collected manually. Each tilted image was comprised of 13 DDD frames (0.5 second exposure) collected in movie-mode with a dose of ~3 e/Ų per image, yielding a total, cumulative dose of ~55–70 e/Ų per tiltseries. Tiltseries with excessive ice contamination, specimens close to the grid bar and/or unexpected specimen shifts during data collection were not processed. A total of 6 tiltseries were deemed optimal for subsequent analysis.

2.2 Motion correction for images in tiltseries

We performed whole-frame movie-mode motion correction on every image in our tiltseries using EMAN2-based software by Direct Electron (Direct Electron LP, San Diego, CA). In this software, a gain reference image is computed by averaging a large number of empty bright-field images (without any specimen) recorded under the same conditions as the data with specimen. This average is normalized so that the mean intensity is one, such that the mean intensity of acquired experimental frames subjected to gain correction remains unchanged. Each raw frame is flat-field corrected by subtracting a dark reference image (collected with the shutter closed; i.e., without incident electrons) and dividing by the gain reference image, prepared as described above (a minimum pixel value of 0.01 is imposed in the gain reference image to avoid divisions by zero). Following flat-field correction, a threshold filter of 8-sigma is applied to each frame to eliminate any possible outlier pixel values (i.e., X-ray pixels or other abnormal noise). The raw frames are then downsampled by a factor of 5 to speed up alignment and band-pass filtered to minimize the effects of artifacts and noise on alignment.

Because later frames for a given specimen area usually move less with respect to each other, frame alignment starts from the last frame as follows: The second to last frame (N-1) is aligned to the last frame (N) by cross correlation, and the two frames are averaged. Frame N-2 is then aligned to this average of frames N and N-1 and a new average is computed (frame N + N-1 + N-2). The algorithm proceeds until all frames are averaged. Then this average is used as a reference for iterative alignment and averaging (the number of iterations is defined by the user). A user-defined number of frames can be excluded at either end of the movie. In our case, we systematically discarded the first frame and ran 6 alignment iterations. Individual, averaged images that still exhibited visible drift after motion correction or other artifacts (grid bar, large ice contaminations, etc.) were removed from the tiltseries being corrected. We also provide tools to plot drift in X and Y as well as total scalar frame drift (the square root of X²+Y²) with respect to the average. For our data comprised of movies with 13 frames, the midpoint of the total drift usually occurs between frames 2 and 3 since early frames drift much more than late frames. This usually corresponds to a change in drift direction in X or Y drift plots (since drift is measured with respect to the average), or a dip in total scalar drift plots.

2.3 Tomographic reconstruction and subtomogram extraction

The motion-corrected and pruned tiltseries were reconstructed into tomograms using IMOD (Kremer et al 1996). EMAN2 was used to manually select 516 VEEV particles from all reconstructed tomograms and for all subsequent processing (subtomogram averaging). We avoided particles superimposed upon the holey carbon support film, close to gold fiducials, near areas with large ice contamination, or too close to the tomogram’s edges (all particle centers were at least 1.5 particle diameters away from the tomogram’s edges).

2.4 Per-image and per-particle CTF determination and correction

The orientation of the tilt axis and the tilt angle of each image are determined by aligning the tiltseries using IMOD (this process rotates each image such that the tilt axis becomes parallel to the Y-axis). Therefore, the defocus across low-dose images (assuming a flat, coplanar specimen) could be geometrically derived (Fernandez et al 2006; Winkler, & Taylor 2003) if the defocus at the center of each image were known.

We automated the determination of the defocus at the center of each image in a tiltseries, using periodogram averaging (Fernández et al 1997) and CTF fitting (Tang et al 2007) for strips parallel to the Y-axis. The following describes our automated, computational procedure, applied individually to each image in a tiltseries (blue boxes in the workflow presented in Supplementary Figure 1):

1. We first obtain a rough approximation of the “global” defocus (average defocus). To do this, we compute the CTF by tiling and periodogram averaging of the entire image (i.e., averaging the Fourier transforms of the tiles for the entire image). The tile size is a user-defined parameter. Depending on the value chosen, there will be a compromise between noise and resolution, as previously described (Fernández et al 1997). The user can also decide whether 50% overlap between tiles will be allowed in either X and/or Y to improve the periodogram average. In our case, we used tiles of 256² pixels, overlapping in both X and Y. We visually assessed the adequacy of tile size choice using our image evaluation tool, e2evalimage.py. A global or average defocus will be incorrect for tilted images, but provides an adequate first approximation. Since EMAN2 needs an estimated range of defocuses to seed CTF fitting (e.g., 0 to 5 μm for standard single particle cryoEM), measuring the global defocus serves to define the center of such a defocus range, which is later adjusted on a strip-by-strip basis. The initial defocus range at the center of each image was set to ±3 μm from the global defocus. Since we know that for images of tilted specimens the defocus will be higher at one end and lower at the other, we geometrically adjust the defocus search range as the defocus estimation moves along the tilt gradient and away from the center of the image.

2. We then determine the optimal width to use in dividing the image into strips parallel to the Y-axis, which are parallel to the tilt axis as well in an aligned tiltseries. Strip width calculation takes ice thickness and tilt angle into account, as described (see Supplement and (Fernandez et al 2006)). The defocus of each strip is determined by tiling it, followed by periodogram averaging of the tiles and automated CTF fitting of the periodogram average. The width of strips will vary with tilt angle (e.g., the entire image will be considered a single strip at 0° but strips get narrower as tilt angle increases). However, the minimum width for a strip is set to the tile size. For our data, strips with the width of a single tile (256 pixels) yield sufficient signal, even at high tilt angle.

3. Once the defocus for all parallel strips in an image is computed, we use linear regression to fit the defocus gradient (Supplementary Figure 2). This linear fit is more robust to noise than the values for any one individual strip.

4. The defocus at the centerline of the image is derived from the linear fit of the defocus gradient computed in step 3. We combine this defocus value with the tilt angle previously determined by IMOD. With this information, we can assign a defocus value to each individual particle in each image of a tiltseries based on the particle’s distance from the centerline of the image.

5. Finally, the per-particle (and per-image) defocus value found in step 4 is adjusted based on the particle’s Z-height (its location in the 3D tomogram), since different particles may sit at different levels within the embedding ice and this will shift their defocus.

We extracted per-particle subtiltseries from each VEEV aligned tiltseries. A subtiltseries corresponds to all the 2D views of one particle, cropped from the tiltseries to include just one particle (Heymann et al 2008; Iwasaki et al 2005; Zhang, & Ren 2012; Galaz-Montoya et al 2015). Using per-particle defocus values (calculated as described above), we phase-flipped every 2D image in each subtiltseries, effectively accounting for both the defocus gradient due to tilted geometry and also due to each particle’s location within the ice. Ice thickness was calculated as the breadth of the distribution in Z of particle centers within the tomogram plus the particle’s diameter (Supplementary Figure 3). The mean defocus plane in our defocus gradient fit (before taking ice thickness into account) was assumed to correspond to the middle Z-plane of the ice. Per-particle defocus shifts due to Z-height differences were calculated based on the distance of each particle to this plane. Changing the assumed location of the mean defocus plane (up to the highest Z-plane and down to the lowest Z-plane of the distribution of particle centers in Z) did not make a significant difference for most tomograms. This is understandable since for most tomograms the breadth of the distribution of particle centers in Z was smaller than the allowable defocus variation limit (or “depth of focus”) at our data’s image sampling, having only marginal effects (~0.2 Å difference in terms of resolution) for our tomogram that had the thickest ice (Supplementary Table 1). Of note, the effect would be more significant for wider distributions of particles in Z (corresponding to thicker ice) or for data at a finer sampling, targeting higher resolution. After CTF correction, our tools recompute each CTF-corrected subtiltseries into a CTF-corrected subtomogram by Fourier inversion using the same tilt angles found during tiltseries alignment.

2.5 Subtomogram alignment

Our previous alignment algorithms in EMAN2 performed rotations and translations in real space, while missing wedge compensation was done in Fourier space, requiring a new Fourier transform to be computed for each tested orientation. Real space transforms (rotations and translations) is a very highly optimized algorithm. Although less optimized, in principle it should be possible to perform rotations and translations in Fourier space at a comparable speed. However, there are a number of challenges faced in Fourier space. First, normal Fast Fourier Transform (FFT) storage used by most applications eliminates redundant data by not including it in the stored data. Therefore, the data arrangement in the 3D FFT has a number of special locations, such as the Y*Z* plane at X*=0 and several specific places on the periphery of the volume. The conditionals required to handle these special cases can slow down the code, unless they are handled in completely separate loops. For example, performing translations involves phase shifts to all of the Fourier components, requiring an expensive trigonometric calculation for each voxel within three nested loops. The total phase shift ΔΦ is set by knowledge of the shift in X* (i.e., ΔX*) and the number of Y* slices (i.e., N_Y*), as follows:

$$\mathrm{\Delta }\mathit{\Phi }=-\mathit{2}\pi \mathrm{\Delta }X\ast /N_{Y\ast }$$ (1)

However, in our implementation, once we have set the initial cosine and sine of the phase Φ, we can update these values by defining constants outside of the innermost loop, k₁=cos(ΔΦ), k₂=sin(ΔΦ), k₃=1/k₁ and k₄= k₂/k₁, and then updating the cosine of the phase as follows:

$$\mathit{cos}(\mathit{\Phi })=k_{\mathit{1}}\mathit{cos}(\mathit{\Phi })-k_{\mathit{2}}\mathit{sin}(\mathit{\Phi })$$ (2)

as well as the sine of the phase:

$$\mathit{sin}(\mathit{\Phi })=k_{\mathit{3}}\mathit{sin}(\mathit{\Phi })+k_{\mathit{4}}\mathit{cos}(\mathit{\Phi })$$ (3)

That is, we can update cos(Φ) and sin(Φ) “in place” without any trigonometric calls in the innermost loop, constituting a less expensive, linear, recursive update to each voxel. This made transforms (including both rotations and translations) in Fourier space as fast as transforms in real space. Finally, we opted to exclude the corners of the transforms at spatial frequencies beyond Nyquist of the X*,Y*,Z* axes, making transforms in Fourier space slightly faster than their real space equivalents (Supplementary Figure 4), with no significant loss in power.

In addition to transforms in Fourier space, our new alignment algorithm uses a coarse-to-fine, multiresolution approach and relies on the fact that, in most cases, the structures being aligned possess features at low resolution that suffice for rough orientation determination. Empirically, we found that for objects with low symmetry, downsampling the subtomograms to a box size of 24³ voxels provides sufficient features to restrict the initial alignment space to a finite number of local regions. This was extensively tested on a variety of real and simulated data sets, including particles with different types of symmetry. The only failure case was for an object with icosahedral symmetry, where there are only a small number of voxels in each asymmetric unit at a size of 24³. For such high symmetry objects (e.g., icosahedral virus capsids, <1000 Å in diameter), we empirically found that a size of 64³ voxels was sufficient.

At the coarsest image sampling level, we perform an exhaustive 3D rotational and translational search, sampling the asymmetric unit uniformly. After alignment at this coarse level, the best N orientations (a minimum of 32) are stored; then, the sampling is increased and alignment is performed at the next level of sampling, with only a local orientation search for each of the best N/2 orientations (limited by the user-requested number of final answers). For instance, if the algorithm at one stage would only refine 4 answers but the user has specified a minimum number of 8 answers to perform local searches on, the best 8 answers will be used for alignment at this as well as all subsequent levels of sampling. This continues until full sampling has been achieved and the best global answer for a pairwise alignment (between any two given subtomograms) has been found. Note that the angular step size is adjusted automatically as a function of box size at each sampling level, achieving a final alignment precision higher than 1° for typical box sizes.

During this multiresolution alignment, the subtomograms are Gaussian lowpass filtered to 2/3 of the downsampled Nyquist. In addition, a highpass filter is applied with a radius of 4 Fourier pixels to eliminate alignment errors due to Cartesian rotation artifacts in the voxels very close to the origin in Fourier space. This procedure eliminates the requirement for the user to decide on an arbitrary filtration level during alignment at each sampling level and acts as a dynamic filter (i.e., at coarser levels of sampling, the effects of the filters will be harsher than at finer sampling, focusing the initial search on only the coarsest, most prominent, low-resolution features in the object, while allowing higher resolution features to contribute to alignment as fuller sampling is reached). By keeping a large number of local minima during alignment at each sampling level, it is highly likely that the neighborhood of the global minimum will be among the potential initial answers. Although there is no guarantee that the correct answer will be found for arbitrary object shapes or all datasets, this approach to alignment has a higher probability of finding the right final answer, compared to exploring only the best answer at each sampling level. As the algorithm progresses towards full sampling, where there may be concern that the alignment may be dominated by noise, the search neighborhoods are already so restricted that the risk of error due to dominating noise is low. While not necessary in most cases, the user is still free to specify additional filters or masks to preprocess the volumes before alignment (e.g., an FSC-based adaptive filtration approach before the data enters the alignment algorithm).

2.6 Missing wedge compensation

Our missing wedge compensation algorithm determines the standard deviation of voxel intensities in each Fourier shell and assumes any values less than 0.01 standard deviations above zero within that shell belong to the missing wedge (this value can be adjusted by the user). In maps or shells that actually have no missing information, this will cause a small fraction of the lowest intensity voxels to be excluded from the similarity computation; however, because this is only a small percentage of the voxels, it has a negligible impact on the similarity metric, meaning the method can be safely used on volumes with or without a missing wedge. When building reference models from scratch (Galaz-Montoya et al 2015), the specific voxels identified as “missing” will automatically change as more particles are added to an average and resolution improves.

As a similarity metric, the new alignment and missing wedge compensation strategy uses (by default) integrated Fourier Shell Correlation (FSC) between the two subtomograms being aligned (the user can choose a different similarity metric), excluding any missing voxels in either subtomogram. This approach works better than the cross correlation map normalization method, the previous default in EMAN2. As noted (Amat et al 2010; Förster et al 2008; Heumann et al 2011; Scheres et al 2009; Schmid, & Booth 2008), when the overlap of non-missing-wedge data between two particles is small, spurious orientations can yield the highest correlation scores and this will vary greatly with different normalization schemes. For this reason, our wedge-aware FSC also returns the precise fraction of non-missing voxel overlap between the two maps being aligned, allowing for the exclusion of alignment answers with minimal overlap. Once the alignment process using the entire dataset has iterated and an average with minimal or no missing wedge is produced, the amount of non-missing voxel overlap is no longer an issue, and any misaligned particles should automatically shift to the correct alignment. (Of course, the amount of non-missing overlap is not an issue when an external reference model with no missing wedge is used). This same dynamic thresholding approach to identify the missing wedge is also used when averaging particles after alignment orientations have been determined. Particles are averaged in Fourier space and all “missing” voxels are correctly excluded from the average and thus do not downweight the corresponding average voxel values.

2.7 Subtomogram iterative refinement and averaging

We extracted a total of 516 subtomograms from six VEEV tomograms. We first built an initial model from each set (one per tomogram) ab initio by self-symmetry alignment (SSA), as described previously for similar specimens (Galaz-Montoya et al 2015). For each set, we performed gold-standard (Henderson et al 2012) iterative refinement, imposing icosahedral symmetry and kept the top 75% of the best-correlating particles for averaging. Our new multiresolution alignment strategy (Methods 2.5 and 2.6) converges very quickly; therefore, we limited refinement to four iterations, with negligible changes occurring beyond the second iteration in most cases. We then combined all our per-tomogram averages and used this new average as an initial model to refine the entire data set of subtomograms from all tomograms.

2.8 Subtomogram simulation

In addition to the results obtained using real data, we repeated the same protocol described above (Methods 2.5–2.7) using simulated data as a control. This allowed to objectively test the accuracy of our new subtomogram alignment and averaging tools. We simulated 240 VEEV particles (PDB ID 3J0C) as previously described (Galaz-Montoya et al 2015), generating projections between −60° to 60°, with a tilt step of 5°, without adding noise or CTF. The particles were in a 256³ box, at 5 Å/pix sampling (matching our experimental data). In addition, we simulated a second data set adding CTF at 300 kV and 10% amplitude contrast as well as 5 μm defocus at the tilt axis and Gaussian noise (SNR 0.5) both before and after applying a CTF.

3. Results

Tests with simulated data revealed that our new automated subtomogram alignment tools are up to ~20 times faster compared to the previous tools in EMAN2 for relatively large particles; e.g., simulated VEEV particles in boxes of 256³ voxels or larger (see Methods 2.8). For these data, alignment speed of the icosahedral asymmetric unit was reduced from ~30 min to ~1.5 min per pair-wise alignment, and accuracy improved from average angular and translational errors of 3.4° and 1.3 pixels to 0.43° and 0 pixels, respectively, for the simulated dataset without CTF or noise. For the simulated data set with noise and CTF, accuracy improved from average angular and translational errors of 3.7° and 1.5 pixels to 0.52° and 0.1 pixels, respectively. Implementing rotations in Fourier space resulted in measurable speed gains (Supplementary Figure 4); e.g., alignments were upwards of ~20% faster for our test specimen here or larger subtomograms (the specific gain in speed will ultimately vary with box size). More importantly, the main factor for the ~20-fold speed up in alignment was the implementation of the coarse-to-fine, multiresolution alignment approach (Methods 2.5). Although EMAN2’s determination of equally-spaced orientations within the asymmetric unit to seed alignment is stochastic, running the same alignment experiment with the same parameters multiple times converged to virtually identical results.

3.1 Motion Correction for Tilted Specimen Images Using a Direct Detection Camera

Each image in each tiltseries of the experimental data set was first corrected for translational drift (Figure 1). During data collection, we selected our imaging magnification (10,000x) such that the entire edge of the carbon hole in the imaging area would be visible in all the images of the tiltseries. This, and the presence of electron-dense gold fiducials, provided enough signal for translational frame alignment in spite of the extremely low dose per frame (Methods 2.2).

Figure 1. Drift correction for cryoET images of a tilted specimen collected with a DE20 camera.

Examples of VEEV images exhibiting significant drift, taken at different tilt angles, shown before (top) and after (bottom) drift correction.

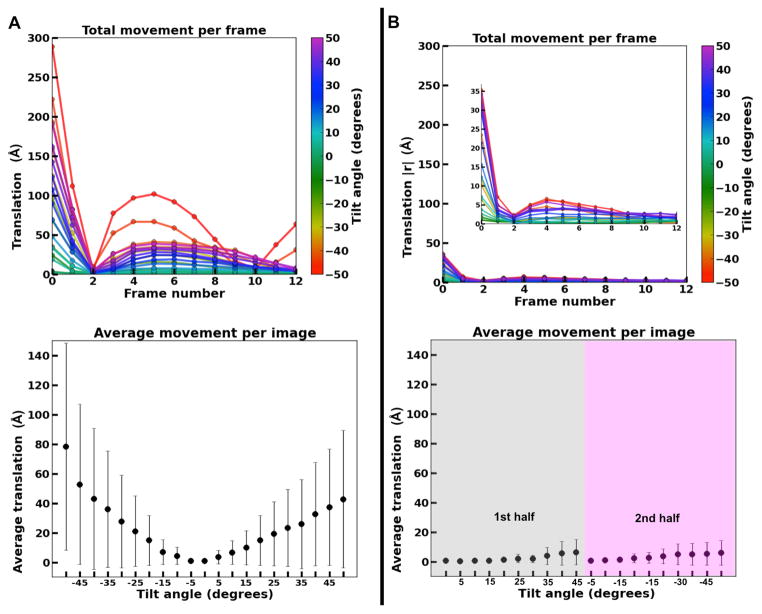
Since the largest motions typically occur in the first frame (Figure 2), we systematically discarded it before computing the average image of aligned frames at each tilt angle. Figure 2A shows that in the worst cases some individual frames (typically the first ones) can undergo large motions, as previously reported for traditional single particle cryoEM (Bai et al 2013; Brilot et al 2012; Campbell et al 2012; Li et al 2013).

Figure 2. Quantification of image drift in cryoET images of a tilted specimen.

Examples of total drift per frame and average drift per image for all images in (A) a “bad” unidirectional tiltseries and (B) a “good” bidirectional tiltseries.

At high tilt angles, the translational motion of early frames can be quite extreme, up to ~300 Å with respect to the average of aligned frames. More commonly (Figure 2B), the motions are an order of magnitude smaller, with single frames moving a maximum of ~30 Å, and less than 10 Å once the first frame is discarded. The movie-mode images exhibiting the largest motions are typically those taken at the highest-tilt angles, which are known to be more susceptible to charging and possibly cryo-holder drift. This is true for unidirectional and bidirectional tiltseries alike, albeit the latter seem to drift less as a whole. In either case, motion correction is able to compensate for this drift in most images recorded with a DE20 camera (Figure 1), rendering images and entire tiltseries usable that would have otherwise been discarded.

3.2 Defocus Measurement from Individual Tilt Images Determined Directly From the Imaging Area

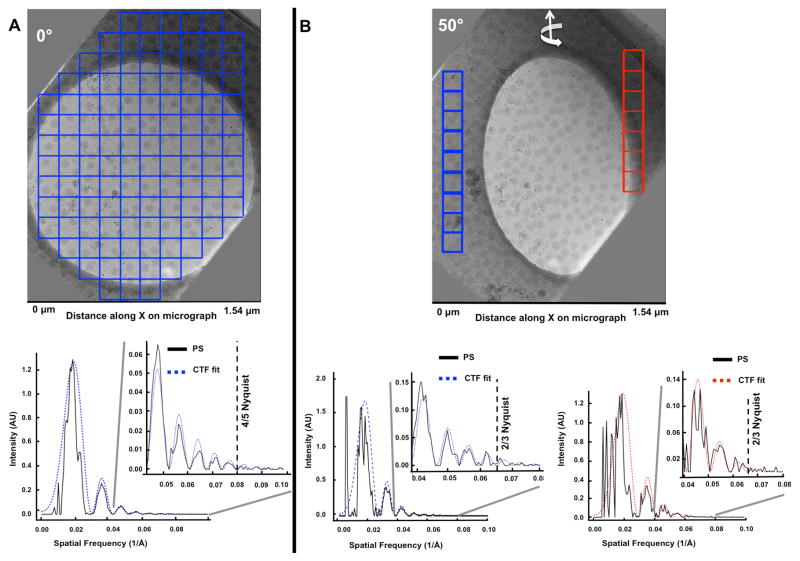
We used IMOD to align the cryoET VEEV tiltseries. We then automatically fitted the defocus gradient for each tilt image (Methods 2.4) and visually confirmed our CTF fitting using EMAN2’s interactive image evaluation graphical user interface, e2evalimage.py. This tool was developed to determine the quality of a micrograph based on the signal present in its power spectrum, by periodogram averaging of manually selected tiles. Our automated CTF determination was successful on both low and high tilt images (Figure 3). At low tilt (Figure 3A) CTF ripples are clearly visible out to 4/5 Nyquist while at high tilt (Figure 3B) the signal from single strips goes out to 2/3 Nyquist. This is understandable since at low tilt the strips are wider (e.g., the entire image is considered a single strip at 0° tilt) and the ice is thinner. On the other hand the path of the electrons through the tilted specimen is considerably longer at high tilt, yielding noisier images. Indeed, increasing ice thickness has been postulated to act as an envelope function that dampens high-frequency amplitudes (Voortman et al 2011). Furthermore, fewer tiles are averaged at high tilt angle, since the strips become quite narrow (down to the width of the tile size).

Figure 3. Interactive CTF fitting in EMAN2.

Examples of periodogram averaging by interactive micrograph tiling for power spectrum (PS) computation and CTF fitting directly from the imaging area for cryoET images of a tilted specimen. (A) Tiling of 0° image from a VEEV tiltseries showing clear CTF ripples out to 4/5 Nyquist. (B) Example of per-strip tiling of a high tilt (50°) image from a VEEV tiltseries, showing clear CTF ripples out to 2/3 Nyquist.

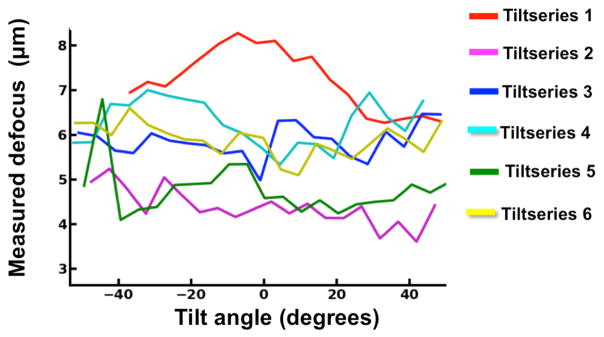
Having defocuses from more than one strip allows fitting of the defocus gradient (Supplementary Figure 2A). This, in turn, permits estimating the tilt angle of each image in the tilt series. Such angle estimates are within 1.40° to 4.85° (mean=2.87°, sigma=1.05°) on average per tiltseries from those determined by IMOD (Supplementary Table 1). IMOD’s tilt angle determination is quite accurate because it uses high contrast gold fiducials for tiltseries alignment. Therefore, for our linear fit of the defocus gradient, we can use IMOD’s tilt angles and only determine the intercept, which is the defocus at the center of the image. Interestingly, angular disagreement increases with tilt angle and cumulative radiation damage (Supplementary Figure 2B). Given the low dose per tilt image, it is difficult to resolve whether these small disagreements imply errors in fitting due to noise or suggest deviations from a flat-geometry (i.e., signal from non-perfectly linear distributions of particles in the ice, or convoluted signals at different Z-heights). Given the size of the micrographs in X, the variation in defocus in the case with the largest angular difference would only result in a ~600 Å shift in defocus, far below the accuracy required to achieve subnanometer resolution (Supplementary Table 3). In our case, variable ice thickness (Supplementary Figure 3) and a wide variation in defocus across individual micrographs and tiltseries (Figure 4) did not hamper our ability to accurately model the defocus gradient per micrograph (Supplementary Figure 2). This is substantiated by the benefits we see from applying our CTF correction, using defocus values assigned to each particle in each micrograph, based on defocus measurements directly from the imaging area (Figure 3).

Figure 4. Measured defocus variation within and across tiltseries.

Plots showing large measured defocus variations within and across six VEEV cryoET tiltseries collected using a JEM3200FSC electron microscope.

3.3 Subtomogram Alignment and Averaging

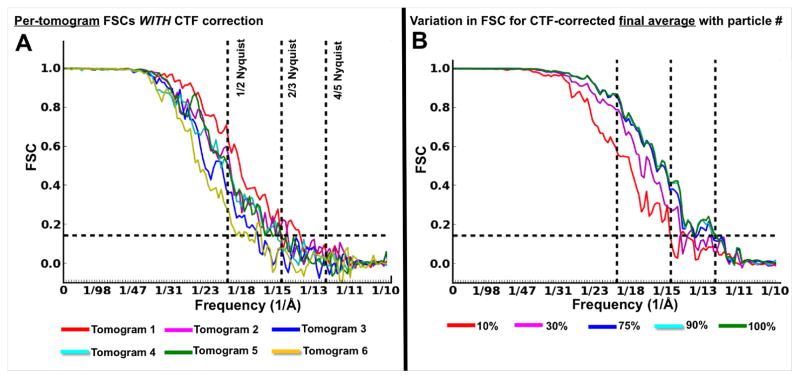
All alignments followed the gold-standard approach (Henderson et al 2012), performing iterative refinement of independent half data sets with icosahedral symmetry imposed. After CTF correction, each of our reference-free VEEV averages (~60–70 subtomograms) computed from each individual tomogram achieved better than ~20 Å resolution (17–14.8 Å; all higher than 1/2 Nyquist and some at 2/3 Nyquist)(Figure 5A). On the contrary, the per-tomogram averages without CTF correction achieved resolutions between 33.9 and 25.7 Å (Supplementary Figure 5A). The resolution of the final averages, containing the top 75% best correlating particles of the datasets combining the subtomograms from all tomograms, was ~25 Å without CTF correction (Supplementary Figure 5B, 6) and ~13.5 Å with CTF correction (Figure 5B), measured by the FSC=0.143 criterion. We tested the effect on resolution of keeping an increasing number of best-correlating particles in the final average, from 10% to 100%, in steps of 10%. Changes were negligible between fractions larger than 70%. The difference in resolution of the final CTF-corrected map was less than 3 Å when keeping only the top 10% correlating particles (51 subtomograms), compared to keeping 100% (516 subtomograms); i.e., ~15 Å and ~12.5 Å respectively (Figure 5B).

Figure 5. Resolution analyses of CTF-Corrected VEEV subtomogram averages.

(A) Per-tomogram FSC curves for six CTF-corrected VEEV subtomogram averages from independent tomograms keeping the top 75% best correlating particles in each average. (B) FSCs for CTF-corrected subtomogram averages comprised of different fractions of particles (~100% / 516 particles; ~90% / 464 particles; ~75% / 387 particles; ~30% / 154 particles; ~10% / 51 particles).

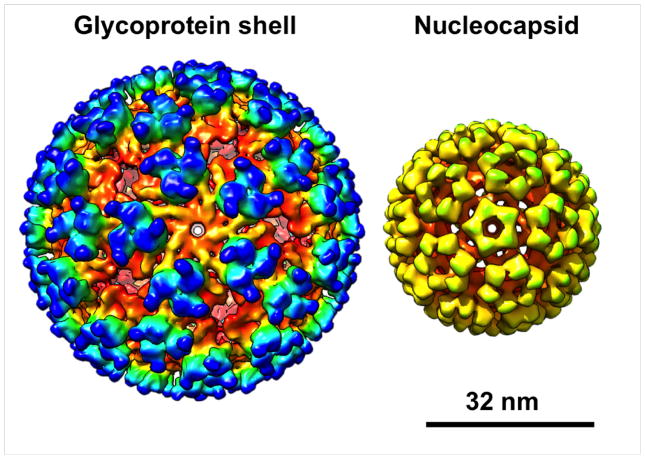
Finally, we applied a structure factor (from epsilon 15 phage) and a Wiener filter to our final subtomogram average, clearly resolving the glycoprotein trimers and the nucleocapsid (Figure 6). Applying these filters makes the Fourier amplitudes at higher spatial frequencies stronger so that the higher resolution features become apparent.

Figure 6. CTF-Corrected Subtomogram Average of VEEV.

Isosurfaces of VEEV subtomogram average comprised of the top 75% best-correlating subtomograms showing the outer glycoprotein shell (top) and the nucleocapsid (bottom).

Although most of the proteins in VEEV are arranged icosahedrally, the RNA inside the nucleocapsid was unresolved in the high-resolution structure (Zhang et al 2011), suggesting that it is not icosahedrally organized. Therefore, we used ResMap (Kucukelbir et al 2014) to analyze local variations in resolution. ResMap highlights the outer glycoprotein layer and the nucleocapsid as being resolved at higher resolution than the lipid membrane and the genome inside the nucleocapsid. Of note, ResMap only yielded sensible results after applying a structure factor. In the absence of a structure factor, the noise in subtomogram averages might be too spatially correlated (not “white” enough), preventing accurate analysis with ResMap.

Discussion

Images in cryoET can show substantial drift at high tilt (Figure 1). Our experiments show that movie-mode alignment of direct electron detector frames is critical for some cryoET images to preserve data beyond 20 Å (Figure 2), particularly at high tilt angles for which drift and charging tend to occur to a larger extent.

The importance of motion correction for cryoET data cannot be emphasized enough in making effective use of the data. The images that typically exhibit the largest drift and charging correspond to high tilt images. Collecting tiltseries from one high tilt end to the other (e.g., −60° to +60°) is simpler and more common than other data collection schemes (e.g., collecting bidirectional tiltseries starting from 0°), albeit more susceptible to charging. Correcting for beam-induced drift in high tilt images (even if at the whole-frame level) allows for constructive use of those frames with the largest drift but the least amount of radiation damage under unidirectional data collection. High tilt images in tiltseries can easily exhibit specimen drift much larger than 20 Å on average in a single movie with multiple frames (Figure 2). Even for the best tiltseries, about 2/3 of the images can be composed of frames spanning a motion range of ~10 Å under our data collection conditions. Understandably, collecting extremely large data sets and excluding “bad data” from the reconstruction process has been a common practice in cryoEM and cryoET. Nonetheless, it has been shown for single particle cryoEM that good structures can be obtained from very small sets of particles by careful application of efficient alignment strategies and correction of image artifacts (Bai et al 2013; Liu et al 2007). Here we demonstrate that alignment and reconstruction with proper handling of artifacts can be rewarding for cryoSPT as well. Indeed, the “worst” tiltseries as measured by the extent of required drift correction yields the single best per-tomogram subtomogram average in terms of FSC (Supplementary Table 1). This observation reinforces the merit of using the direct electron detector DE20 for cryoET studies at this resolution range.

Defocus measurement from micrographs has been demonstrated for a variety of tilted specimens, including 2D crystals (Henderson, & Unwin 1975) and single particles (Mindell & Grigorieff 2003), as well as for negatively stained subcellular samples (Winkler & Taylor 2003). However, such data were either collected with electron doses significantly higher than those typically used for the individual images in a cryoET tiltseries, or else the studies relied on additional, high-dose images. Some other CTF determination methods assumed a eucentric specimen stage and/or accurate defocusing during data collection (Bartesaghi et al 2012; Fernandez et al 2006; Zanetti et al 2009). In other words, the defocus value set by the data collection software was assumed to be within a few nanometers of the actual defocus, and the defocus at the center of the image was assumed to remain constant across all the images in a tiltseries. Using very large datasets (comprising up to hundreds of thousands of asymmetric units) collected under such favorable experimental conditions, cryoSPT has resulted in reconstructions reaching subnanometer resolution (Schur et al 2013; Schur et al 2015). However, specimen stage eucentricity and accurate defocusing are not always guaranteed for all electron microscopes, experimental conditions or data collection protocols. Another CTF correction method was introduced that does not entirely assume stage eucentricity and instead measures the defocus using adjustable subsets of contiguous images in a tiltseries (assuming that defocus variations follow a trend) (Xiong et al 2009). This method required collecting additional images for CTF background estimation. Lastly, an even more involved scheme (Bharat et al 2015; Eibauer et al 2012) requires collection of additional high-dose images away from the imaging area at every tilt angle to permit for CTF fitting and interpolation of the defocus at the imaging area. However, since “cryo-crinkling” of carbon and bending of grids are common artifacts (Booy & Pawley 1993), interpolating the defocus at the imaging area from additional images taken several micrometers away is inherently suboptimal in terms of accuracy. Moreover, this scheme increases data collection time and data processing overhead. This is particularly troublesome now that storage of large datasets is becoming a paramount issue in the cryoEM field in general.

Here we introduce tools for automated CTF fitting and correction for cryoSPT data, estimating ice thickness and defocus variability within tiltseries. Users can also use our interactive tools to directly visualize the power spectrum and fit the CTF by averaging tiles from strips selected manually (Figure 3).

We chose the following experimental conditions to facilitate drift and CTF correction: 1) we used a magnification such that the entire grid hole was visible in every image of the tiltseries. 2) We added a thin carbon film, which has been shown to reduce beam-induced specimen motion (Glaeser et al 2011; Wang et al 2014) and to yield a more consistent specimen distribution as well as additional signal for detection of CTF rings. 3). We used a larger angular step size (5° vs 1°–2°) and reduced the data collection range (±50°, instead of ±60°), which allocated more dose to each image in a tiltseries (and to each frame in each movie). This experimental design allowed measuring the defocus directly from the imaging area without the need to collect high-dose images from neighboring areas. Taking additional images for defocus derivation unnecessarily increases data collection time, data storage needs, and data processing overhead, while likely being inapplicable in cases in which the grid is not flat, and when the carbon support suffers from cryo-crinkling and/or radiation damage. Also, as demonstrated in Figure 4, for some experimental settings the defocus can vary from image to image within a tiltseries; therefore, assuming that all the images in a tiltseries are at the same target defocus or that subsets of images follow a trend will not always work. On the other hand, our study demonstrates the feasibility of quantifying these variations on a per-image basis. Although per-particle correction yielded only small improvements for the thickest tomograms under our experimental conditions (the ice was optimally thin in most tomograms), per-particle defocus corrections should yield greater improvements in resolution when the ice is thick; i.e., for subtomogram averaging of complexes within cells (Asano et al 2015; Dai et al 2013) to achieve resolutions beyond 15–20 Å (Supplementary Table 3).

Subtomograms need to be correctly aligned to each other or to a common reference to accomplish constructive averaging. In turn, compensating for the missing wedge is critical to prevent subtomogram misalignment (Schmid, & Booth 2008). There are multiple methods for missing wedge identification and compensation. Normalization of cross correlation maps has been used successfully (Frangakis et al 2002; Schmid et al 2006). Such method has the advantage of not needing to identify or record the location of the missing voxels in Fourier space. Other algorithms have identified the missing wedge either by explicit knowledge of the wedge location (Stölken et al 2011) or by selecting threshold values in Fourier space to constrain correlation (Bartesaghi et al 2008; Förster et al 2008). Such thresholding is feasible due to the fact that for individual subtomograms ~95% of the structural information is concentrated in approximately the top ~1% strongest Fourier coefficients (Amat et al 2010). Other methods either use an estimate of the true structure (a priori knowledge) (Heumann et al 2011) or “fill in” the missing wedge with the population average (Bostina et al 2007). However, the latter methods assume structural homogeneity among subtomograms. In threshold-based methods, it is assumed that all voxels in Fourier space corresponding to the missing wedge will have very small values and thus a threshold can be easily assigned to identify them. The difficulty with this approach is that simple processing operations, such as lowpass filtration or masking, can alter the values of voxels inside or outside the missing wedge in different ways depending on the operation, leading to misidentification of missing wedge voxels, ultimately causing misalignment. Here we implemented a missing wedge identification method that uses a dynamic, resolution-dependent threshold for each volume shell, designed to be more accurate than the previous, simple normalization of cross correlation maps. The dynamic thresholding we introduce is similar to previous adaptive filtering approaches. These have been demonstrated to yield better results than static filtering, either by deriving a frequency at which to lowpass filter based on resolution (Hrabe et al 2012) or by directly using FSC curves to filter the data (Galaz-Montoya et al 2015). However, our thresholding approach here avoids controversies regarding which FSC cutoff to use (Van Heel, & Schatz 2005) or how to compute a valid FSC (e.g., unmasked vs. masked, and to what extent).

Our new alignment algorithm incorporates several critical improvements, which allow for faster and more accurate subtomogram alignment. In previous studies, which aimed at lower resolutions, larger sampling sizes could be used and typical box sizes were less than 128³ voxels. This permitted reasonable alignment speed performance even with our previous algorithms. However, studies with higher resolution goals need to align thousands of particles in larger boxes (e.g. 256³ to 640³ voxels or larger). With the previous algorithms, a single pair-wise alignment could take upwards of 60–240 minutes, depending on symmetry and the step size used for the finest level of search. With box sizes of 396³ voxels or larger, a single, pairwise, symmetry-free alignment on a single core (3.4 GHz Intel Core i7) could take nearly a day. Even with a large cluster of standard processors, the necessary alignments were untenable in a realistic amount of time, particularly when needing to optimize several parameters and running multiple iterations on large datasets comprised of thousands of subtomograms. This prompted us to develop a new alignment scheme making use of progressive downsampling and dynamic filtering of the data. Our parameter-free, multiresolution alignment algorithm makes our tools very user-friendly.

Without using any external reference models at any point, our CTF-corrected subtomogram averages from single tiltseries using ~60–70 subtomograms each consistently achieved ~2/3 Nyquist resolution (17 Å to 14.8 Å at 5 Å/pixel sampling)(Figure 5), while all previously published CTF-corrected averages for cryoSPT fall short of 1/2 Nyquist (Supplementary Table 2). Our final subtomogram average (Figure 6), combining merely ~350 particles (21,000 asymmetric units) from 6 tomograms, reaches ~13 Å resolution, closely approaching the 4/5 Nyquist mark of ~12.5 Å at 5 Å/pixel sampling. Although this indicates the need for finer image sampling, it also strongly argues for the value of the direct electron detector (DE20 in this case) and the correction of drift and CTF artifacts for cryoET data. Accurate per-image defocus measurements and drift correction could replace the inefficient brute force approach of massive data collection followed extensive by pruning, as is commonly done, while helping to relieve the increasing need for ever larger storage capacity and computational processing time.

At our data sampling, and given that we discarded the first frame in all DDD movies, errors in gold-fiducial based tiltseries alignment and per-particle motions don’t seem to preclude approaching the detector’s theoretical resolution limit. However, tiltseries alignment is known to be error prone due to the individual movements of gold fiducials in vitreous ice (Iancu et al 2006; Noble, & Stagg 2015). Furthermore, in addition to translational drift and radiation damage, single particles undergo out-of-plane rotational motions (Brilot et al 2012), breaking, at the subtomogram level, the central assumption of tomography that all specimen images in a tiltseries are only rotated about a common tilt axis. Therefore, in pushing the field towards achieving subnanometer resolution for cryoSPT consistently, efficiently (without massive data collection) and routinely under various experimental settings, it might be necessary to implement per-particle strategies that bypass tiltseries alignment errors and address per-particle rotations and translations (Iwasaki et al 2005; Zhang, & Ren 2012). This would improve one subtomogram at a time, with subsequent averaging in mind. Indeed, multiple fronts might need to be advanced concertedly in order to routinely push the resolution to the subnanometer level. Our per-particle CTF correction method presented here, which measures the defocuses per tilt image directly from the imaging area and assigns per-particle defocus values, could be combined with whole-frame motion correction followed by damage compensation (Bharat et al 2015), as well as per-particle refinement strategies (Iwasaki et al 2005), which could in the near future include correcting for astigmatism and magnification variations.

Abbreviations

SPT

Single particle tomography

cryoSPT

single particle cryo-electron tomography

CTF

contrast transfer function

SNR

signal to noise ratio