Labeled Graph Kernel for Behavior Analysis

Abstract

Automatic behavior analysis from video is a major topic in many areas of research, including computer vision, multimedia, robotics, biology, cognitive science, social psychology, psychiatry, and linguistics. Two major problems are of interest when analyzing behavior. First, we wish to automatically categorize observed behaviors into a discrete set of classes (i.e., classification). For example, to determine word production from video sequences in sign language. Second, we wish to understand the relevance of each behavioral feature in achieving this classification (i.e., decoding). For instance, to know which behavior variables are used to discriminate between the words apple and onion in American Sign Language (ASL). The present paper proposes to model behavior using a labeled graph, where the nodes define behavioral features and the edges are labels specifying their order (e.g., before, overlaps, start). In this approach, classification reduces to a simple labeled graph matching. Unfortunately, the complexity of labeled graph matching grows exponentially with the number of categories we wish to represent. Here, we derive a graph kernel to quickly and accurately compute this graph similarity. This approach is very general and can be plugged into any kernel-based classifier. Specifically, we derive a Labeled Graph Support Vector Machine (LGSVM) and a Labeled Graph Logistic Regressor (LGLR) that can be readily employed to discriminate between many actions (e.g., sign language concepts). The derived approach can be readily used for decoding too, yielding invaluable information for the understanding of a problem (e.g., to know how to teach a sign language). The derived algorithms allow us to achieve higher accuracy results than those of state-of-the-art algorithms in a fraction of the time. We show experimental results on a variety of problems and datasets, including multimodal data.

1 Introduction

Behavioral analysis is a topic of interest in many areas of science and engineering. For example, in multimedia one may want to annotate actions in a basketball game, actor behavior in a movie or hand and facial gestures associated to speech production [18, 44, 46, 48, 54]. In robotics, behavior analysis is essential for a robot to interact with humans in a natural way [31]. In cognitive science, we wish to relate behavior with input variables, e.g., responses to observed facial expressions of emotion [14] or facial action coding [22]. In psychiatry, we wish to understand how psychopathologies affect behavior [36]. In biology, one may be interested in studying animal behavior [13, 17]. And, in linguistics, one is interested in modeling sign languages [16]. In most of these applications, the number of video sequences that need to be analyzed is staggering. Thus the goal is to achieve robust and accurate automatic analysis of these behaviors using computer vision and machine learning algorithms.

The applications listed above define two inter-related problems of behavior analysis. The first one is classification. In classification, we are interested in categorizing behavior into a set of discrete elements (i.e., categories). For example, in sign language, we want to determine if a video of a sign corresponds to the word apple or onion. The second problem is decoding, where the goal is to understand the behavior variables that allow us to discriminate between these categories. For example, which part of the manual sign discriminates between apple and onion.

To better define these two problems, let us explore the sign language example in more detail. The manual signs in sign languages are a combination of handshapes, hand motions and places of articulation [6]. In general, the handshape, motion and place of articulation are discrete variable whose values must be selected from a set of known elements [43]. In computer vision, one uses algorithms to extract image features from a video of a sentence that can help discriminate between distinct handshapes, motions and places of articulation [12, 33]. Two points need to be addressed here: i) Each possible handshape, motion and place of articulation is a categorical element. This means that the computer vision system needs to learn to identify the variability in handshape, motion and place of articulation associated to each of these categories. ii) Each sign language concept (e.g., each word) can be signed using a slightly different combination of basic elements. The computer vision system must learn which combinations define the same category.

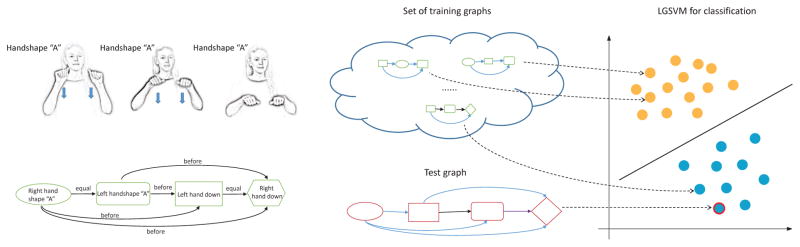
From the discussion above, we see that the manual sign can be modeled using a labeled graph [50]. In this model, the nodes of the graph represent the extracted features (e.g., right hand moves from point a to point b, middle finger and thumb touching), while the edges between nodes represent the temporal structure of these features (e.g., handshape “A” is used in both hands before right hand moves from a to b; left hand moves from point c to d at the same time as the right hand moves from e to f ). This is shown on the left-most part of Figure 1. This model can readily solve the two points defined in the preceding paragraph by learning from sample sequences [12]. These samples will include the distinct handshapes and signer variability needed to address these two classification problems. This is illustrated in the middle section in Figure 1.

Fig. 1.

From left to right: A sign language concept can be described as a labeled graph, which specifies handshapes, motions and/or places-of-articulation. Each video of a sign language concept is a labeled graph. The labeled graphs corresponding to all sample videos form the training set. Our approach is very general and can be plugged into any kernel-based classification method. When using Support Vector Machines, for instance, we obtained a Labeled Graph Support Vector Machine (LGSVM) algorithm which is used to discriminate between samples of different concepts in this set as shown in the image above. The classification of a test graph is readily given by this LGSVM algorithm or the kernel-based classifier of our choosing.

The model just outlined solves the representation problem, i.e., each sign language concept is represented by a labelled graph. Classification of a sign in a test video sequence is directly obtained by finding the graph that best matches the observation in the test video. Unfortunately, the complexity of this matching process grows exponentially with the number of concepts (words) in the database. We derive a classification algorithm to resolve this problem.

To resolve the complexity problem, we derive a labeled graph kernel. A graph kernel is a measure of similarity [47]. A measure of similarity between two labeled graphs should increase as their representations become more similar. This is the same as identifying the number of identical paths in both graphs for all possible paths (i.e., for all paths of every possible length in each graph). We use dynamic programming to derive an efficient, low-cost algorithm to measure this graph similarity. This measure of similarity is then used to derive a kernel-based classifier. For example, we can use Support Vector Machine (SVM) [49] of Regularized Kernel Logistic Regression (RKLR) [5] to learn all the possible variations of a behavior (i.e., variations in handshape, motion and place of articulation used to express the same concept or grammatical function). We call the resulting algorithm Labeled Graph Support Vector Machine (LGSVM), because it corresponds to a SVM for labeled graphs. This is shown on the right-most section in Figure 1.

Thus far we have addressed the classification problem. Let us now look into the decoding problem in more detail. Linear SVM and other linear classifiers learn a linear discriminant function that maximize the margin between the samples of two classes. Moreover, the coefficients (weight associated with each feature) represent the importance of the features defining the discriminant function [23, 45]. Thus, to inverse the problem (i.e., to go from classification to decoding), we need to identify the graph features associated with the largest coefficients. We derive an efficient algorithm to identify the graph features associated to the largest coefficient and illustrate how it can be used in the derived LGSVM.

1.1 Theoretical contribution

Despite the broad investigation of graph kernels in the literature, our graph kernel is different in that it is a path based graph kernel. Graphs can be decomposed into substructures in multiple ways. We employ paths to compute graph kernels while others use random walks [24, 27] or tree walks [24]. A major drawback of walk kernels is that a walk can repeatedly visit the same node, causing the “tottering” problem [29]. This means that a small amount of similar subgraphs can result in a very large kernel value. Path kernels do not have this problem because path nodes cannot be repeated. Unfortunately, this results in an NP-hard problem [21]. In the present paper, we note that, in the temporal domain, events can be ordered according to their starting time and that this ordering allows us to derive an efficient, low-cost algorithm. We show how a dynamic programming implementation of this approach yields polynomial time solutions.

The proposed behavior analysis approach is hierarchical [1] in that we decompose a complex behavior into components called events. Before performing the hierarchical fusion task, we detect the events defining the action. Such detection process is also an information compression process, since we can convert a sequence of images or time series into several events. This results in yet another advantage of our approach, allowing us to incorporate prior knowledge into the system.

Finally, it is well known that basic event detection and their temporal segmentation are very challenging problems. The emergence of novel sensors, including 3D cameras and Inertial Measurement Unit (IMU), facilitate this task. The use of multiple sensors results in a novel problem – the multimodal data fusion problem. This problem is naturally solved by the proposed approach, yielding an elegant, efficient solution for the analysis of behavior from multimodal data. To see this note that events detected from multiple sensors can be modeled as separate nodes in our graph and that edges then describe relationships between them. We show experimental results to illustrate the uses of the derived algorithm in multimodal applications.

1.2 Related work

Bag of Visual Words (BoVW) models [53] have been used in action recognition [25, 35, 51, 52]. The major drawback of Bag of Visual Words models is that they are incapable of capturing spatio-temporal information. Probabilistic graphical models, including Bayesian Networks [41] and Hidden Markov Models [28, 30, 32], solve this problem by including some information about the temporal structure of the data. However, probabilistic graphical models cannot readily model concurrent temporal relations. The conditional probabilities can only model two predicates: before and meet. Other predicates, such as finish and overlap, cannot be properly modeled, limiting the applicability of these algorithms.

In [37], the authors exploit a data mining approach where each video is discretized into a sequence of temporal bins. In combination with the LPBoost classifier, they simultaneously learn the classification function and perform feature selection over the space of all possible sequences. Yet, while sequential temporal information is maintained in their representation, concurrent structures are not. One potential solution is given in [19] which attempts to identify hierarchical temporal structures. However, this method cannot work with large feature spaces and, hence, has to depend on several non-optimal thresholds to prune the feature space before classification is even attempted. This results in sub-optimal classifications.

Finally, the majority of the algorithms described above only address the classification problem. The decoding problem is however equally important. In the sign language example described above, we want to understand which behavior variables code for a word. For example, apple and onion use the same handshape and are distinguished only by their place-of-articulation. Similarly, in biology, one may wish to understand the variables of aggressive behavior in flies [17]. We show how the derived algorithm can readily solve this decoding problem.

1.3 Paper organization

The rest of the paper is organized as follows. Section 2 defines the labeled graph model. Section 3 derives the labeled graph kernel. Section 4 presents the LGSVM algorithm. Section 5 derives the decoding algorithm. Experimental results are in Section 6.7.

2 Modeling Samples of an Action with Labeled Graphs

We decompose actions (e.g., a sign language concept) into events. For instance, the action of a person waving both his hands can be decomposed into four events: left hand moves up, hand moves left to right (which occurs several times), right hand moves up, and hand moves right to left (several times).

In general, the term “action” is used to define what needs to be modeled, while the term “event” is employed to specify the concepts that can be readily detected by a computer vision algorithm. An event will in general be defined by a time interval, during which the event is true (e.g., the time during which the left hand is moving left to right). Then, an action is a combination of events that follow a specific temporal structure. This temporal structure is defined by the temporal relationships between the set of events defining the action. In our example above, handshape “A” happens before right hand moves from a to b; happens before is what we call a temporal relationship (i.e., predicate).

As shown in [2], we can define first-order temporal relationships between two events using seven predicates: before to specify that an event happens before another and that there is a non-empty time interval between these two events; meets to indicate that the time between these two events is zero; overlap when an event v_ki starts and finishes before another event v_{k j} ends but v_{k j} starts before v_ki ends; during to define when an event v_ki starts before another event v_{k j} and finishes after v_{k j} ; starts to indicate that both events start at the same time but end at different times; finishes to specify that both events end at the same time but start at different times; equal to indicate that the two events start and end at the same time; Figure 2.

Fig. 2.

Shown here are the seven possible temporal relationships between two events. Here, k specifies the action and i and j specify the event.

To define the temporal structure of an action, we use a graph where the nodes specify the events and the edges the temporal relationships between events. This is thus a labeled graph [7]. Specifically we will use directed labeled graphs which are defined as follows.

Definition 1

A Directed Labeled Graph is given by a 4-tuple G_k = (V_k, E_k, L, f_k), where V_k = {v_k1, …, v_knk} is a set of nodes, E_k = {e_k12, e_k13, …, e_k1nk, e_k23, …, e_knk−1nk} is the set of edges (e_{ki j}, with i < j ), L = {l_{1 …}, l_p } is a set of labels and f_k : V_k ∪ E_k → L is a function that assigns labels to the nodes and edges of the graph G_k.

The possible labels assigned to an edge are the seven temporal predicates given in Figure 2. The label assigned to a node is the event category it belongs to. Event categories may be different in each application. For example, in sign language recognition, an event category can be right hand moves up or right hands moves down.

Note that we use a directed labeled graph because knowing the predicate describing the temporal relationship between events v_ki and v_{k j} (i.e., L(e_{ki j}) for some i < j ) automatically defines the predicate between v_{k j} and v_ki. E.g., if v_ki is before v_{k j}, then v_{k j} is after v_ki, predicates like after are called inverse predicates. Such predicates would however not add additional information to our model and are therefore omitted.

Since events are in the temporal domain, it is imperative that nodes in the graph be ordered based on their starting time. This can be readily accomplished with the following easy rules: 1. If event v_ki starts before v_{k j} (in time), then v_ki will be before v_{k j} in a way that there is an edge from v_ki to v_{k j} but not vice-versa, i.e., i < j. For example, in Figure 2, before, meets, overlaps, during and finish will have an edge from v_ki to v_{k j} but not from v_{k j} to v_ki. 2. If v_ki and v_{k j} start at the same time, then we define an edge from the event that ends earlier to the one that ends later. For example, in Figure 2, starts will only have an edge from v_ki to v_{k j}. 3. When both events start and end at the same time, there are two edges, one from v_ki to v_{k j} and another from v_{k j} to v_ki. Note, however, that since both edges are identical (i.e., both are labeled equal), in reality we only need to store the information of one of these two edges, yielding a single directed edge. This edge can be selected at random and fixed for all the graphs.

Let the resulting model be called a Sample Action Graph, G_k, with k = 1, …, m, m the number of samples, and e_{ki j} defining a directed edge from event v_ki to event v_{k j} in G_k. Let the adjacency matrix of this action graph be M_k, with entry m_{ki j} equal to one of the seven possible temporal predicates given in Figure 2. The resulting graph is fully connected and, thus, M_k is upper-triangular with $\frac{n_k(n_k-1)}{2}$ entries. The set of all sample graphs is defined as 𝒢 = {G₁, …, G_m}.

3 Labeled Graph Kernel

In the previous section, we have shown how to define a sample of an action as a directed labeled graph. We call the resulting representation a sample action graph and assume there are m such sample graphs. We now wish to calculate the similarity between any two sample action graphs. This can be achieved with the use of a kernel matrix defining the similarity between every pair of sample graphs.

To do this, let a be the total number of possible paths in all m sample action graphs. A path is a non-empty graph P = v₁e₁₂v₂e₂₃ … e_(q−1)qv_q, with e_{i (i +1)} defining the edge between v_i and v_{i +1}, and $v_i\underset{\forall i\ne j}{\ne }{v}_j$. We define a labeled path as P = f (v₁) f (e₁₂) f (v₂) f (e₂₃) … f (e_(q−1)q) f (v_q).

A sample graph G_k can now be defined as a feature vector x_k ∈ ℝ^a, with each entry in x_k specifying the number of times a path P occurs in G_k [11, 24, 27].

Specifically, let $P_b^z$ be a path of length z ≥ 0, b = 1, …, r_z, with r_z the total number of paths of this length in the set of all sample graphs 𝒢. Thus, x_k = (x_k11, …, x_k1r0, …, x_kw1, …, x_kwrw)^T, where x_kzb is the number of times the path $P_b^z$ occurs in G_k, w is the longest path in 𝒢, b = 1, …, r_z, z = 0, …, w, and ${\sum }_{z=0}^w{r}_z=a$.

The similarity of any two graphs, G_k1 and G_k2 in thus given by the inner-product of their feature vectors,

$$\begin{array}{l}K(G_{k_1},G_{k_2})={\mathbf{x}}_{k_1}^T{\mathbf{x}}_{k_2}=\sum _{z=0}^w\sum _{b=1}^{r_z}{x}_{k_{1}zb}{x}_{k_{2}zb}\\ =\sum _{z=0}^w{K}^z(G_{k_1},G_{k_2}).\end{array}$$ (1)

In this equation, K (., .) measures the similarity of two graphs, while K^z(., .) specifies their similarity for a given path length z. K(., .) and K^z(., .) are of course the kernels defining the metric used to measure graph similarity.

Direct computation of K^z (., .) is however computationally demanding – the number of directed paths r_z may grow exponentially with z. We instead employ a dynamic programming technique to only calculate K^z (., .) implicitly. We do this, by noting that x_kzb can be calculated using a function that computes the number of times $P_b^z$ starts at node v_ki, 1 ≤ i ≤ n_k. Let this function be $C_b^z(v_{ki})$, then $x_{\mathit{kzb}}={\sum }_{i=1}^{n_k}{C}_b^z(v_{ki})$. We can thus write,

$$\begin{array}{l}{K}^z(G_{k_1},G_{k_2})=\sum _{b=1}^{r_z}{x}_{k_{1}zb}{x}_{k_{2}zb}\\ =\sum _{b=1}^{r_z}\left[\sum _{i_1=1}^{n_{k_1}}{C}_b^z(v_{k_1{i}_1})\right]\left[\sum _{i_2=1}^{n_{k_2}}{C}_b^z(v_{k_2{i}_2})\right]\\ =\sum _{i_1=1}^{n_{k_1}}\sum _{i_2=1}^{n_{k_2}}\sum _{b=1}^{r_z}{C}_b^z(v_{k_1{i}_1})C_b^z(v_{k_2{i}_2})\\ =\sum _{i_1=1}^{n_{k_1}}\sum _{i_2=1}^{n_{k_2}}{\mathrm{\Gamma }}^z(v_{k_1{i}_1},v_{k_2{i}_2}).\end{array}$$ (2)

The function Λ^z(v_k1i1, v_k2i2) is computed recursively as follows. First, initialize the functions,

$$\{\begin{array}{ll}{\mathrm{\Gamma }}^0(v_{k_1{i}_1},v_{k_2{i}_2})=1,\hfill & \text{if}f(v_{k_1{i}_1})=f(v_{k_2{i}_2}),\hfill \\ {\mathrm{\Gamma }}^0(v_{k_1{i}_1},v_{k_2{i}_2})=0,\hfill & \text{otherwise.}\hfill \end{array}$$ (3)

Then, for z = 1, …, w, when min(n_k1 − i₁ + 1, n_k2 − i₂ + 1) < z or f(v_k1i1) ≠ f(v_k2i2), Λ^z(v_k1i1, v_k2i2) = 0. Otherwise Λ^z(v_k1i1, v_k2i2) use the recursion described next.

The recursion of Λ^z(v_k1i1, v_k2i2) is due to the fact that $P_b^z=f(v_{k_1{i}_1})f(e_{k_1{i}_1{j}_1})P_{\widehat{b}}^{z-1}$. If a common path of G_k1 and G_k2 starts at v_k1i1 and v_k2i2, respectively, its second node can be at v_k1j1, i₁ + 1 ≤ j₁ ≤ n_k1 in G_k1 and v_k2j2, i₂ + 1 ≤ j₂ ≤ n_k2 in G_k2. Therefore, we can write

$$\begin{array}{l}{\mathrm{\Gamma }}^z(v_{k_1{i}_1},v_{k_2{i}_2})=\sum _{b=1}^{r_z}\sum _{j_1=i_1+1}^{n_{k_1}}\sum _{j_2=i_2+1}^{n_{k_2}}\left(C_{\widehat{b}}^{z-1}(v_{k_1{j}_1})C_{\widehat{b}}^{z-1}(v_{k_2{j}_2})I_{i_1,i_2}(j_1,j_2)\right)\\ =\sum _{j_1=i_1+1}^{n_{k_1}}\sum _{j_2=i_2+1}^{n_{k_2}}{I}_{i_1,i_2}(j_1,j_2)\sum _{\widehat{b}=1}^{r_{z-1}}{C}_{\widehat{b}}^{z-1}(v_{k_1{j}_1})C_{\widehat{b}}^{z-1}(v_{k_2{j}_2})\\ =\sum _{j_1=i_1+1}^{n_{k_1}}\sum _{j_2=i_2+1}^{n_{k_2}}{I}_{i_1,i_2}(j_1,j_2){\mathrm{\Gamma }}^{z-1}(v_{k_1{j}_1},v_{k_2{j}_2}),\end{array}$$ (4)

where I_i1,i2(j₁, j₂) is a function that indicates whether the label of the edge e_k1i1j1 is equal to the label of the edge e_k2i2j2,

$$I_{i_1,i_2}(j_1,j_2)=\{\begin{array}{ll}1,\hfill & f(e_{k_1{i}_1{j}_1})=f(e_{k_2{i}_2{j}_2})\hfill \\ 0,\hfill & \text{otherwise.}\hfill \end{array}$$

Since the number of nodes in G_k1 and G_k2 effect the value of this kernel, K^z(G_k1, G_k2), we need to normalize the resulting kernel by the size of the two graphs being compared. Formally,

$$\begin{array}{l}\overline{K^z}(G_{k_1},G_{k_2})=\langle {\overline{\mathbf{x}}}_{k_{1}z},{\overline{\mathbf{x}}}_{k_{2}z}\rangle \\ =\frac{1}{\Vert {\mathbf{x}}_{k_{1}z}\Vert \Vert {\mathbf{x}}_{k_{2}z}\Vert }\langle {\mathbf{x}}_{k_{1}z},{\mathbf{x}}_{k_{2}z}\rangle \\ =\frac{K^z(G_{k_1},G_{k_2})}{\sqrt{K^z(G_{k_1},G_{k_1})}\sqrt{K^z(G_{k_2},G_{k_2})}},\end{array}$$ (5)

where x_kz = (x_kz1, x_kz2, …, x_kzrz)^T, ${\overline{\mathbf{x}}}_{kz}=\frac{{\mathbf{x}}_{kz}}{\Vert {\mathbf{x}}_{kz}\Vert }$ and ||.|| denotes the 2–norm of a vector.

The computation complexity of the above derived kernel is polynomial; specifically, the complexity of K^z(G_k1, G_k2) is $O(z{n}_{k_1}^2{n}_{k_2}^2)$, because we need to compute all Γ^β(i₁, i₂), 0 ≤ β ≤ z, 1 ≤ i₁ ≤ n_k1, 1 ≤ i₂ ≤ n_k2 and each Γ^β(i₁, i₂) needs at most O(n_k1 n_k2) operations.

4 Classification

The approach derived above is general and can be directly plugged into any kernel-based classifier. In our experiments we use Support Vector Machines (SVM) [49] and Regularized Kernel Logistic Regression (RKLR) [5]. A binary Support Vector Machine [49] classifier learns a hyperplane (i.e., (w, o), its norm and bias) that maximizes the margin between two classes of training data. In the dual problem in SVM, we maximize the Lagrangian multipliers α_k’s. After solving the dual problem with respect to α_k’s, we can obtain w as a function of α_k’s in the primal problem,

$$\mathbf{w}=\sum _{k=1}^m{\alpha }_k{y}_k{\overline{\mathbf{x}}}_k$$ (6)

To make a prediction on a test sample labeled graph G_t representing an unknown action, we need to calculate 〈x̄_t, w〉 + o. Replacing w using (6), we can rewrite this quantity as

$$\langle {\overline{\mathbf{x}}}_t,\mathbf{w}\rangle +o=\sum _{k=1}^m{\alpha }_k{y}_k\langle {\overline{\mathbf{x}}}_t,{\overline{\mathbf{x}}}_k\rangle +o.$$ (7)

Since only a few α_k correspond to non-zero support vectors, classification is given by a simple inner product between x̄_t and a few support vectors. Hence, this yields an efficient algorithm for the classification of actions. We call this algorithm Labeled Graph Support Vector Machine or LGSVM for short. Equivalently, we can use Regularized Kernel Logistic Regression (RKLR) to yield a Labeled Graph Logistic Regression (LGLR).

5 Decoding Algorithm

By decoding one generally means we are interested in finding out the most discriminant features from our model. This is explicitly given in the vector w defining the hyperplane of the LGSVM. To see this note that the i^th element w_i of w = (w₁, …, w_a )^T defines the contribution of the i^th feature (i.e., path) to the overall classification. Of course, one does not have w, since this is only computed implicitly. This means we need to compute the value of those elements of w (i.e., w_i ) that may be discriminant before we select the largest value.

The key here is to note that we only need to compute a small number of w_i. This is because most of the paths P are not consistently found in the sample graphs we have used to compute the LGSVM. Note that a path P could be discriminant if the sample graphs of class +1 include it but the sample graphs of class −1 do not. This means that P is present in about 50% of the sample graphs. Another option is for a combination of graphs to be discriminant. For example, ether P₁, P₂ or P₃ are present in the samples of class +1, but none of these are found in the samples of class −1. In this case, these path are present in about 16% of the samples. More generally, a path can only be discriminant if it is present in a minimum number of sample graphs, λ%. For our purposes, we will select all paths that occur in at least 5% of the graphs (λ= 5). Typically, this means that only a few dozen paths are selected.

The selection of these paths can be made really efficient by noting that if P is a non-frequent path (i.e., it is present in less than λ% of our sample graphs) and P is a subpath of path Q, then Q is not frequent [42]. For example, if P = v_k1 is not frequent, then Q = v_k1e_k12 v_k2 is not frequent either. This suggests a simple search algorithm of frequent paths as follows. Start with all possible options of a path having only one node. Eliminate all those that are not frequent. Then, iteratively add an edge and node to the remaining paths and prune those that are not frequent. This efficient procedure thus returns those paths that occur in at least λ% of the sample graphs.

Once we have the frequent paths, we can compute the feature vectors x_ki, its normalized form x̄_ki, and their discriminant factor as

$$w_i=\sum _{k=1}^m{\alpha }_k{y}_k{\overline{x}}_{ki}.$$ (8)

Ordering the frequent paths from largest to smallest w_i yields the list of most to least discriminant paths (features).

6 Experimental Results

We provide experimental evaluation of the proposed classification and decoding algorithms on a variety of databases. First, we show experimental results on three different sign language recognition problems. We then provide experimental results on two additional action recognition problems – one describing generic human behavior and one to demonstrate the use of the derived approach in multimodal modeling and classification. Comparative results with state of the art algorithms demonstrate the accuracy, robustness and low computational cost of the proposed approach. All of our experiments are performed on a 3.40 GHz Intel Core i7 CPU machine using Matlab.

6.1 Graph model for sign language analysis

The three sign language databases used in the experiments below are multi-channel time series. Before computing our graph kernel, we need to extract events from each sample and represent them as an action graph. This is the model to be used in classification and decoding.

The events correspond to a set of three possible movements observed in each channel of a time series. Each tracked fiducial point defines a curve as it moves from one point to another. The three options we consider in each channel are: increasing, flat and decreasing. An interval between a minimum point and a maximum point increases while an interval between a maximum point and a minimum point decreases. Considering noise, if an interval has length less than a threshold and amplitude less than another threshold, its trend cannot be robustly determined; in such cases, the same category as its predecessor is assigned to the current section. A flat interval has amplitude less than the second threshold just mentioned.

Next, adjacent intervals that have the same curve trend are described as a single event. This means that the curve trends of every pair of neighboring intervals are distinct. Thus, each interval and its starting and ending time correspond to an event.

The action graph is given by the ordered events based on their starting time (Section 2). Finally, we compute pairwise temporal relationships of all the events (Figure 2). To handle uncertainty in temporal segmentation, we allow for soft interval, i.e., event A meets event B if and only if |(start of B) − (end of A)| < α, for a small α.

We use the two classification algorithms described in Section 4, LGSVM and LGLR. To determine the optimal length of path z as well as the penalization factor C, we use the leave-one-sample-out cross-validation approach using only the samples in the training set. Grid search is applied in this process, with z = {1, 2, 3, 4, 5, 6} and C = {10, 100, 1000, 10000, 10000}. The same z and C are used for all binary classifiers to avoid overfitting. A one-versus-all approach is used for multi-class classification. Specifically, if there are n classes, we build n binary classifiers. The k^th (k = 1, …, n) classifier is trained with data from the k^th class (i.e., the positive class) and training data of all the other k − 1 classes correspond to the samples of the negative class. To make a prediction on a testing sample, we compute 〈x̄_t, w_k〉 + o_k and use the label of the largest value as the predictor.

Furthermore, in RKLR, we provide results obtained with the l₁ and l₂ regularizers. Also, a 4-fold cross-validation on the training data is done to compute the optimal regularization term from the set {10⁻⁶, 10^−2.5, 10¹}. Additionally, we provide comparative results against the random walk kernel algorithm presented in [24] with SVM as the classifier. Statistical significance is computed using a t-test and p values are given in all experiments. As shown below, the approach derived in the present paper yields statistically significantly better results than those reported in the literature.

6.2 Australian Sign Language (Auslan) dataset

This dataset is included in the UCI Machine Learning repository [20]. Samples of 95 Auslan signs from a single signer (a native Auslan signer) were collected over a period of nine weeks using high-quality position trackers. Three samples of each sign were captured each day. Thus, in total, there are 2, 565 samples, with 27 samples per sign. Each sample is a 22-channel time series representing the (X, Y, Z ) position as well as the roll, yaw and pitch of each hand, and bending measurements of all fingers. The average length of each sample video is 57 frames. We detect curve trends in all the 22 channels, yielding 66 event categories. Experimental results are done as follows.

Each time we randomly select the data of three weeks and use it for training while using the rest (six weeks) for testing. We repeat this process 10 times. This is a more challenging setup than those previously used in [10, 34], since, in these works, the authors use some of the data of each week for training and some for testing. With the LGSVM approach, the mean accuracy and standard deviation are 91.60% and 1.50%. When we use the same experiment setting as [10], our algorithm achieves mean accuracy of 93.44% and standard deviation of 0.30%. The average time of our algorithm for classifying a testing sample from raw data using Matlab is 1.62 seconds. We also run the Matlab implementation of two state-of-the-art algorithms [10, 34] using the same computer. The results, which are in Table 1, show favorable results for our approach in accuracy as well as computational time. Our method is not only more accurate, but also much faster than alternative algorithms.

TABLE 1.

Classification accuracies on the Auslan database for the proposed approach as well as several state-of-the-art methods. OSCM: Order-preserving Sparse Coding Method. TGAK: Triangular Global Alignment Kernels. RW: Random Walk. RKLR: Regularized Kernel Logistic Regression. Also shown are the computational times of three of the algorithms for which the code is available.

Method	Accuracy	Time/Sample
OSCM [34]	70.46% ± 1.73%	9.43 s
TGAK [10]	88% ± 0.5%	14.35 s
RW Kernel + SVM [24]	89.70% ± 1.78%	2.27 s
Path Kernel + RKLR (l1)	89.69% ± 1.73%	–
Path Kernel + RKLR (l2)	90.42% ± 0.67%	–
Path Kernel + SVM	91.60% ± 1.50%	1.62 s

Next, we compute the results using the LGLR algorithm, Table 1. The results are comparable to those obtained with the SVM classifier, demonstrating the effectiveness of the proposed path kernel approach, i.e., the proposed algorithm yields superior results independently of our choice of classifier. A paired-sample t-test to compare our path kernel with the walk kernel algorithm shows our results are significantly better, with a p-value smaller or equal than 0.018.

We can now use the decoding algorithm of Section 5 to identify the most discriminant features in Auslan signing. For example, this process identifies moving the right hand down without any side movement as the most discriminant feature to express and visually recognize the concept (word) “alive.” Additional results are given in Table 2. This is useful, for example, to study grammatical function of behavior in linguistics [4].

TABLE 2.

Most discriminant paths for three Auslan signs. The decoding algorithm of Section 5 returns the most discriminant paths which are readily interpretable and can thus be used to understand a problem or, in this case, teach sign language to novice.

Sign	Most discriminant paths
Cold	(right hand moves up) meets (right pitch increases) before (right roll does not change) (right hand moves up) meets (right pitch increases) before (right yaw does not change) (right hand moves to right) meets (right hand moves up) meets (right pitch decreases)
Different	(left hand roll still) during (right hand roll increases) meets (right hand does not move in depth) (left hand roll still) equals (left little finger bend does not change) meets (right hand roll increases) (left hand yaw still) during (left little finger bend does not change) meets (right hand roll increases)
Danger	(right hand moves up) meets (right pitch increases) before (right hand still about y) (right hand moves down) meets (right pitch decreases) before (right hand still in y) (right hand moves up) meets (right pitch increases) before (right thumb bend does not change)

6.3 DGS Kinect dataset

This dataset is a collection of 40 German Sign Language signs. Each of the 14 subjects performed each of the signs 5 times. The dataset is captured with a Kinect^™ camera. Each sample in the dataset is a 33-channel time series representing how the 3D coordinates of 11 joints in the upper part of the body change across time. This dataset is challenging due to large variations of inter- and intra-subject signing styles.

We divide the subject’s torso and head into multiple regions, Figure 3. This is used to define discrete categories specifying the place-of-articulation [12]. Events are defined as the 3D movement of each hand, the region that each hand is located at, the joint that each hand is closest to, the 3D relative movement of the two hands plus the relative location of the two hands in 3D space (e.g. right hand is above left hand).

Fig. 3.

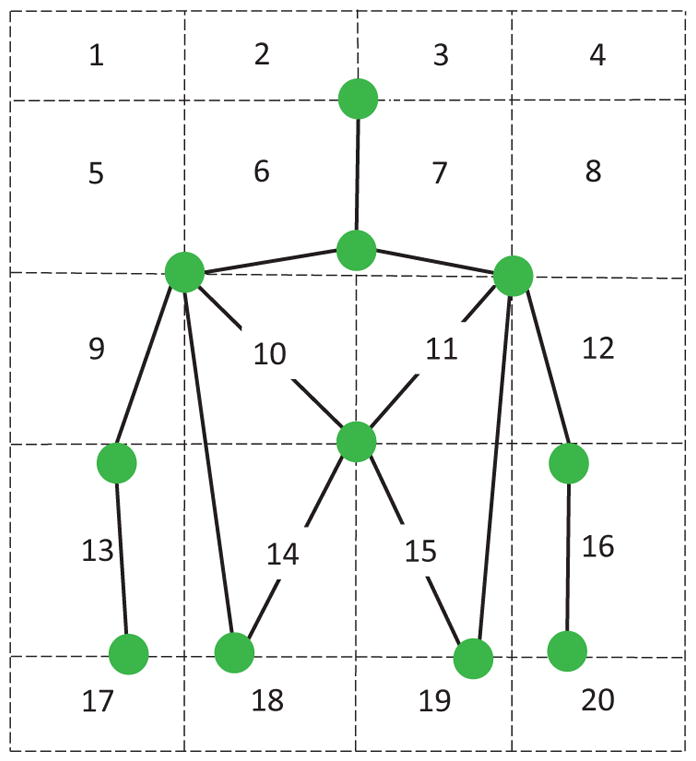
To determine place-of-articulation of a sign, we discretize the image space into twenty regions. The limits of these regions are defined by the skeleton points of the signer. For example, as seen in the figure above, the skeleton point representing the head of the signer divides the space into left and right columns, the average shoulder position separates the top two rows from the bottom three as well as the left- and right-most columns, and the bottom-most points of the torso separate the bottom row from the top four.

Experiments are performed using the more challenging leave-one-signer-out cross-validation approach as in [40]. This means we train the classifier with the samples of all subjects but one and use the samples of the left-out subject for testing. This process is repeated for each of the subjects we can leave out. Our path kernel combined with SVM classifier yields a mean classification accuracy of 70.17% with standard deviation 8.3%. The average time for classifying a testing sign is 4.33 seconds. We report comparative results with state-of-the-art algorithms in Table 3. A t-test shows our improvement is statistically significant, with p < 10⁻¹⁰.

TABLE 3.

Classification accuracies on the DGS dataset for the proposed approach as well as several state-of-the-art methods. SPBoost/Tree: Sequential Pattern Boosting/Tree. RW: Random Walk.

Method	Accuracy	Time/Sample
Markov Chain [40]	50.6% ± 7.1%	–
SPBoost [39]	54.6% ± 8.2%	–
SPTree [40]	55.4% ± 8.4%	–
RW Kernel + SVM [24]	68.87% ± 8.60%	3.86 s
Path Kernel + RKLR (l1)	63.72% ± 10.26%	–
Path Kernel + RKLR (l2)	66.97% ± 9.35%	–
Path Kernel + SVM	70.17% ± 8.3%	2.68 s

As in our previous experiment, we can now use the decoding algorithm presented in Section 5 to find the most discriminate paths in our model. Table 4 shows a few examples.

TABLE 4.

Discriminant paths for a few sample concepts in the DGS dataset.

Sign	Most discriminant paths
Armchair	(right hand in region 17) during (right hand moves up) (right hand moves down) meets (right hand moves up) meets (left hand moves down)
Always	(left hand moves forward) meets (both hands moves away horizontally) before (right hand moves below left hand) (left hand moves forward) before (both hands move away from each other about z) before (right hand below left hand)
Swim	(both hands move away about x) meets (right hand moves to the center of the torso) before (right elbow moves left) (right hand moves left) meets (right hand moves to the center of the torso) before (right elbow moves left)

6.4 ASLLVD dataset

The ASL Lexicon Video Dataset [3] is an extensive database of many glosses signed by several native ASL signers. The videos are captured using four cameras providing two frontal views, one side view and a face view. This is a comprehensive database with samples belonging to many different glosses. Each gloss has at most 15 samples. We select glosses with at least 5 samples, resulting in 1, 612 samples corresponding to 231 classes. These videos include data from 7 signers with signs collected over 24 different sessions. Each of these sessions was filmed on a different month and includes a single signer. No hand tracking is available in this database. To be able to use our algorithm, we manually annotate the positions of both hands in the first and last frame of each sample video and use the tracking algorithm of [9] to determine the movement of the hands in the other frames. We also use the annotated handshapes of the first and last frame which are included in the database.

This database is extremely challenging because of the large number of classes (concepts) and the small number of samples per class.

Events in ASLLVD are defined as the 2D movement of each hand, the region that each hand is located at, the joint that each hand is closest to, the 2D relative movement of the two hands and the relative location of the two hands in 2D space. We also use the handshapes in the first and last frames of each sample video. Place of articulation is defined as above, Figure 3.

We use the leave-one-sample out procedure in each class; i.e., one sample from each class is left out and used for testing. We repeat this procedure 6 times. The mean classification accuracy of the derived approach using SVM is 81.31% with standard deviation 1.53%. The average time for classifying a testing sample is 0.96 seconds.

As with the other sign language datasets, we can now use the derived decoding algorithm to identify the most discriminant paths in our model. A few example results are shown in Table 6. These results are highly interpretable. For instance, “afraid” is signed with handshape 5 (i.e., spread out fingers as if indicating the number 5) with hands in regains 10 (right hand) and 11 (left hand) and a shaking movement. As seen in the table, the discriminant paths define these actions quite accurately.

TABLE 6.

Discriminant paths in the ASSLVD dataset. Shape 5 means all fingers spread out if indicating the number 5. Shape 10 is hand as in a fist. Shape B-L is hand open [3].

Sign	Most discriminant paths
Afraid	(right hand with shape 5) meets (left hand with shape 5) (right hand right of left hand) during (right hand in region 10) meets (right hand moves down) (both hands move away from each in y) starts (right hand right of left hand) starts (both hands in similar y position)
A lot	(both hands move in sync about x) starts (right hand shape 10) (both hands keep distance about x) starts (left hand shape 10) before (left hand shape B-L)

6.5 UCF Kinect dataset

Next, we provide comparative results with a database of generic human actions. This experiment is to demonstrate the versatility and generalization of the derived approach. We used the UCF Kinect database of [15].

This database includes 16 distinct actions as performed by 16 subjects. Each subject performs each action 5 times, resulting in 1, 280 samples. The dataset is collected using a Microsoft Kinect^™ camera to capture 3D videos and the OpenNI platform to estimate skeleton joints. Subjects are defined by the 3D position of 15 joints in each frame. A 45-channel time series represents how the 3D coordinates change with time.

The events in the UCF dataset are also defined as curve trends in each channel. We use a 4-fold cross-validation test to determine the effectiveness of the proposed algorithm. We repeat the experiment 10 times. Average classification accuracies for the derived approach as well as other state-of-the-art algorithms are given in Table 7. When using Support Vector Machine classifier our method achieves 98.70% ± 0.16% accuracy with a mean time of 1.76 seconds. A t-test yields a p-value < 10⁻¹⁰.

TABLE 7.

Results on the UCF human action database. Comparative results with state-of-the-art methods are obtained using a subset of 10 joints, which can be computed extremely fast. The derived approach outperforms state-of-the-art algorithms when using the full set 15 joints. CRF: Conditional Random Fields. TS: Temporal Segment. JAS: Joint Angle Similarity. RW: Random Walk.

Method	Accuracy	Time/Sample
CRF [15]	94.29%	–
BoW [15]	94.06%	–
TS [15]	95.94%	–
JAS [38]	97.37%	–
RW + SVM [24]	97.16% ± 0.26%	2.18 s
Path Kernel + RKLR (l1)	97.99% ± 0.16%	–
Path Kernel + RKLR (l2)	97.78% ± 0.22%	–
Path Kernel + SVM	98.70% ± 0.16%	1.76 s

One may wonder how the behaviors in this database were discriminated by the derived algorithm. A couple of examples are provided in Table 8.

TABLE 8.

Most discriminant paths for a couple of the actions in the UCF dataset.

Actions	Most discriminant paths
Duck	(right shoulder moves down) equals (left shoulder moves down) (left butt moves down) meets (left shoulder moves back) (right hand moves down) equals (left shoulder moves down)
Step front	(right foot moves up) meets (right foot does not move in y) (left foot moves up) meets (left foot does not move in y)

6.6 Multimodal Motion Gesture Dataset

The 6D Motion Gesture dataset (6DMG) [8] contains motion data, including the position, orientation, acceleration, and angular speed information of a set of common motion gestures performed by different users. It combines optical sensing and inertial sensing. The former measures the 3D position of the optical tracker, and the latter estimates the orientation of the tracking device in yaw, pitch and roll. WorldViz PPT-X4 is used as the optical tracking system and MEMS accelerometers and gyroscope embedded in Wii Remote Plus (Wiimote) are used as the inertial sensors. The dataset includes people handwriting by moving their hands in space. Twenty-five (25) people handwrote the uppercase letters, A to Z.

We first do experiments on the position and orientation modality separately. Then, we conduct a third experiment to combine the two modalities. For the position modality we only use the X and Y coordinates, because the Z dimension provides no discriminative information. We detect curve trends in the X and Y coordinates, the relative location of the optical tracker as compared to the initial frame (below or above for X coordinate, left or right for Y coordinate), the optical tracker is close to the top, close to the bottom, between the top and the bottom, the optical tracker is close to the leftmost or rightmost point or between the two. In the orientation modality, we detect curve trends in the orientation of the tracking device in yaw, pitch and roll. Similar to the position modality, events are defined as the orientation of the tracking device relative to its position in the first frame (angle increase/decrease).

We use leave-one-subject-out cross-validation for testing. The average classification accuracy and standard deviation is 99.08% and 0.90% for the position modality, 95.32% and 3.85% for the orientation modality, and 99.22% and 0.82% when using both modalities. This suggests that combing information from different modalities can lead to better classification accuracies. Comparative classification results are in Table 9. Note that [8] uses leave-one-sample-out cross-validation for testing, which is a much easier experiment than the one used herein. The p-values of the corresponding t-tests are 0.014, 10⁻¹⁰ and 0.005, respectively.

TABLE 9.

Classification accuracies for the 6DMG dataset. P: modality to detect position. O: modality to estimate orientation. P+O are the results of modeling the two modalities together using the proposed approach. Comparative results are not available for both modalities in the literature. KSS is the kernel structured sparse algorithm of [26]. RW: Random Walk. Computational time is given in seconds.

Method	P	O	P+O	Time/Sample (P+O)
HMM [8]	96.28	96.19	–	–
SVM [26]	96.32	92.18	–	–
KSS [26]	96.57	86.85	–	–
RW Kernel + SVM	98.74 ± 1.17	93.49 ± 4.90	99.00 ± 0.88	4.33 s
Path Kernel + RKLR (l1)	97.97% ± 1.80%	92.88% ± 4.74%	98.34% ± 1.49%	–
Path Kernel + RKLR (l2)	97.98% ± 1.90%	91.99% ± 5.68%	98.08% ± 1.58%	–
Path Kernel + SVM	99.08 ± 0.90	95.32 ± 3.85	99.22 ± 0.82	2.93 s

6.7 Noisy features

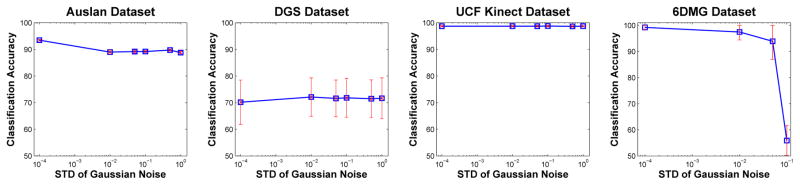
To demonstrate the robustness of our algorithm with respect to noise, we test the derived algorithm with additive zero-mean Gaussian noise and standard deviation σ (with σ = 10⁻⁴, …, 1). We test our algorithms on the Auslan, DGS, UCF Kinect and 6DMG dataset described above. Figure 4 shows the classification accuracy of our algorithm on these four datasets under additive Gaussian noise. As can be seen in the figure, realistic levels of data noise typically found in real-world applications do not deteriorate the performance of the proposed algorithm.

Fig. 4.

The classification accuracies shown above are obtained using the same classification algorithm used in previous sections, but the data (features) now include additive Gaussian noise. The x-axis specifies the variance of the Gaussian used in the noise model. The y-axis shows the classification accuracy. We see that realistic levels of noise do not have much of an effect on the derived algorithm. Note that in the 6DMG dataset the noise is added to both modalities and, hence, this corresponds to twice the amount of noise tested in other datasets.

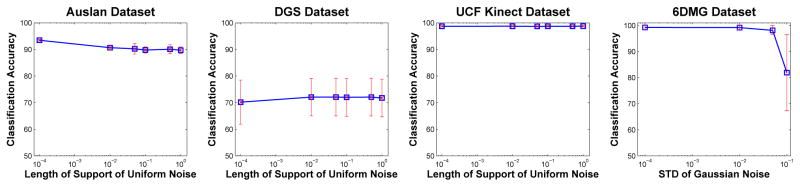
We also test Uniform noise to simulate the complete failure of a detector. To do this, for each sample we randomly select 10% of the fiducial points and add zero-mean Uniform noise U (a, b) (with b − a = 10⁻⁴, …, 1). The results are in Figure 5. As above, we see that realistic levels of data noise (typically found in real-world applications) do not deteriorate the performance of the proposed algorithm.

Fig. 5.

The classification accuracies shown above are obtained using the same classification algorithm used in previous sections, but the data (features) now include additive Uniform noise. The x-axis specifies the length of support of the Uniform Distribution used in the noise model. The y-axis shows the classification accuracy. We see that realistic levels of noise do not have much of an effect on the derived algorithm. Note that in the 6DMG dataset the noise is added to both modalities and, hence, this corresponds to twice the amount of noise tested in other datasets.

7 Conclusions

Automatically classifying and decoding behavior is a challenging problem. Major difficulties include being able to represent the spatio-temporal structure of the data using a model that leads to efficient classification and decoding algorithms, allowing for multiple descriptions of each behavior category, and working with multimodal data.

The present paper derived an algorithm to resolve these problems. This was done by describing behavior categories using a labeled graph. Each graph can represent the multiple ways each category is performed by multiple subjects. Classification is then as simple as graph matching. Unfortunately, graph matching generally comes with a very high computational cost. To resolve this issue, we derived a graph kernel algorithm to only implicitly compute graph similarity. A dynamic programing implementation of this approach is shown to have a low, polynomial-time complexity. This kernel can then be readily plugged into any kernel-based classifier. We have applied it to SVM and RKLR and shown that the results are superior to those reported in the literature regardless of our choice of classifier. Furthermore, the resulting model and classifier are readily interpretable, yielding an efficient decoding algorithm. Experimental results on several databases demonstrated the uses and superior classification abilities of the derived algorithm. Experimental results have also illustrated how the proposed approach can be naturally used to model and classify multimodal data.

TABLE 5.

Classification accuracies on the ASLLVD dataset for the proposed approach as well as the Random Walk Kernel. RW: Random Walk. Computational time needed to classify a sample using our algorithm is given in seconds. The results of the RW kernel and the path kernel are statistically identical.

Method	Accuracy	Time/Sample
RW Kernel + SVM [24]	83.55% ± 2.03%	1.44
Path Kernel + RKLR (l1)	73.09% ± 2.23%	–
Path Kernel + RKLR (l2)	76.19% ± 2.21%	–
Path Kernel + SVM	81.31%± 1.53%	.96