Effects of Anatomical Differences on Electromagnetic Fields, SAR, and Temperature Change

Abstract

Electromagnetic field simulations are increasingly used to assure RF safety of patients during MRI exams. In practice, however, tissue property distribution of the patient being imaged is not known, but may be represented with a pre-existing model. Repeatedly, agreement in transmit magnetic (B₁⁺) field distributions between two geometries has been used to suggest agreement in heating distributions. Here we examine relative effects of anatomical differences on B₁⁺ distribution, Specific Absorption Rate (SAR) and temperature change (ΔT). Numerical simulations were performed for a single surface coil positioned adjacent a homogeneous phantom and bovine phantom, each with slight geometric variations, and adjacent two different human body models. Experimental demonstration was performed on a bovine phantom using MR thermometry and B₁⁺ mapping. Simulations and experiments demonstrate that B₁⁺ distributions in different samples can be well correlated, while notable difference in maximum SAR and ΔT occur. This work illustrates challenges associated with utilizing simulations or experiments for RF safety assurance purposes. Reliance on B₁⁺ distributions alone for validation of simulations and/or experiments with a sample or subject for assurance of safety in another should be performed with caution.

INTRODUCTION

In magnetic resonance imaging (MRI), a radio frequency (RF) magnetic field is used to excite nuclei inside the body while the concomitant electric (E) field deposits RF energy into the body (1), causing Joule heating of tissues. RF safety guidelines, defined by the International Electrotechnical Commission (IEC), recommend limiting localized heating to < 39 °C for “normal” operating mode and 40 °C for “first level controlled” operating mode, while maintaining body core temperature change less than 0.5 °C for normal mode and 1 °C for first level controlled mode (2). Currently, experimental mapping of absolute temperature in vivo using MR-based temperature mapping methods faces challenges due to motion, tissue-dependent variation of the proton resonance frequency shift coefficient, limited sensitivity, $T_2^{\ast }$, T₁ and other factors, limiting its routine use for monitoring patient safety (3). Historically, estimation of temperature change by experiment has mostly been accomplished in phantom studies (4,5), or in human studies where the temperature change was greater than 2 °C (6). Because 2 °C of tissue heating is undesirable in routine clinical use and in vivo temperature mapping remains challenging, these techniques have not been used in common practice (4,6), and patient safety is mostly controlled by limiting the Specific Absorption Rate (SAR) – a measure of the rate at which RF energy is absorbed in tissue (2).

In order to ensure patient safety, both local and whole body SAR need to be controlled. While whole body SAR is routinely monitored in practice with measures of the power delivered to the transmit coil (and estimates of the power delivered to the subject), local SAR is more challenging to monitor (4). In the past, local SAR was mapped accurately in phantom experiments, where the dielectric properties and structure of the phantoms being scanned were well known (4,6). However, in the clinical setting the dielectric distribution of each subject is generally not known and subject-specific computation of local SAR is currently not feasible. In recent years, several experimental techniques have been proposed for subject-specific local SAR estimation (7–9). These techniques utilize various body segmentation techniques that are used to create body models with dielectric property distribution resembling the patient being scanned. The subject-specific models can be used in conjunction with electromagnetic (EM) field simulation software to compute the local SAR distribution and assess patient safety. While these techniques are very promising, they are not yet ready for the clinical setting and robust estimation of tissue property distribution and SAR remains challenging (7,8).

As result, in-vivo local SAR determination currently relies heavily on EM field simulations, where MRI coils are modeled with one or more of several pre-segmented human body models, such as those of the virtual family (10). The body models used typically have a different geometry than the patient being imaged, therefore, geometrical inaccuracies associated with body models may yield inaccurate predictions of local SAR and temperature change (ΔT) distributions in the body (11). Several groups have studied variation in subject anatomy in simulation and its effect on local SAR, specifically, Liu et al. (12), Wolf et al. (13) and Neufeld et al. (14) simulated the local SAR inside a number of human body models. These studies were mostly performed at 3T or below for body coils or for the head at 7T. Similarly, Davis et al. (15) experimentally studied the effect of varying the phantom geometry on heating pattern resulting from exposure to a body coil at 1.5T, observing a three-fold increase in maximum temperature near a low-permittivity, non-conductive inclusion. Furthermore, a number of recent peer-reviewed studies have suggested that agreement between simulated B₁⁺ distributions in simulation and experiment implicitly indicate accurate SAR computation (9,16–18). Therefore, here we investigate whether agreement in B₁⁺ distributions ensures agreement in SAR distributions. Effects of different sample geometries are firstly investigated in simulation for a simple homogeneous muscle tissue geometry with different cylindrical inclusions, then simulations and experiments were conducted for a heterogeneous bovine phantom with different anatomies before simulations are finally performed on two different realistic anatomical body models. This work focuses on use of a local transmit coil positioned next to the body at ultra high field, where much of the attention to local SAR and B₁⁺ is currently devoted. We also examine the mechanism by which a low-permittivity, low-conductivity inclusion can alter heating patterns.

METHODS

Simulation of loop coil against a homogeneous block of muscle tissue with and without low-conductivity inclusions

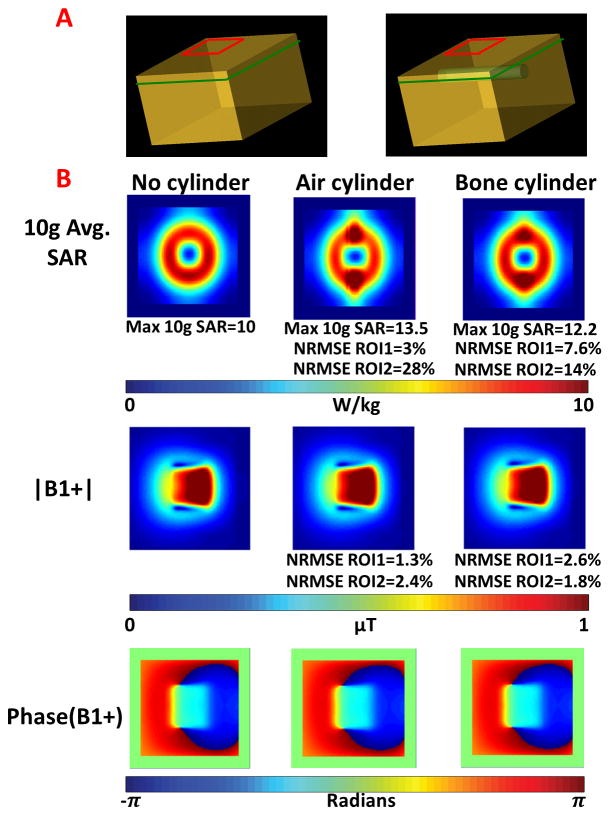
A 6.5 cm by 6.5 cm surface coil was modeled 1 cm above a block of muscle tissue with conductivity (σ) = 0.7 S/m and relative permittivity (ε_r) = 60 (19). The dimensions of the slab of meat were 17×16×10 cm³ (figure 1A). A mesh size of 212×198×148 with resolution of 1×1×1 mm³ was used. The surface coil was tuned to 297.2 MHz using 8 capacitors in series placed across gaps in the conducting path, with a voltage source also across one gap. The coil was matched to −22dB. A seven-layer perfectly matched layer (PML) absorbing boundary condition was applied at all outer boundaries, and the convergence criterion was set to −50dB. Commercial electromagnetic field simulation software (XFDTD version 7.3, Remcom, State College, PA, USA) utilizing the Finite Difference Time Domain (FDTD) was used for the EM field simulations. Upon completion of the simulation, the EM fields and SAR distribution were exported to Matlab (version 8.4, MathWorks, Inc., Natick, MA, USA). This entire process was repeated for two variations on the sample geometry containing a cylinder of low-conductivity tissue. The cylinder diameter was 1.5 cm and it was positioned 1.5 cm beneath the surface of the muscle phantom as shown in figure 1A. In the first variation the cylinder was assigned properties of air (as for a simple representation of a trachea or bowel gas), and in the second the cylinder was assigned properties of bone tissue (as for a simple representation of a rib). The dielectric properties of air and bone at 297MHz are σ = 0 S/m and ε_r = 1 for air, and σ= 0.04 S/m and ε_r = 5.6 for bone tissue. For the three simulations (no cylinder, air cylinder, and bone cylinder) the 10g average SAR was then computed. Then, a scaling factor was determined such that the 10g average SAR of the no-cylinder simulation was 10 W/kg as prescribed by the IEC ‘normal mode’ operation limit (2). The SAR distributions of the three simulations were then scaled using the same scaling factor and the distributions of the scaled 10g average SAR and B₁⁺ were calculated. The maximum 10g average SAR of each of the three simulations was recorded, and the normalized root mean square error (NRMSE) of B₁⁺ and 10g average SAR were calculated as follows (20): $100\ast \frac{\sqrt{\frac{{\mathrm{\sum }}_{\mathrm{n}}{\mid Q_{nc}-Q_C\mid }^2}{\mathrm{n}}}}{max(\mid Q_{nc}\mid )-min(\mid Q_{nc}\mid )}$, where Q_c and Q_nc are the quantity of interest (B₁⁺, SAR, or ΔT) with a cylinder and with no cylinder, respectively, and n is the number of voxels. The NRMSE was computed over two regions of interest (ROI) of 10×10×5 cm³ adjacent the coil (ROI1) and a volume 10cm³ centered at the peak maximum SAR location (ROI2). In the ROIs only voxels where tissue is present in both cases were compared. The average |B₁⁺| inside the ROI was also computed. The scaling of the SAR distribution was used to put the “reference” no-cylinder simulations at the limit of local SAR exposure, then evaluate the effect of minor differences in geometry (addition of cylinders) on B₁⁺ and SAR distributions.

Figure 1.

A. Muscle phantom without (left) and with (right) a cylinder with dielectric properties of air or bone. B. 10g average SAR, |B₁⁺| and phase of B₁⁺ distribution maps for a coronal slice of interest 0.5 cm above the location of the cylinder having different dielectric properties.

Changes in conductivity vs. changes in relative permittivity

In the radiofrequency regime, electrical conductivity and electrical permittivity of human tissues tend to be somewhat correlated, such that in the above simulations the low-conductivity inclusion necessarily also has a low permittivity. To better examine the mechanism whereby the field and SAR distributions were affected by the inclusions, we performed additional simulations where permittivity and conductivity of the cylinder were changed independently. A surface coil was placed next to a homogenous block of muscle tissue. Following the procedures described above, two additional simulations were performed with the following dielectric properties for the cylinder: conductivity of air (σ = 0 S/m) with relative permittivity of muscle (ε_r = 60), and permittivity of air (ε_r = 1) with conductivity of muscle (σ = 0.7 S/m). Upon convergence, the EM fields were extracted and the magnitude of the current density (J) was plotted for these two new simulations for comparison with the cases with no cylinder and a cylinder of air, as simulated previously. A 0.5 × 0.5 cm² region of interest above the position of the cylinder was then selected and the average current density was reported in that region.

Experiments and simulations of a loop coil next to a heterogeneous bovine phantom

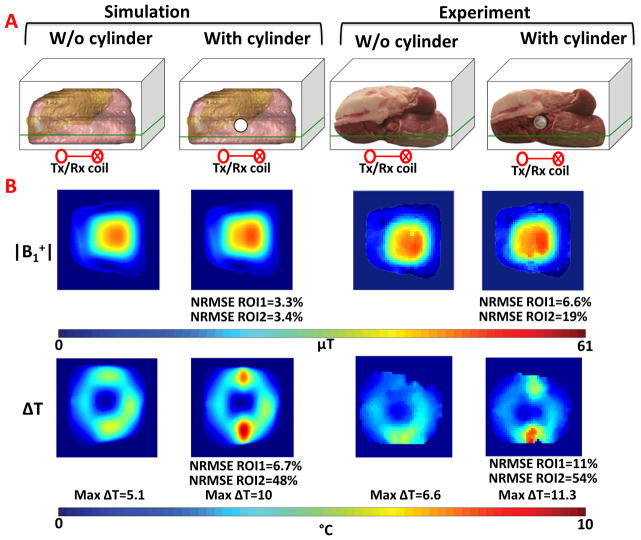
A 16×17×10 cm³ block of top-round beef weighing 2.79 kg was placed inside a rigid plastic container such that the surface of the meat was a fixed 1.5 cm from a transmit/receive surface coil with dimensions of 6.5 cm by 6.5 cm placed at the bottom of the plastic container (Figure 3A) and tuned to 297 MHz with a match of −15dB. The coil was connected to a transmit-receive switch that was controlled by a 7T single channel MR scanner (Siemens Medical Solutions, Erlangen, Germany). Flip angle mapping was conducted using the 3D modified actual flip-angle imaging (MAFI) method (21), with resolution=3×3×4 mm³, TE₁=TE₂=2.5ms, TR₁=40ms, TR₂=200ms, matrix size=64×48×26, flip angle=90° and total acquisition time of 5 minutes. Next, a 3D spoiled gradient-echo (GRE) measurement was acquired with resolution=3×3×4 mm³, TE=15ms, TR=18ms, matrix size=64×48×26, and flip angle=30° using a non-selective pulse and total acquisition time of 22.5 seconds. A high-SAR heating sequence was then run for 2.5 minutes delivering 29.9 Watts of continuous power. The power was measured using a directional coupler positioned at the output of the RF amplifier. Immediately after the heating sequence concluded, a second 3D spoiled gradient echo sequence with the same parameters specified above was acquired. The phase map of the GRE sequence before heating was then subtracted from the phase map of the post-heating GRE sequence and the proton resonance frequency shift method was used to convert heating-related phase change to ΔT (3). The non-thermal phase correction was monitored using the phase in fat within the phantom as a reference. After the ΔT and flip angle distributions were mapped, the phantom was set to cool for 1.5 hours ensuring that the phantom returned to equilibrium with the temperature of the room. Then, a hollow plastic cylinder with diameter of 1.5 cm and length of 15 cm was inserted into the phantom approximately 1.5 cm from the surface of the phantom adjacent the coil. Flip angle and ΔT mapping were conducted as in the first experiment. The NRMSE between the B₁⁺ and ΔT maps of the two experiments was calculated over a large ROI of 10×10×5 cm³ (ROI1) and a localized ROI of 10 cm³ at the location of maximum SAR for the experiment without the cylinder (ROI2). The NRMSE was computed only over voxels containing tissue material in both experiments. The maximum temperature change and |B₁⁺| distribution for each experimental condition were also computed.

Figure 3.

A. Illustration of the simulation and experimental setup for beef phantom with and without a hollow plastic cylinder. Imaging slice (passing through regions of high SAR) is shown in green. B. Normalized B₁⁺ and ΔT maps acquired in the simulation and experiment.

In order to further validate our experimental results, the experimental setup was replicated in a simulation environment. Images of the bovine phantom without the air cylinder were acquired using a resolution of 1×1×1 mm³ with and without a fat saturation pulse. The images were then manually segmented into muscle, fat and air using the MRIcron software package (22) and Matlab. The segmented models were then imported into Commercial electromagnetic field simulation software (XFDTD version 7.3, Remcom, State College, PA, USA). A 6.5 cm by 6.5 cm surface coil was modeled 1.5 cm below the numerical phantom. In simulation, the coil was tuned to the frequency of our 7T system and a match of −17.2dB was achieved. After matching and tuning, a 1V sinusoidal excitation at 297.2 MHz was defined and the steady state fields were computed. The convergence criterion was set to −50dB and the mesh resolution was 1×1×1 mm³. The resulting SAR and B₁⁺ distributions were imported into Matlab. The segmentation and simulation was then performed for the meat phantom with the air cylinder. Matching changed from −17.2dB in the no-cylinder simulation to −14.3dB in the simulation with the air cylinder, indicating minimal effect on the power deposition. The simulated B₁⁺ maps, were scaled such that the simulated |B₁⁺| at the center of the phantom with no cylindrical inclusion matched the experimental |B₁⁺| at the same location. This scaling factor was equally applied to the simulated B₁⁺ maps with and without cylindrical inclusions. In order to scale the temperature simulations, the field distributions (B and E) in simulation were scaled by the same scaling factor as for the |B₁⁺| maps computed in the previous step. An additional factor equal the ratio of the pulse voltage in the heating experiment (125 V) to the pulse voltage in the B₁⁺ mapping experiment (46.9 V), as reported at the console, was applied. In order to compute SAR in simulation accurately, the scaling factor computed in the previous steps was squared and multiplied by the duty cycle (10%) used in the heating sequence. The properly scaled SAR map was then fed into a temperature simulated and the simulated temperature difference maps were computed and plotted.

Simulations with human body models

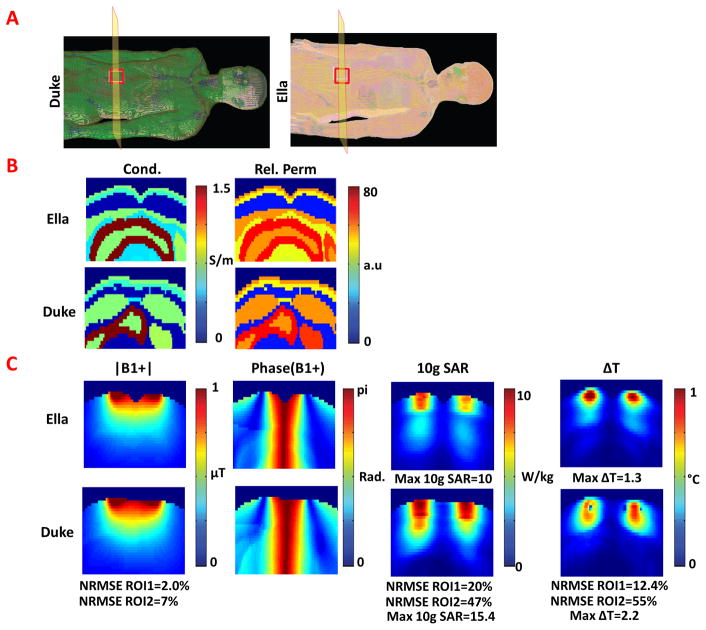
After conducting experiments and simulations on a heterogeneous bovine phantom, we investigated the effects of anatomical variation using human body models. A single surface coil (6.5 cm × 6.5 cm) was modeled 1 cm above the abdomen of the Duke and Ella body models (figure 4A) from the Virtual Family library (10). The mesh resolution was set to 2×2×2 mm³ and the driving frequency was set to 297 MHz. The dimensions of the coils, port settings, boundary conditions and convergence criterion were the same as the previous simulations. Upon convergence of the simulations, the net input power injected per unit drive at the port was recorded for each of the simulations. The SAR distributions from FDTD simulations were then fed into a finite difference temperature simulator (23) to quantify the RF heating effect as modeled with the bio-heat equation (24), while accounting for perfusion effects. The SAR distributions used as input to the temperature simulator were scaled such that the maximum 10g average SAR for the Ella simulation was 10 W/kg for the torso region, equal to the normal operating mode limit specified by the IEC (2). The same scaling factor computed for Ella was used for scaling the SAR in the Duke simulation. The temperature simulations were initialized by allowing the temperature of the body model to reach an equilibrium distribution in an environmental temperature of 23 °C with no RF energy applied. Then the temperature resulting from the scaled SAR distribution applied for 6 minutes was calculated. For an axial slice of interest, the resulting ΔT, |B₁⁺|, and 10g average SAR maps were plotted. The NRMSE of the B₁⁺, 10g average SAR and ΔT maps between the Ella and Duke simulations were computed over an ROI of 10×10×5 cm³ (ROI1) positioned next to the coil and a localized ROI of 10 cm³ at the location of maximum SAR for the Ella simulation (ROI2). The NRMSE was computed only over voxels that contained tissue in both models. The maximum 10g average SAR and ΔT, as well as average |B₁⁺| distribution for each simulation was also recorded.

Figure 4.

A. Duke (left) and Ella (right) human body models used in the EM field simulations. B. Relative permittivity and conductivity maps of the Ella and Duke body models shown for an axial slice of interest passing through the center of the surface coil. C. |B₁⁺|, phase of B₁⁺,10g average SAR, and ΔT distributions shown for same axial slice of interest.

RESULTS

Results comparing simulated fields for a homogeneous block of muscle and a block of muscle with air and bone equivalent cylinders are shown in Figure 1. For each of the three cases (no cylinder, air cylinder, and bone cylinder) the 10g average SAR and |B₁⁺| are plotted in Figure 1B. Results demonstrate that with introduction of the air cylinder, the B₁⁺ distribution remained similar, as the NRMSE between the no cylinder and air cylinder cases was 1.3% for ROI1 and 2.4% for ROI2. The average |B₁⁺| was 0.62μT and 0.64μT for ROI1 and 1.76μT and 1.81μT for ROI2 in the simulations without and with the air cylinder, respectively. The NRMSE in 10g average SAR was 3% for ROI1 and 28% for ROI2, and the maximum 10g average SAR increased by 35% from 10 W/kg to 13.5 W/kg. A comparison between the simulations with no cylinder and with bone cylinder yielded analogous results, as the NRMSE between complex B₁⁺ maps was 2.6% for ROI1 and 1.8% for ROI2 with an average |B₁⁺| of 0.64μT for the bone cylinder case for ROI1 and 1.8μT for ROI2. The NRMSE of the 10g average SAR increased to 7.6% for ROI1 and 14% for ROI2 with a 12.2% increase in maximum 10g average SAR. Regions of high SAR in both cases (air and bone cylinder) occurred at the regions where the nominal B₁+ values were relatively low (<30% of the maximum).

Figure 2 presents the modulus of the current density on an axial slice for different combinations of dielectric properties of the cylinder inserted into the muscle tissue. The axial slice of interest passed through the high-SAR region appearing below the center of figure 1B. For a homogeneous muscle block (Figure 2, upper left), a smoothly varying current density distribution with a maximum current density value of 4.95 A/m² is observed. When a cylinder with conductivity of 0 and the same permittivity as in muscle (ε_r = 60) was introduced (upper right), a similar current density distribution with a maximum current density was 4.86 A/m² results. However, when the conductivity matched that of muscle and the relative permittivity of the cylinder was changed (lower left) from 60 to 1 (that of air) a region of locally high current density appeared above the cylinder and the maximum current density increases to 5.45 A/m². When both the conductivity and permittivity of the cylinder were changed to those of air (lower right), the maximum current density increased to 6.26 A/m². From these simulations it is apparent that the change in relative permittivity makes a greater contribution to the increase in maximum local SAR than the change in electrical conductivity. Furthermore, since SAR at a single location is proportional to the square of current density, the introduction of an air cylinder also resulted in a 60% increase in maximum single-cell SAR.

Figure 2.

Distributions of current density magnitude for an axial slice located at the position where regions of high 10g average SAR occur. Current density maps are shown for a homogeneous muscle tissue (upper left), muscle tissue with a cylinder having conductivity 0 and relative permittivity of 60 (upper right), cylinder having conductivity 0.7 and relative permittivity of 1 (lower left), and cylinder composed of air having conductivity of 0 and permittivity of 1 (lower right).

Simulated and experimental results for the bovine phantoms are shown in figure 3. B₁⁺ and ΔT distributions were plotted for two conditions: the first for a slab of beef, and the second for the same sample of beef with a hollow cylinder inserted (figure 3A). Results were plotted for a coronal slice of interest 1.5 cm from the surface in figure 3B. The average normalized |B₁⁺| for the simulations without and with the cylinder were 0.38μT/V and 0.42μT/V for ROI1 and 1.78μT/V and 1.96μT/V for ROI2, respectively. The NRMSE between the B₁⁺ distributions was 3.3% for ROI1 and 0.42% for ROI2. The NRMSE of the temperature change was 6.7% for ROI1 and 48% for ROI2, respectively, with maximum temperature increase of 5.1 and 10 degrees centigrade, for the simulations without and with the cylinder, respectively. For the experimental setup, the average |B₁⁺| values for the experiments without and with the cylinder were 0.42μT/V and 0.43μT/V for ROI1 and 2.09μT/V and 2.11μT/V for ROI2, respectively, while the NRMSE between the B₁⁺ distributions was 6.6% for ROI and 19% for ROI2. The NRMSE of the temperature change was 11% for ROI1 and 54% for ROI2 with a maximum temperature increase of 6.6 and 11.3 °C for the simulations without and with the cylinder, respectively.

Comparison of simulated fields in the Ella and Duke body models is shown in figure 4. Figure 4A illustrates the geometry of the simulation and the position of the single loop coil next to the Ella and Duke body models. Figure 4B illustrates the conductivity and permittivity maps for the Ella and Duke human body models. Figure 4C shows the |B₁⁺|, 10g average SAR and ΔT distributions for the two body model simulations. The net input power for Ella was 0.38 W and Duke was 0.37 W per unit drive at the port. The average |B₁⁺| in the Ella and Duke body models was 0.55μT and 0.52μT for ROI1 and 1.62μT and 1.62μT for ROI2, respectively. The NRMSE of the B₁⁺ distribution between the two body models was 2.0% for ROI1 and 6.95% for ROI2, while the NRMSE of the 10g average SAR and temperature change were 20% and 12.4% for ROI1 and 47% and 55% for ROI2, respectively. After scaling the Duke and Ella simulations identically such that the maximum 10g average SAR of the Ella simulation was 10 W/kg, results demonstrate a maximum 10g SAR in the Duke simulation that is 54% higher than that of Ella. A similar increase is observed in the ΔT distributions where the maximum temperature change for the Ella and Duke simulations are 1.32 °C and 2.15 °C, respectively. Note that the maximum temperature change occurs outside the slice presented in figure 3C. Differences in the anatomy of the body models introduced maximum 10g average SAR that exceeded the IEC limits for normal operating mode in Duke, yet absolute temperature remained below 39 °C at all locations in both models. In both cases, the whole-body SAR was well below the 2 W/kg normal mode SAR limit (2). Results from the simulations and experiments listed above were summarized in table 1.

Table 1.

Summary of simulated and experimental results.

Quantity	Average |B1+| (μT/V)		NRMSE B1+ (%)		NRMSE SAR/ΔT (%)		Maximum 10g Avg. SAR (W/kg)/ΔT (°C)
Volume	ROI 1	ROI 2	ROI 1	ROI 2	ROI 1	ROI 2	Peak location
Simulation
Homogeneous Phantom
No cylinder	0.62	1.76	-	-	-	-	10
Air cylinder	0.64	1.81	1.3	2.4	3	28	13.5
Bone cylinder	0.64	1.80	2.6	1.8	7.6	14	12.2
Bovine Phantom
Simulated w/o cylinder	0.38*	1.78*	-	-	-	-	5.1
Simulated with cylinder	0.42*	1.96*	3.3	3.42	6.7	48	10
Experiment w/o cylinder	0.42*	2.09*	-	-	-	-	6.6
Experiment with cylinder	0.43*	2.11*	6.6	19	11	54	11.3
Human Body Models
Ella	0.55	1.62	-	-	-	-	10/1.32
Duke	0.52	1.62	2.0	6.95	20/12.4	47/55	15.4/2.15

^*Reference voltage used was 46.9V.

DISCUSSION

In this work, simulations and experiments were used to evaluate the effects of differences in tissue property distribution on B₁⁺, 10g average SAR, and ΔT distributions. A major impetus for this study was the recurring usage of B₁⁺ field distributions as a method for validating experiments and simulations for safety assurance (9,16). Simulations were conducted on simple muscle phantoms to gain a better understanding with regard to the extent in which small differences in the anatomy of a phantom can affect both B₁⁺ and local SAR. Simulations on complex body models from the virtual family were included to further validate our understanding with regard to how changes in the dielectric structure of a multi-tissue object can affect maximum SAR and B₁⁺ distribution. By design, differences between models were similar to or less than what might be expected between a simulation model and an actual subject in a clinical setting. Misrepresentation of subject anatomy can occur due to movement (including respiration, heartbeat, and peristalsis), misalignment of the simulated body model relative to the position of the subject in the magnet, and utilization of a body model that does not precisely represent the subject. The dimensions of the coil were small relative to the dimensions of the sample or subject so that the overall dimensions of the subject had little effect on the power requirements. Notable differences in maximal SAR and ΔT accompanied relatively minor changes in B₁⁺ both for objects with similar overall dimensions (such as in the phantom simulations and experiments with and without the tube) and objects that had slightly different dimensions (such as between the Duke and Ella body models). In the bovine phantom simulations, inserting the cylinder had no effect on coil tuning while matching changed from −17.2dB to −14.3dB. This change corresponds to an increase in reflected power from 2% to 3.7%. This has a minor effect on the net power delivered to the phantom/subject, as is consistent with the minimal change in average B₁⁺ field strength. Change in matching is frequently observed in conventional clinical setting, where coils often cannot be tuned or matched for each subject.

It was demonstrated that relatively small differences in sample geometry resulted in relatively minor differences in the distribution of B₁⁺, but in greater differences in SAR and ΔT, as shown in the NRMSE calculations from simulation and experiment. This was confirmed by using ROI1 and ROI2 for our analysis. The choice of a region of interest that is large (ROI1) was chosen since it allowed us to capture a large section of the phantom volume in our analysis. Similarly, our conclusion that changes in B₁⁺ distribution underestimate changes in local SAR or temperature change was also confirmed for ROI2 where the region of interest was localized to 10 cm³ at the location of maximum SAR in the simulations/experiments without the cylinder. This phenomenon can be attributed to the fact that B₁⁺ fields are primarily produced by currents in the copper coil, while SAR in the sample is very dependent on the distributions of conductivity and permittivity throughout the sample. Changes in conductivity of the tissue properties of the phantom can create new regions of high SAR with relatively little effect on the B₁⁺ field distribution. In principle, characterizing SAR distributions from B₁ would be possible if full knowledge of the RF magnetic field components and tissue properties were measurable (7,8). Further development of methods is ongoing, but while in conventional MR experiments the magnitude of the B₁⁺ is measureable using flip angle mapping techniques, the absolute phase of B₁⁺, magnitude and phase of B₁⁻, and magnitude and phase of B_z are difficult or impossible to determine. Furthermore, since SAR is related to the square of the E field, differences in E are accentuated in SAR.

When comparing the relative effects of permittivity and conductivity, we observe that changes in permittivity alone for a surface coil at this frequency had greater effects on the SAR distribution than did changes in tissue conductivity alone. Clearly, an air inclusion (low permittivity and low conductivity) results in an increase in current density between the inclusion and the surface of the phantom when compared to a homogeneous phantom. This is in agreement with a prior study by Davis et al. in a large volume coil at 64MHz. In this study and in contrast to Davis’, a surface coil was used and the skin effect was much shallower, shielding from non-conductive geometric irregularities. We have focused on ultra high field effects due to surface coils and conclusions regarding arrays and/or volume coils that may heat tissues deep inside the body cannot be straightforwardly made. In our simulations, a slightly higher maximum current density was present at the surface of a phantom containing a cylinder with conductivity of 0 and relative permittivity of 60 than in a homogeneous phantom. This is somewhat non-intuitive, but this slight difference can also occur due to something as minor as small effects of the change in the phantom on coil matching (as reported previously in the discussion section). Importantly, immediately adjacent the low-conductivity, high-permittivity inclusion, current density is higher than in the homogeneous phantom. Interestingly, the effect of setting only the permittivity of the inclusion to that of air has a greater effect than setting only its conductivity to that of air. Based on explanations for the prior experiment, which rely on the idea of conduction currents being forced to flow around a region of low electrical conductivity (15), this might be surprising. Our best current explanation of this comes by considering Gauss’ Law for electric fields in comparison to Gauss’ Law for magnetism. In MRI it is well understood from Gauss’ Law for Magnetism that a low-susceptibility inclusion will result in the lines of magnetic flux flowing around the inclusion, resulting in lower magnetic field strength at the where the lines of flux would have otherwise been perpendicular to the surface of the inclusion, and greater magnetic field strength at the sides where the lines of flux are parallel to the surface of the inclusion. Analogously, Gauss’ Law for electric fields should result in similar effects on current density in bulk tissue, where density of free charges is close to zero. The extent to which permittivity and conductivity make relative contributions to an increase in current density and may depend on the coil and sample geometries and their arrangement relative to each other as well as the frequency of operation, but in this case it appears that the effect of permittivity is much more pronounced than that of conductivity. Several studies in the past have demonstrated that use of high permittivity materials (HPM) outside the subject can reduce the power deposition in a subject to achieve the same B₁⁺ in a region of interest (25,26). In this study, a complimentary effect was shown, where the presence of a lower permittivity material resulted in an increase in maximum local SAR with little effect on B₁⁺ (Figure 1). In the case where a cylinder of air was inserted in the muscle phantom, maximum 10g SAR increased by 35%.

In figure 3A, the segmented phantom appears to have slight geometric differences relative to the experimental illustration of the meat phantom. This can be attributed mainly to the fact that segmentation of the phantom was performed inside the scanner where the meat phantom was placed inside a rigid plastic container to prevent it from moving and ensure consistent phantom placement in experiments with and without the cylinder, while the photographs of the experimental meat phantom with and without the cylinder were taken outside the bore of the scanner (for better visualization) and outside the container. Furthermore, differences between the simulated and experimental B₁⁺ are apparent. This can be attributed to limitations in the accuracy of the manual image segmentation, matching and tuning, representation of driving sources, exact orientation of the meat in the scanner relative to that of the simulation, boundary condition affects, tissue properties, and more. Nonetheless, both in simulation and experiment it is clear that B₁⁺ maps can remain relatively unperturbed by variations in sample geometry that significantly affect the heating pattern. In the experimental demonstration (figure 3), the PRF method was used to reconstruct the temperature change. Studies have shown excellent agreement between temperature change measured using the PRF method and fluoroptic thermal probe measurements (27), but minimum requirements are needed with respect to the signal to noise ratio (SNR) of the thermometry sequence since the accuracy of the phase measurement is proportional to the absolute SNR of the image (3). In order to improve the SNR of the thermometry sequence, the hollow cylinder was placed with its axis parallel to the B₀ field, in order to reduce susceptibility artifacts. This resulted in minimal susceptibility-related artifacts 0.5 cm above the cylinder (imaging slice), and due to the close proximity to the surface coil the SNR at the high-SAR region was >29, which is sufficient for accurate thermometry measurements. In the experimental results, introduction of the cylinder into the meat resulted in a 71% increase in maximum ΔT. Although the tissue property distribution of the meat was not uniform as in the simulations on a homogeneous slab of meat, the region of focal heating was formed in a location that was analogous to the location in which it occurred in simulation. The location was in a region within the muscle tissue adjacent the cylinder introducing large changes in conductivity and permittivity.

For completeness, simulation results were also shown for two different body models taken from the virtual family body model library. These models were selected since they are commonly used for determining RF safety of MRI. Results demonstrate that when an RF coil is positioned at similar locations relative to the abdomen of each model, significant differences in the maximum 10g average SAR (54%) and ΔT (63%) occur. These changes are accommodated by minor changes in NRMSE of the complex B₁⁺ (2% for ROI1 and 6.95% for ROI2), and much greater differences in that of the 10g average SAR (20% for ROI1 and 47% for ROI2) and ΔT (12.4% for ROI1 and 55% for ROI2) distributions, respectively, suggesting that between real-life anatomies, differences in B₁⁺ under-represent differences in the maximal local power deposition and should not be used alone for assuring simulations of one subject will ensure safety for another. Fortunately, the regions of greatest temperature increase are near the surface of the body where the initial absolute temperature was below the core body temperature due to the boundary with the air and the maximum local temperature induced was below 38.2 °C, remaining within the IEC temperature threshold limit of 39 °C (2). As EM field simulations are increasingly used to maintain safety limits for MRI coils, the common assumption that agreement between B₁⁺ field distributions indicates agreement between SAR distributions should be avoided.