Abstract
Energy expenditure (EE) estimation is an important factor in tracking personal activity and preventing chronic diseases, such as obesity and diabetes. Accurate and real-time EE estimation utilizing small wearable sensors is a difficult task, primarily because the most existing schemes work offline or use heuristics. In this paper, we focus on accurate EE estimation for tracking ambulatory activities (walking, standing, climbing upstairs, or downstairs) of a typical smartphone user. We used built-in smartphone sensors (accelerometer and barometer sensor), sampled at low frequency, to accurately estimate EE. Using a barometer sensor, in addition to an accelerometer sensor, greatly increases the accuracy of EE estimation. Using bagged regression trees, a machine learning technique, we developed a generic regression model for EE estimation that yields upto 96% correlation with actual EE. We compare our results against the state-of-the-art calorimetry equations and consumer electronics devices (Fitbit and Nike+ FuelBand). The newly developed EE estimation algorithm demonstrated superior accuracy compared with currently available methods. The results were calibrated against COSMED K4b2 calorimeter readings.
Keywords: Accelerometer, barometer, energy expenditure, machine learning
In this work, we focus on accurate EE estimation for tracking ambulatory activities (walking, standing, climbing upstairs or downstairs) of a typical smartphone user. We use built-in smartphone sensors (accelerometer and barometer sensor) and Bagged Regression Trees, a machine learning technique, to develop a generic regression model for EE estimation that yields up to 96% correlation with actual Energy Expenditure (EE).
I. Introduction
Obesity is an epidemic and a significant health threat both in the United States and all around the world. It is predicted to be the number one preventive health threat in the future [2]. Recent estimates indicate that two-thirds of U.S. adults are overweight [3]. Poor dietary habits and lack of physical activity are the two main contributors to this growing health crisis [4]. New smartphone applications and research projects aim at helping people track their daily food intake [5] and activities. A growing number of smartphone apps are available for consumer download.
Moderate and vigorous physical activity and lifestyle changes can lead to health promotion and disease prevention, while aerobic exercise alone has not shown to be effective [6]. Additionally, increased portion sizes and high caloric intake are important contributors for developing obesity. Provision of tools to accurately measure EE would allow people to actively track expenditure of calories relative to the amount of calories ingested, creating awareness of personal habits that can be modified to promote personal health. However, it is generally very difficult to know exactly how many calories people expend during daily physical activity as it depends on the age, gender, weight, height, type and intensity of activity.
Indirect calorimetry is a commonly used reference method to estimate energy expenditure. A COSMED K4b2 calorimeter uses pulmonary gas exchange to measure caloric expenditure with a very high correlation of 98.2% [7]. Such techniques are not exact and measure pulmonary gas exchange (they measure Oxygen exchange VO2, not actual energy expenditure). The factors such as ratio of macro-nutrients burnt and any lactate accumulation during more intense exercises affect EE values but are not accounted in EE estimation using pulmonary gas exchange. Accounting for this deficiency, indirect calorimetry is the closest we can get to actual EE values in an ambulatory setting. However, such a calorimeter is still impractical for use in daily life settings because of the high cost, complexity and difficulty of use [8]. Pedometers and accelerometer based approximation algorithms offer an alternative solution that is gaining popularity [9]. Many wearable devices, such as Fitbit [10], Jawbone Up [11] and Nike + Fuelband [12] provide a practical solution to monitor the dynamic energy expenditure by unobtrusively collecting data from wearable sensors to estimate EE. Additionally, individuals will need to purchase and carry these devices with them all the time to get a comprehensive assessment of energy expenditure value.
However, the main shortcoming of pedometers or any step-counting algorithms is their poor accuracy in detecting steps at slow speed and insensitivity to gait differences such as the length of the stride. This leads to unreliable estimation of energy expenditure [13]. Another approach uses the accelerometer values directly, and attempt to find an empirical relation between accelerometer data and energy expenditure data measured by a calorimeter, e.g. COSMED K4b2 [13], [14].
With smartphones becoming ubiquitous devices, they are conveniently suited personal devices to measure EE, rather than using dedicated wristbands, heart rate monitors or other tracking devices. The main issue with additional sensors are compliance and cost. Users have to remember to carry them, not lose them and they are prone to damage. Although the cost of commercially-available sensor products are coming down, many of these sensors cost $100 or more at this time and can be prohibitive for some of the population. On the other hand, people already have smartphones and the habit of carrying them along. However, further work needs to be done to improve EE accuracy using smartphone sensors.
In this study, our focus is more on ambulatory activities a person engages in during the course of an individual’s daily life such as walking, climbing upstairs or downstairs etc. Currently existing smartphone apps utilize only the accelerometer data to estimate steps and converts them into METs (Metabolic EquivalenT values) and calories estimates. However, this approach is quite inaccurate.
New smartphones such as Galaxy S3, Galaxy Nexus, iPhone 5 and later models have an integrated barometer sensor in the phone which passively measures atmospheric pressure. Slight variations in atmospheric pressures can be used by these apps/algorithms to detect the work done against gravity, hence improving the results. However, caution should be exercised to not rely on absolute barometer values since these can vary depending on environmental factors as well as differences among devices [15]. Despite these limitations, variations of sensor readings within a time period and extracted features can be useful. Barometer has been used for aiding GPS [16], the main reason behind its introduction into smartphones. Recent work [17] uses barometer as an aid in removing accelerometer drift. Due to its excellent relative accuracy, differential in barometer has been used for floor-change detection [15], [18] and activity classification [19].
Another motivation behind our work is to develop a practical framework for EE estimation. Existing accelerometry equations require heavy computations or require high sampling frequency, both of which will drain the battery of smartphones quickly.
The main contributions of this paper are as follows:
-
1)
We propose and advance the use of machine learning techniques for EE. We have developed an initial linear regression, ANN-based and bagged-regression tree based regression model to obtain a 96% correlation (
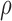 ) accuracy. We demonstrate high accuracy and low error (Root Mean Square Error, RMSE = 0.73).
) accuracy. We demonstrate high accuracy and low error (Root Mean Square Error, RMSE = 0.73). -
2)
Trials were conducted on 12 individuals and validated against reference EE data (provided by COSMED K4b2 calorimeter). We can demonstrate high correlation using basic features and low sampling frequency, which will lead to battery efficiency.
-
3)
We demonstrate the benefit of incorporating barometer smartphone sensor in addition to accelerometer to improve EE estimation accuracy. Unlike many of the currently available calorimetry equations, or usage of complex feature sets (computationally unfeasible on smartphones), our approach uses simple features extracted from barometer and accelerometer sensors, fed to machine learning algorithms to obtain high accuracy and low RMSE values. We demonstrate that using barometer sensor, in addition to accelerometer, improves correlation without computational overhead.
A preliminary version of this work has been reported in a prior conference [1]. We would also like to point out the scopes and limitations of our described model. First and foremost, our analysis have been built and analyzed on the basis of the most basic activities of otherwise normal and healthy human beings. The results can be extended to other physical activities like running, biking, etc, however, these will need further validation testing. Secondly, our proposed model requires an individual to carry a smartphone at all times. This can be problematic as a smartphone may not always be carried by individuals and the sensor location will not always be known. Recognizing the activity type with a non-fixed location of sensor on the body is complex task that will require further work.
The rest of the paper is organized as follows: Section 2 provide an overview of related works in this area. Section 3 discusses the methodology used in the design of the experiment. Section 4 gives a brief summary of the prediction models used in the paper followed by experimental results in Section 5. Section 6 provides summary of study conclusions and discusses directions for future work.
II. Related Work
A. EE Using Body Sensors
Numerous methods have been proposed to measure short- and long-term exercise energy expenditure. This includes using pedometers, heart rate monitors, and accelerometers to measure EE. Most are compared to either doubly-labeled water (DLW) or indirect calorimetry (using a device such as COSMED k4b2 calorimeter) as reference to actual EE values. Pedometer estimates of EE are weak and have a weak correlation to actual values (0.53–0.61% [20], [21]). Similarly, the activity monitor estimates of EE are also low (correlation 0.48–0.60 [20]). It is possible to improve EE accuracy using multiple body sensors (correlation of 0.9–0.95 [22]), but it becomes inconvenient to use multiple body sensors in daily living conditions. Multiple calorimetry equations from accelerometry data have been developed in research literature, but all tend to over- or under-estimate EE depending on type and intensity of the activity [23]. A group of investigators [24] evaluated machine-learning based approaches to estimate EE but considered only treadmill walking and leaves out activities of daily living. However, in prior work [25], the authors determine that height, weight and BMI (Body Mass Index, defined later) are the best indicators for personalized EE for each individuals. Thus, we have chosen those features as inputs in our approach.
Fitbit is a highly popular commercial device which uses accelerometer and altimeter sensors to capture personal activity, a significant improvement over traditional pedometers. However, some experiments have demonstrated that Fitbit is not very accurate as it lacks activity-classification algorithms [26]. Nike + Fuelband has the same limitations. Existing body-sensor based EE estimation employs a body-worn accelerometer and performs signal analysis to estimate calories expended in real-time using regression formulas. However, using a single sensor on the body is not enough to provide accurate measurement for body movement. Instead, multiple sensors are needed to improve the activity estimation performance [27].
In our study, we found many of these devices were accurate in step counts but inaccurate in EE estimation. Step-count based algorithms show high degrees of correlation with EE in scenarios such as walking, running and standing. However, active lifestyle often involves climbing up or down stairs. In these scenarios, accelerometer or pedometer based approaches tend to be inaccurate. For example - in a sample trial we asked some study subjects to climb up 4 flight of stairs and then to climb down the same number of stairs. The EE estimate obtained using commercial products such as Fitbit and Nike + Fuelband (which use pedometer based approach) are shown in Table 1. It is counter-intuitive that one will spend more calories climbing down than upwards. Existing algorithms used in these devices appear to count steps and speed of the movement and attribute higher expenditure based on these variables. Given that our volunteers moved faster when climbing down stairs versus up stairs these devices measured higher caloric expenditure for the less vigorous activity of climbing down versus up. Moreover, the two devices have huge variations in their measurements, leaving user to wonder about their accuracy.
TABLE 1. Average Measurement of EE (Cal) and Step Counts Using Commercial Devices (Nike + Fuelband and Fitbit One) Over Volunteers Performing Climbing Task. The Devices Report More Work Done in Climbing Down Than Up, and Also Have Huge Disparity in Measurements.
Activity in stairs 
|
Up | Down |
|---|---|---|
| Steps (Nike+) | 54.46 ± 22.58 | 59.83 ± 11.45 |
| EE (Nike+) | 3.32 ± 2.15 | 4.38 ± 0.67 |
| Steps (Fitbit) | 61.96 ± 20.44 | 71.38 ± 13.18 |
| EE (Fitbit) | 7.82 ± 2.85 | 9.14 ± 2.92 |
Heart rate monitors have also been used as stand-alone devices or along with accelerometer sensors to collect data and predict energy expenditure. Some devices such as Wahoo heart rate monitor, acquire heart rate data by measuring pulse rate and use a linear relation between heart rate and oxygen uptake to predict energy expenditure. However, heart rate monitors have low accuracy during sedentary behavior and require individual calibration [8], [28].
B. EE Using Smartphones
Accelerometer sensor in smartphone has been used for activity recognition in many studies [29]. CalFit is a widely used Android application that tracks time, location and physical activity patterns of users for health and wellness studies [29]. It uses smartphones GPS receiver to get the location information and the accelerometer for obtaining motion data. It uses a prior algorithm [14] to estimate energy expenditure strictly based on accelerometer data. Another previous work [30] shows how smartphones, along with GPS data, can be used to effectively estimate EE of individuals during biking.
C. Barometer Sensor and Its Application
Traditionally, the barometer sensor is used in meteorology to measure atmospheric pressure. It is also used as pressure sensor which measures relative and absolute altitude through the analysis of changing atmospheric pressure. The barometer sensor can be used for motion detection, but it is mostly used by location-based applications to evaluate elevation. Ohtaki et al. have first introduced the concept of combining barometer with accelerometer for detecting ambulatory movements [31], where authors embed a barometer sensor into a portable device to evaluate daily physical activity and classify the activity type. [32] uses barometer in addition to accelerometer, but consider only linear regression models, thus limiting its accuracy.
III. Methodology
Our primary aim was to build an application capable of accurately estimating EE without leveraging significant computational resources on the smartphones. Low computational and power requirements will make such an algorithm more usable and attractive to consumers.
There are three components of a system developed to estimte EE: (a) sampling and sensing of signal (b) feature calculation and (c) the machine learning algorithm itself. Although the machine learning algorithm is computationally expensive in training, its complexity is very low for testing and practical use. Therefore, we have focused on the other two aspects in this paper: (a) we have used a very low sampling rate of 2Hz and (b) we choose a subset of features which give high correlation to EE but have minimal computational requirements.
A. Smartphone Settings
Researchers have used a sampling frequency of 10–800 Hz [33] for activity detection. However, studies have shown that 0.1–20 Hz is appropriate for most human activities [34]. In this study, however, we restrict our measurements to the default smartphone sampling rate of 2Hz which corresponds to low battery consumption and processing overhead. Both accelerometer and barometer sensors are sampled at 2Hz (corresponding to 2 samples per second).
We use a window of time equivalent to 4 seconds (8 samples) to obtain different feature vectors required for our analysis. We divide these features into two basic categories: basic and derived. The basic features involve direct calculations of mean values from the tri-axial accelerometer and barometer sensors and these computations are simple. The derived features are obtained from basic accelerometer data and selected from existing studies in this domain [8], which we believe will improve the accuracy of our algorithm. However, they require significant computational overhead than the calculation of basic features. We also collect anthropomorphic inputs about the users and use them as feature vector in our machine learning algorithm.
B. Subjects
The study involved 12 otherwise healthy volunteer subjects each performing a specified protocol of human activities. The participants are students in computer science department and were recruited based on open announcement in research group meetings. Participants were made fully aware of the nature of the study, the purpose and any risks/concerns involved. The study protocol was approved by the University IRB. The physical characteristics of the participants is summarized in Table 2.
TABLE 2. Physical Characteristics of Subjects. Values are Means ± for 12 Subjects. The Range (Minimum and Maximum) are Mentioned in Parenthesis.
| Attribute |
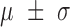 (min, max) (min, max) |
|---|---|
| Age | 25.98 ± 3.3 (22,34) |
| Height (m) | 1.7621 ± 0.06 (1.60,1.84) |
| Weight (kg) | 73.01 ± 17.58 (52,109) |
BMI (kg/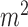
|
23.44 ± 5.32 (18.08,35.59) |
C. Experimental Design
One critical task is to measure reference EE values which are used for training and testing the machine learning algorithm. Direct calorimeter [35] requires observations in a confined metabolic chamber and is therefore impractical in our scenario. Doubly labeled water techniques are also inappropriate in our seting because they calculate EE over a long duration instead of for a single activity. To calibrate energy expenditure values over small time intervals, we used COSMED K4b2 [36] indirect calorimeter, which is portable and can be used with our setup. We used Samsung Galaxy Nexus smartphones to record observations of barometer and smartphone sensors.
During each person’s exercise protocol in the laboratory, smartphone-based tri-axial accelerometer and barometer were measured and recorded simultaneously along with the COSMED K4b2 system. Data were downloaded from the devices after the prescribed physical activity protocol and merged based on time stamps for comparison. Before each test, the oxygen and carbon dioxide analyzers and the flow turbine in the COSMED K4b2 were calibrated according to the manufacturer’s instructions.
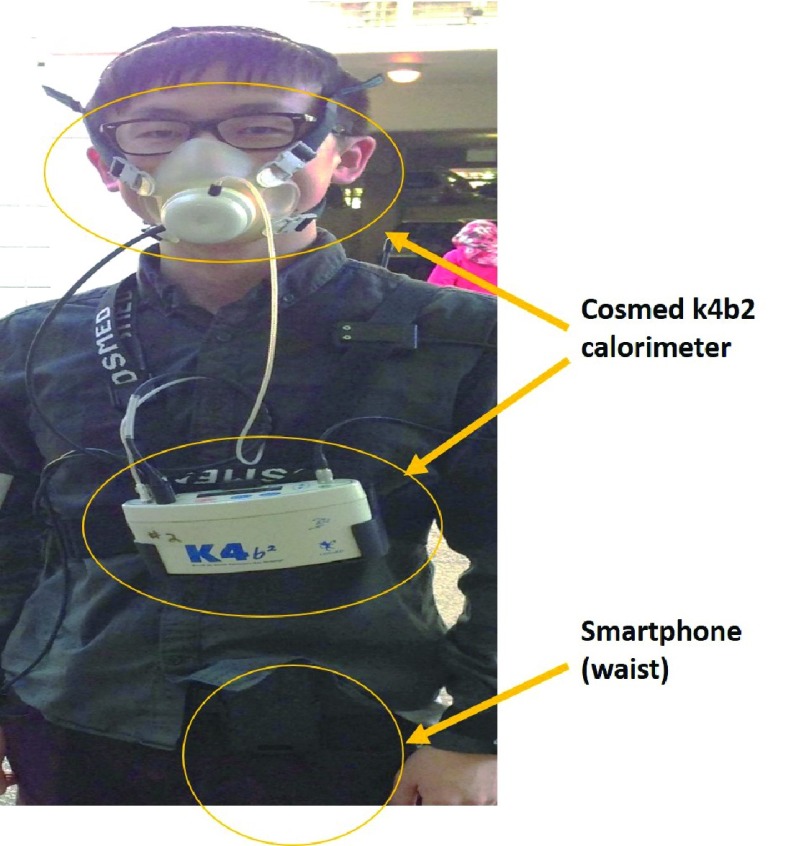
Subjects were asked to perform a series of activities in our exercise laboratory while being simultaneously monitored by the COSMED K4b2 portable metabolic system and a smartphone with built-in accelerometer and barometer sensor (a Galaxy Nexus Android-based phone running a customized software to record and extract accelerometer readings for EE estimation). The smartphone was placed in a waist pouch. Figure 1 shows a snapshot of a subject during the exercise protocol., Subjects were asked to be well hydrated and to rest or perform only light exercise the day before the test. Subjects were advised to not perform any vigorous exercise and take at a normal meal 2–3 hours prior to testing. For each subject, we recorded age, gender, body height and body mass. Body mass index (BMI) was calculated according to the formula: body mass (kg) divided by square of height (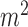 ). During each person’s exercise protocol in the laboratory, smartphone-based tri-axial accelerometry and barometer were measured and recorded simultaneously along with the COSMED K4bc2 system. All systems operated independently. Data were downloaded from the devices after the prescribed physical activity protocol and merged based on time stamps for comparison. Heart rate, oxygen consumption, carbon dioxide production, respiratory exchange ratio (RER) and ventilation rate were continuously monitored. The transitory activities were also considered in addition to steady state readings. A total of 28000 samples were obtained.
). During each person’s exercise protocol in the laboratory, smartphone-based tri-axial accelerometry and barometer were measured and recorded simultaneously along with the COSMED K4bc2 system. All systems operated independently. Data were downloaded from the devices after the prescribed physical activity protocol and merged based on time stamps for comparison. Heart rate, oxygen consumption, carbon dioxide production, respiratory exchange ratio (RER) and ventilation rate were continuously monitored. The transitory activities were also considered in addition to steady state readings. A total of 28000 samples were obtained.
FIGURE 1.
Picture of a participant wearing COSMED metabolic system and smartphone sensor.
Before each test, the oxygen and carbon dioxide analyzers and the flow turbine in the COSMED K4b2 were calibrated according to the manufacturers instructions. Energy expenditure was calculated using the following equation: COSMED K4b2 EE (kcalmin−1) = (3.815 kcalLO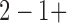 (1.232 kcalLO
(1.232 kcalLO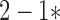 RER))
RER)) 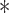 VO2 where VO2 is the oxygen consumption in L per minute, and RER is respiratory exchange ratio.
VO2 where VO2 is the oxygen consumption in L per minute, and RER is respiratory exchange ratio.
D. Subject Protocol
Subjects were asked to perform the following activities, one right after the other, in the sequential order:
-
•
3 minutes of sitting idle on a chair,
-
•
3 minutes of standing still,
-
•
Walking a 100 meter distance in hallway in regular speed
-
•
Climbing up and down three flights of stairs (4 times)
-
•
Moving up and down the elevator (2 times).
E. Basic Features
We use user’s demographic information as feature vectors (FV 1–5) in our machine learning algorithm.
-
•
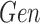 : Gender of the person (1 for male, 2 for female)
: Gender of the person (1 for male, 2 for female) -
•
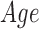 : Age of the person in
: Age of the person in 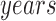
-
•
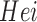 : Height of the person in
: Height of the person in 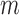
-
•
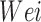 : Weight of the person in
: Weight of the person in 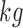
-
•
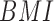 : Body to Mass Index of the person, calculated by dividing the weight with the square of height and measured in
: Body to Mass Index of the person, calculated by dividing the weight with the square of height and measured in 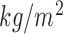 .
.
We use the following feature vectors (FV 6–9) obtained from the accelerometer sensor and barometer values over a window.
-
•
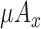 : Mean of x component of Accelerometer signal.
: Mean of x component of Accelerometer signal. -
•
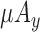 : Mean of y component of Accelerometer signal. x and y refer to horizontal components of accelerometer signal, which are fixed to the local coordinates of smartphone.
: Mean of y component of Accelerometer signal. x and y refer to horizontal components of accelerometer signal, which are fixed to the local coordinates of smartphone. -
•
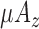 : Mean of z component of Accelerometer signal. This refers to the up-down movement of the human body.
: Mean of z component of Accelerometer signal. This refers to the up-down movement of the human body. -
•
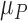 Mean of barometer signal.
Mean of barometer signal.
The FV above are calculated easily from sensor data and are referred to as basic FVs.
F. Derived Features
Next, we define the additional FVs we derived from tri-axial accelerometer data. These features have been useful in human activity recognition and possibly also improve accuracy in our scenario [8]. These are termed as derived FVs (FV 10–34). These features are calculated from the data collected from accelerometer and barometer, which are treated as time series signal. Features are calculated based on time and frequency-domain features. Here, the word energy refers to energy of time-series signal and not the physical EE values.
-
•
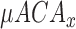 ,
, 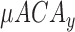 ,
, 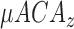 : absolute mean of energy deviation from average of
: absolute mean of energy deviation from average of 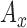 ,
, 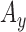 and
and 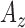 signals.
signals.(for example,
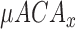 = mean of
= mean of 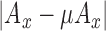 )
) -
•
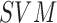 : Signal Vector Magnitude is the root mean square value of AC component along all three axis.
: Signal Vector Magnitude is the root mean square value of AC component along all three axis. -
•
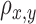 ,
, 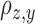 ,
, 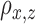 : Correlation between
: Correlation between 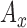 ,
, 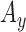 and
and 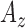 signals (pairwise).
signals (pairwise). -
•
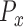 ,
, 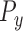 ,
, 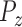 : Pitch of
: Pitch of 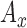 ,
, 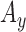 and
and 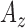 signals.
signals. -
•
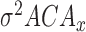 ,
, 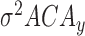 ,
, 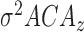 : variance of energy deviation from average energy of
: variance of energy deviation from average energy of 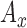 ,
, 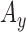 and
and 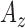 signals.
signals.(for example,
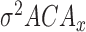 = variance of
= variance of 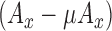 )
) -
•
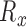 ,
, 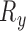 ,
, 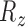 : Range of
: Range of 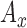 ,
, 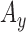 and
and 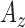 signals in given window.
signals in given window. -
•
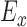 ,
, 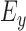 ,
, 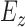 : Energy of
: Energy of 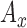 ,
, 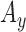 and
and 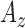 signals in given window.
signals in given window. -
•
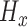 ,
, 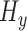 ,
, 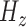 : Entropy of
: Entropy of 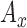 ,
, 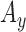 and
and 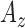 signals in given window.
signals in given window. -
•
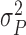 : variance of barometer signal.
: variance of barometer signal. -
•
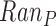 : Range of barometer signal (in given window).
: Range of barometer signal (in given window). -
•
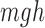 : Work done against gravity.
: Work done against gravity. 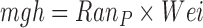 .
.
G. Calorimetry Equations
The activity counts or acceleration values collected using accelerometer can be combined with demographic information and regression techniques [14], [37] or physical models of the human body [38] to produce energy expenditure estimates. We use the popular equation proposed by [14] to obtain EE. This model is also deployed in Calfit [29] used by researchers in California to assess associations between the built environment and physical activity in many case studies. EE estimates given by this method uses the following heuristic relation:
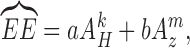 |
where,
-
•
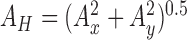
-
•
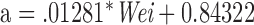
-
•
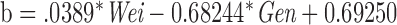
-
•
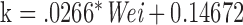
-
•
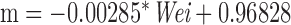
Researchers have reported 60–95% correlation using Equation 1 for ambulatory activities such as walking or running. However, the performance degrades when used for activities involving change of altitude. We use this as FV(35) in our algorithm.
IV. Prediction Models
In this section, we briefly introduce the regression models used in this work. Linear regression is the simplest and most commonly used technique. It is a least squared estimator of single explanatory variable. Artificial Neural Networks are a family of statistical learning models, which have excellent prediction ability. They are simplified representations of the model used by human brain for intelligent functions. Multilayer perceptron is used in this work. We also use an ensemble technique ‘bagging’ in conjunction with regression trees with Reduced-Error-Pruning (REP). Such trees are generated based on information-gain criterion from individual attributes. Pruning is used to avoid over-fitting. Bagging technique ensembles or merges the output of multiple such models to obtain the final prediction. The relative advantage of Bagged REP Regression Trees is in low computational complexity and ability to identify high information attributes.
More details of these models is given in Appendix A.
V. Experiments and Results
In this section, we present our results. The smartphone sensors logged their data using a native Android app into a csv file while COSMED K4b2 calorimeter was used to validate the readings and measure actual EE. The smartphone was kept in waist pouch by the participants, as shown in Figure 1. Unlike, activity specific classification and EE estimation algorithms [28], our focus here is on designing a single robust EE algorithm, that can be applied to a combination of all regular ambulatory activities in a combined manner.
Table 3 gives the performance results using Artificial Neural Networks and Simple Linear Regression models. 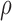 indicates correlation between predicted output and actual EE values. RMSE is the Root Mean Square Error while MAE is Mean Absolute Error. Raw Accelerometer means that only the mean accelerometer values are provided as inputs to machine learning algorithm. ‘All FV’ refer to the case when all 35 FVs mentioned earlier are included in ANN.
indicates correlation between predicted output and actual EE values. RMSE is the Root Mean Square Error while MAE is Mean Absolute Error. Raw Accelerometer means that only the mean accelerometer values are provided as inputs to machine learning algorithm. ‘All FV’ refer to the case when all 35 FVs mentioned earlier are included in ANN.
TABLE 3. Regression Results Indicate Superior Performance of Machine Learning Algorithms Over Linear Regression in Both Cases (a) Using Only Accelerometer Mean Values and (b) All Features.
| Model used | 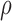 |
RMSE | MAE |
|---|---|---|---|
| Bagged Regression Tree | |||
| Raw Accelerometer (only) | 0.9004 | 1.0302 | 0.5201 |
| All Feature Vectors (FV) | 0.9468 | 0.7910 | 0.4012 |
| Artificial Neural Network | |||
| Raw Accelerometer (only) | 0.7189 | 1.6235 | 1.2244 |
| All Feature Vectors (FV) | 0.8794 | 1.1266 | 0.7347 |
| Linear Regression | |||
| Raw Accelerometer (only) | 0.6028 | 1.8251 | 1.4611 |
| All FVs | 0.5807 | 1.8643 | 1.4797 |
| Demographic features (only) | 0.6040 | 1.8231 | 1.4425 |
It can be clearly seen that linear regression gives very poor performance with only accelerometer as well as all FVs. In both cases the correlation is close to 60% and RMSE is high (≥1.8). There is no improvement in linear regression performance with increase in Feature Vectors. On the other hand, BRT (Bagged REP-regression Trees) and ANN (Artificial Neural Networks) both give higher correlation and lower RMSE values. Thus, the utility of using non-linear models for regression is clear. Using ANN model, we are able to achieve 72% correlation with actual EE values with a RMSE of 1.62 using only accelerometer equations. When all FVs are used, correlation increases to 88% and RMSE reduces to 1.13. BRT gives higher performance than ANN. The RMSE reduces to 0.79 when building BRT with all features, while it is 1.03 when using only raw accelerometer values. These values are improvements over ANN.
Regression Trees are built using Information-theoretic criterion and pick high entropy features on the top. Reduced-Error-Pruning algorithm prunes the redundant leaves of the tree to guard against over-fitting. Bagging is a meta-ensemble algorithm and the results of multiple REP-regression trees are pooled to obtain a higher accuracy than a single REP-regression tree. Thus, we observe that ensemble technique gives higher correlation than ANNs.
Here, we observe that using all FVs does not improve the accuracy of linear regression model for EE over raw accelerometry values, because their impact on EE is non-linear. It is also possibly due to overfitting. Machine learning algorithms are able to capture the non-linearity and thus the correlation is higher (and consequently RMSE is low) when we see the case of neural networks and bagged regression trees.
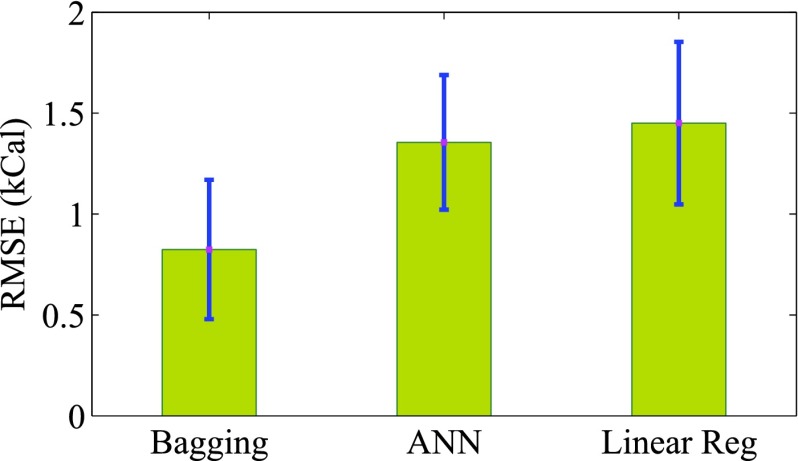
Figure 2 shows the results when we compare the RMSE for leave one out sampling. In leave-one-out sampling, the model is trained with  users and tested on 1 user, and this procedure is repeated for each user. Leave-one-out technique is therefore good to find out the generality of our technique on new users, for whom the model has not been trained. The figure shows that Bagging (BRT) gives lesser RMSE than ANN and Linear Regression techniques. The
users and tested on 1 user, and this procedure is repeated for each user. Leave-one-out technique is therefore good to find out the generality of our technique on new users, for whom the model has not been trained. The figure shows that Bagging (BRT) gives lesser RMSE than ANN and Linear Regression techniques. The 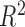 statistics gives the coefficient of determination (range usually 0 to 1). 1 indicates a perfect fit. The
statistics gives the coefficient of determination (range usually 0 to 1). 1 indicates a perfect fit. The 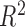 coefficient for ANN was 0.87, but was 0.96 (close to 1) for BRT.
coefficient for ANN was 0.87, but was 0.96 (close to 1) for BRT.
FIGURE 2.
Plot of RMSE (Root Mean Square Error) comparison of three techniques using leave-one-out sampling. The bars show the mean RMSE value while error bars show the variance in values.
A. Baseline Comparison
The models generated using linear regression technique and single accelerometer can be used as a baseline EE algorithm. It obtains 60.28% correlation with output EE values and the Root Mean Square Error (RMSE) is around 1.8251. To serve as another useful baseline, we also tried to study the results when using only a model with demographic information of the participants. It obtains 60.4% correlation and RMSE of 1.8231. The relative absolute error is around 80% for both of them.
B. Influence of Feature Vectors
Figure 3 shows the relative information gain of input FVs obtained using GainRatio criterion. It evaluates the worth of a FV by measuring the gain ratio with respect to the class. The information gain is equal to the total entropy for an attribute if for each of the attribute values a unique classification can be made for the result attribute. In this case the relative entropy subtracted from the total entropy are 0.
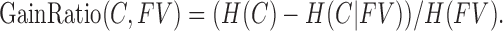 |
where 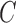 is set of all training examples, and
is set of all training examples, and 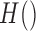 denotes entropy. The missing Merge option distributes counts for missing values. Counts are distributed across other values in proportion to their frequency. Otherwise, missing is treated as a separate value.
denotes entropy. The missing Merge option distributes counts for missing values. Counts are distributed across other values in proportion to their frequency. Otherwise, missing is treated as a separate value.
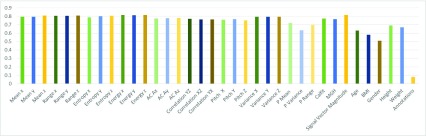
FIGURE 3.
Relative Information Gain Ratio of input Feature Vectors (FVs) obtained using GainRatio criterion. High Information Gain implies high predictive power of a feature to estimate EE.
We can observe that many input features have high information gain ratio in the range of 0.70–0.80. While collecting data, we had annotated different set of activities using manual markers. Here we find that the GainRatio for annotations is pretty low (0.08) indicating that knowledge of activity-type has little correlation to EE values. However, since most of the features such as mean, variance, range, entropy and correlation have high GainRatio, we argue that many of them are correlated and hence redundant.
Next, we use a twofold approach to reduce the attributes to be used in the model. First, we used feature selection algorithms to find the independent features which can give high predictive power. Second, we find the relative computational cost of computing each FV.
Feature selection aims at reducing the number of attributes to be used in the model, while trying to retain the predictive power of the original set of attributes in the pre-processed data. We use the Correlation Feature Selection (CFS) strategy to identify a subset of attributes which were highly correlated with the outcome variable while having low inter-correlation amongst themselves. The CFS technique was used in conjunction with a greedy stepwise search to find the subset 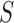 with the best average merit, which is given by:
with the best average merit, which is given by:
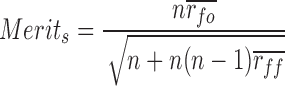 |
where 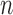 is the number of features in
is the number of features in 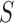 ,
, 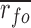 is the average value of feature-outcome correlations, and
is the average value of feature-outcome correlations, and 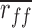 is the average value of all feature-feature correlations. We used the entire dataset for feature selection, which can potentially bias the results and should be avoided in general (cross-validation should be used for feature selection as well). The reason to use the entire dataset for feature selection process is our multi-step strategy, which included a manual screening to eliminate computationally-inefficient coefficients. Using cross-validation for CFS would give slightly different subsets for each fold, which would complicate the manual screening step, and each resulting subset would again give different subsets after the second round of CFS. To simplify the process, we used the entire data at each step and got a single subset of features for the final model.
is the average value of all feature-feature correlations. We used the entire dataset for feature selection, which can potentially bias the results and should be avoided in general (cross-validation should be used for feature selection as well). The reason to use the entire dataset for feature selection process is our multi-step strategy, which included a manual screening to eliminate computationally-inefficient coefficients. Using cross-validation for CFS would give slightly different subsets for each fold, which would complicate the manual screening step, and each resulting subset would again give different subsets after the second round of CFS. To simplify the process, we used the entire data at each step and got a single subset of features for the final model.
Extracting each feature vector from raw sensor inputs can be time consuming. Particularly, on an embedded device like a smartphone, such operations may drain the battery.
We first profile the different FV extraction algorithms in terms of their computational complexity. Since the exact speed of computation is device dependent, we report relative speed (time of execution relative to time of execution of Raw Acc. values (to compute the mean). Let 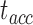 denote the time required to process accelerometer values along one dimension. For a feature
denote the time required to process accelerometer values along one dimension. For a feature 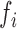 the computation ratio is calculated as follows:
the computation ratio is calculated as follows:
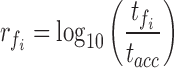 |
where 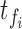 refers to time taken by computation of feature
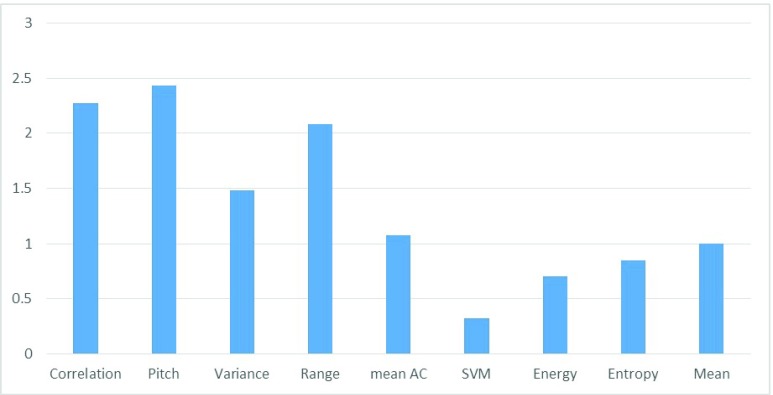
refers to time taken by computation of feature 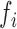 on same device. The values are reported in Figure 4. These computations are performed with a desktop processor running at 2.6 GHz and averaged over 200K computations. The relative computation time is same for mobile processors, but desktop values are reported because we could average them over large sample size. Next, our goal is to prune the FVs with higher computational cost without sacrificing the accuracy of EE estimation. As shown in Figure 4, correlation, pitch and range have an-order of magnitude higher computational cost than mean, energy and entropy.
on same device. The values are reported in Figure 4. These computations are performed with a desktop processor running at 2.6 GHz and averaged over 200K computations. The relative computation time is same for mobile processors, but desktop values are reported because we could average them over large sample size. Next, our goal is to prune the FVs with higher computational cost without sacrificing the accuracy of EE estimation. As shown in Figure 4, correlation, pitch and range have an-order of magnitude higher computational cost than mean, energy and entropy.
FIGURE 4.
Relative Computation cost of Feature Vectors. Different features have different cost of computation, making low-cost features such as energy, SVM, entropy and mean preferred to other features. The y-axis shows 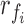 metric which is zero for feature
metric which is zero for feature 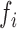 if the computational cost is same as that of mean of accelerometer values (simplest operation).
if the computational cost is same as that of mean of accelerometer values (simplest operation). 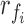 is in logarithmic scale, indicating that increase by 1 indicates
is in logarithmic scale, indicating that increase by 1 indicates 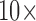 increase in computational requirement on mobile devices.
increase in computational requirement on mobile devices.
We would desire to use the features with least computation cost and high predictive power to form the EE estimation model. Using CFS strategy in conjunction with our knowledge of computational cost, we obtain the following reduced 6 FVs in our final model: 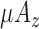 ,
, 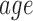 ,
, 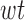 ,
, 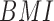 ,
, 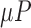 and
and 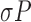 . We note that all derived FVs for acceleromter data are pruned by the CFS algorithm. Both mean and variance of barometer reading is used for EE estimation.
. We note that all derived FVs for acceleromter data are pruned by the CFS algorithm. Both mean and variance of barometer reading is used for EE estimation.
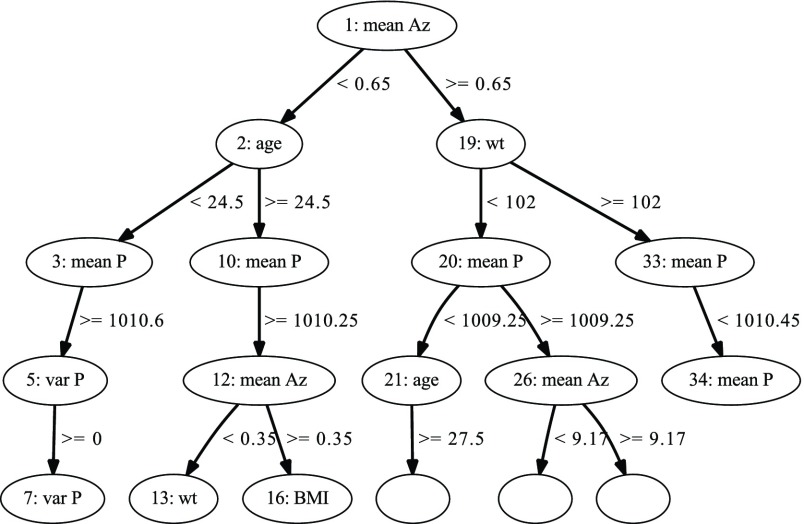
Generating a Bagged REP-regression Tree (BRT) from these FVs give us an correlation of 0.9436, MAE of 0.4243 and RMSE of 0.81. Figure 5 shows the plot of top nodes of the BRT thus obtained. The tree is pruned and only the top attributes, used in tree-branching are shown. It can be seen that 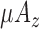 is most significant predictor followed by
is most significant predictor followed by 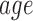 ,
, 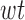 and barometer readings (
and barometer readings (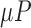 and
and 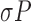 ).
).
FIGURE 5.
Plot of top nodes of Regression Tree. The top nodes are the ones capturing highest information and influencing the EE. We can clearly see mean barometric values (meanP) in the third level of hierarchy, implying clear contribution of barometer sensor in precision of Regression Tree (BRT).
This model is considered the final model.
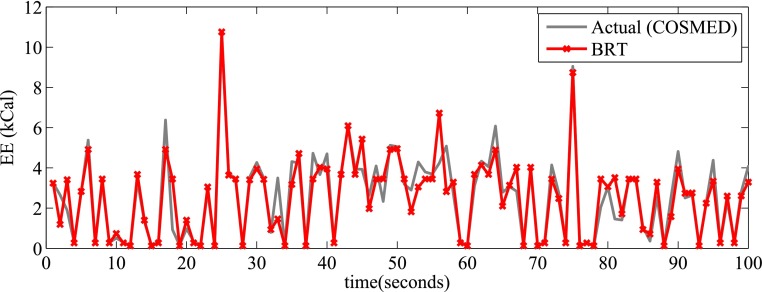
Figure 6 shows the actual EE values and the values estimated using BRT (final model). There is a close agreement between the values.
FIGURE 6.
Sample plot of EE estimates (using Bagged Regression Tree (BRT), a machine learning scheme (final model).) with actual EE values (COSMED). BRT estimates closely match actual COSMED readings with MAE of 0.4.
C. Impact of Calorimetry Equations
Calorimetry Equations (CE) proposed in literature, such as the one used in [14] and [29] have very high computational complexity as they involve fractional arithmetic and are not efficient on smartphone processors. We want to quantify the impact of these calculations on the accuracy of ANN and BRT models. First, we try to see the prediction ability of CE. Although CE estimates roughly followed the trend for most activities, the average correlation was low. Estimation error (along the range of activities) was 89.9788% and correlation was found to be 0.5027. The correlation was particularly low for climbing activities while it was close to 0.65 for other activities [14], [29].
Next, we ran the models with and without this equation along with Accelerometer (basic) features. The results are presented in Table 4. It can be seen that including CE has no (or negative) impact on the accuracy of ANN/ BRT model with Raw Acc. This justifies that we remove this input from our selection of feature vectors.
TABLE 4. Impact of Barometer Values on EE Prediction Using Machine Learning Approaches.
| Model used | 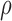 |
RMSE | MAE |
|---|---|---|---|
| Artificial Neural Networks (ANN) | |||
| Raw Accelerometer (only) | 0.7779 | 1.6528 | 1.2321 |
| Raw Acc. + Bar. | 0.8594 | 1.3302 | 1.0001 |
| Raw Acc. + CE | 0.7838 | 1.6642 | 1.2347 |
| Final Model (BRT reduced) | 0.9201 | 1.0020 | 0.6931 |
| Bagged Regression Tree (BRT) | |||
| Raw Accelerometer (only) | 0.9001 | 1.0310 | 0.5229 |
| Raw Acc. + Bar. | 0.9401 | 0.8610 | 0.4730 |
| Raw Acc. + CE | 0.9101 | 0.9701 | 0.4920 |
| Final model (BRT reduced) | 0.9560 | 0.7300 | 0.4015 |
D. Impact of Barometer Sensor
The experimental results validated our assertion that barometric sensor (Bar.) has high correlation with EE accuracy. Appending the mean of barometer values (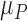 ) improve the correlation of EE to actual energy expenditure for both ANN and BRT as shown in Table 4.
) improve the correlation of EE to actual energy expenditure for both ANN and BRT as shown in Table 4.
E. Comparison With Other Products
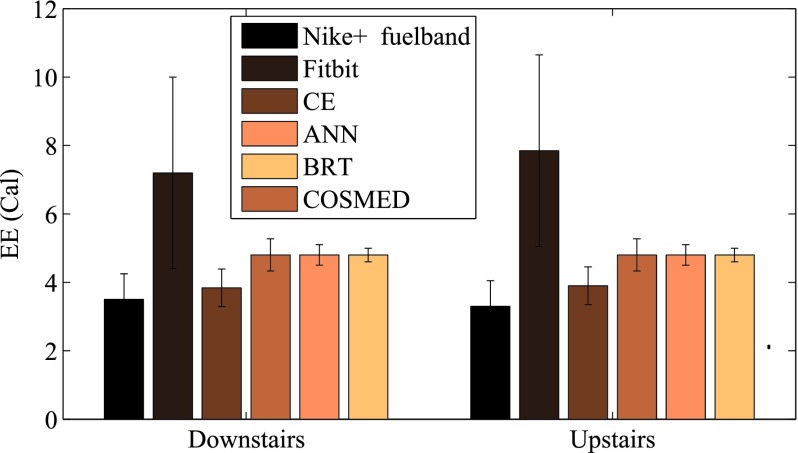
It is not possible to obtain second by second EE from commercial devices such as Fitbit or Nike + Fuel band. However, we did calibrate these values before and after each trial and normalized for each subject’s weight. We present the summary results in Figure 7. The errors in individual measurements sum up and CE algorithm (calorimetry equation used in Calfit) presents an estimate which is within 25% of the COSMED values. ANN and BRT values have same mean as the COSMED values. However, variance of error is smaller in BRT. We can see that Nike + Fuelband tends to underestimate the EE for each individual while Fitbit tends to overestimate the value. The error bars in the figure show the standard deviation for each device/algorithm. Fitbit has an abnormally high deviation. Our algorithm has a smaller deviation over the population considered, which is comparable to actual COSMED values.
FIGURE 7.
Overall absolute EE comparison of COSMED, BRT and ANN with Nike +, Fitbit and Calorimetry equation for two tasks across subjects. The ANN and BRT perform very close to the values obtained from COSMED. All three have same mean estimates but the variances are larger with ANN as against BRT. The variance in Cosmed readings reflect range across subjects. The Calorimetry equations and Nike + product underestimates while Fitbit overestimates the results.
F. Power Efficiency
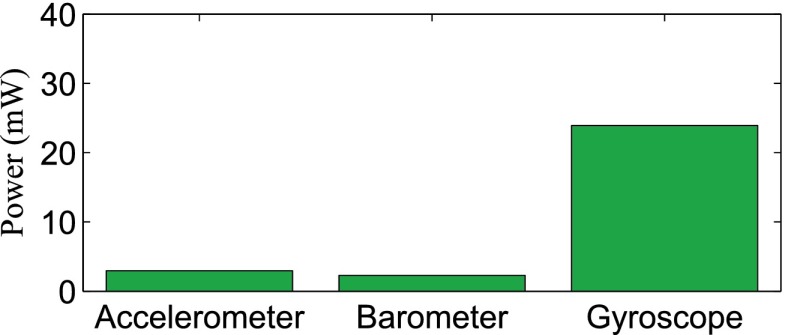
One of the most power consuming operation in EE estimation is sampling of smartphone sensors. Unlike recent works that use gyroscope sensor in addition to accelerometer [39], we directly used the accelerometer and barometer sensor, and use machine learning algorithms to estimate EE. In next set of experiments, we tried to quantify the power savings in making this choice.
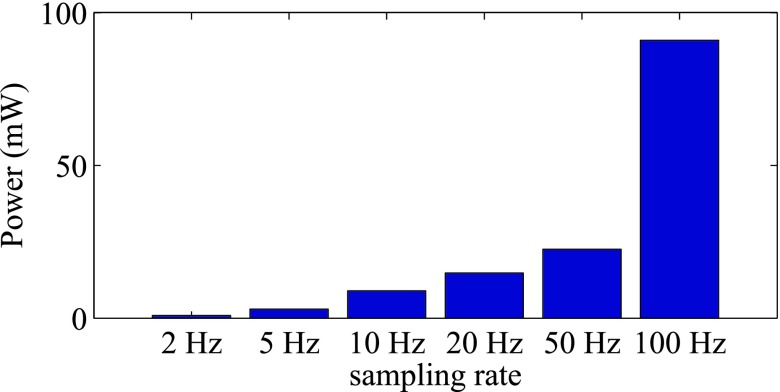
We used Monsoon power monitor to measure the energy consumption of sensors on the smartphone, turned off network interfaces and display and keep all system settings same during the experiments. The sampling rate was kept to be low (at 2 Hz) and the results are averaged over few minutes of observations. Figure 8 shows the relative power expenditure of these sensors (when the smartphone OS is on). These readings clearly demonstrate how accelerometer and barometer sensor has very low power consumption than gyroscope.
FIGURE 8.
Power consumption of smartphone (with display, network and other apps off) reading individual sensor signal at 2 Hz.
Next, we justify our use of low sampling rates to obtain power-efficiency. The impact of different sampling rates on power consumption can be done using the emulation method described in [40] and [41]. The sampling rate can be controlled through the Android API android.hard-ware.SensorManager.registerListener. Figure 9 shows the power consumption with increased sampling rate for accelerometer sensor. A similar trend is obtained with barometer sensor.
FIGURE 9.
Power consumption of smartphone (with display, network and other apps off) reading individual accelerometer sensor signal at different sampling rates.
The training of machine learning algorithm is a power consuming task, but it can be done offline in the cloud. Overall, our framework can be easily implemented in smartphones and has a power consumption less than 30 mW (which will vary a bit with smartphone model and operating system).
VI. Discussions and Future Work
In this work, we proposed a technique for accurate EE estimation in ambulatory settings utilizing machine learning techniques and combining the sensor readings from both the accelerometer and barometer sensors of smart phones. To emulate a practical low-power setting, we used a smartphone and sampled the accelerometer and barometer sensorss at 2Hz only. We then used these values to extract Feature Vectors (FVs) and fit a Bagged Regression Tree which can yield up to 96% correlation and RMSE of 0.70 with very small computational overhead. We observed significant benefits in fusing the input of barometer sensor to an accelerometer sensor as it allows, with use of simpler FVs, achievement of higher correlation and accuracy to reference EE values.
Improved EE estimation will provide important information regarding energy balance for individuals during various physical activities in both clinical and community living settings. Commercially-available wellness devices are becoming popular. In general, they rely on step counts and are expensive. Building accurate EE models is helpful for the masses to measure their caloric expenditure using their already purchased smartphones and make healthy decisions about lifestyles. It is also of great interest to researchers, who can use smartphone-sensed data of individuals to gain insight into EE and gait features as well as trends. Commercial devices such as Fitbit have shared APIs but do not allow access to sensor data, limiting clinical research explorations.
Motivated by the present study’s encouraging results, we plan to collect a more extensive dataset, using a larger sample size of study subjects, along with other physical activities like biking, running, walking/running on inclines, and everyday chores such as gardening/cleaning. In the future, using this larger data set with wider range of activities, we wish to build a more representative model for EE (using Bagged Regression Trees). We then envision building a smartphone application which can be used to obtain accurate EE without significantly impacting the battery life of smartphones.
Biographies

Amit Pande received the bachelor’s degree in electronics and communications engineering from IIT Roorkee, India, in 2007, and the Ph.D. degree in computer engineering from Iowa State University, USA, in 2010. He has been a Research Scientist with the University of California at Davis since 2010. He has authored over 65 peer-reviewed conference and journal papers. His current research interests are in application of data analytics to mobile, health, networking, and other applications and in network security. He received many university research excellence awards and best paper awards at international conferences.

Jindan Zhu received the B.S. and M.S. degrees in information security from Shanghai Jiao Tong University, in 2006 and 2009, respectively. He is currently pursuing the Ph.D. degree with the University of California at Davis.
His research interests include context aware system and services, mobile sensing, and indoor localization.

Aveek K. Das received the B.Tech. degree in electronics and telecommunication engineering from Jadavpur University, India, in 2012. He is currently pursuing the Ph.D. degree with the Department of Computer Science, University of California at Davis. His current research interests include network measurement, network analytics, network data mining, wearables, and network security and privacy.

Yunze Zeng received the B.S. degree in telecommunications engineering from Beijing Jiaotong University, China, in 2012. He is currently pursuing the Ph.D. degree with the Department of Computer Science, University of California at Davis. He was an Exchange Student with the University of California at San Diego in 2011. His current research interests include wireless networking and mobile computing. He was a recipient of the best paper awards from the ACM BodyNets 2013 and the IFIP Networking 2014.

Prasant Mohapatra (F’10) received the Ph.D. degree from Pennsylvania State University, in 1993. He is currently a Professor with the Department of Computer Science and serves as the Associate Chancellor with the University of California at Davis. His research interests are in the areas of wireless networks, mobile communications, cybersecurity, and Internet protocols. He is a fellow of AAAS. He received the Outstanding Engineering Alumni Award in 2008.

Jay J. Han received the bachelor’s degree from Stanford University, in 1993, and the M.D. degree from the UCSF School of Medicine, in 1998. He is board certified in physical medicine and rehabilitation as well as in subspecialties of neuromuscular medicine and electrodiagnostic medicine. He is the Vice Chair of the Department of Physical Medicine and Rehabilitation with the University of California Davis Medical Center. He is a Translational Clinical Researcher specializing in combining technology with clinical medicine.
Appendix A. Linear Regression
Simple linear regression is the least squares estimator of a single explanatory variable. It minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear approximation. The resulting estimator can be expressed by a simple formula, especially in the case of a single regressor on the right-hand side. If 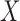 denote the vector of inputs (obtained or derived from accelerometer and barometer readings) and
denote the vector of inputs (obtained or derived from accelerometer and barometer readings) and 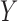 denotes EE obtained using COSMED calorimeter,
denotes EE obtained using COSMED calorimeter, 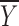 denotes EE values obtained from the model:
denotes EE values obtained from the model:
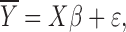 |
where 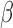 and
and 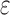 are constants.
are constants.
Appendix B. Artificial Neural Networks
Artificial Neural Network (ANN) is a non-linear techniques have been successfully used in a number of domains [42], [43] for successful prediction. Inspired by biological nervous systems, ANNs are simplified representations of the model used by human brain for intelligent functions. They work by passing feature vectors via layers of small connected computational nodes, called as neurons. Our work uses one hidden layer and one output layer. Each neuron uses a non-linear transfer function to map inputs into outputs [44]. The weights within each neuron is decided in training set.
The number of input layers is determined by the modality of 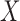 i.e. the number of feature vectors extracted from accelerometer and barometer data. We use one hidden layer, composed of simple elements (called neurons) and each neuron uses a non-linear transfer function to map inputs into outputs [44]. The connections between neurons largely determines the network function. One can train a neural network to perform a particular function by adjusting the values of the connections (weights) between elements. The final layer produces the ANN’s output. The output of a feed-forward neural network with one hidden layer and one output neural network is given by
i.e. the number of feature vectors extracted from accelerometer and barometer data. We use one hidden layer, composed of simple elements (called neurons) and each neuron uses a non-linear transfer function to map inputs into outputs [44]. The connections between neurons largely determines the network function. One can train a neural network to perform a particular function by adjusting the values of the connections (weights) between elements. The final layer produces the ANN’s output. The output of a feed-forward neural network with one hidden layer and one output neural network is given by
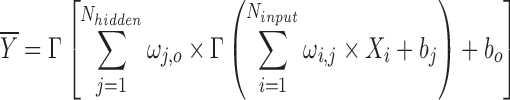 |
where, 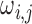 denotes weight between link i and j; all the inputs to a node are summed and passed through transfer function
denotes weight between link i and j; all the inputs to a node are summed and passed through transfer function 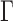 . Input layer neurons uses
. Input layer neurons uses 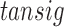 (Tan-Sigmoid) transfer function. Thus, output (y)-input (x) relationship is given by:
(Tan-Sigmoid) transfer function. Thus, output (y)-input (x) relationship is given by:
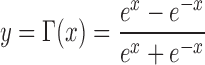 |
It introduces non-linearity into the system and has been observed as most pertinent transfer function for a number of applications [45].
Levenberg-Marquardt (LM) back-propagation optimization algorithm is used to update weights in the network while individual neuron uses gradient descent with momentum weight and bias ( ) learning function. It uses an approximate Hessian matrix and often a more efficient alternative to steepest ascent and its variations [44]. Here, the new weight (
) learning function. It uses an approximate Hessian matrix and often a more efficient alternative to steepest ascent and its variations [44]. Here, the new weight (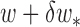 ) is updated from previous step weight change (
) is updated from previous step weight change (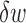 ) based on momentum constant
) based on momentum constant 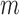 and learning rate
and learning rate 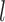
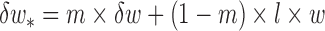 |
The momentum constant and learning rate were selected based on multiple trials and the values corresponding to minimum prediction error (Root Mean Square Error or RMSE) were selected. The learning rate was set to 0.3 and momentum was set to 0.2. These functions are available for implementation as standard routines in Weka toolbox [46] and were used in this work.
Appendix C. Bagged Rep Regression Tree
We used Bootstrapping aggregating (Bagging) [47], ensemble technique with reduced-error pruning decision trees as the underlying regression model to estimate EE. The bagging technique is an ensemble meta-algorithm to improve the stability and accuracy in statistical regression obtained by decision trees. A decision tree is based on build using Information-theoretic criterion for selecting the nodes. Once the tree is built, reduced error pruning is used, where each node, beginning with the leaves, is replaced with its most popular class. The nodes with low information content (and hence reduced error) are pruned to avoid over-fitting.
We divide the data for the model into n = 10 folds, where, 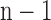 folds are for supervised learning and one fold is used to test the model for errors. The errors obtained in a fold is added to the weights of nodes of next fold in the training set. Ten-fold cross validation was used to evaluate the model in order to ensure that the model was tested on data that it had not seen while training, to minimize chance for over-fitting. Statistical analysis was performed using Weka 3.6.10 and Matlab R2013a (Ver 8.1.0.604) software.
folds are for supervised learning and one fold is used to test the model for errors. The errors obtained in a fold is added to the weights of nodes of next fold in the training set. Ten-fold cross validation was used to evaluate the model in order to ensure that the model was tested on data that it had not seen while training, to minimize chance for over-fitting. Statistical analysis was performed using Weka 3.6.10 and Matlab R2013a (Ver 8.1.0.604) software.
Funding Statement
This work was supported by the Research Investments in the Sciences and Engineering Program through the University of California at Davis.
References
- [1].Pande A., et al. , “Energy expenditure estimation with smartphone body sensors,” in Proc. 8th Int. Conf. Body Area Netw. (BodyNets), 2013, pp. 8–14. [Google Scholar]
- [2].Wang Y., Beydoun M. A., Liang L., Caballero B., and Kumanyika S. K., “Will all Americans become overweight or obese? Estimating the progression and cost of the US obesity epidemic,” Obesity, vol. 16, no. , pp. 2323–2330, 2008. [DOI] [PubMed] [Google Scholar]
- [3].Ogden C. L., Carroll M. D., Kit B. K., and Flegal K. M., “Prevalence of childhood and adult obesity in the United States, 2011–2012,” J. Amer. Med. Assoc., vol. 311, no. 8, pp. 806–814, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Macera C. A. (2003). Promoting Healthy Eating and Physical Activity for a Healthier Nation. [Online]. Available: http://www.cdc.gov/healthyyouth/publications/pdf/pp-ch7.pdf [Google Scholar]
- [5].Khanna N., Boushey C. J., Kerr D., Okos M., Ebert D. S., and Delp E. J., “An overview of the technology assisted dietary assessment project at Purdue University,” in Proc. IEEE Int. Symp. Multimedia (ISM), Dec. 2010, pp. 290–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Thorogood A., et al. , “Isolated aerobic exercise and weight loss: A systematic review and meta-analysis of randomized controlled trials,” Amer. J. Med., vol. 124, no. 8, pp. 747–755, 2011. [DOI] [PubMed] [Google Scholar]
- [7].Pinnington H. C., Wong P., Tay J., Green D., and Dawson B., “The level of accuracy and agreement in measures of FEO2, FECO2 and VE between the COSMED K4 b2 portable, respiratory gas analysis system and a metabolic cart,” J. Sci. Med. Sport, vol. 4, no. 3, pp. 324–335, 2001. [Online]. Available: http://www.sciencedirect.com/science/article/pii/S1440244001800414 [DOI] [PubMed] [Google Scholar]
- [8].Tapia E. M., “Using machine learning for real-time activity recognition and estimation of energy expenditure,” Ph.D. dissertation, Dept. Archit. Program Media Arts Sci, Massachusetts Inst. Technol, Cambridge, MA, USA, 2008. [Google Scholar]
- [9].Bassett D. R. Jr., Wyatt H. R., Thompson H., Peters J. C., and Hill J. O., “Pedometer-measured physical activity and health behaviors in united states adults,” Med. Sci. Sports Exercise, vol. 42, no. 10, pp. 1819–1825, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Fitbit. [Online]. Available: http://www.fitbit.com, accessed Jan. 2015. [Google Scholar]
- [11].Jawbone Up. [Online]. Available: https://jawbone.com/up, accessed Jan. 2015. [Google Scholar]
- [12].Nike+ Fuel Band. [Online]. Available: http://www.nike.com/us/en_us/c/nikeplus-fuel, accessed Jan. 2015. [Google Scholar]
- [13].Bonomi A. G. and Westerterp K. R., “Advances in physical activity monitoring and lifestyle interventions in obesity: A review,” Int. J. Obesity, vol. 36, no. 2, pp. 167–177, 2012. [DOI] [PubMed] [Google Scholar]
- [14].Chen K. Y. and Sun M., “Improving energy expenditure estimation by using a triaxial accelerometer,” J. Appl. Physiol., vol. 83, no. 6, pp. 2112–2122, 1997. [DOI] [PubMed] [Google Scholar]
- [15].Muralidharan K., Khan A. J., Misra A., Balan R. K., and Agarwal S., “Barometric phone sensors: More hype than hope!” in Proc. 15th Workshop Mobile Comput. Syst. Appl., 2014, Art. ID 12. [Google Scholar]
- [16].Zhang J., Edwan E., Zhou J., Chai W., and Loffeld O., “Performance investigation of barometer aided GPS/MEMS-IMU integration,” in Proc. IEEE/ION Position Location Navigat. Symp. (PLANS), Apr. 2012, pp. 598–604. [Google Scholar]
- [17].Tanigawa M., Luinge H., Schipper L., and Slycke P., “Drift-free dynamic height sensor using MEMS IMU aided by MEMS pressure sensor,” in Proc. 5th Workshop Positioning, Navigat. Commun. (WPNC), 2008, pp. 191–196. [Google Scholar]
- [18].Vanini S. and Giordano S., “Adaptive context-agnostic floor transition detection on smart mobile devices,” in Proc. IEEE Int. Conf. Pervasive Comput. Commun. Workshops (PERCOM Workshops), Mar. 2013, pp. 2–7. [Google Scholar]
- [19].Sankaran K., Zhu M., Guo X. F., Ananda A. L., Chan M. C., and Peh L.-S., “Using mobile phone barometer for low-power transportation context detection,” in Proc. 12th ACM Conf. Embedded Netw. Sensor Syst., 2014, pp. 191–205. [Google Scholar]
- [20].Colbert L. H., Matthews C. E., Havighurst T. C., Kim K., and Schoeller D. A., “Comparative validity of physical activity measures in older adults,” Med. Sci. Sports Exercise, vol. 43, no. 5, pp. 867–876, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Gardner A. W. and Poehlman E. T., “Assessment of free-living daily physical activity in older claudicants: Validation against the doubly labeled water technique,” J. Gerontol. A, Biol. Sci. Med. Sci., vol. 53, no. 4, pp. M275–M280, 1998. [DOI] [PubMed] [Google Scholar]
- [22].Zhang K., Pi-Sunyer F. X., and Boozer C. N., “Improving energy expenditure estimation for physical activity,” Med. Sci. Sports Exercise, vol. 36, no. 5, pp. 883–889, 2004. [DOI] [PubMed] [Google Scholar]
- [23].Crouter S. E., Churilla J. R., and Bassett D. R. Jr., “Estimating energy expenditure using accelerometers,” Eur. J. Appl. Physiol., vol. 98, no. 6, pp. 601–612, 2006. [DOI] [PubMed] [Google Scholar]
- [24].Vathsangam H., Schroeder E. T., and Sukhatme G. S., “Hierarchical approaches to estimate energy expenditure using phone-based accelerometers,” IEEE J. Biomed. Health Inform., vol. 18, no. 4, pp. 1242–1252, Jul. 2014. [DOI] [PubMed] [Google Scholar]
- [25].Vathsangam H., Schroeder E. T., and Sukhatme G. S., “On determining the best physiological predictors of activity intensity using phone-based sensors,” in Proc. IEEE Point-Care Healthcare Technol. (PHT), Jan. 2013, pp. 140–143. [Google Scholar]
- [26].Dannecker K. L., Petro S. A., Melanson E. L., and Browning R. C., “Accuracy of fitbit activity monitor to predict energy expenditure with and without classification of activities,” Med. Sci. Sports Exercise, vol. 43, no. 5, p. 62, 2011. [Google Scholar]
- [27].Bosch S., Marin-Perianu M., Marin-Perianu R., Havinga P., and Hermens H., “Keep on moving! Activity monitoring and stimulation using wireless sensor networks,” in Smart Sensing and Context. New York, NY, USA: Springer-Verlag, 2009, pp. 11–23. [Google Scholar]
- [28].Altini M., Penders J., and Amft O., “Energy expenditure estimation using wearable sensors: A new methodology for activity-specific models,” in Proc. Conf. Wireless Health, 2012, Art. ID 1. [Google Scholar]
- [29].Yan P., Lin I., Roy M., Seto E., Wang C., and Bajcsy R., “WAVE and CalFit—Towards social interaction in mobile body sensor networks,” in Proc. 5th Annu. ICST Wireless Internet Conf. (WICON), 2010, pp. 1–2. [Google Scholar]
- [30].Zhan A., Chang M., Chen Y., and Terzis A., “Accurate caloric expenditure of bicyclists using cellphones,” in Proc. 10th ACM Conf. Embedded Netw. Sensor Syst. (SenSys), 2012, pp. 71–84. [Online]. Available: http://doi.acm.org/10.1145/2426656.2426664 [Google Scholar]
- [31].Ohtaki Y., Susumago M., Suzuki A., Sagawa K., Nagatomi R., and Inooka H., “Automatic classification of ambulatory movements and evaluation of energy consumptions utilizing accelerometers and a barometer,” Microsyst. Technol., vol. 11, nos. 8–10, pp. 1034–1040, 2005. [Google Scholar]
- [32].Voleno M., Redmond S. J., Cerutti S., and Lovell N. H., “Energy expenditure estimation using triaxial accelerometry and barometric pressure measurement,” in Proc. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. (EMBC), Aug./Sep. 2010, pp. 5185–5188. [DOI] [PubMed] [Google Scholar]
- [33].Yin J., Yang Q., and Pan J. J., “Sensor-based abnormal human-activity detection,” IEEE Trans. Knowl. Data Eng., vol. 20, no. 8, pp. 1082–1090, Aug. 2008. [Google Scholar]
- [34].Bouten C. V. C., Koekkoek K. T. M., Verduin M., Kodde R., and Janssen J. D., “A triaxial accelerometer and portable data processing unit for the assessment of daily physical activity,” IEEE Trans. Biomed. Eng., vol. 44, no. 3, pp. 136–147, Mar. 1997. [DOI] [PubMed] [Google Scholar]
- [35].Sun M., Reed G. W., and Hill J. Q., “Modification of a whole room indirect calorimeter for measurement of rapid changes in energy expenditure,” J. Appl. Physiol., vol. 76, no. 6, pp. 2686–2691, 1994. [DOI] [PubMed] [Google Scholar]
- [36].McLaughlin J. E., King G. A., Howley E. T., Bassett D. R. Jr., and Ainsworth B. E., “Validation of the COSMED K4 b2 portable metabolic system,” Int. J. Sports Med., vol. 22, no. 4, pp. 280–284, 2001. [DOI] [PubMed] [Google Scholar]
- [37].Freedson P. S., Melanson E., and Sirard J., “Calibration of the computer science and applications, Inc. accelerometer,” Med. Sci. Sports Exercise, vol. 30, no. 5, pp. 777–781, 1998. [DOI] [PubMed] [Google Scholar]
- [38].Jang Y., Jung M., Kang J., and Kim H. C., “An wearable energy expenditure analysis system based on the 15-channel whole-body segment acceleration measurement,” in Proc. 27th Annu. Int. Conf. Eng. Med. Biol. Soc., 2005, pp. 3834–3836. [DOI] [PubMed] [Google Scholar]
- [39].Vathsangam H., Emken A., Schroeder E. T., Spruijt-Metz D., and Sukhatme G. S., “Determining energy expenditure from treadmill walking using hip-worn inertial sensors: An experimental study,” IEEE Trans. Biomed. Eng., vol. 58, no. 10, pp. 2804–2815, Oct. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Yan Z., Subbaraju V., Chakraborty D., Misra A., and Aberer K., “Energy-efficient continuous activity recognition on mobile phones: An activity-adaptive approach,” in Proc. 16th Int. Symp. Wearable Comput. (ISWC), 2012, pp. 17–24. [Google Scholar]
- [41].Qi X., Keally M., Zhou G., Li Y., and Ren Z., “AdaSense: Adapting sampling rates for activity recognition in body sensor networks,” in Proc. IEEE 19th Real-Time Embedded Technol. Appl. Symp. (RTAS), Apr. 2013, pp. 163–172. [Google Scholar]
- [42].Gopalakrishnan K., Agrawal A., Ceylan H., Kim S., and Choudhary A., “Knowledge discovery and data mining in pavement inverse analysis,” Transport, vol. 28, no. 1, pp. 1–10, 2013. [Google Scholar]
- [43].Agrawal A., Misra S., Narayanan R., Polepeddi L., and Choudhary A., “Lung cancer survival prediction using ensemble data mining on seer data,” Sci. Program., vol. 20, no. 1, pp. 29–42, 2012. [Google Scholar]
- [44].Hagan M. T., Demuth H. B., and Beale M., Neural Network Design. Stamford, CT, USA: Thomson Learning, 1996. [Google Scholar]
- [45].Yonaba H., Anctil F., and Fortin V., “Comparing sigmoid transfer functions for neural network multistep ahead streamflow forecasting,” J. Hydrol. Eng., vol. 15, no. 4, pp. 275–283, 2010. [Google Scholar]
- [46].Hall M., Frank E., Holmes G., Pfahringer B., Reutemann P., and Witten I. H., “The WEKA data mining software: An update,” ACM SIGKDD Explorations Newslett., vol. 11, no. 1, pp. 10–18, 2009. [Google Scholar]
- [47].Breiman L., “Bagging predictors,” Mach. Learn., vol. 24, no. 2, pp. 123–140, 1996. [Google Scholar]