High Resolution Single Particle Refinement in EMAN2.1

Abstract

EMAN2.1 is a complete image processing suite for quantitative analysis of greyscale images, with a primary focus on transmission electron microscopy, with complete workflows for performing high resolution single particle reconstruction, 2-D and 3-D heterogeneity analysis, random conical tilt reconstruction and subtomogram averaging, among other tasks. In this manuscript we provide the first detailed description of the high resolution single particle analysis pipeline and the philosophy behind its approach to the reconstruction problem. High resolution refinement is a fully automated process, and involves an advanced set of heuristics to select optimal algorithms for each specific refinement task. A gold standard FSC is produced automatically as part of refinement, providing a robust resolution estimate for the final map, and this is used to optimally filter the final CTF phase and amplitude corrected structure. Additional methods are in-place to reduce model bias during refinement, and to permit cross-validation using other computational methods.

Graphical Abstract

1. Introduction

EMAN was originally developed in 1998 as an alternative to SPIDER [1,2] and IMAGIC [3] the two primary software packages used for single particle reconstruction at that time. Its successor, EMAN2[4], has been under development since 2003, using a modular design which is easy to expand with new algorithms. This also marked the beginning of collaborative development with the SPARX project[5], which is co-distributed with EMAN2.1, and shares the same C++ core library, but has its own set of workflows and its own conceptual framework. It is now one of over 70 different software packages identified as being useful for CryoEM data processing by the EMDatabank. In 2014, based on EMDB statistics, the top seven packages accounted for 96% of published single particle reconstructions: EMAN[4], SPIDER[1,2], RELION[6], IMAGIC[3], SPARX[5], XMIPP[7] and FREALIGN[8]. Surprisingly, each of the seven packages takes a significantly different approach towards the single particle reconstruction problem. With highly homogeneous data with high contrast, it is possible to achieve virtually identical reconstructions using multiple software packages. However, if the data suffers from compositional or conformational variability, a common issue which may often be biologically significant, then each package will be impacted by the variability in different ways, and there can be considerable value in performing comparative refinements among multiple software packages to better understand the specific variations present in the data.

In this manuscript, we will focus not on the problem of heterogeneous data, but rather on a canonical refinement of highly homogeneous data, and the methods used in EMAN2.1 to produce a reliable high resolution structure from the data. The fundamental problem faced by all of these software packages is the same. A field of monodisperse macromolecules is embedded in a thin layer of vitreous ice[9] and imaged on a transmission electron microscope calibrated for optimal parallel-beam conditions. Ideally, each particle will be in a random orientation, and be well away from the perturbing influences of the air-water interface and/or any continuous substrate (carbon or gold). The practical reality often does not match this idealized case. Frequently some level of preferred orientation is observed in the particle population, and there will always be a fraction of particles which have been partially denatured or otherwise perturbed from their idealized conformation, even in the absence of conformational flexibility. Such conformational variability may, in fact, be functionally relevant, rather than an artifact to be eliminated.

Each particle image collected on the microscope represents a projection of the Coulomb potential of the particle, distorted by the properties of the microscope optics and detector, generally described by approximate, but well-understood contrast transfer (CTF) and modulation transfer (MTF) functions[10], respectively, which are corrected for during data processing. These artifacts are largely well understood, and corrections for these are a fundamental part of the reconstruction process in any modern cryoEM software package. Since the particles are in random orientations, the orientation of each particle must be determined before they can be combined to produce a 3-D reconstruction. This can occur via projection matching in real or Fourier space or self or cross-common-lines in Fourier space. In some cases particles are classified and grouped together prior to, or as part of orientation determination. Finally, in some cases, Bayesian methods are used, in which each particle is placed fractionally in multiple orientations when any uncertainty is present. There are advantages and disadvantages of each of these approaches. In the following sections, we will focus on the approach which has evolved over the last 17 years to produce the current EMAN2.12, which can produce high resolution reconstructions very efficiently, often with a small fraction of the computational requirements of its competitors.

2. Single Particle Reconstruction in EMAN

2.1. Project Manager

EMAN2.1 has a graphical workflow manager called e2projectmanager. This program can guide the user through canonical single particle reconstruction, subtomogram averaging and related tasks. It will use standardized naming conventions for folders and image files, producing a well organized project with a complete record of all processing performed therein. In this manuscript, we describe the methodologies and algorithms employed to achieve a high resolution reconstruction. However for those attempting to learn how to use the system, we refer the reader to extensive online tutorials (http://blake.bcm.edu/eman2) and documentation for detailed usage instructions.

2.2. Movie Mode Imaging

Until a few years ago, images were collected on film or CCD cameras in a single exposure, and if there were any stage drift during the, typically ~1 second, exposure the images would be discarded. Similarly, if there were any specimen charging or a significant amount of astigmatism, the images would also be discarded. With the development of direct detectors [11], a single exposure is now often subdivided into many frames forming a ‘movie’ with up to ~100 frames. By aligning the frames before averaging to produce a ‘micrograph’, it is often possible to eliminate the majority of the drift which was previously a large problem[12]. There are additional variants of this methodology which focus on aligning the individual particles within a micrograph, since they may not all move in a uniform way [13,14]. There are a number of software packages for performing whole-frame alignment [15,16], and this issue remains an active area of development. Since this is still such a rapidly evolving area, we will not focus on the details of this process in this manuscript. EMAN2.1 has a program, e2ddd_movie, for whole-frame movie processing and another, e2ddd_particles, for per-particle alignment, both of which are functional, but remain under active research. The user is also free to use any other tool for movie mode alignment they prefer, and can import the resulting averaged micrographs, or particles directly into the refinement pipeline.

2.3. Image Evaluation

Data may be imported at any stage prior to CTF correction. If images are brought into the project as micrographs, rather than boxed out particles, the first steps in processing are micrograph quality assessment, and whole-frame defocus and astigmatism estimation. There is an interactive program (e2evalimage) which segments each micrograph into tiled boxes, then computes the average power spectrum of these tiles as well as their rotational average. The user can assess any residual drift and interactively adjust the automatically determined defocus and astigmatism. There is also an automated program which makes the CTF estimate for all images without user interaction (e2rawdata), as well as programs for importing values from other programs such as CTFFIND [17] and RELION [6] or using the new EMX format (http://i2pc.cnb.csic.es/emx). Typically, for small projects with a few hundred images, the user will interactively assess the image quality as well as ensure accurate initial fitting. This may be impractical for larger projects with thousands of images, so the automatic import tool may be preferable in those situations. There is an opportunity later in the workflow to make automatic quantitative assessments which do a reasonable job of detecting low quality images through use of thresholds in cases where manual assessment is impractical.

2.4. Box Size Selection

Before particle picking/boxing, regardless of what software is used, it is important to select a good box size for your project. There are three concerns when selecting a box size. First, the microscope CTF & MTF (Contrast Transfer Function & Modulation Transfer Function) causes particle information to become delocalized, so for proper CTF correction without artifacts or information loss, the box must be large enough to include this delocalized information. Second, as discussed in section 2.6, EMAN2.1 requires that the box size be 1.5 – 2.5 times larger than the maximum dimension of the particle to perform accurate SSNR (spectral signal to noise ratio) estimations. Third, the specific choice of box size can have a significant impact on refinement speed. Algorithms like the FFT, which are used very heavily during processing, are very sensitive to the specific box dimensions. There are cases where increasing the box size can actually make processing faster, not slower. For example, if using a box size of 244, switching instead to a size of 250 can make the refinement run nearly 2 times faster. There is a full discussion of this issue, and a list of good sizes in the online documentation (http://blake.bcm.edu/emanwiki/EMAN2/BoxSize).

There may be some particles, such as very large viruses, where, due to large particle size, meeting the canonical size requirement would make the box size excessive. For example, a virus with a diameter of 1200 Å, sampled at 1 Å/pixel would technically require a box size of 1800 pixels, which could lead to issues of memory exhaustion, and significant slowdowns in the 3-D reconstruction. In such cases, reducing the box size below recommended limits may be the only practical choice, even if it produces some minor artifacts.

When importing particle data from another software package or non-EMAN particle picking tool, if the box size doesn’t meet EMAN2’s requirements, ideally the particles should be re-extracted from the original micrograph with a more appropriate size. If this impossible due to unavailability of the original micrographs or other problems, then CTF correction should be performed on the particles with their current suboptimal size, and they can be padded to a more appropriate size during the phase-flipping process, along with appropriate normalization and masking to prevent alignment bias. It is critical that particles not be zero-padded or masked prior to CTF/SSNR estimation and phase-flipping. To mask particles in such a situation typically the phase-flipped particles would be processed by setting the mean value around the edge of each particle to zero, resizing the box, then applying a soft Gaussian mask falling to zero around each particle to eliminate the corners of the original box, without masking out any of the actual particle density. These tasks can be completed using e2proc2d.

2.5. Particle Picking

There are a wide variety of particle picking algorithms available in the community developed over the years, and this has been an active area for over two decades[18]. EMAN1 used a reference-based picker, which works quite well, but runs a risk of model-bias when selecting particles from low contrast micrographs. EMAN2.1 currently has two algorithms, an implementation of SWARM[19] and a Gaussian based approach implemented through SPARX (but shared with EMAN2). Neither of these approaches require or are biased by projections of a previous 3-D map. For particles with high symmetry, like icosahedral viruses, there are fully automated approaches such as ETHAN[20] which can do a nearly perfect picking job even with very low contrast images. Various algorithms also vary widely in their ability to discriminate good particles from bad in cases where there is significant contamination or other non-particle objects present in the image. There is an advantage if picking is performed in EMAN2.1 or if coordinates are imported rather than importing the extracted particles. For example, box sizes can be easily altered, and per-particle movie mode alignment cannot be performed without per-particle coordinate information.

2.6. Particle-based CTF and SSNR Assessment

One of the unique features in EMAN2 is its system of particle-based data quality assessment. Standard data assessment methods in Cryo-EM, like the whole micrograph assessment provided in e2evalimage, treat any contrast in the image which produces Thon rings (oscillatory CTF pattern) as signal for purposes of image assessment. There are multiple problems with this assumption. First, if there are contrast producing agents such as detergent or other large-molecule buffer constituents, then these produce contrast across the full depth of the ice layer, which in many cases is 1000+ Å thick, producing CTF pattern averaging over a range of defocuses. At low resolution this will tend to average out to a single defocus value near the center of the ice, which is a good approximation for most purposes, however at high resolution it may cause CTF oscillations to interfere destructively.

A second problem with this assumption is that, from the perspective of the reconstruction algorithm, “signal” refers only to features present in the particle which coherently average into the 3-D reconstruction. If there are broken particles, a carbon film, or detergent producing contrast, they will be treated mathematically as noise by any 3-D reconstruction algorithm. This fact can be critical when assessing whether sufficient contrast exists within an image to proceed with image processing, and for proper relative weighting of the particles from different micrographs.

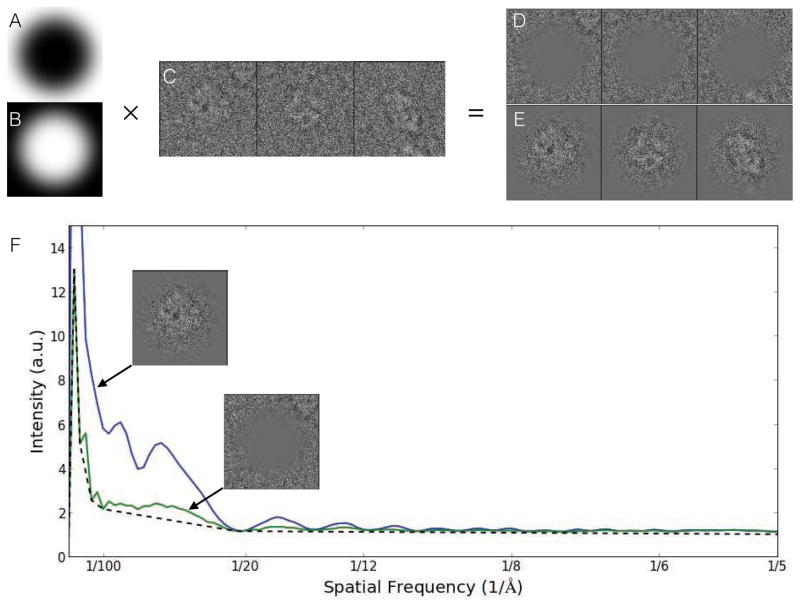
To achieve a better estimate of the true contrast provided by only the particle, we perform this quality estimate on boxed out particles, rather than entire micrographs. This assumes that the selected particles are largely good, well-centered, and that box size recommendations have been followed. The goal of this method is to isolate the contrast due to the particle (signal) from the contrast due to anything else (noise). This is accomplished using a pair of complementary real-space masks acting as windowing functions for the Fourier transform (Fig. 1). The exterior mask isolates a region of each box expected to contain background, using these regions much like the solvent blank in a spectroscopy experiment. While there will be cases, for example, where neighboring particles intrude on this region, unless the crowding is severe, this will simply cause a modest underestimation of the SSNR. The central region of each box is then expected to contain the particle of interest with background noise comparable to the background found in the other region. If the rotationally averaged power spectrum of the middle region is M(s) and of the peripheral region is N(s), then we can estimate the SSNR as (M(s)-N(s))/N(s) which is then averaged over all particles in one micrograph. M(s)-N(s) is the background subtracted power spectrum, which can be used for CTF fitting and structure factor estimation. While this SSNR estimate can be subject to minor errors due to particle crowding, or poor box size selection, it should still be far more accurate than any method based on the entire micrograph, or even particle-based methods which assume a non-oscillatory background.

Figure 1.

Per particle SSNR estimation. A. Exterior mask. B. Central mask. C. Raw unmasked particles. D. Background region. E. Particle region. F. Power spectra for each masked particle stack compared to traditional background estimate (dotted line), which underestimates noise and overestimates signal. SSNR is computed from the two masked curves. In this Beta-galactosidase example, there is only a modest difference between the two background calculations. In specimens with detergent or continuous carbon, the impact on SSNR estimation can be as much as an order of magnitude[33].

In EMAN1, the background subtraction method was based on fitting a sum of exponential decays through the zeroes of the presumed CTF. However, with counting mode detectors now becoming widely used, there is a new problem with coincidence loss at intermediate spatial frequencies. This loss appears as a significant dip in both signal and noise at intermediate resolutions. Rather than trying to build ever more complicated functional models of the expected background, we opt instead to simply measure the background as described above. Once an estimate of the defocus is available, we can also compute a simple background curve which interpolates between the zeroes of the CTF. This curve produces a stronger CTF pattern which can be used for more accurate defocus/astigmatism fitting. Since the fitting is performed directly on particle data, we can be confident that the defocus we are seeing is the average defocus of the actual particles, minimally perturbed by the defocus of any thick or thin carbon present in the image.

Aside from the background and full support for astigmatism correction, the CTF model in EMAN2.1 remains the standard weak-phase approximation used in EMAN1[21]. Phase-flipping corrections are performed as a pre-processing step, including astigmatism if present. Several different algorithms are available for performing CTF amplitude correction and final filtration of the 3-D reconstruction, as discussed in 2.11. CTF parameters are stored in the header of the phase-flipped particles for later use during processing, including the SSNR estimate, which is available as an optional weighting factor in many of the alignment algorithms and similarity metrics.

2.7. Particle Sets

It is frequently desirable to perform multiple refinements using different subsets of the full particle data set. For example, when generating a low resolution initial model, it is often useful to use the highest defocus particles, which have the highest contrast at low resolution. Later in refinement, when high resolution is being targeted, it may be desirable to compare the refinement achieved with only the very best micrographs, with the highest SSNR at high resolution, for example, with a refinement performed using all of the available data. This can help identify any possible issues with model/noise bias and improve confidence in the veracity of the final reconstruction.

EMAN2.1 includes the ability to group particles together into text files with a .lst extension, with each line in the file pointing to a particle in another file containing actual image data. EMAN will treat these .lst files as if they were actual image stack files when viewed as part of a project. Unlike STAR files used in some other packages, these files are used strictly for assembling subsets of particles, and do not contain per particle metadata, which, in EMAN2, is stored centrally for each micrograph in the info/*.json files and/or actual image file headers.

A standard naming convention is used for all particle files in the system. Particles from each micrograph are in a single stack file called, for example, particles/micro1234.hdf. Unlike EMAN1/2.0, in EMAN2.1 variants of each particle data file can be easily generated and may include different sampling and or box-size in addition to any filtration or masking the user may wish to apply as a preprocessing operation. Any such particle variants are named with a “__” (double underscore) separator, e.g. micro1234__ctf_flip.hdf, or micro1234__ctf_filtered.hdf. Each additional stack will include the same particles as the original parent file, but with arbitrary user-specified processing applied. Moreover, when sets are assembled from portions of the particle data, the set generator looks for all variants of each micrograph particle stack and forms additional sets corresponding to each version. In subsequent processing, the user can then use whichever variant they like, regardless of which portion of the data they selected. For example, down-sampled and low-pass filtered particles could be used to generate reference free class averages, and then the corresponding particles at full sampling could be extracted for further processing.

2.8. 2-D Reference Free Class-averaging

While demanding that 2-D class-averages appear like one of the projections of a 3-D map is a powerful restraint, this restriction is undesirable for initial analysis of our 2-D particle data. If, for example the particles exhibit conformational variability, then it will not be possible to construct a single 3-D map which is consistent with all of the data. For this reason, initial class-averaging is performed using reference-free, also known as unsupervised, methods.

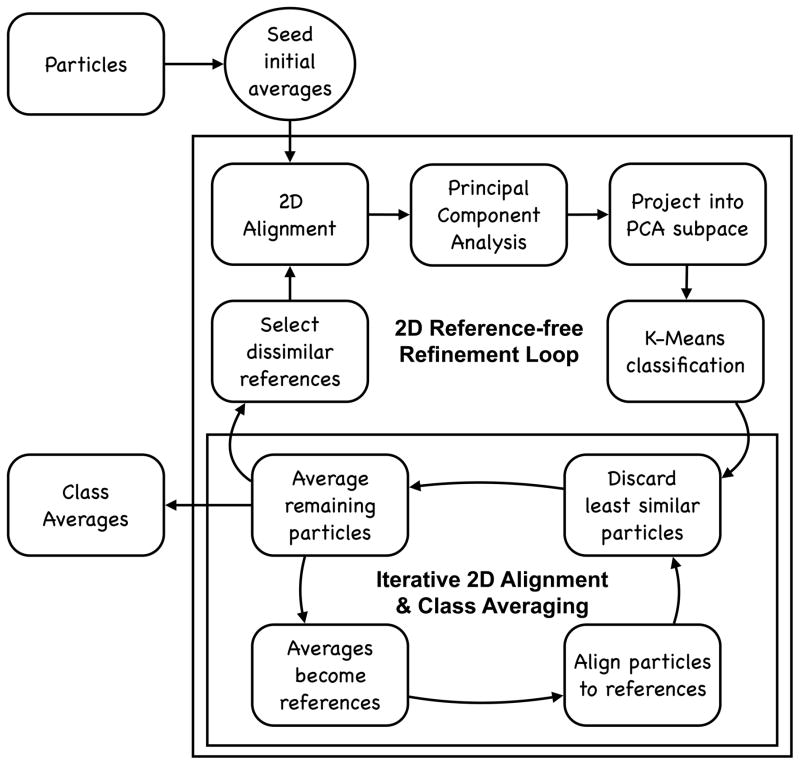
e2refine2d uses an iterative process to generate reference-free class-averages (Fig. 2), which requires an initial set of class-averages as seeds. While the process is termed ‘reference-free’ meaning no external references are provided and no 3-D projections are involved, the previous round of results is used at the beginning of each iteration to align the particles. In the first iteration, alignment references are derived from rotational-translational invariants computed for each particle. These initial ‘seed’ averages are frequently of relatively low quality, and often classes will contain poorly discriminated mixtures of populations. Much like 3-D initial model generation, the sole purpose of this step is to provide some self-consistent alignment references to bootstrap the iterative process.

Figure 2.

An overview of the iterative processing strategy implemented for reference-free class-averaging in e2refine2d.

Once seed averages have been produced, the iterative process begins. A user-selected number of the least-similar initial averages are identified and mutually aligned to one another. The particles are then aligned to each of these initial averages, using the alignment from the best-matching class-average. Note that there is no classification process occurring at this point, this is strictly alignment to try and bring similar particles into a common 2-D orientation, and is based on a small fraction of the reference averages. The similar program in EMAN1 (refine2d) made use of all of the averages as alignment references, but not only did this dramatically slow the process, but it could actually make the particle alignments less self-consistent, as similar class-averages were often in slightly different 2-D orientations.

Once the particles are aligned, PCA (principal component analysis) is performed on the full set of class-averages after mutual alignment similar to that performed on the particles. Since the averages are derived from the particles, the first few basis vectors produced by performing PCA on the averages should be quite similar to those from the full set of particles. A projection vector is then computed for each particle into the subspace defined by the first N PCA images, where N is user selectable (typically ~10). K-means classification is then applied to these particle subspace projections to classify particles into the user specified number of classes.

The classified particles are then aligned and averaged in a separate iterative process for each class-average (Fig. 2, lower loop). In this process, particles are mutually aligned and compared to the previous iteration average. The aligned particles are then averaged, excluding a fraction of the particles which were least-similar to the previous iteration average. This new average then becomes the alignment reference for the next iteration. The number of iterations, selection of alignment and averaging algorithms, and fraction of particles to exclude can all be specified by the user, though the default values are normally reasonable. The final averages then become the seeds for the next round of the overall iterative class-averaging process. These averages can then be used for initial model generation (2.10), heterogeneity analysis, assessment of final reconstructions (2.12), and other purposes.

2.9. Symmetry

When solving a structure by single particle analysis, the internal symmetry of the structure must be specified. The question of symmetry could be viewed as somewhat philosophical, as it should be obvious that at room temperature in solution, even the most rigid protein assembly will not be truly symmetric to infinite resolution. So the question under consideration is whether one should impose symmetry on the map at some specific target resolution or to answer some specific biological question.

For example, icosahedral viruses often have one vertex which differs from the others. However, if full icosahedral (5-3-2) symmetry is imposed, significantly better resolution will be achieved. Even with one different vertex, the other 11 nearly identical vertices will dominate the final average. A common approach in such situations is to impose icosahedral symmetry and refine to the highest possible resolution, then to relax the symmetry and obtain an additional lower resolution map with no symmetry, and use the pair of reconstructions for interpretation.

Another illustrative example is CCT [22]. CCT is a chaperonin, which forms a 16 mer, consisting of 2 back-to-back 8 membered rings. Unlike simple chaperonins such as GroEL or mm-cpn, where the subunits are identical, each CCT ring consists of 8 different, but highly homologous, subunits, which cannot even be structurally distinguished in the closed state until quite high resolution has been achieved. The highest symmetry that could be specified for this system is clearly D8, which might be suitable under some conditions to resolutions as high as 5–6 Å. Beyond this point one would expect the distinct structure of each subunit within a ring to begin to emerge. As the two rings are compositionally identical, it could still be argued that D1 symmetry should still be imposed. However, each subunit also binds and hydrolyses ATP, and differential binding would clearly break even this symmetry. The question is whether this symmetry breaking occurs in any single pattern which would permit multiple particles to be averaged coherently. To examine this question, symmetry would need to be completely relaxed.

When the symmetry of a particular target is unknown, there are various approaches to help elucidate this information directly from the CryoEM data. Very often a simple visual inspection of the reference-free 2-D class averages can answer the question. However, there can be cases where, due to preferred orientation, a 2-D view along the symmetric axes is simply not present sufficiently in the particle population to emerge in 2-D analysis. There can also be situations where the low resolution of the averages combined with a large interaction surface between subunits can make it difficult to observe the symmetry even along the symmetric axis. That is, the symmetric view may appear to be a smooth ring, rather than to have a discrete number of units. In short, there may be situations where the symmetry is not immediately obvious. Performing multiple refinements with different possible imposed symmetries can help resolve ambiguities, but even this may not always resolve the issue at low resolution.

Performing a refinement with no symmetry imposed is guaranteed to produce a structure which is asymmetric to the extent permitted by the data. If the structure were truly symmetric, then symmetry will be broken by model bias. When attempting to relax the symmetry of a map with only very slight structural asymmetries, EMAN2.1 refinement offers the –breaksym option, which will first search for the orientation of each particle within one asymmetric unit, and then perform a second search in that specific orientation among the different asymmetric subunits. This tends to produce much more accurate orientations in the case of near symmetry.

Given that all large biomolecules possess handedness, mirror symmetries are prohibited, leaving us with a relatively small group of possible symmetries to consider, all of which are supported in EMAN[23]: Cn symmetry is a single n-fold symmetry aligned along the Z axis; Dn symmetry is the same as Cn, but with an additional set of n 2-fold symmetry axes in the X-Y plane, one of which is positioned on the X-axis; octahedral symmetry is the symmetry of an octahedron or cube, with a set of 4-3-2 fold symmetries arranged accordingly, with the 4-fold on Z; cubic symmetry is, strangely, not the full symmetry of a cube, but includes only the 3-2 components of that higher symmetry, with the 3-fold on the Z axis; finally, icosahedral symmetry has 5-3-2 fold symmetries, with EMAN using the convention that the 5-fold axis is positioned along Z and a 2-fold on X. For icosahedral symmetry, a commonly used alignment convention is the 2-2-2 convention where orthogonal 2-fold axes are on the X,Y and Z axes. e2proc3d provides the ability to move between these orientation conventions. There is also support for constrained helical symmetry, where the symmetry specification includes a limit on the (otherwise infinite) number of repeats.

Details on all of these supported symmetries is available via the e2help command or in the documentation (http://blake.bcm.edu/emanwiki/EMAN2/Symmetry).

2.10. Initial Model Generation

High resolution 3-D refinement is also iterative, and thus requires an 3-D initial model. There are various strategies in the field for producing initial models ranging from common-lines [24], to random conical tilt [24] to stochastic hill climbing [25] to subtomogram averaging. The canonical approach for low-symmetry structures (with C or D symmetry) is embodied in e2initialmodel. This program is effectively a Monte-carlo performed using a subset of manually selected class averages (discussed in 2.8) as input. The user must identify as broad a set of different particle views as possible without including projections of other compositional or conformational states of the particle.

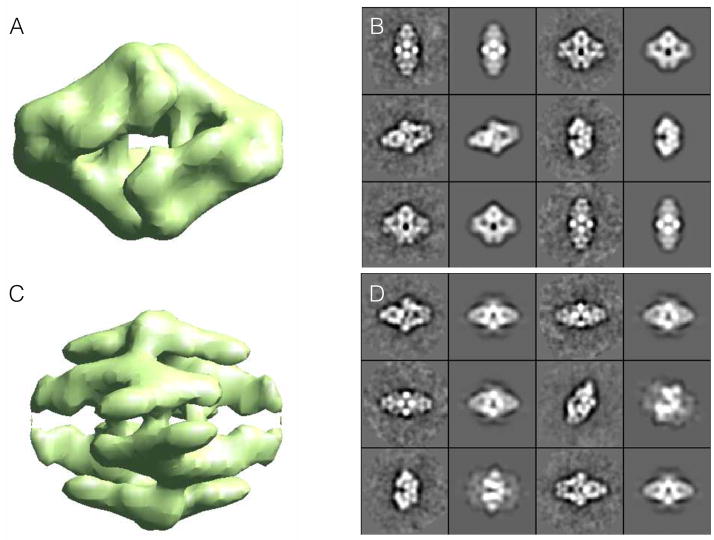
Input class-averages are then treated as if they were particles in a highly optimized form of the method used for high resolution refinement (discussed in 2.11). The class-averages are compared to a set of uniformly distributed projections of an initial model, which is used to identify the orientation of each class-average, which is then in turn used to make a new 3-D model. The initial model is produced by low-pass filtering to 2/5 Nyquist and masking to 2/3 of the box size, pure Gaussian noise, independently for each of N different starting models. The goal of this process is to produce random density patterns roughly the same size as the particle. After refining each of these random starting models, the final set of projections is compared against the class-averages as a self-consistency test, and the results are presented to the user in order of agreement between class-averages and projections (Fig 3).

Figure 3.

Reference-free class-averages used to produce an initial model using Monte-Carlo method implemented in e2initialmodel. Two of the possible 3-D starting maps are shown on the left along with corresponding class-average projection pairs for comparison on the right. For a good starting model, projections (1st and 3rd columns) and class-averages (2nd and 4th columns) should agree very well. The lower map exhibits poor agreement, so the higher ranked upper map would be used for 3-D refinement.

The 2-D images produced in *_aptcl.hdf files consist of pairs of class-average/projections for the corresponding 3-D map. It should be apparent in Fig 3 that the pairs for the better starting model (A) match quite well, whereas the pairs for the poor starting model (B) have significant disagreement. While agreement between projections and class-averages is not proof of an accurate starting model, any significant discrepancies are proof of a bad starting model. For this reason, it is not always possible to identify bad starting models using this method.

There is also a program called e2initialmodel_hisym for particles with octahedral, cubic or icosahedral symmetry. This program also requires class-averages as inputs, but uses a method similar to self-common-lines to identify the correct orientation of each class-average with respect to the symmetry axes, and generally will produce much better initial models for such high symmetry objects.

Other methods such as random conical tilt and subtomogram averaging are also available[26], but each of these methods requires following a complete workflow and collecting specialized data, which is beyond the scope of this paper.

2.11. High Resolution Refinement

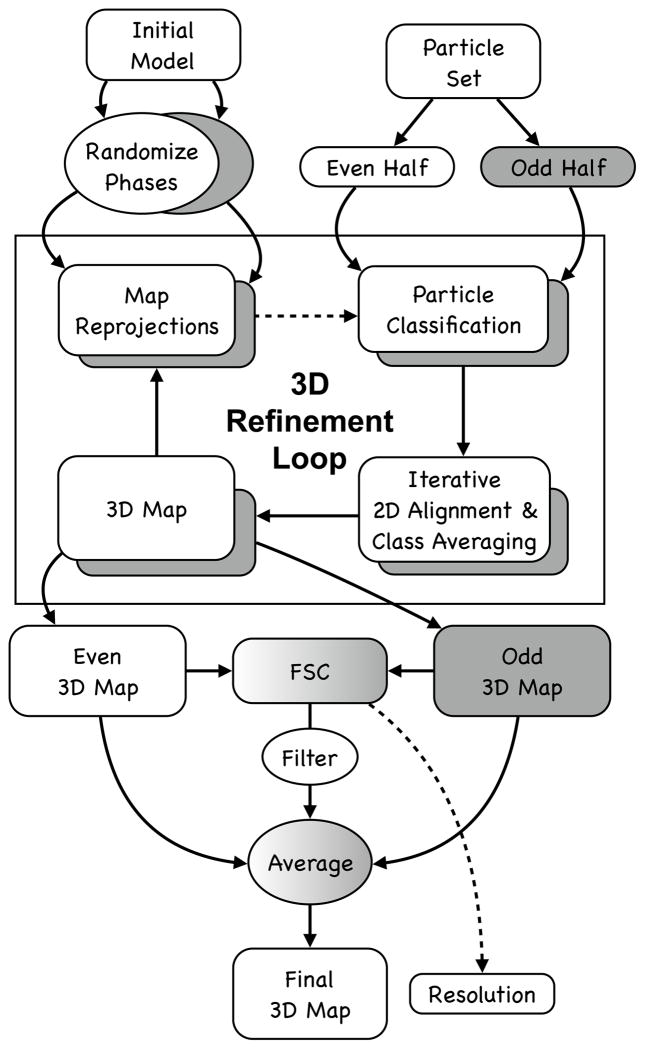
High resolution refinement in EMAN is effectively a fully automated process, using a program called e2refine_easy, once the data has gone through the preprocessing steps above. The internal process used for refinement is outlined in Fig. 4. While the user does not need to understand the details of this process to make use of the program and produce a high resolution reconstruction, understanding the basic process makes it possible to examine some of the intermediate files generated during processing, which can be useful when diagnosing problems should they occur. It should also be mentioned that each time e2refine_easy is run, producing a new refine_XX folder, a refine_XX/report/index.html file is also created with detailed information on all of the specific parameters used in any given reconstruction based on the heuristics built in to e2refine_easy. After completing a refinement, the first thing the user should do is look at this report file.

Figure 4.

Overview of automatic refinement process described in the text and implemented in e2refine_easy. The process begins by splitting a user specified set of particles into even (white) and odd (grey) sets. Following the “gold standard” protocol, the initial model is phase randomized twice at resolutions higher than ~1.5x the target resolution. The two perturbed starting maps are then refined independently against the even and odd halves of the data. Iterative refinement begins by reprojecting the initial map and classifying particles according to their similarity to these projections. Classified particles are then iteratively aligned and averaged as shown in Fig. 2 (lower). The resulting class averages are then reconstructed in Fourier space to form a new 3D map, which becomes the starting map for the next iterative cycle. At the end of a user-specified number of iterations (typically 3–5), the process terminates. A Fourier shell correlation is computed between all pairs of maps produced from refining the even and odd subsets to assess resolution at each iteration and monitor convergence. In the final step, the even and odd maps are averaged, CTF amplitudes are corrected and the FSC is used to create a Wiener filter, ensuring that only the consistent portions of the separate refinements are visualized in the final averaged map.

Technically, e2refine_easy has ~80 different command-line options available, which permit very detailed control of the algorithms used for every purpose during the refinement. However, almost none of these are intended for routine use, and only a small handful are presented to the user via the e2projectmanager graphical interface. If needed, the remainder must be manually added to the command-line. The user generally specifies symmetry, target resolution and a refinement ‘speed’, then e2refine_easy uses a complex set of heuristics based on these values and all of the other information available about the particle data to select values for the other parameters automatically. The speed parameter controls the angular sampling and a few other parameters. The default speed of 5 was computed to provide sufficient sampling to achieve the target resolution with a comfortable margin. Smaller speed values increase angular sampling past this point, compensated by including each particle in multiple class-averages. This makes the refinement take considerably longer to run, but may produce slight resolution increases and slightly improve the smoothness of the map. The specific values of all parameters are available to the user after refinement in a text file called 0_refine_parms.json.

EMAN2 is a modular system, and has a wide range of algorithms for each task in the system. For example, there are over 20 different algorithms which can be used for 2-D alignment, and most of these support specification of an image similarity metric to define mathematically what optimal alignment is. There are 14 choices available for this (3 of which are functionally equivalent to a dot product between images). Through extensive testing over years of development, we have identified which algorithms tend to produce the best results for 3-D refinement in different systems and target resolutions, and these decisions are embedded in the system of heuristics in e2refine_easy. It should be noted that this means that EMAN2 is not intrinsically a “correlation-based refinement”. Indeed, correlation is used as the similarity metric for determining 3-D orientation only for very coarse refinements at low resolution. For higher resolution refinements, the heuristics will normally select a Fourier ring correlation (FRC) metric, with SSNR weighting and a resolution cutoff. For many data sets, this selection of algorithm has little real impact on the final structure, and most reasonable algorithm combinations would produce near identical results.

However, it is possible to find simple examples where commonly used similarity metrics will produce suboptimal results. This is the sort of situation EMAN2’s heruistics are designed to avoid. One of the first macromolecules to inspire development of alternative similarity metrics in EMAN was GroEL. If correlation coefficient is used to determine the orientation of perfect side views of GroEL, but the envelope function of the data is narrower than the envelope function of the 3-D model used as a reference, the extra “blur” of the particles will cause them to match slightly tilted projections better than true side-views. This, in turn, produces a slightly distorted 3-D map, which will not correct itself through iterative refinement. If, however, the data and model are compared using filter-insensitive metrics such as FRC, this problem does not arise, and the correct orientations are found.

In addition to the images themselves, obtaining a 3-D reconstruction requires the CTF/MTF for each image, which we have already determined in step 2.6 above, and the orientation of each particle. Additionally, EMAN2.1 includes an additional step where particles in nearly the same orientation are mutually aligned and averaged in 2-D iteratively prior to 3-D reconstruction. This step permits e2refine_easy to converge typically within 3–5 iterations, whereas the iterative reconstructions in many software packages which simply determine the orientation of each particle and reconstruct immediately can require as much as 50–100 iterations to converge.

When iteratively refining in 3-D, model bias can be a significant issue. The iterative class-averaging process used in EMAN begins with the same projections other software packages use to determine orientation, but then align the particles such that they are self-consistent with each other, rather than with the reference which was used to classify them. This initial step allows the 2-D averages to rapidly shed any initial model bias, and permits the overall 3-D refinement process to converge very quickly. The only negative side effect is that, near convergence, the particles are being aligned to class-averages rather than 3-D projections, and the averages have higher noise levels than the final reconstruction, which was based on all of the data rather than data only in one particular orientation. For this reason, e2refine_easy includes heuristics which gradually reduce the iterative class-averaging process to achieve rapid convergence and the best possible resolution in the final reconstruction. The iterative class-averaging process is identical to the process described above used within e2refine2d (Fig. 2, bottom).

E2refine_easy performs all reconstructions using “gold standard” methods (Fig. 4). In this approach, the particle data is split into even/odd halves at the very beginning of iterative refinement, and the initial model is perturbed independently for each refinement by phase-randomizing at high resolution. This ensures that the starting models are significantly different from one another, and that if high resolution convergence is achieved independently in the even and odd halves that this did not result from any model bias. For symmetries which do not constrain the orientation or center of the 3-D maps, the odd map is oriented to match the even map at the end of each iteration, to make the FSC computed in each iteration meaningful. It should be clear that this approach does not eliminate the bias itself, but only prevents the bias from influencing the resolution determined by FSC. This is mitigated by iterative class-averaging which can effectively eliminate significant model bias.

E2refine_easy also supports the concept of using one version of the particles for alignment, and a different version for the actual reconstruction. This is most commonly used with movie-mode direct detector images for which there remain a range of different theories about the best strategy for achieving high resolution when using such images. One method involves making a high-dose average and a low-dose average of each particle. The high-dose average is then used for alignment, all the way through class-averaging, and the low-dose average is used for the final average after alignment. Another independent method involves performing damage-weighted averaging of all frames in a dose series, where only presumed minimally damaged information is included in the particles. In this strategy only one version of each particle is required, as this average contains both optimal low resolution contrast as well as high resolution detail. The best method remains a topic of active research.

A typical e2refine_easy strategy begins with a quick ~5 iteration refinement using downsampled and lowpass filtered particles to improve the starting model and achieve an intermediate resolution (10–20 Å) map. If this refinement doesn’t converge after 3–4 iterations, it may imply that the initial model was suboptimal. In this situation either additional iterations can be run to try and converge to the correct low resolution structure, or another attempt can be made at initial model generation. After this, the fully sampled unfiltered data can be used, typically with speed set to 5, and refined for ~5 iterations (to ensure convergence). Finally, a third refinement is typically run with speed set to 1 for ~3 iterations, to see if any final resolution improvements can be made.

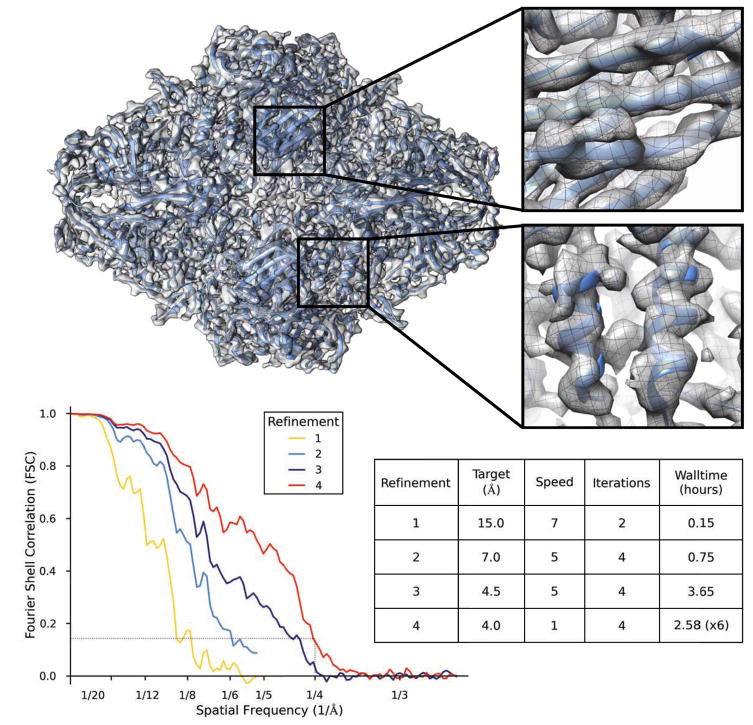
Figure 5 shows the result of the complete analysis process described above, following the instructions for one of our single particle reconstruction tutorials (http://blake.bcm.edu/emanwiki/Ws2015). This tutorial makes use of a small subset of the Beta Galactosidase [27] data from the 2015 CryoEM Map Challenge sponsored by EMDatabank.org. This tutorial set is a small fraction of the original data, downsampled for speed, and is thus not able to achieve the full resolution in the original publication, but the refinement can be completed quickly to near 4 Å resolution on a typical desktop or laptop computer. We extracted 4348 particles (of about 30,000 total particles), and downsampled them to 1.28 Å/pixel. This data set includes a significant number of “particles” which are actually ice contamination, and the tutorial includes instructions for identifying and eliminating these. The final speed=1 refinement to push the resolution past 4 Å can require a somewhat larger computer than a typical laptop, or a somewhat longer run time, but most laptops can get very close to this resolution in the target 24 hour period. The human effort involved in this process should be only a few hours, even for a novice.

Figure 5.

Refinement results of the Beta-galactosidase test data subset from the EMAN2.1 tutorial. e2refine_easy was run 4 times sequentially in this test, and the final FSC curves from each run are combined in one plot. The first 2 runs used downsampled data for speed, so the FSC curves do not extend to as high a resolution. The inset shows that beta-strands can be clearly resolved and alpha helices have appropriate shape. Equivalent results could have been achieved in a single run, but the intermediate results are useful in the context of the tutorial, and require less compute time. The table describes the basic parameters and wall-clock time of each refinement run. The final run was performed on a Linux cluster using 96 cores (~250 CPU-hr).

2.12. Assessing Final Map

Once a final reconstruction has been achieved, it remains to turn this map into useful biochemical/biophysical information. If very high resolution has been achieved (2–5 Å) it may be possible to trace the protein backbone, and even perform complete model building based solely on the CyroEM data[28–30]. At subnanometer resolution, secondary structure should be sufficiently visible to at least confirm that the structure is largely correct. At lower resolutions, additional steps, perhaps even experiments, must be performed to ensure the veracity of the reconstruction[31]. In cases where a model is constructed for the map, or is available from other experimental methods such as crystallography, it is critical that a map-vs-model FSC be computed to assess the resolution at which the model is an accurate representation of the data. When this is combined with the standard model validation methods required in crystallography[32], fairly strong statements about the veracity and resolution of the CryoEM map can be made.

3. Conclusions

There are a wide range of tools available in the community for performing single particle reconstruction as well as related cryoEM image processing tasks. We strive to ensure that EMAN2.1 produces the best possible structures as well as being among the easiest to use and most computationally efficient packages available. However, there are many biomolecular systems in single particle analysis in which flexibility or compositional variability play a key role. Crystallography, by its nature, is ill-suited to collecting data on heterogeneous molecular populations. Single particle analysis data collection, on the other hand, produces solution-like images natively. This shifts the problem of resolving heterogeneity to being computational rather than experimental. In our experience, despite using similar high-level concepts, handling of heterogeneous data is where the various available software packages differ most from one another. While a highly homogenous data set collected to high resolution will generally produce near-identical structures in any of the standard available software packages, in the presence of heterogeneity, different packages will take this into account in different ways, producing measurably different results. This variation can exist at any resolution level, depending on the biophysical properties of the particle under study.

Due to this, it can be very useful to have the ability to cross-compare results from EMAN2.1 with other software packages. We make this a simple process for several software packages through the e2refinetorelion3d, e2refinetofrealign, e2reliontoeman, e2emx and e2import programs. When different results are obtained among two or more packages it is critical to carefully examine each result, and even look at some of the internal validations provided by each software. For example, in EMAN2.1, one might compare 2-D reference-free class-averages with 2-D reference based class-averages with reprojections of the 3-D map, to see if any disagreements match inter-software differences.

The Cryo-EM field has now reached a level of maturity where well-behaved molecular systems studied on high quality microscopes and detectors can readily produce reconstructions in the 3–5 Å resolution range, as demonstrated by the nearly 100 structures published at this resolution so far in 2015. While some of the reason for the even larger number of lower resolution structures published in the same time can be attributed to the lower end equipment many practitioners are still limited to, the larger factor is almost certainly specimen purification and sample preparation, which remain the largest barriers to routine high resolution studies in the field. Some of these issues can be solved by software, and analysis of heterogeneous data is probably the most active area for software development at this time. Indeed, resolution-limiting specimen variability can be used as an opportunity to study solution behavior of macromolecules rather than viewing this as a resolution-limiting factor. In addition to robust tools for high resolution refinement, EMAN2.1 also has a range of tools available for this type of analysis, as described in additional tutorials available on our website. For well behaved specimens, however, it should be possible to rapidly achieve near specimen-limited resolutions using the straightforward methods we have described.