Sample Size Calculations for Micro-randomized Trials in mHealth

Abstract

The use and development of mobile interventions are experiencing rapid growth. In “just-in-time” mobile interventions, treatments are provided via a mobile device and they are intended to help an individual make healthy decisions “in the moment,” and thus have a proximal, near future impact. Currently the development of mobile interventions is proceeding at a much faster pace than that of associated data science methods. A first step toward developing data-based methods is to provide an experimental design for testing the proximal effects of these just-in-time treatments. In this paper, we propose a “micro-randomized” trial design for this purpose. In a micro-randomized trial, treatments are sequentially randomized throughout the conduct of the study, with the result that each participant may be randomized at the 100s or 1000s of occasions at which a treatment might be provided. Further, we develop a test statistic for assessing the proximal effect of a treatment as well as an associated sample size calculator. We conduct simulation evaluations of the sample size calculator in various settings. Rules of thumb that might be used in designing a micro-randomized trial are discussed. This work is motivated by our collaboration on the HeartSteps mobile application designed to increase physical activity.

1. Introduction

The use and development of mobile interventions are experiencing rapid growth. Mobile interventions are used across the health fields and include treatments to improve HIV medication adherence [1, 2], to increase activity [3], supplement counseling/pharmacotherapy in treatment for substance use [4, 5], reinforce abstinence in addictions [6, 7] and to support recovery from alcohol dependence [8, 9]. Mobile interventions for adherence to anti-retroviral therapy and smoking cessation have shown sufficient effectiveness and replicability in trials and have been recommended for inclusion in health services [10].

However, as Nilsen et al. [11] state, “In fact, the development of mHealth technologies is currently progressing at a much faster pace than the science to evaluate their validity and efficacy, introducing the risk that ineffective or even potentially harmful or iatrogenic applications will be implemented.” Indeed reviews, while reporting preliminary evidence of effectiveness, call for more programmatic, data-based approaches to constructing mobile interventions [10, 12]. In particular, these reviews call for research that focuses on data-informed development of these complex multi-component interventions prior to their evaluation in standard randomized controlled trials. But methods for using data to inform the design and evaluation of adaptive mobile interventions have lagged behind the use and deployment of these interventions [11, 13, 14].

Many mobile interventions are designed to be “just-in-time” interventions, meaning that they intend to provide treatments that help an individual make healthy decisions in the moment, such as engaging in a desirable behavior (e.g., taking a medication on time) or effectively coping with a stressful situation. As such, mobile interventions are often intended to have proximal, near-term effects. A first approach toward developing data-based methods for evaluation of mobile health interventions is to provide an experimental design for testing the proximal effects of the treatments. This paper proposes a micro-randomized trial design for this purpose. In a micro-randomized trial, treatments are sequentially randomized throughout the conduct of the study, with the result that each participant may be randomized at the hundreds or thousands of occasions at which a treatment might be provided. This repeated randomization of treatments under investigation enables causal modeling of each treatment’s time-varying proximal effect as well as modeling of time-varying effect moderation. Thus, the micro-randomized trial can be seen as a first experimental step in the development of effective mobile interventions that are composed of sequences of treatments. We propose to size the trial to detect the proximal main effect of the treatments. This is akin to the use of factorial designs for use in constructing multi-component interventions. In these factorial designs [15, 16], a first analysis often involves testing if the main effect of each treatment is equal to 0.

This work is motivated by our collaboration on the HeartSteps mobile application for increasing physical activity, which we will use to illustrate our discussion. One of the treatments in HeartSteps is suggestions for physical activity which are tailored to the person’s current context. HeartSteps can deliver these suggestions at any of the five time intervals during the day, which correspond roughly to morning commute, mid-day, mid-afternoon, evening commute, and post-dinner times. When a suggestion is delivered, the user’s phone plays a notification sound, vibrates and lights up, and the suggestion is displayed on the lock screen of the phone. These suggestions encourage activity in the current context and are intended to have an effect (getting a person to walk) within the next hour.

In the following section, we introduce the micro-randomized trial design. In section 3 we precisely define the proximal main effect of a treatment, using the language of potential outcomes. We develop the test statistic for assessing the proximal effect of a treatment as well as an associated sample size calculator in section 4 and 5. Next we provide simulation evaluation of the sample size calculator. We end, in Section 7, with a discussion.

2. Micro-Randomized Trial

In general an individual’s longitudinal data, recorded via mobile devices that sense and provide treatments, can be written as

$$\{S_0,S_1,A_1,S_2,A_2,\dots ,S_t,A_t,\dots ,S_T,A_T,S_{T+1}\}$$

where, t indexes decision times, S₀ is a vector of baseline information (gender, ethnicity, etc.) and S_t (t ≥ 1) is information collected between time t −1 and t (e.g. summary measures of recent activity levels, engagement, and burden; day of week; weather; busyness indicated by smart phone calendar, etc.). The treatment at time t is denoted by A_t; throughout this paper we consider binary options for the treatments (e.g., the treatment is on or off). The proximal response, denoted by Y_t+1, is a known function of {S_t, A_t, S_t+1}. Here we assume that the longitudinal data are independent and identically distributed across N individuals. Note that this assumption would be violated, if for example, some of the treatments are used to enhance social support between individuals in the study.

In HeartSteps, data (S_t) is collected both passively via sensors and via participant self-report. Each participant is provided a “Jawbone” band, worn at the wrist, which collects daily step count and the amount of sleep the user had the previous night. Furthermore sensors on the phone are used to collect a variety of information at each of the 5 time points during the day, including the time-stamp, location, busyness of planned activities on the phone calendar and other activity on the phone. Each evening, self-report data is collected including utility and burden ratings. The proximal response, Y_t+1, for activity suggestions is the step count in the hour following time t.

A decision time is a point in time at which—based on participant’s current state, past behavior, or current context— treatment may need to be delivered. Decision times vary by the nature of the intervention component. In HeartSteps, the decision times for activity suggestions are 5 times per day over the 42 day study duration. For an alcohol-recovery application that provides an intervention when an individual goes within 10 feet of a high risk location (e.g. a liquor store), decision points might be every 1 minute, the frequency at which the application would get the person’s current location and assess whether she is close to a high-risk location. In a long-term study of an intervention for multiple health behaviors, the decision points might be weekly or monthly at which times, decisions are made regarding whether to change the focus from one behavior (e.g., physical activity) to another (e.g., diet). Finally, in many studies there is an option for an individual to press a “panic” button, indicating the need for help; for such interventions, decision times correspond to times at which the panic button is pressed.

A micro-randomized trial is a trial in which at each decision time t, participants are randomized to a treatment option, denoted by A_t. Treatment options may correspond to whether or not a treatment is provided at a decision time; for example in HeartSteps, whether or not the individual is provided a lock-screen activity suggestion. Or treatment options may be alternative types of treatment that can be provided at the same decision time; for example, a daily step goal treatment might have two options, a fixed 10,000-steps-a-day goal or an adaptive goal based on the user’s activity level on the previous day. Considerations of treatment burden often imply that the randomization will not be uniform. For example in HeartSteps, the randomization probability is 0.4, so that, if an individual is always available, on average 2 lock-screen activity messages are delivered per day.

In designing, that is, determining the sample size for, a micro-randomized trial we focus on the reduced longitudinal data

$$\{S_0,I_1,A_1,Y_2,I_2,A_2,Y_3,\dots ,I_t,A_t,Y_{t+1},\dots ,I_T,A_T,Y_{T+1}\}.$$

The variable, I_t is an “availability” indicator. The availability indicator is coded as I_t = 1 if the individual is available for treatment and I_t = 0 otherwise. At some decision times feasibility, ethics or burden considerations mean that the individual is unavailable for treatment and thus A_t should not be delivered. Consider again HeartSteps: if sensors indicate that the individual is likely driving a car or the individual is currently walking, then the lock-screen activity message should not be sent. Other examples of when individuals are unavailable for treatment include: in the alcohol recovery setting, an “warning” treatment would only be potentially provided when sensors indicate that the individual is within 10 feet of a high risk location or a treatment might only be provided if the individual reports a high level of craving. If the application has a panic button, then only in an x second interval in which the panic button is pressed is it appropriate to provide “panic button” treatments. Individuals may be unavailable for treatment by choice. For example, the HeartSteps application permits the individual to turn off the lock-screen activity messages; this option is considered critical to maintaining participant buy-in and engagement with HeartSteps. After viewing the lock-screen activity message, the individual has the option of turning off the lock-screen messages for 4, 8 or 12 hours. After the specified time interval, the delivery of lock-screen messages automatically turns on again. To summarize, the availability indicator at time t is the indicator for the subpopulation at time t among which we are interested in assessing the proximal main effect of the treatment; we are uninterested in assessing the proximal main effect of a treatment among individuals for whom it is unethical to provide treatment or for whom it makes no scientific sense to provide treatment or among those who refuse to be provided a treatment.

3. Proximal Main Effect of a Treatment

As discussed above, treatments in mobile health interventions are often designed so as to have a proximal effect (e.g., increase activity in near future, help an individual manage current cravings for drugs or food, take medications on schedule, etc.). As a result, a first question in developing a mobile health intervention is whether the treatments have a proximal effect. Here we develop sample size formulae that guarantee a stated power to detect the proximal effect of a treatment. In particular we aim to test if the proximal main effect is zero.

To define the proximal main effect of a treatment, we use potential outcomes [17, 18, 19]. Our use of potential outcome notation is slightly more complicated than usual because treatment can only be provided when an individual is available. As a result, we index the potential outcomes by decision rules that incorporate availability. In particular define d(a, i) for a ∈ {0,1}, i ∈ {0,1} by d(a,0) =“unavailable-do nothing” and d(a,1) = a. Then for each a₁ ∈𝒜₁ = {0,1}, define D₁(a₁) = d(a₁, I₁). Then we denote the potential proximal responses following decision time 1 by { $Y_2^{D_1(1)},Y_2^{D_1(0)}$} and denote the potential availability indicators at decision time 2 by { $I_2^{D_1(1)},I_2^{D_1(0)}$}. Next for each ā₂ = (a₁,a₂) with a₁,a₂ ∈ {0,1}, define $D_2({\overline{a}}_2)=d(a_2,I_2^{D_1(a_1)})$. Define $\overline{D_2({\overline{a}}_2)}=(D_1(a_1),D_2({\overline{a}}_2))$. A potential proximal response following decision time 2 and corresponding to ā₂ is $Y_3^{\overline{D_2({\overline{a}}_2)}}$ and a potential availability indicator at decision time 3 is $I_3^{\overline{D_2({\overline{a}}_2)}}$. Similarly, for each ā_t = (a₁, …,a_t) ∈ 𝒜_t = {(a₁, …,a_t)|a_i ∈ {0,1}, i = 1, …, t}, define $D_t({\overline{a}}_t)=d(a_t,I_t^{\overline{D_{t-1}({\overline{a}}_{t-1})}})$ and $\overline{D_t({\overline{a}}_t)}=(D_1(a_1),\dots ,D_t({\overline{a}}_t))$. For each ā_t = (a₁, …,a_t) ∈ 𝒜_t, the potential proximal response is $Y_t^{\overline{D_{t-1}({\overline{a}}_{t-1})}}$ (following decision time t −1) and potential availability indicator is $I_t^{\overline{D_{t-1}({\overline{a}}_{t-1})}}$ at decision time t.

We define the proximal main effect of a treatment at time t among available individuals by:

$$\beta (t)=E\left(Y_{t+1}^{\overline{D_t({\overline{A}}_{t-1},1)}}-Y_{t+1}^{\overline{D_t({\overline{A}}_{t-1},0)}}|I_t^{\overline{D_{t-1}({\overline{A}}_{t-1})}}=1\right)$$

where the expectation is taken with respect to the distribution of the potential outcomes and randomization in Ā_t−1. This proximal effect is conditional in that the effect of treatment at time t is defined for only individuals available for treatment at time t, that is, $I_t^{\overline{D_{t-1}({\overline{A}}_{t-1})}}=1$. This proximal effect is a main effect in that the effect is marginal over any effects of Ā_t−1. The former conditional aspect of the definition is related to the concept of viable or feasible dynamic treatment regimes [20, 21] in which one assesses only the causal effect of treatments that can actually be provided.

Consider the proximal main effect, β(t), as t varies across time. β(t) may vary across time for a variety of reasons. To see this consider the case of HeartSteps. Here β(t) might initially increase with increasing t as participants learn and practice the activities suggested on the lock-screen. For larger t one might expect to see decreasing or flat β(t) due to habituation (participants begin to, at least partially, ignore the messages). This time variation in β(t) can be attributed to both the immediate effect of a lock-screen activity message as well as interactions between the past lock-screen activity messages and the present activity message; the time variation occurs at least partially due to the marginal character of β(t). Alternately the conditional definition of β(t) means that the effect is only defined among the population of individuals who are available at decision time t. Changes in this population may cause changes in β(t) across time. Again consider HeartSteps. At earlier time points, participants may be highly engaged, yet have not developed habits that in various ways increase their activity, thus most participants will be available. However as time progresses, some participants may develop sufficiently positive activity habits or anticipate activity suggestions, thus at later decision times these participants may be already active and thus unavailable to receive a suggestion. Other participants may become increasing disengaged and repeatedly turn off the lock-screen activity messages; these participants are also unavailable. Thus as time progresses, β(t) may vary due to the subpopulation of participants among whom it is appropriate to assess the effect of the lock-screen activity messages.

Our main objective in determining the sample size will be to assure sufficient power to detect alternatives to the null hypothesis of no proximal main effect, H₀: β(t) = 0, t = 1, … T for a trial with T decision points (if β(t) is nonzero then for the population available at decision time t, there is a proximal effect). The proposed test will be focused on detecting smooth, i.e., continuous in t, alternatives to this null hypothesis.

To express β(t) in terms of the observed data distribution, we assume consistency [18, 19]. This assumption is that for each t, the observed Y_t and observed I_t equal the corresponding potential outcomes, $Y_t^{\overline{D_{t-1}({\overline{a}}_{t-1})}},I_t^{\overline{D_{t-1}({\overline{a}}_{t-1})}}$ whenever Ā_t−1 = ā_t−1. This assumption may be violated if some of the treatments promote social linkages between participants, for example, to enhance social/emotional support or to compete in mobile games. In these cases it would be more appropriate to additionally index each individual’s potential outcomes by other participants’ treatments. The micro-randomization plus the consistency assumption implies that the proximal main effect of treatment at time t among available individuals, β(t) can be written as,

$$\begin{array}{l}\beta (t)=E[Y_{t+1}^{\overline{D_t({\overline{A}}_{t-1},1)}}\mid I_t^{\overline{D_{t-1}({\overline{A}}_{t-1})}}=1]-E[Y_{t+1}^{\overline{D_t({\overline{A}}_{t-1},0)}}\mid I_t^{\overline{D_{t-1}({\overline{A}}_{t-1})}}=1]\\ =E[Y_{t+1}^{\overline{D_t({\overline{A}}_{t-1},1)}}\mid I_t^{\overline{D_{t-1}({\overline{A}}_{t-1})}}=1,A_t=1]-E[Y_{t+1}^{\overline{D_t({\overline{A}}_{t-1},0)}}\mid I_t^{\overline{D_{t-1}({\overline{A}}_{t-1})}}=1,A_t=0]\\ =E[Y_{t+1}^{\overline{D_t({\overline{A}}_t)}}\mid I_t^{\overline{D_{t-1}({\overline{A}}_{t-1})}}=1,A_t=1]-E[Y_{t+1}^{\overline{D_t({\overline{A}}_t)}}\mid I_t^{\overline{D_{t-1}({\overline{A}}_{t-1})}}=1,A_t=0]\\ =E[Y_{t+1}\mid I_t=1,A_t=1]-E[Y_{t+1}\mid I_t=1,A_t=0]\end{array}$$

where the second equality follows from the randomization of the A_t’s and the last equality follows from the consistency assumption.

4. Test Statistic

Our sample size formula is based on a test statistic for use in testing H₀ : β(t) = 0, t = 1, … T against a scientifically plausible alternative. This alternative should be formed based on conversations with domain experts. Here we construct a test statistic to detect alternatives that are, at least approximately, linear in a vector parameter, β, that is, alternatives of the form $Z_t^{\prime }\beta$, where the p ×1 vector, Z_t, is a function of t and covariates that are unaffected by treatment such as time of day or day of week. In the case of HeartSteps, a plausible alternative is quadratic:

$$Z_t^{\prime }\beta =(1,\lfloor \frac{t-1}{5}\rfloor ,{(\lfloor \frac{t-1}{5}\rfloor )}^2)\beta$$ (1)

where β = (β₁,β₂,β₃)′ (p = 3). Recall that in HeartSteps there are 5 decision times per day; $\lfloor \frac{t-1}{5}\rfloor$ translates decision times t to days. This rather simplistic parametrization marginalizes across the day and treats the weekends and weekdays similarly.

We propose to use the alternate, ${\mathrm{H}}_1:\beta (t)=Z_t^{\prime }\beta$, t = 1, …, T to construct the test statistic. We base the test statistic on the estimator of β in a least squares fit of a working model. A simple working model based on the alternative is:

$$E[Y_{t+1}\mid I_t=1,A_t]=B_t^{\prime }\alpha +(A_t-{\rho }_t)Z_t^{\prime }\beta$$ (2)

over all t ∈ {1, …, T}, where ρ_t is the known randomization probability (P[A_t = 1] = ρ_t) and the q ×1 vector B_t is a function of t and covariates that are unaffected by treatment such as time of day or day of week. Note that A_t is centered by subtracting off the randomization probability; thus the working model for α(t) = E[Y_t+1|I_t = 1] is $B_t^{\prime }\alpha$. The estimators α̂, β̂ minimize the least squares error:

$${\mathbb{P}}_N\left\{\sum _{t=1}^T{I}_t{(Y_{t+1}-B_t^{\prime }\alpha -(A_t-{\rho }_t)Z_t^{\prime }\beta )}^2\right\}$$ (3)

where ℙ_N{f (X)}is defined as the average of f (X) over the sample.

Note that from a technical perspective, minimizing the least squares criterion, (3), is reminiscent of a GEE analysis [22] with identity link function and a working correlation matrix equal to the identity. Thus it is natural to consider a non-identity working correlation matrix as is common in GEE. This, however, is problematic from a causal inference perspective. To see this suppose that the true conditional expectation is in fact $E[Y_{t+1}\mid I_t=1,A_t]=B_t^{\prime }{\alpha }^{\ast }+(A_t-{\rho }_t)Z_t^{\prime }{\beta }^{\ast }$, that is, the causal parameter, β(t) is equal to $Z_t^{\prime }{\beta }^{\ast }$. Further suppose that the working correlation matrix has off-diagonal elements and that we estimate β^* by minimizing the weighted (by the inverse of the working correlation matrix) least squares criterion. In this case the resulting estimating equations include sums of terms such as $I_t(Y_{t+1}-B_t^{\prime }\alpha -(A_t-{\rho }_t)Z_t^{\prime }\beta )I_s(A_s-{\rho }_t)Z_s$ for t > s. Unfortunately, both availability at time t, I_t, as well as Y_t+1 may be affected by treatment in the past (in particular, A_s), thus absent strong assumptions $E[I_t(Y_{t+1}-B_t^{\prime }{\alpha }^{\ast }-(A_t-{\rho }_t)Z_t^{\prime }{\beta }^{\ast })I_s(A_s-{\rho }_t)]$ is unlikely to be 0. Recall that a minimal condition for consistency of estimators of (α^*,β^*) is that the estimating equations have expectation 0, thus absent further assumptions, the estimators derived from the weighted least squares criterion are likely biased. Another possibility is to include a time-varying variance term in the least squares criterion, that is the tth entry in (3) might be weighted by a ${\sigma }_t^{-2}$. This would be useful in the data analysis, however for sample size calculations, values of these variances are unlikely to be available. Thus for simplicity we use the unweighted least squares criterion in (3).

Assume that the matrices $Q={\sum }_{t=1}^{T}E[I_t]{\rho }_t(1-{\rho }_t)Z_t{Z}_t^{\prime }$ and ${\sum }_{t=1}^{T}E[I_t]B_t{B}_t^{\prime }$ are invertible. The least squares estimators, α̂, β̂ are consistent estimators of

$$\stackrel{\sim }{\alpha }={\left(\sum _{t=1}^{T}E[I_t]B_t{B}_t^{\prime }\right)}^{-1}\sum _{t=1}^{T}E[I_t]\alpha (t)B_t$$ (4)

and

$$\stackrel{\sim }{\beta }={\left(\sum _{t=1}^{T}E[I_t]{\rho }_t(1-{\rho }_t)Z_t{Z}_t^{\prime }\right)}^{-1}\sum _{t=1}^{T}E[I_t]{\rho }_t(1-{\rho }_t)\beta (t)Z_t$$ (5)

respectively. Furthermore if β(t) is in fact equal to $Z_t^{\prime }\beta$ for some β, then $Z_t^{\prime }\stackrel{\sim }{\beta }=\beta (t)$. This is the case even if $E[Y_{t+1}\mid I_t=1]\ne B_t^{\prime }\stackrel{\sim }{\alpha }$. In the appendix (Lemma 1), we prove these results and also show that, under moment conditions, $\sqrt{N}(\widehat{\beta }-\stackrel{\sim }{\beta })$ is asymptotically normal with mean 0 and variance Σ_β =Q⁻¹WQ⁻¹ where,

$$W=E\left[\left(\sum _{t=1}^T{\stackrel{\sim }{\epsilon }}_t{I}_t(A_t-{\rho }_t)Z_t\right)\times \left(\sum _{t=1}^T{\stackrel{\sim }{\epsilon }}_t{I}_t(A_t-{\rho }_t)Z_t^{\prime }\right)\right]$$

and ${\stackrel{\sim }{\epsilon }}_t=Y_{t+1}-I_t{B}_t^{\prime }\stackrel{\sim }{\alpha }-(A_t-{\rho }_t)I_t{Z}_t^{\prime }\stackrel{\sim }{\beta }$. To test the null hypothesis H₀ : β(t) = 0, t = 1, …, T, one can use a test statistic based on the alternative, e.g.

$$N{\widehat{\beta }}^{\prime }{\widehat{\mathrm{\sum }}}_{\beta }^{-1}\widehat{\beta }$$ (6)

where Σ̂_β = Q̂⁻¹Ŵ Q̂⁻¹ and Q̂ and Ŵ are plug in estimators. Note that this test statistic results from a GEE analysis with identity link function and a working correlation matrix equal to the identity matrix for which sample size formulae have been developed [23]. We build on this work as follows. As Tu et al. [23] discuss, under the null hypothesis the large sample distribution of this statistic is a chi-squared with p degrees of freedom distribution. If N, the sample size, is small, then, as recommended by Mancl and DeRouen [24], we make small adjustments to improve the small sample approximation to the distribution of the test statistic. In particular, they recommend adjusting Ŵ using the “hat” matrix; see the formulae for the adjusted Ŵ as well as Q̂ in Appendix A. Also in small sample settings, investigators commonly suggest that instead of using a critical value based on the chi-squared distribution, a critical value based on the t–distribution should be used [25]. As we are considering a simultaneous test for multiple parameters we form the critical value based on Hotelling’s T–squared distribution [26]. Hotelling’s T–squared distribution is a multiple of the F distribution given by $\frac{d_1(d_1+d_2-1)}{d_2}{F}_{d_1,d_2}$; here we use d₁ = p and d₂ = N−q−p (recall q is the number of parameters in the nuisance parameter vector, α); see the appendix for a rationale. In the following, the rejection region for the test of H₀ : β(t) = 0, t = 1, … T based on (6) is

$$\left\{N{\widehat{\beta }}^{\prime }{\widehat{\mathrm{\sum }}}_{\beta }^{-1}\widehat{\beta }>F_{p,N-q-p}^{-1}\left(\frac{(N-q-p)(1-{\alpha }_0)}{p(N-q-1)}\right)\right\}$$

where α₀ is the desired significance level.

5. Sample Size Formulae

As Tu et. al [23] have developed general sample size formulas in the GEE setting, here we focus on considerations specific to the setting of micro-randomized trials. To size the study, we will determine the sample size needed to detect the alternate, β(t) with:

$${\mathrm{H}}_1:\beta (t)/\overline{\sigma }=d(t),t=1,\dots ,T$$

where ${\overline{\sigma }}^2=(1/T){\sum }_{t=1}^{T}E[\text{Var}(Y_{t+1}\mid I_t=1,A_t)]$ is the average variance and d(t) is a standardized treatment effect. When N is large and H₁ holds, $N{\widehat{\beta }}^{\prime }{\widehat{\mathrm{\sum }}}_{\beta }^{-1}\widehat{\beta }$ is approximately distributed as a non-central chi-squared ${\chi }_p^2(c_N)$, where c_N, the non-centrality parameter, satisfies $c_N=N{(\overline{\sigma }\stackrel{\sim }{d})}^{\prime }{\mathrm{\sum }}_{\beta }^{-1}(\overline{\sigma }\stackrel{\sim }{d})$, and $\stackrel{\sim }{d}={({\sum }_{t=1}^{T}E[I_t]{\rho }_t(1-{\rho }_t)Z_t{Z}_t^{\prime })}^{-1}{\sum }_{t=1}^{T}E[I_t]{\rho }_t(1-{\rho }_t)d(t)Z_t$ [23]. Note that d̃= β̃/σ̄.

Working Assumptions

To derive the sample size formula, we use the form of the non-centrality parameter of the limiting non-central chi-squared distribution, along with working assumptions. The working assumptions are used to simplify the form of ${\mathrm{\sum }}_{\beta }^{-1}$. In particular, we make the following working assumptions:

1. $E(Y_{t+1}\mid I_t=1)=B_t^{\prime }\alpha$, for some α ∈ ℝ^q

2. $\beta (t)=Z_t^{\prime }\beta$ for some β ∈ ℝ^p

3. Var(Y_t+1|I_t = 1, A_t) is constant in t and A_t

4. E[ε̃_tε̃_s |I_t = 1, I_s = 1, A_t, A_s] is constant in A_t, A_s.

   where, as before, ${\stackrel{\sim }{\epsilon }}_t=Y_{t+1}-I_t{B}_t^{\prime }\stackrel{\sim }{\alpha }-(A_t-{\rho }_t)I_t{Z}_t^{\prime }\stackrel{\sim }{\beta }$. See appendix A (Lemma 2) for proof of variance formulas under these working assumptions. The above working assumptions are somewhat simplistic but as will be seen below the resulting sample size formula is robust to moderate violations. First, under these working assumptions the alternative hypothesis can be re-written as

   $${\mathrm{H}}_1:\beta /\overline{\sigma }=d,$$ (7)
   where d is a p dimensional vector of standardized effects. Furthermore, Σ_β is given by

   $${\mathrm{\sum }}_{\beta }={\overline{\sigma }}^2{\left(\sum _{t=1}^{T}E[I_t]{\rho }_t(1-{\rho }_t)Z_t{Z}_t^{\prime }\right)}^{-1},$$
   and thus c_N is given by

   $$c_N=N{d}^{\prime }\left(\sum _{t=1}^{T}E[I_t]{\rho }_t(1-{\rho }_t)Z_t{Z}_t^{\prime }\right)d.$$ (8)

To improve the small sample approximation, we use the multiple of the F-distribution as discussed above. Thus the sample size, N, is found by solving

$$\frac{p(N-q-1)}{N-q-p}{F}_{p,N-q-p;c_N}\left(F_{p,N-q-p}^{-1}\left(\frac{(N-q-p)(1-{\alpha }_0)}{p(N-q-1)}\right)\right)=1-{\beta }_0$$ (9)

where F_{p,N−q−p;cN} is the noncentral F distribution with noncentrality parameter, c_N and 1−β₀ is the desired power. The inputs to this sample size formula are ${\{Z_t\}}_{t=1}^T$, a scientifically meaningful value for d (see below for an illustration), the time-varying availability pattern, ${\{E[I_t]\}}_{t=1}^T$, the desired significance level, α₀ and power, 1−β₀.

Now we describe how the information needed in the sample size formula might be obtained when the alternative is quadratic (p = 3, (1)). In this case we first elicit the initial standardized proximal main effect given by $Z_1^{\prime }\beta /\overline{\sigma }={\beta }_1/\overline{\sigma }$. Second we elicit the averaged across time, standardized proximal main effect $\overline{d}=\frac{1}{T}{\sum }_{t=1}^T{Z}_t^{\prime }\beta /\overline{\sigma }$. Lastly we elicit the time at which the proximal main effect is maximal, i.e. ${\text{argmax}}_t{Z}_t^{\prime }\beta$. These three quantities can then be used to solve for d = (d₁,d₂,d₃)′. For example, in HeartSteps, we might want to determine the sample size to ensure 80% power when there is no initial treatment effect on the first day, and the maximum proximal main effect comes around day 29. We specify the expected availability, E[I_t] to be constant in t and Z_t is given by (1). Table I gives sample sizes for HeartSteps under a variety of average standardized proximal main effects (d̄).

Table I.

Illustrative sample sizes for HeartSteps. The day of maximal treatment effect is 29. The expected availability is constant in t.

E[It]	0.7	0.6	0.5	0.4
d̄
0.10	32	36	42	52
0.09	38	44	51	63
0.08	47	54	64	78
0.07	60	69	81	101
0.06	79	92	109	135
0.05	112	130	155	193

$\overline{d}=(1/T){\sum }_{t=1}^T{Z}_t^{\prime }d$ is the average standardized treatment effect.

In the behavioral sciences a standardized effect size of 0.2 is considered small [27]. Thus given the very small standardized effect sizes, the sample sizes given in Table I seem unbelievably small. Two points are worth making in this regard. First the use of the alternative parametric hypothesis (7) in forming the test statistic, implies that both between-subject as well as within-subject contrasts in proximal responses are used to detect the alternative. To see this, note that if we focused on only the first time point, t = 1, and tested H₀ : β(1) = 0, then an appropriate test would be a two-sample t-test based on the proximal response Y₂, in which case the required sample size would be much larger (akin to the sample size for a two arm randomized-controlled trial in which 40% of the subjects are randomized to the treatment arm). This two-sample t-test uses only between-subject contrasts in proximal response to test the hypothesis. The required sample size would be even larger for a test of H₀ : β(1) = 0, β(2) = 0 in which no relationship between β(1) and β(2) is assumed. Conversely the sample size would be smaller if one focused on detecting alternatives to H₀ : β(1) = 0, β(2) = 0 of the form H₁ : β(1) = β(2) ≠ 0. The use of the alternative, β(1) = β(2) ≠ 0, allows one to construct tests that use both between-subject as well as within-subject contrasts in proximal responses. Our approach is in between these two extremes in that we focus on detecting smooth, in t, alternatives to H₀ : β(t) = 0 for all t. This permits use of both within-as well as between-subject contrasts in proximal responses. The assumption of a parsimonious alternative enables the use of smaller sample sizes. A second point is that, at this time, there is no general understanding of how large the standardized effect size should be for these “in-the-moment” effects of a treatment. Thus these standardized effects may or may not be considered small in future.

6. Simulations

We consider a variety of simulations with different generative models to evaluate the performance of the sample size formulae. In the simulations presented here, we use the same setup as in HeartSteps; see Appendix B for simulations in other setups (Table 4B). Specifically, the duration of the study is 42 days and there are 5 decision times within each day (T = 210). The randomization probability is 0.4, i.e. ρ = ρ_t = P(A_t = 1) = 0.4. The sample size formula is given in (8) and (9). All simulations are based on 1,000 simulated data sets.

Throughout this section the inputs to this sample size formula are $Z_t={(1,\lfloor \frac{t-1}{5}\rfloor ,{\lfloor \frac{t-1}{5}\rfloor }^2)}^{\prime }$, the time-varying availability pattern, τ_t = E[I_t], d, α₀ = .05 and power, 1− β₀ = .80. The value for the vector d is indirectly specified via (a) the time at which the maximal standardized proximal main effect is achieved ( ${\text{argmax}}_t{Z}_t^{\prime }d$), (b) the averaged across time, standardized proximal main effect $\overline{d}=\frac{1}{T}{\sum }_{t=1}^T{Z}_t^{\prime }d$ and (c) no initial standardized proximal main effect ( $Z_1^{\prime }d=d_1=0$). The test statistic used to evaluate the sample size formula is given by (6) in which B_t and Z_t are set to ${(1,\lfloor \frac{t-1}{5}\rfloor ,{\lfloor \frac{t-1}{5}\rfloor }^2)}^{\prime }$.

The simulation results provided below illustrate that the sample size formula and associated test statistic are robust. For convenience we summarize the results here. When the working assumptions hold, then under a variety of availability patterns, i.e., time-varying values for τ_t = E[I_t ] (see Figure 1) the desired Type 1 error and power are preserved. This is also the case when past treatment impacts availability. Furthermore the sample size formula is robust to deviations from the working assumptions, that is, provides the desired Type 1 error and power; this is true for a variety of forms of the true proximal main effect of the treatment (see Figure 2), a variety of distributions and correlation patterns for the errors, and dependence of Y_t+1 on past treatment. In all cases the above robustness occurs as long as we provide an approximately true or conservative value for the standardized effect, d and if we provide an approximately true or conservative (low) value for the availability, E[I_t ].

Figure 1.

Availability Patterns. The x-axis is decision time point and y-axis is the expected availability. Pattern 2 represents availability varying by day of the week with higher availability on the weekends and lower mid-week. The average availability is 0.5 in all cases.

Figure 2.

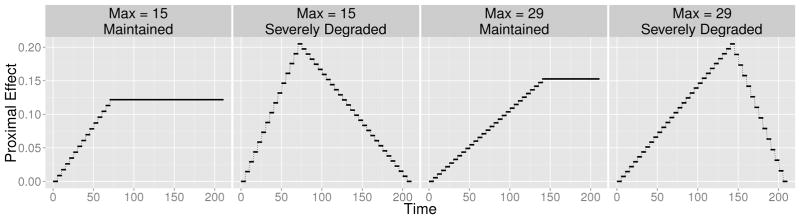
Standardized Proximal Main Effects of Treatment, ${\{d(t)\}}_{t=1}^T$: representing maintained and severely degraded time-varying proximal treatment effects. The horizontal axis is the decision time point. The vertical axis is the standardized treatment effect. The “Max” in the titles refer to the day of maximal proximal effect. The average standardized proximal effect is d̄= 0.1 in all plots.

In our simulations, we note several areas in which the sample size formula is less robust to the working assumption (c); this is when the error variance in Y_t+1 varies depending on whether treatment A_t = 1 or A_t = 0 or with time t. In particular if the ratio of Var[Y_t+1|I_t = 1, A_t = 1]/Var[Y_t+1|I_t = 1, A_t = 0] < 1, then the power is reduced. Also if average variance, E[Var[Y_t+1|I_t = 1, A_t ]] varies greatly with time t, then the power is reduced. See below for details. Lastly as would be expected for any sample size formula, using values of the standardized effect size, d, or availability that are larger than the truth degrades the power of the procedure.

6.1. Working Assumptions Underlying Sample Size Formula are True

First, we considered a variety of settings in which the working assumptions (a)–(d) hold and in which the inputs to the sample size formula are correct (d is correct under the alternate hypothesis and the time-varying availability E[I_t] is correct). Neither the working assumptions nor the inputs to the sample size formula specify the error distribution, thus in the simulation we consider 5 distributions for the errors in the model for Y_t+1 including independent normal, student’s t and exponential distributions as well as two autoregressive (AR) processes; all of these error patterns satisfy ${\overline{\sigma }}^2=1(\text{recall}{\overline{\sigma }}^2=(1/T){\sum }_{t=1}^{T}E[\text{Var}(Y_{t+1}\mid I_t=1,A_t)])$. Furthermore neither the working assumptions nor the inputs to the sample size formula specify the dependence of the availability indicator, I_t on past treatment. Thus we consider settings in which the availability decreases as the number of recent treatments increases. For brevity, we provide these standard results in the Appendix B (Tables 2B and 3B). The results are generally quite good, with very few Type 1 error rates significantly above .05 and power levels significantly below .80.

6.2. Working Assumptions Underlying Sample Size Formula are False

Second, we considered a variety of settings in which the working assumptions are false but the inputs to the sample size formula are approximately correct as follows. Throughout σ̄² = 1.

6.2.1. Working Assumption (a) is Violated

Suppose that the true E[Y_t+1|I_t = 1] ≠ B_tα for any α ∈ ℝ^q. In particular, we consider the scenario in which there is a “weekend” effect on Y_t+1; see other scenario in Appendix B. The data is generated as follows,

$$\begin{array}{l}{I}_t\stackrel{\mathit{Ber}}{\sim }({\tau }_t),A_t\stackrel{\mathit{Ber}}{\sim }(\rho )\\ Y_{t+1}=\alpha (t)+(A_t-\rho )Z_t^{\prime }d+{\epsilon }_t,\text{if}{I}_t=1\end{array}$$

where the conditional mean $\alpha (t)=B_t^{\prime }\alpha +W_t\theta$. W_t is a binary variable: W_t = 1 if day of the week is time t is a weekend day, and W_t = 0 if the day is a weekday. For simplicity, we assume each subject starts on Monday, e.g. for k = 1, …, 6, W_i+35(k−1) = 0, when i = 1, …,25, W_i+35(k−1) = 1, when i = 26, …,35 (recall that we assume in the simulation that there are 5 decision time points per day and the length of the study is 6 week). The values of {α_i, i = 1,2,3} are determined by setting α(1) = 2.5, argmax_t α(t) = T, $(1/T){\sum }_{t=1}^T\alpha (t)-\alpha (1)=0.1$. The error terms ${\{{\epsilon }_t\}}_{t=1}^N$ are i.i.d N(0, 1). The day of maximal proximal effect is 29. Additionally, different values of the averaged standardized treatment effect and four patterns of availability as shown in Figure 1 with average 0.5 and are considered. The type I error rate is not affected, thus is omitted here. The simulated power is reported in Table II; for more details see Table 6B in Appendix B.

Table II.

Simulated power when working assumption (a) is violated. The patterns of availability are provided in Figure 1.

θ	d̄	Availability Pattern
		Pattern 1	Pattern 2	Pattern 3
0.5d̄	0.10	0.80	0.79	0.81
	0.06	0.78	0.83	0.81
1d̄	0.10	0.79	0.78	0.78
	0.06	0.78	0.79	0.79
1.5d̄	0.10	0.78	0.81	0.78
	0.06	0.77	0.81	0.82
2d̄	0.10	0.78	0.79	0.79
	0.06	0.81	0.79	0.78

θ is the coefficient of W_t in E[Y_t+1|I_t = 1]. $\overline{d}=(1/T){\sum }_{t=1}^T{Z}_t^{\prime }d$ is the average standardized treatment effect. Bold Numbers are significantly (at .05 level) greater lower than 0.80.

6.2.2. Working Assumption (b) is Violated

Suppose that the true $\beta (t)\ne Z_t^{\prime }\beta$ for any β. Instead the vector of standardized effect, d, used in the sample size formula corresponds to the projection of d(t), that is, $d={({\sum }_{t=1}^{T}E[I_t]Z_t{Z}_t^{\prime })}^{-1}{\sum }_{t=1}^{T}E[I_t]Z_{t}d(t)$ (recall d(t) = β(t)/σ̄ and ρ_t = ρ). The sample size formula is used with the correct availability pattern, ${\{E[I_t]\}}_{t=1}^T$. The data for each simulated subject is generated sequentially as follows. For each time t,

$$\begin{array}{l}{I}_t\stackrel{\mathit{Ber}}{\sim }({\tau }_t),A_t\stackrel{\mathit{Ber}}{\sim }(\rho )\\ Y_{t+1}=\alpha (t)+(A_t-\rho )d(t)+{\epsilon }_t,\text{if}{I}_t=1\end{array}$$

for the variety of d(t) = β(t)/σ̄ and E[I_t ] patterns provided in Figure 2 and in Figure 1 respectively. The average availability is 0.5. The error terms ${\{{\epsilon }_t\}}_{t=1}^T$ are generated as i.i.d. N(0, 1). The conditional mean, E[Y_t+1|I_t = 1] = α(t) is given by $\alpha (t)={\alpha }_1+{\alpha }_2\lfloor \frac{t-1}{5}\rfloor +{\alpha }_3{\lfloor \frac{t-1}{5}\rfloor }^2$, where α₁ = 2.5, α₂ = 0.727,α₃ = −8.66×10⁻⁴ (so that (1/T)Σ_t α(t)− α(1) = 1, argmax_t α(t) = T).

The simulated powers are provided in Table III. In all cases the power is close to .80; this is because all of the proximal main effect patterns in Figure 2 are sufficiently well approximated by a quadratic in time. See Appendix B for other cases of d(t) and details (Figure 5 and Table 9B).

Table III.

Simulated Power when working assumption (b) is violated. The shape of the standardized proximal effect and pattern for availability are provided in Figure 2 and 1 respectively. The sample sizes are given on the right.

d̄	Availability Pattern	Max	Shape of d(t)		Sample Size
			Maintained	Degraded
0.10	Pattern 1	15	0.78	0.79	43	39
		29	0.80	0.79	38	38
	Pattern 2	15	0.79	0.80	43	39
		29	0.78	0.79	38	38
	Pattern 3	15	0.81	0.77	45	41
		29	0.81	0.78	37	39
0.06	Pattern 1	15	0.81	0.79	111	100
		29	0.81	0.79	96	96
	Pattern 2	15	0.79	0.81	112	100
		29	0.79	0.80	96	96
	Pattern 3	15	0.78	0.81	116	106
		29	0.80	0.80	95	101

$\overline{d}=(1/T){\sum }_{t=1}^T{Z}_t^{\prime }d$ is the average standardized treatment effect. The “Max” in the first row refers to the day of maximal proximal effect. Bold numbers are significantly (at .05 level) lower than .80.

Table 9B.

Simulated Power(%) when working assumption (b) is violated. The shape of the standardized proximal effect, d(t) = β(t)/σ̄ and pattern for availability, E[I_t] are provided in Figure 5 and in Figure (1). The corresponding sample sizes are given in Table 8B.

d̄	Availability Pattern	Max	τ̄			τ̄
			Shape of d(t)
			Maintained	Slightly Degraded	Severely Degraded	Maintained	Slightly Degraded	Severely Degraded
0.10	Pattern 1	15	78.4	78.8	78.6	79.1	80.1	77.6
		22	80.4	79.5	81.2	80.0	76.9	77.9
		29	80.4	79.2	78.9	77.3	76.8	81.1
	Pattern 2	15	78.6	79.9	79.9	80.1	80.4	81.3
		22	78.3	81.2	78.8	79.2	80.8	80.5
		29	77.9	80.8	79.3	78.1	77.7	82.2
	Pattern 3	15	81.0	79.7	77.4	77.9	80.9	77.6
		22	78.9	79.1	80.0	79.7	79.4	75.9
		29	80.9	77.5	77.7	80.6	79.2	78.5
	Pattern 4	15	79.7	79.5	77.9	79.5	81.7	78.0
		22	78.9	77.9	80.4	82.2	78.9	78.8
		29	77.9	79.7	79.0	78.0	80.2	80.8
0.08	Pattern 1	15	80.5	79.5	78.6	80.6	79.2	78.7
		22	78.9	78.7	78.8	78.9	80.7	80.3
		29	76.6	78.0	78.3	80.9	78.6	80.4
	Pattern 2	15	81.0	79.3	78.7	82.0	80.5	80.1
		22	82.4	80.6	80.0	78.0	79.6	79.4
		29	79.2	76.9	81.9	78.3	78.8	79.7
	Pattern 3	15	78.2	81.6	80.9	79.1	79.2	77.5
		22	80.9	79.5	78.6	79.2	78.3	81.4
		29	80.4	79.3	77.5	77.9	80.2	82.3
	Pattern 4	15	79.4	79.4	78.1	78.6	77.4	78.8
		22	81.3	78.4	78.4	80.6	79.4	80.4
		29	79.9	79.3	79.8	79.5	79.7	81.2
0.06	Pattern 1	15	81.2	80.5	79.0	77.8	78.7	79.6
		22	80.0	81.7	79.8	80.7	80.5	80.2
		29	81.2	78.7	79.2	81.2	79.7	80.1
	Pattern 2	15	78.7	77.5	81.4	80.7	81.0	80.7
		22	80.6	81.8	79.2	80.3	81.6	80.2
		29	78.5	80.2	80.0	77.7	78.1	78.0
	Pattern 3	15	78.1	80.0	80.9	79.7	79.3	78.8
		22	81.2	80.2	80.0	78.3	82.2	81.1
		29	79.6	81.6	79.8	80.2	81.6	76.9
	Pattern 4	15	78.2	79.8	78.9	79.5	77.3	79.2
		22	79.2	81.1	79.4	76.8	79.2	80.4
		29	79.9	78.5	79.8	80.1	78.9	81.8

“Max” is the day in which the maximal proximal effect is attained. $\overline{d}=(1/T){\sum }_{t=1}^T{Z}_t^{\prime }d$ is the average standardized treatment effect. Bold numbers are significantly (at .05 level) lower than .80.

6.2.3. Working Assumption (c) is Violated

Suppose that $\text{Var}[Y_{t+1}\mid I_t=1,A_t]=A_t{\sigma }_{1t}^2+(1-A_t){\sigma }_{0t}^2$ where σ_1t /σ_0t ≠ 1. The sample size formula is used with the correct pattern for ${\{Z_t^{\prime }d,E[I_t]\}}_{t=1}^T$. The data for each simulated subject is generated sequentially as follows. For each time t,

$$\begin{array}{l}{I}_t\stackrel{\mathit{Ber}}{\sim }({\tau }_t),A_t\stackrel{\mathit{Ber}}{\sim }(\rho )\\ Y_{t+1}=\alpha (t)+(A_t-\rho )Z_t^{\prime }d+{𝟙}_{\{A_t=1\}}{\sigma }_{1t}{\epsilon }_t+{𝟙}_{\{A_t=0\}}{\sigma }_{0t}{\epsilon }_t,\text{if}{I}_t=1\end{array}$$

where the average across time standardized proximal main effect, $\overline{d}=\frac{1}{T}{\sum }_{t=1}^T{Z}_t^{\prime }d$ is 0.1 and day of maximal effect is equal to 22 or 29. The function α(t) = E[Y_t+1|I_t = 1] is as in the prior simulation. The availability, τ_t = 0.5. The error terms {ε_t } follow a normal AR(1) process, e.g. ε_t = ϕε_t−1 +v_t with the variance of v_t scaled so that Var[ε_t ] = 1. Define ${\overline{\sigma }}_t^2=E[\text{Var}[Y_{t+1}\mid I_t=1,A_t]](=\rho {\sigma }_{1t}^2+(1-\rho ){\sigma }_{0t}^2)$. Recall the average variance σ̄² is given by $(1/T){\sum }_{t=1}^T{\overline{\sigma }}_t^2$. We consider 3 time-varying trends for {σ̄_t} together with different values of σ_1t /σ_0t ; see Figure (3). In each trend, ${\overline{\sigma }}_t^2$ is scaled such that σ̄ = 1; thus the standardized proximal main effect in the generative model is $Z_t^{\prime }d$. In all cases, the simulated type I error rates are close to .05 and thus the table is omitted here (see Appendix B, Table 10B). The simulated power is given in Table IV.

Figure 3.

Trend of σ̄_t : For all trends, ${\overline{\sigma }}_t^2$ is scaled so that $(1/T){\sum }_{t=1}^T{\overline{\sigma }}_t^2=1$. In Trend 3, the variance, ${\overline{\sigma }}_t^2=E[\mathit{Var}[Y_{t+1}\mid I_t=1,A_t]]$ peaks on weekends. In particular, σ̄_7k+i = 0.8 for i = 1, …,5 and σ̄_7k+i = 1.5 for i = 6,7.

Table IV.

Simulated Power when working assumption (c) is violated, σ_1t ≠ σ_0t. The trends are provided in Figure 3. The availability is 0.5. The average proximal main effect, d̄= 0.1 and the day of maximal effect is 22 or 29, and thus the associated sample sizes are 41 and 42.

ϕ	$\frac{{\sigma }_{1t}}{{\sigma }_{0t}}$	Max = 22 (N = 41)			Max = 29 (N = 42)
		trend 1	trend 2	trend 3	trend 1	trend 2	trend 3
−0.6	0.8	0.83	0.84	0.80	0.81	0.89	0.79
	1.0	0.79	0.80	0.75	0.74	0.85	0.70
	1.2	0.76	0.76	0.71	0.72	0.81	0.70
0	0.8	0.85	0.82	0.79	0.81	0.88	0.78
	1.0	0.79	0.81	0.74	0.77	0.86	0.72
	1.2	0.77	0.77	0.71	0.70	0.83	0.70
0.6	0.8	0.83	0.83	0.81	0.77	0.87	0.77
	1.0	0.76	0.79	0.75	0.73	0.85	0.77
	1.2	0.78	0.77	0.73	0.72	0.82	0.69

ϕ is the parameter in AR(1) for ${\{{\epsilon }_t\}}_{t=1}^T$. “Max” is the day in which the maximal proximal effect is attained. Bold numbers are significantly (at .05 level) lower than .80.

In the case of σ_1t < σ_0t, the simulated powers are slightly larger than 0.8, while the simulated powers are smaller than 0.8 in the case of σ_1t > σ_0t. The impact of σ̄_t on the power depends on the shape of treatment effect: when β(t) attains its maximum, more than halfway through the study, at day 29, a increasing {σ̄_t}, trend 1, lowers the power, while a decreasing {σ̄_t}, trend 2, improves the power. When β(t) attains a maximal effect midway through the study, either decreasing or increasing {σ̄_t} does not impact power. A large variation in σ̄_t, e.g. trend 3, reduces the power in all cases. The differing auto correlations of the errors, ε_t, do not affect power; see a more detailed table in Appendix B, Table 10B.

6.2.4. Working Assumption (d) is Violated

We violate assumption (d) by making both the availability indicator, I_t and proximal response, Y_t+1 depend on past treatment and past proximal responses. The sample size formula is used with the correct value of ${\{Z_t^{\prime }d,E[I_t]\}}_{t=1}^T$; in particular d is determined by an average proximal main effect of d̄= 0.1, day of maximal effect equal to 29 (d₁ = 0, d₂ = 9.64×10⁻³, d₃ = −1.72×10⁻⁴) and with a constant availability pattern equal to 0.5. The data for each simulated subject is generated as follows. Denote the cumulative treatment over last 24 hours by $C_t={\sum }_{j=1}^5{A}_{t-j}{I}_{t-j}$. In each time t,

$$\begin{array}{l}{I}_t\stackrel{\mathit{Ber}}{\sim }({\tau }_t+{\tau }_t{\eta }_1(C_t-E[C_t])+{\tau }_t{\eta }_2\text{Trunc}(\frac{1}{5}\sum _{j=1}^5{\epsilon }_{t-j})),A_t\stackrel{\mathit{Ber}}{\sim }(\rho )\\ Y_{t+1}=\{\begin{array}{l}\alpha (t)+{\gamma }_1[C_t-E[C_t\mid I_t=1]]+(A_t-\rho )[Z_t^{\prime }d+Z_t^{\prime }d{\gamma }_2(C_t-E[C_t\mid I_t=1])]+{\sigma }^{\ast }{\epsilon }_t\text{if}{I}_t=1\hfill \\ {\alpha }_0(t)+{\epsilon }_t\text{if}{I}_t=0.\hfill \end{array}\end{array}$$

where ${\{{\epsilon }_t\}}_{t=1}^T$ are i.i.d N(0,1) and Trunc(x) := x𝟙_|x|≤1+sign(x)𝕀_|x|>1 (the truncation is used to ensure that ${\tau }_t+{\tau }_t{\eta }_1(C_t-E[C_t])+{\tau }_t{\eta }_2\text{Trunc}(\frac{1}{5}{\sum }_{j=1}^5{\epsilon }_{t-j})\in [0,1]$). Again α(t) is as in the prior simulation. σ^* is calculated such that the average variance is equal to 1, e.g. $\overline{\sigma }=\frac{1}{T}{\sum }_{t=1}^{T}E[\text{Var}[Y_{t+1}\mid I_t=1,A_t]]=1$. Note that since C_t is centered in both the model for I_t as well as in the model for Y_t+1, the standardized proximal main effect is $Z_t^{\prime }d$ and E[I_t ] = τ_t = 0.5. α₀(t) is the conditional mean of Y_t+1 when I_t = 0. The form of E[Y_t+1|I_t = 0] is not essential: only Y_s+1 −E[Y_s+1|I_s = 0] is used to generate I_t. In the simulation, E[C_t |I_t = 1] and σ^* are calculated by Monte Carlo methods. As before, the simulated type I error are not affected; see Table 11B in appendix B. The simulated powers are provided in Table V.

Table V.

Simulated Power when working assumption (d) is false. The expected availability is 0.5, the average proximal main effect d̄= 0.1 and the maximal effect is attained at day 29. The associated sample size is 42.

Parameters in It	γ2	−0.1	−0.2	−0.3
	γ1
η1 = −0.1,η2 = −0.1	−0.2	0.80	0.81	0.79
	−0.5	0.79	0.81	0.80
	−0.8	0.81	0.82	0.79
η1 = −0.2,η2 = −0.1	−0.2	0.78	0.82	0.79
	−0.5	0.81	0.77	0.77
	−0.8	0.81	0.79	0.78
η1 = −0.1,η2 = −0.2	−0.2	0.78	0.78	0.80
	−0.5	0.80	0.79	0.78
	−0.8	0.78	0.79	0.80

γ₁ and γ₂ are parameters for the cumulative treatments in the model of Y_t+1. η₁ and η₂ are parameters in the model of I_t. Bold numbers are significantly (at .05 level) less than .80.

6.3. Some Practical Guidelines

Third, it is critical to use conservative values of d and availability E[I_t ] in the sample size formula. It is not surprising that the quality of the sample size formula depends on an accurate or conservative values of the standardized effects, d, as this is the case for all sample size formulas. Additionally availability provides the number of decision points as which treatment might be provided per individual and thus the sample size formula should be sensitive to availability. To illustrate these points we consider two simulations in which the data is generated by

$$\begin{array}{l}{I}_t\stackrel{\mathit{Ber}}{\sim }({\tau }_t),A_t\stackrel{\mathit{Ber}}{\sim }(\rho )\\ Y_{t+1}=\alpha (t)+(A_t-\rho )Z_t^{\prime }d+{\epsilon }_t,\text{if}{I}_t=1\end{array}$$

where the ε_t ’s are i.i.d. standard normals and α(t) is as in the prior simulations. In the first simulation, suppose the scientist provides the correct availability pattern, ${\{E[I_t]\}}_{t=1}^T$, the correct time at which the maximal standardized proximal main effect is achieved ( ${\text{argmax}}_t{Z}_t^{\prime }d$) and the correct initial standardized proximal main effect ( $Z_1^{\prime }d=d_1=0$) but provides too low a value of the averaged across time, standardized proximal main effect $\overline{d}=\frac{1}{T}{\sum }_{t=1}^T{Z}_t^{\prime }d$. The simulated power is provided in Appendix B, Table 12B. The degradation in power is pronounced as might be expected.

In the second simulation, suppose the scientist provides the correct ${\text{argmax}}_t{Z}_t^{\prime }d$, correct $Z_1^{\prime }d=d_1=0$, correct $\overline{d}=\frac{1}{T}{\sum }_{t=1}^T{Z}_t^{\prime }d$ and although the scientist’s time-varying pattern of availability is correct, the magnitude is underestimated. The simulation result is in Appendix B, Table 13B. Again the degradation in power is pronounced.

7. Discussion

In this paper, we have introduced the use of micro-randomized trials in mobile health and have provided an approach to determining the sample size. More sophisticated sample size procedures might be entertained. Certainly it makes sense to include baseline information in the sample size procedure, for example in HeartSteps, a natural baseline variable is baseline step count. The inclusion of baseline variables in B_t in the regression (2) is straightforward. An interesting generalization to the sample size procedure would allow scientists to include time-varying variables (in S_t) as covariates in B_t in the regression (2). This might be a useful strategy for reducing the error variance.

An alternate to the micro-randomized trial design is the single case design often used in the behavioral sciences [28]. These trials usually only involve 1 to 13 participants [29] and the data analyses focus on the examination of visual trends for each participant separately. For example during periods when a participant is on treatment the response might be generally higher than the height of the response during the time periods in which the participant is off treatment. An excellent overview of single case designs and their use for evaluating technology based interventions is [30]. This paper illustrates the visual analyses that would be conducted on each participant’s data. A critical assumption is that the effect of the treatment is only temporary (no carry-over effect) so that each participant can act as his own control. We believe that in settings in which treatments are expected to have sufficiently strong effects so as to overwhelm the within person variability in response (thus a visual analysis can be compelling), these designs provide an alternative to the micro-randomized trial design.

Although this paper has focused on determining the sample size to detect the proximal main effect of a treatment with a given power, micro-randomized studies provide data for a variety of interesting further analyses. For example, it is of some interest to model and understand the predictors of the time-varying availability indicator. In the case of HeartSteps we will know why the participant is unavailable (driving a car, already active or has turned off the lock-screen messages) so we will be able to consider each type of availability indicator. Other very interesting further analyses include assessing interactions between treatments, A_t and context, S_t, past treatment A_s, s < t on the proximal response, Y_t+1. Also there is much interest in using this type of data to construct “dynamic treatment regimes”; in this setting these are called Just-in-Time Adaptive Interventions [13]. The sequential micro-randomizations enhance all of these analyses by reducing causal confounding.

Table 8B.

Sample Sizes when working assumption (b) is violated. The vector of standardized effects sizes, d, used in the sample size formula provides the projection of d(t). The sample size formula is used with the correct availability pattern, ${\{E[I_t]\}}_{t=1}^T$. The shape of the standardized proximal effect, d (t) = β(t)/σ̄ pattern for availability, E[I_t] are provided in Figure 5 and in Figure (1). The significance level is 0.05. The desired power is 0.80.

d̄	Availability Pattern	Max	τ̄ = 0.5			τ̄ = 0.7
			Shape of d(t)
			Maintained	Slightly Degraded	Severely Degraded	Maintained	Slightly Degraded	Severely Degraded
0.10	Pattern 1	15	43	41	39	32	31	29
		22	43	41	40	33	31	30
		29	38	37	38	29	28	29
	Pattern 2	15	43	41	39	33	31	30
		22	43	42	40	33	31	30
		29	38	37	38	29	28	29
	Pattern 3	15	45	43	41	33	32	31
		22	44	43	42	33	32	31
		29	37	38	39	28	28	29
	Pattern 4	15	42	39	37	32	30	28
		22	44	41	39	33	31	30
		29	39	38	38	29	28	28
0.08	Pattern 1	15	65	61	58	48	45	43
		22	65	62	60	48	46	44
		29	56	55	56	42	41	42
	Pattern 2	15	65	61	59	48	45	43
		22	65	62	60	48	46	44
		29	56	55	56	42	41	42
	Pattern 3	15	67	64	62	49	47	45
		22	66	64	63	48	47	46
		29	56	56	59	41	41	43
	Pattern 4	15	63	59	55	47	44	41
		22	65	61	58	48	45	43
		29	58	56	56	43	41	41
0.06	Pattern 1	15	111	105	100	81	76	73
		22	112	106	103	81	77	75
		29	96	94	96	70	69	70
	Pattern 2	15	112	105	100	81	77	73
		22	112	106	103	81	77	75
		29	96	94	96	70	68	70
	Pattern 3	15	116	111	106	83	79	76
		22	114	110	108	82	79	78
		29	95	96	101	69	69	72
	Pattern 4	15	108	100	94	79	74	70
		22	112	105	99	81	76	73
		29	100	95	95	72	69	70

“Max” is the day in which the maximal proximal effect is attained. $\overline{d}=(1/T){\sum }_{t=1}^T{Z}_t^{\prime }d$ is the average standardized treatment effect.

Appendix A Theoretical Results and Proofs

Lemma 1 (Least Squares Estimator)

The least square estimators α̂, β̂ are consistent estimators of α̃, β̃ in (4) and (5). In particular, if $\beta (t)=Z_t^{\prime }{\beta }^{\ast }$ for some vector β^*, then β̃ = β^*. Under moment conditions, we have $\sqrt{N}(\widehat{\beta }-\stackrel{\sim }{\beta })\to N(0,{\mathrm{\sum }}_{\beta })$, where the asymptotic variance Σ_β is given by Σ_β = Q⁻¹WQ⁻¹ where $Q={\sum }_{t=1}^{T}E[I_t]{\rho }_t(1-{\rho }_t)Z_t{Z}_t^{\prime },W=E\left[{\sum }_{t=1}^T{\stackrel{\sim }{\epsilon }}_t{I}_t(A_t-{\rho }_t)Z_t\times {\sum }_{t=1}^T{\stackrel{\sim }{\epsilon }}_t{I}_t(A_t-{\rho }_t)Z_t^{\prime }\right]$ and ${\stackrel{\sim }{\epsilon }}_t=Y_{t+1}-B_t^{\prime }\stackrel{\sim }{\alpha }-Z_t^{\prime }\stackrel{\sim }{\beta }(A_t-{\rho }_t)$.

Proof

It’s easy to see that the least square estimators satisfy

$$\widehat{\theta }=(\widehat{\alpha },\widehat{\beta })={\left({\mathbb{P}}_N\sum _{t=1}^T{I}_t{X}_t{X}_t^{\prime }\right)}^{-1}\left({\mathbb{P}}_N\sum _{t=1}^T{I}_t{Y}_{t+1}{X}_t\right)\to {\left(\sum _{t=1}^{T}E(I_t{X}_t{X}_t^{\prime })\right)}^{-1}\left(\sum _{t=1}^{T}E(I_t{Y}_{t+1}{X}_t)\right)$$

where $X_t^{\prime }=(B_t^{\prime },(A_t-{\rho }_t)Z_t^{\prime })\in {ℝ}^{1\times (p+q)}$ is the covariate at time t. For each t,

$$\begin{array}{l}E(I_t{X}_t{X}_t^{\prime })=\left(\begin{array}{cc}E[I_t]B_t{B}_t^{\prime }& B_t{Z}_t^{\prime }E[I_t(A_t-{\rho }_t)]\\ Z_t{B}_t^{\prime }E[I_t(A_t-{\rho }_t)]& Z_t{Z}_t^{\prime }E[I_t{(A_t-{\rho }_t)}^2]\end{array}\right)=\left(\begin{array}{cc}E[I_t]B_t{B}_t^{\prime }& 0\\ 0& E[I_t]{\rho }_t(1-{\rho }_t)Z_t{Z}_t^{\prime }\end{array}\right)\\ E(I_t{Y}_{t+1}{X}_t)=\left(\begin{array}{c}E[I_t{Y}_{t+1}]B_t\\ E[I_t{Y}_{t+1}(A_t-{\rho }_t)]Z_t\end{array}\right)=\left(\begin{array}{c}E[I_t{Y}_{t+1}]B_t\\ {\rho }_t(1-{\rho }_t)E[I_t]\beta (t)Z_t\end{array}\right),\end{array}$$

so that

$$\begin{array}{c}\widehat{\alpha }\to {\left(\sum _{t=1}^{T}E[I_t]B_t{B}_t^{\prime }\right)}^{-1}\sum _{t=1}^{T}E[I_t{Y}_{t+1}]B_t={\left(\sum _{t=1}^{T}E[I_t]B_t{B}_t^{\prime }\right)}^{-1}\sum _{t=1}^{T}E[I_t]\alpha (t)B_t\\ \widehat{\beta }\to {\left(\sum _{t=1}^T{\rho }_t(1-{\rho }_t)E[I_t]Z_t{Z}_t^{\prime }\right)}^{-1}\sum _{t=1}^{T}E[I_t{Y}_{t+1}(A_t-{\rho }_t)]Z_t={\left(\sum _{t=1}^T{\rho }_t(1-{\rho }_t)E[I_t]Z_t{Z}_t^{\prime }\right)}^{-1}\sum _{t=1}^{T}E[I_t]{\rho }_t(1-{\rho }_t)\beta (t)Z_t\end{array}$$

as in (4) and (5). We can see that if $\beta (t)=Z_t^{\prime }{\beta }^{\ast }$, then ${({\sum }_{t=1}^T{\rho }_t(1-{\rho }_t)E[I_t]Z_t{Z}_t^{\prime })}^{-1}{\sum }_{t=1}^{T}E[I_t]{\rho }_t(1-{\rho }_t)\beta (t)Z_t={({\sum }_{t=1}^T{\rho }_t(1-{\rho }_t)E[I_t]Z_t{Z}_t^{\prime })}^{-1}{\sum }_{t=1}^{T}E[I_t]{\rho }_t(1-{\rho }_t)Z_t{Z}_t^{\prime }{\beta }^{\ast }={\beta }^{\ast }$. This is true even if $E[Y_{t+1}\mid I_t=1]\ne B_t^{\prime }\stackrel{\sim }{\alpha }$.

We can easily see that,

$$\begin{array}{l}\sqrt{N}(\widehat{\theta }-\stackrel{\sim }{\theta })=\sqrt{N}\left\{{({\mathbb{P}}_N\sum _{t=1}^T{I}_t{X}_t{X}_t^{\prime })}^{-1}\left[({\mathbb{P}}_N\sum _{t=1}^T{I}_t{Y}_{t+1}{X}_t)-({\mathbb{P}}_N\sum _{t=1}^T{I}_t{X}_t{X}_t^{\prime })\stackrel{\sim }{\theta }\right]\right\}\\ =\sqrt{N}\left\{E{[\sum _{t=1}^T{I}_t{X}_t{X}_t^{\prime }]}^{-1}({\mathbb{P}}_N\sum _{t=1}^T{I}_t{\stackrel{\sim }{\epsilon }}_t{X}_t)\right\}+o_p(\mathbf{1}),\end{array}$$ (10)

where o_p(1) is a term that converges in probability to zero as N goes to infinity. By the definitions of α̃ and β̃, we have

$$E[\sum _{t=1}^T{I}_t{\stackrel{\sim }{\epsilon }}_t{X}_t]=\left(\begin{array}{c}{\sum }_{t=1}^{T}E[I_t](\alpha (t)-B_t^{\prime }\stackrel{\sim }{\alpha })B_t\\ {\sum }_{t=1}^{T}E[I_t]{\rho }_t(1-{\rho }_t)(\beta (t)-Z_t^{\prime }\stackrel{\sim }{\beta })Z_t\end{array}\right)=\mathbf{0}$$

So that under moments conditions, we have $\sqrt{N}(\widehat{\theta }-\stackrel{\sim }{\theta })\to N(0,{\mathrm{\sum }}_{\theta })$, where Σ_θ is given by

$${\mathrm{\sum }}_{\theta }=E{[\sum _{t=1}^T{I}_t{X}_t{X}_t^{\prime }]}^{-1}E[\sum _{t=1}^T{I}_t{\stackrel{\sim }{\epsilon }}_t{X}_t\times \sum _{t=1}^T{I}_t{\stackrel{\sim }{\epsilon }}_t{X}_t^{\prime }]E{[\sum _{t=1}^T{I}_t{X}_t{X}_t^{\prime }]}^{-1}=\left[\begin{array}{cc}{\mathrm{\sum }}_{\alpha }& {\mathrm{\sum }}_{\alpha \beta }\\ {\mathrm{\sum }}_{\alpha \beta }^{\prime }& {\mathrm{\sum }}_{\beta }\end{array}\right].$$

In particular, β̂ satisfies $\sqrt{N}(\widehat{\beta }-\stackrel{\sim }{\beta })\to N(0,{\mathrm{\sum }}_{\beta })$ and Σ_β is given by

$${\mathrm{\sum }}_{\beta }={\left(\sum _{t=1}^{T}E[I_t]{\rho }_t(1-{\rho }_t)Z_t{Z}_t^{\prime }\right)}^{-1}E\left[\sum _{t=1}^T{\stackrel{\sim }{\epsilon }}_t{I}_t(A_t-{\rho }_t)Z_t\times \sum _{t=1}^T{\stackrel{\sim }{\epsilon }}_t{I}_t(A_t-{\rho }_t)Z_t^{\prime }\right]{\left(\sum _{t=1}^{T}E[I_t]{\rho }_t(1-{\rho }_t)Z_t{Z}_t^{\prime }\right)}^{-1}=Q^{-1}W{Q}^{-1}.$$

Lemma 2 (Asymptotic Variance Under Working Assumptions)

Assuming working assumptions (a)–(d) are true, then under the alternative hypothesis H₁ in (7), Σ_β and c_N are given by

$$\begin{array}{l}{\mathrm{\sum }}_{\beta }={\overline{\sigma }}^2{\left(\sum _{t=1}^{T}E[I_t]{\rho }_t(1-{\rho }_t)Z_t{Z}_t^{\prime }\right)}^{-1},\\ c_N=N{d}^{\prime }\left(\sum _{t=1}^{T}E[I_t]{\rho }_t(1-{\rho }_t)Z_t{Z}_t^{\prime }\right)d.\end{array}$$

Proof

Note that under assumptions (b) and (c), we have $Z_t^{\prime }\stackrel{\sim }{\beta }=\beta (t)$ and Var(Y_t+1|I_t = 1, A_t) = σ̄ for each t, and d̃ = d. The middle term, W, in Σ_β can be separated by two terms, e.g. $E\left[{\sum }_{t=1}^T{\stackrel{\sim }{\epsilon }}_t{I}_t(A_t-{\rho }_t)Z_t\times {\sum }_{t=1}^T{\stackrel{\sim }{\epsilon }}_t{I}_t(A_t-{\rho }_t)Z_t^{\prime }\right]={\sum }_{t=1}^{T}E[{\stackrel{\sim }{\epsilon }}_t^2{I}_t{(A_t-{\rho }_t)}^2]Z_t{Z}_t^{\prime }+{\sum }_{i\ne j}^{T}E[{\stackrel{\sim }{\epsilon }}_i{\stackrel{\sim }{\epsilon }}_j{I}_i{I}_j(A_i-{\rho }_i)(A_j-{\rho }_j)]Z_i{Z}_j^{\prime }$. Under assumptions (a), (b) and (c), we have E[ε̃_t |I_t = 1, A_t] = 0 and $E[{\stackrel{\sim }{\epsilon }}_t^2{I}_t{(A_t-{\rho }_t)}^2]=E[I_t]{\rho }_t(1-{\rho }_t){\overline{\sigma }}^2$. Furthermore, suppose i > j, then E[ε̃_iε̃_j I_i I_j (A_i − ρ)(A_j − ρ)]= E[I_i I_j (A_j − ρ)(A_i − ρ)]×E[ε̃_tε̃_s|I_t = 1, I_s = 1, A_t, A_s] = 0, because A_i⫫{I_i, I _j, A_j } and the first term is 0.W is then given by

$$W={\overline{\sigma }}^2\sum _{t=1}^{T}E[I_t]{\rho }_t(1-{\rho }_t)Z_t{Z}_t^{\prime },$$

so that ${\mathrm{\sum }}_{\beta }={\overline{\sigma }}^2{({\sum }_{t=1}^{T}E[I_t]{\rho }_t(1-{\rho }_t)Z_t{Z}_t^{\prime })}^{-1}$ and $c_N=N{(\overline{\sigma }\stackrel{\sim }{d})}^{\prime }{\mathrm{\sum }}_{\beta }^{-1}(\overline{\sigma }\stackrel{\sim }{d})=N{d}^{\prime }\left({\sum }_{t=1}^{T}E[I_t]{\rho }_t(1-{\rho }_t)Z_t{Z}_t^{\prime }\right)d$.

Remark

Working assumption (d) can be replaced by assuming E[Y_t+1|I_t = 1, A_t, I_s = 1, A_s]−E[Y_t+1|I_t = 1, A_t] does not depend on A_t for any s < t, or some Markovian type of assumption, e.g. Y_t+1⫫{Y_s+1, I_s, A_s, s < t}|I_t, A_t. Either of them implies E[ε̃_iε̃_j I_i I_j (A_i−ρ_i)(A_j−ρ_j)]= 0, so that Σ_β and c_N have the same simplified forms.

Rationale for multiple of F distribution

The distribution of the quadratic form, n(X̄−μ)′Σ̂⁻¹(X̄ − μ) constructed from a random sample of size n of N(μ,Σ) random variables in which Σ̂ is the sample covariance matrix follows a Hotelling’s T-squared distribution. The Hotelling’s T-squared distribution is a multiple of the F distribution, $\frac{d_1(d_1+d_2-1)}{d_2}{F}_{d_1,d_2}$ in which d₁ is the dimension of μ, and d₂ is the sample size. Our sample sample approximation replaces d₁ by p (the number of parameters in the test statistic) and d₂ by n−q−p (the sample size minus the number of nuisance parameters minus d₁).

Formula for adjusted Ŵ and Q̂

Define a individual-specific residual vector ê as the T ×1 vector with tth entry ${\widehat{e}}_t=Y_{t+1}-I_t{B}_t^{\prime }\widehat{\alpha }-I_t(A_t-{\rho }_t)Z_t^{\prime }\widehat{\beta }$. For each individual define the tth row of the T ×(p +q) individual-specific matrix X by ( $I_t{B}_t^{\prime }$, I_t(A_t−ρ_t)Z_t). Then define H = X [ℙ_N X′X]⁻¹ X′. The matrix Q̂⁻¹ is given by the lower right p × p block in the inverse of [ℙ_N X′X]; the matrix Ŵ is given by the lower right p × p block in ℙ_N [X^T (I−H)⁻¹êê′(I−H)⁻¹X].

Appendix B Further Simulations and Details

B.1 Simulation Results When Working Assumptions are True

We conduct a variety of simulations in settings in which the working assumptions hold, the scientist provides the correct pattern for the expected availability, τ_t = E[I_t] and under the alternate, the standardized proximal main effect is $d(t)=Z_t^{\prime }d$. Here we will mainly focus on the setup where the duration of the study is 42 days and there are 5 decision times within each day, but similar results can be obtained in different setups; see below. The randomization probability is 0.4, i.e. ρ = ρ_t = P(A_t = 1) = 0.4. The sample size formula is given in (8) and (9). The test statistic is given by (6) in which B_t and Z_t equal to ${(1,\lfloor \frac{t-1}{5}\rfloor ,{\lfloor \frac{t-1}{5}\rfloor }^2)}^{\prime }$. All simulations are based on 1,000 simulated data sets. The significance level is 0.05 and the desired power is 80%.

In the first simulation, the data for each simulated subject is generated sequentially as follows. For t = 1, …,T = 210, I_t, A_t and Y_t+1 are generated by

$$\begin{array}{l}{I}_t\stackrel{\mathit{Ber}}{\sim }({\tau }_t),A_t\stackrel{\mathit{Ber}}{\sim }(\rho )\\ Y_{t+1}=\alpha (t)+(A_t-\rho )d(t)+{\epsilon }_t,\text{if}{I}_t=1\end{array}$$

where $d(t)=Z_t^{\prime }d$ and τ_t are same as in the sample size model. The conditional mean, E[Y_t+1|I_t = 1] = α(t) is given by $\alpha (t)={\alpha }_1+{\alpha }_2\lfloor \frac{t-1}{5}\rfloor +{\alpha }_3{\lfloor \frac{t-1}{5}\rfloor }^2$, where α₁ = 2.5, α₂ = 0.727,α₃ = −8.66 × 10⁻⁴ (so that (1/T) Σ_t α(t) − α(1) = 1, argmax_t α(t) = T). We consider 5 differing distributions for the errors ${\{{\epsilon }_t\}}_{t=1}^T$: independent normal; independent (scaled) Student’s t distribution with 3 degrees of freedom; independent (centered) exponential distribution with λ = 1; a Gaussian AR(1) process, e.g. ε_t = ϕε_t−1+v_t, where v_t is white noise with variance ${\sigma }_v^2$ such that Var(ε_t) = 1; and lastly a Gaussian AR(5) process, e.g. ${\epsilon }_t=\frac{\varphi }{5}{\sum }_{j=1}^5{\epsilon }_{t-j}+v_t$, where v_t is white noise with variance ${\sigma }_v^2$ such that Var(ε_t) = 1. In all cases the errors are scaled to have mean 0 and variance 1 (i.e. E[ε_t |I_t = 1] = 0, Var[ε_t |A_t, I_t = 1] = 1). Additionally four availability patterns, e.g. time varying values for τ_t = E[I_t], are considered; see Figure (1). The simulated type 1 error rate and power when the duration of study is 42 days are reported in Table 2B and 3B. The simulation results in other setups, e.g. the length of the study is 4 week and 8 week, are reported in Table 4B. The associated sample sizes are given in Table 1B.

Since neither the working assumptions nor the inputs to the sample size formula specify the dependence of the availability indicator, I_t on past treatment. In the second simulation, we consider the setting in which the availability decreases as the number of treatments provided in the recent past increase. In particular, the data are generated as follows,

$$\begin{array}{l}{I}_t\stackrel{\mathit{Ber}}{\sim }({\tau }_t+\eta \sum _{j=1}^5(A_{t-j}{I}_{t-j}-E[A_{t-j}{I}_{t-j}])),A_t\stackrel{\mathit{Ber}}{\sim }(\rho )\\ Y_{t+1}=\alpha (t)+(A_t-\rho )d(t)+{\epsilon }_t,\text{if}{I}_t=1\end{array}$$

Note that since we center ${\sum }_{j=1}^5{A}_{t-j}{I}_{t-j}$ in the generative model of I_t, the expected availability is τ_t. The specification of α(t), β(t) and ε_t are same as in the first simulation. The simulated type I error rate and power are reported Table 5B.

B.2 Further Details When Working Assumptions are False

B.2.1 Working Assumption (a) is Violated

Here we consider another setting in which the working assumption (a) is violated, e.g. the underlying true E[Y_t+1|I_t = 1] follows a non-quadratic form(recall that B_t is given by ${(1,\lfloor \frac{t-1}{5}\rfloor ,{\lfloor \frac{t-1}{5}\rfloor }^2)}^{\prime }$). The data is generated as follows

$$\begin{array}{l}{I}_t\stackrel{\mathit{Ber}}{\sim }({\tau }_t),A_t\stackrel{\mathit{Ber}}{\sim }(\rho )\\ Y_{t+1}=\alpha (t)+(A_t-\rho )Z_t^{\prime }d+{\epsilon }_t,\text{if}{I}_t=1\end{array}$$

where α(t) = E[Y_t+1|I_t = 1] is provided in Figure 4. For each case, α(t) satisfies α(1) = 2.5 and $(1/T){\sum }_{t=1}^T-\alpha (1)=0.1$. The error terms ${\{{\epsilon }_t\}}_{t=1}^N$ are i.i.d N(0, 1). The day of maximal proximal effect is assumed to be 29. Additionally, different values of averaged standardized treatment effect and four patterns of availability in Figure 1 with average 0.5 are considered. The simulation results are reported in Table 7B.

B.2.2 Additional Simulation Results When Other Working Assumptions are False

The main body of the paper reports part of the results when working assumptions (b), (c) and (d) are violated. Additional simulation results are provided here. In particular, the simulation result is reported in Table 9B when d(t) follows other non-quadratic forms, e.g. working assumption (b) is false; see Figure 5. The simulated Type 1 error rate and power when working assumption (c) is false are reported in Table 10B. The simulated Type 1 error rate when working assumption (d) is violated is reported in Table 11B.

B.2.3 Simulation Results when d̄ and τ̄ are misspecified

As discussed in the paper, the first scenario considers the setting in which the scientist provides the correct availability pattern, ${\{E[I_t]\}}_{t=1}^T$, the correct time at which the maximal standardized proximal main effect is achieved ( ${\text{argmax}}_t{Z}_t^{\prime }d$) and the correct initial standardized proximal main effect ( $Z_1^{\prime }d=d_1=0$) but provides too low a value of the averaged across time, standardized proximal main effect $\overline{d}=\frac{1}{T}{\sum }_{t=1}^T{Z}_t^{\prime }d$. The simulated power is provided in Table 12B. In the second scenario, the scientist provides the correct ${\text{argmax}}_t{Z}_t^{\prime }d$, correct $Z_1^{\prime }d=d_1=0$, correct $\overline{d}=\frac{1}{T}{\sum }_{t=1}^T{Z}_t^{\prime }d$ and although the scientist’s time-varying pattern of availability is correct, the magnitude, e.g. the average availability, is underestimated. The simulation result is in Table 13B.

Table 1B.

Sample Sizes when the proximal treatment effect satisfies $d(t)=Z_t^{\prime }d$. The significance level is 0.05. The desired power is 0.80.

Duration of Study	Availability Pattern	Max	τ̄= 0.5			τ̄= 0.7
			Average Proximal Effect
			0.10	0.08	0.06	0.10	0.08	0.06
4-week	Pattern 1	15	59	89	154	43	65	112
		22	60	91	158	44	66	114
		29	58	87	152	43	64	110
	Pattern 2	15	59	89	154	43	65	112
		22	60	92	159	44	67	115
		29	58	89	154	43	64	111
	Pattern 3	15	59	90	157	44	66	113
		22	63	96	167	46	69	119
		29	62	94	163	45	67	115
	Pattern 4	15	59	89	155	43	65	112
		22	57	86	150	43	64	110
		29	54	82	142	41	61	105
6-week	Pattern 1	22	41	61	105	31	45	76
		29	42	64	109	32	47	79
		36	41	62	106	31	45	77
	Pattern 2	22	41	61	105	31	45	76
		29	43	64	110	32	47	80
		36	42	62	107	31	46	77
	Pattern 3	22	42	62	106	31	46	77
		29	44	66	114	33	48	82
		36	43	65	112	32	47	80
	Pattern 4	22	41	62	106	31	45	77
		29	41	62	106	31	46	78
		36	40	59	101	30	44	74
8-week	Pattern 1	29	32	47	80	25	35	58
		36	33	49	84	26	37	61
		43	33	48	82	25	36	60
	Pattern 2	29	32	47	80	25	35	58
		36	34	49	84	26	37	61
		43	33	49	82	25	36	60
	Pattern 3	29	33	48	82	25	36	59
		36	35	51	87	26	38	63
		43	34	50	86	26	37	62
	Pattern 4	29	33	48	81	25	36	59
		36	33	49	83	25	36	61
		43	32	47	80	25	35	59

“Max” is the day in which the maximal proximal effect is attained. $\overline{\tau }=(1/T){\sum }_{t=1}^{T}E[I_t]$ is the average availability.

Table 2B.

Simulated Type I error rate (%) when working assumptions are true. Duration of the study is 6-week. The associated sample size is given in Table 1B.

Error Term	Availability Pattern	Max	τ̄ = 0.5			τ̄= 0.7
			Average Proximal Effect
			0.10	0.08	0.06	0.10	0.08	0.06
i.i.d. Normal	Pattern 1	22	3.8	4.5	4.9	4.6	5.3	4.8
		29	4.7	6.0	4.6	4.0	3.2	5.0
		36	5.0	5.4	4.9	4.3	4.8	4.6
	Pattern 2	22	4.8	4.1	4.8	4.4	3.5	4.1
		29	4.3	6.2	3.2	4.6	4.2	4.2
		36	4.5	4.8	5.2	4.5	3.5	5.4
	Pattern 3	22	4.7	4.5	6.3	4.4	4.9	4.9
		29	4.1	5.1	4.6	4.3	6.0	5.6
		36	4.7	4.4	4.6	4.1	5.1	4.4
	Pattern 4	22	5.4	3.5	4.5	4.8	4.7	5.0
		29	5.2	4.5	4.5	5.0	5.0	5.1
		36	3.8	4.1	5.4	4.7	5.0	5.9
i.i.d. t dist.	Pattern 1	22	4.3	4.4	3.2	4.1	4.1	5.2
		29	5.0	3.8	3.2	3.7	4.2	6.3
		36	4.3	4.5	4.0	5.0	5.7	5.4
i.i.d. Exp.	Pattern 1	22	4.5	4.6	4.4	3.7	7.1	3.1
		29	4.5	4.6	4.2	4.5	4.5	4.7
		36	2.7	4.8	4.8	3.9	3.7	3.4
AR(1), ϕ = −0.6	Pattern 1	22	4.3	5.3	4.6	3.8	4.2	4.0
		29	4.6	5.4	5.1	4.0	4.4	4.3
		36	4.7	4.0	4.0	4.1	4.2	3.9
AR(1), ϕ = −0.3	Pattern 1	22	5.8	3.4	4.4	3.3	4.0	5.4
		29	4.9	4.7	4.6	5.5	5.5	4.5
		36	4.0	4.7	4.4	4.9	5.0	4.7
AR(1), ϕ = 0.3	Pattern 1	22	4.6	4.6	4.9	4.3	5.4	4.1
		29	4.8	5.3	4.1	4.3	4.2	5.2
		36	3.6	3.9	4.9	4.8	4.9	4.9
AR(1), ϕ = 0.6	Pattern 1	22	4.4	5.1	4.9	3.6	5.2	3.7
		29	3.7	4.9	4.6	4.5	4.3	5.8
		36	4.4	6.7	5.2	5.6	3.6	5.1
AR(5), ϕ = −0.6	Pattern 1	22	4.4	4.7	5.1	4.2	4.5	5.5
		29	4.3	5.1	4.3	3.2	3.5	4.2
		36	5.3	4.5	6.1	4.2	4.6	5.4
AR(5), ϕ = −0.3	Pattern 1	22	3.7	4.4	6.0	5.0	4.5	3.5
		29	4.4	4.7	5.2	5.3	4.5	5.0
		36	4.5	5.0	5.1	4.1	5.3	4.8
AR(5), ϕ = 0.3	Pattern 1	22	5.3	4.3	5.7	4.8	4.1	4.3
		29	3.9	4.8	4.1	4.0	4.3	4.9
		36	4.2	5.5	5.1	3.6	4.5	3.6
AR(5), ϕ = 0.6	Pattern 1	22	5.1	4.5	4.0	4.5	3.8	5.2
		29	5.2	4.8	4.5	2.9	5.3	4.4
		36	4.1	3.6	4.6	3.9	4.4	4.9

“Max” is the day in which the maximal proximal effect is attained. $\overline{\tau }=(1/T){\sum }_{t=1}^{T}E[I_t]$ is the average availability. ϕ is the parameter for AR(1) and AR(5) process. Bold numbers are significantly(at .05 level) greater than .05.

Table 3B.

Simulated Power (%) when working assumptions are true. Duration of the study is 6-week. The associated sample size is given in Table 1B

Error Term	Availability Pattern	Max	τ̄ = 0.5			τ̄= 0.7
			Average Proximal Effect
			0.10	0.08	0.06	0.10	0.08	0.06
i.i.d. Normal	Pattern 1	22	80.9	80.0	81.0	78.7	77.5	80.7
		29	78.4	80.6	77.8	80.6	78.7	79.0
		36	80.2	80.0	79.6	79.4	80.2	77.0
	Pattern 2	22	80.3	78.1	78.8	80.6	79.6	79.8
		29	80.3	79.1	80.2	77.4	79.9	79.9
		36	76.8	79.3	80.2	78.5	78.4	80.0
	Pattern 3	22	83.5	81.5	77.7	78.5	81.3	78.7
		29	77.9	79.1	78.5	77.8	78.8	79.0
		36	77.3	78.1	79.8	79.8	79.9	79.1
	Pattern 4	22	77.2	79.7	81.8	80.2	79.0	78.8
		29	80.1	78.8	80.3	79.4	80.6	80.1
		36	80.5	79.4	80.0	78.9	79.9	78.1
i.i.d. t dist.	Pattern 1	22	80.4	81.9	81.0	79.7	79.4	80.7
		29	81.7	82.2	82.2	79.1	82.3	77.3
		36	80.8	78.8	79.5	81.8	81.6	79.9
i.i.d. Exp.	Pattern 1	22	81.0	81.6	79.7	77.2	80.1	80.2
		29	80.6	82.4	80.3	79.0	79.8	80.3
		36	82.1	79.8	80.8	79.8	79.5	80.3
AR(1), ϕ = −0.6	Pattern 1	22	78.5	80.3	78.5	82.3	79.8	80.3
		29	78.7	80.8	80.0	77.1	79.5	77.9
		36	77.7	80.3	80.2	78.2	77.4	83.6
AR(1), ϕ = −0.3	Pattern 1	22	77.9	79.0	79.6	80.0	77.8	80.4
		29	77.9	79.1	80.0	79.0	78.0	78.4
		36	78.1	81.2	80.2	80.7	80.9	78.4
AR(1), ϕ = 0.3	Pattern 1	22	80.2	78.5	80.8	80.5	79.6	82.6
		29	78.0	80.0	80.0	78.0	79.4	80.1
		36	77.6	82.5	80.6	77.0	78.9	82.0
AR(1), ϕ = 0.6	Pattern 1	22	80.4	79.8	79.5	80.7	79.5	82.0
		29	78.9	81.5	79.3	79.5	81.3	79.5
		36	79.5	78.4	78.8	80.1	77.9	77.8
AR(5), ϕ = −0.6	Pattern 1	22	79.9	79.4	80.0	78.7	79.2	79.4
		29	80.0	78.3	79.1	76.8	79.6	79.3
		36	80.5	80.0	79.2	80.1	78.0	80.4
AR(5), ϕ = −0.3	Pattern 1	22	79.2	80.4	81.9	81.3	77.7	79.1
		29	80.0	82.3	80.5	80.5	82.2	79.2
		36	75.9	78.7	79.3	79.0	79.4	79.9
AR(5), ϕ = 0.3	Pattern 1	22	79.4	80.8	79.8	79.5	77.3	81.2
		29	78.0	79.2	79.2	79.2	80.5	78.4
		36	78.3	79.1	78.1	80.7	80.5	79.5
AR(5), ϕ = 0.6	Pattern 1	22	80.2	77.9	80.3	78.6	78.4	80.3
		29	76.9	79.3	80.2	79.1	80.6	80.5
		36	78.7	84.0	80.1	78.8	79.3	78.8

“Max” is the day in which the maximal proximal effect is attained. $\overline{\tau }=(1/T){\sum }_{t=1}^{T}E[I_t]$ is the average availability. ϕ is the parameter for AR(1) and AR(5) process. Bold numbers are significantly(at .05 level) less than .80.

Table 4B.

Simulated type 1 error rate(%) and power(%) when the duration of study is 4-week and 8-week. Error terms follow i.i.d. N(0,1). The associated sample size is given in Table 1B.

Duration of Study	Availability Pattern	Max	τ̄ = 0.5			τ̄= 0.7
			Average Proximal Effect
			0.10	0.08	0.06	0.10	0.08	0.06
4-week	Pattern 1	15	4.1	4.7	6.3	5.3	5.5	5.6
		22	5.2	4.4	4.7	3.1	4.7	4.4
		29	5.7	5.5	5.6	4.3	4.2	4.2
	Pattern 2	15	4.8	4.8	5.0	5.0	5.2	5.3
		22	5.1	5.2	4.7	3.7	4.2	3.7
		29	5.6	5.1	4.2	4.2	4.9	4.4
	Pattern 3	15	4.7	5.0	4.6	6.1	5.3	5.1
		22	4.9	4.0	6.6	4.2	3.8	4.1
		29	4.7	4.3	5.1	4.6	5.8	3.5
	Pattern 4	15	4.9	4.6	4.8	3.0	5.9	3.8
		22	3.5	5.1	4.5	5.2	3.8	6.0
		29	4.4	6.4	4.7	4.4	4.3	4.7
8-week	Pattern 1	29	4.1	4.6	4.0	5.3	5.0	5.9
		36	3.3	4.7	6.5	4.6	5.4	4.3
		43	3.2	5.1	5.2	5.0	3.4	5.0
	Pattern 2	29	3.9	5.0	4.5	4.2	3.7	4.1
		36	3.8	4.6	4.9	4.5	3.4	5.2
		43	3.9	5.4	5.0	3.4	3.8	5.0
	Pattern 3	29	4.6	4.2	3.7	5.2	4.1	4.0
		36	4.3	5.1	6.1	4.6	5.0	4.6
		43	4.6	6.0	4.1	5.0	4.9	4.0
	Pattern 4	29	4.5	5.2	2.9	3.6	5.3	4.4
		36	4.5	5.2	3.7	2.7	3.7	4.7
		43	4.2	7.1	4.9	4.4	4.5	4.8
4 week	Pattern 1	15	80.4	79.0	78.5	79.6	82.8	80.3
		22	78.8	78.7	80.7	78.7	79.2	80.0
		29	76.2	80.6	80.1	81.3	80.1	79.1
	Pattern 2	15	82.4	77.8	77.2	75.9	80.0	78.9
		22	77.2	80.3	81.5	75.8	80.7	82.0
		29	80.1	79.3	80.1	78.0	77.7	76.9
	Pattern 3	15	79.3	79.8	79.2	79.1	76.5	80.8
		22	80.0	80.0	79.0	79.0	80.2	81.8
		29	79.4	80.7	79.3	80.4	79.6	79.2
	Pattern 4	15	82.6	78.3	79.2	80.5	80.0	79.5
		22	80.4	80.7	79.3	79.1	78.5	79.2
		29	78.4	79.2	78.5	79.6	79.2	80.5
8 week	Pattern 1	29	79.7	77.3	76.4	79.1	82.2	79.6
		36	78.8	78.6	81.5	80.3	78.2	79.6
		43	80.4	77.8	78.7	79.1	80.3	80.1
	Pattern 2	29	79.3	81.1	79.8	78.7	79.7	80.2
		36	81.2	78.5	79.0	81.3	80.8	78.2
		43	80.3	81.5	77.5	75.1	78.8	78.1
	Pattern 3	29	80.1	79.0	77.1	78.2	80.4	78.8
		36	79.5	79.9	79.6	80.0	80.8	79.6
		43	80.5	79.5	79.6	79.4	79.4	80.2
	Pattern 4	29	82.1	79.7	80.7	79.7	79.0	78.4
		36	77.8	78.2	80.1	77.9	76.9	79.5
		43	79.6	78.5	78.1	79.4	80.6	79.5

“Max” is the day in which the maximal proximal effect is attained. $\overline{\tau }=(1/T){\sum }_{t=1}^{T}E[I_t]$ is the average availability. Bold numbers are significantly(at .05 level) greater than .05 (for type I error)and less than .80 (for power).

Table 5B.

Simulated Type 1 error rate(%) and power(%) when the availability indicator, I_t depends on the recent past treatments with η = −0.2. The expected availability is constant in t and equal to 0.5. Duration of study is 42 days. The associated sample size is given in Table 1B.

Error Term	ϕ	Max	τ̄ = 0.5			τ̄= 0.7			τ̄ = 0.5			τ̄ = 0.7
			Average Proximal Effect
			0.10	0.08	0.06	0.10	0.08	0.06	0.10	0.08	0.06	0.10	0.08	0.06
AR(1)	−0.6	22	4.8	5.4	4.5	3.4	5.8	3.7	81.5	78.0	79.4	81.7	77.9	80.7
		29	4.7	4.4	4.2	4.0	4.9	4.6	79.4	80.9	80.7	78.2	79.2	79.7
		36	4.3	5.3	4.4	4.2	3.9	5.5	79.5	81.5	79.8	80.2	79.2	80.7
	−0.3	22	4.7	3.8	4.4	3.5	4.4	4.6	78.7	81.2	80.3	80.9	77.9	78.5
		29	3.8	4.0	4.9	3.5	5.0	4.4	80.1	79.5	81.2	77.3	79.5	77.1
		36	2.7	5.7	4.0	3.3	4.7	5.2	76.8	80.4	79.9	78.8	79.5	79.4
	0.3	22	4.8	4.1	4.4	5.0	5.4	3.6	83.0	79.8	79.4	81.3	78.9	79.2
		29	4.9	4.6	5.0	4.4	5.5	5.6	79.5	80.3	82.2	78.5	80.7	77.6
		36	4.9	4.9	4.2	3.3	4.5	4.8	80.0	78.9	79.5	81.7	79.4	79.6
	0.6	22	4.5	5.1	4.7	4.3	4.6	4.0	80.3	78.9	81.1	81.2	81.5	77.9
		29	3.4	4.5	5.1	4.4	4.3	4.6	79.3	76.2	79.4	81.3	80.6	79.4
		36	4.8	4.3	4.2	4.1	4.5	4.5	77.5	80.5	80.9	76.7	80.0	79.7
AR(5)	−0.6	22	4.8	4.6	4.3	3.7	4.7	3.5	81.9	81.4	81.6	79.8	78.3	78.9
		29	6.5	4.1	4.5	3.3	4.5	4.8	77.5	79.9	79.8	79.9	79.3	79.3
		36	3.5	5.7	4.4	4.6	4.7	5.7	77.8	80.8	78.6	77.9	79.2	81.7
	−0.3	22	4.3	4.9	4.0	4.3	5.6	5.0	77.7	81.8	80.0	80.1	80.3	81.1
		29	3.9	4.0	5.0	3.2	5.7	5.1	80.0	80.9	80.3	80.6	80.3	77.8
		36	4.0	3.6	4.7	4.8	4.8	3.2	79.0	80.4	80.8	80.1	79.0	76.5
	0.3	22	3.5	4.9	5.0	4.1	3.8	4.1	77.4	82.9	78.5	80.6	81.4	80.2
		29	4.6	6.1	4.7	4.7	4.1	4.1	78.7	82.0	78.0	81.4	76.5	81.3
		36	5.1	4.4	4.0	3.2	3.9	4.7	79.7	81.8	78.6	79.1	77.4	79.0
	0.6	22	5.0	4.6	4.3	4.0	4.0	5.5	80.5	79.4	82.5	79.2	81.1	81.0
		29	5.6	4.3	6.9	5.6	3.4	3.1	78.3	80.0	80.5	80.8	80.4	78.4
		36	4.8	4.8	4.8	3.5	3.7	5.5	78.2	80.5	80.3	77.6	80.5	79.1

“Max” is the day in which the maximal proximal effect is attained. $\overline{\tau }=(1/T){\sum }_{t=1}^{T}E[I_t]$ is the average availability. ϕ is the parameter for AR(1) and AR(5) process. Bold numbers are significantly(at .05 level) greater than .05 and less than .80.

Table 6B.

Simulated type I error rate(%) and power(%) when working assumption (a) is violated. Scenario 1. The average availability is 0.5. The day of maximal proximal effect is 29.

θ	d̄	Availability Pattern
		Pattern 1	Pattern 2	Pattern 3	Pattern 4	Pattern 1	Pattern 2	Pattern 3	Pattern 4
0.5d̄	0.10	5.5	4.6	4.2	5.1	79.7	79.4	80.5	80.1
	0.08	5.1	4.4	5.4	4.6	80.4	78.9	80.4	78.7
	0.06	4.1	5.5	4.6	4.3	77.5	82.7	81.0	81.0
d̄	0.10	4.8	4.3	3.7	4.1	79.3	78.3	77.8	79.4
	0.08	5.4	4.9	4.6	5.5	78.8	79.3	78.0	80.6
	0.06	4.4	3.5	5.1	4.6	78.4	79.3	79.0	80.4
1.5d̄	0.10	4.4	4.1	4.4	4.8	78.3	80.5	78.4	79.9
	0.08	5.0	4.3	4.3	3.9	80.5	79.7	78.7	81.9
	0.06	4.0	5.1	5.5	5.6	77.2	80.8	81.6	80.3
2d̄	0.10	4.1	3.8	5.0	5.5	77.7	78.8	79.0	78.4
	0.08	4.0	5.0	3.7	5.7	79.3	81.5	79.1	79.4
	0.06	4.9	4.3	5.2	5.3	80.8	79.0	77.5	80.9

$\overline{d}=(1/T){\sum }_{t=1}^T{Z}_t^{\prime }d$ is the average proximal effect. θ is the coefficient of Wt in E[Y_t+1|I_t = 1]. Bold Numbers are significantly (at .05 level) greater than .05 (for type I error rate) and lower than 0.80(for power).

Figure 4.

Conditional expectation of proximal response, E[Y_t+1|I_t = 1]. The horizontal axis is the decision time point. The vertical axis is E[Y_t+1|I_t = 1].

Table 7B.

Simulated Type 1 error rate(%) and power (%) when working assumption (a) is violated. Scenario 2. The shapes of α(t) = E[Y_t+1|I_t = 1] and patterns of availability are provided in Figure 4 and Figure 1. The average availability is 0.5. The day of maximal proximal effect is 29. The associated sample size is given in Table 1B.

α(t)	d̄	Availability Pattern
		Pattern 1	Pattern 2	Pattern 3	Pattern 4	Pattern 1	Pattern 2	Pattern 3	Pattern 4
Shape 1	0.10	3.6	4.3	4.7	4.5	77.4	80.2	76.2	75.9
	0.08	5.9	3.8	4.1	3.4	79.7	80.1	78.9	80.6
	0.06	4.6	5.7	4.2	6.5	78.7	76.3	78.3	79.9
Shape 2	0.10	4.8	4.8	4.4	4.1	79.2	79.1	78.5	79.7
	0.08	3.9	5.4	4.8	4.3	77.7	80.4	76.8	80.9
	0.06	5.1	5.5	3.4	4.9	78.3	79.4	79.8	80.2
Shape 3	0.10	5.1	3.5	4.3	4.4	79.1	79.4	75.6	78.0
	0.08	4.6	5.0	6.2	3.8	78.3	78.1	79.1	78.1
	0.06	4.8	4.4	5.4	4.2	78.0	78.3	79.8	77.7

$\overline{d}=(1/T){\sum }_{t=1}^T{Z}_t^{\prime }d$ is the average standardized treatment effect. Bold numbers are significantly (at .05 level) greater than .05 (for type I error rate) and lower than 0.80(for power).

Figure 5.

Proximal Main Effects of Treatment, ${\{d(t)\}}_{t=1}^T$: representing maintained, slightly degraded and severely degraded time-varying treatment effects. The horizontal axis is the decision time point. The vertical axis is the standardized treatment effect. The “Max” in the title refers to the day of maximal effect. The average standardized proximal effect is 0.1 in all plots.

Table 10B.

Simulated Type I error rate(%) and power(%) when working assumption (c) is violated. The trends of σ̄_t are provided in Figure 3. The standardized average effect is 0.1. E[I_t] = 0.5. The associated sample sizes are 41 and 42 when the day of maximal effect is 22 and 29.

ϕ in AR(1)	$\frac{{\sigma }_{1t}}{{\sigma }_{0t}}$	Max = 22				Max = 22
		const.	trend 1	trend 2	trend 3	const.	trend 1	trend 2	trend 3
−0.6	0.8	4.1	4.3	3.3	5.4	4.7	4.9	2.8	4.1
	1.0	4.6	5.0	4.0	4.4	4.4	4.8	4.2	4.3
	1.2	3.8	4.5	5.2	5.5	4.3	4.1	4.5	3.8
−0.3	0.8	5.2	4.7	4.0	3.4	5.4	4.9	6.2	4.5
	1.0	4.9	4.5	4.5	4.3	5.2	5.1	4.0	3.7
	1.2	5.4	4.6	4.1	3.8	3.7	5.2	4.3	5.0
0	0.8	4.8	4.0	4.1	3.9	4.7	5.2	3.7	4.2
	1.0	5.4	4.0	5.8	3.9	4.1	4.0	5.9	5.7
	1.2	4.4	4.9	5.0	4.6	3.7	4.8	4.4	4.9
0.3	0.8	5.3	4.4	4.7	3.2	4.6	5.4	5.6	4.1
	1.0	5.5	4.0	3.4	3.7	5.0	4.6	4.0	3.6
	1.2	3.8	4.5	4.5	4.8	4.5	5.0	6.2	4.3
0.6	0.8	5.5	3.9	5.3	3.8	3.3	3.5	5.1	4.2
	1.0	4.0	3.7	5.2	5.1	4.8	5.1	5.0	4.7
	1.2	4.5	5.1	4.6	4.9	4.5	4.4	4.7	4.8
−0.6	0.8	82.8	82.7	83.7	79.9	83.6	80.6	88.7	79.2
	1.0	81.1	79.1	79.9	74.8	77.7	74.3	84.8	70.4
	1.2	76.6	76.3	76.3	70.6	77.6	72.0	80.7	70.4
−0.3	0.8	83.0	83.0	86.0	80.3	82.7	79.2	87.9	78.0
	1.0	77.6	81.4	80.7	74.9	79.1	74.5	86.0	73.7
	1.2	78.2	76.9	77.3	73.4	74.4	71.2	81.0	70.7
0	0.8	84.6	84.6	82.1	79.0	81.8	81.5	88.0	78.0
	1.0	80.1	78.6	80.9	73.6	77.7	76.5	86.1	71.8
	1.2	76.0	76.7	77.4	70.6	74.5	69.9	83.4	69.6
0.3	0.8	83.6	79.7	84.6	79.7	82.1	81.7	88.2	75.7
	1.0	81.5	82.4	82.3	73.9	79.5	74.6	85.1	71.5
	1.2	74.8	76.6	78.2	71.1	75.5	71.1	82.5	70.1
0.6	0.8	81.4	83.1	83.5	80.5	83.1	77.1	86.6	76.9
	1.0	80.7	76.4	79.0	74.8	80.4	73.4	84.7	76.8
	1.2	77.0	77.5	77.0	73.5	74.4	72.5	81.6	69.4

ϕ is the parameter in AR(1) process for ${\{{\epsilon }_t\}}_{t=1}^T$. Bold numbers are significantly(at .05 level) greater than .05 (for type I error)and less than .80 (for power).

Table 11B.

Simulated Type I error rate(%) when working assumption (d) is violated. E[I_t] = 0.5. The proximal effect $Z_t^{\prime }d$ satisfies the average is 0.1 and day of maximal effect is 29. N = 42.

Parameters in It	γ2	−0.1	−0.2	−0.3
	γ1
η1 = −0.1, η2 = −0.1	−0.2	5.7	3.2	3.9
	−0.5	3.2	4.2	4.9
	−0.8	4.2	5.1	5.5
η1 = −0.2, η2 = −0.1	−0.2	5.4	3.8	3.9
	−0.5	4.4	4.4	4.8
	−0.8	4.7	4.3	4.6
η1 = −0.1, η2 = −0.2	−0.2	4.5	5.0	5.0
	−0.5	4.9	3.8	6.0
	−0.8	4.7	4.8	4.8

η₁, η₂ are parameters in generating I_t . γ₁, γ₂ are coefficients in the model of Y_t+1. All Numbers in this table are significantly (at .05 level) greater than .05.

Table 12B.

Degradation in Power when average proximal main effect is underestimated. The day of maximal treatment effect is attained at day 29 and the average availability is 0.5 in all cases. The associated sample sizes for each value of average treatment effect are provided in first column.

d̄ in Sample Size Formula	True d̄	Availability Pattern
		Pattern 1	Pattern 2	Pattern 3	Pattern 4
0.10 (N = 42)	0.098	76.2	78.9	77.6	78.6
	0.096	75.1	74.6	78.8	74.0
	0.094	73.7	70.7	75.4	73.4
	0.092	71.5	71.6	73.2	71.6
	0.090	68.9	68.4	69.6	67.3
	0.088	65.4	65.6	66.1	65.7
	0.086	66.4	67.9	65.2	66.7
	0.084	62.3	63.4	63.0	59.6
	0.082	60.0	60.2	60.5	58.2
	0.080	58.9	59.8	57.8	61.4
0.08(N = 64)	0.078	78.2	80.2	76.8	75.8
	0.076	77.3	76.7	76.2	75.4
	0.074	73.1	72.2	71.2	71.4
	0.072	70.7	71.0	69.4	68.2
	0.070	68.2	66.0	65.2	66.1
	0.068	65.5	64.3	64.6	65.7
	0.066	62.8	62.3	61.8	59.4
	0.064	61.9	58.5	59.5	62.1
	0.062	53.9	52.6	57.0	56.9
	0.060	54.6	51.1	54.8	53.4
0.06(N = 109)	0.058	75.6	76.9	74.0	78.1
	0.056	73.9	73.1	73.1	72.7
	0.054	68.6	71.1	69.3	68.5
	0.052	65.4	69.4	63.6	66.8
	0.050	61.0	62.8	64.1	63.2
	0.048	57.4	58.6	56.4	56.1
	0.046	53.6	53.4	52.9	54.8
	0.044	52.0	48.9	50.1	53.0
	0.042	45.7	43.9	44.9	46.4
	0.040	40.4	42.2	42.3	42.7

Table 13B.

Degradation in Power when average availability is underestimated. The day of maximal treatment effect is attained at day 29 and the average proximal main effect is 0.1 in all cases. The associated sample sizes are given in first column.

$(1/T){\sum }_{t=1}^T{\tau }_t$ in Sample Size Formula	True $(1/T){\sum }_{t=1}^T{\tau }_t$	Availability Pattern
		Pattern 1	Pattern 2	Pattern 3	Pattern 4
0.5 (N = 42)	0.048	76.4	81.7	76.0	78.2
	0.046	73.9	75.5	73.6	75.8
	0.044	70.6	72.1	71.0	71.7
	0.042	70.8	70.6	74.2	70.3
	0.040	70.3	69.2	65.7	68.6
	0.038	66.0	66.8	67.8	67.0
	0.036	64.0	62.5	62.4	62.9
	0.034	60.8	61.3	59.4	63.9
	0.032	56.4	59.2	54.7	59.8
	0.030	51.4	53.1	51.9	54.5
0.7 (N = 32)	0.068	79.5	76.1	79.1	75.0
	0.066	77.3	75.7	74.0	76.4
	0.064	74.5	74.7	73.5	77.1
	0.062	73.2	73.0	75.1	72.5
	0.060	69.8	70.5	73.5	72.5
	0.058	71.0	69.6	71.3	67.3
	0.056	68.8	70.3	66.6	64.0
	0.054	68.1	65.8	65.3	68.6
	0.052	62.4	64.9	65.6	62.9
	0.050	60.6	63.3	62.8	61.4