Selective spectroscopic imaging of hyperpolarized pyruvate and its metabolites using a single-echo variable phase advance method in balanced SSFP

Abstract

Purpose

In balanced steady state free precession (bSSFP), the signal intensity has a well-known dependence on the off-resonance frequency, or, equivalently, the phase advance between successive radiofrequency (RF) pulses. The signal profile can be used to resolve the contributions from the spectrally separated metabolites. This work describes a method based on use of a variable RF phase advance to acquire spatial and spectral data in a time-efficient manner for hyperpolarized 13C MRI.

Theory and Methods

The technique relies on the frequency response from a bSSFP acquisition to acquire relatively rapid, high-resolution images that may be reconstructed to separate contributions from different metabolites. The ability to produce images from spectrally separated metabolites was demonstrated in-vitro, as well as in-vivo following administration of hyperpolarized 1-13C pyruvate in mice with xenograft tumors.

Results

In-vivo images of pyruvate, alanine, pyruvate hydrate and lactate were reconstructed from 4 images acquired in 2 seconds with an in-plane resolution of 1.25 × 1.25mm² and 5mm slice thickness.

Conclusions

The phase advance method allowed acquisition of spectroscopically selective images with high spatial and temporal resolution. This method provides an alternative approach to hyperpolarized 13C spectroscopic MRI that can be combined with other techniques such as multi-echo or fluctuating equilibrium bSSFP.

Introduction

With the advent of hyperpolarized 13C MRI, non-invasive monitoring of metabolic transformations is becoming more readily studied. Use of hyperpolarized 13C to evaluate metabolism requires a combination of spatial, spectral and temporal information. Acquisition of these data types is complicated by the decay of the hyperpolarized state. As with MRI in general, this often leads to a trade-off between spatial and temporal resolution in dynamic imaging. The utility of dynamic hyperpolarized imaging to monitor metabolic pathways is demonstrated, for example, by investigation of 1-13C pyruvate and its products in cardiac (1,2) and oncologic (3,4) applications.

The utility of hyperpolarized 1-13C pyruvate for tumor diagnosis and characterization lies in inferring metabolic information via its conversion to/exchange with lactate, pyruvate hydrate, alanine and bicarbonate. The large differences in chemical shifts of these products lend themselves to techniques based on simultaneous excitation of all the metabolites, or methods for individual excitation to monitor single metabolite(s). The former includes spiral chemical shift imaging (CSI), and echo-planar spectroscopic imaging in conjunction with compressed sensing, which have combined two- and three- dimensional spectroscopic imaging with strategies to speed up acquisition (5–7). Although useful in some cases, the acquisition of a complete spectrum per voxel may not always be necessary if one has prior knowledge of the metabolites under investigation. The alternative approaches based on excitation of single metabolites include spectral-spatial radiofrequency (RF) pulses combined with echo-planar (8) or spiral readouts to facilitate cardiac gated acquisitions (2).

Balanced steady state free precession (bSSFP) may offer certain advantages relative to gradient- and spin-echo sequences for hyperpolarized imaging. In hyperpolarized imaging the magnetization decays continuously and hence there is no true (non-zero) steady state. With suitable preparation, however, the magnetization can be placed into a ‘pseudo-steady state’ (9) that has many of the properties of the conventional non-hyperpolarized steady state. In particular, the magnetization is refocused during each TR and hence decays at a rate set by T₂ rather than T₂^* as is the case in gradient-echo imaging (10). Consequently, relative to gradient-echo sequences, bSSFP enables imaging over a longer period of time or, alternatively, imaging at a higher tip angle (and with higher SNR) over the same period of time. Spin-echo sequences also refocus the magnetization, but, unlike bSSFP, require high tip-angle refocusing pulses. These refocusing pulses can rapidly consume the magnetization if there are errors in the tip angle calibration or significant B₁ inhomogeneities. The refocusing properties of bSSFP are relatively robust against such errors. The main disadvantage of bSSFP is its well-known sensitivity to off-resonance effects that can result in so-called ‘banding’ artifacts. The low gyromagnetic ratio of 13C reduces the sensitivity of bSSFP to off-resonance by roughly a factor of four (at a given TR) relative to proton imaging, enabling use of this technique at higher field strengths than would be readily achievable in proton imaging. In general, however, off-resonance artifacts are expected to be more common at higher field strengths, and bSSFP techniques may be best suited to imaging at low to moderate field strength.

Several strategies for spectroscopic imaging based on bSSFP have been described in the literature, including methods aimed at hyperpolarized 13C imaging. One approach is to acquire multiple echoes during each TR and generate spectroscopically selective images in a manner similar to conventional fat/water separation in proton MRI (11,12). An alternative approach is to exploit the off-resonance sensitivity of bSSFP to selectively excite a single metabolite (13,14). Both methods have some undesired sensitivity to off-resonance effects. Multi-echo methods generally require long TR values (which increase the sensitivity of bSSFP to off-resonance), while selective excitation schemes have a very narrow excitation bandwidth (BW) that generally requires combining several images acquired at slightly different frequency offsets.

Here we describe a method based on single-echo bSSFP that excites all metabolites simultaneously and acquires a series of images with different values of the phase advance between successive RF pulses. The method then uses a priori knowledge of the dependence of a given metabolite’s signal on the phase advance to reconstruct spectroscopically selective images. As with the multi-echo approach, this work holds its foundations in previous literature concerned with separation of water from fat (15). With suitable choice of repetition time TR, each metabolite’s signal has a distinct dependence on the phase advance. As described by Miller (16), the RF phase advance is closely related to the off-resonance frequency, so the method can be alternatively formulated in terms of the signal dependence on center frequency of the acquisition. Using this method, it is possible to correct off-resonance effects during the reconstruction process.

Theory

As noted above, there is no (non-trivial) steady state for hyperpolarized bSSFP imaging. However, with suitable preparation the magnetization can be placed in a pseudo-steady state that has many of the properties that are familiar from standard proton bSSFP imaging.

The orientation of the magnetization in the pseudo steady state can be determined using spinor methods. Spinor notation in MRI has been more fully explored in order to simplify considerations of rotation in three dimensions (17). In particular, the spinor formalism is adopted for mathematical simplification of the Shinnar-Le Roux algorithm used in RF pulse design (18,19). The reader is invited to look at the referenced (and other) works for greater detail regarding spinors, but for the purposes of brevity, this work continues under the assumption of a rudimentary understanding.

Consider a nuclear spin with chemical shift Δω rad s⁻¹under the influence of a series of RF pulses having tip angle α and applied with phases such that the axis of rotation in the xy-plane rotates clockwise by angle ϕ with each successive pulse. In the approximation that T₁ and T₂ are much longer than TR, and treating the RF pulses as instantaneous rotations, the evolution of the magnetization from one TE to the next is given by free precession about the z-axis for TR/2, an RF rotation about the appropriate axis by angle α, and a second free precession for TR/2 (9,17,20). The analysis is simplified in a modified rotating frame that rotates clockwise by ϕ radians per TR relative to the rotating frame defined by the center frequency of the scanner. In this frame, all of the RF pulses are applied with zero phase and can be treated as rotations about the x-axis. In addition, the off-resonance Δω is transformed into Δω+ϕ/(2πTR), and the evolution of the magnetization between successive echoes is:

$$\overrightarrow{M}({\text{TE}}_n)=R_z([\mathrm{\Delta }\omega \text{TR}+\varphi ]/2){\mathrm{R}}_x(\alpha )R_z([\mathrm{\Delta }\omega \text{TR}+\varphi ]/2)\overrightarrow{M}({\text{TE}}_{n-1})$$ (1)

where R_x,z are rotations about the x- and z-axes. The pseudo-steady state magnetization must be constant from one TE to the next. Since the evolution during this time is a pure rotation, the pseudo-steady state must be oriented along the net axis of rotation over one TR. Using spinor notation, a rotation by angle θ about axis â is given by R_â(θ) = cos(θ/2) + i(â.σ)sin(θ/2), where σ is the vector of Pauli matrices (17,19). The axis of any rotation R can be determined, up to an overall constant, by â ∝ Tr(iσR). Applying this to the above expression, we find that the axis of rotation, and hence the magnetization in the pseudo-steady state, is oriented along the axis:

$$\overrightarrow{M}({\text{TE}}_n)\propto \text{Tr}[i\sigma R_z(\mathrm{\Omega })R_x(\alpha )R_z(\mathrm{\Omega })]\propto [sin(\alpha /2)csc(\mathrm{\Omega }),0,cos(\alpha /2)]$$ (2)

where Ω = (ΔωTR+ϕ)/2 and the overall constant of proportionality is irrelevant. For small tip angles, the transverse magnetization is small except near ‘singular points’ (SPs) where Ω = 0, ±π, ±2π, …. The above expression determines orientation of the pseudo-steady state magnetization as a function of Ω, while the phase of the complex signal M = (M_x + iM_y)/√2 depends on the receiver phase. A convenient choice of phase is e^−iΩ, which, in the pseudo-steady state, yields:

$$M({\text{TE}}_n)\propto e^{-i\mathrm{\Omega }}csc(\mathrm{\Omega })sin(\alpha /2)$$ (3)

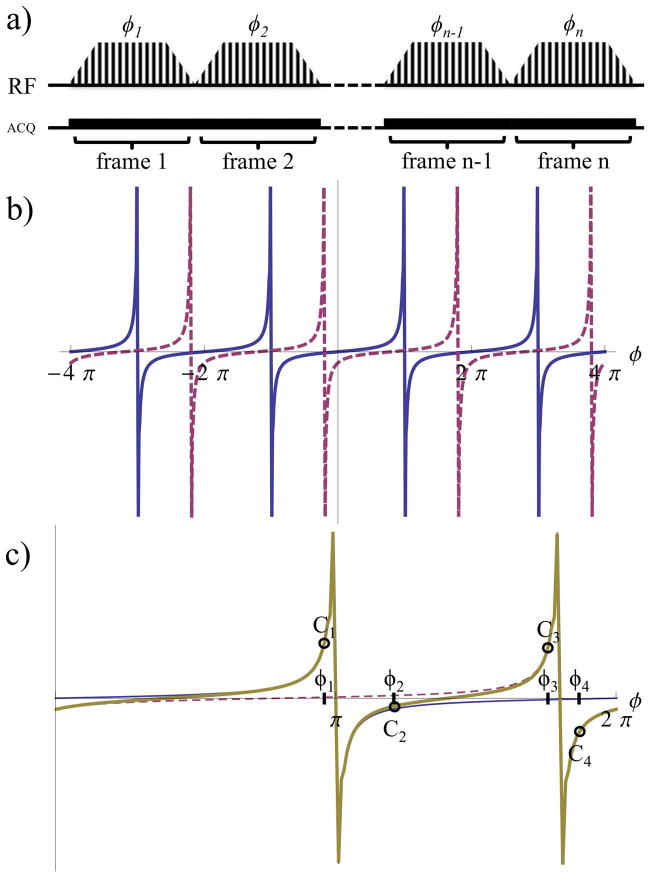
Numerical simulations were used to demonstrate that hyperpolarized spins with long relaxation times can be placed in the above pseudo-steady state by means of a suitable preparation. To place the magnetization in the pseudo-steady state, the RF tip angle was adiabatically increased from zero at the beginning of each acquisition to a maximum value and then adiabatically decreased to zero at the end of each acquisition (Fig. 1a). The adiabatic decrease serves to restore the magnetization to the z-axis after each image is acquired.

Figure 1.

a) Diagram of bSSFP sequence illustrates modulation of the RF pulses with a distinct phase advance value, ϕ for acquisition of a single image. The value of ϕ used to acquire N subsequent images cycles through the n phase advances calculated to allow separation of the signal from M metabolites. bSSFP signal profiles (real component) as functions of the phase advance value, ϕ shows b) repetition every 2π from metabolites A (blue, solid) and B (magenta, dashed); and c) the sum of the signal (gold, bold) from metabolites A and B. This combined signal C, for example, can be sampled at phase advance values ϕ_1-4 to surround the expected SPs for reconstruction using Equations 4–6.

An acquisition with 256 phase encoding steps was simulated utilizing a Fermi function modulation for the RF pulses. The signal after 128 RF pulses as a function of the offset frequency, Δω=2πΔf was simulated with: α_max=2.5° and TR=2ms, for two example metabolites (A and B) spectrally separated by Δf=1200Hz. With the above phase conventions, the signal response as a function of ϕ is repeated every 2π period (Fig. 1b). Figure 1c shows this signal evolution from metabolites A and B as a function of the phase advance within a 2π interval. SPs are observed in the signal from each metabolite. Thus, with a suitable choice of TR, for M metabolites there are M distinct SPs. The numerical simulations show good agreement with the signal response derived above (Fig. 1c and Eq. 3). Hence, for a series of N images acquired at phase advance values ϕ_n (Fig. 1a), the signal in the n^th image from a metabolite m at chemical shift Δω_m is:

$$S_{nm}\propto e^{-i[\mathrm{\Delta }{\omega }_m\text{TR}+{\varphi }_n]/2}csc([\mathrm{\Delta }{\omega }_m\text{TR}+{\varphi }_n]/2)$$ (4)

For suitable choices of TR, the signal depends on the chemical shift and the phase advance in a manner that can be used to extract individual metabolite signals from a series of images acquired at distinct phase advance values.

This approximation will be valid provided that the acquisition is fast enough (i.e. TR ≪ T₁, T₂), and the tip angle small enough (21), that relaxation can be neglected over the course of the acquisition of N images at different phase advance values necessary to reconstruct the M metabolites’ signals. Note that all metabolite signals have a common overall factor of sin(α/2) that is assumed constant over the series of images and is irrelevant to determining the relative signals of different metabolites. In the two-metabolite example shown in Fig. 1c, the combined signal from both metabolites (gold, bold line) is a combination of the signals from both metabolites. To extract individual metabolite signals from a series of images, acquired at distinct phase advance values, we note that the pixel-by-pixel image intensities C_n are linear combinations of the individual metabolite signals μ_m weighted by the frequency response found above. Hence we have a system of linear equations:

$$C_n={\sum }_{m=1}^M{e}^{-i[\mathrm{\Delta }{\omega }_m\text{TR}+{\varphi }_n]/2}csc([\mathrm{\Delta }{\omega }_m\text{TR}+{\varphi }_n]/2){\mu }_m\equiv {\sum }_{m=1}^M{S}_{nm}{\mu }_m$$ (5)

In matrix notation, the metabolite signals may be determined by inverting the matrix S. The least squares solution can be found using the Moore-Penrose pseudo-inverse:

$$\mathbf{\mu }={({\mathbf{S}}^{\mathrm{H}}\mathbf{S})}^{-1}{\mathbf{S}}^{\mathrm{H}}\mathbf{C}$$ (6)

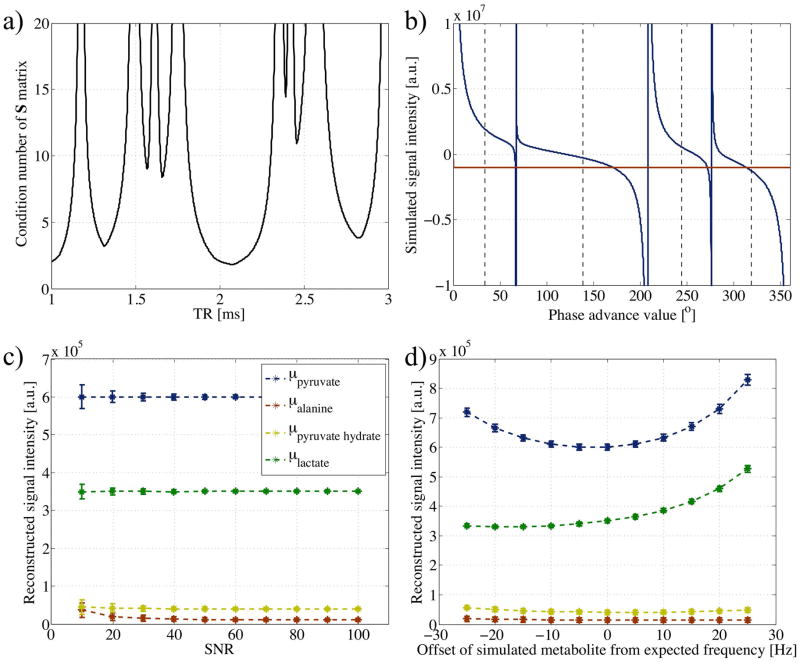
To acquire spectrally selective images with this technique it is necessary to choose TR and a set of phase advance values ϕ_n. These values should be chosen to minimize sensitivity to off-resonance effects (reducing artifacts), while ensuring that each metabolite’s signal has a unique dependence on the phase advance to enable robust separation of different metabolite signals. The gap between SPs associated with M metabolites avoids overlap thereby improving the ability to separate each metabolite’s signal. The SP of a metabolite is dependent on TR such that ϕ_m,SP=−Δω_mTR(modulo 2π). As in regular bSSFP, off-resonance effects may appear as artifacts at SPs but are reduced with shorter TRs. Thus TR should be chosen as short as possible (typically ~1.5–3ms) while maximizing the separation between adjacent metabolite SPs within 1/TR. The bSSFP signal as a function of ϕ (given by Eq. 4 and shown in Figs. 1b–c) varies more rapidly closer to SPs, making it more sensitive to off-resonance effects. To minimize sensitivity to off-resonance, data should be acquired at phase advance values ϕ_n located as far as possible from ϕ_m,SP. The simplest choice, which minimizes the number of images required for metabolite reconstruction and thereby provides the highest temporal resolution during dynamic scans, is to acquire N=M images at the midpoints between adjacent SPs.

To further guide the choice of phase advance values and TR, so as to induce the smallest deviation in the calculated signal contributions, μ, the condition number of the S matrix can be calculated for different achievable TRs.

In the presence of B₀ inhomogeneities, the metabolite profiles as a function of the phase advance ϕ will be shifted by an amount δϕ=−2π.δf.TR, where δf is the local off-resonance in Hz, such that:

$$\mathrm{\Delta }{{\omega }_m}^{\prime }=\mathrm{\Delta }{\omega }_m+2\pi .\delta f$$ (7)

These effects can be incorporated retrospectively into the reconstruction of Equation 6 in at least two ways. A proton field-map can be used to determine the local 13C frequency shift δf, and this shift can be incorporated into Equations 5–6 (replacing Δω_m with Δω_m′) during the reconstruction process. Alternatively, for over-determined systems, the frequency shift δf can be incorporated as a variable into Equations 5–6 via Equation 7, and then δf can be adjusted on a pixel-by-pixel basis to minimize the residual error |Sμ − C| in the solution of Equation 6.

Methods

All experiments were conducted on a 9.4T horizontal small-bore scanner (Bruker, Billerica, USA) using a commercial 84mm volume coil for 1H MRI in combination with custom-built 13C saddle and surface coils for in-vitro and in-vivo acquisitions respectively.

Phantom studies were performed to test the sensitivity of the multi-phase advance method to off-resonance effects. A 5mm NMR tube containing 2.8M 13C labeled deuterated tert-butanol (22) in water was embedded in agar gel inside a 30mm plastic tube. This phantom was then placed within a 36mm saddle coil and situated at the isocenter of the scanner with the axis of the NMR tube parallel to the main magnetic field. A region within the NMR tube 30mm long was shimmed to obtain field homogeneity of approximately 0.03ppm. The field homogeneity was verified using dual gradient echo proton field-maps (FOV=64×48×128mm³; matrix=64×48×64; NEX=2; TE₁/TE₂/TR=2.0/6.3/20). The 13C center frequency was placed at the center of the tert-butanol spectral line, which had a width (FWHM) of approximately 7Hz over the 30mm shimmed region.

Three sets of images were acquired: First, a standard bSSFP image was acquired to provide a reference for image intensity that included effects of partial volume and B₁ inhomogeneity. Second, an image was acquired using the low-tip angle selective excitation strategy. Finally, a variable phase advance image was acquired using the parameters outlined in Table 1.

Table 1.

Scan parameters for the variable phase advance bSSFP acquisitions. All in vivo data were acquired with a read BW of 42kHz.

Experiment	ϕs [°]	αmax [°]	frames	matrix	TE/TR [ms]	in-plane resolution [mm2]	slice thickness [mm]	scan time for M metabolites [s]
Tert-butanol	36; 108; 180; 252; 324	10	5	48×256	1.00/2.00	1.25×1.25	10	2.560
Multi-metabolite	78; 178; 258; 338	20; 10; 5	10	48×256	1.16/2.32	1.0×1.0	10	2.373
In vivo 1 (A549 cell line)	34; 139; 244; 319	2.5	45	48×256	1.04/2.08	1.25×1.25	5	2.133
In vivo 2 (A498 cell line)	35; 139; 241; 318	2.5	46	48×256	1.04/2.08	1.25×1.25	5	2.133
In vivo 3 (A498 cell line)	12; 114; 215; 293	2.5	46	48×256	1.04/2.08	1.25×1.25	5	2.133
In vivo 4 (A498 cell line)	27; 104; 206; 309	2.5	46	48×256	1.04/2.08	1.25×1.25	5	2.133
In vivo 5 (A498 cell line)	36; 137; 215; 293	2.5	46	48×256	1.04/2.08	1.25×1.25	5	2.133

As k-space was traversed, the RF tip angle α was modulated by a Fermi function such that $\alpha (x)={\alpha }_{max}{e}^{-\frac{1}{2}(\frac{2}{x}-\frac{4}{1-x})}$, where x measures the phase encoding position: x=k/(N−1), k=1, 2, … N is the phase encoding step, and N is the matrix size. This Fermi function was used to modulate the RF pulses in subsequent phantom and in-vivo variable phase advance bSSFP acquisitions. The standard bSSFP image was acquired with α_max=20°, the selective excitation image was acquired with α_max=0.5°, and the variable phase advance image was acquired with α_max=10°. In the case of the selective excitation image, the sum of the tip angles from the beginning of the acquisition to the center of k-space was approximately 30°. To obtain sufficient SNR, the bSSFP image was acquired with 32 signal averages separated by delays to allow full T₁ recovery. The selective excitation and variable phase images were acquired with 16 signal averages. Following these acquisitions, a linear 0.247mT/m z-gradient was applied. This gradient shifted the 13C frequency by ±40Hz over the (formerly homogeneous) 30mm region. The variable phase advance and selective excitation images were then re-acquired as before. The standard bSSFP image and the two selective excitation images (acquired before and after the application of the z-gradient) were reconstructed using standard Fourier transforms. The variable phase advance images were reconstructed using Equation 6, with an off-resonance correction derived from the dual gradient echo proton field-maps. The reconstructed magnitude images were smoothed with bilinear interpolation for display.

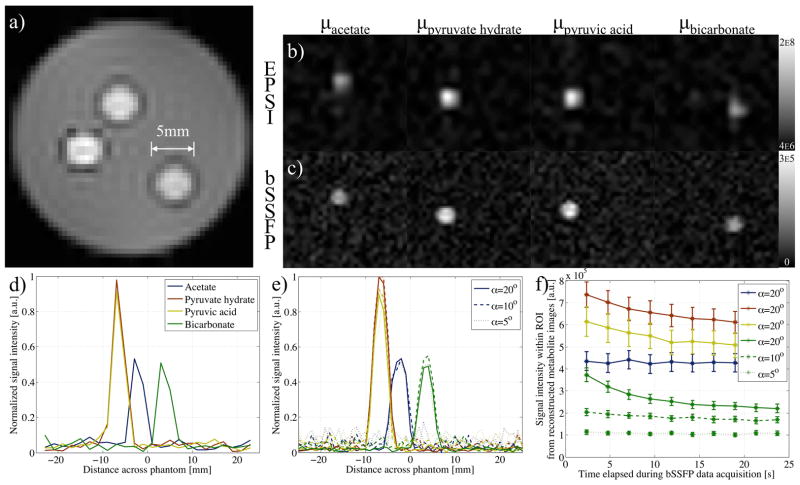
A multi-metabolite phantom was also prepared to illustrate the spectral selectivity of the technique: 5mm NMR tubes were filled with aqueous solutions of 13C labeled bicarbonate (stabilized by addition of sodium hydroxide), pyruvic acid, and acetate, and then placed in agar (Fig. 3a). Variable phase advance bSSFP data were again acquired following shimming and acquisition of proton field-maps with the dual gradient echo sequence. The chemical shifts of the metabolites present were determined by 13C echo-planar spectroscopic imaging (EPSI), with scan parameters of: 512 complex points; 5° tip angle; FOV=32×48mm²; matrix=16×24; slice thickness=10mm; spectral width (SW)=4.9kHz; and TR=134.5ms. EPSI and variable phase advance bSSFP acquisitions were repeated 8 times for signal averaging purposes, with repetitions separated by 3 minutes to allow for signal recovery. In this case and in-vivo, the condition number of the S matrix was used to select a suitable TR for the variable phase advance bSSFP acquisition, based on phase advance values ϕ_ns halfway between the singular points ϕ_m,SPs. As outlined above, this choice was a simple strategy to mitigate off-resonance effects. The proton field-map was used during reconstruction to provide data on any local B₀ inhomogeneities (after scaling by the ratio of the 13C and 1H center frequencies), with any measured offset in frequency, δf added via Equation 7. EPSI data were processed with 30Hz line broadening and used to form metabolite images by integration of their respective peaks (and bicubic interpolation).

Figure 3.

a) 1H gradient echo image (from field-map acquisition) shows multi-metabolite phantom. b) Images reconstructed from EPSI data, by integration of peaks at the offset frequencies, Δf, of acetate, pyruvate hydrate, pyruvic acid and bicarbonate, show the metabolites separated in space. c) Similar images are formed from data acquired with the variable phase advance bSSFP acquisition (α=5°) and for corresponding Δω values. Plots of the normalized signal intensity taken across a single line of interest within the images reconstructed using d) EPSI, and e) bSSFP data show comparable peaks. f) A plot of the mean signal intensity (with error bars of standard error) from a ROI within each metabolite image, reconstructed using the variable phase advance scheme, shows decay towards steady state with time. The time to reach a consistent signal value is reduced for smaller tip angles used during the variable phase advance bSSFP sequence.

Prior to in-vivo experiments, since the nature of phantom experiments allow multiple acquisition to compound the signal, the expected signal from pyruvate and its metabolites were simulated as a function of the phase-advance. The chemical shifts of pyruvate, alanine, pyruvate hydrate and lactate (0, 570.4, 849.9, and 1239.5Hz relative to pyruvate) were determined from prior experiments. Taking the complex signal as simulated using Equation 5 across the 4 metabolites for 1000 sets of samples, noise was added to the real and imaginary components to produce SNR levels between 10 and 100. The absolute simulated signal contributions, μ from pyruvate, alanine, pyruvate hydrate and lactate were: 6.0; 0.1; 0.4; and 3.5, × 10⁵, respectively.

Pre-clinical imaging was performed with Institutional Animal Care and Use Committee approval in athymic nude mice bearing A549 and A498 cell line xenograft tumors. An acetate phantom was present equidistant from the surface coil as the coil was from the tumor, for preliminary calibration of the RF pulses. The mice were anesthetized using isoflurane in oxygen, and an 18G needle connected to an extension tube was placed in the tail vein. The animal was then situated within the scanner with body temperature maintained at 36°C using a warm air circulator (SA Instruments, Stony Brook, USA), and respiration was maintained at a rate of roughly 80 breaths/min. To ensure good B₀ homogeneity within the tumor, a thin (~3mm) layer of ultrasound gel was initially placed over the A549 cell line tumor, and in subsequent experiments on A498 cell line xenografts the tumors were immersed in D₂0, to eliminate the air-water susceptibility mismatch at the surface of the tumor.

Hyperpolarized pyruvate was prepared as described previously (23). Briefly, pyruvic acid was combined with 15mM trityl radical (OX063, GE Healthcare, London, UK) and a gadolinium contrast agent (ProHance, Bracco, Italy) to obtain 0.5mM Gd concentration. 34.1mg of this mixture was placed in an open sample cup, which was then inserted into a commercial DNP hyperpolarizer (Oxford Instruments, Oxfordshire, UK) at 1.4K and subjected to 100mW microwave radiation at a frequency of 94.110GHz for solid-state 13C polarization. The sample was polarized for >40mins to ensure solid-state polarization reached at least 95% of its maximum, saturated value. Upon thaw and ejection of the sample from the system using 4ml hot USP saline (0.45% NaCl) with 50mM Tris and 25mg/100ml disodium EDTA, the solution was mixed with sufficient 1N sodium hydroxide to obtain a pH~7.5±0.5. The resultant mixture (approximately 90mM hyperpolarized pyruvate) was injected via tail vein into the mouse (already within the scanner).

For the first 2 in-vivo experiments, intravenous administration was achieved in two doses: A small 20μl pre-injection was used to determine and account for any shift in frequency of the pyruvate peak, which was used as a reference (i.e. SP of pyruvate at ϕ=0°). Automatic calculation of Δω_pyruvate was achieved with a slice selective spectroscopic experiment (4096 complex points; SW=10kHz; θ=10°; TR=412ms), directly prior to the variable phase advance bSSFP acquisition. Upon commencement of the variable phase advance bSSFP sequence (t=0s), the remaining 160μl hyperpolarized pyruvate was injected.

Further in-vivo experiments (numbered 3–5) allowed comparison of the variable phase advance bSSFP acquisition with EPSI. Dynamic information was obtained from 64 repetitions of an EPSI scan with: 512 complex points; 5° tip angle; FOV=40×40mm²; matrix=16×16; slice thickness=5mm; SW=4.0kHz; and TR=134ms. EPSI was initiated directly prior to injection of 160μl hyperpolarized pyruvate. The chemical shifts of the pyruvate and its metabolites were thus determined by processing the EPSI data, and then used to calculate optimal phase advances. 3D dual gradient data was acquired between scans to further account for any drift in the center frequency and/or B₀ inhomogeneities. The mouse remained in the scanner for approximately 60mins between the EPSI and bSSFP acquisitions to allow a second sample to polarize. 160μl hyperpolarized pyruvate was again injected into the mouse via tail vein prior to the variable phase advance bSSFP scan.

Prior experiments showed that there is no appreciable bicarbonate signal in tumors of this kind, hence only the signal at chemical shifts relating to pyruvate, alanine, pyruvate hydrate and lactate were considered. A proton field-map, to assess local offsets in frequency δf, was acquired for all in vivo experiments, and used (via Eq. 7) to account for B₀ inhomogeneities in all reconstructions of signals from the four separate metabolites (associated with injection of hyperpolarized pyruvate) using variable phase advance bSSFP.

Dynamic information from EPSI and variable phase advance bSSFP data was extracted using a ROI from within the tumor. A parameter proportional to the rate of pyruvate to lactate conversion was calculated using the ratio of the areas under the curve from lactate to pyruvate (24), based on the dynamic plots of signal in the ROI.

The parameters for the variable phase advance acquisitions are outlined in Table 1. These parameters varied between experiments since the bSSFP sequence was optimized based on the expected spectral species present in each experiment.

Results

Figure 2a shows the standard bSSFP image and provides a reference prior to application of the additional z-gradient. The selective excitation images acquired in the absence and presence of the gradient (left and right images in Fig. 2b) show signal dropouts at the top and bottom of the image. By comparison the variable phase advance images show improved homogeneity (Fig. 2c). In the variable phase advance method, for the TR and phase advance values employed (Table 1), as the 13C off-resonance approaches ±50Hz (Fig. 2d) the RF excitation pulses approach a singular point (SP), resulting in a breakdown of Equation 6 and concomitant signal dropouts. Over the region where the 13C off-resonance is less than ±22Hz, the signal change (in the reconstructed multi phase advance image) resulting from the gradient is less than 10%.

Figure 2.

Coronal images of the tert-butanol phantom from data acquired with: a) standard bSSFP, b) selective excitation bSSFP, c) variable phase advance bSSFP; and d) dual gradient echo. b–c) The images on the left appear as in (a) prior to the additional gradient, but show signal dropouts at the top and bottom following application of the 0.247mT/m z-gradient. Inclusion of the field-map from (d) during reconstruction of variable phase advance bSSFP data results in reduced signal dropout, apart from around SPs.

Data reconstructed from the variable phase advance bSSFP sequence compares well with that from EPSI of the multi-metabolite phantom (Fig. 3). Reconstructed images from both EPSI and bSSFP data show high intensity at the distinct chemical shift frequencies relating to pyruvate hydrate and pyruvic acid from within the same vial. Line scans through both the EPSI and bSSFP images relating to the four metabolites within the phantom show the peak intensity from acetate and bicarbonate to be half that from the metabolites in the pyruvic acid vial (Figs. 3d–e). Although little difference is observed in the line scan from bSSFP images for tip-angles between 5 and 20°, the average signal from ROIs encompassing the vials show a decrease with time for dynamic acquisitions when α=20° (Fig. 3f). However this effect is alleviated for smaller tip-angles as demonstrated by a steady signal for α≤10° from the metabolite with the shortest T₂ (bicarbonate).

Calculation of phase advance values and TR (Table 1) for initial in-vivo acquisition were based on the expected chemical shifts of lactate, alanine and pyruvate hydrate relative to pyruvate from previous experiments and the condition number of S matrix (Fig. 4a). A minimum was present at the achievable and chosen TR of 2.083ms. A plot of the combined simulated signal from the metabolites showed four SPs that corresponded to phase advances of 0, 67, 276, and 208°, for pyruvate, alanine, pyruvate hydrate, and lactate respectively (Fig. 4b). Sampling at the midpoints, illustrated by the dashed black vertical lines, non-zero signals were seen to exist to allow reconstruction of μ from Equation 6. Above a SNR of 20, the mean values of μ calculated for each metabolite using the pseudo-inverse were as expected, with the standard deviation over the 1000 simulated sample datasets increasing for lower SNR (Fig. 4c). Below this SNR, the reconstructed alanine signal was higher than its simulated value. Simulation of chemical shifts of each independent metabolite occurring at a frequency different from that expected showed the reconstructed signal to be more greatly affected by variations in more abundant metabolites (Fig. 4d). However the reconstructed signal remained within 10% of its expected value for absolute offsets ≤10Hz.

Figure 4.

a) Plot of condition number of matrix S (Equation 4), using chemical shifts for pyruvate, alanine, pyruvate hydrate and lactate of 0, 570.4, 849.9, and 1239.5Hz respectively. For simplicity, phase advance values were fixed midway between SPs. At feasible TR values, a minimum is observed around 2.08ms, the TR selected for in-vivo acquisition. b) Plot of the simulated cumulative signal (real component in blue and imaginary in magenta) as a function of the phase advance value as calculated from Equation 5 using a TR of 2.08ms and chemical shifts as in (a). Dashed vertical lines illustrate points of sampling for reconstruction of separate metabolite contributions. Plots of mean metabolite contributions as calculated by the pseudo-inverse from simulated data samples c) with normally distributed noise added for varying SNR levels, and d) with Δω values adjusted up to ±25Hz from expected (SNR = 30). Error bars reflect the standard deviation over 1000 sample datasets.

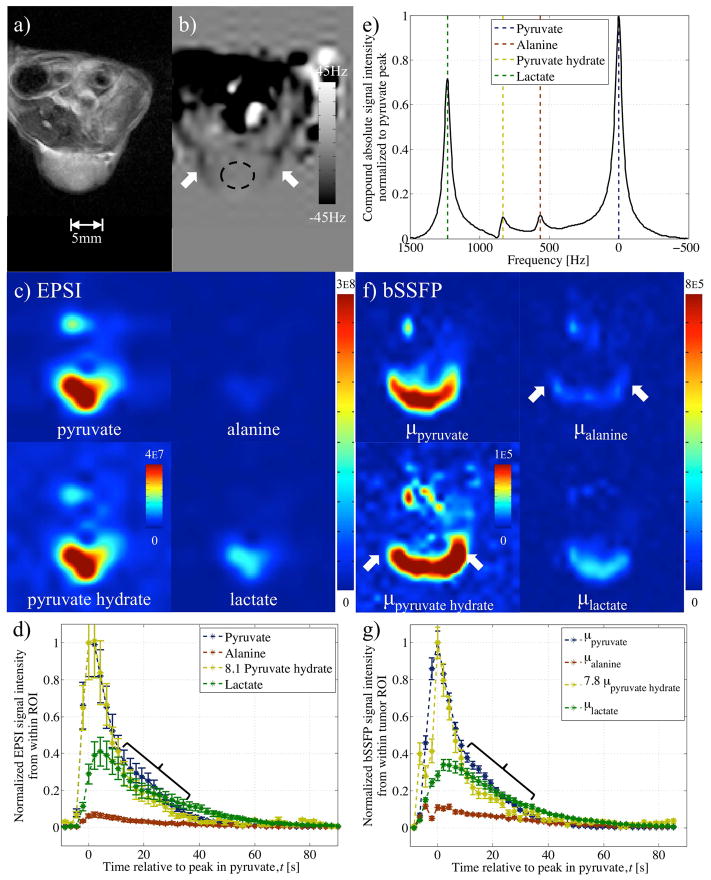
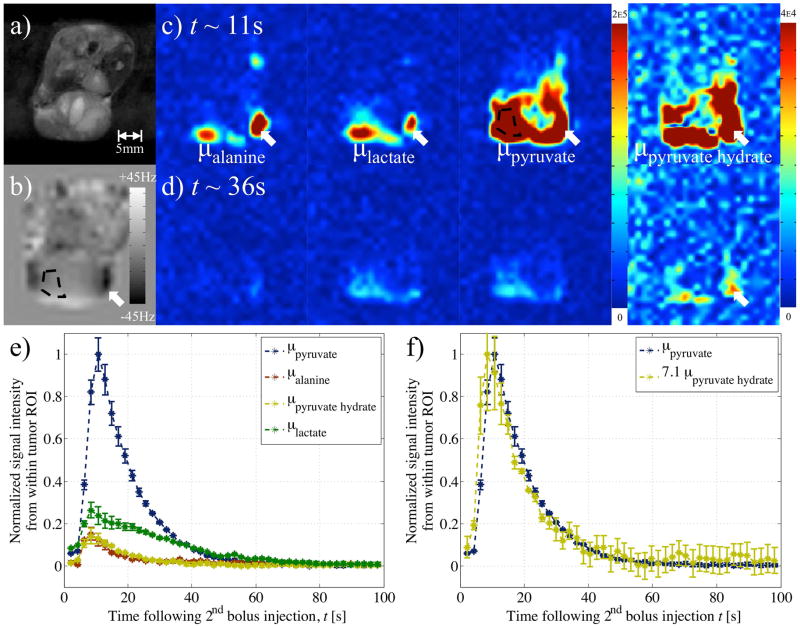
Application of variable phase advance bSSFP in-vivo in mouse xenograft tumor models showed separation of the 4 metabolites using 4 phase advance values (Figs. 5–7). Images from in-vivo experiments involving tail vein injection of a second, larger hyperpolarized pyruvate bolus showed a bright pyruvate signal from a blood vessel and an initial build-up in the tumor. Signs of metabolic activity were evident from the signal also visible within the tumor region of the reconstructed alanine, pyruvate hydrate and lactate images. 35–40s after the second injection, the signal reconstructed at the lactate frequency was the strongest (Fig. 5d), or as strong (Fig. 6d), as the pyruvate signal, whilst the signal within the tumor from the other 2 metabolites had dissipated.

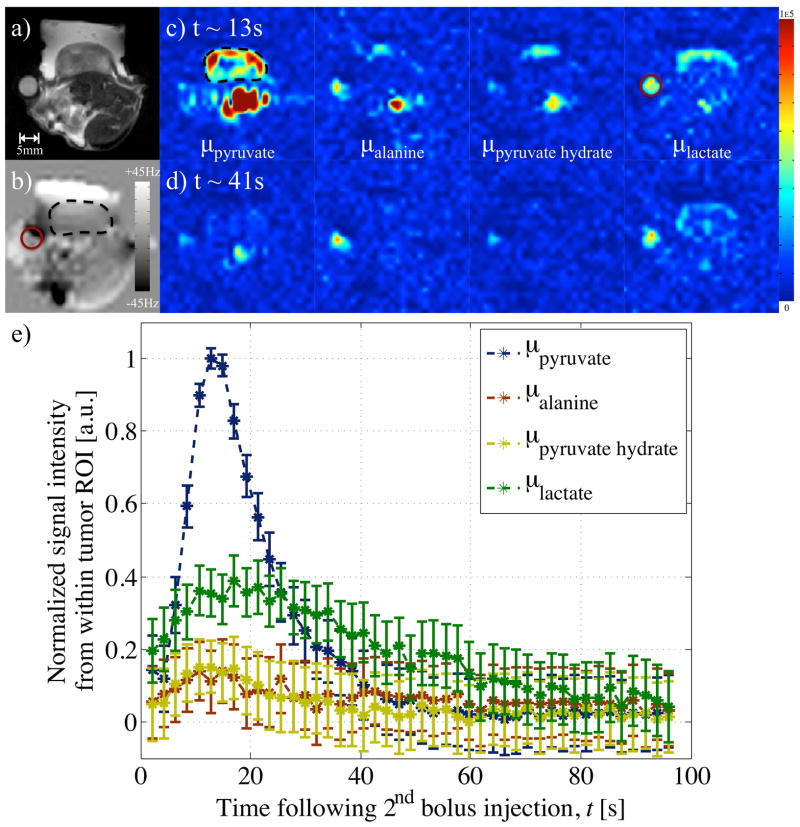
Figure 5.

Images from a) 1H rapid acquisition with refocused echoes (RARE), and b) field-map, with ROIs in tumor (black, dashed outline) and acetate vial (magenta, solid circle), acquired from the tumor bearing mouse as part of in-vivo experiment 1 and used to reconstruct variable phase advance bSSFP data. Separated images reconstructed for metabolites at the pyruvate, alanine, pyruvate hydrate and lactate chemical shift frequencies at approximate time points of c) 13s, and d) 41s after injection of the second, larger bolus of hyperpolarized pyruvate. e) A plot of the normalized signal from an area within the bulk of the tumor provides dynamic metabolic information.

Figure 7.

Results from in-vivo experiment 3 comparing EPSI and variable phase advance bSSFP in A498 cell line xenograft tumor model following injection of hyperpolarized pyruvate. Images from: a) proton RARE serve as reference; and b) field-map acquisition used during reconstruction of variable phase advance bSSFP data. Data from EPSI: c) reconstructed into separate metabolic images at the peak in pyruvate time point; d) used to form dynamic plots based on the signal from a ROI within the tumor; and, e) reconstructed into spectra with the sum over the entire experiment plot using odd echoes only. Multiplication of pyruvate hydrate signal by 8.1 (based on peak in pyruvate) in (d) to emphasize consistency with pyruvate time course Similar f) metabolite images and g) dynamic plots were produced from bSSFP data in the same mouse. Unusual points of hyper-intense alanine and pyruvate hydrate signals coincided with hypo-intensities in the field-map (white arrows). Dynamic signal from pyruvate hydrate in (g) multiplied by 7.8 (based on peak value) shows similar correspondence with pyruvate as for EPSI results, in (d), including deviation from pyruvate at time points encompassed by braces.

Figure 6.

Results from in-vivo experiment 2: a) RARE image, and b) field-map, used in reconstruction to account for local B₀ inhomogeneities (Eq. 7). Reconstructed images of the four metabolites at c) 11s and d) 36s after hyperpolarized pyruvate injection. Signals in the metabolite images that coincided with severe B₀ inhomogeneity in the field map were considered spurious (white arrows). e) A ROI (black, dashed outline) within a perfused area of the tumor provided a plot of the (normalized) dynamic signal from each metabolite. f) Plot of dynamic signal from pyruvate corresponded with that from pyruvate hydrate (multiplied by 7.1 to equalize peak values).

The variable phase advance bSSFP acquisition also allowed analysis of the in-vivo change in signal from the 4 metabolites. Dynamic information was provided using an average of the signal from within tumor ROIs (Figs. 5e, 6e–f, 7g, 8f). The time course of the pyruvate hydrate signal, which is expected to be proportional to the pyruvate signal, evolved in a manner similar to that from pyruvate. This was more evident upon multiplication of the pyruvate hydrate signal by a factor to equalize its peak with the peak in pyruvate (Figs. 6f, 7g). Comparison of the shape of dynamic curves from pyruvate hydrate and pyruvate showed similarity between data acquired with the EPSI and that from the bSSFP sequence in Figure 7. However disparities between the pyruvate hydrate and pyruvate curves from phase advance bSSFP were also apparent (relative to EPSI). In Figure 7 a decrease in the pyruvate hydrate to pyruvate ratio between 10 and 35s was observed in both EPSI and bSSFP data (braces in Figs. 7d, g). Also, in Figure 8, the pyruvate hydrate signal at early time points is greater than expected. For this experiment, a multiplicative factor of 11.3 was determined by a linear least squares fit (Fig. 8f) since pyruvate hydrate peaked before the pyruvate signal.

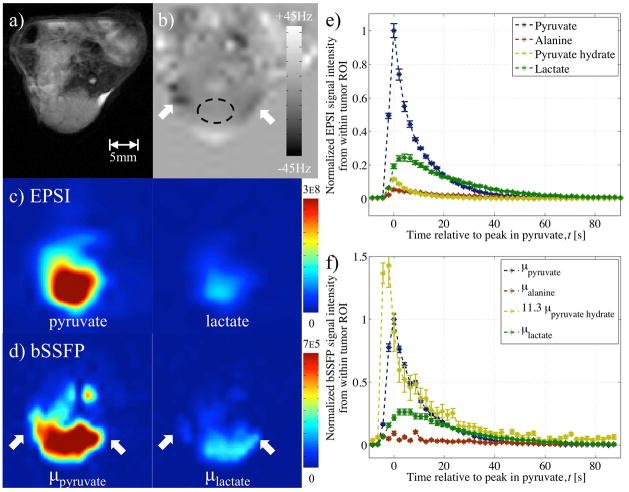
Figure 8.

EPSI and variable phase advance bSSFP data in A498 cell line xenograft tumor model following injection of hyperpolarized pyruvate (in-vivo experiment 4). Images from a) proton RARE and b) field-map acquisition (with ROI) serve as reference. Reconstructed pyruvate and lactate metabolite images from c) EPSI and d) variable phase advance bSSFP data (using the field-map to inform on any local off-resonance) interpolated (bicubic) to the same resolution shows spatial distribution. Plots of the signal from a ROI within the tumor using e) EPSI and f) variable phase advance bSSFP data provides dynamic information. Plot of dynamic signal from pyruvate hydrate in (f) multiplied by 11.3 based on linear least squares fit to pyruvate time course.

Spatial heterogeneity from the metabolites’ signal within the tumor was also visible. From in-vivo experiment 1, pyruvate and lactate were observed at the periphery of the tumor (Figs. 5c,d). The pyruvate signal at t~11s from the second in-vivo experiment showed a void in the middle of the tumor, which corresponded with a region of hyper-intense signal based on the T₂-weighted reference proton image (Figs. 6a, c). Figures 6c–d also show the pyruvate hydrate images with the intensity scale modified to brighten the image intensity. These images show a similar spatial distribution to the pyruvate signal, except for a region of large off-resonance indicated by the arrows. This is also evident in Figure 7f where again the intensity of the pyruvate hydrate image has been adjusted to facilitate comparison with the pyruvate image. The spatial distributions of pyruvate and pyruvate hydrate were similar, but the pyruvate hydrate signal was not correctly reconstructed in regions of large off-resonance. These spurious pyruvate hydrate signals were observed in the regions with the largest off-resonances (white arrows in Figs. 6–7 corresponding to approximately −40Hz off-resonance), and, as for the tert-butanol phantom, such signals were attributed to acquisition at singular points, where the assumptions underlying the reconstruction break down.

Reconstructed variable phase advance bSSFP data from in-vivo experiments 3–5 compared well with the results from EPSI: The relatively low resolution EPSI scan provided a concentrated, blurred signal from within the tumor at the pyruvate frequency (Figs 7c, 8c). At a similar time-point during the bSSFP scan, the reconstructed pyruvate image more closely resembled the shape of the tumor provided by the reference (Figs. 7a,f, 8a,d). Comparison of the dynamic information based on the average signal from a ROI within the tumor showed similar patterns of a pyruvate influx following its injection, a peak in lactate to between 0.3 and 0.50 of pyruvate’s peak and early non-zero signal from the other two metabolites (Figs. 7d,g, 8e–f).

Discussion

An expression for the bSSFP signal as a function of the phase advance was described by Equation 4 and used to successfully separate images of different metabolites. Thus, as with multi-echo acquisitions (11,12), the contribution from a chemical species at a specific frequency could be determined in a least squares manner via the Moore-Penrose pseudoinverse (Eq. 6).

The initial in-vitro demonstration provided evidence of a reduced sensitivity to B₀ inhomogeneity compared to a low tip angle bSSFP image acquired at the resonance frequency of tert-butanol (Fig. 2). Although the results were only for a single chemical species and an overdetermined system (since 5 ϕs were acquired), provided the linewidth of multiple metabolites does not result in an overlap it was assumed that such B₀ insensitivity could continue to be achieved through inclusion of an off-resonance correction in the reconstruction process (Eq. 7). Indeed, simulation of the bSSFP signal for the case of hyperpolarized pyruvate showed the reconstructed signal to be within 10% of that expected for absolute frequency offsets less than 10Hz (Fig. 4d). For a simulated offset in a single metabolite’s signal, the largest deviations were apparent for errors in the most abundant metabolites, and even contributed to further errors in the other reconstructed species. Thus, in our case, spurious results are likely to be the result of miscalculation of the expected pyruvate (and lactate) frequency.

An attempt to compensate for the sensitivity to B₀ inhomogeneity was made by inclusion of the results from a field-map in the Δω term during reconstruction (Eq. 7) (25). However, as in the phantom experiments (Fig. 1c), severe changes in B₀ that might place a phase advance acquisition close to a SP resulted in unreliable signals in-vivo (red circle and white arrows in Figs. 6b–c, 7b,f, 8b,d). Thus scrutiny is required in looking at the metabolite images, as the source of unexpected metabolite signal (e.g. alanine) may be the result of sharp off-resonances. Such spurious signals might be reduced by acquisition of additional phase advance values, the data from which could be used in minimization of the residual error (see Theory). Thus a tradeoff is necessary with regards to the number of phase advance values to acquire, since with fewer phase advance values to acquire, any additional frames can be used to further improve upon the temporal resolution (Table 1).

Nevertheless, separate images for all identifiable peaks in the multi-metabolite phantom experiment showed that reconstruction of 4 metabolites was possible with 4 acquired ϕs (Fig. 3). The reconstructed images from the variable phase advance bSSFP technique showed similar signal to that acquired by EPSI. However instabilities of the signal were present and were thought to be a response to deviation from the assumed small tip-angle and long T₂ approximation; A decrease in the average signal with successive repetition of the bSSFP acquisition at α=20° was observed (Fig. 3f). The rate of decrease was related to T₂ in that a negligible decrease is observed from the acetate vial (measured T₂=3.4s), whereas the average signal from within the bicarbonate vial fell faster (measured T₂=0.5s). Concentrating on the bicarbonate signal, the results showed that a consistent signal level was achieved at 10 or 5°. Thus a stable signal during repetitive acquisition from shorter T₂ metabolites was achievable by reducing the tip-angle, and in order to account for possible B₁ inhomogeneities from the surface coil employed in-vivo, a tip-angle of 2.5° was considered sufficient.

Application of the variable phase advance bSSFP acquisition in-vivo to hyperpolarized experiments allowed reconstruction of separate images of the associated metabolites (Figs. 5–8). The signal from ROIs within the tumor of each metabolite image plotted over the entire acquisition were similar to that expected from previous experiments and literature (26): An initial rapid increase in the pyruvate contribution was associated with a bolus injection and by conversion/exchange, the lactate signal persisted for a longer period over the acquisition. The time course of pyruvate hydrate was found to follow that of pyruvate, with which it is in equilibrium (23). The correlation between the time courses of pyruvate and pyruvate hydrate was made more apparent upon multiplication by a scale factor based on their respective peaks from in-vivo experiments 2–3 (Figs. 6f, 7g). However for in-vivo experiment 4 a linear least squares fit between the time courses was necessary as pyruvate hydrate peaked before pyruvate (Fig. 8f). This mismatch was most likely the result of data at different variable phase advance values being acquired successively as opposed at the same time. The reconstruction assumes that the signals at different phase advance values were acquired at the same time, when in fact there is a short delay between successive phase advances. Since a complete image was acquired at one phase before moving on to the next, the temporal variation from one phase advance to the next can result in artifacts at time points when the signals are rapidly changing, for instance immediately following the bolus injection. Although this did not always occur (Fig. 7g), a possible solution is to use temporal interpolation to estimate the signal values from all phase advances at a single time point. In Figures 5–6, the early presence of a significant lactate signal before pyruvate reached its peak was most likely a consequence of the 20μl pre-injection used for phase advance/frequency adjustment in the first two in-vivo experiments. The effect of this was also evident from the nonzero lactate signal at time, t=0 after the second bolus injection (Figs. 5e, 6e).

In-vivo acquisition of the variable phase advance bSSFP acquisition following EPSI showed comparable and complete dynamic curves (Figs. 7d,g, 8e–f) for pyruvate and lactate, the dominant metabolites. In the images of pyruvate and lactate, the increased spatial resolution afforded by the variable phase advance bSSFP technique was apparent from signal conforming to the dome shape of the tumor (Fig. 8d). The spatial distributions of signals from less abundant metabolites, i.e. alanine and pyruvate hydrate, were less reliably reconstructed. Although a similarity in the overall shape of bulk signal was observed in the pyruvate hydrate and pyruvate images (Figs. 6c–d, 7f), the pyruvate hydrate signal (which should be proportional to the pyruvate signal) is artifactually enhanced near the edges of the tumor, where off-resonance is large. Similar enhancements are seen in the alanine signal. This highlights a potential limitation of the bSSFP method, namely that accurate reconstruction of small metabolites requires a very precise cancellation between large signals from other metabolites. Small errors in the pseudo-inverse matrix (Eq. 6) can result, for instance, in a portion of the large signal from pyruvate or lactate being erroneously reconstructed as pyruvate hydrate or alanine. This is particularly likely in regions with large off-resonance, where the metabolites may approach a singular point and the assumptions underlying the reconstruction may fail. This is one possible explanation of the artifactual pyruvate hydrate signal enhancements, and indeed the proton field maps show that these regions do in fact correspond to regions of large off-resonance. Another feature of the enhanced pyruvate hydrate and alanine signals is that they appear to be strongest at the edges along the read direction (arrows in Fig. 7f). This suggests another potential source of the artifact, namely that chemical shift displacements in the read direction result in spatial misregistration between the different metabolite signals. Given the ~1.2kHz chemical shift between pyruvate and lactate, together with the 0.9kHz/pixel read bandwidth, it is possible that pixels at extreme ends of the read direction will contain signals dominated by pyruvate alone or by lactate alone, so that these two large signals cannot undergo the necessary cancellation to yield small reconstructed signals for alanine and pyruvate hydrate. This situation can be improved by increasing the readout bandwidth or by incorporating the chemical shift displacement into Eq. 6, a possibility that we leave to future work. Kinetic modeling was still possible from both sets of data, and averages in the parameter proportional to the pyruvate to lactate conversion rate constant (as calculated from areas under the pyruvate and lactate curves (24)) were comparable (Table 2).

Table 2.

Table of parameter proportional to rate of conversion from pyruvate to lactate, calculated from dynamic EPSI and variable phase advance bSSFP data. Values provided as: average ± standard error, from within the A498 cell line xenograft tumors.

Experiment	Ratio of total lactate/total pyruvate
	EPSI	bSSFP
In vivo 3	0.75 ± 0.07	0.74 ± 0.08
In vivo 4	0.62 ± 0.02	0.61 ± 0.05
In vivo 5	0.62 ± 0.03	0.66 ± 0.05

In general, TR is chosen to be as short as possible to increase the distance (in Hz) between SPs, where the bSSFP technique breaks down. As the field strength increases, the range of chemical shifts Δf and linewidths of individual metabolites increase. As the field strength increases and Δf exceeds 1/TR for the shortest achievable TR, it becomes increasingly difficult to avoid banding artifacts because the width of the lines may exceed the distance between adjacent SPs. The results presented here therefore provide proof-of-principle evidence that bSSFP techniques can yield good results even at high field strengths. Further investigation will be needed too assess performance at lower field strengths.

As with other previously established techniques based on an imaging sequence, the variable phase advance bSSFP technique for spectrally selective imaging of hyperpolarized pyruvate was reliant on prior information regarding the chemical shift(s) of any metabolite(s) of interest (2,11,12,14). Simulation of errors in the chemical shift from that expected showed variable results based on the metabolites’ concentrations (Fig. 4d). Decreased sensitivity to such off-resonance related errors might be achieved by inclusion of variable phase advance values in calculation of the condition number of S matrix. The current scheme involving a small pre-injection of hyperpolarized pyruvate to determine its chemical shift seemed prudent and necessary. This method was used to acquire in-vivo data with high spatial and temporal resolution, and a more rigorous approach might be developed using a combination of variable phase advance bSSFP with existing techniques, such as multi-echo acquisition and/or spatial-spectral RF pulses.

Conclusions

A spectrally selective technique for imaging based on the signal from a variable phase advance bSSFP sequence was presented. Its application in-vitro and in-vivo allowed separation of multiple metabolites with a single echo and short TR sequence. Although sensitivity to off-resonances was still present, the technique allowed for optimization by prudent selection of phase advance values, TR, and the use of field-map(s). Its application to in-vivo imaging of hyperpolarized pyruvate in tumor models provided images ascribed to the metabolites: pyruvate; alanine; pyruvate hydrate; and lactate, with 1.25×1.25mm² in-plane resolution, and dynamic information at a temporal resolution of ~2s. The technique might be explored for imaging of other (hyperpolarized) media, where both spectral and spatial information are required.