Velocity-Selective-Inversion Prepared Arterial Spin Labeling

Abstract

Purpose

To develop a Fourier-transform based velocity-selective inversion (FT-VSI) pulse train for velocity-selective arterial spin labeling (VSASL).

Methods

This new pulse contains paired and phase cycled refocusing pulses. Its sensitivities to B0/B1 inhomogeneity and gradient imperfections such as eddy currents were evaluated through simulation and phantom studies. Cerebral blood flow (CBF) quantification employing FT-VSI prepared VSASL was compared with conventional VSASL and pseudo-continuous ASL (PCASL) at 3T.

Results

Simulation and phantom results of the proposed FT-VSI pulse train demonstrated excellent robustness to B0/B1 field inhomogeneity and eddy currents. The estimated CBF of gray matter and white matter for the FT-VSI prepared VSASL, averaged among eight healthy volunteers, were 49.5 ± 7.5 mL/100g/min and 14.8 ± 2.4 mL/100g/min, respectively. Excellent correlation and agreement between the FT-VSI method and conventional VSASL and PCASL were found. The averaged SNR value in gray matter of the FT-VSI method was 39% higher than VSASL using conventional double refocused hyperbolic tangent (DRHT) pulses and 9% lower than PCASL.

Conclusion

A novel FT-VSI pulse train was demonstrated to be a suitable labeling module for VSASL with robustness of velocity-selective profile to B0/B1 field inhomogeneity and gradient imperfections. Compared to conventional VSASL, FT-VSI prepared VSASL produced consistent CBF maps with higher SNR values.

INTRODUCTION

Current arterial spin labeling (ASL) techniques largely rely on the tagging of the supplying arterial blood located proximal to the imaging volume. For instance, when measuring cerebral blood flow (CBF), pseudo-continuous ASL (PCASL) (1) inverts the water spins (¹H) within the arterial blood flowing through a plane perpendicular to both the internal carotid arteries and vertebral arteries. Although this type of spatially-selective ASL is conceptually straightforward, it does require a lengthened arterial transit time (ATT) for the labeled tracers to arrive at the imaging voxels. For healthy subjects, the ATT values for cerebral cortices are in a range of about 1~2 sec (2-5), which are comparable to the longitudinal relaxation time constants of arterial blood (T_1,a) at 3 T (6-9). Since the arterial input function (AIF) of PCASL is proportional to exp(- ATT / T_1,a) (3,10), longer ATT causes reduced sensitivity of ASL signals. For patients with vascular disorders where the bolus are markedly delayed, such as ischemia, the resulting low signal-to-noise ratio (SNR) could lead to an overestimated area of hypoperfusion (11,12).

In order to minimize the ATT between the labeled bolus and the capillary-tissue exchange-bed, a labeling strategy has been proposed to tag all the upstream blood in the vascular tree that is flowing above a cutoff velocity (V_c, ideally corresponding to the arterioles), which was termed velocity-selective ASL (VSASL) (13). In spite of holding great promise for perfusion measurements, only one clinical application using this approach has been reported (14), and improvements to this approach are needed before widespread utilization is possible. Traditional VSASL implementations (13-17) employ a simple VS preparation module consisting of a 90°_x-refocus-90°-_x pulse train with velocity-encoding gradients surrounding the refocusing pulses, which can produce only a velocity-dependent cosinusoidal function with the period of 2V_c. Technical challenges for this setup include sensitivity to B0/B1 field inhomogeneity (13,15) and eddy currents (ECs) (17,18). In terms of SNR, it is equivalent to the use of VS saturation (VSS) pulses when assuming a laminar flow distribution in vivo.

Compared to saturation, VS inversion (VSI) has the advantage of increased perfusion signal sensitivity (13,19). The combination of non-selective RF pulse trains with embedded velocity encoding gradients, based on the excitation k-space formalism (20-22), has allowed its implementation. In fact, Fourier-transform (FT) based velocity-selective pulse trains (FT-VS) can be constructed to produce almost arbitrary velocity-selective profiles. Regretfully, the original scheme (without refocusing pulses) suffers from off-resonance effects which are manifested as excitation profile shifting along the velocity direction (23). As previously shown for VSS prepared peripheral MR angiography (MRA) at 1.5T (24), the susceptibility to B0 field inhomogeneity can be alleviated, by incorporating one composite refocusing pulse within each velocity encoding step and modifying the RF and gradient waveforms accordingly. Recently, by adding paired refocusing pulses within each velocity encoding step accompanied by phase cycling, further improved immunity to B0/B1 field inhomogeneities was realized for VSS prepared cerebral MRA at 3T (25).

In this work, a FT-based VSI pulse train with paired and phase cycled refocusing pulses is introduced and its labeling performance for VSASL evaluated. First, sensitivities of the FT-VSI pulse train to effective T2 decay, B0/B1 field inhomogeneities, acceleration, and eddy currents were gauged using simulations. Then, sensitivity of this pulse train to gradient imperfections was assessed through phantom experiments. Lastly, we demonstrated its utility in a 2D multi-slice VSASL protocol for CBF measurement on a human 3T scanner. Comparisons with existing VSS pulse trains were also conducted.

METHODS

Label Modules

Based on the proposed VS pulse train II in a recent study (25), the FT-VSI pulse train employed in the current work is composed of a series of 9 excitation pulses (20° each), interleaved with pairs of 180° refocusing pulses each of which is surrounded by a pair of encoding gradient lobes with alternating polarity, providing 8 velocity encoding steps (total duration T_VS = 48 ms, Figure 1a). Note that all RF pulses are hard pulses and the phase cycling scheme of the refocusing pulses is MLEV-16. The velocity field of view (FOV_v) was set to be 45 cm/s with a targeted inversion band within ±4 cm/s.

Figure 1.

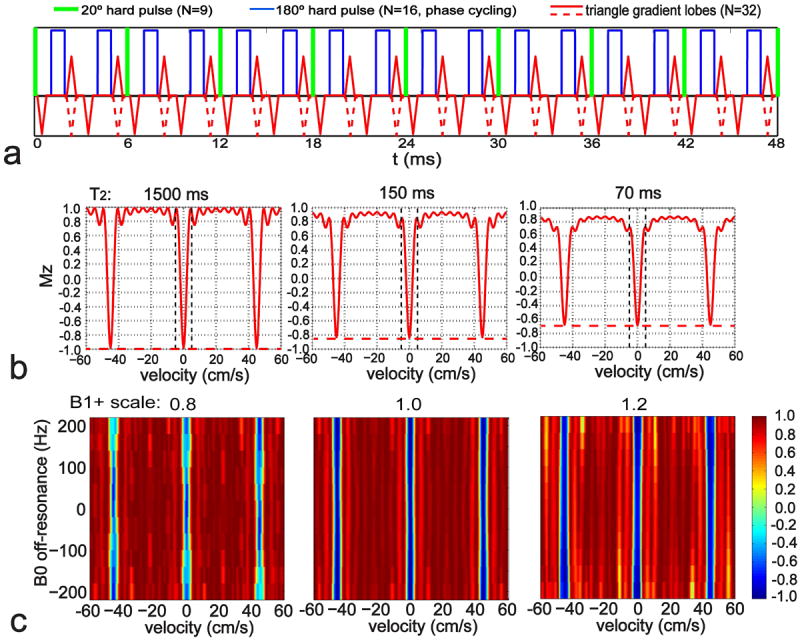
(a) Diagram of the FT-VSI pulse train with paired and phase-cycled refocusing pulses in each velocity encoding step, gradients with alternating polarity surrounding refocusing pulses for velocity-sensitized waveform (red solid lines) and uni-polar gradients for velocity-compensated waveform (red dashed lines for the polarity-switched gradient lobes). (b) The simulated Mz-Velocity responses of the pulse (a) with different T₂ relaxation effects: 1500 ms (CSF), 150 ms (arterial blood), and 70 ms (tissue). The vertical dashed lines indicate the inversion band (±4 cm/s). The horizontal dashed lines illustrate the universal inversion response of the FT-VSI pulse train for the control scan. (c) The simulated Mz-velocity responses of the labeling pulse (a) at different B0 conditions with representative B1+ scales of 0.8, 1.0, and 1.2.

For comparison purposes, another FT-VSI pulse train with the same velocity selective profile but less eddy current effect (less gradient amplitude and longer gaps between the gradients and subsequent RF pulses) was also designed (T_VS = 64 ms). By halving the flip angles of the excitation pulses from these two FT-VSI pulse trains, two corresponding FT-VSS pulse trains were devised. Finally, a basic VS module consisting of ±90° hard pulses enclosing a pair of adiabatic refocusing pulses with surrounding velocity encoding gradients, was built with T_VS = 20 ms. Contrary to previous implementations, double refocused hyperbolic tangent (DRHT) pulses, instead of hyperbolic secant pulses (13,18), were chosen here for refocusing pulses as they offer the advantage of providing adiabaticity with relatively short pulse durations (2,26,27) (5 ms, tanh/tan, maximum amplitude of 575 Hz and a frequency sweep of 8 KHz). Specific parameters for the FT-VS pulse trains and DRHT pulse train are listed in Table 1.

Table 1.

Parameters for the labeling modules of VSASL used in this study with FT-VS applying to both FT-VSS and FT-VSI.

	TVS (ms)	Nstep	Tstep (ms)	Tref (ms)	TG (ms)	Tramp (ms)	Gmax (mT/m)	Tgap (ms)	Δ (ms)	Vc (cm/s)	b-value (s/mm2)
DRHT	20.0	1	20.0	5.00	0.60	0.30	25.0	1.59	10.0	3.9	0.1
FT-VS	48.0	8	6.0	0.87	0.60	0.30	29.0	0.34	3.0	2.8	0.2
	64.0	8	8.0	0.87	0.60	0.30	21.8	0.79	4.0	2.8	0.2

T_VS: duration for the entire VS pulse train; T_step: duration for each velocity encoding step; T_ref: duration of each refocusing pulse; T_G: duration of each gradient lobe; T_ramp: ramp time for each gradient lobe; G_max: maximum gradient strength of gradient lobes; T_gap: the gap between the gradient and the following RF pulse; Δ: the separation between gradient lobes of the same polarity; V_c: cut-off velocity.

Control Modules

Conventionally, the control module for VSASL is just the RF pulse train of the labeling module (velocity-sensitive) with the gradient lobes turned off (velocity-insensitive) (13-17). When calculating the ASL difference signal between the label/control sequences, any diffusion attenuation on the static tissue at the end of the labeling pulse train would lead to an overestimation of CBF (13,18). Using typical apparent diffusion coefficients (ADC) of gray matter (0.49 × 10^-3 mm²/s) and CSF (3.19 × 10^-3 mm²/s) (28), diffusion losses are negligible for the b-values used in this work (0.1 ~ 0.2 s/mm², Table 1). When a higher b-value (e.g. 1.0 s/mm²) is employed for lower V_c, a subtraction error (1 - exp(- b × ADC)) would be generated, of 0.05% for gray matter and 0.32% for CSF, the magnitude of which is comparable to the perfusion signal which is typically about 1% of the tissue signal. In order to obviate the issue of the unbalanced b-value, an alternative configuration for the control module of FT-VSASL is to keep the same gradient lobes employed in the labeling module for the FT-VS pulse trains, but with uni-polar gradient lobes (velocity-compensated) (i.e.: positive gradient lobes replaced with negative ones as indicated by red dashed lines in Figure 1a).

For the DRHT pulse train, the velocity-compensated waveform may be acceleration-sensitive given its cutoff acceleration (A_c) as 22 m/s² (29). Acceleration-selective ASL with a much lower A_c (2~3 m/s²) has been proposed for CBF measurement (30,31). Thus the control module for DRHT in this work is still the corresponding velocity-insensitive pulse train for its complete insensitivity to acceleration.

Numerical Simulation

Numerical simulations using the Bloch equations based on matrix rotation were performed to assess the properties of the proposed FT-VSI pulse train using Matlab (MathWorks, Inc., Natick, MA, USA). Responses of the longitudinal magnetizations (M_z) following both the label and control pulse trains under various conditions were calculated for velocities from -60 cm/s to 60 cm/s with intervals of 0.5 cm/s. First, the effect of the transverse relaxation time (T₂) over the duration of the proposed VSI pulse train (48 ms) was considered for three different T₂ values at 3T: 1500 ms (CSF, (32)), 150 ms (arterial blood, (33,34)), and 70 ms (tissue, (35)), respectively; Second, the sensitivity to a typical range of B0/B1 offset incurred in the brain at 3T (B0 field : ±200 Hz; B1+ scale (ratio of actual flip angle to nominal input flip angle): from 0.8 to 1.2) was evaluated; Third, to mimic pulsation or tortuous flow as conducted in (23,25), the velocity selective profiles of the DRHT, FT-VSS and FT-VSI pulse trains were simulated, respectively, for velocities with ±5%, ±10% and ±20% linear temporal-variation (acceleration) during a 50 ms period; Finally, the effect of eddy currents on the static spins at the end of the DRHT, FT-VSS and FT-VSI pulse trains were examined with eddy current amplitude of 0.25% and time constants of 10^-4 - 1 s, as described in (17,18). For the last two simulations, both the velocity-sensitized and the velocity-compensated waveforms of FT-VS pulse trains were studied.

Experiments

Experiments were conducted on a 3T Philips Achieva scanner (Philips Medical Systems, Best, The Netherlands) using the body coil for RF transmission (maximum amplitude 13.5 μT) and a 32-channel head-only coil for signal reception. The combined maximum strength and slew rate of our standard gradient coil are 40 mT/m and 200 mT/m/ms, respectively.

Phantom Experiments

To evaluate effects of eddy currents and other gradient imperfections, an experimental setup and a spherical silicone oil phantom (T₁ / T₂ = 1111 / 227 ms) were used following those in (18). The DRHT, FT-VSS, and FT-VSI pulse trains specified in Table 1 were tested with the velocity-compensated control and velocity-sensitive label modules placed 10 ms before image acquisition. The 48 ms FT-VS pulse trains paired with the velocity-insensitive control modules were also tested on the phantom for comparison. The gradients of the VS pulse trains were applied either along the anterior-posterior (A-P), left-right (L-R) or superior-inferior (S-I) direction to examine the effect of velocity-encoding orientations. A final comparison was made with the 48 ms FT-VSI pulse train along the S-I direction without any phase-cycling scheme for the refocusing pulses. Using a TR = 4.0 s, the total measurement time after 12 repetitions was about 1.7 min for each pulse train configuration. Proton density-weighted image of signal intensity (SI_PD) was also acquired with TR = 10 s. The parameters used for the phantom images (5 slices of 2D acquisition) were identical with the human studies detailed below.

Since the static spins experience different flip angles for DRHT (0°), FT-VSS (90°), and FT-VSI (180°), the averaged signal difference for the label/control pairs across repetitions were normalized to the SI_PD image in order to facilitate comparisons between different VS pulse trains. For each pulse train configuration, the mean and standard deviation (STD) of the normalized differences from all the pixels within the 5 slices of the phantom were calculated.

In Vivo Experiments

Eight healthy volunteers (30-56 yrs old, five males and three females) were enrolled after providing informed consent in accordance with the Institutional Review Board guidelines. A subgroup of subjects (three) were first scanned with the 48 ms FT-VSS preparation pulses for cerebral MRA (25), and compared with the results for the velocity-compensated and velocity-insensitive counterparts, to visualize the effect of the latter two control waveforms on large vessels. For perfusion measurements on each volunteer, four types of labeling techniques (48 ms FT-VSI, 64 ms FT-VSS, 20 ms DRHT and PCASL) paired with their corresponding control counterparts were ordered randomly. Subjects were instructed to stay awake and kept still with their head stabilized with foam pads inside the head-coil.

For the DRHT and FT-VS prepared VSASL sequences, a tailored hard-pulse train for global saturation (65°, 83°, 143°, 162°) (36), chosen for its reduced RF power deposition compared to adiabatic saturation pulses such as BIR-4 (37), was applied following image acquisition and a delay of 3.6 s before the label/control modules. During the 1.5 s post-labeling delay (PLD), two or three non-selective adiabatic inversion pulses were applied to suppress the static tissues (background suppression (BGS) (38)): DRHT, N_BGS = 2, [0.04, 1.14] s following labeling pulse; FT-VSS, N_BGS = 3, [0.02, 1.12, 1.46] s after labeling; FT-VSI, N_BGS = 3, [0.56, 0.58, 1.14] s after labeling. Given that M_z of static tissue is preserved after DRHT, saturated after FT-VSS, and inverted after FT-VSI, respectively, the number of BGS inversion pulses serves to achieve positive residual tissue M_z at the end of the PLD, for consistent ASL signal analysis. The timing of the BGS inversion pulses were tailored through a home-made iterative minimization algorithm in Matlab, to have residual signal intensities of 1% - 25% for a broad range of T_1,t values (from 0.5 s to 4.4 s in 0.3 s interval). PCASL (39) was implemented with labeling duration τ of 1.8 s, PLD of 1.9 s, and BGS pulses with a slab-selective saturation pulse (1.5 s before labeling), a slab-selective inversion (0.05 s before labeling), and three non-selective inversion pulses [0.06, 1.22, 1.74] s post-labeling).

For all ASL protocols, following a fat-suppression module (spectral presaturation with inversion recovery, SPIR) at the end of the PLD, an axial 2D single-shot echo-planar imaging (EPI) scheme was performed with inserted motion-sensitized bipolar gradients along the slice direction (duration: t_bp = 7 ms; amplitude: 33 mT/m; V_c = 3 cm/s) for suppressing large-vessel signals (3,40). For VSASL (encoding velocity along the slice direction), this is to ensure acquisition of only the tagged spins that flow downstream along the arterial tree (from V > V_c to V < V_c) (13,15,16). Acquisition parameters: the transverse field of view (FOV) was 220 × 220 mm² with five slices acquired at a slice thickness of 4 mm and gaps of 4 mm; the acquisition resolution was 3.9 × 4.2 mm² and the reconstructed voxel size was 2.8 × 2.8 mm²; with the EPI factor (the number of k-space lines collected per echo train) of 29 and sensitivity encoding (SENSE) factor of 2, the echo train duration is 14.8 ms and the effective echo time is 16.1 ms (including t_bp). With TR = 5.5 s, the total measurement time after 30 averages of interleaved label and control was about 5.5 min for each of the four ASL scans.

In addition, proton density-weighted image (SI_PD) (TR = 10 s) was acquired for CBF quantification purposes (0.3 min) and a double inversion recovery (DIR) image to visualize gray matter only (TR = 10s; TI_1 = 3.58 s; TI_2 = 0.48 s; 0.3 min). All of these images were collected with the same resolution and acquisition scheme as the ASL protocols.

Data Analysis

Experimental data were processed using Matlab. For each subject, a binary gray matter mask (GM) was obtained from the DIR image using an empirical threshold and an ROI within the white matter (WM) was drawn manually using the SI_PD image.

Standard equations were used for CBF quantification of both the VSASL and PCASL scans. For VSASL applied with DRHT and FT-VSS pulse trains, CBF was calculated as described in (13,14):

$$\mathit{CBF}=\frac{6000·\mathrm{\lambda }·({\mathit{SI}}_{\mathit{control}}-{\mathit{SI}}_{\mathit{label}})·e^{\frac{\mathit{PLD}}{{\mathrm{T}}_{1,\mathrm{a}}}}}{{\mathrm{\alpha }}_{\mathit{label}}·{\mathrm{\alpha }}_{\mathit{BGS}}·{\mathrm{SI}}_{\mathit{PD}}·e^{-\frac{t_{\mathit{bp}}}{T_{2,t}^{\ast }}}·\mathit{PLD}}$$ [1]

When a FT-VSI pulse train is applied, a factor of 2 is added in the denominator to reflect the nature of inversion:

$$\mathit{CBF}=\frac{6000·\mathrm{\lambda }·({\mathit{SI}}_{\mathit{control}}-{\mathit{SI}}_{\mathit{label}})·e^{\frac{\mathit{PLD}}{{\mathrm{T}}_{1,\mathrm{a}}}}}{2·{\mathrm{\alpha }}_{\mathit{label}}·{\mathrm{\alpha }}_{\mathit{BGS}}·{\mathrm{SI}}_{\mathit{PD}}·e^{-\frac{t_{\mathit{bp}}}{T_{2,t}^{\ast }}}·\mathit{PLD}}$$ [2]

For PCASL the calculation is (41):

$$\mathit{CBF}=\frac{6000·\mathrm{\lambda }·({\mathit{SI}}_{\mathit{label}}-{\mathit{SI}}_{\mathit{control}})·e^{\frac{\mathit{PLD}}{{\mathrm{T}}_{1,\mathrm{a}}}}}{2·{\mathrm{\alpha }}_{\mathit{label}}·{\mathrm{\alpha }}_{\mathit{BGS}}·{\mathrm{SI}}_{\mathit{PD}}·e^{-\frac{t_{\mathit{bp}}}{T_{2,t}^{\ast }}}·T_{1,a}·(1-e^{-\frac{\tau }{T_{1,a}}})}$$ [3]

Note that the sign of the difference of the averaged signal intensities from the control/label images, (SI_control–SI_label), depends on the control/label profiles and BGS inversion pulses applied during PLD. The correction factor for perfusion signal loss due to BGS was set to be 0.93 for each inversion pulse employed (27). The labeling efficiency α_label for DRHT was set to be 0.88 given its effective TE of 20 ms and a T₂ of arterial blood at 3T assumed to be 150 ms (33,34). For FT-VSS and FT-VSI sequences, α_label values were estimated by referencing the averaged gray matter ASL signal differences of FT-VS scans to those measured in the DRHT scans and averaged across the eight subjects. The overall BGS-induced signal loss factor α_BGS and the labeling efficiency α_label for each VSASL method are listed in Table 2. For PCASL, α_BGS and α_label were assumed to be 0.80 (N_BGS = 3) and 0.85 (1,41), respectively. The exponential factor in the denominator of eqn. [3] takes into account the extra decay of the tissue during the time that bipolar gradients are played out right before the EPI acquisition and $T_{2,t}^{\ast }=40\mathrm{ms}$ (42). T₁ of arterial blood (T_1,a) at 3T was taken as 1.65 s as commonly chosen (6). Note that higher blood T₁ values (1.7-1.9s) were found recently when measured in vivo (7-9) and this will affect CBF estimation. Here λ (= 0.9 ml/g) is the brain-blood partition coefficient (43) and SI_PD is the signal intensity of tissue at equilibrium magnetization. CBF units are mL/100g/min, which is converted from mL/g/s through the factor of 6000.

Table 2.

Labeling efficiencies of FS-VS pulse trains.

	ASL signal differences referenced to DRHT	αBGS	αlabel
DRHT	1.00	0.86 (NBGS=2)	0.88
FT-VSS	0.94±0.05	0.80 (NBGS=3)	0.89±0.04
FT-VSI	1.21±0.06	0.80 (NBGS=3)	0.57±0.03

Voxel-wise mean CBF maps from the CBF time courses measured repeatedly (30 times) and temporal SNR maps (ratio of the mean value to the STD of the CBF time courses) were produced for all the scans of every subject. Averaged CBF and SNR values from GM and WM ROIs were calculated for each ASL method. Paired two-tailed t-Tests were performed on the differences of these SNR values (significance detection level: P = 0.05). To evaluate the consistency of the measured CBF values between the proposed FT-VSI prepared VSASL and the DRHT prepared VSASL and PCASL, their respective correlation was checked using linear regression and agreement was estimated through Bland–Altman plots.

RESULTS

Numerical Simulations

Mz responses (y-axis) of the proposed FT-VSI pulse train (Figure 1a) over the velocities (x-axis) are shown in Figure 1b for three different T₂ relaxation times (1500 ms, 150 ms, 70 ms), for both the labeling and control modules. Note that for labeling (solid profiles), the static spins (v = 0 cm/s) as well as the spins flowing at velocities around integer multiples of the FOV_v (45 cm/s) experience inversion as a result of the FT; for control (dashed lines), all spins are inverted regardless of the speed. When the T₂ values of arterial blood (150 ms) and tissue (70 ms) are taken into account, the inversion efficiency of this relatively long pulse train (T_VS = 48 ms) reduces to 0.84 and 0.69, respectively. In fact, this signal drop can be estimated by, exp(- (T_VS / 2) / T₂), the exponential decay of the T₂ relaxation starting from the middle of the pulse train, which is the center of the excitation k-space (20) for amplitude-modulated symmetric RF pulses.

Figure 1c displays the Mz responses of the FT-VSI pulse train over the plane of velocity (x-axis) vs. B0 off-resonance frequency (y-axis) at three different B1+ scales (0.8, 1.0, and 1.2) respectively. The simulated VS profiles of the labeling module are well maintained at different B0/B1 conditions and the Mz signal intensity within the inversion band still suffers from B1 inhomogeneity due to the hard pulses used at the beginning of each velocity encoding step, similar to the results shown for the FT-VSS pulse train (25). In contrast, the Mz responses of the employed velocity-compensated control pulse train increasingly deteriorate for flowing spins when the B1+ scales are further away from the correct setting (Supporting Figure S1). This indicates a more stringent requirement of perfect refocusing pulses for the proposed velocity-compensated waveform to eliminate any velocity sensitivity.

The Mz responses for a range of temporal changes in blood velocity (0%, red; ±5%, green; ±10%, blue; and ±20%, magenta) during the DRHT, FT-VSS and FT-VSI pulse trains are summarized in Figures 2a-c, respectively, with solid lines for labeling and dashed lines for control. For all three pulse trains, the spins with slow velocities are not affected by the velocity changes. For DRHT (Figure 2a), the velocity selective profiles are still close to cosinusoidal but larger velocity changes led to more shortened periods at the fast-velocity side of the passband, reflecting acceleration-related phase addition during the pulse train. For the two FT-VS pulse trains (Figures 2b,c), temporal changes of velocities during the pulse give rise to signal loss for the fast-velocity spins. For the temporal changes of velocities of 10% (blue solid lines) and 20% (magenta solid lines), the signal for fast moving blood spins is more reduced at the end of the 48 ms FT-VSI pulse train (Figure 2c) than the 64 ms FT-VSS one (Figure 2b). The profiles of the corresponding control pulse trains (dashed lines) for the FT-VS approach are also slightly susceptible to changes for fast moving spins (Figures 2b,c), compared to the complete insensitivity of the DRHT control pulse to this change (Figure 2a).

Figure 2.

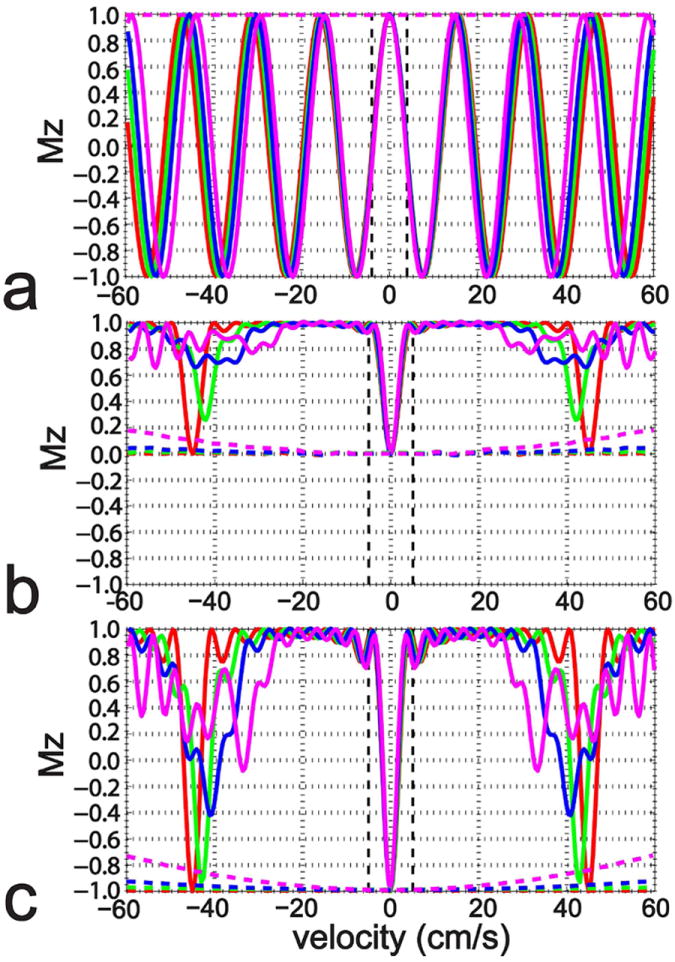
The simulated Mz-velocity responses of the 20 ms DRHT (a), 64 ms FT-VSS (b), and 48 ms FT-VSI pulse trains (c) when encountering linear temporal velocity changes within 50 ms: constant velocities (red), from 95% to 105% (green), from 90% to 110% (blue), and from 80% to 120% (magenta). The dashed lines illustrate the responses for the control scans of these three pulse trains. No B0 or B1+ inhomogeneity or T₂ effects were included in this simulation.

Using the 20 ms DRHT pulse as reference (Figure 3a), the simulated sensitivities of static spins to eddy current (EC) effects for the FT-VSS and FT-VSI pulse trains are shown in Figures 3b and 3c respectively, both for the 48 ms and 64 ms length. The sensitivities for the velocity-compensated control counterparts are also displayed. The sensitivities are shown as the signal differences between Mz affected by EC and ideal Mz (DRHT: 1; FT-VSS: 0; FT-VSI: -1) normalized to SI_PD (1). Compared to the velocity-sensitized pulse trains, the velocity-compensated ones are affected almost 10 times more by ECs (Figures 3b,c), which we attribute to reduced self-cancelation of ECs due to the shape of its gradient waveform. The range of time constants that the velocity-sensitized pulse trains are sensitive to (10^-2 - 10^-1 s) is also smaller than that of the velocity-compensated ones (10^-3 - 10^-1 s). Notice that EC sensitivity is reduced for the 64 ms FT-VS pulses (both label and control) compared to the 48 ms ones (Figures 3b,c), due to the increased gaps between gradients and subsequent RF pulses (Table 1). Interestingly, the velocity sensitive FT-VSI pulse trains (Figure 3c) are less sensitive to ECs than both the FT-VSS pulse trains (Figure 3b) and the DRHT one (Figure 3a). Considering the gradient-RF gaps employed in the 48 ms FT-VS pulse trains (0.34 ms) vs. in the 20 ms DRHT pulse (1.59 ms) (Table 1), the reduced EC sensitivity of the former is remarkable.

Figure 3.

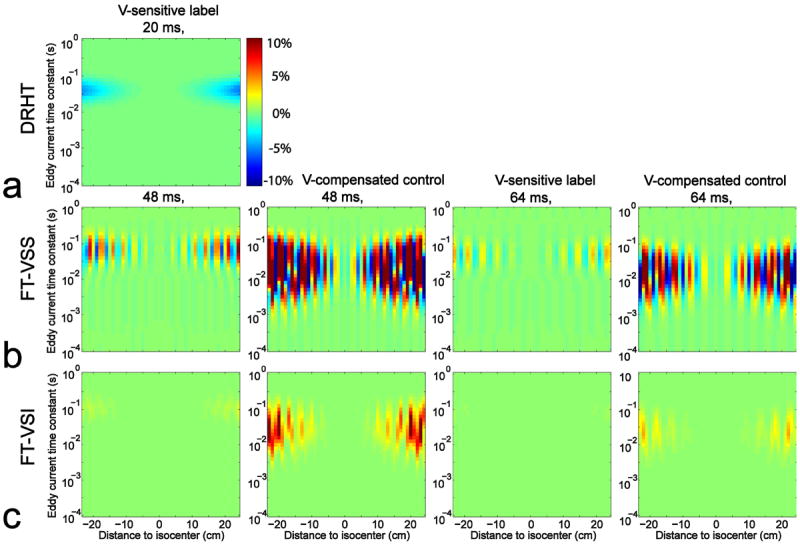
The simulated differences of the Mz of static spins at different distances to isocenter, following the 20 ms DRHT (a), the 48 ms and 64 ms FT-VSS (b), the 48 ms and 64 ms FT-VSI pulse trains (c), in the presence of EC effects with different time constants, to the Mz at EC-free conditions. Velocity-sensitive (V-sensitive) labeling and velocity-compensated (V-compensated) control waveforms are both tested for each FT-VS configuration. B0/B1 inhomogeneity and T₂ effects were not taken into account.

Phantom Experiments

Fig. 4 displays the effects of gradient imperfections for three orthogonal directions across 5 slices of the phantom, using normalized and then averaged signal differences of the label/control pairs for different pulse train conditions. The results of DRHT (Figure 4a), FT-VSS (Figure 4b) and FT-VSI (Figure 4c) interleaved with controls using velocity-insensitive waveforms are shown at the left column. For DRHT (Figure 4a), the normalized subtraction errors (mean ± STD) along A-P, L-R and S-I directions are 0.40 ± 0.41%, 0.11 ± 0.17%, and 0.07 ± 0.14%, respectively. The performance of the FT-VS pulse trains paired with velocity-compensated controls are displayed in the middle column (the same 48 ms) and the right column (64 ms) (Figures 4b,c). When paired with velocity-compensated controls, the normalized subtraction errors of the 48 ms and 64 ms FT-VS pulse trains along the S-I direction are much lower compared to the corresponding ones with velocity-insensitive waveforms (FT-VSS: -0.07 ± 0.07% and 0.05 ± 0.17% vs. 0.28 ± 0.40%; FT-VSI: -0.03 ± 0.12% and -0.05 ± 0.10% vs. -0.24 ± 0.44%). For the A-P and L-R directions, the FT-VS pulse trains with 64 ms configurations generate considerably less gradient-related artifacts than the 48 ms ones, as expected, and all of these directions would be suitable for use. Supporting Figure S2 unambiguously demonstrates that phase cycling of the refocusing pulses during the FT-VS pulse trains greatly reduces EC artifacts (by more than 100 times). For the CBF measurements in vivo, the 20 ms DRHT, the 64 ms FT-VSS and the 48 ms FT-VSI pulse trains, all along the S-I direction, were selected for their overall robustness to eddy currents and other gradient imperfections (Figures 3,4).

Figure 4.

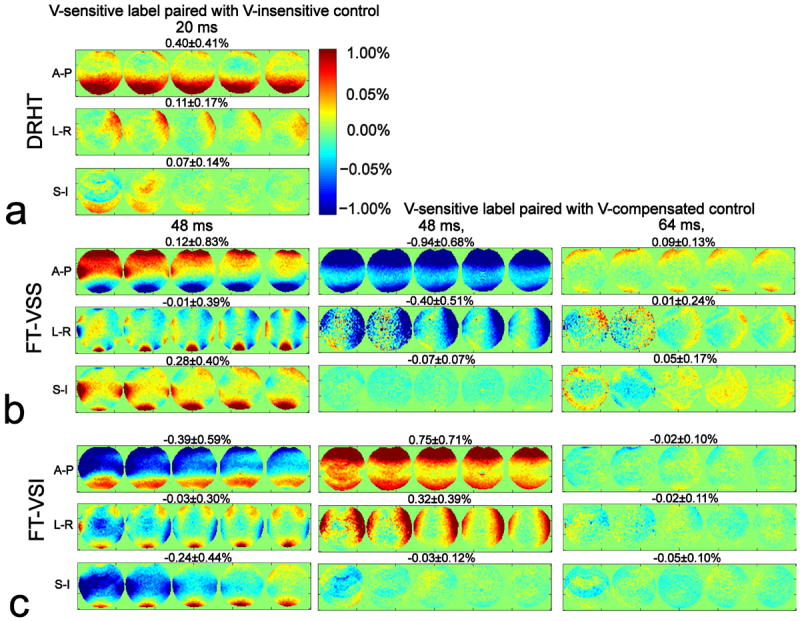
Signal difference errors on a phantom for different VS label/control configurations, (a) 20 ms DRHT, (b) 48 ms and 64 ms FT-VSS, (c) 48 ms and 64 ms FT-VSI pulse trains, caused by gradient imperfections (such as EC) along different gradient orientations. Results for velocity-sensitive (V-sensitive) labeling paired with velocity-insensitive (V-insensitive) control are shown in the left column; the middle and right column display the results with velocity-compensated (V-compensated) controls. Error maps are normalized to SI_PD (percentage displayed). All acquired 5 slices are shown with the averaged error percentage (mean ± STD) displayed at the top of each row.

In Vivo Experiments

Compared with the VSS prepared cerebral MRA (25), the results with the preparation modules using the velocity-compensated saturation pulse train and the velocity-insensitive one are depicted in the Supporting Figure S3. The velocity-non-selective effects are comparable between the two control modules.

Representative data from one female subject (#8) are shown in Fig. 5 with all 5 slices obtained: the image of SI_PD, the GM-only image from the DIR sequence, the segmented GM mask and chosen WM ROIs, quantified CBF maps estimated using PCASL as well as the VSASL scans labeled using DRHT, FT-VSS, and FT-VSI trains, respectively. The CBF maps and SNR images from the middle of the 5 slices of all 8 subjects are arrayed in Figure 6. No apparent artifacts related to eddy-currents were observed in any FT-VS labeled CBF maps. All four labeling techniques showed comparable perfusion results in cortical areas as well as deep brain regions.

Figure 5.

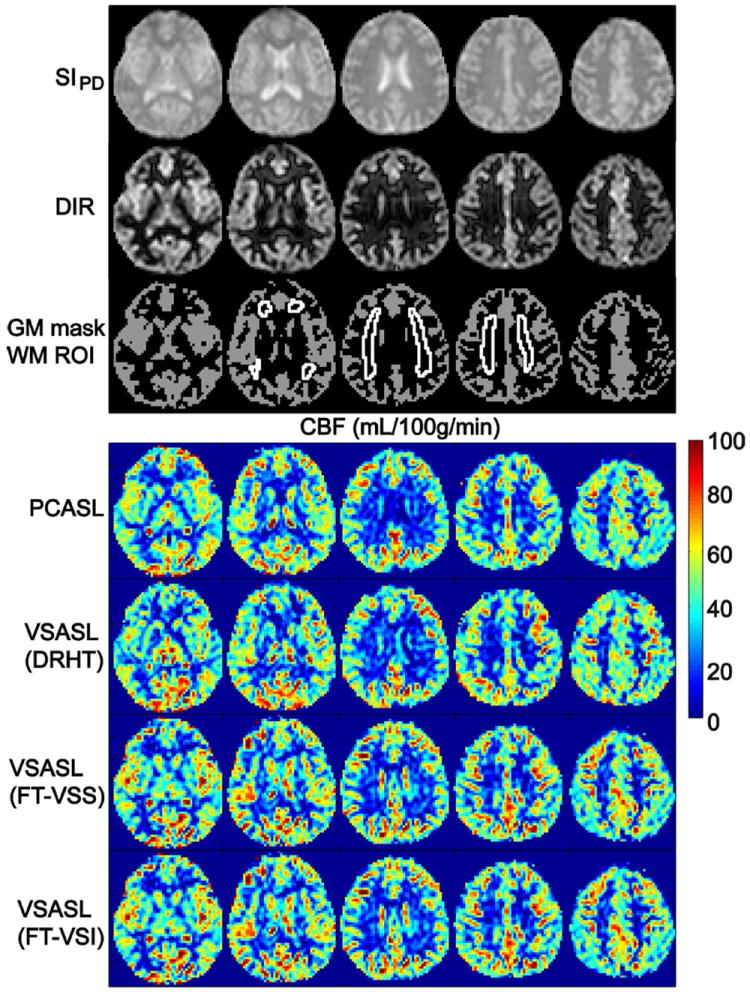
Representative data of all 5 slices acquired from subject 8: images of the SI_PD; image of gray matter only from the DIR sequence, the segmented GM mask and WM ROI, quantified CBF maps using PCASL and VSASL scans employing DRHT, FT-VSS, and FT-VSI labeling techniques, respectively.

Figure 6.

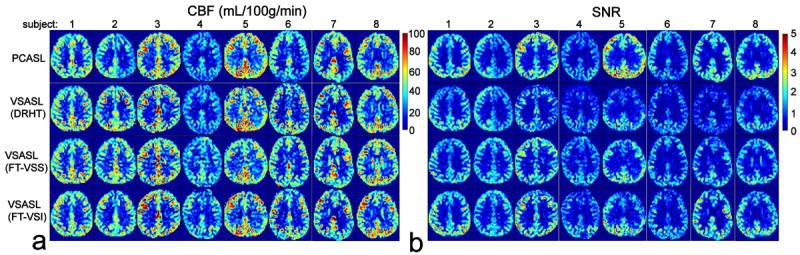
Examples of the estimated CBF maps (a) and SNR images (b) of 8 subjects (only one slice shown), using PCASL and VSASL scans employing DRHT, FT-VSS, and FT-VSI labeling techniques, respectively.

Noticeable left-right asymmetry is present for the CBF and SNR maps from PCASL in two subjects (#2, 6). Compared to the VSASL results, underestimation of CBF on one side of the hemispheres by PCASL indicates a non-uniform labeling efficiency across the main brain feeding arteries. Labeling efficiency of PCASL is sensitive to local B0/B1 inhomogeneities and flow velocities in large vessels (1,44-46) (subject #2 has a curled internal carotid artery on the left, known from previous angiogram study, data not shown).

Averaged CBF and SNR values within GM and WM ROIs and their GM/WM ratios are reported in Table 3. For the proposed FT-VSI prepared VSASL, the averaged GM and WM CBF values are 49.5 ± 7.5 and 14.8 ± 2.4 mL/100g/min, with a GM/WM ratio of 3.36. The averaged SNR value in GM of FT-VSI (1.76 ± 0.34) is 39% higher than that of DRHT (1.27 ± 0.29), 10% higher than that of FT-VSS (1.76 ± 0.34), and 9% lower than that of PCASL (1.93 ± 0.46); in WM, SNR of FT-VSI (0.42 ± 0.07) is 17% higher than that of DRHT (0.36 ± 0.08), 17% higher than that of FT-VSS (0.36 ± 0.08), and 2% higher than that of PCASL (0.41 ± 0.11). Significant differences in SNR values were observed between FT-VSI and DRHT methods for both GM (P = 0.003) and WM (P = 0.031) and between FT-VSI and FT-VSS for WM (P = 4.34×10^-4). No significant differences in SNR were observed between FT-VSI and PCASL methods for both GM (P = 0.180) and WM (P = 0.371) and between FT-VSI and FT-VSS for GM (P = 0.105) only.

Table 3.

Averaged CBF and SNR values (mean ± STD, n = 8) in GM and WM ROIs and their GM/WM ratios of the four different ASL methods.

		CBF (mL/100g/min)			SNR
		GM	WM	GM/WM ratio	GM	WM	GM/WM ratio
PCASL		48.0±11.1	14.5±3.2	3.31	1.93±0.46	0.41±0.11	4.72
VSASL	DRHT	49.5±6.7	15.5±2.6	3.19	1.27±0.29	0.36±0.08	3.50
	FT-VSS	49.3±6.5	15.1±2.5	3.26	1.60±0.20	0.36±0.08	4.40
	FT-VSI	49.5±7.5	14.8±2.4	3.36	1.76±0.34	0.42±0.07	4.14

Figure 7 shows linear regression and Bland-Altman analyses of the averaged individual CBF values from both GM and WM comparing FT-VSI prepared VSASL with PCASL (Figures 7a,b) and DRHT prepared VSASL (Figures 7c,d), respectively. Excellent correlation and agreement across different methods are demonstrated.

Figure 7.

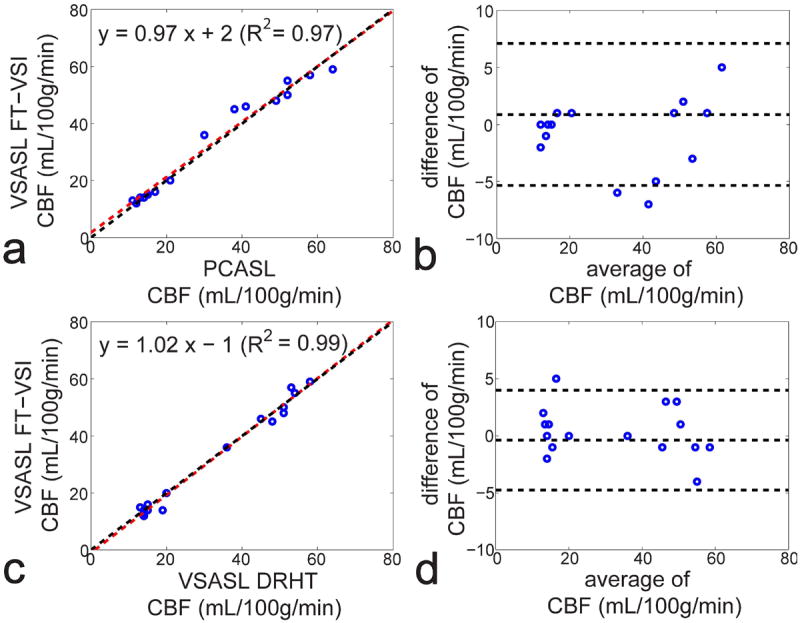
Correlation (a,c) and agreement plots (b,d) of the averaged individual CBF values of both GM and WM (open circles) measured by FT-VSI prepared VSASL with PCASL (a,b) and DRHT-prepared VSASL (c,d), respectively. For the correlation plots (a,c), red dashed lines are the linear regression curves with the fitted equations shown at the top of the figures. The black dashed lines show the unity line y = x. For the agreement plots (b,d), the difference of the two methods are plotted against the mean (Bland-Altman plot), with the middle of the three horizontal dashed lines indicating the mean difference of all subjects, and the top and bottom dashed lines indicating the mean difference ± two times of the standard deviation of their differences.

DISCUSSION

The proposed FT-VSI pulse train, by inserting paired and phase-cycled refocusing pulses, was able to greatly mitigate artifacts of the velocity-selective profiles from B0/B1 field inhomogeneities (Figure 1c) and eddy currents (Figures 3-4, Supporting Figure S2). As shown in a recent MRA application (25), a similarly designed FT-VSS pulse train can adequately separate both large and small vessels from the static tissue in the head and neck. The effects of these velocity-sensitive, -compensated, and -insensitive waveforms are illustrated in Supporting Figure S3. The utility of this technique for CBF measurement was demonstrated using a VSASL protocol on a clinical 3T scanner with very consistent results compared to conventional VSASL and PCASL methods (Figures 5-7).

The averaged FT-VSI to DRHT ratio of ASL signal differences and SNR of GM were 1.21 (Table 2) and 1.39 (Table 3), respectively. This is much less than the sensitivity improvement of a factor of 2.00 expected when changing from saturation to inversion labeling in theory. The estimated labeling efficiency for FT-VSI in this work was 0.57± 0.03 (Table 2), compared to 0.88 for DRHT (Table 2) and 0.85 for PCASL (1,41). The two main factors that bear the blame for this low labeling efficiency are spatial variation in the B1+ field and temporal variation of velocity during the pulse.

First, the hard pulses used at the beginning of each velocity encoding step for k-space weighting are still influenced by the inhomogeneity of B1+ field and directly affect the flip angles of spins within the inversion band (Figure 1c). Considering B1+ scales in the brain at 3T range from 0.8 to 1.2, the ASL signal differences produced by the FT-VSI label/control pair are maximum when 180° flip angle is achieved (B1+ scale = 1.0) and less with either lower or higher flip angles (from 144° to 216°), whereas FT-VSS pulse train generates more ASL signal differences with higher labeling flip angles (from 72° to 108°). In fact, this may also help explain the low FT-VSI to FT-VSS ratio of the averaged ASL signal differences (1.21 / 0.94 = 1.29, Table 2) and SNR (1.76 / 1.60 = 1.10, Table 3) of GM. The bulk of the blood being labeled within the large intracranial arteries (25) may experience the B1 transmission field close to the center of the cranium with a B1+ scale higher than 1.0 (47-49). To overcome the spatially-dependent labeling efficiency due to B1 inhomogeneity and eddy currents, a variant of VSS using B1 insensitive rotation (BIR) pulses was introduced (17,18). Further studies are warranted to realize more B1-insensitive FT-VS pulse trains.

Second, blood velocity variation during the pulse (such as arterial blood pulsation or blood vessel tortuosity) will lead to signal loss for the flowing spins with fast-velocities at the end of the FT-VS pulse trains (Figure 2). Interestingly, the response to the FT-VSI pulse (Figure 2c) seems to be more degraded by this temporal change of velocities than that to the FT-VSS pulses (Figure 2b). In the FT-VSS prepared MRA study (25), 20-30% signal reduction was reported for large arteries when one and two VS modules applied successively were compared. This can be alleviated by further shortening the duration of FT-VS pulses with better RF coil (higher maximum B1 amplitude) and gradient systems (higher maximum amplitude and slew rate, and less eddy currents).

The reduction of labeling efficiency induced by T₂-decay during the FT-VSI pulse train is 0.84 (Figure 1b), close to 0.88 of DRHT, although with more than twice the train duration (48 ms vs. 20 ms). This is due to the difference in time that the magnetizations spend in the transverse plane during these two pulse trains, with about half the pulse duration (24 ms) for FT-VSI and almost the entire pulse duration (20 ms) for DRHT. Note that the assumed arterial blood T₂ for the simulation is 150 ms, which is based on a calculation with hematocrit (Hct) of 0.41, oxygenation level (Y) of 0.98, and CPMG inter-echo spacing (τ_CPMG) of 10 ms (33,34). A more realistic arterial blood T₂ with the same Hct and Y values for FT-VSI (τ_CPMG = 3 ms) should be higher than 170 ms, considering an effective T₂ of 165 ms for τ_CPMG = 5 ms (34). This actually will only cause a very small increase of estimated T₂-induced signal reduction for FT-VSI pulse train from exp(- 24 / 150) = 0.85 to exp(- 24 / 170) = 0.87.

In this work, the control module of the FT-VSI method employed a velocity-compensated waveform instead of the velocity-insensitive RF pulse train typically used in VSASL (13-17). The original motivation of this implementation was to avoid unbalanced diffusion attenuation between label and control signals. While this effect was negligible in this study (Table 1), FT-VS pulse trains paired with velocity-compensated waveforms along the S-I direction showed minimum artifacts in the axial slices, compared to corresponding results either with velocity-insensitive waveforms or with other velocity-encoding directions (Figure 4). The gradient imperfections related to this technique are perhaps not dominated by ECs, since simulations actually showed that velocity-compensated FT-VS pulse trains were almost 10 times more sensitive to the EC effects than velocity-sensitive ones (Figure 3). Other gradient imperfections may include gradient-switching induced mechanical vibration, thermal variation and B0 field drifting and could be characterized by impulse response measurements (50). The exact mechanisms of how different gradient configurations exhibit different levels of robustness to gradient imperfections at various conditions are still unknown. In contrast to the velocity-sensitive labeling pulse train (Figure 1c), the employed velocity-compensated control pulse train is sensitive to the B1 inhomogeneity (Supporting Figure S1), which could be a major factor contributing to the low labeling efficiency observed in our study. Another caveat of applying this velocity-compensated waveform as the control module is its potential sensitivity to acceleration selectivity (30,31). Although no significant acceleration effect was observed in the FT-VSS prepared MRA experiments (Supporting Figure S3), a slight undermining of labeling efficiencies in the presence of 2^nd order motion during the FT-VS pulse trains was noticed when using the control module with velocity-compensated waveforms (dashed lines in Figure 2).

SNR efficiency of VSS prepared VSASL has recently been shown to be improved by setting the proper PLD based on knowing the bolus durations and utilizing multiple VSS modules (51). In this study, a 1.5 s PLD was chosen which was similar to other VSASL reports (13,18,51,52). Our FT-VSS prepared cerebral MRA (25) with a wide angiographic coverage indicated equivalent bolus durations for the DRHT prepared VSS method. In addition, SNR efficiency of FT-VSI prepared VSASL might be further enhanced by repeating the labeling modules (51,53).

With the implementations on healthy subjects here, the SNR attained by FT-VSI preparation was only 9% lower than PCASL (Table 3), which is attractive considering the desired benefit of insensitivity to transit times for VSASL on patients with large vessel occlusions. Two recent publications on velocity- and acceleration-selective ASL also demonstrated SNR values comparable to or higher than PCASL (31,51). Other advantages of VSASL techniques over PCASL include: 1) a significant reduction in reported SAR values (PCASL: 33%; DRHT: 12%; FT-VSS: 16%; FT-VSI: 17%; The percentages are relative to 3.2 W/kg, the head averaged SAR limit of the scanner); 2) Elimination of the need for operators to manually place labeling slabs onto the feeding arteries; 3) Avoidance of the high-pitch acoustic noise associated with PCASL. Here the emphasis was on VSI pulse trains applied for ASL. However, it should be noted that FT-VSI pulse trains can be devised for velocity-selective profiles of arbitrary shape and extended to other applications, e.g., acceleration-selective ASL (30) or MR angiography (23-25,54).

CONCLUSION

Using the k-space formalism, we developed a novel FT-based velocity-selective inversion pulse train. Simulation studies showed that the velocity-selective profile of the labeling pulse train is robust to B0/B1 field inhomogeneity and the signal intensity within the inversion band depends on the B1+ scale. However, the velocity-compensated control module for FT-VSI remains sensitive to B1 inhomogeneity. Phantom studies employing the FT-VSI labeling pulse train paired with the velocity-compensated control module revealed little artifacts with gradient imperfections such as eddy currents. The CBF values measured in vivo using this FT-VSI prepared VSASL approach were consistent with those from conventional VSASL and PCASL methods. The SNR produced with the FT-VSI method was higher than that of the conventional VSASL and close to the PCASL method. Further investigation among patients with cerebral vascular disorders is needed to explore the clinical value of the proposed technique.

Supplementary Material

Supp FigureS1-S3

Supporting Figure S1: The simulated Mz-velocity responses of the employed velocity-compensated control pulse train (red solid lines) for different B1+ scales of (a) 1.0, (b) 0.9, (c) 1.1, (d) 0.8, and (e) 1.2. The blue dashed lines illustrate the corresponding responses of the velocity-insensitive pulse train. When B1+ scales depart 10% (b,c) or 20% (d,e) from the correct setting (a), the Mz-velocity responses of the velocity-compensated pulse train increasingly deteriorate for the flowing spins, as compared to the Mz responses of the velocity-insensitive pulse train where the only changes are in the inversion degree.

Supporting Figure S2: Gradient-imperfection induced subtraction errors on a phantom of the 48 ms FT-VSI pulse trains, velocity-sensitive (V-sensitive) labeling paired with velocity-compensated (V-compensated) controls, with (top row) and without (bottom row) MLEV-16 phase-cycling scheme. Note that the scale of the normalized error percentage in the bottom row is 30 times more than in the top row, indicating great reductions of gradient related artifacts by complete phase cycling of refocusing pulses.

Supporting Figure S3: MIPs of VS-MRA from one subject: double implementation of the 48 ms FT-VSS pulse train encoded along superior-inferior direction using (a) velocity-sensitive (V-sensitive), (b) velocity-compensated (V-compensated), (c) velocity-insensitive (V-insensitive) waveforms.