Abstract
Purpose
To design array-compressed parallel transmit radiofrequency (RF) pulses and compare them to pulses designed with existing transmit array compression strategies.
Theory and Methods
Array-compressed parallel RF pulse design is proposed as the joint optimization of a matrix of complex-valued compression weights that relate a full-channel physical array to a reduced-channel virtual array, along with a set of RF pulses for the virtual array. In this way, the physics of the RF pulse application determine the coil combination weights. Array-compressed pulse design algorithms are described for four parallel transmit applications: accelerated 2D spiral excitation, multislice RF shimming, small-tip-angle kT-points excitation, and slice-selective spokes refocusing. Array-compressed designs are compared in simulations and an experiment to pulses designed using four existing array compression strategies.
Results
In all cases, array-compressed pulses achieved the lowest root-mean-square excitation error among the array compression approaches. Low errors were generally achieved without increasing root-mean-square RF amplitudes or maximum local 10-gram specific absorption rate. Leave-one-out multisubject shimming simulations demonstrated that array-compressed RF shimming can identify useful fixed coil combination weights that perform well across a population.
Conclusion
Array-compressed pulse design jointly identifies the transmit coil array compression weights and RF pulses that perform best for a specific parallel excitation application.
Keywords: SVD, RF pulse design, selective excitation, array compression, parallel transmission, spokes pulses, kT points pulses, RF shimming, tailored excitation, optimization
Introduction
Parallel radiofrequency (RF) transmission (pTx) is an important technique for high field MRI in which different RF waveforms are simultaneously played through the elements of a multicoil transmit array, in order to dynamically shape the combined transmit RF field [1, 2]. Just as it is desirable to use a large number of receive coils in parallel receive, it is also desirable to use a large number of transmit coils for pTx [3]. For example, when accelerating multidimensional spatially-selective excitations, with more transmit coils the RF pulse duration can be decreased without sacrificing excitation accuracy, which reduces sensitivity to off-resonance and makes the pulses compatible with a wider range of pulse sequences. A large number of transmit coils is desirable for RF shimming [4–6], since with more coils one can more finely shape the total field to mitigate subject-specific variations. Arrays with many coil elements can also provide better control of specific absorption rate (SAR) [2, 6].
While a large number of coils is desirable in pTx, the high cost, large footprint and cabling requirements of the corresponding RF power amplifier arrays have limited the number of transmit channels that have been installed in practice. Most ≥ 7 Tesla scanners today are equipped with at least 32 receive channels, but only 2 or 8 transmit channels. Furthermore, power monitoring and SAR prediction becomes increasingly complicated as the number of transmit channels is increased, and pTx pulse design time increases with the number of transmit channels. Thus, it is desirable to use only a few transmit channels with independent RF waveforms, while maintaining as much as possible the performance provided by a large number of transmit coils. Previous work has been done to compress transmit arrays by identifying coil combinations or modes that are most important for parallel transmission [7, 8], or that can improve mapping accuracy or speed [9– 13]. However, in all these cases the set of available coil combinations was fixed prior to pulse design or shim optimization.
In this work, we propose an array-compressed pTx pulse design framework in which the amplitudes and phases of the transmit coil array compression weights are jointly optimized with RF pulses for the compressed array. In this way, the excitation spin physics directly informs the construction of the compressed coil array. We first show how this concept can be integrated with four representative small- and large-tip-angle pTx pulse design problems, by iteratively constraining the rank of the RF pulse or shim weight matrix during pulse design. Then we demonstrate the potential advantages of this approach compared to fixed array compression weights derived by multiple methods in simulations and pseudo-pTx experiments. The comparisons also include a related hybrid RF shimming and pulse design method that was presented at the same ISMRM meeting as a preliminary account of the present work [14].
Theory
The goal of array-compressed pTx pulse design is to jointly determine a matrix of complex-valued compression weights that relate the elements of a transmit coil array to a reduced-channel virtual array, along with a set of RF pulses for the reduced-channel virtual array. Depending on the application, the compression weights would then be implemented using a hardware or software array compression network as illustrated in Fig. 1a. In the following sections we formulate array-compressed pulse design problems for four representative parallel pulse types, and describe approaches to solve those problems. In all cases, the basic optimization problem we solve is:
| [1] |
where B is a matrix whose columns are vectors of waveform samples or shim weights for the Ncoils physical array, one column for each physical coil. Ψ (B) is the excitation error metric plus any regularization terms, and is different for each problem as defined below. Compressed pulses and compression weights can be obtained from the singular value decomposition (SVD) of a solution to Eq. 1:
| [2] |
where the orthonormal matrices U and V contain the left- and right-singular vectors, respectively, Σ is an Namps × Namps diagonal matrix of singular values, and the H superscript denotes a Hermitian matrix transpose. Matrices of compressed pulses and compression weights can be derived from Eq. 2 in two ways; in this work we define the Ncoils × Namps compression weights matrix to be V* where * denotes complex conjugation of each matrix element, and the array-compressed pulse matrix to be UΣ, which will have a row dimension equal to the number of RF waveform time points or RF shim weights, and a column dimension of Namps. In the following sections we define Ψ (B) in Eq. 1 for accelerated spiral pulse design, RF shimming, 3D kT-points pulse design, and large-tip-angle spokes pulse design, and describe methods to solve the resulting problems.
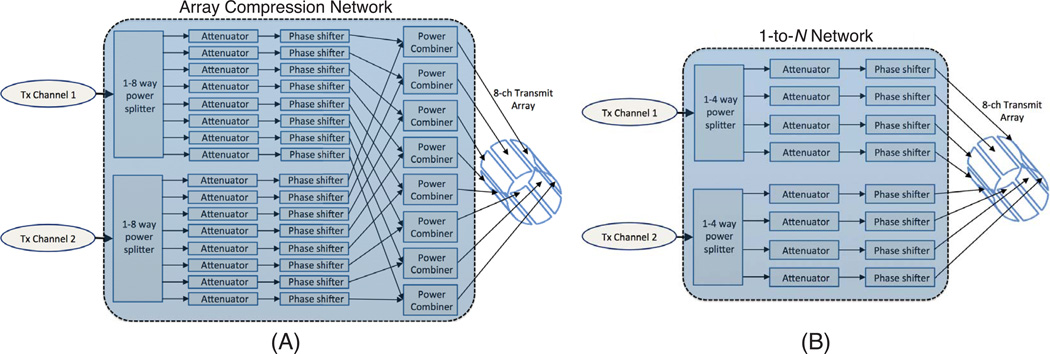
Figure 1.
(a) Illustration of an array compression network. In this example, the network takes Namps = 2 input transmit channels, splits them to each of the Ncoils = 8 coils, and applies optimized attenuations and phase shifts to each of the split signals. Then for each coil the weighted signals are summed across the two input channels. (b) Illustration of the 1-to-N coil combination network proposed by Floser et al [27]. In this example, the Namps = 2 input transmit channels are each split 4 ways, and each coil receives a weighted signal from one transmit channel.
Spiral pulses
Spiral parallel transmit pulses are typically used to excite a localized 2D region for reduced-FOV imaging [1, 15]. The array-compressed spiral pulse design problem is developed as an extension of the small-tip-angle pTx pulse design method of Ref. [16]:
| [3] |
where d is a vector of samples of a target excitation pattern, Si is a diagonal matrix containing coil i’s map, A is a Fourier system matrix defined by the spiral excitation k-space trajectory, bi is coil i’s sampled RF pulse waveform, λ is a regularization parameter, and R is a regularization matrix that can be set (for example) to an identity matrix to control integrated power, or to a finite differencing matrix to control rapid changes in the pulses’ envelopes [17]. The pulse design typically only considers spatial locations within the imaged object.
To solve this problem, we use an iterative procedure in which we alternately perform a few conjugate gradient (CG) iterations starting with the most recent set of RF pulses, and perform singular value truncation of the B matrix formed from the most recent set of pulses. The singular value truncation procedure comprises calculating the SVD of B, setting the last Ncoils – Namps singular values to zero in the Σ matrix, and then re-constituting the resulting rank-reduced B matrix. After the iterations converge, the first Namps columns of the V* matrix are taken to be the compression weights. This procedure is inspired by the singular value thresholding algorithm proposed in Ref. [18] for low-rank matrix completion.
Multislice RF shimming
In multislice RF shimming, RF shim weights are optimized and played out on a slice-by-slice basis [5], with the goal of producing a combined field with uniform amplitude in each slice. The array-compressed idea can be applied to multislice RF shimming by jointly determining a set of array compression weights that apply to the entire volume of slices, along with the compressed shim weights for each slice. This problem can be stated as:
| [4] |
where the vectors di (ϕi) contain each slice’s sampled target excitation patterns which have phase patterns ϕi and uniform amplitudes, the matrices Si contain the Ncoils maps for each slice as their columns, and the vectors bi contain the Ncoils RF shim weights for each slice. In contrast to the spiral pulse design above, in this problem the rows (rather than the columns) of the matrix B are formed from the vectors bi. The phase patterns ϕi are optimized along with the RF shim weights B to obtain a magnitude least-squares solution, since only the magnitudes of the combined fields need to be spatially uniform [19].
As in the array-compressed spiral pulse design, we solve this problem by alternately updating the shim weights for each slice independently using a few CG iterations, and then forming the B matrix and truncating its singular values. Then the target phase patterns ϕi are set equal to the phase produced by the singular value-truncated shim weights, and the process is repeated until the squared-error objective stops decreasing. It is important to note that when Namps ≥ Nslices, the matrix B can have rank no greater than Nslices, so singular value truncation is not necessary to obtain a compressed solution. In that case, each slice’s RF shim weights can be taken directly as an array compression matrix. This situation is not likely to arise in spiral pulse design since the number of time points in spiral pulses will typically be much larger than Namps.
3D kT - Points pulses
kT-Points pulses comprise trains of weighted hard pulses interleaved with gradient blips, and are typically used to excite uniform flip angle patterns over 3D volumes [20]. The small-tip-angle array-compressed kT-points pulse design problem is developed as an extension of the interleaved greedy and local optimization spokes and kT-points pulse design method of Ref. [21]:
| [5] |
where the vector d(ϕ) contains samples of the uniform 3D target excitation pattern with phase pattern ϕ and uniform amplitude, Si is a diagonal matrix containing coil i’s 3D map, A(𝕂) is the Fourier system matrix defined by the set of excitation k-space locations 𝕂 visited by the kT-points trajectory, and the vectors bi contain the coils’ hard pulse weights, one for each excitation k-space location visited by the trajectory. ϕ and 𝕂 are jointly optimized with the pulses. In this problem (like the spiral problem), the columns of B are formed from the vectors bi.
The interleaved greedy and local optimization algorithm starts with a single kT-point and alternately updates the RF weights and target phase pattern ϕ until the excitation error stops decreasing. Then a greedy method is used to select the excitation k-space location of the next kT-point, and the RF weights, ϕ, and the k-space locations are again alternately updated until convergence. The steps are repeated until all the kT-points have been added to the pulse. Full details are provided in Ref. [21]. The algorithm is extended to array-compressed pulse design by replacing the original algorithm’s regularized pseudo-inverse RF update step with a few CG iterations followed by singular value truncation, once the number of kT-points in the pulse exceeds Namps.
Spokes pulses
Similar to kT-points pulses, spokes pulses comprise trains of weighted subpulses interleaved with gradient blips, however spokes pulses use slice-selective subpulses and are used to excite uniform flip angle patterns within 2D slices [22, 23]. The large-tip-angle array-compressed spokes pulse design problem is developed as an extension of the joint RF and gradient blip design algorithm of Ref. [24], which applies to large-tip spokes and kT-points pulses:
| [6] |
where αd (ϕα) and βd (ϕβ) contain samples of the uniform 2D target spinor patterns [25] with phase patterns ϕα and ϕβ and uniform amplitudes, and are the 2D spinor patterns produced by the spokes pulses with subpulse weights bfull and gradient blip moments , and bfull is the vector of all coils’ weights, stacked end-on-end. The matrix B is constructed by reshaping the bfull vector so that each column contains one coil’s subpulse weights. The pulse design typically only considers spatial locations in the center of the excited slice and within the imaged object.
The algorithm of Ref. [24] works by alternately updating the RF subpulse weights and the gradient blip moments using the non-linear CG algorithm, and updating the target phase patterns by setting them equal to the phase of the current excited spinor patterns. It is extended to array-compressed pulse design by adding a singular value truncation step after each RF update, assuming the number of spokes is greater than Namps. The algorithm is initialized with small-tip-designed pulses; in this work, the algorithm described for array-compressed kT-points pulse design will also be used to design the initial small-tip spokes pulses.
Methods
All pulse designs and related processing were performed in MATLAB R2014b (Mathworks, Natick, MA, USA). Code to implement all designs is available for download at https://bitbucket.org/wgrissom/acptx/.
Comparisons
Array-compressed pulses were compared to pulses designed using four other array compression approaches. Three of those approaches worked by compressing the maps down to the target number of channels prior to pulse design. Then pulses were designed using those maps and the same algorithms as the array-compressed designs but without singular value truncation. Specifically, all pulse design cases included comparisons to array compression using singular value truncation of the map matrix (“ SVT”), wherein the masked maps of all Ncoils channels were arranged as columns in a matrix S, and singular value truncation was applied to that matrix to obtain the desired Namps compressed channels [11, 26]. Mathematically, the compressed map matrix is given by:
| [7] |
where is the matrix of right singular vectors of the matrix S corresponding to the largest Namps singular values. Since the 7T 8-channel head coil (described further below) that was used in the spiral, kT-points and spokes simulations had a concentric configuration, in those cases we also compared the array-compressed pulses to the coil’s “Modes” [7], where mode i was obtained by summing the coils’ maps with phase shifts of i2π/Ncoils between adjacent coils. The first Namps modes were used for each comparison. The same pulse design cases also included comparisons to “Split CP” (circularly polarized) combinations, wherein the maps were adjusted to be in-phase at the center of the target imaging volume prior to summation, and each consecutive set of Ncoils/Namps coils was assigned to a compressed channel. For this compression approach, the number of compressed channels was restricted to a divisor of Ncoils. For example, 8 physical channels could be combined to 1, 2, or 4 compressed channels. This comparison was intended to complement the “Modes” case by using amplitude modulation of the coil elements rather than phase modulation to obtain orthogonal sets of virtual coil combination weights. We chose to group the coils into consecutive sets rather than interleave them since consecutive coil groupings consistently led to lower excitation errors and RF power (results not shown).
The spiral, kT-points and spokes pulse designs for the 7T 8-channel concentric head coil also included comparisons with a contemporary array compression approach proposed by Flöser et al [27], which we refer to as the “1-to-N” approach. In that method, transmit coils in a concentric array are grouped into Namps coil subsets either consecutively or in an interleaved fashion, and each group is assigned to a transmit channel. This is illustrated in Fig. 1b. The method then solves for both the weights that link the transmit channels to the coils, and the pulses for the compressed channels. In the original work, the authors used a gradient-based approach to solve for the weights and pulses. For the comparisons presented here, we adapted the SVT rank-constraint step used for array-compressed designs to solve for 1-to-N coil combination weights and pulses as follows: the B matrix is formed as described for each pulse design problem, and is then divided into multiple sub-matrices, each of which contains the pulse waveforms for the coils assigned to one transmit channel. Then, SVT is applied to each submatrix to reduce its rank to 1, and the full B matrix is reconstituted from the rank-constrained sub-matrices. In all other aspects the array-compressed and 1-to-N pulse design algorithm implementations were identical. As in the split CP combinations, in 1-to-N combinations the number of compressed channels were restricted to a divisor of Ncoils. Also like the split CP case, for the 1-to-N designs we chose to group the coils into consecutive sets rather than interleave them since consecutive coil groupings consistently led to lower excitation errors and RF power (results not shown).
For the spiral experiment and spokes simulations, pulses were compared in terms of their flip angle root-mean-square-error (RMSE) (degrees). For the spiral and kT-points simulations, pulses were compared in terms of flip angle normalized RMSE (NRMSE) (%), which were calculated as the flip angle RMSE divided by the RMS amplitude of the target excitation pattern. RF Shim solutions were compared in terms of their RMSE (%). The pulses were also compared in terms of their RMS RF amplitude after transforming them back to the original coil space. Additionally, since electric field and conductivity maps were available for the 7T 8-channel head coil used for the spiral, kT-points and spokes pulse designs, the maximum 10-gram local SAR in the head model was calculated for all of those pulses, and reported relative to the all-channels pulses [28].
Spiral simulations and experiment
Small-tip-angle spiral pulses were designed for a simulated 8-channel 7 Tesla brain transmit coil [29]. RF field simulations were performed in XFDTD (Remcom Inc, State College, PA, USA), and the static magnetic (B0) field in the same human head model was calculated using the method of Ref. [30] and used in the pulse designs. The target pattern (the Vanderbilt University logo) and field maps were defined on a brain-masked 100 × 100 grid with FOV 18 cm. The designs used a spiral-in excitation trajectory with 7 cm FOV, 0.36 cm resolution and 8 ms duration, and the resulting pulses were undersampled by a factor of 2.32 considering the width of the brain mask. Pulses were designed using all 8 coils, and with all compression methods for Namps = 1 – 4 compressed channels. Non-uniform fast Fourier transforms were used for multiplications with the Fourier system matrix A in Eq. 3 [31]. The RF updates used 3 CG iterations and waveform roughness regularization [17].
Small-tip-angle spiral pulses were also designed to excite a selective pattern in an 18 cm homogeneous gel phantom using a 7T Philips Achieva scanner (Philips Healthcare, Cleveland, OH, USA). Since hardware to apply the array compression weights was not yet available and the scanner had only two transmit channels, receive sensitivity maps were measured in an axial slice using a 32-channel head coil (Nova Medical Inc., Wilmington, MA, USA) and were used in place of the transmit fields for pulse design. The 16 channels with the lowest amplitudes in the selected slice were discarded for pulse design. The designs targeted a 20 degree flip angle on a masked 100 × 100 grid with FOV 20 cm. The designs used a spiral-in excitation trajectory with 5 cm FOV, 0.3 cm resolution, and 6 ms duration, so the resulting pulses were undersampled by a factor of 18/5 = 3.6. Pulses were designed using all 16 coils, and with SVT and array-compressed pulse design for Namps = 2 compressed channels. Then experiments were performed to measure the excitation patterns produced by the designed pulses. The experiments used the pseudo transmit SENSE method [32] which exploits the commutative property of small-tip-angle excitation by designing pulses using the maps of a receive coil array, then imaging the pulses’ excitation patterns individually and summing the images to obtain the total excitation pattern. The spiral pulses were used for excitation, a slice-selective 180° refocusing pulse was used for slice selection, and a 2DFT readout was used for imaging.
Multislice RF shimming simulations
Multislice RF shim weights were designed using maps measured in 5 healthy human subjects for the 32-channel head coil. Human scanning was done with approval of the Institutional Review Board at Vanderbilt University. The designs were performed over 10 axial slices (3 mm thickness, 5 mm slice gap). To evaluate performance of the compression approaches across the number of compressed channels, in one representative subject shim weights were designed using all 32 channels, and with SVT and array-compressed shimming with Namps = 1 – 9. The array-compressed shim weight updates used 3 CG iterations. To evaluate whether the array-compressed pulse design approach can identify coil combinations that perform well across multiple subjects, a leave-one-out cross validation was also performed in which the array-compressed RF shim weight design problem was solved after concatenating four of the five subjects’ maps into a single multislice volume. The resulting array compression weights were then applied to the fifth subject’s maps, and a conventional multislice shim weight optimization was performed using the same shimming algorithm without singular value truncation. This procedure was performed for all 5 subjects, and the results were compared to shimming using SVT coil combinations derived from four of five subjects’ concatenated maps, as well as subject-specific all-channel shimming. For each slice and Namps, the SVT shim optimizations were repeated with multiple initial target phase maps, including zero phase maps and phase maps obtained from the all-channel shim, and the result with the lowest final objective function value (Eq. 4) was used in the comparison.
kT - Points simulations
Small-tip-angle kT-points pulses were designed for the simulated 8-channel brain coil. The pulses targeted a volume FOV of 18 × 18 × 12 cm. The kT-points pulses comprised 7 hard subpulses, each with 0.1 ms duration. The RF subpulse weight updates used 3 CG iterations. Pulses were designed with all 8 coils and with each array compression approach with Namps = 1 – 6. The integrated RF power penalty λ was updated dynamically over algorithm iterations as described in Ref. [21]. All compressed designs were repeated with multiple initial target phase maps, including zero phase maps and phase maps obtained from the all-channels pulse, and in each case the result with the lowest final objective function value (Eq. 5) was used in the comparison.
Spokes simulations
180° Spokes pulses were also designed for the simulated 8-channel brain coil. The pulses were designed to excite a 3 mm-thick axial slice in the middle of the simulated brain volume with an 18 × 18 cm design FOV, and comprised 7 slice-selective subpulses (time-bandwidth product 2, 1.3 ms duration) with a bipolar slice-select gradient trajectory. Pulses were designed with all 8 coils and with each array compression approach with Namps = 1 – 6. The integrated RF power penalty λ was updated dynamically over algorithm iterations as described in Ref. [24]. As in the RF shimming and kT-points designs, all compressed designs were repeated with multiple initial target phase maps, including zero phase maps and phase maps obtained from the all-channels pulse, and in each case the result with the lowest final objective function value (Eq. 6) was used in the comparison.
Results
Spiral simulations and experiment
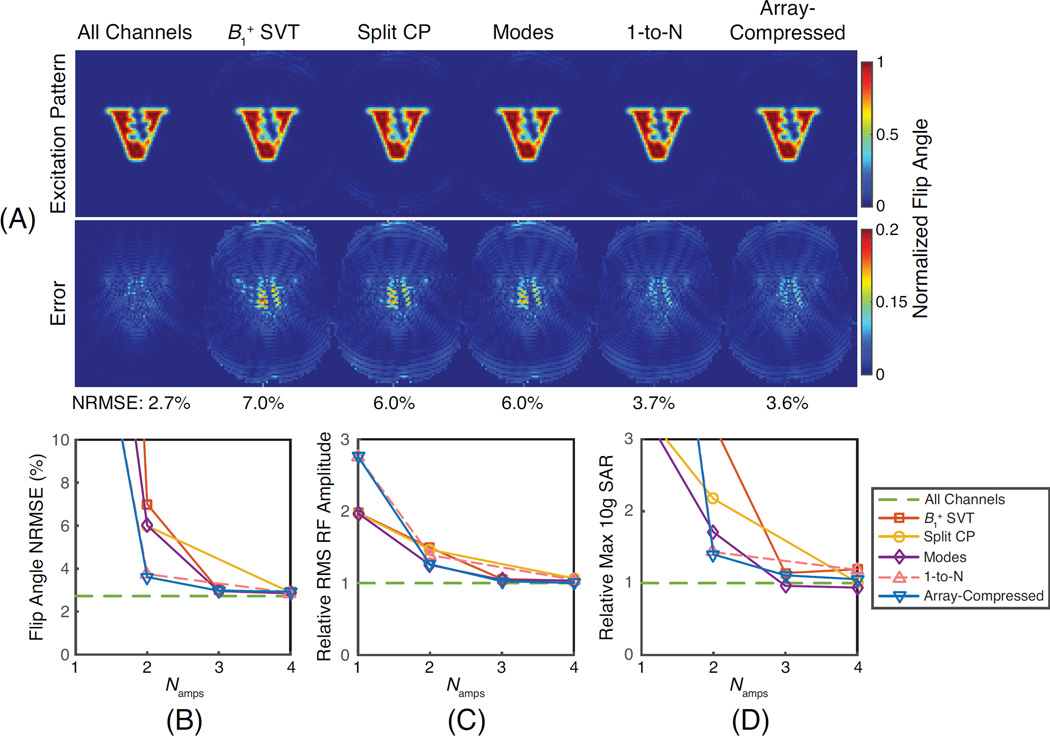
Figure 2 shows the accelerated spiral simulation results. Comparing excitation patterns in Fig. 2a, the all-channels flip angle pattern had the least error and visible distortion, while the two-channel array-compressed pulses had the lowest flip angle RMSE of the compressed designs. Figure 2b shows that the array-compressed pulses had the lowest flip angle RMSE among the compressed designs, for all Namps. For Namps = 2 – 4 the array-compressed pulses had the lowest or nearly the lowest RMS RF amplitude and max 10g local SAR of the compressed designs. The 1-to-N designs were the same as the array-compressed designs for Namps = 1 as expected, but they had slightly higher error and power than the array-compressed designs for Namps = 2 and 4. The curves in Fig. 2b,c,d also suggest that as Namps increases, all compressed designs would eventually converge to the same error and power as the all-channels design. Designing the Namps = 2 array-compressed pulses whose pattern is shown in Fig. 2a required 753 singular value truncations.
Figure 2.
Simulated spiral small-tip-angle excitation results. (a) Excitation and error patterns for pulses designed with all channels and with two channels (Namps = 2) using each coil combination method. Flip angle RMSE’s are reported for each pattern. (b) Flip angle NRMSE, (c) relative RMS RF amplitude, and (d) relative maximum 10-gram local SAR for each method as a function of the number of compressed channels (Namps). The all-channel results appear across the plots for reference.
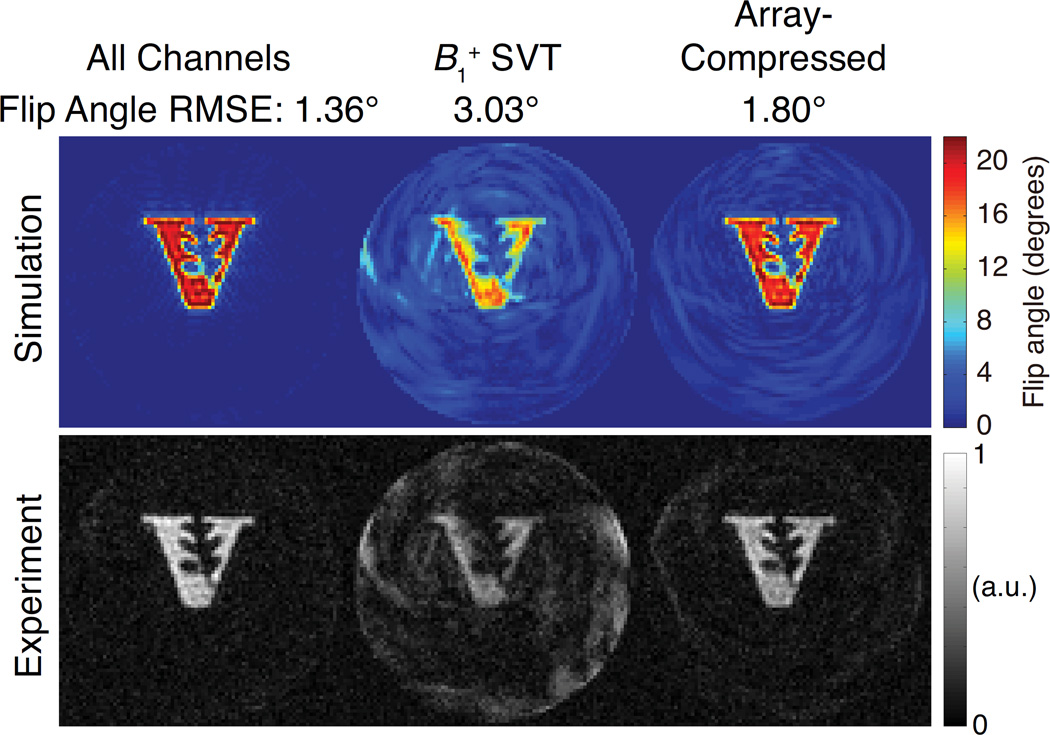
Figure 3 shows the accelerated spiral experiment results. As in the simulations, the all-channels flip angle pattern had the least error (measured from the simulated patterns) and visible distortion, while the two-channel array-compressed pulses had 40% lower simulated flip angle RMSE than the SVT pulses. The simulated and experimental patterns matched closely, in terms of the patterns of excitation errors visible in the compressed pulses’ patterns. In these two channel-compressed designs, the spiral undersampling factor (3.6×) was 1.8 × higher than the number of effective transmit channels.
Figure 3.
Spiral small-tip-angle (20°) excitation experiment results. Simulated (top) and experimental (bottom) excitation patterns for pulses designed with all 16 channels and with two channels (Namps = 2) using SVT and array-compressed pulse design. Flip angle RMSE’s are reported above each simulated pattern.
Multislice RF shimming simulations
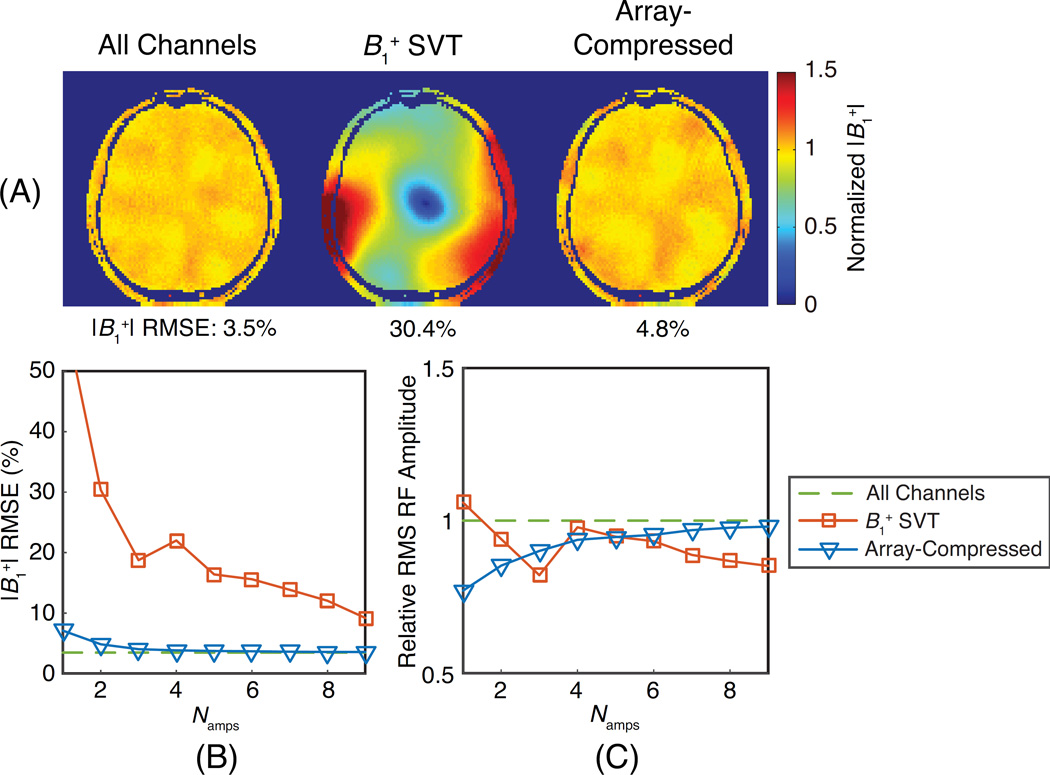
Figure 4 shows the multislice RF shimming results in one subject, across a range of Namps. Figure 4a shows shimmed all-channels and two-channel maps for the fifth slice of the 10-slice volume. The array-compressed shims have the lower RMSE of the two compressed designs. Figures 4b,c plot RMSE and relative RMS RF amplitude for the two compression methods as a function of the number of compressed channels (Namps). The array-compressed shims had a lower RMSE than the SVT shims for all Namps (77% lower on average). The SVT and array-compressed shims had on average 8% lower RMS RF amplitudes than the all-channels shims. As is suggested by their RMSE curve, the SVT shims eventually converge to the all-channels shims for large Namps; by construction, the array-compressed shims exactly coincide with the all-channels shims for Namps ≥ 10. Design of the Namps = 2 array-compressed solution required 2356 singular value truncation steps.
Figure 4.
Multislice RF shimming simulation results. (a) Total fields in a representative slice for shim weights designed with all channels and with two channels (Namps = 2) using SVT and array-compressed pulse design. Normalized RMSE is reported across the whole brain for each method. (b) Normalized RMSE and (c) relative RMS RF amplitude for each pulse design method as a function of the number of compressed channels (Namps).
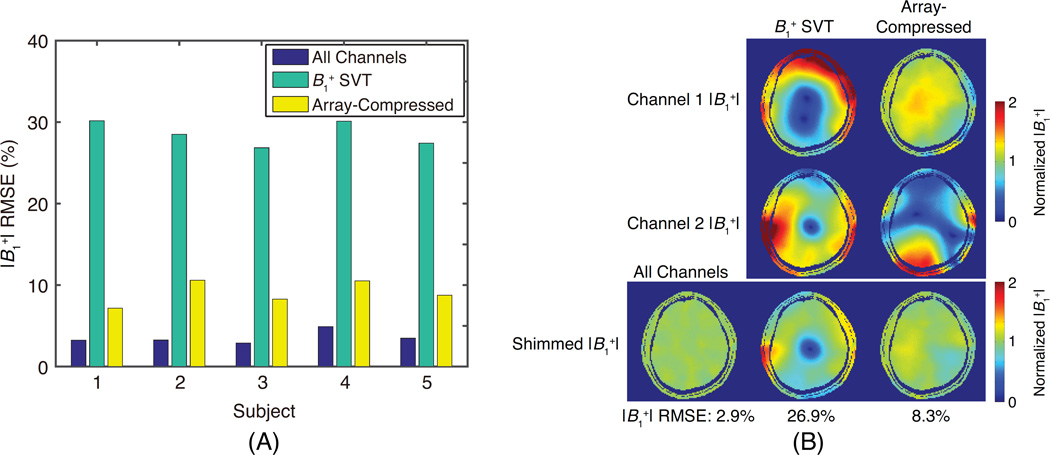
Figure 5 shows the multisubject multislice shimming results. The bar chart in Fig. 5a shows RMSE’s for two-channel compressions, which as expected all have higher shimmed RMSE’s than the subject-specific all-channel shims. As in the subject-specific array-compressed shimming results of Fig. 4, the two-channel array-compressed RMSE’s are lower for all subjects than SVT combinations. Averaged across subjects, determining the compression weights using the leave-one-out array-compressed designs resulted in an 86% increase in RMSE compared to subject-specific array-compressed shimming, and the RMSE of the array-compressed designs were 2.54 × higher than subject-specific all-channel shimming. The SVT RMSE’s were on average 8.04 × higher than subject-specific all-channel shimming.
Figure 5.
Multisubject multislice RF shimming simulation results. (a) Normalized RMSE for an all-channels shim for each subject, compared to RF shimming using two-channel (Namps = 2) compressed arrays where the compression weights were determined in a leave-one-out fashion using SVT or array-compressed shimming. (b) Representative axial shimmed maps in subject 3. (Top two rows) maps for the two-channel compressed array as determined by each compression method. (Bottom row) Shimmed maps for all-channel shimming, and two channel-compressed shimming using the two compression methods. Normalized volumetric shimmed RMSE is reported in this subject along the bottom for each method.
kT-Points simulations
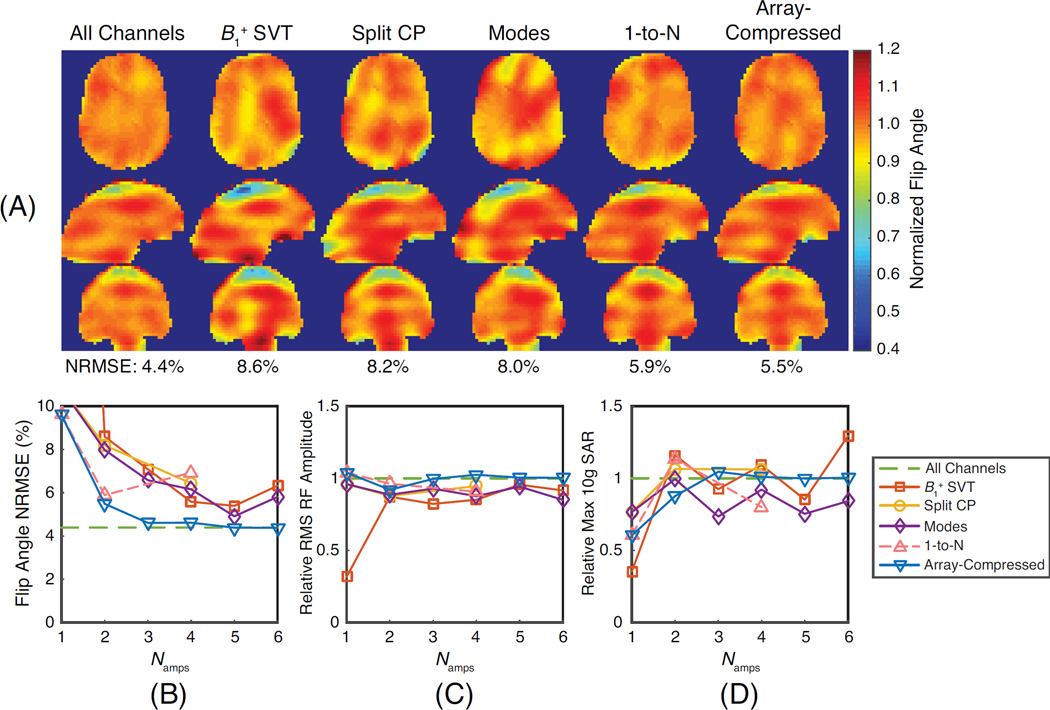
Figure 6 shows the kT-points excitation pulse design results. Figure 6b–d show that the array-compressed pulses had the lowest flip angle RMSE of all the compression methods for every Namps, while its power and maximum 10-gram local SAR was not significantly higher than the all-channels design for any degree of compression, and did not tend to increase as Namps decreased. On average, the array-compressed RMS RF amplitudes were 0.2% lower than the all-channels designs, and the max local SAR was 7.7% lower. As the number of channels increased, the flip angle RMSE of the array-compressed pulses converged smoothly to that of the all-channels pulses. Among the other compressed designs, the 1-to-N pulses came closest to the array-compressed pulses for Namps = 2 and 4, and had an average 4.3% lower RMS RF amplitude and 1.7% lower max local SAR, but an average 20% higher flip angle RMSE. Design of the Namps = 2 array-compressed pulses whose excitation pattern is shown in Fig. 6a required a total of 1,431 singular value truncation steps.
Figure 6.
kT-Points small-tip-angle excitation pulse design simulation results. (a) Simulated flip angle patterns from three orthogonal planes of the brain, for pulses design with all channels and with two channels (Namps = 2) using each coil combination method. Each plane was taken from the middle of the brain. (b) Flip angle NRMSE, (c) relative RMS RF amplitude, and (d) relative maximum 10-gram local SAR for each method as a function of the number of compressed channels (Namps). The all-channel results appear across the plots for reference.
Spokes simulations
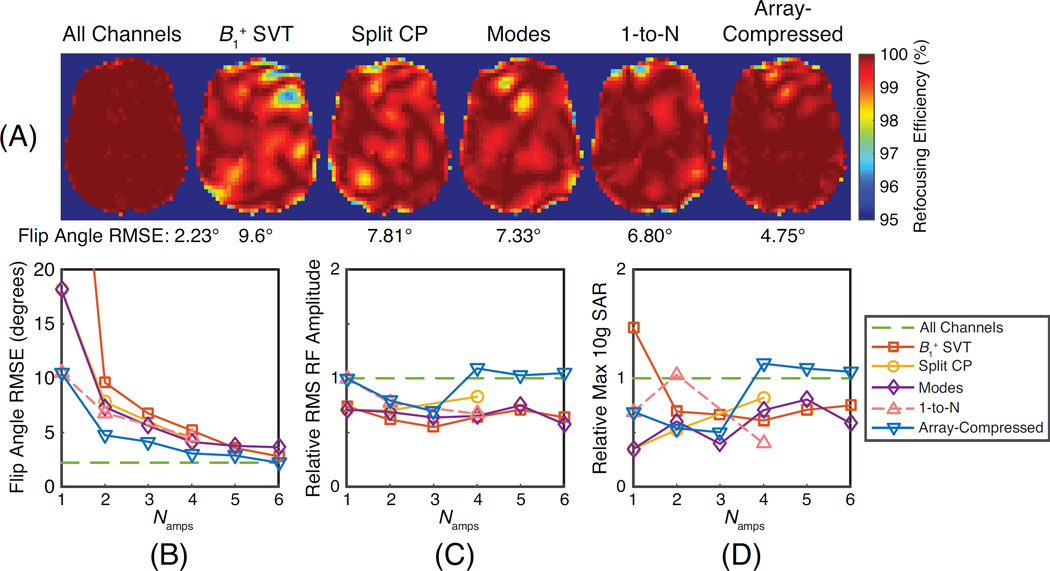
Figure 7 shows the spokes refocusing pulse design results. Figure 7a shows refocusing efficiency patterns for the all-channels pulses and each of the two-channel-compressed pulses (Namps = 2), where refocusing efficiency is defined as |β|2 × 100 (%). Figure 7b shows that for all Namps, the array-compressed pulses had the lowest flip angle RMSE of any coil-compressed design method. Figures 7c shows that none of the compressed designs resulted in significantly higher RMS RF amplitude or max local SAR than the all-channels pulses; on average the array-compressed designs had 5.8% lower RMS RF amplitudes and 16.5% lower max local SAR than the all-channels pulses. Design of the Namps = 2 array-compressed pulses whose refocusing pattern is shown in Fig. 7a required a total of 2,394 singular value truncation steps.
Figure 7.
Spokes refocusing pulse design simulation results. (a) Simulated refocusing efficiency patterns for pulses designed with all channels and with two channels (Namps = 2) using each coil combination method. (b) Flip angle RMSE, (c) relative RMS RF amplitude, and (d) relative maximum 10-gram local SAR for each method as a function of the number of compressed channels (Namps). The all-channel results appear across each plot for reference.
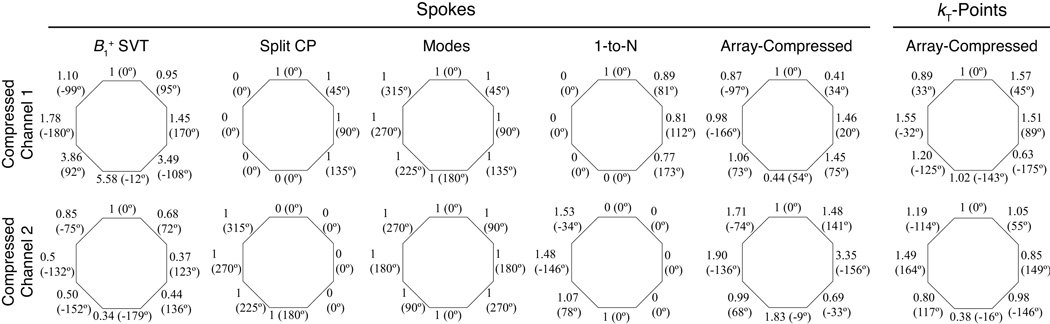
Figure 8 shows two-channel combination weights determined by each method for the spokes pulse design, as well as two-channel array-compressed weights for the kT-points design. For each combination the weights are normalized in amplitude and phase to the top coil of the array. The array-compressed weights have a distribution of amplitudes and phases that is not like any other combination method. For example, in the spokes Channel 2 combination, the largest array-compressed weight is 4.9 × larger than the smallest weight, a uniquely large span among the combination methods, the rest of which had either more uniform weight amplitudes ( SVT, modes, 1-to-N), or binary amplitudes (split CP, 1-to-N). The array-compressed weights also vary significantly between pulse design problems, as indicated by the large differences between array-compressed weights for the spokes and kT-points designs. For example, the right-most element in the array-compressed Channel 2 combination has a 3.9 × larger weight in the spokes design than it does in the kT-points design. Similarly, some of the phase differences between spokes and kT-points array-compressed designs for the same coil and compressed channel were more than 100°.
Figure 8.
Comparison of spokes coil compression weights for all methods, and between spokes and kT-points compression weights for the array-compressed method. Each side of the octagon represents one element of the 8-channel head coil used for the designs, and for each element an amplitude and phase angle (in degrees) is reported. The amplitudes and phases are normalized to the top coil in each combination.
Discussion
Summary of results
Array-compressed pulse design was demonstrated in four pTx applications. In the accelerated spiral experiment, it enabled 3.6× acceleration with two transmit channels and only a small increase in excitation error compared to a full 16-channel design. Array-compressed multislice RF shims achieved RMSE‘s at least 2.6× smaller than the SVT compression method. The multisubject multislice RF shimming results further showed that array-compressed RF shimming can identify coil compression weights that perform better across multiple subjects than SVT compression, which may have implications for RF coil design as discussed below. Though we presented multisubject array compression for multislice RF shimming, the concept would also apply to 3D shimming. In small-tip kT-points excitation and spokes refocusing pulse designs, array-compressed pulses always had the lowest flip angle RMSE of any compression method, without significantly higher power or max local SAR than all-channels pulses. The 1-to-N compression approach of Flöser et al [27] came closest to the performance of array-compressed pulse design, especially in the spiral case. However, to our knowledge that approach only applies to concentric transmit arrays, whereas array-compressed pulse design is not restricted to a coil geometry.
In only one pulse design scenario (spiral simulation) did there appear to be a trend of increasing RF amplitude and maximum 10-gram local SAR with increasing array compression (for Namps = 2, the array-compressed pulses had 26% higher RMS RF amplitude and 40% higher max 10-gram local SAR compared to all-channels pulses; these were the lowest levels among the compression methods). In the other scenarios array compression came only at the cost of increased excitation error. Thus, though hard constraints on SAR and power were not used in these designs, our results are close to what would be obtained if they had been incorporated and used to limit power and SAR to be no larger than the all-channels designs. In general, array compression must come at some cost in excitation fidelity, power, SAR, or all three, and it should be expected that (conversely to our results) if excitation error were constrained to be no larger than all-channels designs (which could be achieved using algorithm or gradient trajectory adjustments), then power and SAR would increase with increasing compression. Our results show that array-compressed pulse design simply achieves a consistently better tradeoff between compression and these pulse characteristics compared to other approaches.
Potential applications
Array-compressed pulse design could find multiple applications. The most straightforward and immediately realizable of these is to use it to identify optimal coil combinations that would be held fixed across subjects, which would accelerate online pTx pulse computations and simplify RF shimming. For example, the RF shimming results demonstrated that a 32-channel head coil could be compressed to two channels with little penalty in RMSE over a multislice volume in multiple subjects. This is significant since two-channel RF shimming is particularly simple to implement because (if the two channels are fixed) it requires optimization of only the relative amplitude and phase between the two channels, and lookup tables can be used to predict SAR. For this reason two-channel RF shimming is the first embodiment of pTx that vendors have fully implemented in clinical scanners. This embodiment of array-compressed pulse design would be analogous to receive coil array compression for accelerating parallel imaging reconstruction [33, 34].
Another potential application is to optimize pTx coil arrays for specific applications. For example, for a given coil former and transmit channel budget, an overcomplete set of candidate coil conductors or field basis functions [6] could be defined on the former and array-compressed pulse or shim designs could be performed jointly over a representative set of body models and geometries, as in the multisubject multislice RF shimming scenario presented here. The resulting array compression weights would then indicate the best placement and density of coil elements or conductors on the coil former. In this way, the actual spin physics of the excitation problem would directly inform the coil design. Sparsity regularization could also be applied in the physical coil dimension to more effectively prune the set of coil candidates [8].
Finally, array-compressed pulse design could be used to reduce the number of power amplifiers required for many-coil pTx while maintaining as much of the performance of a many-coil array as possible. Whereas transmit array compression approaches (such as the modes approach) that use fixed coil combinations selected before mapping or pulse design could have reduced mapping and SAR and pulse computation requirements compared to both full-channel and array-compressed pTx, as demonstrated in this work array-compressed pTx achieves a considerably better tradeoff between compression, excitation accuracy and SAR. Array-compressed pTx would require the development of tunable amplitude and phase shifting networks (illustrated in Fig. 1a) analogous to Butler matrices that provide access to coil modes [7], to enable coil combination weights to be set on a scan-to-scan or subject-to-subject basis. For mapping of each coil in an array, the networks would also need to be capable of switching individual coils on and off, or of implementing an invertible set of modes. The insertion loss of the components making up these networks may also increase total RF power requirements. Overall, though it is not yet clear what engineering challenges will be faced in developing these networks, their development and integration with array-compressed pulse design could finally enable pTx to reach coil counts similar to those currently enjoyed in parallel receive.
Relationship to other work
The array-compressed pulse design framework introduced here is most closely related to work by Zelinski et al on sparse pTx pulse design to optimally select coil modes [8], and to the 1-to-N approach of Flöser et al [27]. Zelinski et al demonstrated a parallel pulse design algorithm that applies a sparsity penalty across the coil dimension to simultaneously optimize pulses and select the best 8 modes of a 16-mode coil. In that work the algorithm was also given an overcomplete set of coils and was expected to select the Namps best coils to use, though unlike the present work the combination weights were fixed prior to pulse design. In every design example Zelinski’s algorithm selected the first two coil modes, and in most cases it selected all of the first five, indicating that the results obtained with that algorithm would be similar to the ‘modes’ results presented here for Namps = 1–5. Furthermore, as mentioned above Zelinski’s sparse approach could be combined with array-compressed pulse design to select a subset of coils (or modes) while simultaneously determining the best way to combine the remaining coils.
Flöser et al’s 1-to-N approach has the same basic goal as our approach but was formulated in a more constrained manner. Specifically, prior to pulse design they divided the physical array into Namps coil subsets, each comprising Ncoils/Namps coils, and assigned one subset to each transmit channel. Also unlike the present approach they explicitly solved for the weights and the pulses for the compressed array using a gradient-based approach, without a rank constraint. Our results showed that the performance of 1-to-N compressed pulses was closer to that of array-compressed pulses than any other coil combination method. The 1-to-N problem construction would have the practical advantage of reduced hardware complexity to apply the optimized coil weights, since it would require fewer phase shifters and attenuators, and no power combiners. However, the ultimate performance of 1-to-N designs were shown to be less optimal than array-compressed pulses due to these additional constraints. The requirement that the user select the mapping of coil to transmit channels is also a disadvantage of the 1-to-N approach. Also of note is the fact that Flöser et al found that their optimized coil combinations also outperformed modes combinations.
Algorithm considerations
In this work, array compression was incorporated with each iterative pulse design algorithm by introducing a singular value truncation step immediately after the RF pulse update. This approach was chosen for its simplicity and consistency across applications. More advanced rank-constraining methods may provide faster or more robust convergence. For example, nuclear norm minimization by singular value soft-thresholding is a widely-investigated approach for low-rank matrix completion [18], and is a convex relaxation of rank minimization that may converge more robustly than singular value truncation, but would require tuning a threshold parameter to achieve the desired number of compressed channels. Furthermore, in practice it will be desirable to incorporate peak and total power and SAR constraints with array-compressed pulse designs [35], which are not precluded by the present framework and will be the subject of future development.
Conclusion
A framework for array-compressed pTx pulse design was proposed that jointly optimizes both coil array compression weights and RF pulses for a specific application. It was applied in simulations and an experiment to four pTx pulse design problems and achieved lower excitation errors than other coil compression approaches, generally without increasing RF power or maximum local SAR. The approach has implications for accelerating and simplifying pTx pulse design, designing transmit coil arrays for specific applications based on excitation physics, and increasing the number of coils that can be driven by a fixed set of transmit channels.
Acknowledgment
This work was supported by NIH R01 EB016695.
References
- 1.Katscher U, Börnert P, Leussler C, van den Brink JS. Transmit SENSE. Magn Reson Med. 2003;49:144–150. doi: 10.1002/mrm.10353. [DOI] [PubMed] [Google Scholar]
- 2.Zhu Y. Parallel excitation with an array of transmit coils. Magn Reson Med. 2004;51:775–784. doi: 10.1002/mrm.20011. [DOI] [PubMed] [Google Scholar]
- 3.Grissom WA, Sacolick L, Vogel MW. Improving high-field MRI using parallel excitation. Imaging in Medicine. 2010;2:675–693. [Google Scholar]
- 4.Ibrahim TS, Lee R, Baertlein BA, Abduljalil AM, Zhu H, Robitaille PM. Effect of RF coil excitation on field inhomogeneity at ultra high fields: a field optimized TEM resonator. Magn Reson Imag. 2001;19:1339–1347. doi: 10.1016/s0730-725x(01)00404-0. [DOI] [PubMed] [Google Scholar]
- 5.Mao W, Smith MB, Collins CM. Exploring the limits of RF shimming for high-field MRI of the human head. Magn Reson Med. 2006;56:918–922. doi: 10.1002/mrm.21013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lattanzi R, Sodickson DK, Grant AK, Zhu Y. Electrodynamic constraints on homogeneity and radiofrequency power deposition in multiple coil excitations. Magn Reson Med. 2009;61:315–334. doi: 10.1002/mrm.21782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Alagappan V, Nistler J, Adalsteinsson E, Setsompop K, Fontius U, Zelinski AC, Vester M, Wiggins GC, Hebrank F, Renz W, Schmitt F, Wald LL. Degenerate mode band-pass birdcage coil for accelerated parallel excitation. Magn Reson Med. 2007;57:1148–1158. doi: 10.1002/mrm.21247. [DOI] [PubMed] [Google Scholar]
- 8.Zelinski AC, Alagappan VA, Goyal VK, Adalsteinsson E, Wald LL. Sparsity-Enforced Coil Array Mode Compression for Parallel Transmission; Proceedings of the 16th Scientific Meeting, International Society for Magnetic Resonance in Medicine; Toronto, Canada. 2008. p. 1302. [Google Scholar]
- 9.Brunner DO, Pruessmann KP. SVD based calibration of transmit arrays; Proceedings of the 18th Scientific Meeting, International Society for Magnetic Resonance in Medicine; Stockholm, Sweden. 2010. p. 242. [Google Scholar]
- 10.Brunner DO, Pruessmann KP. interferometry for the calibration of RF transmitter arrays. Magn Reson Med. 2009;61:1480–1488. doi: 10.1002/mrm.21893. [DOI] [PubMed] [Google Scholar]
- 11.Nehrke K, Börnert P. Eigenmode analysis of transmit coil array for tailored B 1 mapping. Magn Reson Med. 2010;63:754–764. doi: 10.1002/mrm.22239. [DOI] [PubMed] [Google Scholar]
- 12.Padormo F, Beqiri A, Malik SJ, Hajnal JV. PRIMO: Precise radiofrequency inference from multiple observations. Magn Reson Med. 2014 doi: 10.1002/mrm.25404. [DOI] [PubMed] [Google Scholar]
- 13.Sbrizzi A, Raaijmaker AJE, Hoogduin H, Lagendijk JJW, Luijten PR, van den Berg CAT. Transmit and receive RF fields determination from a single low-tip-angle gradient-echo scan by scaling of SVD data. Magn Reson Med. 2014;72:248–259. doi: 10.1002/mrm.24912. [DOI] [PubMed] [Google Scholar]
- 14.Cao Z, Grissom WA. Array-compressed parallel transmit pulse design; Proceedings of the 23rd Scientific Meeting, International Society for Magnetic Resonance in Medicine; Toronto, Canada. 2015. p. 547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ullmann P, Schubert F, Haueisen R, Junge S, Seifert F, Wick M, Ruhm W, Hennig J. Flexible Feature Specific Inner-Volume Selection with Transmit SENSE: Methods and Applications in Humans, Animals and Biological Samples; Proceedings of the 14th Scientific Meeting, International Society for Magnetic Resonance in Medicine; Seattle, USA. 2006. p. 598. [Google Scholar]
- 16.Grissom WA, Yip CY, Zhang Z, Stenger VA, Fessler JA, Noll DC. Spatial domain method for the design of RF pulses in multicoil parallel excitation. Magn Reson Med. 2006;56:620–629. doi: 10.1002/mrm.20978. [DOI] [PubMed] [Google Scholar]
- 17.Grissom WA, Kerr AB, Stang P, Scott GC, Pauly JM. Minimum envelope roughness pulse design for reduced amplifier distortion in parallel excitation. Magn Reson Med. 2010;64:1433–1440. doi: 10.1002/mrm.22512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cai JF, Candes EJ, Shen Z. A singular value thresholding algorithm for matrix completion. SIAM J Optim. 2010;20:1956–1982. [Google Scholar]
- 19.Hoyos-Idrobo A, Weiss P, Massire A, Amadon A, Boulant N. On variant strategies to solve the magnitude least squares optimization problem in parallel transmission pulse design under strict SAR and power constraints. IEEE Trans Med Imag. 2014;33:739–748. doi: 10.1109/TMI.2013.2295465. [DOI] [PubMed] [Google Scholar]
- 20.Cloos MA, Boulant N, Luong M, Ferrand G, Giacomini E, Le Bihan D, Amadon A. kT-Points: Short three-dimensional tailored RF pulses for flip-angle homogenization over an extended volume. Magn Reson Med. 2011;67:72–80. doi: 10.1002/mrm.22978. [DOI] [PubMed] [Google Scholar]
- 21.Grissom WA, Khalighi MM, Sacolick LI, Rutt BK, Vogel MW. Small-tip-angle spokes pulse design using interleaved greedy and local optimization methods. Magn Reson Med. 2012;68:1553–1562. doi: 10.1002/mrm.24165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Saekho S, Yip CY, Noll DC, Boada FE, Stenger VA. Fast-kz three-dimensional tailored radiofrequency pulse for reduced B1 inhomogeneity. Magn Reson Med. 2006;55:719–724. doi: 10.1002/mrm.20840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhang Z, Yip CY, Grissom W, Noll DC, Boada FE, Stenger VA. Reduction of transmitter B1 inhomogeneity with transmit SENSE slice-select pulses. Magn Reson Med. 2007;57:842–847. doi: 10.1002/mrm.21221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cao Z, Donahue MJ, Ma J, Grissom WA. Joint design of large-tip-angle parallel RF pulses and blipped gradient trajectories. Magn Reson Med. 2015 doi: 10.1002/mrm.25739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pauly JM, Le Roux P, Nishimura D, Macovski A. Parameter relations for the Shinnar-Le Roux selective excitation pulse design algorithm. IEEE Trans Med Imag. 1991;10:53–65. doi: 10.1109/42.75611. [DOI] [PubMed] [Google Scholar]
- 26.Nehrke K, Börnert P. Eigenmode Analysis of Transmit Coil Array for SAR-reduced B1 Mapping and RF shimming; Proceedings of the 17th Scientific Meeting, International Society for Magnetic Resonance in Medicine; Honolulu, USA. 2009. p. 368. [DOI] [PubMed] [Google Scholar]
- 27.Flöser M, Bitz AK, Jost S, Orzada S, Gratz M, Kraff O, Ladd ME. Hybrids of static and dynamic RF shimming for body imaging at 7T; Proceedings of the 23rd Scientific Meeting, International Society for Magnetic Resonance in Medicine; Toronto, Canada. 2015. p. 2391. [Google Scholar]
- 28.Carluccio G, Erricolo D, Oh S, Collins CM. An approach to rapid calculation of temperature change in tissue using spatial filters to approximate the effects of thermal conduction. IEEE Trans Biomed Eng. 2013;60:1735–1741. doi: 10.1109/TBME.2013.2241764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Cao Z, Park J, Cho ZH, Collins CM. Numerical evaluation of image homogeneity, signal-to-noise ratio, and specific absorption rate for human brain imaging at 1.5, 3, 7, 10.5, and 14T in an 8-channel transmit/receive array. J Magn Reson Imag. 2014 doi: 10.1002/jmri.24689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Collins CM, Yang B, Yang QX, Smith MB. Numerical calculations of the static magnetic field in three-dimensional multi-tissue models of the human head. Magn Reson Imag. 2002;20:413–424. doi: 10.1016/s0730-725x(02)00507-6. [DOI] [PubMed] [Google Scholar]
- 31.Fessler JA, Sutton BP. Nonuniform fast Fourier transforms using min-max interpolation. IEEE Trans Sig Proc. 2003;51:560–574. [Google Scholar]
- 32.Zhang Z, Stenger VA. Validation of Transmit SENSE with Reciprocity; Proceedings of the 10th Scientific Meeting, International Society for Magnetic Resonance in Medicine; Miami, Florida, USA. 2005. p. 2434. [Google Scholar]
- 33.Huang F, Vijayakumar S, Li Y, Hertel S, Duensing GR. A software channel compression technique for faster reconstruction with many channels. Magn Reson Imag. 2008;26:133–141. doi: 10.1016/j.mri.2007.04.010. [DOI] [PubMed] [Google Scholar]
- 34.Zhang T, Pauly JM, Vasanawala SM, Lustig M. Coil compression for accelerated imaging with Cartesian sampling. Magn Reson Med. 2013;69:571–582. doi: 10.1002/mrm.24267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Brunner DO, Pruessmann KP. Optimal design of multiple-channel RF pulses under strict power and SAR constraints. Magn Reson Med. 2010;63:1280–1291. doi: 10.1002/mrm.22330. [DOI] [PubMed] [Google Scholar]