An estimated glomerular filtration rate equation for the full age spectrum

Abstract

Background

Glomerular filtration rate (GFR) is accepted as the best indicator of kidney function and is commonly estimated from serum creatinine (SCr)–based equations. Separate equations have been developed for children (Schwartz equation), younger and middle-age adults [Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) equation] and older adults [Berlin Initiative Study 1 (BIS1) equation], and these equations lack continuity with ageing. We developed and validated an equation for estimating the glomerular filtration rate that can be used across the full age spectrum (FAS).

Methods

The new FAS equation is based on normalized serum creatinine (SCr/Q), where Q is the median SCr from healthy populations to account for age and sex. Coefficients for the equation are mathematically obtained by requiring continuity during the paediatric–adult and adult–elderly transition. Research studies containing a total of 6870 healthy and kidney-diseased white individuals, including 735 children, <18 years of age, 4371 adults, between 18 and 70 years of age, and 1764 older adults, ≥70 years of age with measured GFR (inulin, iohexol and iothalamate clearance) and isotope dilution mass spectrometry–equivalent SCr, were used for the validation. Bias, precision and accuracy (P30) were evaluated.

Results

The FAS equation was less biased [−1.7 (95% CI −3.4, −0.2) versus 6.0 (4.5, 7.5)] and more accurate [87.5% (85.1, 89.9) versus 83.8% (81.1, 86.5)] than the Schwartz equation for children and adolescents; less biased [5.0 (4.5, 5.5) versus 6.3 (5.9, 6.8)] and as accurate [81.6% (80.4, 82.7) versus 81.9% (80.7, 83.0)] as the CKD-EPI equation for young and middle-age adults; and less biased [−1.1 (−1.6, −0.6) versus 5.6 (5.1, 6.2)] and more accurate [86.1% (84.4, 87.7) versus 81.8% (79.7, 84.0)] than CKD-EPI for older adults.

Conclusions

The FAS equation has improved validity and continuity across the full age-spectrum and overcomes the problem of implausible eGFR changes in patients which would otherwise occur when switching between more age-specific equations.

INTRODUCTION

Glomerular filtration rate (GFR) is generally accepted as the best indicator of kidney function. As direct measurement of GFR is complex, GFR is commonly estimated based on serum creatinine (SCr) concentration. Height-dependent [1, 2] and height-independent equations [3, 4] have been suggested for children and adolescents [5]. The Modification of Diet in Renal Disease (MDRD) equation [6], and the more recent Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) equation [7], are widely recognized equations to estimate GFR in adults, and the Berlin Initiative Study 1 (BIS1) equation [8] was designed for older adults. There is also a consensus that SCr should be obtained by isotope dilution mass spectrometry (IDMS) traceable creatinine methods in all these modern equations [9].

During the last few years, we have gained experience in developing estimated GFR (eGFR) equations for children, adolescents and young adults [2, 4, 5]. We also studied the way SCr concentration changes with age from birth through 100 years of age [10]. As all SCr-based eGFR equations can be seen as gender/race/age-adjusted SCr, we have proposed a different way to build an eGFR equation. We adjust SCr by normalizing it with the median SCr value (Q) obtained in a specific (healthy) subpopulation. Using this approach, it is possible not only to derive eGFR equations for children, adolescents and young adults [4, 5], but also to reshape adult equations, like the MDRD and CKD-EPI equations, into normalized SCr-based eGFR equations [11–13]. Many more equations have been proposed, both for children and adults [6–8, 14–16]. A major issue is the large discrepancy in eGFR when switching from equations developed for children to equations developed for adults or from equations developed for adults to equations developed for older adults.

In this article, we derive a single (age-knotted) eGFR equation that is applicable for all ages by first normalizing SCr for age (for children and adolescents) and gender (for adolescents and adults). A full age spectrum (FAS) equation remediates the discontinuity when switching from paediatric equations to adult equations or from adult to older adults equations. As examples of this discontinuity problem, with a clear clinical impact, consider the following cases:

Example 1: A healthy 18-year-old male with a body height (L) of 180 cm and SCr of 0.90 mg/dL:

•  Paediatric equation (Schwartz): eGFR = 0.413 × L/SCr = 0.413 × 180/0.90 = 83 mL/min/1.73 m².

•  Adult equation (CKD-EPI): eGFR = 141 × (0.90/0.90)^−1.209 0.993¹⁸ = 124 mL/min/1.73 m².

Switching from the Schwartz equation to the CKD-EPI equation at the age of 18 years would result in a 50% increase in eGFR.

Example 2: A female, aged 70 years, with SCr = 3.5 mg/dL:

•  Adult equation (CKD-EPI): eGFR = 144 × (3.5/0.7)^−1.209 0.993⁷⁰ = 13 mL/min/1.73 m².

•  Older adults equation (BIS1): eGFR = 3736 × (3.5)^−0.87 × 70^−0.95 × (0.82 if female) = 18 mL/min/1.73 m².

Switching from the CKD-EPI equation to the BIS1 equation at the age of 70 years would result in a 44% increase and move this female subject from GFR Category 5 back to 4.

These discontinuities are physiologically implausible and may cause confusion. Therefore, we aimed to construct an equation for estimating eGFR that overcomes this discontinuity and consequently fits for all ages. A subsequent aim of this study was to validate the new equation against measured GFR (mGFR) and to compare it with the current recommended equations for children (Schwartz equation), adults (CKD-EPI equation) and older adults (CKD-EPI and BIS1 equations).

Recently published SCr-based eGFR equations have been obtained by statistical modelling of mGFR data against demographic information [age, gender, ethnicity, height (for children)] and blood marker information (e.g. SCr or cystatin C). In this article, we develop a new eGFR equation using population-normalized SCr. We do not base this new equation on statistical modelling, but we connect a previously published and validated paediatric equation [4, 5] with the previously published and validated BIS1 equation for older adults [8], requiring continuity across the full age-spectrum.

MATERIALS AND METHODS

Overview of study design

The current study consists of two parts, the development and construction of the equation (see Supplementary data, Appendix) and validation of the new equation. For the validation study, 14 different datasets were obtained to form a representative lifespan sample of the general population and renal disease patients from nephrology clinics, covering 735 children and adolescents (aged <18 years), 4371 adults (aged between 18–70 years) and 1764 older adults (aged ≥70 years). These datasets were obtained from cross-sectional cohorts in Europe (France, Norway, Germany, UK) and the USA (Rochester, MN) using a wide variety of GFR measurement methods and IDMS-equivalent SCr methods. The datasets were centralized for data analysis. According to Belgian and French laws, retrospective studies using anonymized data do not require Institutional Review Board (IRB) approval, however, most of the validation datasets were obtained from previous IRB-approved studies (Berlin, Tromsø, Rochester, Saint-Etienne, Kent).

Data sources and participants

Patient characteristics of each separate database (DB) are described in the Supplementary data, Table S1.

Data from Lyon, France

Published (DB3–6, DB11) and unpublished data (DB1–2, DB13) from Lyon, France, were collected by the specialized Renal Function Exploration Unit (RFEU) of the University Hospital in Lyon. These data were collected as routine measurements of the RFEU. Patients were informed that their data could be used (in an anonymous way) for research purposes.

DB1 (n = 153) contains unpublished data selected from a cohort of consecutive paediatric patients, aged between 3–14 years, with a suspected kidney pathology who were referred to the paediatric nephrology department in the period January 2010–January 2012. The selection criteria for this dataset were age ≤14years, iohexol GFR measurement and SCr enzymatic test.

DB2 (n = 185) contains unpublished data, based on the same selection criteria as DB1, but for the inulin GFR measurement method.

DB3–5 are subsets from one larger dataset (n = 750) with unique entries (serial measurements were omitted from the dataset described by Selistre [17], collected between 2003 and 2010) of 10–14-year-old children (n = 273), 15–18-year-old adolescents (n = 151) and 19–25-year-old young adults (n = 326). The database was here subdivided into subsets to allow for better detailed comparison with the Schwartz equation (valid for children and adolescents) and with the CKD-EPI equation (for young adults).

DB11 represents an extended dataset from the n = 224 to n = 310 older adult patients (>70 years) with suspected or established renal dysfunction referred to the RFEU between 2010 and 2014 [18]. Selection criteria were age ≥70 years, inulin measurement, enzymatic SCr and suspected or established renal dysfunction.

DB13 (n = 1416) contains adult patients with various kidney pathologies representing a cross section of all CKD stages. Selection criteria for this dataset were consecutive recruitment with enzymatic SCr (after 2010) and mGFR <90 mL/min/1.73 m².

In all datasets, only subjects from Caucasian or North African origin were selected.

Data from Saint-Etienne (DB7)

All patients (n = 203) were >18 years old and had confirmed HIV status. Patients were Caucasian (n = 188) or of North African origin (n = 15) and enrolled in 2011–2012 [19].

Data from Tromsø (DB8)

The subjects (n = 1627) from the Renal Iohexol Clearance Survey In Tromsø 6 (RENIS-T6), recruited in 2007–08, form a representative sample of the middle-aged general Norwegian population [20]. A total of 1521 patients were free from cardiovascular disease, diabetes, CKD or albuminuria. A total of 33 participants had diabetes, 34 had CKD according to an mGFR<60 mL/min/1.73² and 44 had albuminuria. All subjects were Caucasian.

Data from Rochester, MN, USA (DB9, DB10)

The subjects were recruited between 2006 and 2011 from two white community-based cohorts [21]. The Genetic Epidemiology Network of Arteriopathy (GENOA) cohort and the Epidemiology of Coronary Artery Calcification (ECAC) cohort consisted of 687 and 406 individuals with complete data, respectively. ECAC was representative of the general population and GENOA of the hypertensive population.

Data from Berlin, Germany (DB12)

The BIS recruited 570 subjects, aged ≥70 years, in 2010 and 2011 with eight iohexol measurement samples [8]. This cross-sectional dataset was obtained from the random community-based population of the largest statutory health insurance in Berlin. All participants were Caucasian.

Data from Kent, UK (DB14)

Participants (n = 394) from this prospective cohort were recruited between 2008 and 2011 from nephrology clinics (38%) and the community (62%) [22]. All participants were Caucasian and >74 years of age. About 55% were hypertensive, 19% had diabetes and 44% had a vascular disease.

Measurements

GFR measurements

Participants were asked fast for at least 4–6 h before the GFR measurement, except for water intake.

Iohexol measurement

In Lyon (DB1, DB13) and Saint-Etienne, France (DB7) and Kent, UK (DB14), the slope-intercept iohexol method with Bröchner-Mortensen correction was used [23]. Lyon and Kent used three samples (120, 180 and 240 min) and Saint-Etienne used two samples (120 and 240 min) after intravenous bolus injection of iohexol (Omnipaque 240 or 300, GE Healthcare).

In Tromsø, Norway (DB8), GFR was measured as the single-sample plasma clearance of iohexol (Jacobsson's method [24]). Details have been published previously [25].

In Berlin, blood samples were obtained at 30, 60, 90, 120, 150, 180, 240 and 300 min after injection of 5 mL iohexol. The concentration–time curve was fitted and the area under the curve was calculated using a two-compartment model.

In all cohorts, iohexol concentration in the plasma samples was assayed by high-performance liquid chromatography.

Inulin measurement (DB2–6, DB11)

GFR was measured by renal clearance of inulin (polyfructosan infusion, Inutest, Fresenius Kagi, Graz, Austria) [26] using a continuous infusion of inulin after a loading dose and urine collection. Inulin clearance was calculated using the standard UV/P formula [(urinary inulin × urine flow)/plasma inulin]. Plasma and urine polyfructosan measurements were obtained with the same enzymatic method [27].

Iothalamate measurement (DB9, DB10)

GFR was measured from the clearance of non-radiolabelled iothalamate assayed with capillary electrophoresis from timed plasma (P) and urine (U) samples [21].

Serum creatinine measurement

SCr was measured by enzymatic IDMS-traceable methods in Lyon (after 2010), Saint-Etienne, Tromsø, Berlin and Rochester, or directly by IDMS in Kent. Before 2010, the SCr assay results in Lyon were calculated back to the IDMS-equivalent SCr concentration [8, 17–22].

Data analysis

Development of the FAS equation

The current study presents a new SCr-based eGFR equation, called the FAS equation:

$$\text{FAS}-\text{eGFR}=\frac{107.3}{(\text{SCr}/Q)}\mathrm{for}2\le \text{age}\le 40\text{years}$$

$$\text{FAS}-\text{eGFR}=\frac{107.3}{(\text{SCr}/Q)}\times {0.988}^{(\mathrm{Age}-40)}\text{for age}>40\text{years}$$

Q-values are the mean or median SCr value for age-/sex-specific healthy populations, listed in Table 1, obtained from a previous SCr reference interval study [10]. Q was matched with age or with median height obtained from Belgian national growth curves [5]. The development and derivation of the FAS equation is described in detail in the Supplementary data, Appendix.

Table 1.

Q-values [=median serum creatinine in µmol/L (mg/dL)] for the FAS equation, according to age or height (from refs [4, 5, 10])

Age, years	Heighta, cm	Qb, µmol/L (mg/dL)
Boys and girls
1	75.0	23 (0.26)
2	87.0	26 (0.29)
3	95.5	27 (0.31)
4	102.5	30 (0.34)
5	110.0	34 (0.38)
6	116.7	36 (0.41)
7	123.5	39 (0.44)
8	129.5	41 (0.46)
9	135.0	43 (0.49)
10	140.0	45 (0.51)
11	146.0	47 (0.53)
12	152.5	50 (0.57)
13	159.0	52 (0.59)
14	165.0	54 (0.61)
Male adolescents
15	172.0	64 (0.72)
16	176.0	69 (0.78)
17	178.0	72 (0.82)
18	179.0	75 (0.85)
19	180.0	78 (0.88)
Male adults
≥20	≥181.5	80 (0.90)
Female adolescents
15	164.5	57 (0.64)
16	166.0	59 (0.67)
17	166.5	61 (0.69)
18	167.0	61 (0.69)
19	167.5	62 (0.70)
Female adults
≥20	≥168.0	62 (0.70)

^aHeight is the median height of a child or adolescent at the specified age (Belgian growth curves).

^bMathematical expressions for the Q-age and Q-height relationship for children, adolescents and young adults can be obtained from Hoste et al. [5].

GFR estimating equations

The following equations were evaluated for children and adolescents:

• Schwartz equation: eGFR = 0.413 × L/SCr [1]

• FAS equation, with Q matching age (Table 1) [5]

• FAS-height equation, with Q matching height (Table 1) [5]

and for adults:

• CKD-EPI equation [7]

• FAS equation with Q = 0.70 mg/dL for females and Q = 0.90 mg/dL for males

and for the oldest adults we also added the comparison results of the BIS1 equation [8].

Statistical analysis

Performance results of eGFR equations are presented as bias (constant bias: eGFR–mGFR; proportional bias: eGFR/mGFR), precision [root mean square error (RMSE)] and accuracy (P10 and P30, defined as the percentage of patients within 10% and 30% of mGFR, respectively), along with 95% CIs. Paired t-tests to compare bias and McNemar's test to compare proportions were used. Statistical significance was considered at the 5% significance level. A Bland–Altman plot (difference versus average) with quantile regression lines (2.5th, median and 97.5th percentile lines) is presented. All analyses were done in SAS 9.3 (SAS Institute, Cary, NC, USA).

RESULTS

The clinical characteristics of the participants are shown for each validation dataset (Supplementary data, Table S1) and for the pooled dataset (Table 2).

Table 2.

Patient characteristics (N = 6870)

Age group (years)	Sex	n	Mean (SD)
			Age, years	Height, cm	Weigth, kg	mGFR, mL/min/1.73 m²	SCr, mg/dL	SCr, µmol/L
<18	M	414	11.1 (3.1)	141.8 (19.1)	37.0 (14.4)	95.0 (32.8)	0.69 (0.33)	61 (29)
	F	321	11.3 (3.3)	140.4 (18.0)	37.2 (14.4)	93.9 (29.2)	0.63 (0.27)	56 (24)
18–70	M	2293	52.6 (12.7)	174.7 (7.1)	81.4 (15.8)	78.4 (28.1)	1.10 (0.50)	97 (44)
	F	2078	53.5 (12.7)	162.5 (6.7)	69.8 (16.0)	78.8 (24.3)	0.83 (0.38)	73 (34)
≥70	M	935	77.7 (5.5)	171.4 (7.2)	81.0 (14.4)	53.7 (21.0)	1.35 (0.61)	119 (54)
	F	829	77.2 (5.3)	158.7 (6.8)	69.7 (14.8)	57.7 (20.3)	0.98 (0.45)	87 (40)

The performance results of the FAS equation and the recommended eGFR equations are presented, in Supplementary data, Table S2 for each dataset, and for the pooled data, categorized according to age group and mGFR below and above 60 mL/min/1.73 m² (Table 3) and according to age group and gender (Table 4).

Table 3.

Prediction performance results of different eGFR equations on the pooled databases according to age group and measured GFR categories (mGFR below or above 60 mL/min/1.73 m²)

Pooled data	eGFR equivalent	RMSE (95% CI)	Constant bias (95% CI)	Proportional bias (95% CI)	P10, % (95% CI)	P30, % (95% CI)
Children and adolescents <18 years
All (n = 735) mGFR = 94.5	FAS	20.1 (18.5, 21.6)	−1.7 (−3.1, −0.2)*,†	1.01 (0.99, 1.03)*,†	40.1 (36.6, 43.7)	87.5 (85.1, 89.9)*
	FAS-height	19.8 (18.1, 21.4)	−2.7 (−4.1, −1.3)*,‡	1.00 (0.98, 1.01)*,‡	41.9 (38.3, 45.5)	88.8 (86.6, 91.1)†
	Schwartz	21.7 (19.5, 23.7)	6.0 (4.5, 7.5)†,‡	1.09 (1.07, 1.11)†,‡	40.1 (36.6, 43.7)	83.8 (81.1, 86.5)*,†
mGFR < 60 (n = 99) mGFR = 45.1	FAS	14.6 (8.5, 18.9)	6.2 (3.6, 8.9)*,†	1.15 (1.09, 1.21)*,†	34.3 (24.8, 43.9)	75.8 (67.2, 84.3)
	FAS-height	13.5 (4.2, 18.6)	4.7 (2.2, 7.2)*,‡	1.12 (1.06, 1.17)*,‡	39.4 (25.6, 49.2)	77.8 (69.4, 86.1)*
	Schwartz	16.7 (8.2, 22.1)	9.4 (6.7, 12.2)†,‡	1.22 (1.16, 1.28)†,‡	31.3 (22.0, 40.6)	70.7 (61.6, 79.8)*
mGFR ≥ 60 (n = 636) mGFR = 102.2	FAS	20.8 (19.1, 22.4)	−2.9 (−4.5, −1.3)*,†	0.99 (0.97, 1.00)*,†	41.0 (37.2, 44.9)	89.3 (86.9, 91.7)*
	FAS-height	20.6 (18.9, 22.3)	−3.8 (−5.4, −2.3)*,‡	0.98 (0.96, 0.99)*,‡	42.3 (38.4, 46.1)	90.6 (88.3, 92.8)†
	Schwartz	22.4 (20.0, 24.5)	5.4 (3.7, 7.1)†,‡	1.07 (1.05, 1.09)†,‡	41.5 (37.7, 45.3)	85.8 (83.1, 88.6)*,†
Adults 18–70 years
All (n = 4371) mGFR = 78.6	FAS	17.2 (16.6, 17.8)	5.0 (4.5, 5.5)*	1.12 (1.11, 1.12)*	40.4 (38.9, 41.9)*	81.6 (80.4, 82.7)
	CKD-EPI	16.4 (15.8, 16.9)	6.3 (5.9, 6.8)*	1.13 (1.12, 1.14)*	42.5 (41.1, 44.0)*	81.9 (80.7, 83.0)
mGFR < 60 (n = 1089)	FAS	19.0 (17.7, 20.2)	13.4 (12.6, 14.2)*	1.35 (1.33, 1.37)*	19.1 (16.8, 21.4)*	52.2 (49.3, 55.2)*
mGFR = 42.3	CKD-EPI	19.2 (18.1, 20.3)	12.7 (11.8, 13.5)*	1.31 (1.29, 1.34)*	21.9 (19.4, 24.3)*	55.2 (52.2, 58.1)*
mGFR ≥ 60 (n = 3282)	FAS	16.6 (15.9, 17.2)*	2.2 (1.6, 2.7)*	1.04 (1.03, 1.04)*	47.5 (45.8, 49.2)*	91.3 (90.3, 92.3)
mGFR = 90.6	CKD-EPI	15.3 (14.7, 15.8)*	4.2 (3.7, 4.7)*	1.07 (1.06, 1.07)*	49.4 (47.7, 51.1)*	90.7 (89.7, 91.7)
Older adults ≥70 years
All (n = 1764) mGFR = 55.6	FAS	11.2 (10.7, 11.7)*	−1.1 (−1.6, −0.6)*	1.02 (1.01, 1.03)*	39.7 (37.5, 42.0)*	86.1 (84.4, 87.7)*
	CKD-EPI	12.9 (12.4, 13.4)*	5.6 (5.1, 6.2)*	1.13 (1.12, 1.15)*	35.0 (32.8, 37.3)*	77.6 (75.7, 79.6)*
	BIS1a	12.0 (11.4, 12.6)	−1.2 (−1.9, −0.6)	1.05 (1.03, 1.07)	34.7 (32.0, 37.4)	81.8 (79.7, 84.0)
mGFR < 60 (n = 986) mGFR = 40.7	FAS	9.5 (8.8, 10.1)*	2.2 (1.6, 2.7)*	1.09 (1.07, 1.11)*	36.6 (33.6, 39.6)*	81.0 (78.6, 83.5)*
	CKD-EPI	13.1 (12.3, 13.8)*	6.9 (6.2, 7.6)*	1.19 (1.17, 1.21)*	29.5 (26.7, 32.4)*	67.7 (64.8, 70.7)*
	BIS1a	9.7 (9.0, 10.3)	3.7 (3.0, 4.4)	1.16 (1.13, 1.18)	35.3 (31.8, 38.8)	75.4 (72.2, 78.5)
mGFR ≥ 60 (n = 778) mGFR = 74.4	FAS	13.1 (12.3, 13.8)	−5.2 (−6.1, −4.4)*	0.94 (0.93, 0.95)*	43.7 (40.2, 47.2)	92.4 (90.6, 94.3)
	CKD-EPI	12.7 (12.1, 13.3)	4.1 (3.2, 4.9)*	1.07 (1.06, 1.08)*	42.0 (38.6, 45.5)	90.1 (88.0, 92.2)
	BIS1a	14.8 (13.7, 15.7)	−8.6 (−9.7, −7.5)	0.90 (0.88, 0.91)	33.9 (29.6, 38.1)	91.5 (89.0, 94.0)

The same symbols (*,^†,^‡) within each subgroup and column indicate significant differences (paired t-test for constant and proportional bias, McNemar's test for P10 and P30 = % of subjects with an eGFR value within 10% and 30% of measured GFR).

^aFor the BIS1 performance results, the data (n= 570) from the BIS1 study were not included (therefore, no comparisons with FAS and CKD-EPI were made).

Table 4.

Prediction performance results of different eGFR equations on the pooled databases according to age group and gender

Pooled data	eGFR equivalent	RMSE (95% CI)	Constant bias (95% CI)	Proportional bias (95% CI)	P10, % (95% CI)	P30, % (95% CI)
Children and adolescents <18 years
Males (n = 414) (mGFR = 95.0)	FAS	20.0 (18.1, 21.7)	−5.2 (−7.0, −3.3)*	0.97 (0.95, 0.99)*	39.6 (34.9, 44.3)	87.4 (84.2, 90.6)
	FAS-height	19.4 (17.5, 21.1)	−5.5 (−7.3, −3.7)†	0.96 (0.95, 0.98)†	41.3 (36.5, 46.1)	89.4 (86.4, 92.4)
	Schwartz	19.8 (17.5, 22.0)	+2.9 (1.0, 4.8)*,†	1.05 (1.03, 1.07)*,†	43.7 (38.9, 48.5)	88.2 (85.0, 91.3)
Females (n = 321) (mGFR = 93.9)	FAS	20.2 (17.2, 22.8)	2.8 (0.6, 5.0)*,†	1.06 (1.04, 1.09)*,†	40.8 (35.4, 46.2)	87.5 (83.9, 91.2)*
	FAS-height	20.4 (17.2, 23.1)	1.0 (1.3, 3.2)*,‡	1.04 (1.01, 1.06)*,‡	42.7 (37.2, 48.1)*	88.2 (84.6, 91.7)†
	Schwartz	23.9 (19.9, 27.3)	10.0 (7.6, 12.4)†,‡	1.14 (1.11, 1.16)†,‡	35.5 (30.3, 40.8)*	78.2 (73.7, 82.7)*,†
Adults 18–70 years
Males (n = 2293) (mGFR = 78.4)	FAS	17.8 (17.0, 18.6)	4.9 (4.2, 5.6)*	1.12 (1.11, 1.13)	38.8 (36.8, 40.8)*	79.2 (77.6, 80.9)*
	CKD-EPI	16.3 (15.5, 17.0)	5.2 (4.6, 5.9)*	1.12 (1.11, 1.13)	42.0 (40.0, 44.0)*	81.4 (79.8, 83.0)*
Females (n = 2078) (mGFR = 78.8)	FAS	16.6 (15.6, 17.4)	5.0 (4.3, 5.7)*	1.11 (1.10, 1.12)*	42.2 (40.1, 44.3)	84.1 (82.5, 85.7)*
	CKD-EPI	16.5 (15.7, 17.2)	7.5 (6.9, 8.1)*	1.14 (1.12, 1.15)*	43.1 (41.0, 45.2)	82.4 (80.7, 84.0)*
Older adults ≥70 years
Males (n = 935) (mGFR = 53.7)	FAS	11.0 (10.3, 11.8)*	−0.6 (−1.3, 0.1)*	1.04 (1.02, 1.06)*	39.8 (36.6, 42.9)*	84.9 (82.6, 87.2)*
	CKD-EPI	12.6 (11.9, 13.3)*	5.3 (4.5, 6.0)*	1.14 (1.12, 1.16)*	35.0 (31.9, 38.0)*	76.8 (74.1, 79.5)*
	BIS1a	12.1 (11.1, 12.9)	−1.1 (−2.1, −0.2)	1.07 (1.04, 1.10)	34.5 (30.7, 38.3)	79.3 (76.1, 82.5)
Females (n = 829) (mGFR = 57.7)	FAS	11.4 (10.6, 12.1)	−1.6 (−2.4, −0.8)*	1.00 (0.99, 1.02)*	39.7 (36.3, 43.0)*	87.3 (85.1, 89.6)*
	CKD-EPI	13.2 (12.5, 13.9)	6.0 (5.2, 6.8)*	1.13 (1.11, 1.15)*	35.1 (31.8, 38.4)*	78.5 (75.7, 81.3)*
	BIS1a	11.9 (11.1, 12.7)	−1.3 (−2.3, −0.4)	1.03 (1.01, 1.05)	35.0 (31.4, 38.9)	84.5 (81.5, 87.4)

The same symbols (*,^†,^‡) within each subgroup and column denote significant differences (paired t-test for constant and proportional bias, McNemar's test for P10 and P30 = % of subjects with an eGFR value within 10% and 30% of measured GFR).

95% CI, 95% confidence interval; FAS, full age spectrum equation; eGFR eq., estimated glomerular filtration rate equation; mGFR, measured glomerular filtration rate; CKD-EPI, Chronic Kidney Disease Epidemiology Collaboration equation; BIS1, Berlin Initiative Study; RMSE, root mean square error.

^aFor the BIS1 performance results, the data (n = 570) of the BIS1 study were not included (therefore, no comparisons with FAS and CKD-EPI were made).

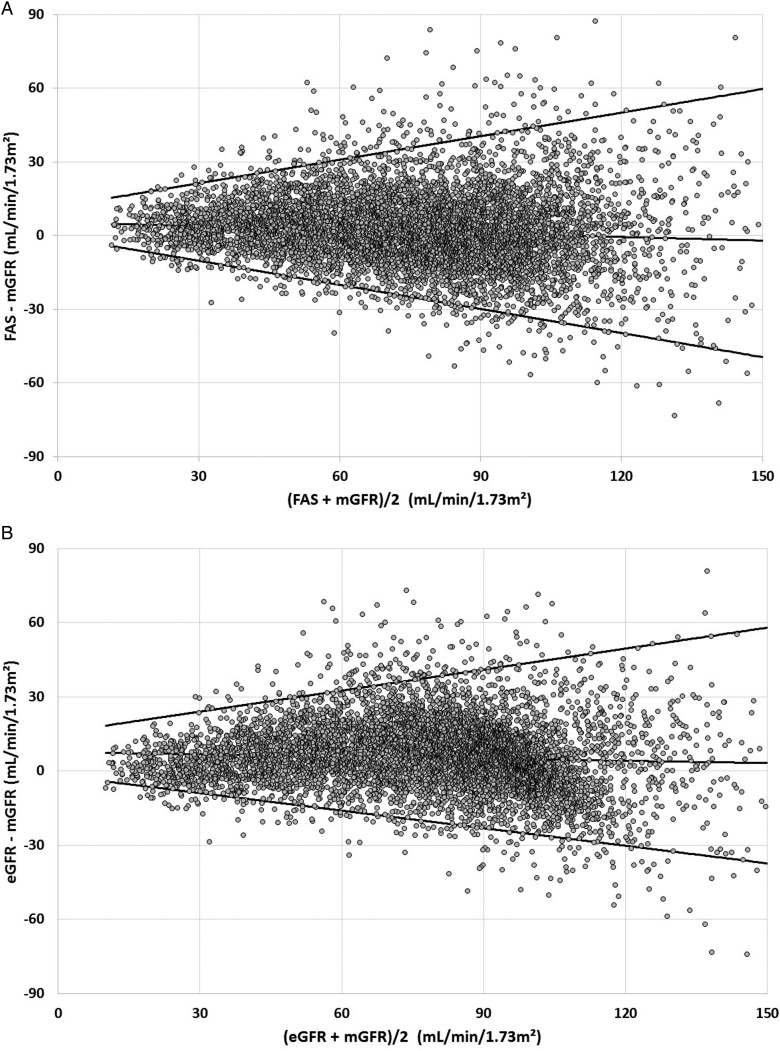
Figure 1 shows the performance of the FAS equation (Figure 1A) and the combined use of the Schwartz and CKD-EPI equations (Figure 1B). The median bias over the full age spectrum is 1.9 mL/min/1.73 m² [interquartile range (IQR) −6.7–11.0)] for FAS and 5.4 mL/min/1.73 m² (IQR −2.7–14.5) for the combined use of the Schwartz and CKD-EPI equations (P < 0.0001).

FIGURE 1:

(A) Difference between estimated (FAS equation) and measured GFR versus the average of both methods. Quantile regression lines (2.5th, 50th and 97.5th percentiles) are shown, without excluding any data. Median difference = 1.9 mL/min/1.73 m². (B) Difference between estimated (Schwartz up to age 18 years, CKD-EPI beyond 18 years) and measured GFR versus the average of both methods. Quantile regression lines (2.5th, 50th and 97.5th percentiles) are shown, without excluding any data. Median difference = 5.4 mL/min/1.73 m².

The external validation (Supplementary data, Table S2) shows that for children up to 14 years of age, the FAS equation with Q corresponding with age (Table 1) has smaller constant and proportional bias in DB1, DB2 and DB3 compared with the Schwartz equation. Also, the accuracy (P10 and P30) is better than for the Schwartz equation in these cohorts of children. The FAS-height equation with Q corresponding with height (Table 1) performs equivalently for children, but for adolescents and young adults (DB4, DB5), height is a better predictor than age for Q-values, leading to improved performance of the FAS-height compared with the FAS equation with Q-age values. The FAS-height equation shows equivalent performance as the Schwartz equation in adolescents (DB4) and better results than the CKD-EPI equation in young adults (DB5). For adults and older adults, the FAS equation has smaller constant and proportional bias when compared with the CKD-EPI equation in 7 of 10 datasets. Precision and accuracy (RMSE, P10 and P30) was comparable in younger and middle-aged adults and equivalent or better in older adults.

Categorization according to mGFR (Table 3) shows that the FAS equation is the best in children <18 years of age, both in the subgroup <60 and ≥60 mL/min/1.73 m²; the FAS equation is equivalent to the CKD-EPI equation for adults 18–70 years in both the <60 and ≥60 mL/min/1.73 m² subgroups and the FAS equation is better than the CKD-EPI equation for older adults in the <60 mL/min/1.73 m² subgroup, but performs differently in the ≥60 mL/min/1.73 m² subgroup.

Categorization according to gender (Table 4) shows that the FAS equation performs equivalently for male and female children and better than the Schwartz equation for females; the FAS equation performs better than CKD-EPI equation for both adult males and adult females and also for older males and females.

Table 5 shows the classification comparison of GFR categories according to mGFR, the FAS equation and the recommended equations (Schwartz and CKD-EPI). This table is more detailed in the Supplementary data, Tables S3–S5, for the separate age groups. Using mGFR as the reference method, the FAS equation correctly classified subjects into GFR categories in 68.2% (67.3–69.1) of the cases, compared with 66.6% (65.6–67.5) (P = 0.001) by the combined use of the two equations (Schwartz, CKD-EPI). In children, FAS correctly classified subjects into GFR categories in 74.8% (72.1–77.5) of cases, compared with 77.8% (75.2–80.3) (P = 0.037) for the Schwartz equation. In adults, FAS correctly classified subjects into GFR categories in 65.7% (64.5–66.9) of cases, compared with 63.6% (62.4–64.8) (P = 0.0003) for the CKD-EPI equation. Finally, in the older adults subgroup, FAS correctly classified subjects into GFR categories in 71.5% (69.7–73.3) of cases, compared with 69.4% (67.5–71.2) (P = 0.038) for the CKD-EPI equation. However, in this last age group, if the CKD-EPI equation predicts an eGFR ≥60 mL/min/1.73 m², it is correct in 74.9% of cases (compared with 84.7% for FAS) and if the CKD-EPI predicts an eGFR <60 mL/min/1.73 m², it is correct in 92.7% of cases (compared with 83.1% for FAS).

Table 5.

Comparison of GFR category classification based on mGFR between FAS and recommended equations

	Schwartz/CKD-EPI
FAS	>90	60–89	30–59	15–29	<15	Total	% Total
mGFR > 90 mL/min/1.73 m²
>90	1537	0	0	0	0	1537	73.5
60–89	273	275	0	0	0	548	26.2
30–59	0	4	1	0	0	5	0.2
15–29	0	0	0	0	0	0	0.0
<15	0	0	0	0	0	0	0.0
Total	1810	279	1	0	0	2090	100.0
% Total	86.6	13.3	0.0	0.0	0.0	100.0
mGFR = 60–90 mL/min/1.73 m²
>90	584	3	0	0	0	587	22.5
60–89	415	1367	5	0	0	1787	68.6
30–59	0	146	86	0	0	232	8.9
15–29	0	0	0	0	0	0	0.0
<15	0	0	0	0	0	0	0.0
Total	999	1516	91	0	0	2606	100.0
% Total	38.3	58.2	3.5	0.0	0.0	100.0
mGFR = 30–60 mL/min/1.73 m²
>90	40	4	0	0	0	44	2.5
60–89	21	441	29	0	0	491	27.9
30–59	0	169	989	9	0	1167	66.3
15–29	0	0	17	41	0	58	3.3
<15	0	0	0	0	0	0	0.0
Total	61	614	1035	50	0	1760	100.0
% Total	3.5	34.9	58.8	2.8	0.0	100.0
mGFR = 15–30 mL/min/1.73 m²
>90	1	0	0	0	0	1	0.3
60–89	2	6	1	0	0	9	2.4
30–59	0	2	136	32	0	170	45.8
15–29	0	0	10	170	6	186	50.1
<15	0	0	0	0	0	5	1.3
Total	3	8	147	202	6	366	98.7
% Total	0.8	2.2	39.6	54.4	1.6	98.7
mGFR <15 mL/min/1.73 m²
>90	0	0	0	0	0	0	0.0
60–89	0	0	0	0	0	0	0.0
30–59	0	0	2	3	0	5	11.6
15–29	0	0	0	27	4	31	72.1
<15	0	0	0	0	7	7	16.3
Total	0	0	2	30	11	43	100.0
% Total	0.0	0.0	4.7	69.8	25.6	100.0

Italics represent agreement with mGFR for either FAS or the recommended equations.

DISCUSSION

In this study, we derived a novel eGFR equation based on the concept of population-normalized SCr, denoted as SCr/Q. By extending the previously published [4] and validated paediatric equation [5, 28–30] and by connecting this equation to the previously published [8] and validated BIS1 equation [18, 31–33], we developed a new equation, called the FAS equation, introducing continuity across the full age-spectrum and with important advantages over the currently recommended equations. First, it is a reasonable alternative to commonly used existing eGFR equations for children, adolescents, young adults, adults and older adults, as the FAS equation is valid across the full age-spectrum. Second, the correction for age (for children) and sex is at the level of SCr, not at the level of GFR, which makes sense, as there is a clear increase in SCr with age during childhood and a difference between sexes, but the average GFR, expressed in mL/min/1.73 m², is not age dependent in children and the (clinically relevant) difference in GFR between sexes is still a matter of debate [34, 35]. The FAS equation, therefore, does not require further correction for age or sex, and probably not for other ethnicities, although Q-values specific for other ethnicities still need to be obtained [12]. Third, the equation solves the discontinuity when switching from paediatric to adult eGFR and the discontinuity between adult and the BIS1 equation developed for older adults. Key in requiring continuity between paediatric and adult equation is the introduction of an age cut-off, where renal decline begins. Up to now, the recommended adult equations (MDRD, CKD-EPI) have assumed that the decline starts at the age of 18 years, which is an unreasonable assumption. Indeed, some authors have shown that the decrease in GFR is continuous from the age of 40 or 50 years on [36–41] and others point out that it starts continuously but accelerates (and doubles) from the fourth or fifth decade on [34, 35, 42, 43]. A rule of thumb is that the GFR stays within the normal range until the age of 40 years and then declines at approximately 1 mL/min/year [44]. This decline appears in both males and females. This decrease in GFR might vary according to the studies ranging from 6 [45] to 12 mL/min/1.73 m² per decade [39]. During the development of our new equation, we assumed that the paediatric equation could be used up to an age cut-off and by mathematically matching our equation with the BIS1 equation we found that this age cut-off is 40 years, confirming most of the literature, with a decline rate constant equal to 0.988^Age. Fourth, the equation is simple and intuitive and every coefficient in the equation has a specific meaning: (i) 107.3 mL/min/1.73 m² may be considered as the average GFR value for healthy children, adolescents and young adults. This value was obtained from a previously published meta-analysis [4] and is supported by the literature studies [34]. (ii) The equation assumes an inverse relationship with SCr, or more specifically with SCr/Q, where the exponent is simply −1, and not −1.209 (CKD-EPI), or −1.154 (MDRD) or −0.87 (BIS1). This inverse relationship simplifies the overall relationship. (iii) SCr/Q = 1 corresponds to the average healthy subject and is independent of age and sex because all age/sex information is absorbed in the Q-value. (iv) The age decline rate matches the decline rate of the BIS1 equation, i.e. 0.988^Age, which is equivalent to about 1 mL/min/1.73 m²/year.

The large external validation shows that the FAS equation is the most unbiased equation in this comparison and demonstrates better performance than the Schwartz and CKD-EPI equations. All equations performed worse in the pooled database subsets defined by mGFR <60 mL/min/1.73 m², but FAS shows better accuracy and precision, although for older adults with mGFR ≥60 mL/min/1.73 m², FAS underestimates and CKD-EPI overestimates mGFR, an observation also made by Fan et al. [46]. As the FAS equation has been designed based on SCr/Q requirements valid for the healthy population, it was expected that the FAS equation would perform better in the healthy and general population than in the CKD population, which is confirmed in this validation study; however, the validation results in the mGFR <60 mL/min/1.73 m² subgroups are not worse than with the CKD-EPI equation. The FAS equation performed equivalent to the Schwartz equation for male children but much better for female children. The FAS equation, with Q based on age, performed reasonably well for adolescents, but worse than the Schwartz equation. However, it has been shown previously that the same (FAS-height) equation using a height-dependent Q-value (FAS-height) performed better than the Schwartz equation [5, 28, 29]. The fact that the Schwartz equation shows a better categorization into GFR categories than FAS is due to the large number of children with mGFR >90 mL/min/1.73 m² in our study, combined with the systematic overestimation of mGFR by the Schwartz equation. An advantage of the age-dependent FAS equation over the height-dependent FAS equation for children and adolescents is that it can be used by the clinical laboratory, where height information is usually not available. Therefore, automatic reporting of FAS predictions along with the SCr value by the clinical laboratory can be done for all ages, without continuity problems at the paediatric–adult and adult–elderly transition. The FAS equation was equivalent to the CKD-EPI equation for adult males, slightly better for adult females and superior in the oldest adults, and was also better than the BIS1 equation for older adults, and again slightly better for females than for males (Table 4). Overall, these approximately equivalent performance results for males and females indicate that correction at the SCR level for gender works well and is equivalent to corrections made at the GFR level. Finally, the overall classification into mGFR categories based on FAS and the established equations is approximately equivalent (Table 5).

This study has some limitations. First, the FAS equation does not improve the imprecision, which remains a problem for all currently used and recommended eGFR equations. Second, as Belgium is central in Europe, the Belgian growth curves are quite representative for European children, however, matching national growth curves to Q-values might be more optimal [28, 29]. For adults, the constant Q-values are very robust. Third, validation data in the age range of 20–40 years includes a limited number of healthy subjects. Fourth, cystatin C equations are not considered in the comparison. Fifth, in case of severe muscle wasting (very low SCr), the power coefficient of −1 may cause an overestimation of GFR, but this is a limitation of all SCr-based equations [47, 48]. Finally, the validation is for Caucasians only. We believe that the FAS equation can be extended to other ethnicities as well, with appropriate Q-values to normalize SCr, but this will require further studies.

In conclusion, the FAS equation is an alternative to the Schwartz, CKD-EPI and BIS1 equations. It enables continuity of eGFR prediction across the full age-spectrum and has a very simple form, especially for adults, and older adults where fixed Q-values can be used. The FAS equation is of particular interest for longitudinal follow-up, but this potentially added value needs to be confirmed in further studies.

SUPPLEMENTARY DATA

Supplementary data are available online at http://ndt.oxfordjournals.org.

CONFLICT OF INTEREST STATEMENT

None declared.

(See related article by Van Biesen and Nagler. A Swiss army knife for estimating kidney function: why new equations will not solve the real problem. Nephrol Dial Transplant 2016; 31: 685–687)