Activator-inhibitor coupling between Rho signaling and actin assembly make the cell cortex an excitable medium

Abstract

Animal cell cytokinesis results from patterned activation of the small GTPase Rho, which directs assembly of actomyosin in the equatorial cortex. Cytokinesis is restricted to a portion of the cell cycle following anaphase onset in which the cortex is responsive to signals from the spindle. We show that shortly after anaphase onset oocytes and embryonic cells of frogs and echinoderms exhibit cortical waves of Rho activity and F-actin polymerization. The waves are modulated by cyclin-dependent kinase 1 (Cdk1) activity and require the Rho GEF (guanine nucleotide exchange factor), Ect2. Surprisingly, during wave propagation, while Rho activity elicits F-actin assembly, F-actin subsequently inactivates Rho. Experimental and modeling results show that waves represent excitable dynamics of a reaction diffusion system with Rho as the activator and F-actin the inhibitor. We propose that cortical excitability explains fundamental features of cytokinesis including its cell cycle regulation.

INTRODUCTION

Cytokinesis begins with activation of Rho in a narrow zone at the plasma membrane¹. Rho directs assembly of the cytokinetic apparatus, a transient array of F-actin and myosin-2. Spindle-derived cues specify the Rho zone; accordingly, considerable effort has been directed at characterization of these signals and their transport. The current consensus is that the centralspindlin complex interprets spindle microtubule organization to concentrate Ect2 at the equator, thus defining the Rho zone^2,3.

The cortex is not a passive substrate in cytokinesis, but rather may actively process and amplify spindle-derived signals during a discrete window of the cell cycle. Physical manipulations of echinoderm embryos showed that the cortex becomes responsive (as manifest by furrowing) shortly after anaphase onset and remains so until shortly before the next M-phase⁴ whereas experimental M-phase arrest prevents development of this responsiveness⁵. Similarly, manipulations of cultured mammalian cells showed that forced anaphase entry results in ~50 minutes of ectopic cortical contractility even after ablation of the spindle, leading to the concept of “C-phase” (“Cytokinetic-phase”), a period of the cell cycle during which large-scale cortical contractility can be focused by signaling⁶.

Here we describe the discovery of a cell cycle entrained behavior that we propose reflects the capacity of the cortex to support cytokinesis – cortical excitability. This behavior is manifest as mutually coordinated cortical waves of Rho activity and F-actin assembly that are Ect2-dependent and modulated by cyclin dependent kinase 1 (Cdk1). We show that cortical excitability is present in vertebrates and invertebrates, that it coincides with the ability of different cells to respond to spindle signals, and that it involves F-actin dependent Rho inactivation.

RESULTS

Cortical F-actin waves in activated Xenopus eggs and embryos

Previous low resolution imaging of cytokinesis in Xenopus embryos revealed cortical “flickers” of F-actin outside the furrow⁷. Remarkably, when imaged at higher resolution, the flickers resolved into waves of F-actin (Figures 1a,b; Supplementary Videos 1,2), similar to those previously described in chemotactic cells⁸. F-actin waves can be detected using two different F-actin probes, UtrCH⁹ (Figures 1a,b) or Lifeact¹⁰ (see Supplementary Figure 1a). Apparently identical structures exist in fixed, uninjected embryos stained with phalloidin (Fig. 1c), demonstrating that they are endogenous to the system. Waves traverse the cortex in an apparently random manner at 0.22 ± 0.1 μm/s (mean ± SD; n=80 waves) with a period of 80–120 s (Figures 1b,d; Supplementary Videos 1,2). Waves that were unambiguously observed to undergo collision annihilated each other (Supplementary Figure 1d). Waves occur in artificially activated eggs, which do not cleave but otherwise mimic embryos (Figure 1b, Supplementary Figure 1b), but not oocytes arrested in prophase of meiosis I (Supplementary Figure 1c).

Figure 1.

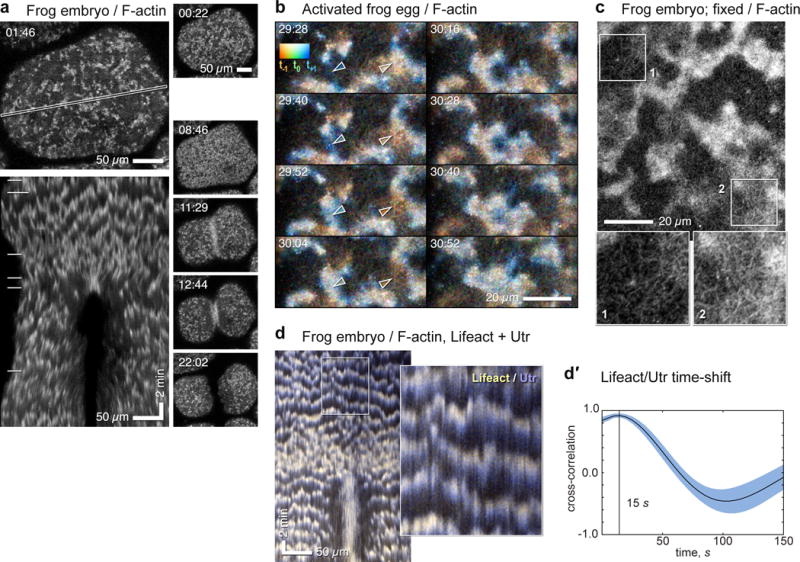
Cortical waves of actin assembly and disassembly in activated frog eggs and embryos. (a) Surface view of frog blastomere expressing GFP-UtrCH to label F-actin. Top left: single frame; cortical F-actin consists of irregularly sized patches throughout cortex, which, as illustrated in the kymograph made from the outlined region (bottom left) travel continually across the surface (see Supplementary Video 1). In the kymograph, F-actin waves create slanted bands with semi-regular spacing. Right: sequential frames from the same sequence throughout cytokinesis; horizontal lines in kymograph indicate times corresponding to individual en face frames shown to the right. For this and all other figures, time in min:sec. (b) High magnification time-lapse sequence of activated frog egg expressing GFP-UtrCH (see Supplementary Video 2), color coded by rendering the current frame malachite, next frame blue, last frame copper: thus new F-actin is bluish, old F-actin reddish. On left, leading edge of F-actin wave progresses downward while trailing edge disappears. On lower right, old F-actin wave dissipates. Cables of F-actin are apparent within and between receding waves. Swatch shows colors resulting from blending RGB channels with low (bottom of swatch) to high (top of swatch) overlap. Arrowheads indicate rising (left) and falling (right) wave fronts (arrow color sampled locally). (c) Fixed frog embryo stained with fluorescent phalloidin to reveal endogenous cortical F-actin; closely resembles Fig. 1b. 2× enlarged insets (bottom) correspond to areas indicated by boxes. Inset 1 shows region between waves, inset 2 shows wave. Cables are present in both but are brighter and denser in wave. (d) Kymograph from time-series of frog embryo co-expressing GFP-Lifeact (yellow) and mCherry-UtrCH (blue) to label newer and older actin, respectively (see Supplementary Video 3, Supplementary Figure 1d); inset is a 3× blowup. Leading edges of each wave (top of bands in kymograph) have proportionately more Lifeact and trailing edges (lower part of bands) more UtrCH, even though both probes qualitatively label the same features (Sup. Fig. 1d). (d′) Cross-correlational analysis showing 15s delay between recruitment of Lifeact and UtrCH. Images are representative of at least 40 (a), at least 30 (b), and 3 (c, d) independent experiments, respectively.

To test if the waves reflect actin assembly and disassembly, we double-labeled embryos with GFP-Utr and mCherry Lifeact since Utr-based probes bind to F-actin slower than probes that also label G-actin, like Lifeact^9,11. Although both probes clearly reveal the same features (Supplementary Figure 1d), the leading edges of waves had more Lifeact than Utr, and the trailing edges more Utr than Lifeact (Figures 1d,d′; Supplementary Video 3), demonstrating that the waves represent new assembly followed by disassembly, not cortical contraction or irruption from below. Further, the myosin-2 inhibitor, blebbistatin¹² had no significant effect on wave period (Con = 78 ± 11 s; Blebbistatin = 83 ± 8 s; mean ± SD; p=.46; n=270 correlation curves; Anova). However, by suppressing cortical contraction, blebbistatin reduced side-to-side movement of the cortex which permitted quantification of wave run length (maximum run length = 25 μm; mean = 3.7 μm).

Ect2 regulates cortical Rho waves in activated Xenopus eggs and embryos

C3 exotransferase, a specific Rho inhibitor, eliminated actin waves, but not other forms of actin assembly, such as comets (Figures 2a″,b, Supplementary Figure 2a). A dominant negative Ect2^13,2 (the conserved GEF involved in cytokinesis) also eliminated the actin waves (Figures 2a′,b, Supplementary Figure 2b). We therefore sought to detect concomitant waves of cortical Rho activity. A probe for active Rho (GFP-rGBD¹⁴) did not express quickly enough to detect any Rho patterning other than the cytokinetic Rho zone. However Rho activity waves could be detected in activated eggs expressing 3XGFP-rGBD (Figure 2c, Supplementary Video 4) or in embryos microinjected with recombinant GFP-rGBD protein (Figure 2c). In addition, anillin, a Rho effector protein¹⁵, also displays cortical waves (Figure 2d) while low level over-expression of wild-type Ect2 resulted in a striking increase in the amplitude and regularity of the Rho waves (Figure 2d, Supplementary Figure 2e; Supplementary Video 5).

Figure 2.

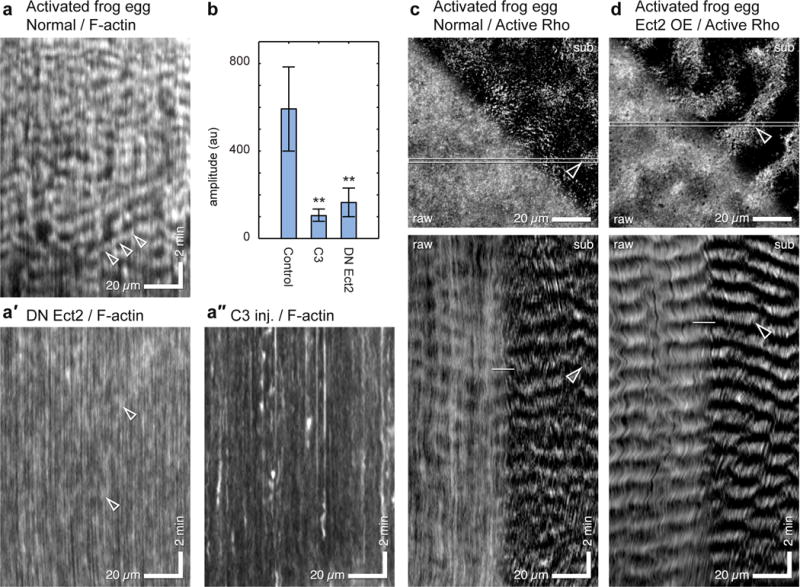
Cortical F-actin waves in activated frog eggs are Rho-dependent and are accompanied by Rho activity waves. (a) Kymograph from control activated frog expressing GFP-UtrCH to label F-actin; (a′) Kymograph from activated frog egg expressing GFP-UtrCH and dominant negative Ect2; (a″) Kymograph from activated frog egg expressing GFP-UtrCH and C3 exotransferase to inactivate Rho. Arrowheads indicate waves. (b) Plot of wave amplitude in controls versus cells expressing dominant negative Ect2 or C3. Results are mean ± SD; n=100 waves; p=0.00012 for C3 vs. control and 0.00015 for DN Ect2 versus control; t-test. (c) Activated frog egg expressing 3xGFP-rGBD to label active Rho (see Supplementary Video 4): single frame (top) and kymograph (bottom), raw (left) and subtracted data (right, t₀–t₋₃), highlighting rising Rho activity. The kymograph demonstrates that what otherwise looks like mundane inhomogeneity in the still image actually reflects regular waves of Rho activity; these are more evident in the processed half of both the image and kymograph. (d) Activated frog egg expressing 3xGFP-rGBD to label active Rho and subjected to low-level overexpression of wild-type Xenopus Ect2 (see Supplementary Video 5); figure processed and presented as in 2c. Waves are sharper (i.e. have higher amplitude) and more continuous than normal cells (compare to 2c) and are clearly evident even without processing. 2c and 2d are derived from average projections of 4 1 micron sections at 10 sec intervals. Images are representative of at least 30 (a) 3 (a′, a″, b). 4 (c) and 6 (d)3–6 independent experiments, respectively.

Cortical Rho waves in starfish oocytes and embryos

In parallel experiments we discovered that P. miniata (starfish) oocytes and embryos display cortical Rho activity waves that, in contrast to frog, are clearly visible only during a ~10–15 min window post-anaphase. At anaphase of meiosis I, Rho activity spread from the vegetal pole toward the animal pole, culminating in polar body emission (Figure 3a; Supplementary Video 6). Low-level overexpression of wild-type Ect2 profoundly amplified meiotic Rho activity and extended its duration, producing extremely regular, persistent (maximum run length = 55.8 μm; mean = 6.5 μm), high-amplitude waves kinematically similar to those in frogs, including overtly-spiral repeating patterns (Figures 3b,c; Supplementary Videos 7). Higher magnification movies of normal starfish oocytes (i.e., oocytes not subject to Ect2 overexpression) showed that much of the meiotic Rho activity comprised low-amplitude, rapidly damped cortical waves (Figure 3d; Supplementary Video 8). Rho activity subsided before onset of meiosis II, reappeared coincident with anaphase of meiosis II, again spreading from the vegetal to the animal pole, and culminated in polar body emission (not shown). In the largest mitotic cells, waves of cortical Rho activity also formed at anaphase onset, but were rapidly lost from polar regions and instead were confined to the equatorial cortex (Figure 3e, Supplementary Figures 3a,b). Waves initially dominated the furrow region itself, but as the furrow ingressed, relatively stable patches of Rho activity eventually merged into a coherent cytokinetic Rho zone (Figure 3c, Supplementary Figure 3b). As cells decreased in size, the time window in which polar waves were apparent after anaphase onset became narrower, as did the prominence of waves in the furrow itself (Supplementary Figure 3c,d).

Figure 3.

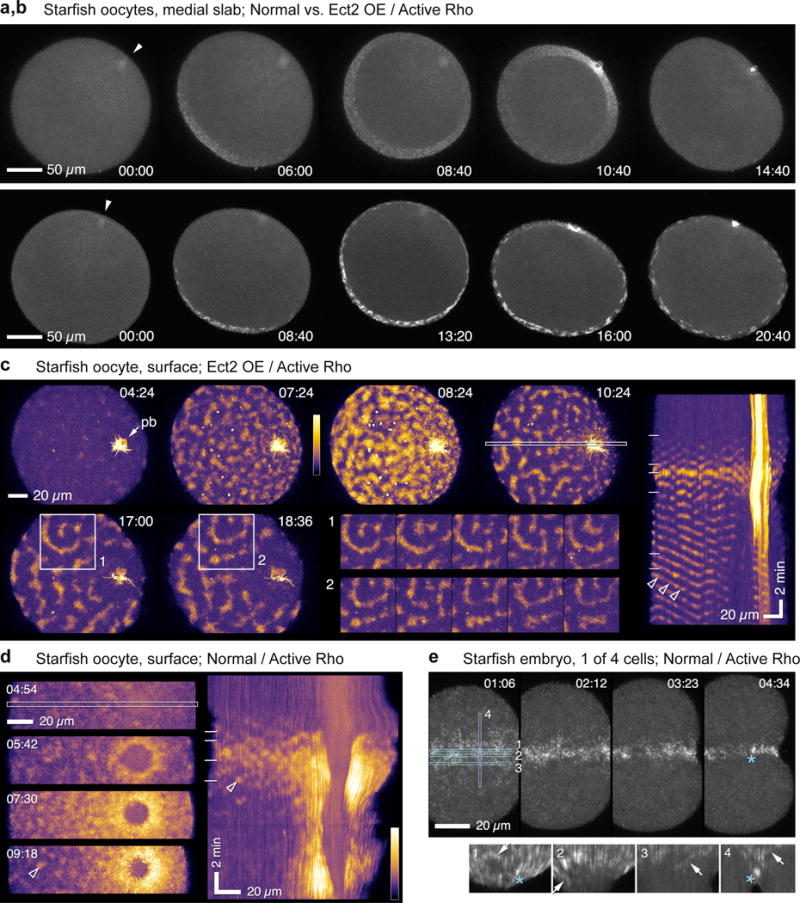
Rho activity waves in starfish oocytes and embryos. (a,b) Frames from time-lapse sequences of Rho activity during meiosis I in normal starfish oocyte (top; projection of 8 1 micron sections) and oocyte overexpressing wild-type S. purpuratus Ect2 (bottom; projection of 8 1.5 micron sections). See Supplementary Video 6. Arrow indicates animal pole. Rho activity appears at vegetal pole, spreads upward, and converges on nascent polar body, forming cytokinetic Rho zone. In Ect2-expressing oocytes the global pattern of Rho activity mirrors that of controls but waves are much brighter, travel further, and persist after polar body emission. (c) Surface view of cortical Rho activity in meiosis II oocyte overexpressing Ect2 (see Supplementary Video 7; pb = polar body; projection of 14 1 micron sections). High amplitude waves form and settle into repetitive, often spiral, patterns. Inset montages are successive 60 s time points from boxed region on left starting at 17:00 (1) or 18:36 (2), showing patterns that approximately replicate on ~ 70 sec time scale (1 is spiral, 2 is center-surround with a slash underneath). Kymograph on right generated from area indicated by outlined strip, 4th frame. Diagonal bands span half the oocyte, showing that waves travel at least this far. Horizontal lines in kymograph mark times of frames shown on left. Arrowheads point to wave front that traverses tens of microns at steady speed (d). Surface view of cortical Rho activity in normal starfish oocyte, single frames (left) and kymograph (right). Rho waves appear, brighten, and coalesce into continuous zone around nascent polar body (see Supplementary Video 8). Arrowheads indicate wavelet that appears in both kymograph and still frame. (e) Rho activity in normal starfish blastomere (1 of 4 cells), still frames and kymographs generated from strips outlined in blue: 1, furrow center; 2, furrow periphery; 3, just outside furrow; 4, across furrow. Rho waves focus at equator before ingression, appear in the furrow (arrows), and eventually merge into a coherent Rho zone. Asterisk indicates particularly bright focus that appears in 4th still frame and kymographs 1 and 4. Images are representative of 10 (a, d), 20 (b, c) and 4 (e) independent experiments, respectively.

Spatiotemporal coordination of Rho and actin waves

Simultaneous imaging of active Rho and F-actin within the cleavage furrow of control starfish zygotes and frog blastomeres revealed another surprise: instead of overlapping, F-actin assembly fronts directly follow Rho activity waves (Figure 4a,b; Supplementary Video 9). The same pattern (high-amplitude Rho waves followed by F-actin waves) was triggered globally in both activated frog eggs and starfish oocytes or mitotic cells by Ect2 overexpression (Figures 4c–e; Supplementary Videos 10–12). In all cases (except once waves cede to coherent zones, e.g., in progressing furrows) peak actin assembly coincides spatially with decreasing Rho activity, and a latent period with relatively low cortical Rho and actin follows each cycle. Although superficially similar to calcium waves that develop following expression of exogenous neurotransmitter receptors¹⁶, the Rho and actin waves are ~10 times slower than calcium waves and are not associated with elevated calcium (not shown).

Figure 4.

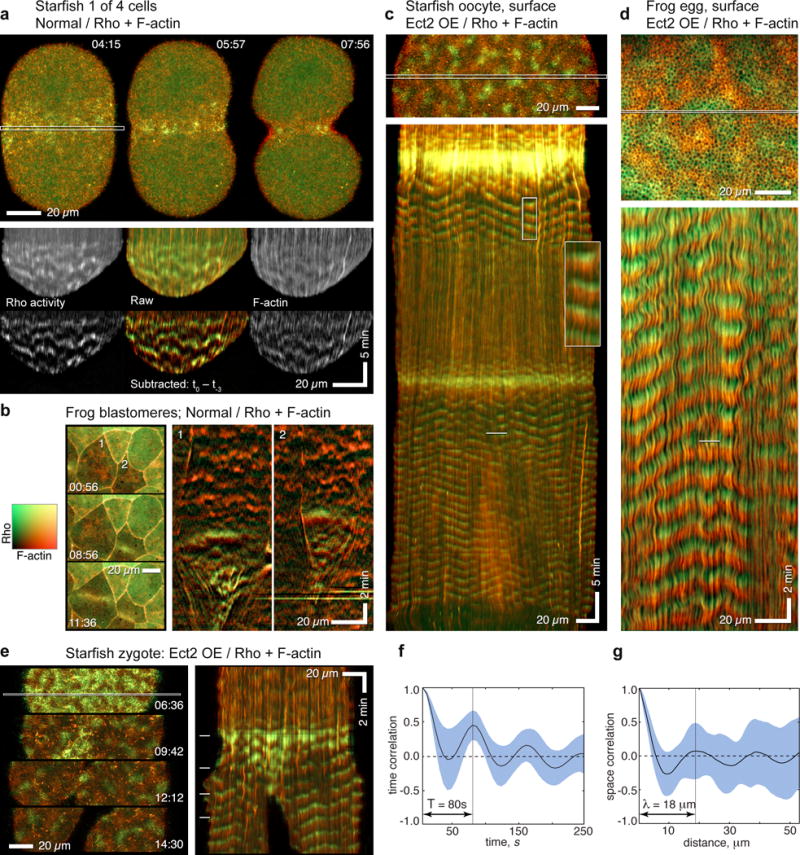
F-actin assembly fronts directly follow, but overlap minimally with, Rho activity waves. Color table shown in (b) applies to all images in this figure. (a) Normal starfish blastomere co-expressing GFP-rGBD (malachite; Rho activity) and GFP-Utr (copper; F-actin), selected frames (top) from time-lapse sequence of cytokinesis (Supplementary Video 9), and raw and subtracted kymographs (bottom) made from outlined strip. In still images, cytokinetic furrow is populated by apparently random densities of active Rho and F-actin; kymographs show these correspond to wavelets in which Rho activity rises, then falls as actin assembles. (b) Still images (left) and kymographs (right) from time-lapse movie of cortical F-actin and Rho activity in frog embryo showing two cells (1, 2) undergoing cytokinesis. Rho waves in furrow are followed by F-actin assembly waves. (c) Rho activity and F-actin in a starfish oocyte modestly overexpressing wild-type Ect2; kymograph (bottom) made from strip outlined in still frame (top). See Supplementary Video 10. Except during the global burst of Rho activity accompanying each meiotic cytokinesis, Rho activity waves immediately precede F-actin assembly, and F-actin disassembly precedes each Rho activation wave. Inset magnifies 4 cycles from wave train after first meiosis, emphasizing minimal overlap (yellow) between malachite and copper, and dark zone separating copper from next malachite wave. (d) Activated frog egg subjected to Ect2 overexpression, probes and presentation as in 4c (see Supplementary Video 11). Although waves are more tightly packed in frog eggs, kymographs show strikingly similar relationship between Rho and actin waves as in normal starfish. (e) Starfish zygote overexpressing Ect2 (see Supplementary Video 12), probes and presentation as in 4c and 4d, positions of still frames (left) indicated by dashes in kymograph (right). Faint waves precede global rise in Rho activity that focuses equatorially, leaving lower-amplitude waves in non-furrow regions; throughout, F-actin assembly follows peak Rho activity, and dark phases precede each Rho wave. (f) Temporal correlation plot of Rho waves from starfish oocytes overexpressing Ect2. Wave period ~80s. (g) Spatial correlation plot of Rho waves from starfish oocytes overexpressing Ect2. Wavelength 18 μm. Images are representative of 4 (a, b) 8 (c), or 5 (d) independent experiments, respectively.

To quantitatively characterize the wave pattern, we performed spatial and temporal autocorrelation analyses^17,18. These analyses demonstrated that in starfish oocytes both Rho and actin waves had wavelength of 18 μm and propagated with the same velocity, ~0.225 μm/s (Figures 4f,g). In activated frog eggs, the waves were slower, ~0.18 μm/s, and longer, ~21 μm. Importantly, analysis of the cross-correlation between Rho and F-actin signals showed that F-actin waves followed Rho with a fixed delay, 18 s in starfish and 48 s in frog. Thus, Rho and F-actin waves are mutually coordinated parts of the same wave pattern. Furthermore, such a constant time delay suggests that F-actin might effectively suppress Rho activation.

Rho-actin waves represent cortical excitability leading to spiral turbulence

Propagating waves that undergo self-annihilation upon collision suggest excitable dynamics¹⁹. Excitable media generate waves that travel without damping because they are generated de-novo by rapid local autoactivation at their front and extinguished at their wake by delayed negative feedback. Rho is a good candidate for the activator as small GTPases can indirectly activate themselves autocatalytically²⁰. Based on our kinematic observations, F-actin seemed a promising candidate for negative feedback. To test this possibility, we exploited the fact that quantitative relationships between Rho and F-actin can be directly inferred from imaging data¹⁷ (see Methods). In cortical loci (image pixels) with low F-actin signal, the rate of Rho signal change and the value of Rho signal itself are statistically positively correlated (Figure 5a). Since F-actin concentration is low at the front of the excitable wave, this correlation implies that, at the wave front, Rho amplifies itself in a positive feedback loop, which is the required property of the activator. Likewise, F-actin assembly positively correlates with Rho activity at the wave front (Figure 5b), while Rho activity negatively correlates with F-actin accumulation at the wave back (Figure 5c). We already established that Rho activity is required for actin assembly waves and that amplifying Rho activity elicits excess actin assembly; the correlative image analysis, thus, quantitatively confirms the dynamic relationship expected for the activator-inhibitor coupling (see Supplementary Figures 4a–c).

Figure 5.

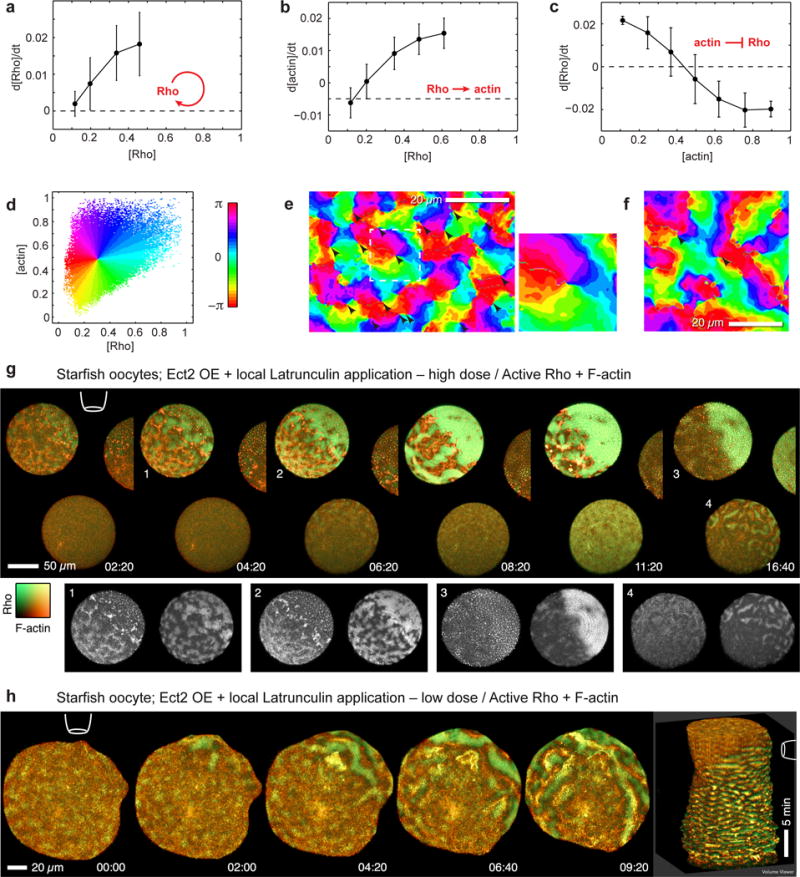
Analysis of Rho and F-actin dynamics reveals cortical excitability and spiral turbulence. (a) Rho activation rate (mean ± SD) increases with Rho activity signal indicating that Rho activates itself in a positive feedback loop. Correlation assessed from pixels with low F-actin signal (see Supplementary Figures 4a). (b) F-actin accumulation rate is positively correlated with Rho activity (assessed from pixels with low F-actin signal). (c) Rho activation rate is inversely correlated with F-actin signal, to the point of switching to inactivation at high F-actin density (assessed from pixels with high Rho activity signal). Results are mean ± SD; n=900 cycles. (d) Each cortical locus (image pixel) can be mapped by its particular values of Rho activity and F-actin density to a single phase value, an angle between 0 and 2π, shown in rainbow colors: Cortical loci at the front of waves appear green, loci at Rho wave crests as cyan, at F-actin wave crests as dark blue-magenta, and loci at the back of the wave are red and orange. (e) Phase reconstruction for starfish oocyte overexpressing Ect2 (Supplementary Video 13). Points where all rainbow colors (phase values) merge indicate spiral cores (arrowheads). Inset: magnification of spiral wave core neighborhood outlined by dashed line. (f) Phase reconstruction for activated frog egg overexpressing Ect2. (g) Meiotic Ect2-overexpressing starfish zygotes containing GFP-rGBD (Rho activity; malachite) and mCherry-Utr (F-actin; copper), time-lapse sequence after application of high concentration of LatB (10 uM) from agarose-filled pipette (position indicated by cartoon); treatment causes rapid cortical F-actin collapse and corresponding burst of Rho activation (see Supplementary Video 14). Insets: single channel images of cells/stages indicated by numerals: 1) initial response, 2) wave regime on far side, collapse on near side, 3) total collapse, 4) wave regime on near side of distant oocyte (h) Similar to (g), but low-dose (1 uM) LatB induces shift from typical Ect2-enhanced wave regime to higher-amplitude, longer-period wave regime, in which large scale Rho waves propagate away from site of local F-actin disassembly (see Supplementary Video 15); rightmost image is kymocube rendered using ImageJ. Images are representative of 5 independent experiments.

What factors shape the wave patterns? Random fluctuations in F-actin density and concentrations of other proteins are necessary to induce dynamics in excitable cellular systems¹⁹. However, occasionally visible fragments of spiral waves (Figure 3c, Supplementary Videos 7,10,11) suggest an underlying behavior much more complex than simply uncorrelated spatiotemporal noise. To reveal it, we reconstructed the phase of the excitable dynamics using a recently developed procedure²¹ (Figures 5d–f and Methods). This approach revealed multiple spiral waves (normally obscured by noise) whose cores spontaneously emerge, erratically move and disappear generating spiral wave turbulence. While the majority of spiral cores were very short-lived (few seconds), some persisted for up to ~59 min (Supplementary Video 13), reminiscent of the self-sustained spiral waves that emerge from the ends of broken wave fronts of cardiac excitation and cause atrial fibrillation in the heart²².

Antagonism of Rho by F-actin

The excitability model predicts that restricting F-actin assembly would extend the rising phase of Rho activation, resulting in waves with higher amplitude and crest widths. Treatment of starfish oocytes overexpressing Ect2 with latrunculin B to reduce F-actin caused global collapse of cortical F-actin and increased Rho activity (Supplementary Figure 5a) while treatment with jasplakinolide to stabilize F-actin attenuated Rho waves (Supplementary Figures 4e,e′). Local F-actin disruption via latrunculin B-filled microneedles positioned near the cell surface was more informative: high needle concentrations (> 5 μM) of latrunculin caused rapid local dissolution of cortical actin and a parallel burst of Rho activity (Figure 5g; Supplementary Video 14), which tapered off after the entire cortical actin network dissolved. Lower concentrations (1–0.5 μM; Figure 5h; Supplementary Video 15), or greater distance from the needle (Figure 5g, lower cell), resulted in slower loss of cortical F-actin and a corresponding amplification of Rho wave amplitude and crest width. Importantly, when applied at concentrations that permitted some residual actin assembly to cells with active waves, latrunculin induced a sustained shift to higher wave amplitude and longer period (Figure 5h). Similar results, albeit less dramatic, were observed in latrunculin-treated normal cells (Supplementary Figure 5). This directly confirms that F-actin assembly somehow suppresses Rho activation, supporting a model of cortical excitability in which F-actin-dependent Rho inhibition represents the essential negative feedback.

Cdk1-dependent control of excitability

To better characterize the relationship between cell cycle progression and excitability, cortical microtubules were used as a marker for cell cycle progression²³ and compared to either cortical F-actin (frogs) or cortical Rho (starfish). Cortical microtubule abundance changed rhythmically with the cell cycle in frog embryos, with high levels in interphase and very low levels in M-phase, while cortical actin waves were present throughout (Figure 6a). However, in starfish oocytes or embryonic cells overexpressing Ect2, cortical Rho waves were evident for ~63% of the cell cycle, disappearing and appearing in concert with cortical microtubules (Figure 6b). In control cells, Rho waves were normally visible for ~20% of the cell cycle (not shown).

Figure 6.

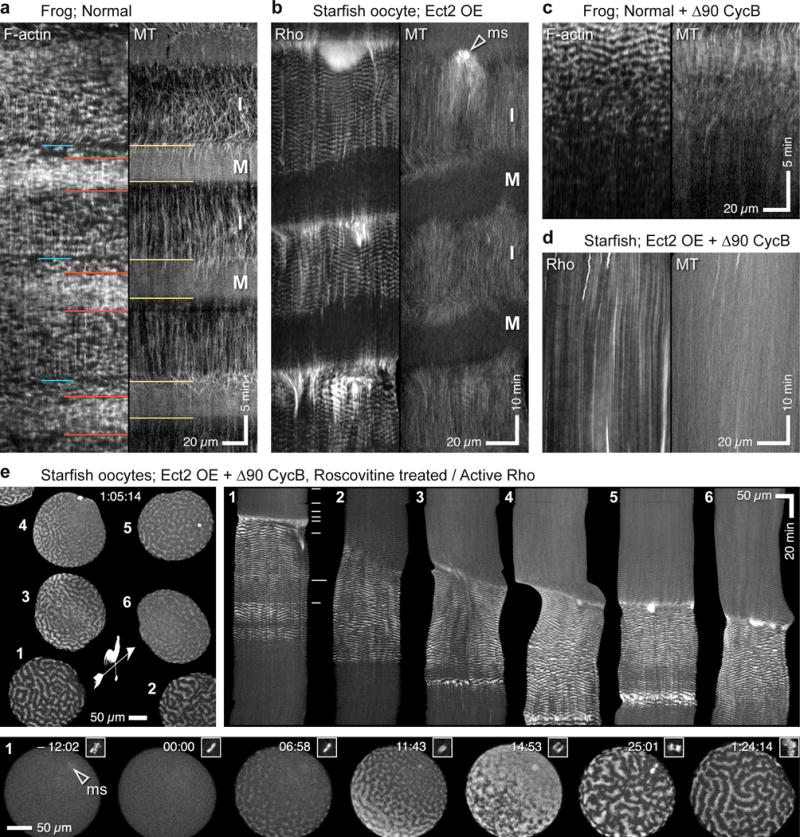
Cdk1 gates excitability. (a) Kymograph from normal frog embryo showing waves of cortical F-actin (left) and cortical microtubules (right). I=Interphase; M=M-phase; Yellow lines on right indicate M-phase onset, as revealed by loss of cortical microtubules. Actin waves persist throughout M-phase but wave density varies: at M-phase onset (blue line on left), waves are spaced farther apart; this is followed by period of same length as M-phase but slightly delayed in which F-actin waves are brighter (red lines). (b) Kymograph from double-labeled starfish oocyte overexpressing Ect2 showing waves of cortical Rho activity (left) and cortical microtubules (right). Rho waves cease in each M-phase and reappear in each interphase. ms = meiotic spindle. (c) Kymograph of frog blastomere expressing Δ90 cyclin B showing cortical F-actin (left) and cortical microtubules (right). As time of high Cdk1 activity lengthens (revealed by loss of cortical microtubules) cortical F-actin waves progressively disappear. (d) Kymograph of Ect2-overexpressing starfish oocyte expressing Δ90 cyclin B as well, showing cortical Rho activity (left) and cortical microtubules (right). Rho waves fail to appear as cell remains arrested with high Cdk1 activity. (e) Top left: Rho activity in starfish oocytes overexpressing Ect2 and expressing Δ90 Cyclin B, 65 min after treatment with 40 μM roscovitine to inhibit Cdk1 (see Supplementary Video 16). Weather vane indicates direction of roscovitine flow. Roscovitine-containing seawater perfused around tight-packed oocytes from Southeast to Northwest at time 00:00; cells 1 and 2 are at cluster edge, cells 5 and 6 are in cluster center; hence, weathervane indicates presumed gradient of drug exposure. All oocytes show robust Rho waves at this time point. Top Right: kymographs of oocytes (identified by numerals) showing development of cortical Rho activity waves following Roscovitine treatment. Note that onset of waving follows expected rate of Cdk1 inhibition based on access to drug in perfused media. Bottom: successive frames showing oocyte 1 alone; inset shows chromosomes, arrowhead indicates position of meiotic spindle. Rho waves are well developed at least five minutes before anaphase begins. Images are representative of 4(a), 3(b), 5(c) and 6(d) independent experiments, respectively.

Because M-phase results from activation of cyclin dependent kinase 1 (Cdk1), we microinjected cells with mRNA encoding Δ90 cyclin B, which prevents Cdk1 inactivation²⁴. In frogs, this resulted in progressive disappearance of actin waves coincident with complete disappearance of cortical microtubules (Figure 6c). Similarly, in starfish, Δ90 cyclin B produced an indefinite cessation of Rho waves (Figure 6d). Thus, Cdk1 activity suppresses excitability in both systems. To determine whether Cdk1 inactivation initiates excitability, Ect2 overexpressing starfish oocytes were microinjected with Δ90 cyclin B mRNA, and subsequently treated with roscovitine to inhibit Cdk1²⁵. Roscovitine treatment triggered reappearance of cortical Rho waves in a manner that paralleled the expected exposure to the drug (Figure 6e; Supplementary Video 16). Moreover, simultaneous imaging of active Rho and fluorescent histone demonstrated that Roscovitine treatment actually released Rho waves even before anaphase onset (Figure 6e; Supplementary Video 16). Thus, Cdk1 inactivation is indeed a trigger of excitability.

DNA, centrosomes, microtubules and excitability

C-phase onset and cessation are regulated independently of the spindle⁶. To determine whether excitability is likewise spindle-independent, starfish oocytes overexpressing Ect2 were microdissected to produce pairs of cytoplasts that contain or lack essential spindle components—DNA and centrosomes²³. Cytoplasts that contained neither DNA nor centrosomes nonetheless displayed excitability (Figure 7b; Supplementary Video 17), and the timing and character of waves were remarkably similar to those of nucleated cytoplasts or whole cells (Figure 7a,b), with the exception of a long delay between meiosis and first mitosis in anucleates (Figure 7b′). Thus, neither DNA, nuclei, nor spindles are required for temporal regulation of excitability.

Figure 7.

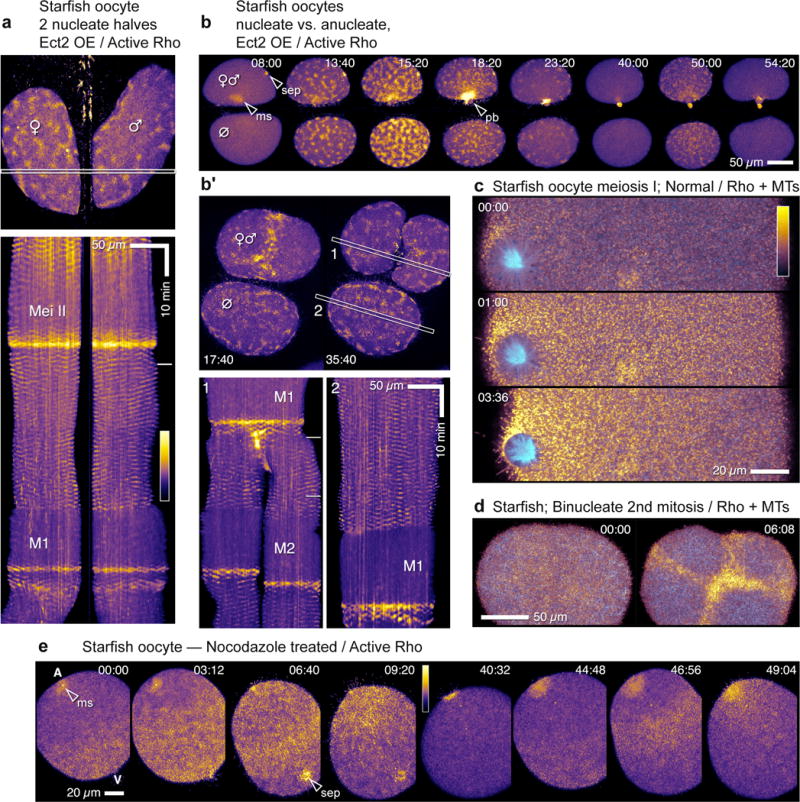
Excitability does not require spindles but is locally modulated by microtubules (a) Still frame (top) and kymograph (bottom) from time-lapse movie showing cortical Rho activity in two nucleate fragments derived from bisection of Ect2-overexpressing starfish oocyte. Waves of Rho activity appear and disappear in synchrony in each half. Pseudocolor table shown applies to a,b,b′, and e; in a and b′, outlined strips indicate kymograph region, dashes in kymographs are times of still frames. (b) Frames from time-lapse movie showing cortical Rho activity in nucleate half (top) and anucleate cytoplast (bottom) after bisection of Ect2-overexpressing starfish oocyte just before meiosis I. Waves appear and disappear on time in anucleate cytoplast in spite of the fact that it lacks spindle, chromosomes, or even centrosomes (see Supplementary Video 17) (b′) Similar bisection but after meiosis; two frames (top), during and after first cleavage, and kymographs (bottom, 1: nucleated, 2: anucleate). Cortical Rho waves appear and disappear in both halves, although first mitosis is delayed in the anucleate cytoplast. (c) Frames from time lapse movie showing microtubules (cyan) and active Rho (gold) in normal starfish oocyte during meiosis I. Rho activity is suppressed in the region occupied by spindle aster. (d) Frames from time lapse movie showing microtubules (cyan) and active Rho (gold) in starfish zygote with two spindles. Rho activity waves are excluded from regions occupied by spindle asters leading to focusing of Rho waves into cruciform Rho zone. (e) Meiotic Rho activity in normal starfish oocyte after treatment with 5 uM nocodazole to depolymerize microtubules (see Supplementary Video 18). The overall pattern of Rho activation is similar to controls – initiation at vegetal end, rapid progression to animal pole, inactivation in M-phase – except that animal pole is a Rho hotspot instead of a suppressed area; sep=sperm entry point, ms=meiotic spindle. Images are representative of 3(a, b), 12(c),17 (d) and 3(e) independent experiments, respectively.

While the temporal regulation of C-phase is independent of microtubules, microtubules nevertheless spatially regulate cortical contractility during C-phase⁶. Simultaneous imaging of microtubules and Rho activity in starfish oocytes and embryos illustrates that excitability is subject to spatial regulation by microtubules, as expected for a manifestation of C-phase: Rho waves were suppressed in regions where astral microtubules densely populate the cortex (Figure 7c,d). Further, microtubule disassembly by nocodazole prevented formation of the wave-free region at the animal pole in oocytes (Figure 7e; Supplementary Video 18) but had no apparent effect on the timing of wave appearance or disappearance (Figure 7e), indicating that while microtubules do not control the timing of excitability, they are nonetheless responsible for locally modulating it.

A model for cortical excitability suggests the route to furrow formation

To better understand cortical excitability, we developed a simple model (Figure 8a,b) that incorporates membrane-cytoplasmic shuttling of inactive Rho, its Ect2-dependent autocatalytic activation and its inactivation via a slower, F-actin-mediated negative feedback (see Methods). The spatiotemporal excitable dynamics of the model driven by molecular noise (Fig. 8, Supplementary Figures 6b,c) faithfully recapitulates the pattern of spontaneously emerging, erratically moving and colliding waves. Moreover, the wave pattern and kymograph signature of the global wave-like rise in Rho activity observed during meiosis are captured by the model simply by including a transient peak in Ect2 activity (Figures 8c–e, Supplementary Figures 6b,c; Supplementary Video 19), suggesting that the overall increase in Rho activity and specific changes in the wave pattern following anaphase onset reflect the rise in Ect2 activity.

Figure 8.

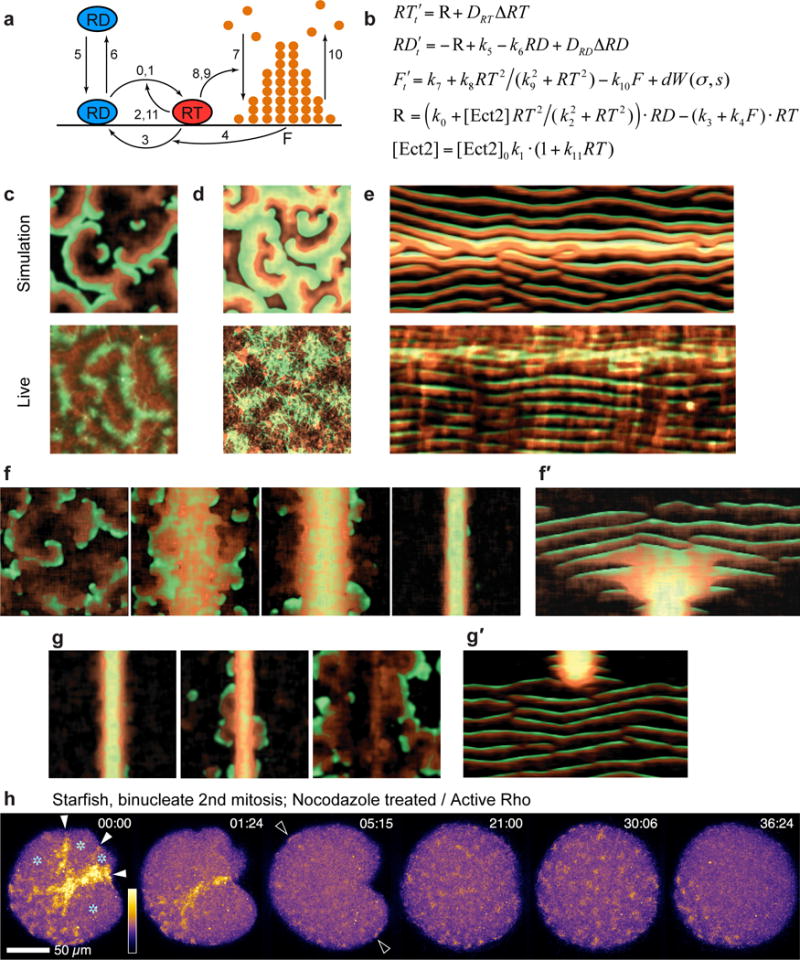
Model of excitable dynamics predicts that Ect2 spatio-temporal distribution determines the pattern of Rho-actin cortical activity. (a) Schematic diagram of the molecular processes described by the model (see Methods). Numbers on the arrows correspond to numbers of rate constants in b. (b) Model equations (see Supplementary Figure 6a and Methods). (c) Top: Simulation of wave turbulence with Ect2 level representing interphase wave pattern in starfish oocytes with extra Ect2 (see Supplementary Video 19), active Rho (malachite) and F-actin (copper). Bottom: image of cortical Rho (malachite) and F-actin (copper) from Ect2-overexpressing starfish oocyte for comparison. (d) Top: Model dynamics at the peak of global Ect2 activity – representing polar body emission phase – demonstrates a characteristic wave pattern with broad crests, substantial overlap of Rho and F-actin maxima and narrow refractory zones between wave crests (see also Supplementary Figures. 6b,c and Methods). Bottom: image of cortical Rho (malachite) and F-actin (copper) from Ect2-overexpressing oocyte at time of polar body emission for comparison. (e) Top: Model kymograph of Rho activity and F-actin prior to, during, and after polar body emission (see Supplementary Video 19). Bottom: experimental kymograph for comparison. (f) Emergence of furrow through condensation of waves in a simulation representing mitotic starfish cells with progressive focusing of Ect2 at the cell equator (see Supplementary Video 20). (f′) Kymograph along a line perpendicular to the furrow for model behavior in f. (g) Simulation of rapid microtubule depolymerization after furrow zone formation: furrow signal dissipates and spatially-homogeneous waves return. (g′) Kymograph of simulation shown in f. (h) Behavior of cortical Rho waves following experimental microtubule depolymerization by nocodazole in binucleate starfish zygote at the onset of cytokinesis. Cytokinetic Rho zones dissipate quickly and waves repopulate the entire cortex. Asterisks indicate spindle pole positions; solid arrowheads indicate Rho zones in nascent furrows; hollow arrowheads point out instances of cortical Rho waves in once-bare territory (see Supplementary Video 21). Images in h are representative of 3 independent experiments.

We further asked if the transition of mitotic cells from uniform wave dynamics to equatorially focused waves could reflect microtubule-mediated redistribution of Ect2 towards the cell equator. Indeed, model simulations demonstrated a transition from a weak global excitability to progressively narrower and more intense excitability at the equator (Figures 8f,f′, Supplementary Video 20). Driving Ect2 localization to an even narrower band with higher local concentration caused the model to transition from excitability to a new steady state in which both Rho activity and F-actin density are high and stable, which corresponds to the behavior observed in mature ingressing furrows. Excitable dynamics could still be visible on furrow margins where Ect2 concentration sharply drops, just as it is seen in vivo (Figures 3e,4a). Finally, we modeled the consequences of rapid microtubule depolymerization on the established cytokinetic zone. This produced a rapid loss of high excitability from the furrow and reemergence of weaker excitability elsewhere (Figures 8g,g′). This model prediction was tested by treating Ect2 overexpressing starfish zygotes with nocodazole after the formation of the cytokinetic Rho zone. This completely reversed the sequence of events seen in wild-type cells: the furrow disassembled and waves re-appeared throughout the cell cortex (Figure 8h; Supplementary Video 21), in close agreement with model simulations.

Discussion

We have discovered that the cortex of vertebrate and invertebrate oocytes and embryos is an excitable medium, which is based on Rho autoactivation and F-actin mediated Rho inhibition (Figure 8). Positive feedback (Rho autoactivation) would allow the cortex to respond to spindles experimentally deprived of astral or midzone microtubules²³ via auto-amplification at the cortex. Conversely, the negative feedback (F-actin-mediated Rho inhibition) would efface established Rho zones and cytokinetic apparatuses upon repositioning of the spindle^4,26,27. Thus, excitability explains both the sensitivity of the cortex to spindle-generated signals and the rapid adaptation of the cortex to changes in spindle position.

The relationship between cortical excitability and the cell cycle, together with the fact that cytokinesis ensues when excitability becomes confined to the equator, provide a simple explanation for C-phase: it represents the period of the cell cycle in which cortical excitability is fully enabled. Consistent with this proposal, Rappaport has shown that furrowing in sand dollar zygotes normally occupies about 20% of the cell cycle but can be extended to ~60% by manipulation of spindle position⁴, closely paralleling our observation that Rho waves are normally evident for about 20% of the cell cycle but can be extended to about ~60% by overexpression of Ect2. Further, early frog blastomeres display continuous excitability consistent with the observation that C-phase of one cell cycle overlaps with C-phase of the next cell cycle such that multiple furrows may be found in a single cell⁴.

How, exactly, is excitability regulated? The results point clearly to Cdk1. Not only does cessation of excitability in starfish oocytes and zygotes coincide precisely with the onset of M-phase, waves are stripped from the cortex in an animal-to-vegetal pole manner, following the known spatial pattern of Cdk1 activation^28,29. Further, suppression of Cdk1 inactivation arrests cells in a non-excitable state, which is rapidly converted to excitable by experimental inhibition of Cdk1. Thus, excitability in echinoderms is negatively regulated by Cdk1 and it is extremely likely that the characteristic top-to-bottom stripping of the waves from the cortex reflects the underlying “trigger wave” of Cdk1 activation³⁰. Ect2 is a potential target of Cdk1 in this context, in that Cdk1 phosphorylation compromises the ability of Ect2 to bind the plasma membrane¹³. Why waves are not fully suppressed in M-phase in frogs remains to be seen, but based on the demonstration that these cells are metachronous^28,31 and the fact that they do terminate wave activity when forced into a prolonged M-phase, we speculate that their normal Cdk1 activity levels fail to reach the threshold needed to suppress excitability.

The F-actin mediated antagonism of Rho activity observed here seems counterintuitive to the point of deviance given traditional views on collaboration of Rho and F-actin in contractile arrays. However, at least two parallels are found in other processes. During single cell wound repair, a ring-like wave of Rho activity forms in a region of low cortical F-actin density⁹; as the Rho wave closes, it is “chased” inward by a surrounding, ring-like wave of F-actin. Similarly, during blebbing, it is thought that Rho activity rapidly rises in regions of the cortex from which F-actin is cleared, and as Rho activity falls, F-actin rises^32,33,34. Further, while not yet directly demonstrated, negative feedback from F-actin to Rho family GTPases explains essential features of cell locomotion-associated F-actin waves^35,36.

Finally, two other striking points emerge from this study. First, the fact that furrowing commences as overlapping waves of Rho activity and F-actin become confined to the equator suggests that the continuous and relatively stable structures envisioned in textbook models of the cytokinetic apparatus need revision. Second, the observation that Ect2 overexpression produces a cell-wide version of what occurs at the equator during cytokinetic apparatus specification suggests that cytokinetic signaling by the spindle might simply reflect redistribution of Ect2 from non-equatorial regions to the equator. More complex scenarios, in which astral microtubules stimulate Rho GAPs in non-equatorial regions or otherwise inhibit Rho, may not be necessary.

Methods

Xenopus oocytes and artificially activated eggs

Chunks of ovaries were removed from anesthetized, adult female Xenopus laevis, rinsed in 1X Barths solution (87,4mM NaCl, 1 mM KCl, 2.4 mM NaHCO₃, 0.82 mM MgSO₄, 0.6 mM NaNO₃, 0.7 mM CaCl₂ and 10 mM HEPES at pH 7.4), and then collagenase treated for 1 hour at 17° C. After extensive rinsing in 1X Barths, oocytes were allowed to recover overnight at 17° C. After recovery, oocytes were injected with 40 nL of mRNA (0.01–1 mg/ml needle concentration). Oocytes destined to be imaged as full grown oocytes were maintained at 17° C overnight and imaged the next day. Oocytes destined to be converted to activated eggs were maintained at RT for 3–6 h, then treated with 5 ug/ml progesterone for 15 min and transferred to 17° C overnight. The following day, meiotically mature eggs were activated with 10 ug/ml ionomycin in 0.1X MMR for 2–4 min. Activated eggs (identified by pigment contraction) were rinsed 3X in 1X Barths and then maintained at 17° C for 2 hour prior to imaging. In experiments involving Ect2 overexpression, eggs were subject to a second round of microinjection after 30 min post activation with 10 nL of 0.01 mg/ml Ect2 mRNA (needle concentration).

Xenopus Embryos

Ovulation was induced by injecting adult female Xenopus laevis with 600–800 U HCG followed by overnight maintenance at 18° C. The next day, eggs release was promoted by gentle squeezing of the abdomen. Eggs were maintained in 1X MMR (100 mM NaCl, 2 mM KCl, 2 mM CaCl₂, 1 mM MgCl₂, 5 mM Hepes, pH 7.4), fertilized and then dejellyed in 2% cysteine in 0.1X MMR. At the two-cell stage, embryos were microinjected with 5 nL of mRNA at 0.01–1 mg/ml (needle concentration) or, for the protein version of GFP-rGBD, 5 nL of protein at 1 mg/ml (needle concentration). In some experiments, a second round of injections took place at the 4-cell stage; such injections used a volume of 2.5 nL. Embryos were maintained at 17° C until imaging.

Starfish

Patiria miniata was purchased from Marinus Scientific of Long Beach, California and kept in flowing natural seawater at OIMB. Fragments of gonad were obtained by penetrating the body wall of one arm with a 4 mm biopsy punch. Ovaries were rinsed in calcium-free artificial seawater (CFSW; Stricker and Schroeder’s recipe), then teased apart with forceps and shaken gently to release full-size oocytes. We used only oocytes from batches in which the majority of large oocytes were full sized, and in which the spontaneous maturation rate after an hour in CFSW was less than ~25%. Several rinses in CFSW over the course of 1–2 hr was sufficient to fully defolliculate oocytes, which were then transferred to 0.22-micron filtered natural seawater (MFSW) prior to injection. Testis fragments were kept dry in microfuge tubes until needed, then sperm were obtained by perforating a swollen lobe in MFSW.

Starfish egg handling

While sitting in a dish of seawater, starfish oocytes tend to release mucus that makes handling difficult. Therefore, just before injection, defolliculated oocytes were passed repeatedly through a mouth pipette cut to a diameter slightly exceeding the outer diameter of the oocytes plus jelly coat, ~250 microns. For injection, oocytes were arranged by mouth pipette in rows on coverslip-bottomed dishes (MatTek) which had been coated by washing 30 sec. with 1% protamine sulfate in distilled water, followed by rinsing in water and air drying. Following injection, oocytes were incubated in MFSW in their injection dishes or transferred to uncoated 35 mm petri dishes, often with the addition of 50 μg/ml streptomycin, and kept either at seatable temperature (12–16°C) or on a Peltier cold plate (Torrey Pines Scientific) at 12–16°C.

Maturation was induced by addition of 1 mM 1-methyladenine in water to a final concentration of 10⁻⁶–10⁻⁵. After germinal vesicle breakdown, which usually takes 45–60 min at temperatures used, maturing oocytes were inseminated by aspirating a suspension of motile sperm from the vicinity of a just-poked testis fragment. Sperm activity, oocyte binding, and fertilization success (as judged by envelope elevation) were observed carefully under dissecting microscope, because of the high risk of polyspermy in microinjected oocytes.

For some experiments, fertilized eggs were deprived of their envelope by brief treatment with 1% sodium thioglycolate in MFSW at pH 9.5–10.0 followed by several transfers to normal MFSW. Thioglycolate solution was made fresh within an hour or two of use, and titrated by addition of 1 M KOH while stirring vigorously. During and after envelope dissolution, eggs were kept well separated in agarose-coated 35 mm petri dishes. Gentle shearing with a mouth pipette during treatment speeds removal of coats (i.e., before full dissolution), limiting time spent in high-pH seawater.

Microinjection and micromanipulation

For Xenopus, pressure microinjections were performed with a PLI-100 picoinjector (Medical Systems Corp.; Greenvale, NY) using needles pulled from capillary tubes and calibrated using oil and a stage micrometer. Oocytes were microinjected in 1X Barths in 5 ml petri dish with plastic mesh affixed to the bottom; embryos were microinjected in 0.1X MMR + 5% ficoll in a meshed dish.

Starfish oocytes were injected in coverslip-bottomed dishes on an inverted microscope at 18–20°C using an oil-hydraulic manipulator (Narishige), pressure injector (Dagan), and glass needles pulled from 1 mm OD filament-containing capillaries (Sutter) using a P-97 Flaming-Brown puller (Sutter). Prior to loading, pulled needles were silanized by adding ~100 μl hexamethyldisilazane to a closed box containing the needles. Backfilled needles were broken to appropriate size (3–5 μm) against a coverslip fragment held to the bottom of the injection dish with high-vacuum grease. In our hands, starfish oocytes tend to eject the germinal vesicle if the needle penetrates it, therefore we systematically injected into the cytoplasm a puff corresponding to <1% of oocyte volume.

To generate anucleate cytoplasts or locally apply drugs, fertilized eggs were stripped of their fertilization envelopes and then arranged in coverslip-bottom dishes. Bisections were performed with an injection needle held by an oil-hydaulic micromanipulator. Local drug applications were conducted by filling a large-bore (20–50 μm), fire-polished drawn capillary with 0.5% low-melt agarose containing Latrunculin B at 0.5–5 μM. Roscovitine and nocodazole treatment do not require envelope removal, and global, timed drug application was accomplished by trapping small groups of oocytes between slide and coverslip, then flooding one open chamber edge with drug-containing MFSW while wicking away medium from the opposite opening with filter paper.

Actin staining

Xenopus embryos were rinsed 3X in PBS (Phosphate Buffered Saline–100 mM NaCl, 3 mM KCl, 10 mM Na₂HPO₄, 2 mM KH₂PO₄, pH 7.4) and fixed for 1 h at RT in Zevon’s Fixative (100 mM KCl, 10 mM Hepes, 3 mM MgCl2, 1 mM EGTA, pH 7.6) + 3.7% fresh paraformaldehyde, 0.1% glutaraldehyde, 0.1% Triton X-100, and 1 U/ml AX-488 Phalloidin (Molecular Probes). Embryos were then washed 3X 10 min in PBS, and then 1 h in TBSN (Tris Buffered Saline—50mM Tris, pH 7.5, 150 mM NaCl + 0.1% NP-40).

Imaging

Frog oocytes, activated eggs, and embryos were imaged using a Prairie View Laser Scanning Confocal (Bruker Nano Surfaces, Middleton, WI) on a Nikon Eclipse Ti. Samples were prepared as described previously³⁷ and imaged using a 40X 1.0 NA or a 60X 1.4 NA objectives.

All imaging of starfish oocytes and embryos was conducted on an Olympus FluoView 1000 laser-scanning confocal on an IX81 inverted stand, using 60× 1.2NA or 40× 1.15 NA water-immersion objectives, or 20× dry 0.75 NA objective. Cells were either held between slide and coverslip separated by two ridges of high-vacuum grease (Dow Corning) and compressed to trap the cells, or were filmed in ethanol-cleaned coverslip-bottomed dishes; clean glass clings just enough to demembranated oocytes that they are prevented from drifting off, but not rendered overtly abnormal. To keep cells at viable temperatures, we used stage-mounted Peltier cooling adaptors (Dagan) set to 12–14°C. When using coverslip-bottomed dished filled with seawater and water-immersion objectives, in-bath measurements and comparison of developmental rates to controls suggest an effective temperature 1–3°C above the set point, slightly more for cells held in slide chambers. Volumes of seawater and numbers of oocytes per dish or slide were limited to avoid anoxia (10–20 embryos per slide prep; <50 in dishes).

Constructs and in vitro synthesis of mRNA

The following constructs used were described previously and for both frog and starfish injected at concentration ranges as follows: eGFP-rGBD¹⁴, 100–500 ng/μl; mCh-UtrCH⁹, 100–200 ng/μl; mCh-H2B, 50 ng/μl; 2xmCh EMTB 50–200 ng/μl²³; 1xGFP, 3xGFP- or 3xmCh-SpEct2², 10–50 ng/μl; anillin-3XGFP 100 ng/ul³⁸. 3XGFP-rGBD was generated by cloning rGBD into pCS2+ downstream of 3 tandemly repeated GFPs and was injected at 800 ng/nL. Xenopus Ect2 (Open Biosystems) was cloned into pCS2+ and dominant negative Xenopus Ect2 was made by changing the conserved residues 593PVQR596 in the catalytic domain to alanines^2,13 using a Quikchange kit (New England Biolabs) and the following primers: F: cttatcagagctg ctgcagcattaccaagcgtcgctcttcttctg.

R: gcgacgcttggtaatgctgcagcagctctgataagtaactcgac. Wild type Xenopus Ect2 was injected at 5–10 ng/ul; dominant negative Xenopus Ect2 was injected at 50–100 ng/nl. Δ90 cyclin was made by cloning full length human cyclin B into pCS2 and then removing the first 270 nucleotides; it was injected at 50 ng/μl for both frog and starfish. mRNAs were transcribed from linearized plasmids in vitro using mMessage mMachine SP6 kit (Ambion) and were polyadenylated using a Poly(A) tailing kit (Ambion).

Expression of FLAG-GFP-rGBD

A 5′ terminal Kozak consensus sequence and FLAG epitope were added to the GFP-rGBD construct from¹⁴ using PCR. The resultant amplicon was inserted into the bacmid donor plasmid pFastBac1 to generate recombinant bacmid DNA in DH10BAC (Invitrogen) bacteria. Recombinant baculovirus was produced in Sf21 insect cells and used to infect additional Sf21 monolayers. Recombinant protein was purified using anti-FLAG M2 affinity resin (Sigma) with Arg-based elution³⁹. Elution fractions were pooled and the protein concentrated to 50 μM in 25 mM HEPES, 100 mM KCl pH 7.5 prior to oocyte injections.

Image processing

All image processing (projection, brightness and contrast, averaging, etc.) was conducted in ImageJ, except for false-coloring and figure composition in Photoshop CS6. All kymographs were prepared in ImageJ by re-slicing a strip of a time series (as shown by outlines in figures), 6 or 12 pixels wide (~1 μm), then averaging the re-slicing planes and stretching along the time axis for clarity, with or without bicubic interpolation. Subtraction was performed in ImageJ using the image calculator function, and then median filtered (3×3) to reduce noise. No other convolution filters or other image processing was applied to any image. For grayscale images, adjustments were limited to white and black point, preserving linearity intensity range between. For certain data, pseudocolor tables were used to perceptually balance bright versus dim features while preserving luminosity in single-channel images (the Abattoir Blues lookup table in Figs. 3c,d, 7a,b,e, and 8h) or to blend two channels while providing a distinct color for co-localization (the Copper/Malachite lookup table in Figs. 4a–e, 5g,h, 8a–g, and Supplementary Figure 5). Color tables for both are reproduced adjacent to several figure panels that make use of the range. Identical color tables used for supplementary videos, but with gamma adjustment to un-do a non-user-controlled gamma adjustment applied by QuickTime H.264 codec.

Data analyses

For most analyses, the data were extracted with ImageJ from experimental time-lapse movies of Rho and F-actin dynamics in the form of kymographs, i.e., matrices $u_{i,j}^R,u_{i,j}^A$, where index i represents time and index j is the spatial position of an image pixel along a chosen linear segment. Spatial and time correlation analyses were performed according to the standard signal processing method, e.g., time autocorrelation function for the Rho signal at a specific pixel j is given by

$$C_j^R(\tau )={\displaystyle {\int }_0^t{u}_j^R(t+\tau )}{u}_j^R(t)dt,$$

where the integral is taken along the j-th column of the data kymograph. To obtain statistical information (Fig. 4f,g), computed spatial and time correlation functions were averaged over multiples lines and columns of the kymograph, respectively. Furthermore, for the computation of spatial autocorrelation function, kymographs were taken over multiple varied spatial directions on the images.

To compute statistical distribution of wave runs, the above kymographs were first normalized to lie within [0,1] and then processed using Matlab function countourf () that performs non-polynomial interpolation and contour extraction in 2D images. The candidate positions of wave front were then extracted at locations of the contour computed at the half maximal height, 0.5. At each contour point its slope was computed with centered 5-point template. To separate waves from non-propagating excitable dynamics, only points with slope above a suitable threshold calculated on the basis of spatial and temporal resolution of the original time-lapse movie were retained for the following analysis. All candidate runs shorter than 4 consecutive time points (frames) were discarded from the analysis. The lengths of these unbroken wave runs were then binned and used for the calculation of histogram representing statistical distribution of wave runs.

For the kinetic analysis¹⁷ (Figs. 5a–c, Supplementary Figures 4a–c), in addition to signal values, time derivatives d[Rho]/dt and d[actin]/dt were calculated numerically from the kymographs using finite difference approximation. The data were then suitably binned and the average and standard deviation were computed per bin to reveal the dependences between the Rho and F-actin signals. To reconstruct phase of the excitable dynamics, we implemented Morlet wavelet analysis²¹ using Matlab. For the time series of Rho or F-actin signal at a given image pixel, this method generates two 2-dimensional functions, amplitude and phase (Supplementary Figure 4d). The maximal value of amplitude for each given time point defines the dominant value of the time period T(t), which need not be the same for all time points. Morlet wavelet analysis, thus, allows to determine phase even when the periodicity of the signal changes with time. In the case shown in Supplementary Figure 5d, T = 80 s uniformly within the time series. The curve of amplitude maxima (in this case – a straight line segment) is then transferred onto the Morlet phase function and the value of phase at each time t is read along the curve. The value of phase (−π: π) is then computed in each image pixel and time point and plotted as a color-coded value (Fig. 5d–f). This method reveals spiral wave cores that are seen as the spatial points in which all rainbow colors come together even in very noisy data, where interaction of multiple unstable spiral waves makes it impossible to directly observe contiguous spirals by eye.

Change in the wave pattern of cortical dynamics observed throughout the cell cycle prompted us to introduce the activity ratio, an easily computable from experimental data heuristic measure of the fraction of full period that the system spends in the excited state. To compute the activity ratio in space (Supplementary Figures S6b,c), the average, value of the normalized signal of Rho or F-actin is computed first along the i-th line of the data kymograph. The data is then converted to 1 if the pixel value is above the average and to 0 if below. Activity ratios are then computed as shown in Supplementary Figure 6b for every spatial period and averaged along the i-th line of the kymograph. This value is the activity ratio at time t (Supplementary Figure 6c). Larger statistics was obtained by averaging over multiple kymographs. As shown in Supplementary Figure 6, thus defined activity ratio is easily computed even from noisy experimental data and can be readily compared with the behavior of the model (see below).

Modeling

The model (Fig. 8a,b) consists of three reaction-diffusion equations representing dynamics of active (RT) and inactive (RD) Rho²⁰ as well as the density of polymeric F-actin (F) that does not diffuse. Diffusion of RT and RD is explicitly represented by the diffusion terms D_RT ΔRT, D_RDΔRD, where Δ is the Laplace operator. The numbers on the reaction arrows in Figure 8a (shown in curly braces { } below) correspond to the numbers of the reaction rate constants in Figure 8b (values given in Supplementary Figure 6a). In our model, we explicitly consider only the dynamics of membrane bound active and inactive forms of Rho and assume that the inactive form, RD, is freely exchanging with a constant large pool in the cytoplasm ({5} k₅, {6} −k₆RD). Reaction term R describes nucleotide cycling of Rho and includes activation of Rho potentially by several GEFs ({0} k₀RD) of which GEF activity of Ect2 is singled out explicitly ({1,2,11} $[\text{Ect}2]R{T}^{2}RD/(k_2^2+R{T}^2)$, $[\mathit{Ect}2]={[\mathit{Ect}2]}_0{k}_1\cdot (1+k_{11}RT)$) to highlight the autocatalytic character of Rho activation by means of Ect2. Inactivation of Rho is assumed to be both constitutive ({3} −k₃RT) and F-actin-dependent ({4} –k₄F·RT), the latter term reflects F-actin mediated negative feedback to the activity of Rho. F-actin polymerization is a weak constitutive process in the absence of Rho activity ({7} k₇) and is significantly stimulated by the active Rho ({8,9} $k_{8}R{T}^2/(k_9^2+R{T}^2)$). Depolymerization of actin, for simplicity, is taken to be an unregulated first order reaction ({10} −k₁₀F). Molecular fluctuations that are necessary for the induction of excitable dynamics are taken into the consideration by the stochastic term dW(σ,s) that denotes spatially-distributed Gaussian white noise with mean 0, standard deviation σ and spatial correlation length s. Unknown membrane diffusion coefficients of active and inactive Rho, D_RT, D_RD, were varied in the ranges shown (Supplementary Figure 6a). Other model parameters were chosen to fit the dynamics observed experimentally in starfish cells. In particular, the model reproduces the characteristic wavelength and the temporal period of excitable dynamics as well as the time delay between the Rho and F-actin maxima.

To model wave dynamics observed in starfish oocytes between consecutive M-phases (Figs. 8c–e, Supplementary Figure 6c), it was assumed that temporal activity of Ect2 is governed by a Gaussian function $TG(t)={[\mathrm{Ect}2]}_0(1+exp(-{(t-t_0)}^2/2{\tau }^2)$, where t₀ and τ = 80 sec were estimated from the imaging data. To simulate furrow formation in mitotic starfish cells (Fig. 8f,f′), Ect2 temporary activity given by TG(t) was assumed to be further modulated by a spatially-dependent term $SG(x,t)=\exp {(-x-x_0)}^2/2\beta {(t)}^2$, where x is the spatial dimension that spans the pole to pole distance L of a mitotic cell and β(t) decreases linearly in time from L to l_f = 7 μm, the furrow width estimated from the data. To simulate depolymerization of microtubules by nocodazole (Fig. 8g,g′), Ect2 concentration profile was rapidly relaxed to a spatially uniform distribution with equivalent total quantity of Ect2. Model reaction-diffusion equations were solved with standard forward Euler finite-difference method using custom-developed C code.

All computer codes generated in this study are freely available from the authors upon request.

Reproducibility of Experiments

All of the results reported were replicated at least three times to ensure repeatability; the basic results—eg. Ect2-amplifiable actin and Rho waves—were replicated 60 or more times. The only issues with reproducibility arose when probes were under or over expressed or when too much Ect2 was expressed (this resulted in contractions that were either too extreme to film or which resulted in cell lysis). The specific number of repeats is indicated in each figure legend.