Three-Dimensional QSAR Analysis and Design of New 1,2,4-Oxadiazole Antibacterials

Abstract

The oxadiazole antibacterials, a class of newly discovered compounds that are active against Gram-positive bacteria, target bacterial cell-wall biosynthesis by inhibition of a family of essential enzymes, the penicillin-binding proteins. Ligand-based 3D-QSAR analyses by comparative molecular field analysis (CoMFA), comparative molecular shape indices analysis (CoMSIA) and Field-Based 3D-QSAR evaluated a series of 102 members of this class. This series included inactive compounds as well as compounds that were moderately to strongly antibacterial against Staphylococcus aureus. Multiple models were constructed using different types of energy minimization and charge calculations. CoMFA derived contour maps successfully defined favored and disfavored regions of the molecules in terms of steric and electrostatic properties for substitution.

The profligate use of antibiotics has accelerated not just the evolution of antiobiotic resistance, but also the epidemiological landscape, of both the Gram-positive and Gram-negative bacteria. Among the many examples of this transformation is the transition of the β-lactam antibiotic-resistant Gram-positive pathogen Staphylococcus aureus from the hospital into the community.^1–4 The breadth and the rapidity of this transformation (and others like it) have been suggested to correspond to the dawn of a post-antibiotic era.⁵ This credible—and no less fearful—prospect has engendered numerous strategic proposals to push back this dawn,^6–10 including especially the importance of the discovery of new antibacterial structure^{11, 12} and the provision of new economic incentives to revitalize commercial antibacterial development.^13–15 Here, we provide an overview of our extensive effort to systematically probe the structure-activity relationship of a new class of 1,2,4-oxadiazole antibacterials with unprecedented anti-Gram positive activity.

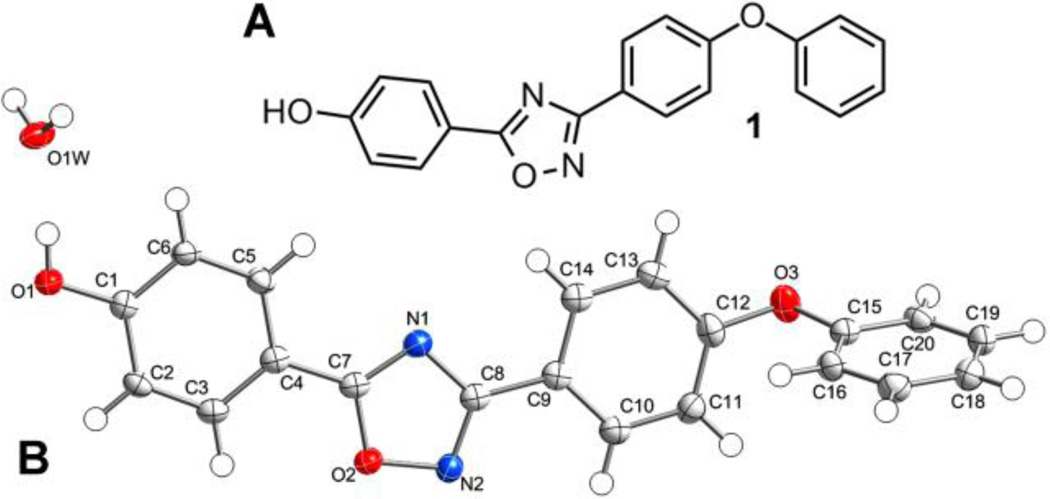
Through computational docking and scoring procedures carried out in our laboratory, we discovered the class of 1,2,4-oxadiazole antibiotics active against Gram-positive bacteria, including S. aureus.¹⁶ This antibiotic class inhibits bacterial cell-wall biosynthesis by targeting the function of the penicillin-binding proteins (PBPs). The lead compound (1, Figure 1A) was the basis for extensive structure-activity analysis.^{17, 18} Here, we use the results of this effort to build a three-dimensional quantitative structure-activity relationship (3D-QSAR) model for these compounds in order to assist the design of novel analogues with improved activity.

Figure 1.

(A) Chemical structure of antibiotic 1; (B) the ORTEP structure for the crystal structure of 1 shown at 50% probability level. H atoms are shown as spheres of arbitrary radii.

The 3D-QSAR methods rely on the principle that the three-dimensional geometric and electronic features of molecules correlate with their biological activities.¹⁹ 3D-QSAR plays an important role in the optimization of pharmacologically active compounds and in the prediction of the biological activity of newly synthesized compounds.²⁰ Cramer has elegantly captured the reasons behind a QSAR renaissance for ligand-based design.²¹ Comparative molecular field analysis (CoMFA)²² aligns molecules in a three-dimensional lattice and calculates their steric (Lennard-Jones potential) and electrostatic (Coulomb potential) molecular descriptors. These CoMFA descriptors can be used to build a partial least squares (PLS) statistical model that correlates the molecular structures with the biological activity. Comparative molecular shape indices analysis (CoMSIA) incorporates hydrophobic and hydrogen-bond donor/acceptor descriptors in addition to steric and electrostatic descriptors. Contour maps obtained from CoMFA calculations identified favored and disfavored regions of the lead oxadiazole compound in terms of steric and electrostatic properties for further lead optimization. Based on the investigation, recommendations for the design of new oxadiazole analogs are proposed.

The performance of the standard CoMFA and CoMSIA procedures requires the specification of both the conformations and alignments of the molecules. All of our structures were superimposed onto the X-ray crystal structure of 1 (Figure 1B). Selection of appropriate and accurate methods to assign partial charges of each atom in a molecule is a critical step in QSAR study. Energy minimization with different charge methods is required to create robust CoMFA and CoMSIA models.²³ Molecular mechanics (MM) methods are most commonly used to derive molecular charges for CoMFA and CoMSIA calculations. We first used the standard Tripos Molecular Mechanics force field to determine the Gasteiger-Hückel charges. Our second method applied the Powell method via the Merck Molecular Force Field and added MMFF94 charges to the molecular dataset.²⁴ This method has been given increasing attention as a more accurate general-use empirical partial charge method.²³ In order to further improve the accuracy, a third method used quantum-mechanical charge calculation to introduce restrained electrostatic potential (RESP) charges.²⁵ The molecular alignments for the compounds that were energy minimized containing Gasteiger-Hückel and QM charges are shown from two different viewpoints (Figure S2 in the Supporting Information). Additionally, Field-Based QSAR, a 3D-QSAR method developed by Schrödinger Inc., was also used.

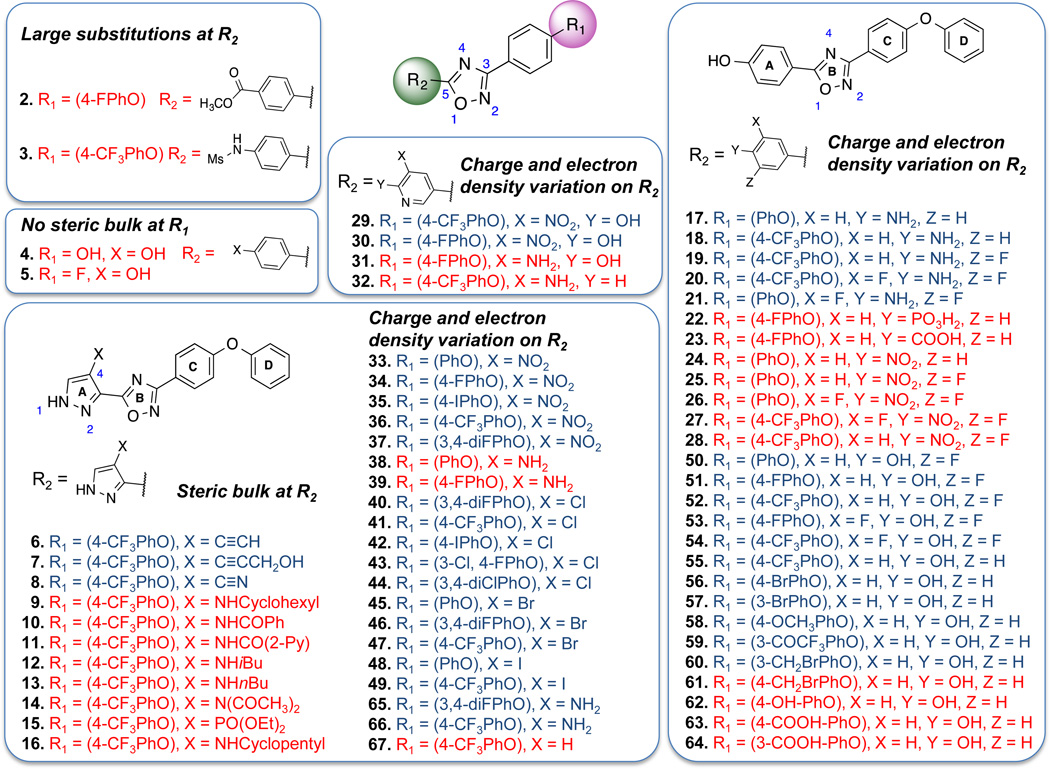
The dataset of 102 synthetic oxadiazoles was randomly divided into a training set of 77 compounds and a test set of 25 compounds (see Figure 2 for a representative set of compound structures and Table S1 in the Supporting Information for full set of compounds). Both sets represent equally well the chemical and biological properties of the entire data set, as per recommendations of Golbraikh et al.²⁶ The measurement of antibacterial activity was expressed as pMIC (pMIC = −log_e(MIC/MW), where the MIC values were experimental ones determined against S. aureus. The compounds in our data set represent an activity range of greater than five log units, from a minimum pMIC of 0.63 (least active) to a maximum pMIC of 7.4 (most active). Data analysis by PLS regression linearly correlated CoMFA and CoMSIA values with the calculated field descriptors as independent variables and the pMIC values as dependent variables.²²

Figure 2.

Representative 1,2,4-oxadiazole structures of the 102 compound set, demonstrating the molecular diversity used in the analyses. Compound activity was assessed by MIC determinations against a standard, methicillin-sensitive strain of S. aureus (ATCC 29213). Active compounds (MIC ≤ 8 µg/ml) are in blue letters, while inactives (MIC > 8 µg/ml) are in red letters. The pMIC value of 1 is 5.8. This figure includes all of the compounds more active than 1. These compounds are 6 (pMIC = 7.4, the most active compound of the entire series), 18, 34, 40, 41, 42, 44, 45, 46 and 55. The complete dataset of structures and biological activity is given as Table S1 of the Supporting Information.

The dataset with Gasteiger-Hückel charges was first analyzed by CoMFA. The training set provided a cross-validation correlation coefficient q² of 0.52 with the leave-one-out method (LOO) to evaluate internal predictive quality.^27,28 A non-validated r² value of 0.82 was obtained using five components (see Table 1), thus demonstrating a satisfactory level of internal predicting power.²⁹ However, Golbraikh and Tropsha state that q² alone is not sufficient for reliable predictive power. The only way of validating predictive power reliably is by the use of an external test set.^{27, 29, 30} The activity values for the predictive compounds (the test set) gave an r²_pred of 0.55, thus indicating a reasonable predictive power of the model. This predicted r² assesses the robustness of the QSAR model. A graph of the experimental versus the residual values showed that the residual values were mostly lower than the standard error of estimate (SEE) of 0.90, as a measure of the accuracy of the predictions (see Figure S3-B in the Supporting Information).

Table 1.

Statistical results for CoMFA, CoMFA + cLogP, CoMSIA and Field-based QSAR

	CoMFA			CoMFA + cLogP			CoMSIA			Field-based QSAR
										force field			Gaussian
charge calculation	GH	MM FF 94	QM	GH	MM FF 94	QM	GH	MMF F 94	QM	GH	MMF F 94	QM	GH	MM FF 94	QM
Values
q2a	0.52	0.70	0.52	0.55	0.71	0.60	0.63	0.66	0.46	0.64	0.68	0.32	0.55	0.61	0.47
r2	0.82	0.85	0.88	0.83	0.85	0.89	0.90	0.90	0.75	0.91	0.92	0.73	0.88	0.90	0.72
SEEb	0.90	0.84	0.72	0.88	0.82	0.71	0.70	0.69	1.01	0.64	0.62	1.05	0.75	0.86	1.06
nc	5	5	6	6	6	7	7	6	3	6	6	4	7	5	3
F-test	66.2	77.6	74.8	57.8	68.3	66.3	83.9	103.5	65.2	120.5	130.3	43.4	72.1	73.1	56.1
r2pred	0.55	0.77	0.61	0.31	0.44	0.56	0.61	0.58	0.39	0.68	0.74	0.14	0.68	0.69	0.22
Field distribution %
steric	35.6	37.1	39.9	35.0	35.0	37.4	6.6	7.6	8.5	34.1	33.1	40.0	32.0	35.4	36.2
electrostatic	64.4	62.9	60.1	60.2	59.6	58.4	32.0	34.4	33.4	65.9	67.9	60.0	13.2	12.5	9.2
cLogP				4.8	4.5	4.2
hydrophobic							16.3	13.7	10.7				15.5	13.5	20.2
donor							26.5	26.5	32.6				23.4	24.9	16.8
acceptor							17.4	17.9	14.8				15.9	13.6	17.7

^aq² from the Leave-One-Out

^bStandard error of estimate

^cOptimum number of components

3D-QSAR CoMFA analysis of the data set with empirical MMFF94 charges was generated in an identical manner. The cross-validated q² value of 0.70 for the same training set improved in comparison to the one obtained with Gasteiger-Hückel charges (q² = 0.52), whereas the non-validated r² value (0.85) was in the same range. Analyzing the test set by the model gave a much higher r²_pred of 0.77 (see Table 1, and Figure S4 in the Supporting Information).

More complex ab initio quantum-mechanical charge calculations were carried out in an effort toward improvement of the accuracy to describe molecular interactions. The RESP method (ab initio energy minimization of structures at the Hartree-Fock level, using the 6–31G(d) basic set) was used to determine the electrostatic charges. Gaussian 09 performed these calculations, and the antechamber module of Amber 12 applied the derived RESP changes. The internal cross-validation q² (0.52) and the non-validated r² value (0.88) were similar to those with the empirical Gasteiger-Hückel charges (q² = 0.52, r² = 0.88). Validation using the test set of 25 compounds gave an acceptable r²_pred value of 0.61 (see Table 1 and Figure S5 in the Supporting Information).

Based on previous reports that the inclusion of hydrophobic properties could improve a QSAR model, the value of including LogP as an added descriptor was assessed.³¹ When cLogP (CambridgeSoft ChemBioDraw Ultra 2010, 12.0) was introduced as a lipophilicity molecular descriptor, the model carrying Gasteiger-Hückel charges improved slightly from a q² value of 0.52 and an r² value of 0.82 to a q² of 0.55 and an r² of 0.83, respectively (see Table 1). However, the r²_pred value of the test set decreased from 0.55 to 0.31. For the model with MMFF94 charges, adding cLogP as an extra descriptor gave an inconsequential improvement for q² (from 0.70 to 0.71). At the same time, r²_pred value decreased drastically from 0.77 to 0.44 for the test set, indicating reduced predictive ability. For the model using QM charges and cLogP, the q² and r² values improved to 0.60 and 0.89 in comparison to 0.52 and 0.88, respectively. The r²_pred value of 0.56 was slightly lower than that for the model without the use of cLogP (0.61). The models with cLogP required additional PLS components. Cramer and Wendt indicate that small improvements of q² as a result of incorporating cLogP is offset by the increase in PLS components.³⁰ These results indicated that the addition of a cLogP descriptor did not give improved models.

We applied a second method, CoMSIA, which incorporates hydrophobic and hydrogen-bond donor/acceptor features in addition to steric and electrostatic descriptors. For the CoMSIA method with Gasteiger-Hückel charge calculation, better results were achieved in comparison with CoMFA. However, this model required additional PLS components. The CoMSIA analysis for the same training and test sets using MMFF94 charges (q² = 0.66, r² = 0.90; n = 6) gave comparable results to the CoMFA analysis (q² = 0.70, r² = 0.85; n = 5). The predicted r² for CoMSIA was lower (r²_pred = 0.58) than the one obtained with CoMFA (r²_pred = 0.77), indicating that CoMFA had more predictive ability. The quantum-mechanical results for the CoMSIA analysis produced less satisfactory results in comparison to CoMFA.

Field-Based QSAR (Schrödinger Inc.) is a 3D-QSAR approach similar to CoMFA/CoMSIA but uses different parameters.³² In the force-field method of this approach, the ligands were given Lennard-Jones steric potentials from OPLS2005 force field and previously calculated atomic charges for the electrostatic properties. For the Gaussian method, molecular hydrophobicity was determined according to Ghose et al. via ALOGP and CLOGP methods.³³ Hydrogen-bond donor and hydrogen-bond acceptor pharmacophore features were provided by PHASE. The CoMFA and CoMSIA models with Gasteiger-Hückel and MMFF94 charges were compared to force field and Gaussian methods, respectively. As seen in Table 1, the MMFF94 charge calculations provided the best model for the force field as well as for the Gaussian method with q² values of 0.68 and 0.61, non-validated r² of 0.92 and 0.90, and r²_pred of 0.74 and 0.69, respectively. The model carrying Gasteiger-Hückel charges also resulted in good values for both the force field (q² = 0.64, r² = 0.91, n = 6) and the Gaussian approach (q² = 0.55, r² = 0.88, n = 7). Results for models that used quantum-mechanical charges were less satisfactory than the other two models.

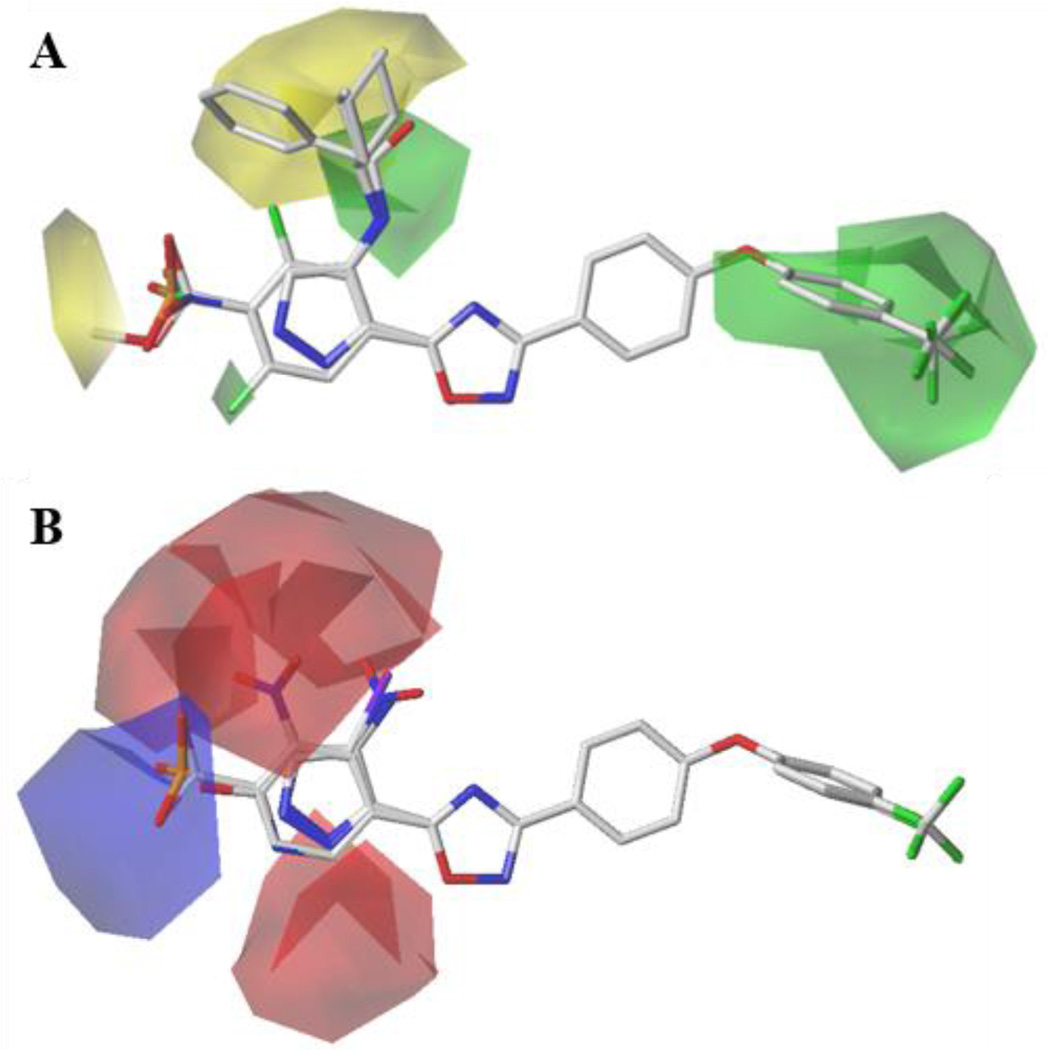
The graphic representation of CoMFA contour maps in 3D space was created using the data from the PLS analysis. With these maps, the steric and electrostatic features of the compounds were analyzed. The steric CoMFA map indicates the areas where steric bulk is favored (green contours) or disfavored (yellow contours), as shown in Figure 3A. The electrostatic contour map is shown in Figure 3B. The blue polyhedrals represent favorable regions for electropositive substituents, and the red polyhedrals represent favorable regions for electronegative substituents. The two sub-classes of compounds, i. e. the 5-phenyl- and 5-(pyrazol-3-yl)-substituted 1,2,4-oxadiazoles, contributing to this model were examined (see Figure S1).

Figure 3.

(A) CoMFA steric contour maps: Green contours represent steric-bulk-favored region and yellow contours show steric-disfavored position. (B) CoMFA electrostatic contour maps: Blue maps display favorable regions for electropositive substituents, while the red polyhedrals show favorable regions for electronegative substituents. The generation of a single map encompassing the phenyl- and pyrazolyl-substituted oxadiazoles (superimposed at the far left) supports the selection of the pyrazolyl rotamer that is shown in this Figure as the biologically active conformation.

Compounds in the training set were initially analyzed to identify the features of the antibiotic activity in relation to the maps. For the 5-phenyl-1,2,4-oxadiazoles, large substitutions at the para-position of the phenyl ring are not tolerated, as indicated by the yellow contour. For example, both 2 (p-CO₂Me) and 3 (p-NHSO₂Me) are inactive. This map also suggests that a steric feature is favored at the 3-phenoxyphenyl group of the 1,2,4-oxadiazole (R₁ position), as shown by the green contour. This conclusion is supported by the inactive compounds that lack this ring (4, and 5). The small green contour at position 4 of the 5-(pyrazol-3-yl)-1,2,4-oxadiazoles indicates that steric substitutions are preferred close to that region, as exemplified by the iodo-substituted active compounds 48 and 49. However, further increasing the bulk at the same position, and thus extending substitutions to the steric-disfavored yellow map region in the vicinity, is proposed to be detrimental to the activity. This suggestion by the model is corroborated by inactive compounds with bulkier substitutions (9, 10, 11, 12, 13, and 14).

Furthermore, electrostatic features were visualized by blue and red contours, which indicate favorable electropositive and electronegative groups, respectively (Figure 3B). When 5-phenyl-1,2,4-oxadiazoles were analyzed, a blue contour was observed close to the para-position of the phenyl ring, which recommends positively charged substitutions to enhance antibacterial activity. 5-(4-Aminophenyl)-1,2,4-oxadiazoles (17, 18, 19, 20, and 21) follow this trend. Accordingly, compounds 22, 23, 24, 25, 26, and 27, which carry high partial negative charge in this region, are inactive. At the ortho- and meta-positions of the phenyl ring, red contours indicate that increased electron density improves activity. Therefore, compounds with higher electron density like meta-NO₂ (29 and 30) are active, while substitution with meta-NH₂ group make 31 inactive. Similarly, for 5-(pyrazol-3-yl)-1,2,4-oxadiazoles, substitution with NO₂ group is favored at the 4-position of the pyrazole ring, and thus the compounds 33, 34, 35, and 36 are active. Replacing NO₂ group with NH₂ (compounds 38 and 39) is detrimental to the activity, thus demonstrating unfavorable positive charge at this position.

Analysis of the compounds in the test set reveal that the features of the map correlated well with their respective activities. Acetylene functionality of 4-acetylene-substituted 5-(pyrazol-3-yl)-1,2,4-oxadiazole 6 favorably occupies the small steric map region and shows good activity. Active compounds 7 and 8 also fit well in the steric-favored contour map. At the same time, compounds with bulkier diethyl phosphonate (15) and cyclopentane (16) substitution in this region extends to the steric disfavored yellow contour map and were inactive. Compound 37 with nitro substitution at this position was active, as supported by the red contour map in the vicinity. As just noted, the positively charged amine substitution of compound 38 is against the recommendation made by the maps, and results in loss of activity. The 5-phenyl-1,2,4-oxadiazole derivative 28 with the nitro substitution at the para position of the phenyl ring (ring A) was inactive. Our model recommends positive charge at this position. Electropositive amine substitution at the meta-positions of the phenyl ring renders 32 inactive.

Analogous steric and electrostatic contour maps for CoMSIA were generated (shown in Figure S7A and S7B in the Supporting Information). The CoMSIA hydrophobic contour map (Figure S7E) revealed hydrophilic preference around the 5-phenyl and 5-(pyrazol-3-yl) ring of the 1,2,4-oxadiazole for increasing activity. Indeed, compounds like 9, 12, 13, and 16 have hydrophobic groups in this region, and they are inactive. However, the hydrophobic contour map at the 3-phenoxyphenyl region did not correlate with the activity of the compounds. Similarly, hydrogen-bond donor/acceptor maps (see Figure S7C and S7D) failed to provide a satisfactory explanation of the activities.

Supported by these analyses, we formulated guidelines toward the synthesis of analogues of 5-phenyl- and 5-(pyrazol-3-yl)-substituted 1,2,4-oxadiazoles with improved biological activity. The CoMFA steric and electrostatic contour maps of the model generated with MMFF94 charges were used to identify different regions on the molecular template, where any changes could alter the biological activity of the compounds. At the 3-position of the 3-phenyl-1,2,4-oxadiazole (R₁), a bulky para-substituent is favorable for the activity, as indicated by the steric contour map. Compounds with small substituents like hydroxyl (4) or fluoride (5) at this position are inactive. An aromatic ring at this position (ring D, see Figure 2) appears to be critical for activity. Activity is mostly retained by substitution of F, Cl, I and CF₃ at the meta- or para-positions of this phenyl ring of the 4-chloro (40, 41, 42, 43 and 44), 4-bromo (45, 46, and 47), and 4-iodo (48 and 49) (pyrazol-3-yl)-1,2,4-oxadiazoles. A similar observation can be made for 5-phenyl-1,2,4-oxadiazoles 50, 51, 52, 53, 54, and 55. In addition, compounds 56 and 57 show that meta- or para-bromo substitutions were also acceptable. CoMFA green contour map towards the meta- and para-position suggest that bulkier groups can be accomodated at this region. This is exemplified by methoxy (58), trifluoroacetyl (59) and meta-bromomethyl (60) substitutions at this region. However, contrary to this recommendation, para-bromomethyl (61) analog was inactive. Loss of activity was also observed for hydroxyl (62), and carboxylic acid (63 and 64) substitutions. CoMFA steric or electrostatic maps were unable to rationalize these activities.

For the 5-phenyl-1,2,4-oxadiazoles, large substitutions at the para-position of the phenyl ring (ring A, see Figure 2) are not tolerated as indicated by compounds 2 and 3. At the same position, positively charged substitutions like an amine group (17, 18, 19, 20, and 21) are favored by the CoMFA electrostatic map. For the same reason, the nitro group and negatively charged carboxylate at this position (22, 23, 24, 25, 26, and 27) rendered the compounds inactive. At the ortho- and meta-positions of the phenyl ring, or at the 3- and 4-positions of the pyrazole ring, the CoMFA electrostatic map recommended negatively charged or electron-dense substitutions. Thus the NO₂-substituted compounds (29, 30, 33, 34, 35, 36 and 37) were active, while the amino-substituted compounds (31, 32, 38 and 39) were inactive. However, compounds 65 and 66 did not follow this trend. Bulky substituents like cyclohexyl, cyclopentyl or benzamide at the 4-position of the 5-(pyrazole-3-yl)-1,2,4-oxadiazoles are not favored (9, 10, 11, 12, 13, 14, 15, and 16). On the other hand, smaller substituents are recommended by the maps at the same place. The importance of substitution at this position is exemplified by the unsubstituted compound (67), which is inactive compared to chloro-, bromo-, or iodo- substituted analogs (41, 47 and 49 respectively).

A limitation of these calculation is their use of MIC values as the experimental biological descriptor. MIC values represent the sum of separate biological contributors such as penetration through the cell wall or the collective interaction within the many members of the family of penicillin-binding proteins, the target enzymes of these antibiotics. But since PBPs are found at the surface of the outer leaflet of the membrane of Gram-positive bacteria, the compounds need only to diffuse through the cell wall to reach their target. The compounds do not need to pass through the membrane. Diffusion through the cell wall for these small molecules may not be strongly dependent on structure (within this antibiotic class). Similarly, if inhibition of a single PBP (out of the five found in MRSA), for example PBP2a, is the critical biological target, this conclusion is even more reasonable. These observations bolster confidence in the models studied in this report as foundational for the future design of more potent antibacterials within this class.

Abbreviations

CoMFA

comparative molecular field analysis

CoMSIA

comparative molecular shape indices analysis

GH

Gasteiger-Hückel

LOO

Leave-One-Out method

MIC

minimum inhibitory concentration

MM

molecular mechanics

MMFF94

Merck Molecular Force Field 94

PLS

partial least squares

QM

quantum mechanical

SEE

standard error of estimate