Abstract
The accurate diagnosis of Alzheimer’s disease (AD) at different stages is essential to identify patients at high risk of dementia and plan prevention or treatment measures accordingly. In this study, we proposed a new AD staging method for the entire spectrum of AD including the AD, Mild Cognitive Impairment with and without AD conversions, and Cognitive Normal groups. Our method embedded the high dimensional multi-view features derived from neuroimaging data into a low dimensional feature space and could form a more distinctive representation than the naive concatenated features. It also updated the testing data based on the Localized Sparse Code Gradients (LSCG) to further enhance the classification. The LSCG algorithm, validated using Magnetic Resonance Imaging data from the ADNI baseline cohort, achieved significant improvements on all diagnosis groups compared to using the original sparse coding method.
I. Introduction
Alzheimer’s disease (AD) is the most common neurodegenerative disorder among aging people and its dementia symptoms gradually deteriorate over years. AD usually develops in 3 stages as the pathology evolves from cognitive normal (CN) through mild cognitive impairment (MCI) to dementia. MCI represents the transitional state between AD and CN with a high conversion rate to AD. There are 40% MCI patients from the Alzheimer’s Disease Neuroimaging Initiatives (ADNI) [1] baseline cohort converted to AD within two years, whereas only 3.9% for normal aging subjects developed AD during the same period [2]. The accurate diagnosis of AD at different stages, especially the early detection, is important in identifying subjects at high risk of dementia, thereby taking appropriate intervention or prevention measures accordingly.
Neuroimaging, such as Magnetic Resonance Imaging (MRI) and Positron Emission Tomography (PET), is a fundamental component in the diagnosis of AD and MCI, and also an important indicator in disease monitoring and therapy assessments. A variety of neuroimaging-based classification methods in AD and MCI have been proposed [3–7]. Most of current studies of AD and MCI simplified the classification problem into two-class classification problems, i.e., AD vs. CN [3–6] and/or MCI vs. CN [4–7]. However, the staging of AD is indeed a multi-class classification problem leading to the necessity of the investigation of whole spectrum of AD, i.e., AD, MCI and CN subjects need to be identified in a single setting. The MCI subjects could be further classified into two subgroups, MCI converter (cMCI) and MCI non-converter (ncMCI), depending on whether they developed into AD in the short term (usually 0.5 to 3 years). The classification of AD, CN and MCI (ncMCI and cMCI) is challenging because there are more interferences in a multi-class model than in a two-class model.
There are several studies [8–11] on multi-class classification in AD, cMCI and ncMCI. These studies were conducted in the same fashion. The features were first extracted from the neuroimaging data, usually MRI [8–11] and/or PET [9], and sometimes combined with others biomarkers, e.g., cerebrospinal fluid (CSF) measures [9], genetic biomarkers [10] and clinical assessment scores [10]. The concatenated features [11] or a subset of the features selected using feature selection algorithms, e.g., feature selection based on stability of sparse codes [10], were subsequently used to train the classifiers, e.g., support vector machines (SVM). Finally, the derived classifiers were used to solve the classification [8, 9] or detection [10, 11] problems.
We believe the workflow of the above-mentioned studies could be optimized in two ways. 1) Instead of concatenating the multi-modal/multi-view features into a high dimensional feature vector or selecting a subset of features to represent the subjects, we may embed the high dimensional multi-modal/multi-view features into a low dimensional space. Such embeddings may reduce the complexity of high dimensional feature space without discarding less important features. 2) The classifiers, e.g., SVMs, enforce the global consistency and continuity of the boundaries and ignore the local classification. However, we believe we could incorporate such local information in addition to the subject’s feature values to further enhance the classification. For example, the oriented gradient in a subject’s local neighborhood could reveal the most possible change of the subject over time and help to classify the subject with stronger confidence.
Therefore, in this study, we proposed a new multi-class classification enhancing method for the entire spectrum of AD based on the Localized Sparse Coded Gradients (LSCG) incorporating the information of the subjects’ local neighborhoods. This method is capable of integrating multi-view features to form a more distinctive representation than the naive features, and also could automatically update testing set based on LSCG. The proposed method was validated on 4 diagnosis groups from the ADNI baseline cohort and it showed a great potential to enhance the AD staging.
II. Methods
A. Neuroimaging Data Pre-processing
The neuroimaging data used in this work were obtained from the ADNI database (adni.loni.ucla.edu) [1]. In total, 331 subjects were randomly selected from the ADNI baseline cohort, and a T1-weighted volume acquired on a 1.5 Tesla MR scanner was retrieved for each subject. The sample dataset included 85 AD cases, 169 MCI cases and 77 cognitive normal subjects. The MCI group was further divided into two sub-groups. There were 67 MCI subjects converted to AD in half to 3 years from the first scan, and they were considered as the MCI converters (cMCI). The other 102 MCI subjects in the MCI group were then considered as the non-converters (ncMCI).
All ‘raw’ 3D MRI data were converted to the ADNI format following the ADNI MRI image correction protocol [11]. We then nonlinearly registered the MRI images to the ICBM_152 template [12] using the Image Registration Toolkit (IRTK) [13]. We mapped 83 brain structures in the template space using the multi-atlas propagation with enhanced registration (MAPER) approach [14] on each registered MRI image.
B. Feature Extraction
Three types of features extracted from multi-views were used in this study including the Grey Matter (GM) volume, solidity and convexity. The grey matter volume features of 83 brain regions were extracted from each registered MRI image as the representations in the first view for the ith image. We further normalized the for each brain region (indexed by j) by the volume of the brain mask as a fraction of the whole brain.
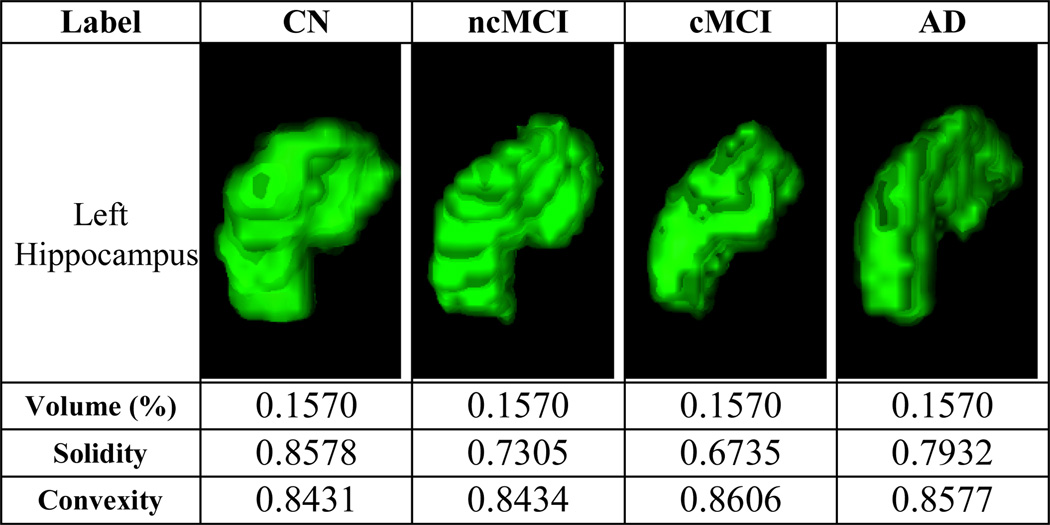
While the GM volume feature had been widely used in many studies [2–6], it was not reliable due to anatomical variability between subjects. Figure 1 shows 4 examples from the 4 diagnosis groups of the same brain region, the left hippocampus, which is an important biomarker in AD. The GM volume features were not able to distinguish the differences between the 4 subjects, because the GM volume values were identical, although the AD subject presented clear atrophy. Therefore, we proposed two other features, the convexity and solidity in addition to the GM volume features. Both convexity and solidity required the convex hull. The was defined as in the ratio of the convex hull surface area to the surface area of jth region of interest; and the was the ratio of the volume of jth region of interest to the volume of the convex hull. The convexity and solidity provided the complementary information to the volume features in describing the brain region atrophy. Figure 1 also shows the convexity and solidity values of the left hippocampus for the 4 subjects.
Figure 1.
The volume, convexity and solidity features. The 3D volume-rendered images were generated using the 3D Slicer software (Version 4.1) [15][16].
The three types of features extracted from multi-views were then concatenated to form a tripled sized feature vector, a(i) ∈ ℝ1×249, as a naive representation of each subject.
C. Sparse Auto-encoder
Given the concatenated feature vectors, a ∈ ℝM×NI (M = 331, NI = 249), we then computed the sparse codes using a sparse auto-encoder [17]. The sparse auto-encoder is a special case of the neural-network. A sparse auto-encoder has three layers, the input layer, hidden layer, and output layer. The outputs of a sparse auto-encoder are constrained to be the same as the inputs. We set such constrains to find the internal structure of the input data and thus optimally embed the original input feature space to a new feature space. Assuming a sparse auto-encoder has NH-hidden-neurons, thus the sparse codes for each input vector is .
The goal of a sparse auto-encoder is to minimize the following cost function, as in (1):
| (1) |
where â(i) is the estimated output of a(i), W1 and W2 are NI × NH and NH × NI matrices representing the weights on the neurons in conjunctive layers, ρ̂j is the average activation of jth hidden neuron, KL(*‖*) is the Kullback-Leibler divergence between two variables. We could use λ, β and ρ to control the ratios of the 3 cost functions, error cost, weight cost and sparsity cost. In this study, we solved this optimization problem through L-BFGS algorithm [18]. The sparse codes were then derived as in (2):
| (2) |
where a ∈ ℝM×NI, W1 ∈ ℝNI×NH, and aSC ∈ ℝM×NH. NI is usually set of a value smaller than NH, thus the high dimensional inputs could be embedded into a low dimensional space. Therefore the sparse auto-encoder completed multi-view feature embedding and dimension reduction simultaneously.
D. Localized Sparse Code Gradient
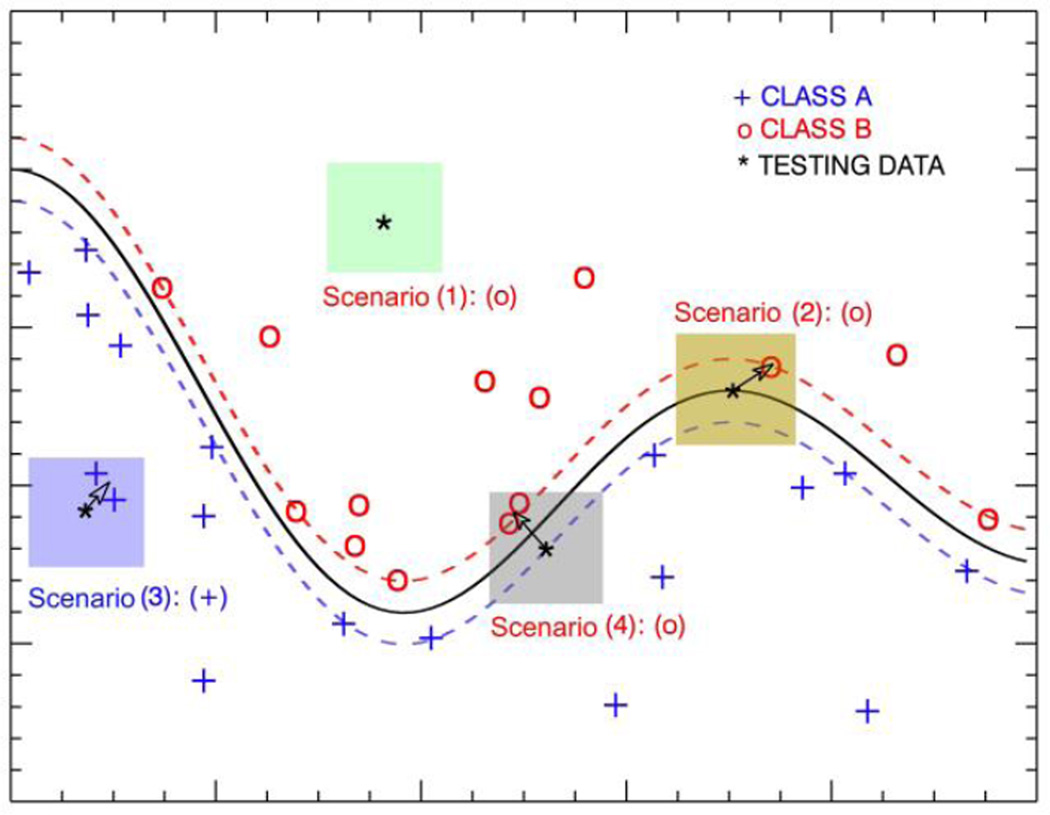
We assumed that the classification of a given case was not just based on the feature values of the subject in the feature space, but also affected by the local circumstance. Although SVM defined the hard boundaries in the kernelized space, the localized information could reduce the bias of the testing subjects near boundaries. It could be useful especially when a large number of support vectors were used in SVM. Figure 2 shows a toy example of 4 scenarios of a simple SVM. The color boxes indicate the neighborhoods. If we update the subjects’ positions in the feature space by its local gradients as indicated by the arrows, then we may retain the correct classification of scenarios (1) and (3), and increase the margin of scenario (2), and correct the classification of scenario (4).
Figure 2.
The toy examples of the 4 scenarios (shown in different color boxes) in the proposed LSCG algorithm. The localized gradients are determined by the center of gravity of the neighborhoods. Note that in scenario (1), the subject has no neighbors in the neighborhood, so the subject’s position will not change.
The sparse codes (aSC ∈ ℝM×NH) derived from the sparse auto-encoder were divided into 2 subsets, a training set with MU subjects and a testing set with MV subjects. We then modeled the localized information of given as local sparse code gradients (LSCG). In the feature space of aSC, we defined a local neighborhood space with radius of r for each subject in the testing subset, . We then detected the training subjects within the local neighborhood of . The detected formed a subset of the training subjects and we believe it could provide important local information for . We argued that the neighbors could help to reveal the circumstance of the subjects in addition to the feature values alone. We then calculated the LSCG as in (3):
| (3) |
where was the control function, and was the smallest distance between and subjects in . The control function controlled the magnitudes of the gradients to assign more weights of closer neighbors and also ensured the largest possible movement is less than the b. Finally, we update the to generate the as in (4):
| (4) |
where α is the amplitude parameter to control the overall oscillations of .
When using LSCG algorithm, the SVMs were trained with the same training set as the original sparse codes, but the testing set was updated based on LSCGs, which provide important insight of the local neighborhood and enhance the overall classification with the local information.
E. Performance Evaluation
The proposed method was validated using the entire spectrum of AD, including 331 subjects in 4 diagnosis groups, as described in Section II.A. We built a set of binary SVMs with the radial basis function (RBF) kernels as the classifiers and the average classification accuracy of 4 diagnosis groups was used to evaluate the performance of different features. A leave-50%-out 10-fold cross-validation paradigm was adopted throughout the whole process of performance evaluation. The optimal trade-off parameter (C) and the kernel parameter (γ) for SVM were estimated via grid-search. All SVM based cross-validations and performance evaluations were conducted using LIBSVM library [19].
We first evaluated the performance of the naive concatenated features and then compared the best performance of it to that of the sparse coding methods with different sparsity settings. We intuitively tested the n2 sequences with 1 < n ≤ 10, based on the assumption that the performance increased slower as the number of hidden neurons became larger. The optimal SVM settings of the desired sparse auto-encoder were inherited in LSCG evaluation, because the LSCG algorithm did not change the training set and the optimal parameter settings for SVM remained the same. Furthermore, we also used grid-search to determine the optimal radius parameter (r) and amplitude parameter (α) in the LSCG algorithm.
III. Results
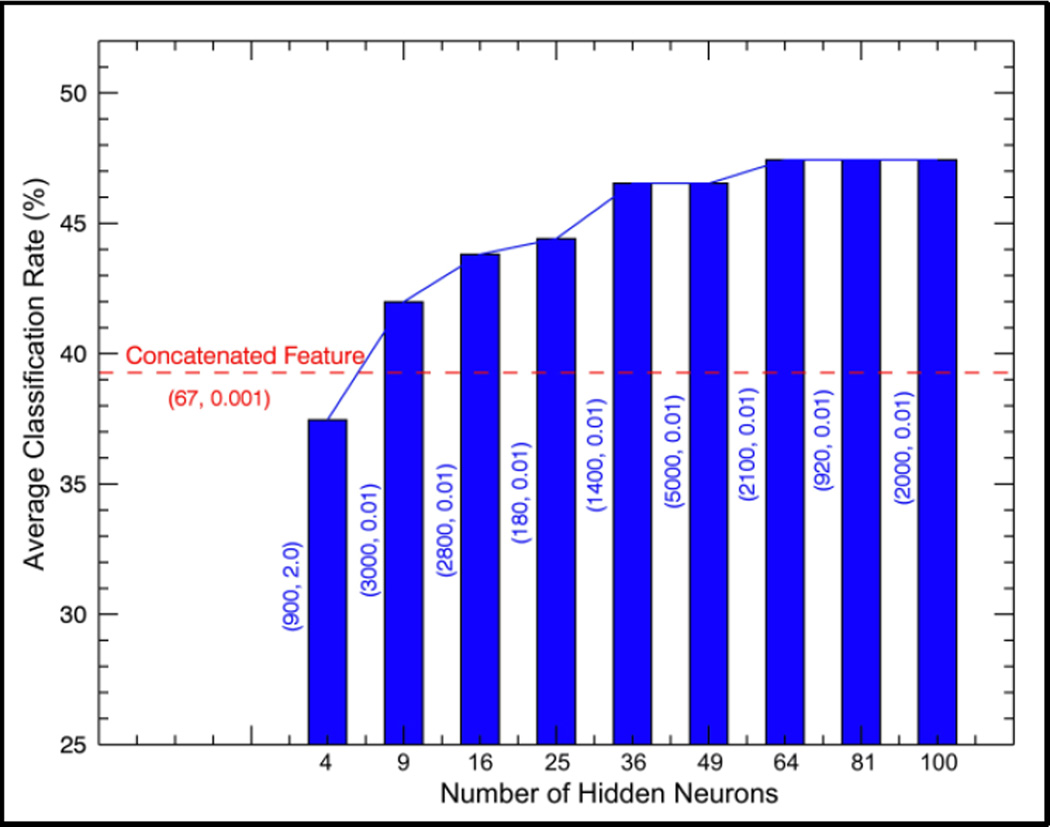
Figure 3 shows the performance of naive concatenated features and the sparse codes with different sparsity settings. The two values in each bracket represent optimal setting of C and γ in SVM with RBF kernels. The x-axis represents the number of hidden neurons, and also the dimension of the derived sparse codes. The best performance achieved by the naive concatenated features (249 dimensional) has a 10-fold cross validation average accuracy of 39.9%, as indicated by the red dashed line. When the number of hidden neurons were larger than 4, the sparse codes could outperform the naive concatenated features. This proved that sparse auto-encoder was very effective in multi-view feature embedding. In addition, when the number of neurons was set larger than 36, the performance improved slowly. Therefore, we set the number of hidden neurons in the sparse auto-encoder as 36, and then applied the optimal SVM settings (C = 1400, γ = 0.01) to the LSCG algorithm.
Figure 3.
The performance of naive concatenated features and the sparse codes with different number of hidden neurons.
Table I. shows the results of the proposed LSCG algorithm compared to the original sparse codes (SC) using the optimized RBF SVMs. The optimal parameter setting of LSCG algorithm are (α = 0.5, r = 0.21), obtained through grid-search. The LSCG method formed discriminating representations based the original SC and outperformed the original SC thoroughly. The largest improvements were achieved on CN and AD groups with an increase of 18.5% and 11.9% respectively. The cMCI and ncMCI groups also showed slight increase, yet with poor performance. The classifier had the lowest classification accuracy in cMCI, and most of the type 1 errors occur between ncMCI and cMCI.
TABLE I.
Classification rate (%) of the proposed algorithm compared to the original sparse codes (SC). Both methods were based on optimized SVM with (C = 1400, γ = 0.01).
| Algorithm | Prediction | CN | ncMCI | cMCI | AD |
|---|---|---|---|---|---|
| Diagnosis | |||||
| Original SC | CN | 44.7 | 44.7 | 5.3 | 5.3 |
| ncMCI | 27.5 | 49.0 | 13.7 | 9.8 | |
| cMCI | 11.8 | 38.2 | 26.5 | 23.5 | |
| AD | 14.3 | 16.7 | 4.7 | 64.3 | |
|
Proposed LSCG |
CN | 63.2 | 28.9 | 2.6 | 5.2 |
| ncMCI | 27.5 | 52.9 | 7.8 | 11.8 | |
| cMCI | 8.8 | 35.3 | 32.4 | 23.5 | |
| AD | 4.8 | 14.3 | 4.7 | 76.2 |
IV. Discussion
In this study, we applied the sparse auto-encoder to embed the concatenated multi-view features in a lower feature space in one step instead of two steps taken by the conventional multi-view feature embedding methods: 1) embedding the single-view features separately; and 2) concatenating the embedded features to synthesized features. This is because the sparse auto-encoder automatically updates weights towards the lowest overall cost, and requires no manual concatenation of the sparse codes of single-view features. We further proposed the LSCD to model the local information of the testing dataset based on the assumption that a large number of support vectors were used in the SVMs. When we built the SVMs for the entire AD spectrum with different settings, we found the number of support vectors varied from 70 to 140 (with 166 or 165 training subjects). This large number of support vectors enables our method to work more effectively.
V. Conclusions and future work
In this study, we present an AD staging method on the entire spectrum of AD based on the localized sparse coded gradients. This method is capable of integrating the multi-view features and optimally embedding them in a lower dimension feature space to form a more distinctive representation. The method also automatically updates testing set based on LSCGs and thereby could further enhance the AD and MCI classification. Marked improvements are achieved by the proposed method on all diagnosis groups, yet the classifications of cMCI and ncMCI are still more challenging than AD and CN. Therefore, in our future work, more efforts will be put on the MCI group and other imaging biomarkers that are able to detect the subtle functional and anatomical changes, such as PET and DTI, will be investigated.
Acknowledgments
This work was supported in part by the ARC, AADRF, NA-MIC (NIH U54EB005149), and NAC (NIH P41RR013218).
Contributor Information
Sidong Liu, Biomedical and Multimedia Information Technology (BMIT) Research Group, School of Information Technologies, University of Sydney, Australia.
Weidong Cai, Biomedical and Multimedia Information Technology (BMIT) Research Group, School of Information Technologies, University of Sydney, Australia.
Yang Song, Biomedical and Multimedia Information Technology (BMIT) Research Group, School of Information Technologies, University of Sydney, Australia.
Sonia Pujol, Surgical Planning Laboratory, Department of Radiology, Brigham and Women's Hospital, Harvard Medical School, Boston, USA.
Ron Kikinis, Surgical Planning Laboratory, Department of Radiology, Brigham and Women's Hospital, Harvard Medical School, Boston, USA.
Lingfeng Wen, Biomedical and Multimedia Information Technology (BMIT) Research Group, School of Information Technologies, University of Sydney, Australia; Department of PET and Nuclear Medicine, Royal Prince Alfred Hospital, Sydney, Australia.
David Dagan Feng, Biomedical and Multimedia Information Technology (BMIT) Research Group, School of Information Technologies, University of Sydney, Australia; Med-X Research Institute, Shanghai Jiao Tong University, China.
References
- 1.Jack CR, Bernstein MA, et al. The Alzheimer’s Disease Neuroimaging Initiative (ADNI): MRI Methods. J. Magnetic Resonance Imaging. 2008;27(4):685–691. doi: 10.1002/jmri.21049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Fan Y ADNI. Ordinal Ranking for Detecting Mild Cognitive Impairment and Alzheimer’s Disease based on Multimodal Neuroimages and CSF Biomarkers. MBIA2011. 2011:44–51. [Google Scholar]
- 3.Kloppel S, et al. Automatic Classification of MR Scans in Alzheimer’s Disease. Brain. 2008;131:681–689. doi: 10.1093/brain/awm319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Liu S, Cai W, Wen L, Eberl S, Fulham M, Feng D. Localized Functional Neuroimaging Retrieval using 3D Discrete Curvelet Transform. ISBI2011. 2011:1877–1880. [Google Scholar]
- 5.Liu S, Cai W, Wen L, Feng D. Multiscale and Multiorientation Feature Extraction with Degenerative Patterns for 3D Neuroimaging Retrieval. ICIP2012. 2012 [Google Scholar]
- 6.Iglesias JE, et al. Classification of Alzheimer's Disease Using a Self-Smoothing Operator. MICCAI2011. 2011;Part III:58–65. doi: 10.1007/978-3-642-23626-6_8. [DOI] [PubMed] [Google Scholar]
- 7.Liu T, et al. Identifying Neuroimaging and Proteomic Biomarkers for MCI and AD via the Elastic Net. MBIA2011. 2011:27–34. doi: 10.1007/978-3-642-24446-9_4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Liu S, Cai W, Wen L, Feng D. Neuroimaging Biomarker based Prediction of Alzheimer’s Disease Severity with Optimized Graph Construction. ISBI2013 [Google Scholar]
- 9.Petersen RC, Smith GE, et al. Mild Cognitive Impairment: Clinical Characterization and Outcome. Arch. Neurol. 1999;56:303–308. doi: 10.1001/archneur.56.3.303. [DOI] [PubMed] [Google Scholar]
- 10.Ye J, Farnum M, et al. Sparse Learning and Stability Selection for Predicting MCI to AD Conversion using Baseline ADNI Data. BioMed Central Neurology. 2012;12(46) doi: 10.1186/1471-2377-12-46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Shannon L, Saykin AJ, et al. Baseline MRI Predictors for Conversion from MCI to Probable AD in the ADNI Cohort. Current Alzheimer Research. 2009;6:347–361. doi: 10.2174/156720509788929273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mazziotta J, et al. A Probabilistic Atlas and Reference System for the Human Brain: International Consortium for Brain Mapping (ICBM) Phil. Trans. Royal Soc. B Biol. Sci. 2001;356(1412):1293–1322. doi: 10.1098/rstb.2001.0915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Schnabel JA, et al. A Generic Framework for Non-rigid Registration based on Non-uniform Multi-level Free-form Deformations. MICCAI2001. 2001:573–581. [Google Scholar]
- 14.Heckemann RA, Keihaninejad S, et al. Automatic Morphometry in Alzheimer’s Disease and Mild Cognitive Impairment. Neuroimage. 2011;56:2024–2037. doi: 10.1016/j.neuroimage.2011.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pieper S, Lorensen B, Schroeder W, Kikinis R. The NA-MIC Kit: ITK, VTK, Pipelines, Grids and 3D Slicer as an Open Platform for the Medical Image Computing Community. Proc. 3rd ISBI 2006. 2006;1:698–701. [Google Scholar]
- 16. www.slicer.org. [Google Scholar]
- 17.Raina R, Battle A, et al. Self-taught learning: Transfer learning from unlabeled data. ICML 2007 [Google Scholar]
- 18.Kullback S. Letter to the Editor: The Kullback–Leibler distance. The American Statistician. 1987;41(4):340–341. [Google Scholar]
- 19.Chang CC, Lin CJ. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intel. Sys. Tech. 2011;2(27):1–27. [Google Scholar]