A parsimonious statistical method to detect groupwise differentially expressed functional connectivity networks

Abstract

Group‐level functional connectivity analyses often aim to detect the altered connectivity patterns between subgroups with different clinical or psychological experimental conditions, for example, comparing cases and healthy controls. We present a new statistical method to detect differentially expressed connectivity networks with significantly improved power and lower false‐positive rates. The goal of our method was to capture most differentially expressed connections within networks of constrained numbers of brain regions (by the rule of parsimony). By virtue of parsimony, the false‐positive individual connectivity edges within a network are effectively reduced, whereas the informative (differentially expressed) edges are allowed to borrow strength from each other to increase the overall power of the network. We develop a test statistic for each network in light of combinatorics graph theory, and provide p‐values for the networks (in the weak sense) by using permutation test with multiple‐testing adjustment. We validate and compare this new approach with existing methods, including false discovery rate and network‐based statistic, via simulation studies and a resting‐state functional magnetic resonance imaging case–control study. The results indicate that our method can identify differentially expressed connectivity networks, whereas existing methods are limited. Hum Brain Mapp 36:5196–5206, 2015. © 2015 Wiley Periodicals, Inc.

INTRODUCTION

Group‐level region‐based whole brain connectivity analyses have been conducted to identify differentially expressed connectivity patterns between cohorts with different clinical or experimental conditions [Craddock et al., 2009; Fornito et al., 2013; Ginestet et al., 2014; Guo et al., 2014; Park and Friston, 2013; Shehzad et al., 2014; Zalesky et al., 2012b]. However, the high dimensionality of connectivity features and the complex correlation structure between them pose difficulties to detect the truly differentially expressed connectivity features without introducing substantial false‐positive findings. Mass‐univariate statistical analyses on connections naturally require multiple testing adjustment methods, such as family‐wise error rate (FWER) or false discovery rate (FDR), to control false‐positive findings [Simpson et al., 2013b; Varoquaux and Craddock, 2013]. Different from other types of high‐dimensional data (e.g., genomics), the correlation between connectivity features could be affected by an explicit topological structure comprised of brain areas (nodes). Ignoring such topological structure‐related correlation may lead to overly conservative multiple testing adjustments and a substantial loss of statistical power (i.e., no positive findings) [Fan et al., 2012]. There have been few attempts to investigate the topological structure of the differentially expressed connectivity features. Graph/network‐based population‐level connectivity analyses seem to be a good solution to identify differences of connections with topological structures by leveraging both statistical and graph theoretical models [Guo et al., 2014; Simpson et al., 2012; Zalesky et al., 2012b]. Graph theoretical models are often used to model brain functional connectivity networks [Braun et al., 2012; Bullmore and Sporns, 2009; Rubinov and Sporns, 2010; Simpson et al., 2011, 2013a; Simpson and Laurienti, 2015; Sporns, 2011, 2012]. The nodes/vertices in the graph represent brain areas/regions and the edges express connections between the brain areas [Rubinov and Sporns, 2010; Sporns, 2011]. Because most connectivity metrics are continuous (e.g., Pearson correlation), all edges are weighted, and the overall graph including all nodes is a weighted complete graph [Rubinov and Sporns, 2010, 2011; Zalesky et al., 2010, 2012a]. The group‐wise statistical inferences are conducted based on the weighted complete graphs.

There are mainly two types of commonly used group‐wise connectivity graph/network analysis methods: (1) global network metric‐based (GNM) methods, which first calculate graph theoretical metrics, such as “small‐worldness,” modularity, and transitivity or cross‐entropy/mutual information, for each individual, and then conduct statistical testing or regression analysis on the metrics at a group level [Marrelec et al., 2008; Rubinov and Sporns, 2010; Sporns, 2011, 2012; van den Heuvel et al., 2010] and similarly; (2) differentially expressed network (DEN) methods, such as network‐based statistics (NBS) and spatial pairwise clustering (SPC), which first perform mass‐univariate statistical analysis for each edge at the group level and next assembles the edges as a network using optimization algorithms [Zalesky et al., 2010, 2012b]. For example, the NBS method first applies a breadth‐first method to detect the network and then conducts permutation tests to adjust for multiple tests in the weak sense. Both NBS and SPC methods have been successfully applied to neuroimaging studies and yielded many interesting findings [Achard et al., 2006; Bassett et al., 2011, 2012; Fornito et al., 2012; Honey and Sporns, 2008; van den Heuvel et al., 2008, 2009] In general, the GNM method does not involve multiple testing corrections for a single graph theoretical metric, because the edges are combined into a single metric. However, the GNM results often only include overall graph theoretical properties without information of localized nodes and edges [Zalesky et al., 2010]. In contrast, the DEN method can reveal spatially specific information rather than only averaged/summarized metrics, but it requires adjustment for multiple comparisons [Fornito et al., 2013]. The NBS and SPC methods by Zalesky et al. (2010, 2012b) are two widely used DEN methods, which successfully incorporate family‐wise error control with network detection by applying permutation testing. Kim et al. (2014) conducted comprehensive comparisons of several DEN testing/detection methods and concluded that the NBS method outperforms the others, given appropriate threshold values. However, these two methods may still be subject to lack of power when the testing results contain high false‐positive noises. The noises may cause the detected networks to include many nodes and a small proportion of supra‐threshold connections such that the permutation testing results turn out to be not statistically significant.

The main contribution of this article is to present a novel method to detect DENs with greatly improved power and reduced false‐positive edges by leveraging the concept of parsimony (constraining the number of nodes). The penalized objective function (e.g., “lasso” or elastic net methods) has been widely applied to high‐dimensional data analysis because the parsimonious selection of features may greatly improve a model's reliability and reproducibility [Hastie et al., 2009]. The effects of parsimony (of nodes) are more marked when the features are edges in networks, because the number of edges is power order of the number of nodes. For example, if the detected network including n nodes and n(n − 1)/2 edges increases its size by adding one more node, then the increased network contains n + 1 nodes and n(n + 1)/2 edges with n more edges than the original network. Such increasing trends between the number of nodes and the number of edges could give rise to the power loss and high false‐positive rates for network detection, because even adding one more node (to the existing network of n nodes) by mistake could increase nα false‐positive edges and introduce other noises. Thus, we propose a parsimonious differential brain connectivity network detection method (Pard) that includes most significantly differentially expressed connectivity edges within networks with constrained number of nodes. We construct an objective function that maximizes the combined significance levels of the edges in the target networks when using the number of nodes of each network as a penalty term. The objective function can be effectively and efficiently solved by spectral graph theory models [Von Luxburg, 2007]. In addition, the detected networks reveal the topological structure of the differentially expressed edges. We apply permutation tests to control the family‐error rate in the weak sense, which is a similar strategy to the NBS method [Zalesky et al., 2010]. The detailed statistical model is introduced in Methods section, and followed by model evaluation and comparison using a simulation study and an example of analyzing resting‐state functional magnetic resonance imaging (rs‐fMRI) data.

METHODS

In many group‐level studies, we seek to answer the question whether two groups exhibit differential connectivity patterns. The general statistical test can be described as: the null hypothesis H ₀ that the two groups have no difference in connectivity vs. H_a that there are differentially expressed connectivity networks between the two groups. To conduct the statistical test, we first define the networks by Pard and then evaluate the probability of the networks assuming the null hypothesis is true (by using permutation tests). Clearly, the power and Type I error rate are greatly impacted by the network detection method and, thus, that is our main focus in this section.

Model Background

The connectivity network in neuroimaging studies is often represented by a graph with a set of nodes and edges G = {V,E}; the set of nodes V denote a set of distinct brain areas, and the edges E are the connections between those nodes. To investigate the differential connectivity expressions between two groups of subjects (e.g., controls vs. cases), two sample tests are often conducted for all edges. For example, $p_{ij}$ is the test p‐value between a pair of nodes i and j. Based on all these testing results, we obtain a |V| by |V| testing significance weight matrix $W_0=\left\{w_{ij}\right\}$ with $w_{ij}=-log(p_{ij})$. We utilize the “−log” transformation of p to express that the edges of small p‐values may contain important information and, hence, are highly weighted. In addition, we note that the empirical distribution of $-\log (p_{ij})$ often follows a Gamma distribution (with both parameters equal to 1 based on maximum likelihood estimation).

Objective Function of Network Detection

The primary goal of differential connectivity detection is to identify the significantly differentially expressed edges with well‐controlled false‐positive discovery rates. In contrast to other high‐throughput genomic or proteomic expression features, the brain connectivity features (edges) are spatially constrained by nodes and, thus, are not independent. The NBS and SPC methods have wisely used this property to select features with more power [Zalesky et al., 2010, 2012b]. We also leverage this property to construct our objective function and furthermore add a penalty term of the number of nodes. The main objective function is to search the C‐component clustering of the whole graph, denoted, ${\left\{A_c\right\}}_{c=1}^C$ where ${\cap }_{c=1}^C{A}_c=V$ and $A_c\cap A_{c\text{'}}=Ø$, which allocates most significant edges within networks of small number of nodes:

$${\text{argmin}}_{{\left\{A_c\right\}}_{c=1}^C}{\displaystyle \sum _{c=1}^C\frac{{\sum }_{i\in A_c,j\cancel{\in }{A}_c}^{}-\log (p_{ij})}{\left|A_c\right|}}$$ (1)

where $\left|A_c\right|$ represents the size (number of nodes) of the detected network cluster $A_c$. The objective function minimizes the weights of edges between the selected networks and the rest of G, which ensures the edges of heavy weights (more significant) are included in some networks rather than left between networks. Only the edges in the detected networks are included as biomarkers, and the optimization process can be intuitively considered to cover more informative/supra‐threshold edges by using small‐sized networks.

The first step of the optimization is the screening step, which thresholds the noisy edges of larger p‐values, for example to let $w_{ij}=0$ if $p_{ij}>p_0$, and we refer to the thresholded weight matrix as W. Then, the Laplacian matrix based on the thresholded W matrix is

$$L=D-W,$$ (2)

where the degree matrix D is defined as the diagonal matrix with diagonal element $d_1,\cdots ,d_n$ and $d_i={\sum }_{j=1}^{\left|V\right|}{w}_{ij}.$

Next, we investigate how many disconnected components/subgraphs are there in the overall graph G with the thresholded W matrix. We denote $G_q$ as a disconnected subgraph/subset of G (q = 1,⋯,Q and $G={\cup }_{q=1}^Q{G}_q$) such that $G_q\subset G$, and there is no edge with weight > 0 connecting between $G_q$ and its complement subset $G\backslash G_q$. To identify the disconnected subgraphs, we conduct the eigen‐decomposition on the Laplacian matrix L, and the number of zero‐valued eigenvalues equals the number of disconnected subgraphs [Von Luxburg, 2007]. The corresponding eigenvectors of zero‐valued eigenvalues exhibit the allocation of nodes to the disconnected subgraphs. This step is equivalent to the network detection step in NBS, but a spectral graph model is used rather than the breadth first search by NBS. The objective function in Eq. (1) is at minimum and equals zero, if C the total number of network clusters in Eq. (1) is the same as Q (Q > 1) the number of disconnected subgraphs in G. However, rather than stopping at this step and performing family‐wise error control, we further conduct parsimonious network detection within each unconnected component to identify smaller networks with a higher proportion of significant edges. Thus, the overall objective function becomes parsimonious network detection within each unconnected subgraph:

$${\text{argmin}}_{{\left\{{\stackrel{\sim }{A}}_k\right\}}_{k=1}^{K_q}}{\displaystyle \sum _{k=1}^{K_q}\frac{{\sum }_{i\in {\stackrel{\sim }{A}}_k,j\cancel{\in }{\stackrel{\sim }{A}}_k}-\log (p_{ij})}{\left|{\stackrel{\sim }{A}}_k\right|}}$$ (3)

where $K_q$ is the number of clusters in a disconnected subgraph $G_q$ and $C={\sum }_{q=1}^Q{K}_q$, which links between Eqs. (2) and (3). However, the direct optimization of Eq. (3) is an nondeterministic polynomial time (NP) problem. We seek the solution by using spectral graph models. After discretization relaxation, it turns into the RatioCut spectral clustering problem, which has been well developed by Hagen and Kahng (1992). The details of the implementation of the RatioCut algorithm are illustrated in the following detailed algorithm. Then, the only tuning parameter for each disconnected subgraph is $K_q$, which chooses the number of clusters for K‐means clustering. Rather than applying the conventional methods, such as silhouette criteria, we develop a novel and connectivity network specific criteria to choose $K_q$ objectively by maximizing the of product of (1) the ratio of the total number of significant edges in all $K_q$ clusters to the total number of non‐zero edges in the disconnected subgraph (quantity) and (2) the ratio of the total number of significant edges to the number of edges within all $K_q$ clusters (quality):

$$\frac{{\sum }_{k=1}^{K_q}{\sum }_{i\in {\stackrel{\sim }{A}}_k,j\in {\stackrel{\sim }{A}}_k}^{}I(W_{ij}>0)}{{\sum }_{i<j}^{}I(W_{ij}>0)}·\frac{{\sum }_{k=1}^{K_q}{\sum }_{i\in {\stackrel{\sim }{A}}_k,j\in {\stackrel{\sim }{A}}_k}^{}I(W_{ij}>0)}{{\sum }_{k=1}^{K_q}{\sum }_{i\in {\stackrel{\sim }{A}}_k,j\in {\stackrel{\sim }{A}}_k}^{}1}.$$ (4)

The criteria in Eq. (4) provides a data‐driven and objective pathway to select tuning parameters $K_q$ that tries to maximize the proportion of significant edges in the selected networks and to include most significant edges of W in the detected differential networks.

Moreover, we provide an approach to automatically select $p_0$ by a grid search algorithm. We search $p_0$ in the range of (0.05, 0.1) by increments of 0.005 and select $p_0$ that maximizes the criteria below:

$$\frac{{\sum }_{k=1}^{K_q}{\sum }_{i\in {\stackrel{\sim }{A}}_k,j\in {\stackrel{\sim }{A}}_k}^{}-\log (p_{ij})}{{\sum }_{k=1}^{K_q}{\sum }_{i\in {\stackrel{\sim }{A}}_k,j\in {\stackrel{\sim }{A}}_k}^{}1}÷\frac{{\sum }_{k=1}^{K_q}{\sum }_{i\in {\stackrel{\sim }{A}}_k,j\cancel{\in }{\stackrel{\sim }{A}}_k}^{}-\log (p_{ij})}{{\sum }_{k=1}^{K_q}{\sum }_{i\in {\stackrel{\sim }{A}}_k,j\cancel{\in }{\stackrel{\sim }{A}}_k}^{}1},$$ (5)

which is the ratio of the average intensity of $-\log (p_{ij})$ (information intensity) within selected networks and the average intensity of $-\log (p_{ij})$ outside of selected networks. Note that $K_q$ is selected by Eq. (4). Overvall, Eqs. (4) and (5) ensure that most of the information differentiating the two groups of subjects is contained in the selected networks while minimizing the sizes of the networks needed (for higher concentration). Rather than applying a penalty term to control the network sizes, we implement the rule of parsimony by optimizing tuning parameters for objective functions. Thus, our approach is not only computationally convenient but also less ad hoc (to provide more reproducible results).

Last, we apply a permutation test to provide the p‐value of selected networks while controlling family error rates, which is similar to the family error control in NBS [Zalesky et al., 2010].

We summarize the overall parsimonious differential brain connectivity network detection (Pard) algorithm as follows:

1. Conduct statistical tests on all edges E and calculate the weight matrix W by screening (e.g., thresholding values $p_0$):

   $$w_{ij}=\{\begin{array}{cc}-\log (p_{ij})\hfill & \text{if} p_{ij}\le p_0;\hfill \\ 0\hfill & \text{else}.\hfill \end{array}$$

2. Detect disconnected subgraphs in G: first eigen decompose the Laplacian matrix L = D − W and the number of zero eigenvalues of L equals the number of disconnected subgraphs, and the allocation of nodes to disconnected subgraphs is based on the eigenvectors with zero eigenvalues.

3. Within each disconnected subgraph $G_q$, search networks that include most informative/significant edges with constrained numbers of nodes for each network. Although the direct optimization of this step is NP, it can be solved by the RatioCut algorithm after discretization relaxation:

   1. Compute the first $K_q$ eigenvectors $[u_1,\cdots ,u_{K_q}]$ of L, with eigenvalues ranked from the smallest.

   2. Let $U=[u_1^T,\cdots ,u_{K_q}^T]$ be a $\left|V\right|\times K_q$ matrix containing all $K_q$ eigenvectors.

   3. Perform K‐means clustering algorithm on $U$ with $K=K_q$ to cluster |V| nodes into $K_q$ networks: ${\stackrel{\sim }{A}}_{K_q}^1,\mathrm{...}, {\stackrel{\sim }{A}}_{K_q}^{K_q}$.

4. Try all possible $K_q$ for each disconnected subgraph and select the optimum number of networks by Eq. (4).

5. Select $p_0$ by using the criteria of Eq. (5).

6. Perform permutation testing to control FWERs for each detected network $A_c$:

   1. Shuffle the group labels for each subject T times (e.g., T = 5,000) and calculate W with the same threshold $p_0$ at each shuffling t.

   2. Obtain the most significant test statistic (e.g., Fisher's combination test) of $A_c$ as $m_t$ in each permutation and let $m_0$ represent the test statistic with $w_{ij}>0$ for original labeling.

   3. Calculate the permutation p‐value as how many $m_t$ are larger than $m_0$ divided by T, $P_{A_c}=\frac{\#(m_t>m_0)}{T}$ and determine whether the network is significant at a predetermined α‐level.

7. Output the significant networks with permutation test p‐values.

SIMULATIONS

In this section, we simulate a case–control connectivity study including 30 healthy controls and 30 subjects with neural disorders to evaluate the performance of our Pard algorithm. We generate an overall graph $G_s$ of 90 ROIs as nodes and 4,005 edges for a subject s (s = 1,⋯60) to represent the widely used first 90 automated anatomical labeling regions in functional connectivity analysis [Tzourio‐Mazoyer et al., 2002; Zalesky et al., 2010, 2012b].

We assume that the normalized connectivity metrics (e.g., correlations after Fisher's transformation and z‐score normalization) follow a standard normal distribution. Within the overall graph G, we generate a truly differentially expressed connectivity network $G_D$ of size 10 (10 nodes and 45 edges). Thus, we simulate the connectivity metrics for all subjects by

$$Z_{ij}^s\sim \{\begin{array}{cc}N(0,{\sigma }^2)+d\hfill & \text{if}\hspace{0.17em}i,j\in G_D\hspace{0.17em}\text{and subject}\hspace{0.17em}s\hspace{0.17em}\text{is from the healthy control group};\hfill \\ N(0,{\sigma }^2)\hfill & \text{otherwise}.\hfill \end{array}$$

Then, we conducted two sample t‐tests to obtain p‐values and weight matrix $W_0$. The simulated data are summarized in Figure 1: Figure 1a illustrates the truth: the truly DEN by the red color; Figure 1b is the heatmap of $-log(p_{ij})$ based on the p‐values of two sample t‐tests between the two cohorts of the simulated data; and Figure 1c is the shuffled version of Figure 1b (i.e., the labels of all nodes are permuted), which may better reflect the real spatial distribution of significant edges in practice (Fig. 1c is the input data for the differential network detection algorithm). We repeat the procedures above to obtain 100 simulated data sets by using each set of parameters.

Figure 1.

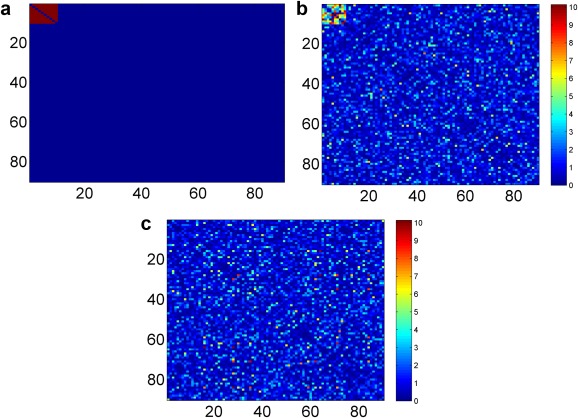
(a) The heatmap of truth: the connectivity between the first 10 nodes are differentially expressed between the two groups. (b) Heatmap of two sample t‐test −log(p) values of the simulated connectivity based on 60 subjects (30 cases vs. 30 controls). (c) Heatmap with shuffled region number of (b) is used as the input of our method. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

We then performed our Pard algorithm on $W_0$ to identify DENs. After thresholding ( $p_0$), there are no disconnected subgraphs (i.e., G is connected) due to false‐positive significant edges. Thus, the only network size tuning parameter is C, the number of clusters for the overall graph G. The optimum number C ranges from 49 to 62, and most $p_0$ are between 0.08 and 0.10 across the 100 simulated sets. The individual edges or networks with a few nodes are rarely detected as significant based on the permutation test results. Figure 2 shows how the tuning parameter selection criteria function changes with an increasing number of clusters for one simulated data set, and the score is highest at C = 59 (for a simulation data set). Then, we perform our algorithm with C = 59, and the DEN $G_D$ is successfully detected. We then conduct permutation testing based on 10,000 times permutation and $P_{G_D}<0.001$, which indicates that the detected network is significant after controlling for the FWER. The final results are demonstrated by Figure 2b, which reveals the true DEN accurately.

Figure 2.

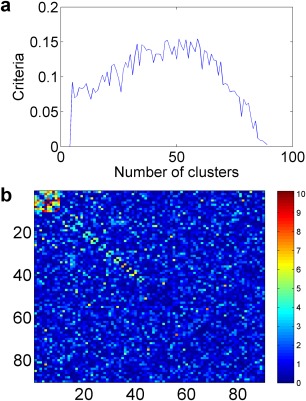
(a) The number of cluster selection criteria function: scores of the function vs. the number of clusters. (b) The resulting heatmap of −log(p): the detected network is at the left‐top corner. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

For comparison, we apply the NBS algorithm for differential network detection by default parameter (t‐statistic =3.1) and several other threshold values; for example, 2, 2.7, and 4. We also apply it to detect the differentially expressed edges by using FDR as a reference for false‐positive rates and negative rates without considering networks as output biomarkers, and we use q = 0.1 as a cut‐off. In comparison, we consider many scenarios by using different sets of parameters including network sizes (5, 10, and 15) and different significance levels of truly differentially expressed edges. The significance levels of truly differentially expressed edges are generally determined by three factors: effect sizes (d), noise levels ( ${\sigma }^2$), and sample sizes, and we only tune noise levels ( ${\sigma }^2$) because it is redundant to tune all three factors (the same p‐values). We let d = 0.8, and sample sizes for cases and controls are both 30. Table 1 summarizes the means and standard errors of false‐positive (FP) and false‐negative (FN) findings under different settings.

Table 1.

Simulation results under different settings

	Pard			FDR			NBS
	FP	FN	Network	FP	FN	Network	FP	FN	Network
Size = 10; σ 2 = 1	0.3 ± 0.17	0	Yes	0.29 ± 0.06	40.42 ± 0.35	No	0	45	No
Size = 5; σ 2 = 1	4.519 ± 0.47	0	Yes	0.19 ± 0.05	9.45 ± 0.10	No	0	10	No
Size = 20; σ 2 =1	1.33 ± 0.51	0	Yes	3.21 ± 0.18	134.43 ± 1.12	No	0	190	No
Size = 10; σ 2 = 0.25	0	0	Yes	1.04 ± 0.11	31.91 ± 0.49	No	6.37 ± 1.17	27.28 ± 2.20	Yes
Size = 10; σ 2 = 5	19.64 ± 2.12	16.28 ± 1.44	Yes	0.05 ± 0.02	44.88 ± 0.04	No	0	45	No

The true DEN is detected and tested as significant in 100 of the 100 data sets by using the Pard algorithm for different network sizes and most noise levels, though there is a small chance that false‐positive nodes (the number of nodes ranges 2∼4) could be included. As a contrast, the FDR method misses most of the true positives while effectively controlling the false‐positive rates. The power increase of the Pard method relies on both the combined significance levels of all edges in the network and the size of the detected network, because a network with more significant edges and smaller number of nodes is more likely to be significant based on permutation testing. In addition, the NBS method could not detect the DENs in most settings, and we apply different thresholds (ranging from 2 to 4) and report the results (of the threshold value) with the best performance. One possible reason could be the false‐positive edges connecting a large number of nodes and, thus, a large network is detected by breadth first search, but within the detected large network, there is only a small proportion of edges that are significant, and the number of significant edges is similar to those of the networks from permutations. Therefore, by applying the rule of parsimony (constraining the number of nodes of the detected networks), our method increases the power substantially and excludes false‐positive edges effectively. In summary, the simulation study indicates that our proposed Pard algorithm is effective for differentially expressed connectivity network detection and less affected by noises (false‐positive edges).

DATA EXAMPLE

This data set was collected at the Yale child study center in Yale School of Medicine, one of the data collecting sites in the Autism Brain Imaging Data Exchange (ABIDE) (Di Martino et al., 2014). The imaging was performed on Siemens magneto Trio scanners. The imaging data were obtained using a gradient echo T2*‐weighted echo planar imaging sequence, echo time TE = 25 ms, repetition time TR = 2,000 ms, 64 × 64 matrix with 34 slices 4.0 mm thick, skip 0 mm, resulting in whole brain coverage with a voxel size of 3.4 mm × 3.4 mm ×4.0 mm. The publically available data set includes 28 participants (typical controls, TC) and 28 patients with Autism spectrum disorders, and the two groups exhibit no significantly different demographics (e.g., age and gender). During the MRI scanning, all subjects were asked to lie as still as possible, keep their eyes open, try not to fall asleep, and think about whatever they wanted. A black background with a gray central fixation cross was presented during the resting state scan, although participants were not asked to fixate, it was verified that they had not fallen asleep at the end of the scan.

We performed rs‐fMRI data preprocessing based on the Configurable Pipeline for the Analysis of Connectomes (http://fcp-indi.github.io). The rs‐fMRI data were first slice time and motion corrected. The data were next registered to a standard MNI space with voxel size 2 mm ${}^3$ and normalized to be percent signal change. The masks of the white matter (WM), the gray matter, and the cerebrospinal fluid (CSF) were created in the standard MNI space. The mean time series from the WM and the CSF were calculated. The mean time series of the WM, CSF, and the six movement parameters were regressed from the gray matter. A linear trend was removed from all the signals. The fMRI time series were filtered using a bandpass with passing band (0.009–0.08 Hz) and spatially smoothed with a 6‐mm full width at half maximum Gaussian kernel. We then use the first 90 automated anatomical labeling ROIs as nodes, and take the weighted average of all voxels' temporal profiles within each ROI as the region level signal for all subjects. The Pearson correlation coefficients were calculated between the 90 nodes. In this analysis, we focus on the differential connectivity network detection between TC and Autism spectrum disorders.

We first conducted two sample t‐tests to obtain p‐values and $-log(p_{ij})$ for all edges between TC and TSD (Fig. 3a), and then calculated the weight matrix $W_0$. Next, we applied the parsimonious differential connectivity network detection method to the $W_0$ matrix. We excluded singleton nodes in G, which have all edges $p_{ij}>p_0$ connected to the rest of the nodes. Then, there was no disconnected subgraph in G. We implemented the optimization algorithm for network detection and selected the tuning parameter based on the criteria function. Based on Eq. (5) in Methods section, we selected $p_0$ as 0.1. Figure 3b shows the relationship between the tuning parameter selection criteria function and the number of clusters, and the maximum value is reached at C = 31. Therefore, the final results were detected by using the tuning parameter C = 31. The results are summarized in Figure 3c, and we note that all significant edges tend to be along the diagonal because of the shrinkage effect. Two networks are detected and tested as significant by permutation tests: the first network includes 15 nodes (P < 0.001), and the second network includes 10 nodes (P < 0.001).

Figure 3.

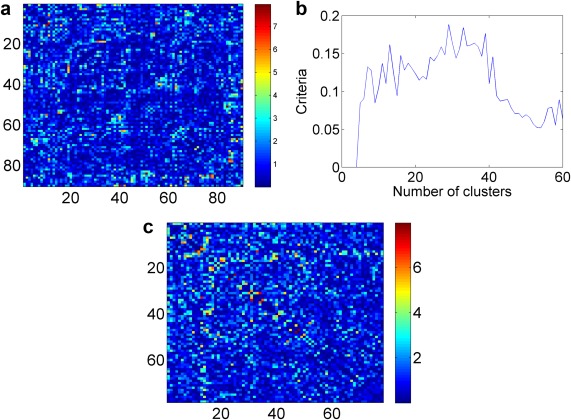
(a) Heatmap of −log(p) values for all edges between TC and TSD. (b) Tuning parameter selection criteria function. (c) The resulting heatmaps: detected networks along the diagonal. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figures 4 and 5 show the differentially expressed edges within the two detected networks (figures are generated by using BrainNet Viewer by Xia et al., 2013). Many differentially expressed edges have been found in previous studies [Cherkassky et al., 2006, Di Martino et al., 2014; Tyszka et al., 2014]. The first cluster mainly exhibits altered connectivity expressions between prefrontal cortex, parietal cortex, middle inferior temporal cortex, and basal ganglia. The second cluster mainly shows differences between superior frontal cortex, limbic system, and occipital cortex. The details are included in Supporting Information Tables S1 and S2.

Figure 4.

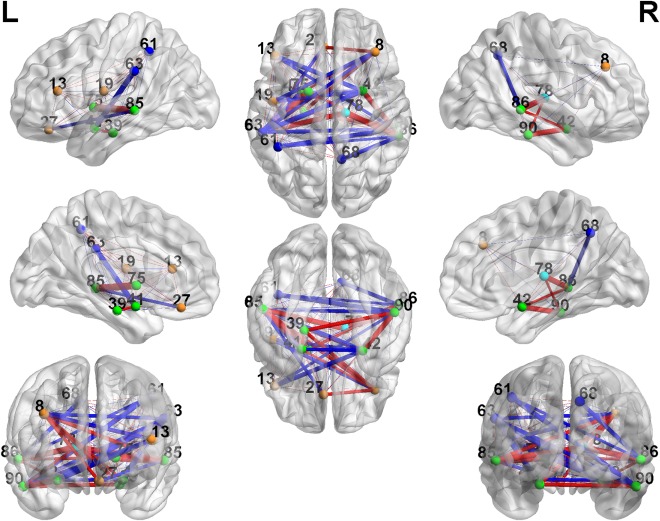
Cluster 1: 3D plots of the differentially expressed edges. The width of the edges reflects the significance level, and the color is coded as red (TC < TSD) and blue (TC > TSD). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 5.

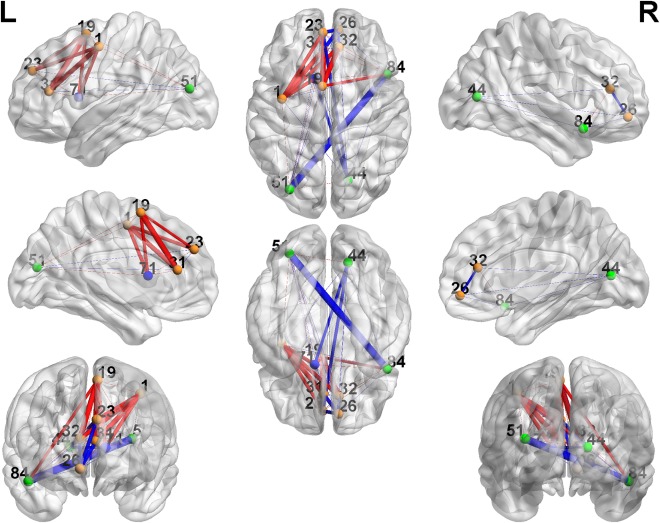
Cluster 2: 3D plots of the differentially expressed edges. The width of the edges reflects the significance level, and the color is coded as red (TC < TSD) and blue (TC > TSD). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

For comparison, we applied both the NBS method (with several threshold values from 2 to 4) for DEN detection and the false‐positive discovery rate (FDR) control for individual differentially expressed edge detection. Neither of these two methods detect significant results, which may be caused by the noise of false‐positives (NBS) and ignorance of correlation between edges (FDR) (similar atlas‐based results by Tyszka et al., 2014).

DISCUSSION

Group‐wise whole brain connectivity analyses using atlas regions have been facing trade‐offs between false‐positive findings and lack of statistical power (false‐negatives). Traditional multiple testing adjustment methods often could not detect truly differentially expressed features when trying to avoid false‐positive findings. Some studies conduct group‐wise connectivity analyses within predefined regions rather than the whole brain to lower the stringent level required for multiple testing adjustment and to increase the likelihood of detecting statistically significant findings. Clearly, such procedures may lead to limited and inaccurate results. The DEN type network‐based methods, such as NBS, provide a pathway to improve the statistical power while controlling the FWER. DEN methods select a significant edge not only by the criteria of the test p‐value but also the distribution of p‐values of its neighborhood edges. Therefore, the DEN methods naturally incorporate the topological structure of the edges for significant connectivity detection and improve statistical power. Note that our method only controls the FWE in the weak sense, and thus, we can make inferences only on networks rather than individual edges.

The statistical power of the existing DEN methods (e.g., NBS) depends on the proportion of supra‐threshold edges within the connected subgraphs, and a smaller proportion may lead to an insignificant permutation test result. From the aspect of graph combinatrics, the probability of all edges with small p‐values clustering in a small network is extremely low, and therefore, the permutation test p‐value is very small, and the organized structure of such p‐values yields important topological information of differentially expressed connectivity networks. Hence, if the detected network includes truly differentially expressed edges, but the proportion of significant edges is low, the statistical power to detect these truly significant edges is very low because the detected network is very likely to be tested as nonsignificant using a permutation test. Therefore, the objective function of our Pard algorithm aimed: (i) to include most significant edges in the detected networks; ii) by constraining the number of nodes of the networks to increase the proportion of significant edges within the detected networks. The constraint of the network size in the objective function is critical to reduce the (false‐positive) noise to improve statistical power. Therefore, our Pard algorithm improves the statistical power of network detection by allowing edges to borrow power between each other; and meanwhile effectively controls the false‐positive findings because false‐positive edges are more likely to be randomly distributed rather than concentrated within a small network. The detected networks, in turn, reveal the topological structures of the significant edges, and the parsimonious networks are more informative because the shrinkage procedure removes substantial noises.

We implement the optimization step by using the RatioCut algorithm. Although most spectral clustering algorithms primarily aim to allocate similar nodes to the same cluster, our objective function is to capture most significant edges within constrained networks. Fortunately, the algorithms have been well developed to implement the optimization of our objective function without intensive computational load. However, for most spectral clustering algorithms, the selection of number of clusters can be an arbitrary and ad hoc procedure [Von Luxburg, 2007]. We developed a new tuning parameter selection criteria function specifically for brain connectivity analysis to choose the number of clusters objectively. In addition, we provide a similar procedure to choose $p_0$. We express the importance (weight) of a edge by using −log transformation of the test p‐value rather than raw p‐value or t statistic, because the scale is more appropriate to differentiate the small p‐values (e.g., 0.001 and 0.0001) and is naturally linked to Fisher's combined probability test [that has been used in cluster activity intensity analysis by Hayasaka and Nichols, 2004]. From the computational statistics point of view, we developed a novel procedure to fuse network size shrinkage and ad hoc tuning parameter selection, which avoids use of penalty terms (e.g., lasso and elastic nets methods) and reduces computational cost. Further asymptotic properties of such procedure will be studied.

In the simulation study, the truly DEN can only be accurately detected and tested as significant by using our Pard algorithm. The ABIDE data provide another example of increased statistical power of our method, where the differential networks can only be detected by our Pard algorithm. The edges can borrow power from each other within the network, and the high proportion of small p‐value edges leads to significant permutation results. The detected networks exhibit many significantly differentially expressed edges that have been found in previous studies. As we focus on methods and models in this article, because of the space limit, we do not intend to discuss the results in more detail from the neurophysiological aspect. We provide the list the edges with p‐values less than 0.05 for the two clusters in Supporting Information Tables S1 and S2. We plan to further verify the results by applying our methods to several data sets, including rs‐fMRI data sets from other sites of the ABIDE project.

In summary, we have presented a novel parsimonious differential brain connectivity network detection method to discover differentially expressed connectivity features at the group level for fMRI data. The simulation study and data example have shown that the statistical inferences based on our Pard method are more powerful and reliable (lower false‐positive discovery rate). We are also optimistic that the Pard method is ready to be applied to connectivity analyses for task‐induced fMRI data and structural connectivity network analyses.

Supporting information

Supporting Information Tables