Identification of Unintuitive Features of Sumoylation through Mathematical Modeling

Abstract

Sumoylation is a multistep, multienzymatic post-translational modification in which a small ubiquitin-like modifier protein (SUMO) is attached to the target. We present the first mathematical model for sumoylation including enzyme mechanism details such as autosumoylation of E2 and multifunctional nature of SENP. Simulations and analysis reveal three nonobvious properties for the long term response, modeled as an open system: (i) the steady state sumoylation level is robust to variation in several enzyme properties; (ii) even when autosumoylation of E2 results in equal or higher activity, the target sumoylation levels are lower; and (iii) there is an optimal SENP concentration at which steady state target sumoylation level is maximum. These results are qualitatively different for a short term response modeled as a closed system, where e.g. sumoylation always decreases with increasing SENP levels. Simulations with multiple targets suggest that the available SUMO is limiting, indicating a possible explanation for the experimentally observed low fractional sumoylation. We predict qualitative differences in system responses at short post-translational and longer transcriptional time scales. We thus use this mechanism-based model to explain system properties and generate testable hypotheses for existence and mechanism of unexpected responses.

Introduction

Cellular proteins are regulated at several levels, viz. epigenetic, transcriptional, post-transcriptional, translational, and post-translational. Sumoylation is a post-translational modification in which small ubiquitin-like modifier (SUMO)² protein is attached to a lysine on the target protein. In most cases, the lysine is part of the consensus sequence ϕKX(E/D) (1). Sumoylation has been shown to be involved in regulation of many cellular processes such as maintaining genome integrity, regulating transcription, replication, and nuclear trafficking of cellular proteins. SUMO modification of the target can modulate target levels, can lead to its conformational change, and can change target properties such as binding affinity/specificity and specific activity (2–5).

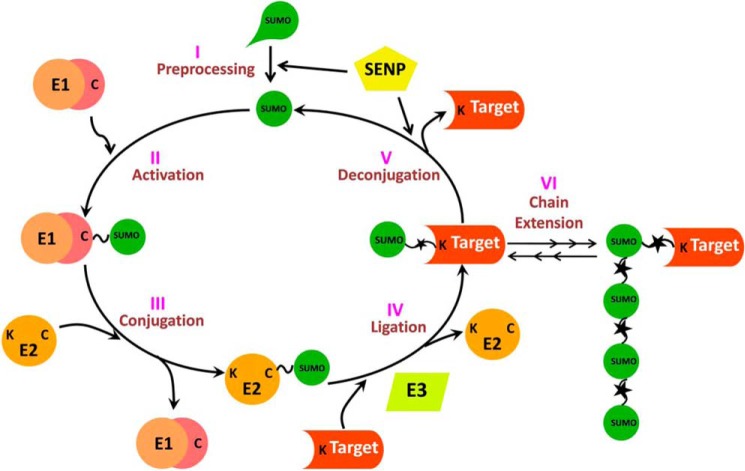
Sumoylation is a multistep process (Fig. 1) consisting of the concerted activity of four enzymes, viz. sentrin/SUMO-specific protease (SENP in Fig. 1); heterodimeric activating enzyme, SAE1/UBA2 (E1); conjugating enzyme, UBC9 (E2); and SUMO ligase (E3). SUMO is translated in an immature precursor form (presumo) that has to be processed. In the first step (preprocessing), SENP with its C-terminal hydrolase activity cleaves presumo to expose its diglycine residues and converts it into a mature form (SUMO; step I in Fig. 1). In the next step (activation), SUMO is activated by E1 in the presence of ATP. SUMO attaches to the cysteine residue on E1 by a thioester bond to form sumoE1 (step II in Fig. 1). In the third step (conjugation), SUMO is transferred from the cysteine of E1 to the cysteine of E2, resulting in a thioester bond to form sumoE2 (step III in Fig. 1). Step IV in Fig. 1 (ligation) is the target modification step. SUMO from cysteine of E2 is transferred to the target lysine residue, forming an isopeptide bond. Ligation specificity is enhanced in presence of E3 (step IV in Fig. 1). SUMO modification of the target is reversible. During deconjugation, the SUMO attached to the target is cleaved off by the isopeptidase activity of SENP (step V in Fig. 1). Sumoylated target can be retargeted to add another SUMO to the lysine of existing SUMO to form poly-SUMO chain on the target (step VI in Fig. 1) (2) or to add SUMO to another lysine residue on the target. In addition to other lysine-containing target proteins, the system enzymes E1, E2, and SENP may also be sumoylated. SUMO modification of the enzymes might change their activity and level, affecting the sumoylation process efficacy and dynamics (6–8).

FIGURE 1.

Schematic representation of the multistep sumoylation pathway.

The intricate multistep cyclic nature of the modification system, together with the automodification capability and presence of multifunctional enzyme SENP, makes an intuitive analysis of the system very difficult. A mathematical model is a useful tool to understand the properties of such nonlinear networks with autoregulation. There are a few studies that have mathematically modeled multienzyme modification systems such as ubiquitination, for instance, to study the role of degradation kinetics in promoting oscillations, to understand the paradoxical role of ubiquitin ligase E3, or to understand the role of ubiquitin activating enzyme E1 (9–11). The enzymology and kinetics of individual sumoylation steps have been studied. However, to the best of our knowledge, an integrated analysis of the entire cyclic sumoylation system has not yet been published. We use published information about the kinetics of individual steps to construct the first mathematical model of the sumoylation system. Our model considers details of each step of the cycle. We use the model to analyze the system properties, in particular, the effect of varying enzyme activities, the effect of varying the Janus-like SENP, and the effects of changes in sumoylation efficiency caused by automodification of E2. With the model simulations, we highlight the qualitative differences in the short term and long term responses modeled as a closed (no transcription/degradation) and open system, respectively.

We show that in the long term, change in the properties of binding enzymes (E2) and the enzymatic transformation rate constants has no effect on steady state target sumoylation. For these situations, the extent of target sumoylation is mathematically independent of the values of these parameters and therefore absolutely robust to changes in enzyme activity. We approximate the effects of automodification by modeling the sumoylation of E2. The model simulations demonstrate that even for the case when the efficacy of the sumoylated E2 is unchanged or increased, autosumoylation of E2 results in a decrease in sumoylated target levels. Analysis suggests an explanation of this nonobvious result in terms of sequestration of the enzyme. Our simulations also reveal the existence of an optimal SENP level for maximum target sumoylation for an open system, whereas for the closed system, increasing SENP levels always result in a decrease in target sumoylation. These results are in agreement with published experimental results that were not used in model construction or parameter estimation. Lastly, we simulate multitarget sumoylation to suggest an explanation for the observation that most proteins exhibit low levels of sumoylation. Mathematical analysis of the system suggests that available SUMO for the modification of the targets is limiting, leading to lower percentage sumoylation of each target.

The mathematical description of the sumoylation system presented here explains previously reported experimental observations and hypothesizes, with a mechanistic explanation, the ability of the system to exhibit unintuitive responses. It will serve as a starting point for further modeling and analysis of sumoylation.

Experimental Procedures

Model Development and Parameters

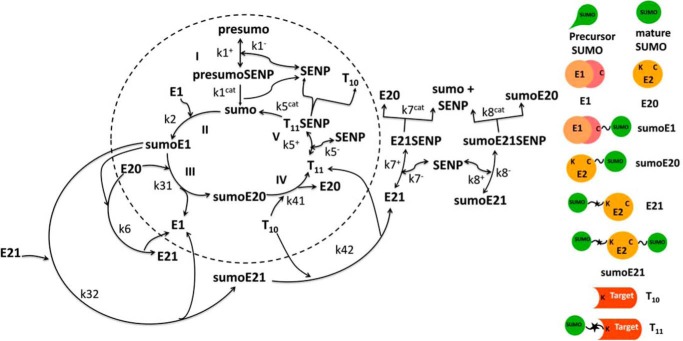
A deterministic model was constructed for the system with simultaneous sumoylation of more than one target. We also considered sumoylation of E2. A pictorial representation of the constructed model for monosumoylation of one target and E2 is shown in Fig. 2. Each step of the sumoylation process shown in Fig. 1 is modeled as a chemical reaction. Reactions in the dashed circle are for sequential addition of one SUMO molecule to the target (T₁₀) and desumoylation of the modified target (T₁₁), whereas the reactions outside the circle depict modification of E2 and the involvement of modified E2 in target modification. These reactions for a closed system represent short term events where there is no protein synthesis or degradation. To model longer term events, representing an open system, zero order formation of enzymes and the targets and their first order degradation are included in the model (not shown in Fig. 2). Simple mass action kinetics was written for each step of the cycle. The parameters for formation (“birth”) and degradation of the species are denoted by b and d, respectively, followed by species name in subscript (e.g. b_SENP, d_SENP). We modeled E3-independent, single site sumoylation of the targets and did not consider the detailed activation step involving ATP usage. The various SUMO and SENP isoforms known in the human system were also not considered in the model. Our model does not distinguish between sumoylation of multiple lysines on a single target and polysumoylation at the single lysine on a modified target but merely tracks the number of SUMO moieties conjugated to a target. The ordinary differential equations (ODEs) that govern the dynamics of each component of an open system with simultaneous polysumoylation of multiple targets and monosumoylation of E2 are represented below. ODEs are written for system having targets T_ij, where i is the index specific to a target, with values from 1 to the total number of targets N_T; and j is the index for the number of SUMOs on the target, taking values from 0 to N_sumomax(i). E20 represents unmodified E2, and E21 represents E2 with one SUMO moiety. Subscripts for rate constants are omitted for situations where there is one monosumoylated target. Each differential equation arises from a simple mass balance for the corresponding protein or complex. For instance, the first equation equates the rate of change in presumo concentration to the net difference in the rates of reactions where it is formed (birth/formation, complex dissociation) and removed (degradation/complex formation). The reactions below are for an open system. For a closed system, the formation and degradation rate constants are set to 0, and the initial concentration chosen depends on the total concentration of each protein (supplemental materials, section D). For the open system, the steady state reached is independent of the choice of the initial (non-negative) concentration.

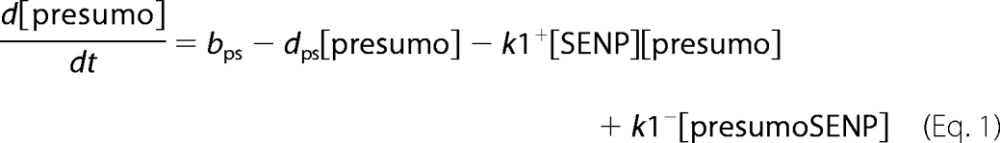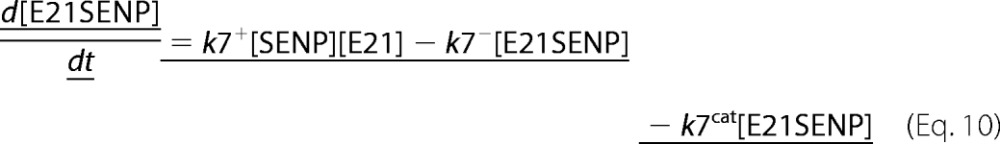FIGURE 2.

Pictorial representation of complete sumoylation system for monosumoylation of one target used for construction of the mathematical model. Reactions within the dashed circle represent the simple closed system with sumoylation of only the target. Steps outside of the dashed circle represent the reactions that occur in E2 autosumoylated system. Zero order formation and first order degradation reactions of presumo, SENP, E1, E2, and target used for simulating the open system are not shown. Similarly, first order degradation of SUMO, modified targets, and intermediate SUMO complexes are not shown.

For i = 1 … N_T, j = 0

For i = 1 … N_T, j = N_sumomax(i)

For i = 1 … N_T, j = 1 … N_sumomax(i) − 1

For i = 1 … N_T, j = 1 … N_sumomax(i)

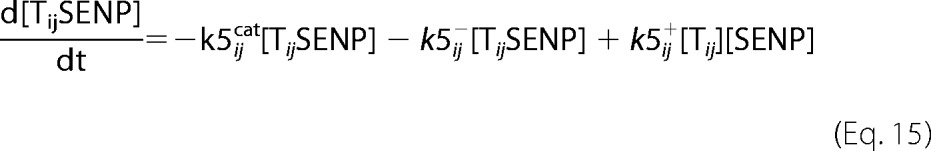Following the known biochemistry, SUMO modification of E2 was modeled differently than the targets. E2 was modeled to receive its SUMO directly from cysteine of E1 and not from cysteine of E2 like the other targets (7). Excluding the underlined rates results in a simpler system where E2 is not modified. Because the SUMO modification step is the same as the conjugation step (having same reactants sumoE1 and E20), we assumed the parameter for sumoylation of E2 (k6) to be same as the known conjugation parameter (k31). Also, sumoylation of E2 is known not to impair its thioester formation property; hence the parameter for conjugation of E21 (k32) was assumed to be same as that of conjugation of E20 (k31) (12). The parameter for modification of the target by E21 was denoted as k42. Deconjugation activity of SENP toward modified targets E21 and sumoE21 was assumed to be the same. The parameters for zero order formation and first order degradation were calculated from the previously reported values of mRNA copy number average, average translation rate constant and average protein half-life (t_½) values (13). The degradation parameter was calculated as ln(2)/t_½. The formation rate was calculated as the product of the number of molecules of the protein molecules translated per mRNA (translation rate constant) and mRNA copy number. The characteristic cell volume for humans was considered to be 2.25e-12 L (BNID 100434) (14) for molar calculations. Michaelis-Menten constants K_m and V_max and the derived parameter k_cat were obtained from literature for individual steps of the cycle. We assumed the parameter (k1⁺,k5⁺) for forward reaction of complex formation for steps involving SENP for calculating the k⁻ and k_cat parameters using quasi-steady state assumptions. The parameters for activation, conjugation, and ligation steps were calculated from k_cat/K_m values. The rate constant for degradation of presumo was assumed to be same as that of SUMO. Modified and unmodified target were assumed to have same degradation rate constant. Degradation of SUMO complex with E1 and E2 was considered to be the same as that of free E1 and E2, respectively. The parameters thus estimated and used as reference values for simulations are tabulated in Table 1. Closed systems were modeled by setting all formation and degradation rates b_i and d_i, respectively, to 0.

TABLE 1.

Values for reaction rate parameters used for simulations

Reaction	Value	Reference
Formation of presumo	bps: 6.286e-3 μm/h	Ref. 13
Degradation of presumo	dps: 2.218e-2 h−1	Assumed to be same as ds
Degradation of mature SUMO	ds: 2.218e-2 h−1	Ref. 13
Formation of E1	bE1: 2.426e-2 μm/h	Ref. 13
Degradation of E1	dE1: 4.313e-3 h−1	Ref. 13
Formation of E20	bE20: 4.416 e-2 μm/h	Ref. 13
Degradation of E20	dE20: 4.132e-3 h−1	Ref. 13
Formation of SENP	bSENP: 3.212e-4 μm/h	Ref. 13
Degradation of SENP	dSENP: 3.454e-2 h−1	Ref. 13
Formation of the target (RanGAP1)	bT10: 4.591e-2 μm/h	Ref. 13
Degradation of target (RanGAP1)	dT10: 1.938e-2 h−1	Ref. 13
Degradation of sumoylatedtarget	dT11: 1.938e-2 h−1	Assumed to be same as dT10
Preprocessing of presumo	Km: 27.9 ± 3.7 μm	Ref. 22
	kcat: 0.72 ± 1.5 s−1
Activation: transfer of SUMO on E1	kcat: 0.78 ± 0.49 s−1	Ref. 24
	Km: 0.17 ± 0.096 μm
Conjugation: transfer of SUMO to E20	kcat/Km: 1.06 ± 0.05 μm−1 s−1	Refs. 12 and 25
Ligation of target (RanGAP1) by E20	kcat: 0.66 ± 0.14 s−1	Ref. 26
	kd: 2.9 ± 0.96 μm
Deconjugation of modified target (RanGAP1)	Km: 33.1 ± 3.2 μm	Ref. 22
	kcat: 50.4 ± 2.2 s−1

The system was simulated using ODE solver (ode15s) and the function fsolve of MATLAB (version 7.6.0.324-R2008a). Analytical steady state analysis was carried out in Mathematica (Wolfram) version 7.

Results

The First Mathematical Model for Sumoylation

We constructed a deterministic mathematical model for simultaneous polysumoylation of multiple targets and E2. Referring to the known sumoylation biology, we represented each step of the SUMO cycle (Fig. 2) as a chemical reaction, and mass balance equations were written for each species. The parameters for each step of the cycle were approximated from the enzyme kinetics experiments as represented in Table 1. To the best of our knowledge, this is the first mathematical description of the sumoylation system. For the most comprehensive model, the ODEs that govern the concentration dynamics of each component are given under “Experimental Procedures.”

The modeled system can be used to simulate various experimental scenarios. Depending on the time scale of the system being studied, it may be important to include change in the total protein levels through formation and degradation. This is modeled as an open system where mass enters and leaves the system through transcription/translation and protein degradation. If the phenomena to be simulated occur at shorter time scales, it may be sufficient to consider the total protein levels to be constant and just track the change in fractional amounts of modified/associated proteins. This is a closed system where there is no formation or degradation or any other input or output. Simulation as a closed system reflects an in vitro experiment where the total amounts of each protein are constant, although the bound/unbound or modified/unmodified fraction may change, whereas the open system simulation is more appropriate for long term in vivo dynamics. Our constructed model has the ability to simulate both these conditions. For each of the two conditions (open/closed), we have also included the reactions that enable the modeling and simulation of (i) multiple targets, (ii) different levels of polysumoylation of individual targets, and (iii) sumoylation of E2, with the sumoylated E2 participating in the same reactions as the unmodified E2, but with different rate constants. This results in a comprehensive model that can simulate a very large range of experimental conditions, each being one specific combination of the multiple possible states of each aspect of the process. For instance multiple targets, each with a different polysumoylation capacity, with E2 modified, and a closed system is but one of several possible combinations that can be simulated. Therefore we chose not to include sumoylation of other enzymes and not to track the polysumoylation on each target. However, the model can be extended to include factors that may be considered important in a given situation. Here, we only report the results for a system with targets undergoing sumoylation once.

First, we present the results on the robustness of a simple system with sumoylation of only one target and no autosumoylation of E2. The ODEs for this system can be derived from the equations under “Experimental Procedures” by setting N_T = 1 and N_sumomax = 1 (Equations SI1–SI11 in the supplemental materials). To calculate the steady state levels of sumoylated target ([T₁₁]_ss) and other moieties, for a simple system without any degradation of intermediates (d_se1 = d_se20 = 0), we set all derivatives to 0. The resulting set of algebraic equations is shown in the supplemental materials (Equations SI 12–SI 22). From the equations and from Fig. 2, it is clear that when there is no degradation of intermediates, there are two enzymatic reactions responsible for the change in concentration of each SUMO-enzyme complex. One reaction increases the concentration, and the other decreases the concentration. If the rate of the reaction that increases the concentration is greater, the intermediate will continuously accumulate, and no steady state is possible. A trivial example is when the target concentration [T₁₀]_ss is forced to be 0 by setting the formation rate b_T10 to 0. In this case, sumoE20 accumulates and a steady state is not possible. Because there is a sequence of reactions that move SUMO from E1 to E2 to target, each reaction rate has to be the same. An exact mathematical constraint on the reaction rate parameters that ensures that none of the intermediates accumulate is given by Equation SI 23 in the supplemental materials, which can be derived from the requirement of a finite non-negative steady state concentration for all model constituents (see supplemental materials, section A for details). An examination of this condition reveals that when b_T10 > b_SENP, the constraint is always satisfied. Henceforth, we will assume that the requirement for the existence of a steady state is fulfilled. We calculate the steady state sumoylated target concentration and examine the factors to which it is sensitive, and interestingly those reactions to which it is robust.

Target Modification Does Not Depend on the Properties of Its Modifying Enzyme E2

For a simple open system with one target (N_T = 1), no autosumoylation of E2 (k6 = 0), and no degradation of intermediate SUMO complexes, sumoE1 and sumoE20 (d_se1 = d_se20 = 0), the steady state concentration of each moiety was obtained by solving Equations SI 12–SI 22 in the supplemental materials. Some of the solutions are given as Equations SI 24–SI 27 in the supplemental materials, exactly describing the role of each reaction rate parameter in determining the steady state concentration of a particular entity. Because none of the equations include initial conditions as a parameter, it is clear that the steady state reached is independent of the choice of (non-negative) initial concentration. The analytical steady state concentration of the sumoylated target ([T₁₁]_ss) as a function of the reaction rate parameters is given by Equation 16.

It is clear that the steady state value depends on several parameters, including obvious ones such as formation rates of the protease that desumoylates the target and the presumo that provides the sumo for target sumoylation. However, interestingly, the rate constants for enzymatic conjugation and ligation (k31 and k41) do not appear in Equation 16. This absence implies that [T₁₁]_ss does not depend on k31 and k41. Neither does it depend on the formation and degradation rates of E20. This directly leads to the testable hypothesis that, given the model assumptions, the steady state target sumoylation levels are robust to changes in the concentration and activity of E2. Because this is a mechanism-based model, it also is capable of suggesting an explanation of this unexpected result through further analysis and examination of the rates of the individual reactions. Using an analogy of flow through various segments of a pipe, the sequential activation-conjugation-ligation steps can be imagined as pipe segments through which SUMO is transported (transformed). When the flow (reaction rate) through the various segments is equal, there will be no accumulation in the pipe. Conversely, for steady state, flow through segments of the pipe is independent of the properties of the segment, because the properties can adjust (different intermediate steady state concentrations) to ensure that exactly the same amount that enters from one end exits through the other. For [T₁₁]_ss, the flow is decided by the first activation step, which is seen in the dependence on E1 and SUMO (reflected in the rate constants that govern steady state concentrations of these entities). Once this flow rate is specified, the flow and hence the sumoylated target level is robust to changes in the properties of the succeeding steps (conjugation, ligation). Of course, both mathematically and in the analogy, the derivation and logic holds only when there is a pipe, i.e. the formation rate of E2 is not 0.

Simulation of [T₁₁]_ss as a function of various parameters is used to demonstrate this robustness, and the role of various model assumptions in the conclusion that [T₁₁]_ss is robust to changes in conjugation and ligation parameters. From the black solid lines in A and B of Fig. 3, it can be observed that changing k31 and k41, respectively, did not alter [T₁₁]_ss. Surprisingly, as long as the parameters are not 0, varying the parameters for formation and degradation of E20 and the target (b_E20, d_E20, b_T10, and d_T10) also had no effect on [T₁₁]_ss. The conclusion of this analysis is that, for an open system with sumoylation of one target, the activity of modifying enzyme E20 or the target formation rate have no effect on [T₁₁]_ss. This can be interpreted as a set of experimentally testable hypotheses directly arising from the modeling and analysis. For instance, under these assumptions (no degradation of intermediates, long term steady state), the increase in target protein transcription/translation rates should not cause any change in the steady state sumoylated target protein concentration.

FIGURE 3.

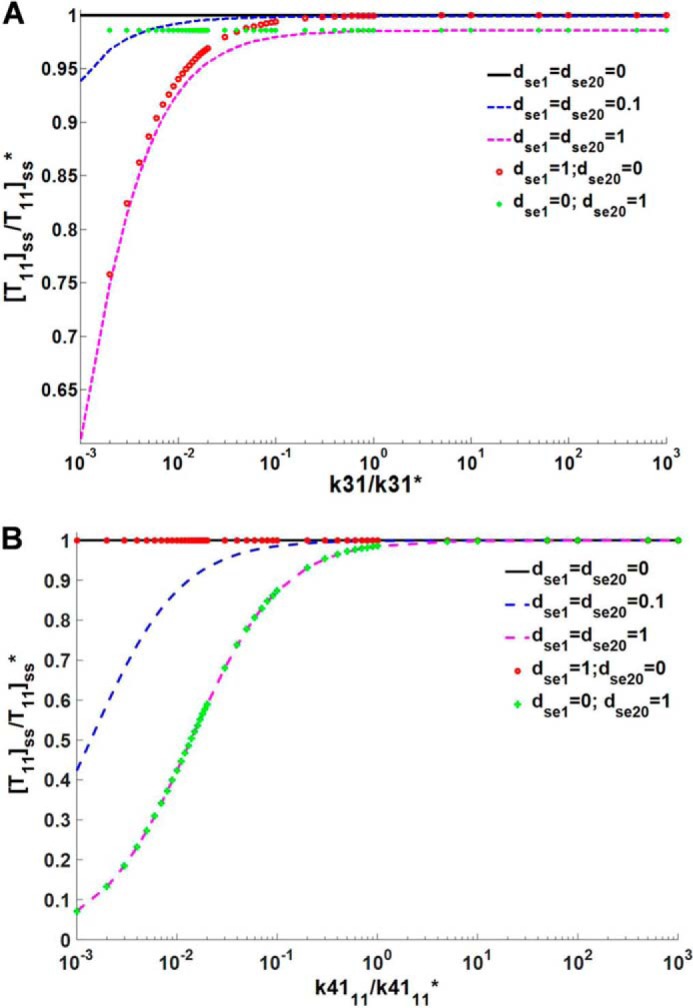
Effect of varying the conjugation and ligation step parameters k31 (A) and k41 (B), respectively, on [T₁₁]_ss in a simple open system with no E2 autosumoylation for varied values of the parameter for the degradation of intermediate SUMO complexes (d_se1 and d_se20). k31* and k41* represent the parameter values as reported in Table 1, and [T11]_ss* is the steady state sumoylated target concentration for the parameters in the Table 1.

In our model, we consider that the intermediate SUMO complexes formed from the activation and conjugation steps (sumoE1 and sumoE20, respectively) are immediately used up in the next step. However, it is possible that either or both of the intermediates are used up in different reactions or the intermediates can get degraded. We observe different steady state dynamics on introducing degradation of these intermediates. On simultaneous degradation of both the intermediates (d_se1 and d_se20 ≠ 0), it was observed that varying k31 and k41 has an effect on [T₁₁]_ss (pink and blue dashed lines in Fig. 3, A and B). If only sumoE1 was degraded (d_se1 ≠ 0 and d_se20 = 0), it was observed that modified target steady state levels are robust to change in k41 but were affected on varying k31 (curve with red open circles in Fig. 3, A and B)_. This case where only sumoE1 is degraded is similar to the system having simultaneous sumoylation of both the target and E2 as a part of sumoE1 is now used in modifying E2. Similarly, when a system has two targets, part of sumoE20 is used in sumoylation of the second target and such system can be compared with system with one target and degradation of only sumoE20 (d_se1 = 0 and d_se20 ≠ 0). Here we observed that varying k31 had no effect on [T₁₁]_ss, whereas it varied with change in k41 (curve with green plus marker in Fig. 3, A and B).

To investigate whether these observations were specific to sumoylation as modeled here, we analyzed a cyclic system with n intermediate complexes/enzymes on which the modifier is transferred before its final attachment on the target. Analytical steady state analysis of this n intermediate generalized cyclic system with single modification of the single target showed that the steady state levels of sumoylated target are robust to the intermediate parameters (supplemental materials, section B). Similar result is also reported by Junli Liu (15), who conducted a study to derive kinetic constraints for biochemical networks to attain non-negative finite steady states for all species of the network.

Effect of Autosumoylation of E2 on Target Sumoylation

One of the interesting features of the system is modification of its own enzymes. Along with the other substrates, the system enzymes E1, E2, and SENP are also targeted for modification. We investigated whether the system acquires additional properties on modification of its own enzymes. Reaction with parameter k6 in Fig. 2 represents autosumoylation of E2. To gain insight into the effect of the automodification on the target sumoylation, we simulated and compared [T₁₁]_ss for two cases: first, as control, we considered a system with sumoylation of only the target (k6 = 0), and second, with autosumoylation of E2 (k6 ≠ 0) along with the target. Sumoylation of E2 might alter its structure so that it now has changed binding affinity for the target.

It has been experimentally observed that sumoylation of E2 either has increased, decreased, or had no effect on target sumoylation (12). We simulated the cases in which we varied the target binding parameter of E21 (k42) from that of the E20 (k41). Knipscheer et al. (12) in their study report that E2 sumoylation does not alter its property of thioester formation; hence we consider the parameters k31 and k32 to be the same.

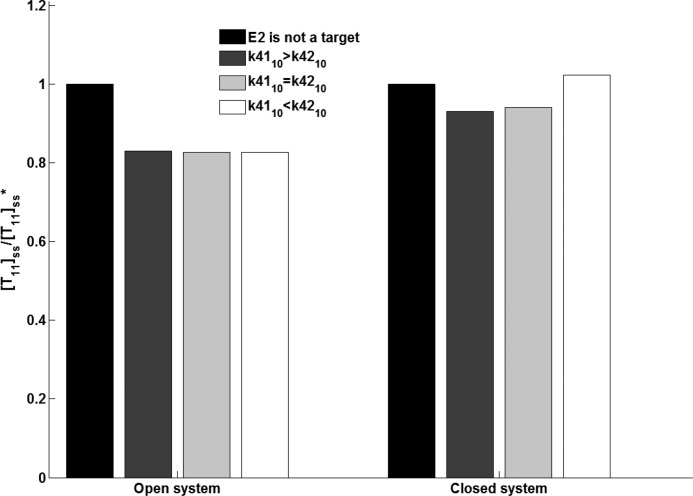
Fig. 4 shows [T₁₁]_ss for these four simulated conditions: no autosumoylation of E2 and E2 sumoylation resulting in increased, decreased, and unchanged target binding property (k42). For the open system, [T₁₁]_ss levels were observed to be lower in E2 modified system compared with its levels in system with no E2 modification. Even for the case when modification of E2 enhances its binding to the target (i.e. when k42 > k41), target sumoylation was lower (Fig. 4). However, for some cases of the closed system, as expected, the modification that made enzyme less active resulted in lower levels of [T₁₁]_ss compared with its level when there was no E2 modification, whereas the E2 modification that increased its binding with the target resulted in higher [T₁₁]_ss (Fig. 4). The reason for such unintuitive observation in open and for some cases of the closed system can be explained in terms of sequestration of E2. The effective modification rate depends on the product of the reaction rate constant (k41, k42) and the enzyme level ([sumoE20], [sumoE21]). Thus the weighted level of available E2 measured as: (k41 * [sumoE20] + k42 * [sumoE21]), decides the sumoylation rate in a system with E2 automodification. For all the cases of the open system we simulated, the system was found to have lower weighted levels of enzymatic E2 available for target modification in E2 modified system compared with k41 * [sumoE20] in the system with no E2 modification, resulting in the higher target sumoylation in the later system.

FIGURE 4.

Effect of automodification of E2 on steady state levels of the modified target ([T11]_ss) in open and closed system. In an open system with one target, the binding affinity of sumoE21 (k42) toward the target was enhanced (k41₁₀ < k42₁₀), lowered (k41₁₀ > k42₁₀), and kept the same (k41₁₀ = k42₁₀).

Role of SENP in Regulating Target Modification

Another interesting quirk of this system is dual and seemingly opposite function of SENP. SENPs are involved in both sumoylation and desumoylation of the targets. With their hydrolase activity, SENPs process the presumo to a mature form for its attachment to the target and by their isopeptidase activity cleave off the attached SUMO from the target. Such a dual role with opposite effects makes it difficult to intuitively predict the effect of change in SENP levels on target sumoylation.

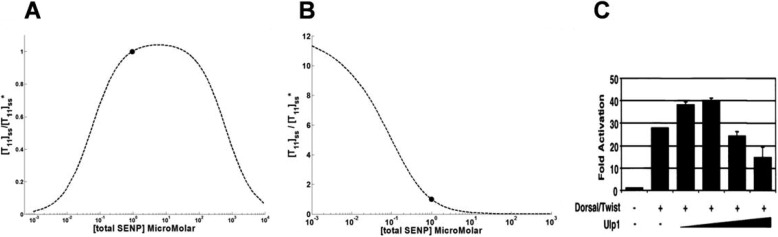
Fig. 5 shows the effect of changing total SENP level on target sumoylation. For the open system, we observed that maximum target sumoylation is seen for a particular SENP level. This trend was observed irrespective of E2 modification and even on degrading the intermediate SUMO complexes (Fig. 5A), whereas for the closed system, increasing SENP levels always led to a decrease in [T₁₁]_ss levels (Fig. 5B). This difference between open and closed systems can be explained in terms of presumo steady state levels. For a closed system, there is no formation (or degradation) of proteins including presumo. When the closed system reaches equilibrium conditions, the initial presumo is completely converted to mature SUMO. Hence all the available SENP is available for deconjugating the target, resulting in lower modified targets levels on increasing SENP. In contrast, the steady state of open system always has some presumo; hence the available SENP participates in both preprocessing and deconjugation. This result of the open system is in accordance with a study of Smt3 conjugation to Dorsal protein in Drosophila S2 cells, where increasing the amounts of Ulp1 expression vectors showed a biphasic response to the expression of Dorsal-dependent reporter activity (16). Their result figure is reprinted as Fig. 5C. Fold activation on y axes were calculated by dividing the relative luminescence of reporter having Dorsal/Twist to that of the relative luminescence of reporter alone.

FIGURE 5.

A and B, effect of total SENP levels on target sumoylation in open system (A) and in closed system (B). The plot is for the system in which E2 is not sumoylated and only one target is sumoylated. The dot indicates the value for reference of the total SENP concentration. C, reprint of the Fig. 3D from Ref. 16 (license agreement number 3805320570691) that represents a biphasic response of Dorsal to increasing amounts of Ulp1 reporter in Drosophila S2 cells.

Limitation in Availability of SUMO Is the Reason for Lower Levels of Sumoylated Target

One of the notable features of the SUMO system is that only a small fraction of any target is detected in sumoylated form in a cell at any given time. It is thought that the change in the function and localization of the target on sumoylation is retained even after it is desumoylated, and thus the system has low levels of the sumoylated target (17–19). From a mathematical analysis of this system, we conclude that one reason for low levels of SUMO modified forms of the target may be that the SUMO available for target modification is limiting.

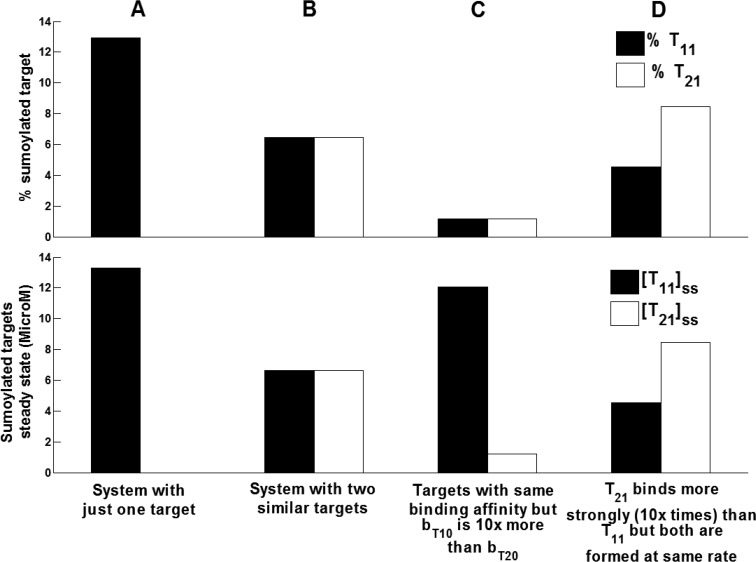
We simulated a simple open system using reported reaction rate parameters (Table 1) with either one or two targets. For the system having sumoylation of only one target, 12.9% target sumoylation was observed (Fig. 6A). We simulated three different cases for systems with two targets. First, we simulated a system having two targets with identical properties and hence reaction rate parameters and observed that steady state of sumoylated target and percent sumoylation was reduced to half (Fig. 6B). Second, we changed the formation rate (b_T10 = b_T20 * 10) for one target (T1) such that simulated steady state T₁₀ is at larger levels than T₂₀. It was interesting to note the steady state level of T₁₁ was more than T₂₁, but the percentage of sumoylation of each target was same (Fig. 6C). Third, we simulated a case of two targets at same total levels but with different binding affinities toward sumoE20 (k41₂₀ = k41₁₀ * 10). Here we observed that both percentage of target sumoylation and sumoylated targets steady state was more for the second target with increased binding efficiency but was not more than the single target in case A (Fig. 6D). From these simulations, it can be observed that having more concentration of one target or having many targets reduced the percentage of target sumoylation of each target. In this case, SUMO is the limiting factor and gets distributed over the available targets, thereby reducing individual percent target sumoylation. This observation suggests the hypothesis that SUMO available for modifying various known targets is limiting and hence results in lower levels of each sumoylated target in the system. Experimentally, it has also been shown that SUMO levels are limiting (18). These results support the conclusion independently reached from this modeling approach.

FIGURE 6.

Plots for percentage of the total target that is sumoylated at steady state and the steady state sumoylated target concentrations for simple open system with no E2 modification for following cases. A, simulation of the system with one target and for the reference parameters tabulated in Table 1. B, for the system with two similar targets that are monosumoylated (T₁₀ and T₂₀). C, system with two targets having same binding affinity (k42) but different formation rate (b_T10 = b_T20 * 10). D, system with two targets with same formation rate but different binding affinity (k41₂₀ = k41₁₀ * 10).

Discussion

Sumoylation is a post-translational modification in which small ubiquitin-like modifier is first processed and then attached to the target protein. Sumoylation of the target is not permanent, and the attached SUMO can be cleaved off by the bifunctional enzyme SENP recycling back the modifier SUMO and the initial unmodified target. With the concerted function of the enzymes SENP, E1, and E2 (sumoylated and native), the sumoylation system regulates modification and demodification of the target. We have mathematically modeled and analyzed this cyclic, autoregulated, multistep SUMO system. To the best of our knowledge, this is the first mathematical model for sumoylation. Most of the parameters of the model are obtained from literature (Table 1). These are derived from experimental single reaction, single-enzyme studies. Our framework uses parameters obtained from these individual experimental results for the simultaneous analysis of the entire sumoylation system. Simulation results in certain predictions of the response to changes in one or more parameters or concentrations. We have compared these predictions wherever possible to published experimental results. In all cases, these experimental results have not been used either in the formulation or parameterization of the model and hence provide independent support for the conclusions of this simulation study.

We have formulated a model for multiple levels of sumoylation of multiple targets for open and closed systems. Simulations and analysis revealed several unexpected results: (i) for an open system with one target and no autosumoylation of E2, simulations and analysis show that when there is no degradation of intermediate SUMO complexes, target sumoylation is robust to changes in properties of the conjugation and ligation steps; (ii) when E2 is autosumoylated, for the open system, [T₁₁]_ss levels were always higher in the system with no modification of E2 compared with [T₁₁]_ss levels in system with E2 modification even when E2 modification resulted in more efficient enzyme; (iii) for an open system, there is an optimal concentration of the bifunctional enzyme SENP that results in a maximum [T₁₁]_ss, but for the closed system, an increase in SENP levels always resulted in lower[T₁₁]_ss; and (iv) only a small fraction of each target is sumoylated.

Unlike a puzzling experimental observation or correlation, the cause of any result obtained from a mechanism-based mathematical model can be identified through dissection of the underlying mechanism because all the data are already available and linked to a biological process, in this case enzymatic transformation steps. Our analysis revealed that this unexpected result can be explained through further simulations and mathematical analysis of the sumoylation system model.

Robustness to parameters has been investigated in other enzymatic systems. It has been previously proposed that antagonistically bifunctional “paradoxical” enzymes can provide robustness to the system (20). For this system, we found that bifunctionality of SENP is not the cause for robustness. We simulated a system having two SENP isoforms and tested two situations: (i) each having only preprocessing and only deconjugation activity, respectively, and (ii) each having both the functionalities. For both these scenarios, modified target steady state levels were robust to the parameters of intermediate catalyzing steps ([T₁₁]_ss expression for both the cases is given in supplemental materials, section C). We further checked whether the robustness of [T₁₁]_ss levels to the parameters of conjugation and ligation steps was restricted only to sumoylation-like system having two steps before target modification. We investigated the flux or reaction rate of each step and the modulation by the concentration of intermediate complexes and discovered the explanation for the robustness, which is that the flux or reaction rate during the modification steps is determined by the first step, and the concentration of the intermediates adjusts so that an equal flux is maintained at steady state.

To understand the role of E2 sumoylation on target sumoylation, we calculated the effective enzyme activity (k41 * [sumoE20] + k42 * [sumoE21]) and found that it was lower in E2 modified system, even when E21 activity was increased. Thus the cause of the unexpected lower [T₁₁]_ss levels compared with when there was no E2 modification could be explained. This simulation result suggests the hypothesis that the system may show differing qualitative steady state behavior over long time scale (open system) than for short time scale (pseudo), steady state behavior (closed system). Therefore the results of experiments where the initial response is monitored (in vitro) may be qualitatively different from results where the long term response (in vivo) is monitored.

SENP helps in both modification of the target by processing presumo, as well as in demodifying the target, by cleaving off the tagged SUMO from the target. SENPs show more preference for their deconjugating isopeptidase activity over SUMO processing hydrolase activity. This observation was reviewed previously (21) and also is reflected in k_cat values of SENP for the two reactions (22). In the case of species having only one SENP isoform as assumed here, it can be inferred that SENP levels in the system are the deciding factors for modified targets levels. For an open system, we observed maximum target sumoylation for a particular SENP level, and [T₁₁]_ss decreases when SENP concentration either increases or decreases from this optimal level. Experimental validation of this result is shown in Fig. 5C. The data from the experiment were not used in model construction or parameter estimation, and this experimental observation independently supports the predictions of the model. This result is independent of modification of E2 and binding affinity of E2 toward the target. The result was also consistent even upon degrading the intermediate SUMO complexes: sumoE1 and sumoE20. However, at the equilibrium of the closed system, because the presumo is completely converted to SUMO and none is available on which SENP can have its preprocessing activity, increased SENP levels resulted in increased deconjugation of T₁₁ and hence lower [T₁₁]_ss. Once again, there is a qualitative difference between the results for the open and closed systems.

Lastly, from the analysis from our model, we hypothesize that limitation of available SUMO might be the reason for having only less than 5% sumoylation for most targets. Intuitively, it is possible that increasing desumoylation of the modified target or increasing its degradation can also be the reasons to have lower sumoylated levels. There are some studies that focus on linking the SUMO and ubiquitin cycle together. In targets like PML and BMAL1, it is reported that sumoylation of these targets is a signal for their ubiquitination (23). Thus sumoylation of the target may lead to its degradation and hence result in lower sumoylated target levels. By comparing the parameters for deconjugation and ligation, it is clear that desumoylation occurs more rapidly than sumoylation of the target. However, even on simulating the system having one target with known deconjugation parameter, just 12.9% of the total target was found to be sumoylated in the system (Fig. 6A). On introducing the second target in the system, the level of sumoylated targets of either of the targets is never above 12.9%, even when varying their total amount or their ligation affinity. This result thus supports our hypothesis that limitation of available SUMO to sumoylate all the available targets in the cell might be the reason for the lower levels of sumoylated targets. Further, on simulating the case in which SUMO was not limiting, i.e. when we simulated the system by setting equal formation rates for presumo and target (b_ps = b_T10) and by keeping the same deconjugation rates, we observed that almost 94% of target is sumoylated at steady state (results not shown). Thus we can speculate that one of the reasons for having lower fractions of post-translationally modified substrates can be that, given the vast number of targets, the modifier is not enough to modify all the available substrate(s). Experimentally it has also been shown that SUMO levels are limiting (18). Again, because data from this experiment was not used in construction or simulation of the model, it independently supports the finding of the simulation study. From Fig. 6C, it can also be noted that increasing the amount of one target in the system increased the steady state sumoylation level of that target even if the percentage of target sumoylation remained same. Hence the model simulations result in the testable prediction that increasing the total amount of the target in the experiments can be one of the methods adopted to have an increase in the detection of the sumoylated target.

We have simulated only a handful of the combinatorially large number of possible sumoylation scenarios. The parameters that we used related to the target (as tabulated in Table 1) are for the nuclear membrane associated protein RanGap1. We varied all the eight target related parameters by 5-fold and observed that the results did not change qualitatively (results not shown). We believe that this model can serve as a starting point for many modeling studies for specific situations that help analyze the corresponding experimental studies. The model simulations led to several hypotheses that are experimentally testable, because all parameters are linked to one or more molecules that participate in sumoylation. Although the analysis and simulation results presented here are mathematically and computationally accurate and a direct consequence of the model assumptions, an iterative cycle of modeling-driven hypotheses and experimentation will result in ever-increasing understanding of the complex sumoylation system.

Author Contributions

S. S. P. was responsible for model development, steady state and detailed analysis, code development and simulations, parameter variation simulations, initial draft, and modification and revision of the manuscript. D. N. performed steady state analysis, initial model and code development and simulations, and analysis of simulation results. P. S. was responsible for initial model development, analysis of the generic modification system, and analysis of simulation results. C. J. G. initiated the study and participated in model formulation, analysis of the model and simulation results, and modification and revision of the manuscript. All authors read and approved the final manuscript.