Abstract
The global diabatic potential energy surfaces which are correlated with the ground state 1A′ and the excited state 2A′ of the Li(2p) + H2 reaction are presented in this study. The multi-reference configuration interaction method and large basis sets (aug-cc-pVQZ for H atom and cc-pwCVQZ for Li atom) were employed in the ab initio single-point energy calculations. The diabatic potential energies were generated by the diabatization scheme based on transition dipole moment operators. The neural network method was utilized to fit the matrix elements of the diabatic energy surfaces, and the root mean square errors were extremely small (3.69 meV for 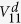 , 5.34 meV for
, 5.34 meV for 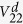 and 5.06 meV for
and 5.06 meV for 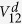 ). The topographical features of the diabatic potential energy surfaces were characterized and the surfaces were found to be sufficiently smooth for the dynamical calculation. The crossing seam of the conical intersections between the
). The topographical features of the diabatic potential energy surfaces were characterized and the surfaces were found to be sufficiently smooth for the dynamical calculation. The crossing seam of the conical intersections between the 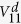 and
and 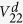 surfaces were pinpointed. Based on this new analytical diabatic potential energy surfaces, time-dependent wave packet calculation were conducted to investigate the mechanism of the title reaction. At low collision energies, the product LiH molecule tends to forward scattering, while at high collision energies, the forward and backward scatterings exist simultaneously.
surfaces were pinpointed. Based on this new analytical diabatic potential energy surfaces, time-dependent wave packet calculation were conducted to investigate the mechanism of the title reaction. At low collision energies, the product LiH molecule tends to forward scattering, while at high collision energies, the forward and backward scatterings exist simultaneously.
Chemical reactions involving Li atom and H2 molecule play an important role in early cosmic evolution1,2,3,4,5,6,7,8,9,10. Moreover, LiH molecule makes a considerable contribution to the cosmic background radiation7,8,9. The elementary reactions Li(2s, 2p) + H2(X1Σ+g) ↔ H + LiH(X1Σ+) have great influence on the formation and depletion of LiH7,8. Therefore, the research concerning the LiH2 system plays a vital role in understanding the early evolution of the universe.
Over the past decades, the ground state of the LiH2 system has received extensive attention in theoretical studies9,10,11,12,13. The first three-dimension adiabatic potential energy surface (PES) for the ground state of the LiH2 molecule was constructed by Dunne et al.11. This PES shows an unphysical well at the Li(2s) + H2(X1Σ+g) asymptotic valley. In 2009, two PESs of the ground states of LiH2 system were reported by Prudente et al. and Wernli et al.12,13 Recently, Chen and co-workers presented a high-precision PES for the ground state of the LiH2 system14. All the four PESs were employed to study the reaction dynamics of the LiH(X1Σ+) + H → Li(2s) + H2(X1Σ+g) reaction using the quasi-classical trajectory (QCT) and time-dependent wave packet (TDWP) method12,15,16,17.
Although the LiH(X1Σ+) + H → Li(2s) + H2(X1Σ+g) reaction has been widely studied in theory, less attention has been paid to experimental studies. In contrast, a large number of experimental studies have been carried out on the Li(2p) + H2(X1Σ+g) → LiH(X1Σ+) + H reaction18,19,20,21. Mysers et al.18 measured the reaction cross section (σ = 0.10 ± 0.03 Å2) of the Li(2p) + H2(X1Σ+g) reaction at a temperature of T = 788 K. In 2001, Lin and co-workers19 measured the rotational population distribution of LiH(v = 0) for this reaction by using a pump–probe technique, and observed that the reactive collisions are dominated by insertion mechanism. Bililign et al.20 observed that the Li(2p) + H2 reaction occurs preferentially within bent geometry (near C2v) by using the far-wing scattering spectroscopy. Chen et al.21 studied the effect of vibrational excitation of H2 on the rotational state distributions of LiH(v = 0) for the Li(2p) + H2(v = 1) → LiH(X1Σ+) + H reaction using a pump-probe technique.
Although, many experimental studies have focused on the Li(2p) + H2(X1Σ+g) → LiH(X1Σ+) + H reaction, few theoretical studies of this reaction have been reported22,23. The reactants Li(2p) + H2(X1Σ+g) and the products LiH(X1Σ+) + H correlate with two different adiabatic states (22A′, 12A′). Thus, the Born-Oppenheimer (BO) approximation is not valid in the vicinity of the conical intersection24. To appropriately deal with the breakdown of the BO approximation, a proper diabatization scheme should be chosen to adequately treat the coupling between the two states. In 1999, Lee et al.22 investigated the Li(2p) + H2 collisions. The PES used in their research is limited to three different point group symmetries: C∞v, C2v and Cs where the molecular axis of the H2 molecule makes an angle of π/4 with respect to the velocity vector of the lithium atom. Since this PES is not global, it cannot accurately describe all the features of the intermolecular interaction potential of the Li(2p) + H2 reaction. In 2011, two adiabatic global PESs of LiH2 (12A′, 22A′) were constructed by Hsiao et al.23, and the QCT calculations were carried out based on their PESs. In their QCT calculations, the trajectories initially evolve on the excited state surface 22A′ and hop to the ground state 12A′ at the exit channel. The transition probability between the two states (12A′, 22A′) was assumed to be unity, which is an approximate method for treating the diabatic process of the reaction. A valid method for describe the effect of the diabatic process for the molecular reaction accurately, is to construct a set of diabatic PESs for the coupled electronic states. However, for the title reaction, there are no such a set of diabatic PESs that can be employed for dynamical calculations. To meet these requirements above mentioned, a set of global diabatic PESs was constructed for the lowest two 2A′ states of LiH2 system using the neural network (NN) method25. Based on the diabatic PESs, the reaction dynamics of the title reaction were investigated using the TDWP method.
Results
PESs topographical attributes
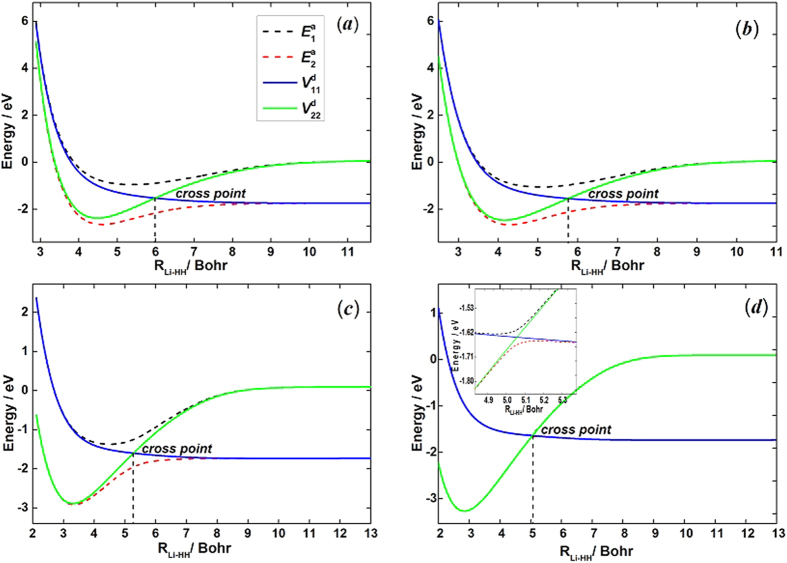
The accuracy of the ab initio computations can be assessed by comparing the calculated spectroscopic constants with the experimental values. The spectroscopic constants of H2 and LiH obtained from the diabatic PESs and the corresponding experimental data are listed in Table 1. The H2 and LiH spectroscopic constants were calculated in the supermolecule approach with the other atom (Li and H, respectively) at a distance of 30 a0. Obviously, all of the theoretical results have a good agreement with the corresponding experimental results26,27. The calculated equilibrium bond lengths and harmonic vibrational frequencies of H2 and LiH are nearly identical with the experimental values. Both of the dissociation energies of H2 and LiH are slightly smaller than the corresponding experiment data. The small error of anharmonic constants for H2 and LiH are 0.8 cm−1 and 3.4 cm−1, respectively. Figure 1 shows the adiabatic and diabatic potential curves for a fixed internuclear distance of HH molecule (rHH = 2.9 a0) as function of RLi-HH for various values of θ, which is the angle between RLi-HH and rHH. It is noted that the cross point shifts to the smaller RLi-HH with the increase of θ. At large θ, the adiabatic potentials strongly avoid each other in the neighborhood of the crossing point; on the contrary, the diabatic potentials cross over with each other smoothly. Furthermore, in all cases, the adiabatic and diabatic energies become identical when the molecular geometries are far from the crossing point. Figure 2 shows the corresponding mixing angles which were used to constructed diabatic potential curves shown in Fig. 1. It can be seen from this figure that in the vicinity of the crossing point, the change rate of the mixing angle becomes steeper with the increase of θ. The mixing angle reaches an asymptotic value gradually with the increase of RLi-HH. Otherwise, according to Eqs (2) and (3), the cross point appears when the mixing angle θ equals to 45° and this conclusion is in agreements with the result of Fig. 1. Figure 3 shows the coupling potentials obtained from the corresponding mixing angle and the adiabatic potentials. The value of the coupling potential decreases more rapidly with the increase of θ and the coupling potential gradually decrease to zero, while the RLi-HH increases to a large value. According to Eq. (4), it is can be concluded that the smaller value of the difference between 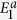 and
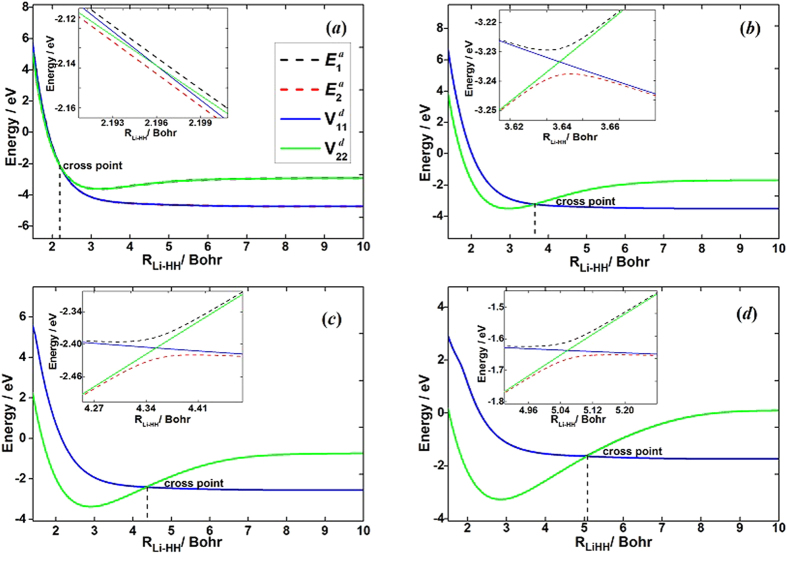
and 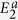 is, the smaller value of coupling potential is. This conclusion is consistent with the result obtained from Fig. 3. Figure 4 shows the adiabatic and diagonal diabatic potential energy curves for θ = 90° as a function of RLiHfor various HH bond lengths rHH. It clearly shows that the cross point shifts to larger RLi-HH with the increase of HH bond length. The three-dimensional diabatic PESs and the corresponding contour plots of the differences
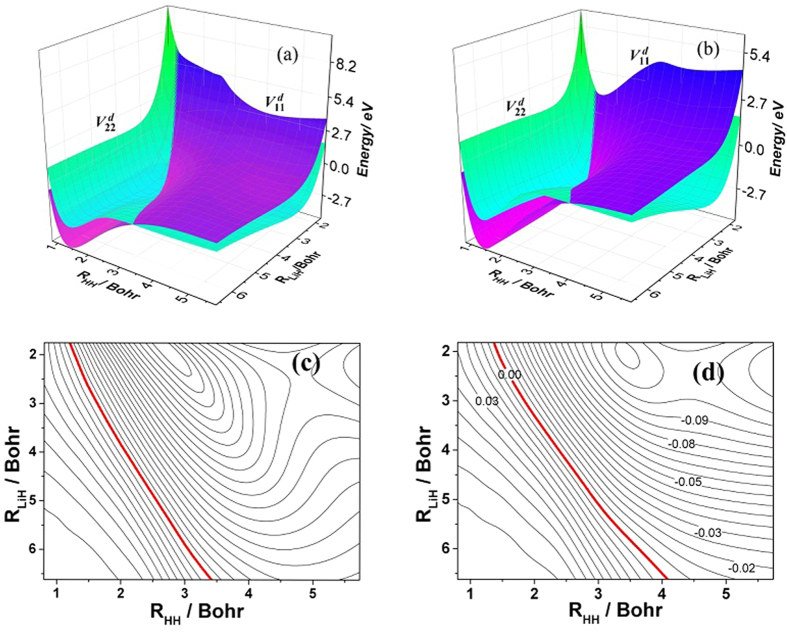
is, the smaller value of coupling potential is. This conclusion is consistent with the result obtained from Fig. 3. Figure 4 shows the adiabatic and diagonal diabatic potential energy curves for θ = 90° as a function of RLiHfor various HH bond lengths rHH. It clearly shows that the cross point shifts to larger RLi-HH with the increase of HH bond length. The three-dimensional diabatic PESs and the corresponding contour plots of the differences 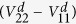 of the two diabatic states are presented in Fig. 5. From the upper panel of Fig. 5, it can be seen that for the top state, the reactant region was dominated by
of the two diabatic states are presented in Fig. 5. From the upper panel of Fig. 5, it can be seen that for the top state, the reactant region was dominated by 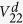 and the product region was dominated by
and the product region was dominated by 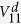 , whereas the bottom state shows a reverse case. It can be seen that the transition of the title reaction occurs in the vicinity of interaction region. The lower panel of Fig. 5 shows the exact position of the crossing seam. The red lines in these contour plots represent the isopotential line
, whereas the bottom state shows a reverse case. It can be seen that the transition of the title reaction occurs in the vicinity of interaction region. The lower panel of Fig. 5 shows the exact position of the crossing seam. The red lines in these contour plots represent the isopotential line 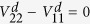 , i.e., the conical intersection seam of the two surfaces. The Li(2p) + H2 → LiH(X1Σ+) + H reaction processes on the
, i.e., the conical intersection seam of the two surfaces. The Li(2p) + H2 → LiH(X1Σ+) + H reaction processes on the 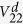 surface. The minimum energy paths of the title reaction as function of RHH − RLiH coordinate for various values of θ are shown in Fig. 6. From this plot it can be seen that there is a deep well (about 0.8 eV) along the reaction path. This well has a great impact on the reaction. The reactant zero point energy (ZPE) is 0.273 eV and the product ZPE is 0.086 eV, so that the endothermicity of the title reaction is 0.225 eV, taking into consideration the ZPEs of reactant and product.
surface. The minimum energy paths of the title reaction as function of RHH − RLiH coordinate for various values of θ are shown in Fig. 6. From this plot it can be seen that there is a deep well (about 0.8 eV) along the reaction path. This well has a great impact on the reaction. The reactant zero point energy (ZPE) is 0.273 eV and the product ZPE is 0.086 eV, so that the endothermicity of the title reaction is 0.225 eV, taking into consideration the ZPEs of reactant and product.
Table 1. Spectroscopic constants for LiH(X1Σ+) and H2(X1Σg +).
Figure 1.
Adiabatic and diabatic potential energies at (a) θ = 3.0°, (b) θ = 30.0°, (c) θ = 60.0°, (d) θ = 90.0° for fixed rHH = 2.9 a0 vs RLi-HH. The solid lines represent the diabatic potential energies and the dashed lines represent the adiabatic potential energies.
Figure 2.
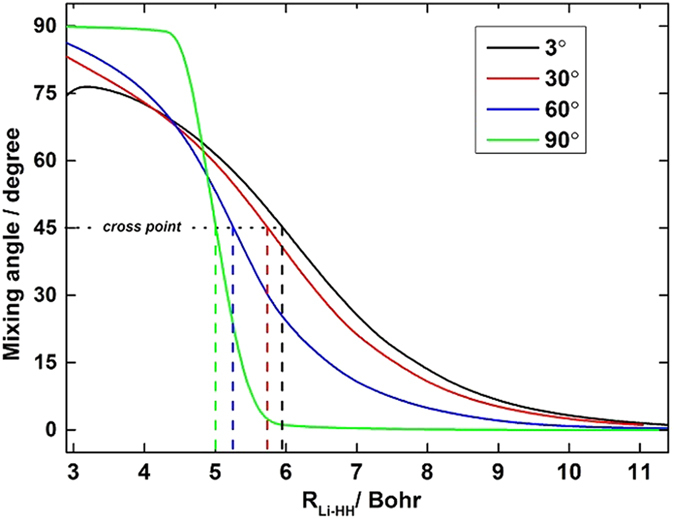
Mixing angles as function of RLi-HH for fixed rHH = 2.9 a0 and (a) θ = 3.0°, (b) θ = 30.0°, (c) θ = 60.0°, (d) θ = 90.0°.
Figure 3.
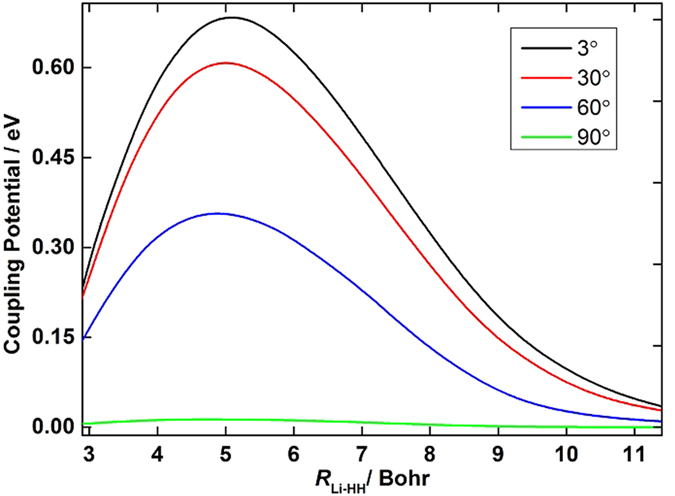
Coupling potentials as function of RLi-HH for fixed rHHand (a) θ = 3.0°, (b) θ = 30.0°, (c) θ = 60.0°, (d) θ = 90.0°.
Figure 4.
Adiabatic and diabatic potentials at (a) rHH = 1.4 a0, (b) rHH = 2.1 a0, (c) rHH = 2.5 a0, (d) rHH = 2.9 a0 for fixed θ = 90.0° vs RLi-HH. The solid lines represent the diabatic energies and the dashed lines represent the adiabatic energies.
Figure 5.
Three dimension PESs of the diabatic states 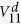 and
and 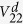 for Li-H-H with a bond angle of (a) 60.0° and (b) 90.0°. The corresponding contour plot of their differences (
for Li-H-H with a bond angle of (a) 60.0° and (b) 90.0°. The corresponding contour plot of their differences (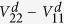 ) are showed in (c,d), respectively. The red lines represent the position of the diabatic crossing.
) are showed in (c,d), respectively. The red lines represent the position of the diabatic crossing.
Figure 6. Minimum energy paths of diabatic PES 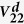 for Li-H-H angle fixed at 60.0° and 90.0°.
for Li-H-H angle fixed at 60.0° and 90.0°.
Dynamical calculations
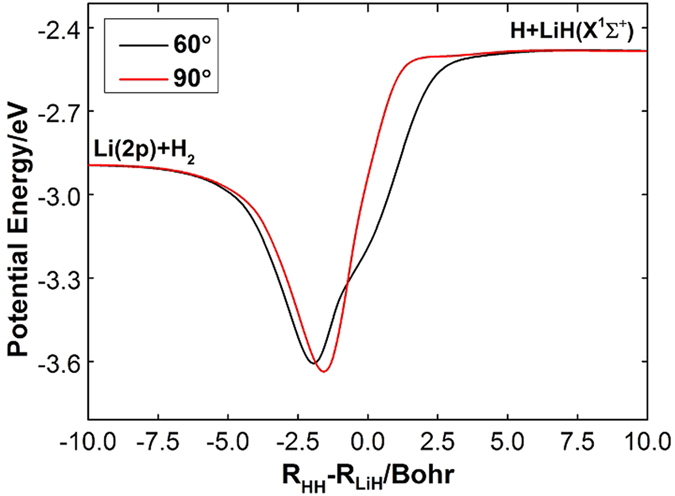
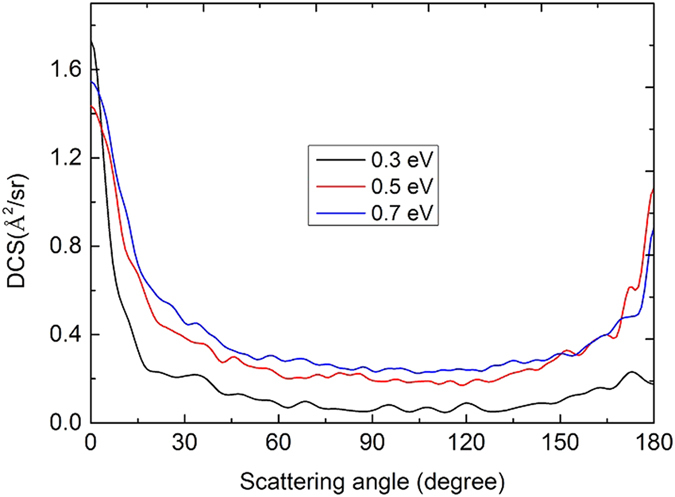
Figure 7 shows the initial state-specified (v = 0, j = 0) total reaction probabilities at five total angular momentum quantum number J values (0, 20, 30, 40, 50) as a function of the collision energy. For the reaction probabilities of J = 0, there is a threshold about 0.225 eV which corresponds to the endothermicity of the reaction. With the increase of the J value, the threshold increases due to the emergence of a centrifugal barrier. In the curves of the reaction probabilities, there are a mass of peaks, especially at low collision energies, which is a typical feature of quantum resonance. The feature probably corresponds to long-lived resonances associated with the well (about 0.8 eV relative to the Li(2p) + H2(X1Σ+g) asymptote) on the  . The amplitude of the oscillations decreases with the collision energy increasing, because of the decrease in lifetime of the intermediate complex. In TDWP calculation, the maximum total angular momentum quantum number is 65, which is large enough to calculate the integral cross sections (ICSs) and differential cross sections (DCSs) at the collision energies under 1.0 eV. Figure 8 shows the total and vibrationally resolved ICSs of Li(2p) + H2 (X1Σ+g) → LiH(X1Σ+) + H reaction calculated by the S-matrix method. There are a small amount of tiny oscillations on the ICSs curves, which is different from the intense and sharp peaks on the curves of probability. It is because the resonance structure is erased by summing over all the partial waves. For the total ICSs, the threshold is 0.225 eV which is consistent with the probability for J = 0. With the collision energy increasing, the total ICSs increases and the four vibrational excitation states of product appear in the order of v′ = 1 to v′ = 4. With the collision energy increasing, the ICS of ground vibrational state increases until reaching the maximum value at collision energy of 0.505 eV. When the collision energy increases from 0.505 eV, the ICSs for the vibrational excitation states still increases, but it decreases for the ground vibrational state. Therefore, the increase of the total ICSs comes from vibrational excitation states when the collision energy is higher than 0.505 eV. Figure 9 presents the DCSs of the Li(2p) + H2(X1Σ+g) → LiH(X1Σ+) + H reaction at three collision energies to study the angular distribution of the product LiH. As shown in the figure, the product molecule LiH tends to be forward scattering at low collision energy (0.3 eV). With the collision energy increasing, the peak at 180° appears, which implies that the trend of the backward scattering of LiH molecule becomes more and more obvious. However, the peak at 0° is still higher than that at 180°, thus the forward scattering is dominant in the title reaction.
. The amplitude of the oscillations decreases with the collision energy increasing, because of the decrease in lifetime of the intermediate complex. In TDWP calculation, the maximum total angular momentum quantum number is 65, which is large enough to calculate the integral cross sections (ICSs) and differential cross sections (DCSs) at the collision energies under 1.0 eV. Figure 8 shows the total and vibrationally resolved ICSs of Li(2p) + H2 (X1Σ+g) → LiH(X1Σ+) + H reaction calculated by the S-matrix method. There are a small amount of tiny oscillations on the ICSs curves, which is different from the intense and sharp peaks on the curves of probability. It is because the resonance structure is erased by summing over all the partial waves. For the total ICSs, the threshold is 0.225 eV which is consistent with the probability for J = 0. With the collision energy increasing, the total ICSs increases and the four vibrational excitation states of product appear in the order of v′ = 1 to v′ = 4. With the collision energy increasing, the ICS of ground vibrational state increases until reaching the maximum value at collision energy of 0.505 eV. When the collision energy increases from 0.505 eV, the ICSs for the vibrational excitation states still increases, but it decreases for the ground vibrational state. Therefore, the increase of the total ICSs comes from vibrational excitation states when the collision energy is higher than 0.505 eV. Figure 9 presents the DCSs of the Li(2p) + H2(X1Σ+g) → LiH(X1Σ+) + H reaction at three collision energies to study the angular distribution of the product LiH. As shown in the figure, the product molecule LiH tends to be forward scattering at low collision energy (0.3 eV). With the collision energy increasing, the peak at 180° appears, which implies that the trend of the backward scattering of LiH molecule becomes more and more obvious. However, the peak at 0° is still higher than that at 180°, thus the forward scattering is dominant in the title reaction.
Figure 7. Total reaction probabilities of the Li(2p) + H2(X1Σg+) → LiH(X1Σ+) + H reaction calculated by TDWP method at J = 0, 20, 30, 40 and 50.
Figure 8. Total and vibrationally resolved ICSs of the Li(2p) + H2(X1Σg+) → LiH(X1Σ+) + H reaction calculated by TDWP method.
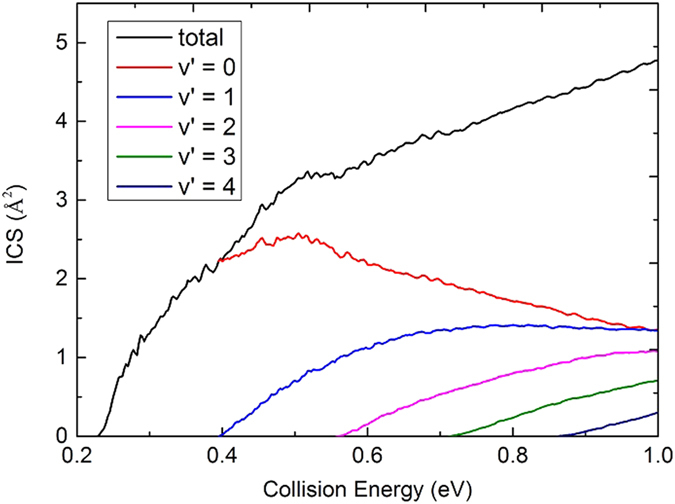
Figure 9. DCSs of the Li(2p) + H2(X1Σg+) → LiH(X1Σ+) + H reaction calculated by TDWP method at three energies.
Discussion
A set of diabatic potential energy surfaces for the ground and first excited state of LiH2 system was constructed using a proper diabatization scheme and high-quality ab initio energy data. The diabatization scheme is based on transition dipole moments which could reflect the correct transition properties through the conical intersection. The ab initio calculations were performed by internally contracted multi-reference configuration interaction (MRCI)28,29 method. The augmented correlation-consistent polarization valence quadruple-ζ (AVQZ)30 atomic basis was employed for H atom and the Dunning-weighted correlation consistent polarized core-valence quadruple-ζ (WCVQZ)30 atomic basis was employed for Li atom. The NN methods are used to fit the diabatic potential energy surfaces and three high-accuracy potential surfaces were constructed with extremely small root mean square error (RMSE) (3.69 meV for 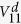 , 5.34 meV for
, 5.34 meV for 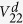 and 5.06 meV for
and 5.06 meV for 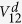 ). The endothermicity of Li(2p) + H2(X1Σg+) → LiH(X1Σ+) + H reaction is 0.225 eV. There is a deep potential well about 0.8 eV exists in the reaction pathway. On the new PESs, the TDWP method was used to study the reaction of Li(2p) + H2 (X1Σ+g) → LiH(X1Σ+) + H. The reaction probabilities, ICSs and DCSs of the title reaction were calculated. The threshold is about 0.225 eV which corresponds to the endothermicity of the reaction. A mass of peaks are found on the curves of reaction probabilities especially at low collision energies, and this feature probably corresponds to the long-lived complex formed in the well. However, there is only a small amount of tiny oscillations on the total ICS curve, because the resonance is eased by summing over all the partial waves. The DCS results show the product LiH tends to be forward scattering at low collision energy (0.3 eV). With the collision energy increasing, the forward and backward scatterings both exist in the reaction. To our knowledge, there are no experimental results that can directly compare with theoretical results presented here. We are eagerly looking forward to a molecular beam experiment for the title reaction in the future, so that a comparison between theory and experiment can be fulfilled.
). The endothermicity of Li(2p) + H2(X1Σg+) → LiH(X1Σ+) + H reaction is 0.225 eV. There is a deep potential well about 0.8 eV exists in the reaction pathway. On the new PESs, the TDWP method was used to study the reaction of Li(2p) + H2 (X1Σ+g) → LiH(X1Σ+) + H. The reaction probabilities, ICSs and DCSs of the title reaction were calculated. The threshold is about 0.225 eV which corresponds to the endothermicity of the reaction. A mass of peaks are found on the curves of reaction probabilities especially at low collision energies, and this feature probably corresponds to the long-lived complex formed in the well. However, there is only a small amount of tiny oscillations on the total ICS curve, because the resonance is eased by summing over all the partial waves. The DCS results show the product LiH tends to be forward scattering at low collision energy (0.3 eV). With the collision energy increasing, the forward and backward scatterings both exist in the reaction. To our knowledge, there are no experimental results that can directly compare with theoretical results presented here. We are eagerly looking forward to a molecular beam experiment for the title reaction in the future, so that a comparison between theory and experiment can be fulfilled.
Methods
Potential Energy Surface
Diabatizaton scheme
The Li(2p) + H2 → LiH(X1Σ+) + H reaction is correlated with 12A′ and 22A′ of LiH2 molecule in Cs symmetry. For LiH2 system, the 12A′ state corresponds to 12A1 state in C2v symmetry, while the 22A′ state corresponds to 12B2 state in C2v symmetry. There are many methods of diabatization for the construction of the diabatic states31,32,33,34,35,36,37,38,39,40. In this work, the molecule property which could reflect the character of the transition between those coupled states is used to construct the diabatic PESs. The diabatization scheme used in this work is briefly described here and more detail presentation can be found in previous literatures33,34,35. Considering two coupling states, the diabatic wave functions 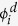 can be constructed from adiabatic wave functions
can be constructed from adiabatic wave functions 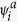 by the following unitary transformation
by the following unitary transformation
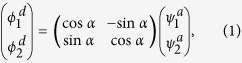 |
where α is the mixing angle. The diabatic energies 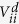 can be obtained in terms of adiabatic energies
can be obtained in terms of adiabatic energies 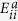 by
by
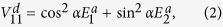 |
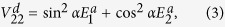 |
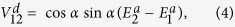 |
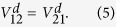 |
The 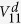 and
and 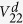 are the corresponding diabatic potential energies in the diabatic states, and the
are the corresponding diabatic potential energies in the diabatic states, and the 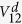 and
and 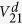 are the coupling potential energies between the two states. The mixing angle α can be obtained by molecular properties35,36,37,39,40. In our work, the transition dipole moments are used to obtain the mixing angle. According the Eq. (1), the matrix elements
are the coupling potential energies between the two states. The mixing angle α can be obtained by molecular properties35,36,37,39,40. In our work, the transition dipole moments are used to obtain the mixing angle. According the Eq. (1), the matrix elements 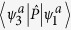 and
and 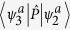 can be written as follows:
can be written as follows:
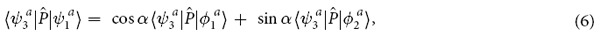 |
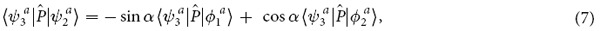 |
where 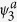 is a third state which not involved in the coupling. The operator
is a third state which not involved in the coupling. The operator 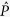 is taken to be dipole moment
is taken to be dipole moment 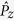 which is parallel to the z axis. An approximate treatment is that the
which is parallel to the z axis. An approximate treatment is that the 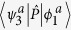 is set as zero and the
is set as zero and the 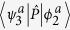 was set as one not just for the high symmetry geometries (C2v, D2h), but for all geometries. Then the mixing angle α can be derived from:
was set as one not just for the high symmetry geometries (C2v, D2h), but for all geometries. Then the mixing angle α can be derived from:
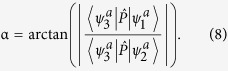 |
Ab initio calculations
The Jacobi coordinates are employed to generate the ab initio grid points. All of the three atoms are located in the x-z plane and the Li atom is fixed along the z axis. The center of mass of HH is set as the origin. The energy grid points are defined by 0.0 ≤ RLi-HH /a0 ≤ 30.0, 0.6 ≤ rHH/a0 ≤ 30.0 and 0.0 ≤ θ/deg ≤ 90 for Li-H2 reactant region, and 0.0 ≤ RH-LiH /a0 ≤ 30.0, 1.3 ≤ rLiH/a0 ≤ 30.0 and 0.0 ≤ θ/deg ≤ 180 for H-LiH product region, R, r and θ are the atom-diatom Jacobi coordinates. The coverage is sufficiently large for guaranteeing the quality of the asymptotic channels and the dynamic calculation. Otherwise, high-density grid points are distributed in connection region between strong interaction and asymptotic region for ensuring the accuracy of this region. In order to warrant the quality of the fitting, 15398 geometries are chosen to generate the ab initio energy points. Different step size of R and r are applied for generate the grid points. More specifically, the step size of R and r in interaction region, asymptotic region and connection region between the interaction and asymptotic region are about 0.2 Bohr, 2.0 Bohr and 0.5 Bohr, respectively. Moreover, the ab initio energy points above 20.0 eV relative to the energy of the Li-H-H dissociation limit are excluded from the fitting process. All of these ab initio energy points are calculated at the internally contracted MRCI level and using the complete active space self-consistent field (CASSCF)41,42 wave function as reference. Three valence electrons are included in eleven active orbitals and three states (12A′, 22A′ and 12A″) of LiH2 are set equal weight in state-averaged CASSCF calculations. In both the CASSCF and MRCI calculations, the WCVQZ and the AVQZ basis sets are employed for the Li and H atoms, respectively. For the two states (12A′, 22A′) of LiH2, 30796 ab initio adiabatic energy points are obtained to construct the diabatic energies. The transition dipole moments mentioned above are also calculated. All ab initio calculations in this work are performed by MOLPRO43 package.
Fitting the diabatic PESs
The diabatic potential energies are obtained by the diabatization scheme mentioned above from the raw ab initio adiabatic energies. All of the diabatic potential energies are fitted by NN method. The back-propagation NN model is chosen in the fitting procedure. To ensure the quality of the fitting, there were two hidden layers in our NN method and 15 neurons were included in each hidden layer. There are 322 free parameters in the NN. The cross validation method was employed to detect and prevent over fitting of the training procedure. In this work, the ab initio energy points were separated into three sets, called training set, testing set and validation set. The training set was used for adapting the weights of the neural network and the validation set was used for early stopping of the training process. Moreover, the PESs have been checked by scanning the profiles for guaranteeing the non-physical behavior does not exist. A single neuron is a basic unit of the NN. Every neuron receives a set of input signals {xi} from the last layer and emits an output signal yi, which can be expressed as:
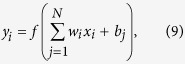 |
where bj ( j = 1, 2, 3….N) are the bias and wi are the connection weights between the two hidden layers. The transfer function f(x) is a critical factor for the quality of fitting the PES. The form of the transfer function in this work can be written as:
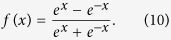 |
In order to include the permutation symmetry induced by the two H atoms, the permutation invariant polynomials44,45 are used in our fitting work. The final NN expansion can be presented as:
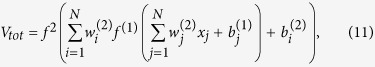 |
where the superscript represents the sequence number of different hidden layers. Finally, three high accuracy analytical PESs are constructed based on the diabatic energies and the RMSE of 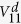 ,
, 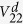 and
and 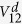 are 3.69, 5.34, 5.06 meV, respectively.
are 3.69, 5.34, 5.06 meV, respectively.
Reaction Dynamics
On the new diabatic PESs, TDWP calculation was performed for the Li(2p) + H2 (X1Σ+g) → LiH(X1Σ+) + H reaction. The TDWP method is a powerful tool to calculate initial state selected reactive collision and has been applied widely in many reactions14,46,47,48,49,50. A brief introduction of TDWP method which used here is given in this work and the detailed discussions can be found in relevant literature48,49. The TDWP method used in this work is based on the reactant coordinate based (RCB) approach and the method was developed by Sun et al.49. The basic theory RCB is to propagate an initial wave packet in the reactant Jacobi coordinates as in an initial state-selected total reaction probability calculation to obtain a scattering wave function for the product channels directly before the wave packet is absorbed in the product region. This method could treat the diabatic effect efficiently for studying non-adiabatic reaction, such as Cl + H2 reaction51. For a non-adiabatic reaction which take place over two coupled PESs, the Hamiltonian of the system is a 2 × 2 matrix. The off-diagonal elements of the matrix were employed to evaluate the transition probability between the diagonal elements. The Hamiltonian can be written as
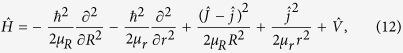 |
where R is the distance from the Li atom to the mass center of the H2 molecule and r is the bond length of the H2 molecule. μR and μr are the corresponding reduced masses.  and
and 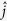 are the angular momentum operators of LiH2 system and reactant diatom molecule.
are the angular momentum operators of LiH2 system and reactant diatom molecule. 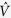 denotes the 2 × 2 matrix representation of the potential energies. The RCB method is used to extract the state-to-state S-matrix
denotes the 2 × 2 matrix representation of the potential energies. The RCB method is used to extract the state-to-state S-matrix 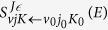 49. The state-to-state reaction probability is obtained by
49. The state-to-state reaction probability is obtained by
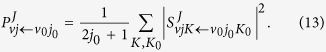 |
The state-to-state ICSs are calculated by
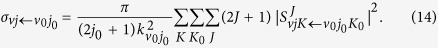 |
The DCSs are obtained by
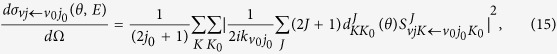 |
where θ is the scattering angle.
The initial rovibrational state of the reactant molecule H2 is set as v0 = 0, j0 = 0.The parameters used in the TDWP method are determined by numerous tests, and main parameters are listed in the Table 2.
Table 2. Numerical parameters used in the TDWP calculations. (Atomic units are used).
| Li(2p) + H2(X1Σ+g) → LiH(X1Σ+) + H | |
|---|---|
| Grid/basis range and size | R ∈ [0.01, 15.0], NR = 149 |
| r ∈ [0.01, 15.0], Nr = 149 | |
| Nj = 69 | |
Initial wave packet 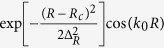
|
Rc = 10.0 |
 = 0.25 = 0.25 | |
 with E0 = 0.5 eV with E0 = 0.5 eV | |
| Total propagation time | 40000 iterations |
| Highest J value | 65 |
Additional Information
How to cite this article: He, D. et al. Global diabatic potential energy surfaces and quantum dynamical studies for the Li(2p) + H2(X1Σ+g) → LiH(X1Σ+) + H reaction. Sci. Rep. 6, 25083; doi: 10.1038/srep25083 (2016).
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No. 11374045), and Program for New Century Excellent Talents in University (Grant No. NCET-12-0077).
Footnotes
Author Contributions M.C. supervised the project, D.H. calculated the ab initio energy points, J.Y. fitted the potential energy surface and performed the time-dependent wave packet calculations, D.H., H.L. and M.C. wrote the paper.
References
- Galli D. & Palla F. The chemistry of the early Universe. Astron. Astrophys. 335, 403–420 (1998). [Google Scholar]
- Signore M. et al. The Lithium Problem with Iram, Osse, and Integral. Astrophys. J. Suppl. S. 92, 535–537 (1994). [Google Scholar]
- Maoli R., Melchiorri F. & Tosti D. Molecules in the Postrecombination Universe and Microwave Background Anisotropies. Astrophys. J. 425, 372–381 (1994). [Google Scholar]
- Lepp S. & Shull J. M. Molecules in the Early Universe. Astrophys. J. 280, 465–469 (1984). [Google Scholar]
- Stancil P. C. et al. Cosmological recombination of lithium and its effect on the microwave background anisotropies. Astrophys. J. 580, 29–35 (2002). [Google Scholar]
- Dubrovich V. K. & Lipovka A. A. Distortions of the Cosmic Blackbody Spectrum Due to Luminescence of H2D+ Molecules. Astron. Astrophys. 296, 301–306 (1995). [Google Scholar]
- Stancil P. C. & Dalgarno A. Stimulated radiative association of Li and H in the early universe. Astrophys. J. 479, 543–546 (1997). [Google Scholar]
- Bovino S., Wernli M. & Gianturco F. A. Fast LiH destruction in reaction with H: quantum claculations and astrophysical consequences. Astrophys. J. 699, 383–387 (2009). [Google Scholar]
- Bodo E., Gianturco F. A. & Martinazzo R. The gas-phase lithium chemistry in the early universe: elementary processes, interaction forces and quantum dynamics. Phys. Rep. 384, 85–119 (2003). [Google Scholar]
- Clarke N. J. et al. Classical and quantum dynamics on the collinear potential energy surface for the reaction of Li with H2. Chem. Phys. 233, 9–27 (1998). [Google Scholar]
- Dunne L. J., Murrell J. N. & Jemmer P. Analytical potential energy surface and quasi-classical dynamics for the reaction LiH(X, 1Σ+) + H(2S) → Li(2S) + H2(X, 1Σg+). Chem. Phys. Lett. 336, 1–6 (2001). [Google Scholar]
- Prudente F. V., Marques J. M. C. & Maniero A. M. Time-dependent wave packet calculation of the LiH plus H reactive scattering on a new potential energy surface. Chem. Phys. Lett. 474, 18–22 (2009). [Google Scholar]
- Wernli M., Caruso D., Bodo E. & Gianturco F. A. Computing a Three-Dimensional Electronic Energy Manifold for the LiH + H ↔ Li + H2 Chemical Reaction. J. Phys. Chem. A. 113, 1121–1128 (2009). [DOI] [PubMed] [Google Scholar]
- Yuan J. C., He D. & Chen M. D. A new potential energy surface for the ground electronic state of the LiH2 system, and dynamics studies on the H(2S) + LiH(X1Σ+) → Li(2S) + H2(X1Σ+g) reaction. Phys. Chem. Chem. Phys. 17, 11732–11739 (2015). [DOI] [PubMed] [Google Scholar]
- Padmanaban R. & Mahapatra S. Quantum wave-packet dynamics of H + HLi scattering: Reaction cross section and thermal rate constant. J. Chem. Phys. 121, 7681–7691 (2004). [DOI] [PubMed] [Google Scholar]
- Liu Y. F., He X. H., Shi D. H. & Sun J. F. Stereodynamics of the reaction H + LiH(v = 0, j = 0) → H2 + Li and its isotopic variants. Comput. Theor. Chem. 965, 107–113 (2011). [Google Scholar]
- Roy T. & Mahapatra S. Quantum dynamics of H + LiH reaction and its isotopic variants. J. Chem. Phys. 136, 174313 (2012). [DOI] [PubMed] [Google Scholar]
- Myers E. G., Murnick D. E. & Softky W. R. Isotope Selective Laser Enhancement of the Li + H2 Reaction. Appl. Phys. B-Photo. 43, 247–251 (1987). [Google Scholar]
- Chen J. J. et al. Reaction pathway, energy barrier, and rotational state distribution for Li(22PJ) + H2 → LiH(X1Σ+) + H. J. Chem. Phys. 114, 9395–9401 (2001). [Google Scholar]
- Bililign S., Hattaway B. C., Robinson T. L. & Jeung G. H. Far-wing scattering studies on the reaction Li*(2p, 3p) + H2 → LiH(v″ = 1, 2, J″) + H. J. Chem. Phys. 114, 7052–7058 (2001). [Google Scholar]
- Chen J. J. & Lin K. C. Influence of vibrational excitation on the reaction Li(2 2PJ) + H2(v = 1) → LiH(X1Σ+) + H. J. Chem. Phys. 119, 8785–8789 (2003). [Google Scholar]
- Lee H. S., Lee Y. S. & Jeung G. H. Potential energy surfaces for LiH2 and photochemical reactions Li* + H2 ↔ LiH + H. J. Phys. Chem. A. 103, 11080–11088 (1999). [Google Scholar]
- Hsiao M. K., Lin K. C. & Hung Y. M. Quasiclassical trajectory calculations for Li(22PJ) + H2 → LiH(X1Σ+) + H: Influence by vibrational excitation and translational energy. J. Chem. Phys. 134, 034119 (2011). [DOI] [PubMed] [Google Scholar]
- Smith F. T. Diabatic and Adiabatic Representations for Atomic Collision Problems. Phys. Rev. 179, 111–124 (1969). [Google Scholar]
- Rabitz H. & Alis O. F. General foundations of high-dimensional model representations. J. Math. Chem. 25, 197–233 (1999). [Google Scholar]
- Huber K. P. & Herzberg G. In Molecular Spectra and Molecular Structure IV. Constants of Diatomic Molecules Ch. 2, 424–440 (Springer: US,, 1979). [Google Scholar]
- Stwalley W. C. & Zemke W. T. Spectroscopy and Structure of the Lithium Hydride Diatomic-Molecules and Ions. J. Phys. Chem. Ref. Data. 22, 87–112 (1993). [Google Scholar]
- Werner H. J. & Knowles P. J. An Efficient Internally Contracted Multiconfiguration Reference Configuration-Interaction Method. J. Chem. Phys. 89, 5803–5814 (1988). [Google Scholar]
- Knowles P. J. & Werner H. J. An Efficient Method for the Evaluation of Coupling-Coefficients in Configuration-Interaction Calculations. Chem. Phys. Lett. 145, 514–522 (1988). [Google Scholar]
- Kendall R. A., Dunning T. H. & Harrison R. J. Electron-Affinities of the 1st-Row Atoms Revisited-Systematic Basis-Sets and Wave-Functions. J. Chem. Phys. 96, 6796–6806 (1992). [Google Scholar]
- Dobbyn A. J. & Knowles P. J. A comparative study of methods for describing non-adiabatic coupling: diabatic representation of the 1Sigma + /1Pi HOH and HHO conical intersections. Mol. Phys. 91, 1107–1123 (1997). [Google Scholar]
- Baer M. Introduction to the theory of electronic non-adiabatic coupling terms in molecular systems. Phys. Rep. 358, 75–142 (2002). [Google Scholar]
- Schwenke D. W. et al. Converged quantum-mechanical calculations of electronic-to-vibrational, rotational energy transfer probabilities in a system with a conical intersection. Chem. Phys. Lett. 203, 565–572 (1993). [Google Scholar]
- Halvick P. & Truhlar D. G. A New Diabatic Representation of the Coupled Potential-Energy Surfaces for Na(3p2 P) + H2 → Na(3s2 S) + H2 or NaH + H. J. Chem. Phys. 96, 2895–2909 (1992). [Google Scholar]
- Peric M., Buenker R. J. & Peyerimhoff S. D. Ab initio investigation of the vibronic structure of the C2H spectrum ІІ. Calculation of diabatic potential surfaces for the 3 lowest-lying electronic states in C2H. Mol. Phys. 71, 673–691 (1990). [Google Scholar]
- Hirsch G., Buenker R. J. & Petrongolo C. Abinitio study of NO2 Part ІІ: Nonadiabatic Coupling between the two lowest 2A′ states and the construction of a diabatic representation. Mol. Phys. 70, 835–848 (1990). [Google Scholar]
- Alexander M. H. Adiabatic and approximate diabatic potential energy surfaces for the B…H2 Van der Waals molecule. J. Chem. Phys. 99, 6014–6026 (1993). [Google Scholar]
- Simah D., Hartke B. & Werner H. J. Photodissociation dynamics of H2S on new coupled ab initio potential energy surfaces. J. Chem. Phys. 111, 4523–4534 (1999). [Google Scholar]
- Werner H. J. & Meyer W. Mcscf study of the avoided curve crossing of the 2 lowest 1Σ+ states of LiF. J. Chem. Phys. 74, 5802–5807 (1981). [Google Scholar]
-
Petrongolo C., Hirsch G. & Buenker R. J.
Diabatic representation of the Ã2A1/
 2B2 conical intersection in NH2. Mol. Phys.
70, 825–834 (1990). [Google Scholar]
2B2 conical intersection in NH2. Mol. Phys.
70, 825–834 (1990). [Google Scholar] - Werner H. J. & Knowles P. J. A. 2nd Order Multiconfiguration Scf Procedure with Optimum Convergence. J. Chem. Phys. 82, 5053–5063 (1985). [Google Scholar]
- Knowles P. J. & Werner H. J. An Efficient 2nd-Order Mc Scf Method for Long Configuration Expansions. Chem. Phys. Lett. 115, 259–267 (1985). [Google Scholar]
- Werner H. J. et al. Molpro: a general-purpose quantum chemistry program package. Wires. Comput. Mol. Sci. 2, 242–253 (2012). [Google Scholar]
- Jiang B. & Guo H. Permutation invariant polynomial neural network approach to fitting potential energy surfaces. J. Chem. Phys. 139, 054112 (2013). [DOI] [PubMed] [Google Scholar]
- Braams B. J. & Bowman J. M. Permutationally invariant potential energy surfaces in high dimensionality. Int. Rev. Phys. Chem. 28, 577–606 (2009). [DOI] [PubMed] [Google Scholar]
- Cheng D. H., Yuan J. C. & Chen M. D. State-Resolved Time-Dependent Wave Packet and Quasiclassical Trajectory Studies of the Adiabatic Reaction S(3P) + HD on the (13A″) State. J. Phys. Chem. A. 118, 55–61 (2014). [DOI] [PubMed] [Google Scholar]
- Yuan J. C., Cheng D. H. & Chen M. D. Time-dependent wave packet and quasiclassical trajectory studies of the Au plus HD reaction: competition between the reactive channels. RSC. Adv. 4, 36189–36195 (2014). [Google Scholar]
- Sun Z. G., Lee S. Y., Guo H. & Zhang D. H. Comparison of second-order split operator and Chebyshev propagator in wave packet based state-to-state reactive scattering calculations. J. Chem. Phys. 130, 174102 (2009). [DOI] [PubMed] [Google Scholar]
- Sun Z. G., Lin X., Lee S. Y. & Zhang D. H. A Reactant-Coordinate-Based Time-Dependent Wave Packet Method for Triatomic State-to-State Reaction Dynamics: Application to the H + O2 Reaction. J. Phys. Chem. A. 113, 4145–4154 (2009). [DOI] [PubMed] [Google Scholar]
- Yuan J. C., He D. & Chen M. D. A new potential energy surface for the H2S system and dynamics study on the S(1D) + H2(X1Σ+g) reaction. Sci. Rep. 5, 14594 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun Z., Zhang D. H. & Alexander M. H. Time-dependent wavepacket investigation of state-to-state reactive scattering of Cl with para-H2 including the open-shell character of the Cl atom. J. Chem. Phys. 132, 034308 (2010). [DOI] [PubMed] [Google Scholar]