Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2016 Mar 24;10(4):4004–4010. doi: 10.1021/acsnano.6b01419

In Situ Transmission Electron Microscopy Modulation of Transport in Graphene Nanoribbons

Julio A Rodríguez-Manzo 1, Zhengqing John Qi 1, Alexander Crook 1, Jae-Hyuk Ahn 1, A T Charlie Johnson 1,*, Marija Drndić 1,*
PMCID: PMC4850503  PMID: 27010816

Abstract

graphic file with name nn-2016-01419s_0005.jpg

In situ transmission electron microscopy (TEM) electronic transport measurements in nanoscale systems have been previously confined to two-electrode configurations. Here, we use the focused electron beam of a TEM to fabricate a three-electrode geometry from a continuous 2D material where the third electrode operates as side gate in a field-effect transistor configuration. Specifically, we demonstrate TEM nanosculpting of freestanding graphene sheets into graphene nanoribbons (GNRs) with proximal graphene side gates, together with in situ TEM transport measurements of the resulting GNRs, whose conductance is modulated by the side-gate potential. The TEM electron beam displaces carbon atoms from the graphene sheet, and its position is controlled with nanometer precision, allowing the fabrication of GNRs of desired width immediately prior to each transport measurement. We also model the corresponding electric field profile in this three-terminal geometry. The implementation of an in situ TEM three-terminal platform shown here further extends the use of a TEM for device characterization. This approach can be easily generalized for the investigation of other nanoscale systems (2D materials, nanowires, and single molecules) requiring the correlation of transport and atomic structure.

Keywords: in situ TEM, electronic transport, modulation, side gate, graphene nanoribbons, two-dimensional materials

Growing interest in performing in situ TEM electronic transport measurements is motivated by the need to understand transport in devices that keep shrinking in size and by a surge of specialized TEM sample holders allowing such measurements. The concept of in situ measurements is particularly attractive because standard TEMs offer a unique combination of materials-characterization techniques (high-resolution imaging, electron diffraction, electron-based spectroscopy, etc.) that can be used concurrently to correlate a material’s structure and chemistry—down to the atomic scale—with its electronic properties. However, in situ TEM transport measurements have been confined to two-electrode configurations, by using either two static electrodes or a movable scanning probe tip operating as an electrode. Examples include measurements of chains of Au atoms;1−3 C4−6 and BN tubes;7,8 Si,9 Ge2Sb2Te5,10 and MoSe wires;11 CNT–metal junctions;12 graphene constrictions13−15 and ribbons;16−18 atomic C chains;19 and nanobatteries.20,21 Modulating the conductance in some of these nanoscale systems by tuning the charge carrier density requires addition of a third electrode: the gate electrode in a field-effect transistor (FET) configuration.

In this Article, we describe the implementation of a three-terminal transport platform inside the TEM, extending its use beyond two-terminal in situ characterizations. Specifically, we present the steps to achieve in situ TEM fabrication of a three-electrode graphene device nanosculpted from a continuous graphene sheet, with one graphene electrode operating as a side gate, to perform in situ TEM transport measurements in a freestanding graphene nanoribbon (GNR) serving as a FET channel. The top- or bottom-gate configuration typically used to modulate the charge charrier density in a FET channel is incompatible with in situ TEM transport studies, where the goal is to image and fabricate the channel with the electron beam. For these types of studies, the side-gate configuration offers a valid alternative by removing the gate from the path of the electron beam, which then can be used to image and modify the channel via beam-induced modifications without interruption. In the side-gate configuration the coupling between gate and channel is weaker than in the top/bottom-gate configuration but, as we show here, sufficiently large to modulate the electronic properties of a GNR FET channel. In summary, this three-terminal device design enables the simultaneous characterization of the channel’s structural, chemical, and transport properties within the TEM column (Figure 1a).

Figure 1.

Figure 1

Open in a new tab

In situ TEM side-gate transport measurement in a freestanding graphene nanoribbon (GNR) fabricated in situ in the TEM. (a) Scheme of three-electrode chip configuration used to perform in situ TEM transport measurements of a GNR. The electron beam is shown focused, as in the STEM mode. (b) TEM image of typical GNR obtained after sculpting a graphene sheet with the electron beam. Source, drain, and side-gate metal electrodes are visible on top of the SiNx film. The distance between the gate extension carved from graphene and the GNR is ∼80 nm. Two voltage sources (Vb and Vg) and an ammeter compose the electrical circuit. (c) Color plot of GNR conductance showing transport modulation as a function of source–drain and side-gate voltages Vb and Vg for a GNR with a width and length of 68 ± 2 and 187 ± 3 nm, respectively. The distance between the GNR and gate extension was 80 ± 5 nm. The measurement was performed at room temperature within the TEM.

In our experiments, the GNRs are suspended between source and drain electrodes and in proximity to the side-gate electrode (Figure 1b). The GNRs and graphene side gates are fabricated with nanometer precision by cutting continuous graphene sheets with a focused electron beam by operating the TEM in scanning mode (STEM).22,23 After the in situ device fabrication we measure the current I flowing through the GNR for a fixed source–drain voltage Vb while the gate potential Vg is varied. In this way, we modulate the GNR conductance within the TEM column at room temperature (Figure 1c). The sign and magnitude of the measured changes in GNR conductance are explained by considering the electric field strength at the GNR channel, which we estimate with numerical simulations to be a maximum of ∼107 V m–1 in our experiments. This study demonstrates in situ TEM implementation and fabrication of three-terminal devices with nanometer features from a 2D material and, importantly, their in situ operation. Extending this work, we envision a wide range of in situ TEM transport experiments in nanoscale systems that exploit the TEM’s atomic precision to study and understand correlations between transport phenomena and atomic structure.

Results and Discussion

Observations were carried out with an electron microscope (JEOL 2010F) operated at 200 kV. TEM-compatible chips were mounted in a sample holder with electrical feedthroughs (Hummingbird Scientific) for electronic-transport measurements. Chips were fabricated with standard photolithography, electron-beam lithography, and etching processes (a detailed description is given in the Methods section). Briefly, we used 100-nm-thick SiNx films spanning areas of ∼60 × 60 μm2 as insulating supports for metal electrodes and graphene and as electron-transparent windows. In each chip, graphene was patterned into a 2-μm-wide strip in contact with the three electrodes. Freestanding-graphene areas were obtained by making gaps in the SiNx film with a focused ion beam prior to graphene deposition (Figure 2a). Electron diffraction and electron energy-loss spectroscopy confirmed the presence of graphene between the electrodes (see Supporting Information SI-1).

Figure 2.

Figure 2

Open in a new tab

Fabrication of freestanding GNRs in TEM-compatible chips. (a) SEM image of a three-electrode chip in an electron-transparent SiNx window. The magnified area (right) shows the initial graphene strip in contact with all electrodes; dashed lines mark the graphene strip borders. (b) Cutting of a line in freestanding graphene. The top HAADF STEM image served as reference for the cutting path indicated by the dotted line. The bottom image shows the same area with a 7-nm-wide line cut, after the electron beam was rastered through the path. The SiNx-gap ends are visible as gray areas. (c) TEM image of a GNR in proximity to the graphene gate extension. The double-headed arrow indicates the distance dg between the GNR and extension. Dotted lines illustrate cutting paths used for sculpting the graphene strip. (d) TEM images showing GNR width reduction (from top to bottom). Dotted lines indicate the first and second cutting paths used to reduce the width of the same GNR. The images’ brightness and contrast were modified for clarity.

We made the GNR and graphene gate electrode of each device with the same in situ fabrication process by appropriately cutting the continuous freestanding graphene strip with the electron beam. The beam was focused into a probe and scanned over the sample in STEM mode following a preprogrammed series of parallel and perpendicular lines designed to achieve the desired geometry: a single GNR with an isolated graphene side gate nearby. The beam energy onset for displacement of carbon atoms from graphene is ∼90 keV.24 Hence, set at 200 keV, the beam used in our experiments can cut through graphene. For this energy the knock-on displacement cross section for a carbon atom in graphene is ∼15 barn.24,25 Therefore, to displace all carbon atoms from an area of 1 nm2 requires ∼109 electrons (1 nm2/15 barn). This corresponds to an irradiation dose (charge per unit area) of 108 C m–2. A lower dose would cause less damage to the lattice. High-angle annular dark-field (HAADF) STEM images are composed with the signal from electrons scattered with angles > 50 mrad with each pixel’s intensity proportional to the mass probed by the beam. This mass contrast readily distinguishes the presence and absence of graphene in HAADF STEM images. Bearing in mind the above considerations, the procedure to sculpt graphene comprises the following steps:22,23 (1) acquiring a HAADF STEM reference image with a low irradiation dose (∼103 C m–2) to minimize damage in the graphene area to be modified, (2) designing a cutting path using the acquired reference image, and (3) driving the beam through the designed path with a dosage high enough to cut graphene (∼108 C m–2). The beam can be placed at any point within the reference HAADF STEM image. Thus, any pattern can be engraved in graphene, as illustrated in Figure 2b with the cutting of a line. We used a 2-nm-diameter probe with a current of 3 nA (current density ∼109 A m–2). HAADF STEM reference images were acquired with irradiation dwell times per pixel on the order of 1 μs, with 256 × 256 pixels and a pixel size of <10 nm. Similar imaging conditions induced only minimal changes in the conductance of GNRs supported by SiNx films.16 To cut graphene, the dwell time per pixel was increased 5 orders of magnitude to 0.1–0.5 s.

To maximize the capacitive coupling between GNR and gate electrode, the separation between them was kept minimal to around 50–150 nm by sculpting a gate extension from the graphene strip (Figure 2c), connected to a larger Au electrode. As explained below, according to numerical calculations the electric field at the GNR channel is expected to be ∼3 times stronger with than without the graphene gate extension (i.e., only the Au electrode). We also used the electron-beam-based sculpting procedure to reduce the GNR’s width in each device by gradually reducing the width of the original GNR (Figure 2d).

Graphene was annealed via Joule heating before, during, and after sculpting with currents up to 10–4 A, yielding current densities on the order of 1012 A m–2 (see Supporting Information SI-2). With these conditions graphene can be heated to temperatures above 1000 K.26 Annealing avoids contamination by enhancing diffusion of mobile hydrocarbons, increases the rate of recombination of defects (interstitials and vacancies), and induces crystallization of amorphous carbon.18,26−28 The described annealing effects help to contain electron-irradiation-induced damage in the GNRs.

To model the effect of the side gate on the GNR conductance in our in situ TEM transport measurements, we estimated numerically the electrostatic potential V at the channel for the electrode geometry in our experiment (Figure 3a). In this analysis, the central point of the channel closest to the gate electrode is defined as p0, and the distance between channel and gate is defined as dg. From each electric potential distribution V, we derived the electric field strength E (see Supporting Information SI-3 for details). The effect of extending the gate spatially, from the Au electrode toward the channel, on the electric field E is shown in Figure 3b, where we plot E at p0 for different dg as a function of Vg. It is at this point in the area covered by a GNR that the E is strongest. Hence, with our chip configuration we expect maximum values of E ≈ 107 V m–1 at p0. To put this value in perspective, we compare it to the E in a back-gate FET device with a 300 nm thick SiO2 gate layer, an arrangement commonly used for GNR devices. For a 1 V gate potential the electric field strength is about the same, E ≈ 0.3 × 107 V m–1 at p0, in both the back- and side-gate configurations, when dg = 100 nm in the latter case. However, the charging effect will be approximately 4 times stronger in the back-gate configuration because the permittivity of SiO2 is 3.9 × permittivity of vacuum (the pressure in the TEM column is 10–5 Pa). In addition, the E magnitude decays as the distance in the channel from the side-gate electrode increases (Figure 3c).

Figure 3.

Figure 3

Open in a new tab

Numerical calculations of electrostatic potential and electric field induced by side-gate electrode. (a) Electrostatic potential for side-gate voltage Vg = 1 V and source and drain electrodes grounded (V = 0 V). In this example, the distance from the extended gate to the channel dg = 100 nm. The dash-dotted line indicates the plane from which the cross section (right) was taken. The potential at p0, the closest point from gate to channel in this model, is not zero. (b) Electric field strength E at p0 as a function of Vg for six different distances dg. When dg = 150 nm the extension of the gate, carved from graphene in the experiment, is zero in this model. (c) Electric field strength E as a function of distance from the side gate in a line passing through p0. Here, we use the same geometrical parameters as in (a).

We present results from three nanosculpted devices tested at room temperature, the TEM’s column operating temperature. During all transport measurements the electron beam was blocked to avoid the electron-beam-induced damage of the GNRs. The Vg sweep was restricted to a ±10 V range to prevent leakage currents through the SiNx film and the devices’ mechanical collapse due to electrostatic forces.29 Details of the measurements and leakage current analysis are provided in Supporting Information SI-4. Figure 4a and b show the conductance G and ΔG = G – G0, respectively, where G0 is G evaluated at Vg = 0, as a function of Vg for three GNRs with widths W of 113 ± 2, 68 ± 2, and 31 ± 3 nm. The GNR length L in each device is defined by the SiNx gap’s length. Since the GNR that was 68 nm wide was obtained by cutting the GNR that was initially 113 nm wide (see Figure 2d), these two same-chip devices had the same L (187 ± 3 nm) and dg (80 ± 5 nm). The GNR with a width of 31 nm wide was patterned in another chip with L = 182 ± 2 nm and dg = 58 ± 4 nm. The quoted distances for W and dg correspond to values averaged along each GNR length. For these measurements the source–drain voltage was set to Vb = 0.1 V.

Figure 4.

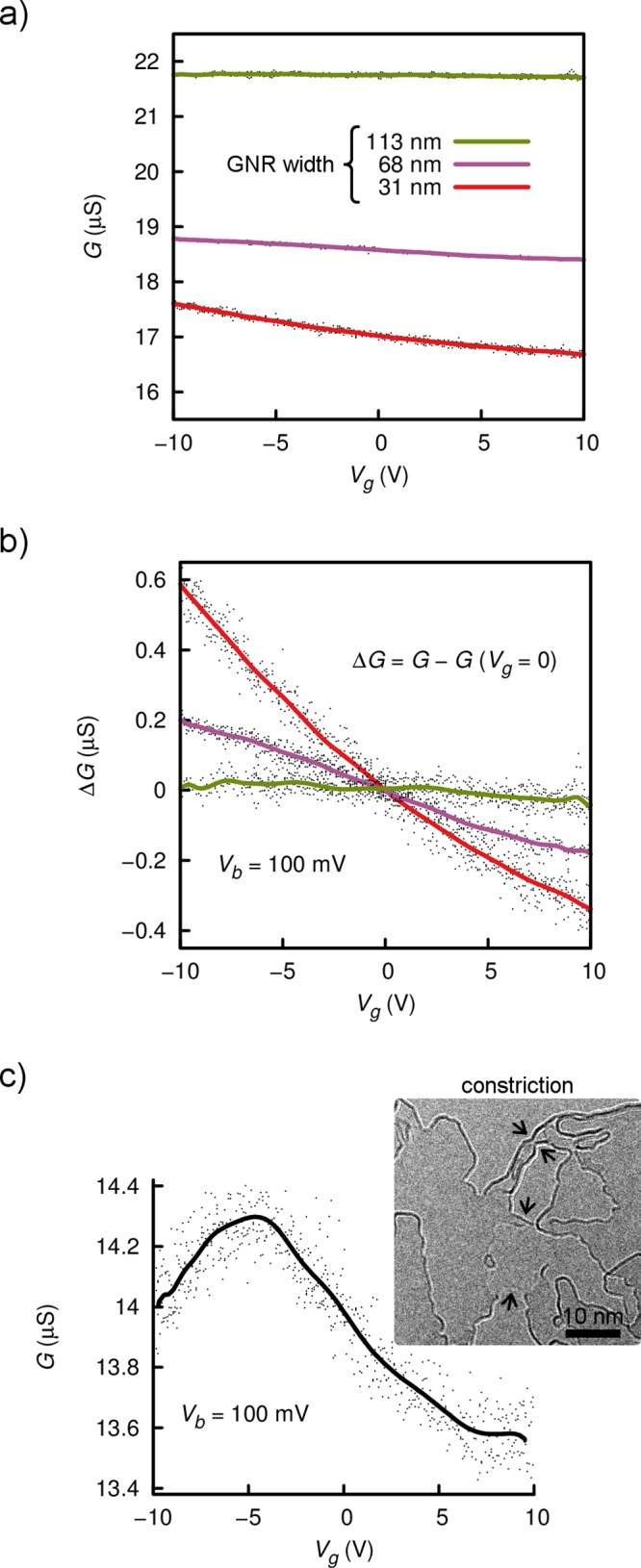
Figure 4

Open in a new tab

Side-gate modulation of GNR conductance within the TEM column. (a) GNR conductance G and (b) ΔG = G – G0, where G0 is G evaluated at Vg = 0, as a function of Vg in three GNRs with widths of 113 ± 2, 68 ± 2, and 31 ± 3 nm. Values of ΔG ≠ 0 indicate that the GNR conductance was modulated by the side-gate potential. (c) Conductance as a function of Vg in a graphene-derived constriction. Inset: TEM image of channel composed of two paths (indicated by arrows) separated by a hole in the structure. The paths are 12 and <2 nm wide at their narrowest points. During these measurements the source–drain voltage was set to Vb = 0.1 V. All lines are a noise-reduction fit to each raw data set (black points).

In addition to demonstrating the modulation of a GNR channel’s conductance with a side-gate electrode within a TEM column, these results indicate that the side-gate electrode’s capacity to modulate the conductance increases as the GNR width decreases. In particular, changes in G were only registered as the GNR width in each device was reduced from an initial value of W ≈ 1 μm to a few tens of nanometers. The trend is evident when comparing the GNRs’ ΔG values (Figure 4b). The GNR that was 113 nm wide shows ΔG ≈ 0 for all Vg in contrast to the other two narrower GNRs for which ΔG ≠ 0 in the same Vg range. In general, as the W/L channel ratio of a FET device increases, short-channel effects result in a weakened gate capacity to control transport.30 This effect has been observed in back-gated GNR devices31 but should be more pronounced in our devices because the electric field strength decreases along the GNR width (see Figure 3c). In addition, GNRs have energy gaps ∼1/W that lead to larger Ion/Ioff ratios for narrower GNRs.32,33 These effects coincide qualitatively with our result that the side-gate’s capacity to modulate transport is stronger for narrower GNRs.

The GNR conductance of the analyzed GNRs (G ≈ 17, 19, and 22 μS for GNR width W = 31 ± 3, 68 ± 2, and 113 ± 2 nm, respectively) is close to the expected minimum conductance of ∼(e2/h) × (W/L) for a GNR at room temperature,32 suggesting that the as-fabricated GNRs are not in the on-state. However, the gate-voltage range (|Vg| ≤ 10 V) prevented us from establishing the full on/off-state response of the studied GNR devices. Considering the sense of the registered changes in G as a function of Vg (ΔG/ΔVg < 0), our measurements are consistent with that of p-type GNRs that are in an electronic state close to the minimum conductance with a charge-neutrality point at Vg > 0. The shift of the charge-neutrality point is most likely caused by impurities and substrate effects in graphene areas adjacent to the freestanding channel. For the narrowest GNR device (W = 31 ± 3 nm) we estimated a subthreshold swing S ≈ ΔVg/Δ(log I),30 which quantifies the efficiency to turn on and off a FET-type device, of S ≈ 860 V dec–1. By comparison, a back-gated (300-nm-thick SiO2 gate layer) GNR that is 24 nm wide (from exfoliated graphene) was shown to have an S ≈ 80 V dec–1 at room temperature.32 Assuming similar graphene conductivity in both cases, the side-gate device is 10 times less efficient, in agreement with a lower channel-gate capacitive coupling in the side-gate configuration, recalling that for this configuration we estimate a 4-fold weaker charging effect (at p0) from the calculated electric field. Possible improvements to boost the coupling between side-gate and channel include reducing the distance dg, adding dielectric layers to partially fill the vacuum gap between gate and channel, and patterning an additional side-gate electrode opposite the first to reduce the asymmetry of the electric field at the channel and increase its strength. In the end, changes in chip configuration will have to be tailored according to a channel’s material and size.

The combination of GNR width reduction and annealing produced channels a few nanometers wide that ultimately failed by channel rupture. The graphene-derived structures obtained before failure resembled constrictions13−15 rather than well-defined ribbons but also displayed modulation in G as a function of Vg. An example of a constriction and its conductance response is shown in Figure 4c. This constriction was formed in the middle of a GNR (W = 50 ± 2 nm and L = 180 ± 3 nm) and consisted of two separated channels with an average length of roughly 10 nm. One channel resembles a 12-nm-wide GNR and the other, with a < 2 nm span at its narrowest point, a carbon nanotube. For this constriction G showed a peak (about Vg = −5 V) similar to those observed in devices possessing negative differential conductance. At this point we can only speculate the origin of this peak, but given the relative short length of the constriction, a resonant tunneling effect cannot be discarded, and more studies would be needed to fully understand this observation. For example, by increasing the image resolution with an aberration-corrected TEM, this observation could be correlated with the precise atomic arrangement and edge structure (armchair, zigzag, roughness, etc.) of the GNR.

Conclusions

In summary, we carried out in situ TEM transport measurements with devices fabricated in situ that contain a side-gate electrode that modulates the carrier density in a freestanding channel a few nanometers wide. In particular, we outline the STEM procedure to form gated graphene structures, and we demonstrate the resulting side-gate-induced modulation of conductance at room temperature in GNRs fabricated within the TEM column. This emphasizes that our approach enables both a full characterization of the active channel in an FET-type configuration and structural modifications of the device via electron-beam sculpting. With state-of-the-art instrumentation the spatial resolution of both the channel characterization (structural and chemical) and beam-induced modifications can be pushed to the atomic level. The combined method of beam-induced channel modifications with in situ TEM transport measurements is especially well-suited for other 2D materials, provided that the specific beam energy and dose requirements have been met. With slight modifications this method can be applied to investigate transport phenomena in nanoscale systems, such as single-molecule transport or metal-to-insulator transitions dependent on channel width or edge structure, where the resolution of the channel’s atomic structure is of paramount importance.

Methods

Graphene Growth

We used graphene grown via atmospheric pressure chemical vapor deposition on Cu foil (99.8% purity).34 For graphene growth the Cu foil is sonicated in acetone for 10 min and then dried with N2 after rinsing in deionized water. Then, the foil is inserted into a sealed 1 in. quartz tube furnace. A mixture of Ar (500 sccm) and H2 (50 sccm) is introduced into the tube for 10 min to flush the tube. Afterwards, the furnace is set to 1057 °C, the H2 flow is reduced to 25 sccm, and 2 sccm of a 1% CH4 in an Ar mixture is flowed into the tube. After 100 min of growth the furnace is turned off and the tube is moved to a position where the foil is 2 in. away from the furnace entrance. Once the oven reaches 850 °C, the flow rates for Ar, H2, and CH4 are changed to 1000, 7, and 0 sccm, respectively. Finally, the foil is removed when the tube reaches room temperature.

Fabrication Details of TEM-Compatible Chips

Si/SiNx substrates (from WRS Materials) consisting of 300-nm-thick Si wafers covered by 100-nm-thick low stress (<100 MPa) SiNx films were patterned and etched to fabricate 5 × 3.5 mm2 chips, with each chip containing an area ∼60 × 60 μm2 of freestanding SiNx film resembling a “window”. The SiNx window is transparent to the electron beam and supports the device’s metal electrodes and graphene. The windows were fabricated by, first, etching the SiNx with SF6 from squares (450 × 450 μm2) patterned with photolithography in one side of the wafer and, second, etching the exposed Si with a KOH bath. T-shaped Au/Cr electrodes with thicknesses of 50–100/10 nm were fabricated in the windows with photolithography followed by metal thermal evaporation. To allow for freestanding graphene areas, a fork-shaped gap 150–200 nm wide was made in the windows containing electrodes with a focused ion beam with Ga source. Then, the windows were completely covered by CVD-grown graphene. After transferring a continuous film of graphene into the SiNx window a protective strip 2 μm wide of poly(methyl methacrylate) (PMMA) covering the graphene was patterned at the intersection of the electrodes with electron-beam lithography. The graphene outside the protective strip was etched with O2 plasma and, finally, the PMMA resist was removed. For in situ TEM transport measurements, the TEM-compatible devices were pasted and wire-bonded to TEM chip carriers, which in turn were mounted to a sample holder with electrical feedthroughs (Hummingbird Scientific).

Acknowledgments

We acknowledge support from NIH Grants R21004767 and R21HG007856 and access to the TEM NSF-MRSEC facility at the University of Pennsylvania. Z.J.Q. and A.T.C.J. acknowledge support from SRC Contract No. 2011-IN-2229, associated with NSF AIR Program ENG-1312202. Z J.Q. acknowledges support from the IBM Ph.D. Fellowship and the NSF IGERT program (Grant DGE02-21664). The authors thank Andrés R. Botello-Méndez and Prof. Vincent Meunier for fruitful discussions.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.6b01419.

  • Details for graphene characterization and annealing via Joule heating; calculation of the electrostatic potential and electric field; and transport measurements and leakage current analysis (PDF)

Author Present Address

§ Department of Electronic Engineering, Kwangwoon University, Seoul 01897, South Korea.

Author Contributions

‡ J. A. Rodríguez-Manzo and Z. J. Qi contributed equally to this work.

Author Contributions

J.A.R.-M., Z.J.Q., A.T.C.J., and M.D. designed the experiments; J.A.R.-M., Z.J.Q., and A.C. prepared the samples. J.A.R.-M. and Z.J.Q. performed in situ TEM transport measurements. All authors contributed to data analysis and the manuscript writing.

The authors declare no competing financial interest.

Supplementary Material

nn6b01419_si_001.pdf (505KB, pdf)

References

  1. Ohnishi H.; Kondo Y.; Takayanagi K. Quantized Conductance Through Individual Rows of Suspended Gold Atoms. Nature 1998, 395, 780–783. 10.1038/27399. [DOI] [Google Scholar]
  2. Erts D.; Olin H.; Ryen L.; Olsson E.; Thölén A. Maxwell and Sharvin conductance in gold point contacts investigated using TEM-STM. Phys. Rev. B: Condens. Matter Mater. Phys. 2000, 61, 12725–12727. 10.1103/PhysRevB.61.12725. [DOI] [Google Scholar]
  3. Kizuka T.; Umehara S.; Fujisawa S. Metal-Insulator Transition in Stable One-Dimensional Arrangements of Single Gold Atoms. Jpn. J. Appl. Phys. 2001, 40, L71. 10.1143/JJAP.40.L71. [DOI] [Google Scholar]
  4. Wang Z. L.; Poncharal P.; de Heer W. A. Measuring Physical and Mechanical Properties of Individual Carbon Nanotubes by In Situ TEM. J. Phys. Chem. Solids 2000, 61, 1025–1030. 10.1016/S0022-3697(99)00350-9. [DOI] [Google Scholar]
  5. Huang J. Y.; Chen S.; Jo S. H.; Wang Z.; Han D. X.; Chen G.; Dresselhaus M. S.; Ren Z. F. Atomic-Scale Imaging of Wall-by-Wall Breakdown and Concurrent Transport Measurements in Multiwall Carbon Nanotubes. Phys. Rev. Lett. 2005, 94, 236802. 10.1103/PhysRevLett.94.236802. [DOI] [PubMed] [Google Scholar]
  6. Wang M. S.; Wang J. Y.; Chen Q.; Peng L. M. Fabrication and Electrical and Mechanical Properties of Carbon Nanotube Interconnections. Adv. Funct. Mater. 2005, 15, 1825–1831. 10.1002/adfm.200500215. [DOI] [Google Scholar]
  7. Cumings J.; Zettl A. Field Emission and Current-Voltage Properties of Boron Nitride Nanotubes. Solid State Commun. 2004, 129, 661–664. 10.1016/j.ssc.2003.11.026. [DOI] [Google Scholar]
  8. Golberg D.; Mitome M.; Kurashima K.; Zhi C. Y.; Tang C. C.; Bando Y.; Lourie O. In situ electrical probing and bias-mediated manipulation of dielectric nanotubes in a high-resolution transmission electron microscope. Appl. Phys. Lett. 2006, 88, 123101. 10.1063/1.2186987. [DOI] [Google Scholar]
  9. Kizuka T.; Takatani Y.; Asaka K.; Yoshizaki R. Measurements of the Atomistic Mechanics of Single Crystalline Silicon Wires of Nanometer Width. Phys. Rev. B: Condens. Matter Mater. Phys. 2005, 72, 035333. 10.1103/PhysRevB.72.035333. [DOI] [Google Scholar]
  10. Nam S.-W.; Chung H.-S.; Chieh Lo Y.; Qi L.; Li J.; Lu Y.; Johnson A. T. C.; Jung Y.; Agarwal R. Electrical Wind Force–Driven and Dislocation-Templated Amorphization in Phase-Change Nanowires. Science 2012, 336, 1561–1566. 10.1126/science.1220119. [DOI] [PubMed] [Google Scholar]
  11. Lin J.; Cretu O.; Zhou W.; Suenaga K.; Prasai D.; Bolotin K. I.; Cuong N. T.; Otani M.; Okada S.; Lupini A. R.; Idrobo J.-C.; Caudel D.; Burger A.; Chimire N. J.; Yan J.; Mandrus D. G.; Pennycook S. J.; Pantelides S. T. Flexible Metallic Nanowires with Self-Adaptive Contacts to Semiconducting Transition-Metal Dichalcogenide Monolayers. Nat. Nanotechnol. 2014, 9, 436–442. 10.1038/nnano.2014.81. [DOI] [PubMed] [Google Scholar]
  12. Rodríguez-Manzo J. A.; Banhart F.; Terrones M.; Terrones H.; Grobert N.; Ajayan P. M.; Sumpter B. G.; Meunier V.; Wang M.; Bando Y.; Golberg D. Heterojunctions between Metals and Carbon Nanotubes as Ultimate Nanocontacts. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 4591–5. 10.1073/pnas.0900960106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Lu Y.; Merchant C. A.; Drndić M.; Johnson A. T. C. In Situ Electronic Characterization of Graphene Nanoconstrictions Fabricated in a Transmission Electron Microscope. Nano Lett. 2011, 11, 5184–5188. 10.1021/nl2023756. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Barreiro A.; Börrnert F.; Rümmeli M. H.; Büchner B.; Vandersypen L. M. K. Graphene at High Bias: Cracking, Layer by Layer Sublimation, and Fusing. Nano Lett. 2012, 12, 1873–1878. 10.1021/nl204236u. [DOI] [PubMed] [Google Scholar]
  15. Börrnert F.; Barreiro A.; Wolf D.; Katsnelson M. I.; Büchner B.; Vandersypen L. M. K.; Rümmeli M. H. Lattice Expansion in Seamless Bilayer Graphene Constrictions at High Bias. Nano Lett. 2012, 12, 4455–4459. 10.1021/nl301232t. [DOI] [PubMed] [Google Scholar]
  16. Puster M.; Rodríguez-Manzo J. A.; Balan A.; Drndić M. Toward Sensitive Graphene Nanoribbon–Nanopore Devices by Preventing Electron Beam-Induced Damage. ACS Nano 2013, 7, 11283–11289. 10.1021/nn405112m. [DOI] [PubMed] [Google Scholar]
  17. Qi Z. J.; Rodríguez-Manzo J. A.; Botello-Méndez A. R.; Hong S. J.; Stach E. A.; Park Y. W.; Charlier J.-C.; Drndić M.; Johnson A. T. C. Correlating Atomic Structure and Transport in Suspended Graphene Nanoribbons. Nano Lett. 2014, 14, 4238–4244. 10.1021/nl501872x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Qi Z. J.; Daniels C.; Hong S. J.; Park Y. W.; Meunier V.; Drndić M.; Johnson A. T. C. Electronic Transport of Recrystallized Freestanding Graphene Nanoribbons. ACS Nano 2015, 9, 3510–3520. 10.1021/nn507452g. [DOI] [PubMed] [Google Scholar]
  19. Cretu O.; Botello-Mendez A. R.; Janowska I.; Pham-Huu C.; Charlier J.-C.; Banhart F. Electrical Transport Measured in Atomic Carbon Chains. Nano Lett. 2013, 13, 3487–3493. 10.1021/nl4018918. [DOI] [PubMed] [Google Scholar]
  20. Yamamoto K.; Iriyama Y.; Asaka T.; Hirayama T.; Fujita H.; Fisher C. A. J.; Nonaka K.; Sugita Y.; Ogumi Z. Dynamic Visualization of the Electric Potential in an All-Solid-State Rechargeable Lithium Battery. Angew. Chem., Int. Ed. 2010, 49, 4414–4417. 10.1002/anie.200907319. [DOI] [PubMed] [Google Scholar]
  21. Huang J. Y.; Zhong L.; Wang C. M.; Sullivan J. P.; Xu W.; Zhang L. Q.; Mao S. X.; Hudak N. S.; Liu X. H.; Subramanian A.; Fan H.; Qi L.; Kushima A.; Li J. In Situ Observation of the Electrochemical Lithiation of a Single SnO2 Nanowire Electrode. Science 2010, 330, 1515–1520. 10.1126/science.1195628. [DOI] [PubMed] [Google Scholar]
  22. Börrnert F.; Fu L.; Gorantla S.; Knupfer M.; Büchner B.; Rümmeli M. H. Programmable Sub-nanometer Sculpting of Graphene with Electron Beams. ACS Nano 2012, 6, 10327–10334. 10.1021/nn304256a. [DOI] [PubMed] [Google Scholar]
  23. Xu Q.; Wu M.-Y.; Schneider G. F.; Houben L.; Malladi S. K.; Dekker C.; Yucelen E.; Dunin-Borkowski R. E.; Zandbergen H. W. Controllable Atomic Scale Patterning of Freestanding Monolayer Graphene at Elevated Temperature. ACS Nano 2013, 7, 1566–1572. 10.1021/nn3053582. [DOI] [PubMed] [Google Scholar]
  24. Meyer J. C.; Eder F.; Kurasch S.; Skakalova V.; Kotakoski J.; Park H. J.; Roth S.; Chuvilin A.; Eyhusen S.; Benner G.; Krasheninnikov A. V.; Kaiser U. Accurate Measurement of Electron Beam Induced Displacement Cross Sections for Single-Layer Graphene. Phys. Rev. Lett. 2012, 108, 196102. 10.1103/PhysRevLett.108.196102. [DOI] [PubMed] [Google Scholar]
  25. Egerton R. F.; Li P.; Malac M. Radiation Damage in the TEM and SEM. Micron 2004, 35, 399–409. 10.1016/j.micron.2004.02.003. [DOI] [PubMed] [Google Scholar]
  26. Westenfelder B.; Meyer J. C.; Biskupek J.; Kurasch S.; Scholz F.; Krill C. E.; Kaiser U. Transformations of Carbon Adsorbates on Graphene Substrates under Extreme Heat. Nano Lett. 2011, 11, 5123–5127. 10.1021/nl203224z. [DOI] [PubMed] [Google Scholar]
  27. Florian B. Irradiation Effects in Carbon Nanostructures. Rep. Prog. Phys. 1999, 62, 1181. 10.1088/0034-4885/62/8/201. [DOI] [Google Scholar]
  28. Moser J.; Barreiro A.; Bachtold A. Current-Induced Cleaning of Graphene. Appl. Phys. Lett. 2007, 91, 163513. 10.1063/1.2789673. [DOI] [Google Scholar]
  29. Bolotin K. I.; Sikes K. J.; Jiang Z.; Klima M.; Fudenberg G.; Hone J.; Kim P.; Stormer H. L. Ultrahigh Electron Mobility in Suspended Graphene. Solid State Commun. 2008, 146, 351–355. 10.1016/j.ssc.2008.02.024. [DOI] [Google Scholar]
  30. Schwierz F. Graphene Transistors. Nat. Nanotechnol. 2010, 5, 487–496. 10.1038/nnano.2010.89. [DOI] [PubMed] [Google Scholar]
  31. Shu-Jen H.; Zhihong C.; Bol A. A.; Sun Y. Channel-Length-Dependent Transport Behaviors of Graphene Field-Effect Transistors. IEEE Electron Device Lett. 2011, 32, 812–814. 10.1109/LED.2011.2131113. [DOI] [Google Scholar]
  32. Han M. Y.; Özyilmaz B.; Zhang Y.; Kim P. Energy Band-Gap Engineering of Graphene Nanoribbons. Phys. Rev. Lett. 2007, 98, 206805. 10.1103/PhysRevLett.98.206805. [DOI] [PubMed] [Google Scholar]
  33. Li X.; Wang X.; Zhang L.; Lee S.; Dai H. Chemically Derived, Ultrasmooth Graphene Nanoribbon Semiconductors. Science 2008, 319, 1229–1232. 10.1126/science.1150878. [DOI] [PubMed] [Google Scholar]
  34. Luo Z.; Lu Y.; Singer D. W.; Berck M. E.; Somers L. A.; Goldsmith B. R.; Johnson A. T. C. Effect of Substrate Roughness and Feedstock Concentration on Growth of Wafer-Scale Graphene at Atmospheric Pressure. Chem. Mater. 2011, 23, 1441–1447. 10.1021/cm1028854. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn6b01419_si_001.pdf (505KB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES