NETWORK ASSISTED ANALYSIS TO REVEAL THE GENETIC BASIS OF AUTISM

Abstract

While studies show that autism is highly heritable, the nature of the genetic basis of this disorder remains illusive. Based on the idea that highly correlated genes are functionally interrelated and more likely to affect risk, we develop a novel statistical tool to find more potentially autism risk genes by combining the genetic association scores with gene co-expression in specific brain regions and periods of development. The gene dependence network is estimated using a novel partial neighborhood selection (PNS) algorithm, where node specific properties are incorporated into network estimation for improved statistical and computational efficiency. Then we adopt a hidden Markov random field (HMRF) model to combine the estimated network and the genetic association scores in a systematic manner. The proposed modeling framework can be naturally extended to incorporate additional structural information concerning the dependence between genes. Using currently available genetic association data from whole exome sequencing studies and brain gene expression levels, the proposed algorithm successfully identified 333 genes that plausibly affect autism risk.

1. Introduction

Autism spectrum disorder (ASD), a neurodevelopmental disorder, is characterized by impaired social interaction and restricted, repetitive behavior. Genetic variation is known to play a large role in risk for ASD [Gaugler et al. (2014), Klei et al. (2012)], and yet efforts to identify inherited genetic variation contributing to risk have been remarkably unsuccessful [Anney et al. (2012), Liu et al. (2013)]. One explanation for this lack of success is the large number of genes that appear to confer risk for ASD [Buxbaum et al. (2012)]. Recent studies estimate this number to be near 1000 [He et al. (2013), Sanders et al. (2012)].

The advent of next generation sequencing and affordable whole exome sequencing (WES) has led to significant breakthroughs in ASD risk gene discovery. Most notable is the ability to detect rare de novo mutations (i.e., new mutations) in affected individuals. These studies examine ASD trios, defined as an affected child with unaffected parents, to determine rare mutations present in the affected child, but not in the parents. A fraction of these mutations cause loss of function (LoF) in the gene. And when these rare damaging events are observed in a particular gene for multiple ASD trios, it lends strong evidence of causality [Sanders et al. (2012)]. While this approach has revolutionized the field, the accumulation of results is slow, relative to the size of the task: to date, analysis of more than two thousand ASD trios has identified less than two dozen genes clearly involved in ASD risk [Iossifov et al. (2012), Kong et al. (2012), Neale et al. (2012), O'Roak et al. (2011, 2012), De Rubeis et al. (2014), Sanders et al. (2012), Willsey et al. (2013)]. Extrapolating from these data suggest that tens of thousands of families would be required to identify even half of the risk genes [Buxbaum et al. (2012)]. At the same time, a single de novo LoF (dnLoF) event has been recorded for more than 200 genes in the available data. Probability arguments suggest that a sizable fraction of these single-hit genes are ASD genes [Sanders et al. (2012)], indicating that genetic data are already providing partial information about more ASD genes. Thus, there is an urgent need to advance ASD gene discovery through the integration of additional biological data and more powerful statistical tests.

The large number of genes with rare coding mutations identified by exome sequencing presents an opportunity for the next wave of discoveries. Fortunately a key element in the path forward has recently been identified. ASD-related mutations have been shown to cluster meaningfully in a gene network derived from gene expression in the developing brain—specifically during the mid-fetal period in the frontal cortex [Willsey et al. (2013)]. These results support the hypothesis that genes underlying ASD risk can be organized into a much smaller set of underlying subnetworks [Ben-David and Shifman (2012), Parikshak et al. (2013), Willsey et al. (2013)]. This leads to the conjecture that networks derived from gene expression can be utilized to discover risk genes. Liu et al. (2014) developed DAWN_α, a statistical algorithm for “Detecting Association With Networks” that uses a hidden Markov random field (HMRF) model to discover clusters of risk genes in the gene network. Here we present DAWN, a greatly improved approach that provides a flexible and powerful statistical method for network assisted risk gene discovery.

There are two main challenges to discovery of ASD genes: (1) weak genetic signals for association are spread out over a large set of genes; and (2) these signals are clustered in gene networks, but the networks are very high dimensional. Available data for network estimation are extremely limited, hence the dimension of the problem is orders of magnitude greater than the sample size. A weakness of DAWN_α lies in the approach to gene network construction. The algorithm is based on discovering gene modules and estimating the edges connecting genes within a module based on the pairwise correlations. In contrast, DAWN estimates the conditional independence network of the genes under investigation. It achieves this goal utilizing a novel network estimation method that achieves a dimension reduction that is tightly linked to the genetic data. Our approach to network assisted estimation is based on three key conjectures: (i) autism risk nodes are more likely to be connected than nonrisk nodes; (ii) by focusing our network reconstruction efforts on portions of the graph that include risk nodes we can improve the chance that the key edges in the network that connect risk nodes are successfully identified and that fewer false edges are included; and (iii) the HMRF model will have greater power to detect true risk nodes when the network estimation procedure focuses on successfully reconstructing partial neighborhoods in the vicinity of risk nodes.

The remainder of this paper is organized as follows. Section 2 presents data and background information. Section 3 presents the main idea of our testing procedure within a graphical model framework. First, we develop an algorithm for estimating the gene interaction network that integrates node-specific information. Second, we describe the HMRF model. Third, we extend our model to include the directed network information. Last, we develop in theory to motivate why our network estimation procedure is more precise when node-specific information is integrated. In Section 4 simulation experiments compare our approach with other network estimation algorithms. In Section 5 we apply our procedure to the latest available autism data.

2. Background and data

2.1. Genetic signal

DAWN requires evidence for genetic association for each gene in the network. While this can be derived from any gene-based test for association, a natural choice is TADA, the Transmission And De novo Association test [He et al. (2013)]. For this investigation, TADA scores were calculated using WES data from seventeen distinct sample sets consisting of 16,098 DNA samples and 3871 ASD cases [De Rubeis et al. (2014)]. Using a gene-based likelihood model, TADA produces a test statistic for each gene in the genome. Based on these data, 18 genes incurred at least two dnLoF mutations and 256 incurred exactly once. Any gene with more than one dnLoF mutation is considered a “high confidence” ASD gene and those with exactly one are classified as a “probable” ASD genes due to the near certainty (>99%) and relatively high probability (>30%) the gene is a risk gene, respectively [Willsey et al. (2013)]. Based on TADA analysis of all genes covered by WES, 33 genes have false discovery rate (FDR) q-values <10% and 107 have q-values <30%. Thus, in total, this is a rich source of genetic data from which to make additional discoveries of ASD risk genes and subnetworks of risk genes.

2.2. Gene networks

The major source of data from which to infer the gene–gene interaction network is gene expression levels in specific tissues, which are obtained by high throughput microarray techniques. Using the BrainSpan transcriptome data set [Kang et al. (2011)], Willsey et al. (2013) examined the coexpression patterns across space and time of genes with at least one dnLoF mutation. The data originate from 16 regions of the human brain sampled in 57 postmortem brains ranging from 6 weeks postconception to 82 years of age. By identifying the region and developmental period of the brain in which ASD genes tend to cluster, their investigation confirmed that gene expression networks are meaningful for organization and inter-relationships of ASD genes. Specifically, they identified prefrontal and motor-somatosensory neocortex (FC) during the mid-fetal period as the most relevant spatial/temporal choice. While each brain is measured at only one point in time, combining gene expression from the five frontal cortex regions with the primary somatosensory cortex, multiple observations can be obtained per sample. Nevertheless, the sample size was very small: for example, for fetal development spanning 10–19 weeks post-conception, 14 brains, constituting 140 total samples, were available from which to determine the gene network.

Another type of network is the gene regulation network, which is a directed network. By studying the ChIP-chip data or the ChIP-seq data, one can obtain which genes are regulated by particular transcription factors (TFs). Many available gene regulation networks have already been studied and integrated into a large database called ChEA [Lachmann et al. (2010)]. But this kind of network is far from complete. Here we incorporate the TF network for a single gene (FMRP) to illustrate how this type of information might be utilized in the hunt for ASD risk genes.

2.3. Network estimation

To estimate the gene co-expression network by expression levels, in general, there are three types of approaches. The most straightforward way is to apply a correlation threshold: the connectivity of two genes is determined by whether the absolute correlation is larger than a fixed threshold. This is the approach taken in the popular systems biology software tool known as Weighted Gene Co-expression Network Analysis (WGCNA) [Langfelder and Horvath (2008)]. This tool is frequently used to discover networks of genes, or modules, with high coexpression. The DAWN_α algorithm used this principle to construct a gene correlation network [Liu et al. (2014)]. Using WGCNA, modules were formed based on the dendrogram with the goal of partitioning genes into highly connected subunits. Next, to generate a relatively sparse network within each module, genes with very high correlation were clustered together into multi-gene supernodes. The motivation for pre-clustering highly correlated genes as supernodes was to create a network that is not dominated by local subsets of highly connected genes. By grouping these subsets of genes into supernodes, the broader pattern of network connections was more apparent. Finally, the gene network was constructed by connecting supernodes using a correlation threshold.

A major innovation of the DAWN algorithm developed in this paper is a more efficient network estimation method with better statistical interpretation. Constructing a network based on correlations has two advantages: it is computationally efficient and the edges can be estimated reliably using a small sample. In contrast, the conditional independence network is sparser and has greater interpretability, but it is much harder to estimate. Assuming that the gene expression levels follow a multivariate normal distribution, the conditional independence can be recovered by estimating the support of the inverse covariance matrix of the expression data. One approach is to estimate the inverse covariance matrix directly using penalized maximum likelihood approaches [Cai, Liu and Luo (2011), Cai, Liu and Zhou (2012), Friedman, Hastie and Tibshirani (2008), Ma, Xue and Zou (2013)]. Alternatively, the neighborhood selection method is based on sparse regression techniques to select the pairs of genes with nonzero partial correlations. For instance, Meinshausen and Bühlmann (2006) applied LASSO for the neighborhood selection of each gene and then construct the adjacency matrix by aggregating the nonzero partial correlation obtained for each regression. Peng, Zhou and Zhu (2009) proposed a joint sparse regression method for estimating the inverse covariance matrix. A challenge for both the neighbor selection method and the maximum likelihood approach is that the number of expression samples available is two orders of magnitude smaller than the number of genes. In most applications that utilize LASSO-based methods this challenge is diminished by simply estimating the gene network for several hundred genes. For example, Tan et al. (2014) use a sample of size 400 to estimate a gene network for 500 genes. For this application we wish to explore the full range of genes that might be involved in risk for autism, and thus we cannot reduce the dimension in a naive manner. One may also consider inverting an estimated covariance matrix [Opgen-Rhein and Strimmer (2007), Schäfer and Strimmer (2005)]. But in high dimensions the matrix inversion may be too noisy. DAWN takes a novel approach to dimension reduction to optimize the chance of retaining genes of interest.

2.4. Networks and feature selection

Many previous papers have discussed how to incorporate the estimated network into the feature selection problems, namely, DAPPLE [Rossin et al. (2011)], GRAIL [Raychaudhuri et al. (2009)] metaRanker [Pers et al. (2013)], Hotnet [Vandin, Upfal and Raphael (2011)], VEGAS [Liu et al. (2010)] and penalized methods [Mairal and Yu (2013)]. However, none of these methods control the rate of false discovery.

Motivated by the work of Li, Wei and Maris (2010) and Wei and Pan (2008), DAWN_α applied a HMRF model to integrate the gene network into a powerful risk gene detection procedure. In principle, this approach captures the stochastic dependence structure of both TADA genetic scores and the gene–gene interactions, while being able to provide posterior probability of risk association for each gene and thus control the rate of false discovery. In practice, DAWN_α has a weakness due to the multi-gene nodes that define the networks. This complication led to several statistical challenges in the implementation of the algorithm. Notably, a post-hoc analysis is required to determine which gene(s) within a multi-gene node are associated with the phenotype. With DAWN we can capture the strengths of the natural pairing of the gene network and the HMRF model without these added challenges.

3. Methods

The TADA scores together with the gene–gene interaction network provide a rich source of information from which to discover ASD genes. To obtain useful information from these data sets, we will need to utilize existing tools and also to develop novel statistical procedures that can overcome several challenges. Our model incorporates 3 main features: (1) Based on DAWN_α, a HMRF model combines the network structure and individual TADA scores in a systematic manner that facilitates statistical inference. (2) To obtain the most power from this model, we require a sparse estimate of the gene–gene interaction network, but the sample size is insufficient to yield a reliable estimate of the full gene network (approximately 100 observations and 20,000 genes). However, based on the form of the HMRF model, it is apparent that it is sufficient to estimate the sub-network of the gene–gene interaction network that is particularly relevant to autism risk. We provide a novel approach to achieving this goal. (3) Finally, the statistical model efficiently incorporates additional covariates, for instance, the targets of key transcription factors that may regulate the gene network, to predict autism risk genes.

Feature two is the most challenging. Under the high-dimensional setting, the existing network estimation approaches are neither efficient nor accurate enough to successfully estimate the network. To optimize information available in a small sample size, we need to target our efforts to capture the dependent structure between disease-associated genes and their nearest neighbors. DAWN uses a novel partial neighborhood selection (PNS) approach to attain this goal. By incorporating node-specific information, this approach focuses on estimating edges between likely risk genes so that it reduces the complexity of the large-scale network estimation problem and provides a disease-specific network for the HRMF procedure.

To incorporate the estimated network into the risk gene detection procedure, feature one involves simplifying the HMRF model already developed for DAWN_α to integrate the estimated network and the genetic data. By applying the proposed model, the posterior probability of each gene being a risk gene can be obtained based on both the genetic evidence and neighborhood information from the estimated gene network.

If additional gene dependence information such as targets of transcription factor networks are available, they can be incorporated naturally into the risk gene detection procedure so that better power can be achieved. To this end, for feature three, we extend the Ising model by adding another parameter to characterize the effect of such additional dependence information. This allows simple estimation and inference using essentially the same procedure.

3.1. Partial neighborhood selection for network estimation

To estimate a high-dimensional disease-specific gene network with small sample size data, we propose the partial neighborhood selection (PNS) method. Let X₁, . . . , X_n be the samples from d-dimensional Gaussian random variables with covariance matrix Σ. Our goal at this stage is to estimate the support of the inverse matrix of Σ, which is an adjacency matrix Ω. To maximize the power of the follow-up HMRF algorithm, the estimated adjacency matrix should be as precise as possible. But, given the high dimensionality and the small sample size, estimating the support of the entire precision matrix is a very ambitious goal. To overcome this challenge, it has been noted that ignoring some components of the high-dimensional parameter will lead to better estimation accuracy [Levina and Bickel (2004)]. Here we follow this rationale by estimating entries Ω(i, j) for a set of selected entries (i, j), and setting $\widehat{\Omega }(i,j)=0$ for other entries. Such a selective estimation approach will inevitably cause some bias, as many components of the parameter of interest are assigned a null value. However, this approach has the potential to greatly reduce the estimation variance for the selected components, as the reduced estimation problem has much lower dimensionality. Such a procedure is particularly useful in situations where some low-dimensional components of the parameter are more important for subsequent inference. We will need to choose the zero entries carefully so that the bias is controlled. Because our ultimate goal is to detect the risk genes associated with a particular disease, the dependence structure between risk genes is more essential in the procedure rather than the dependence between nonrisk genes. Specifically, we target Ω(i, j) for genes i and j with higher TADA scores and their high correlation neighbors. Such a choice can be supported by the HMRF model described in Section 3.2 as well as the theoretical results in Section 3.4.

In the PNS algorithm (Algorithm 1), the p-values for each gene are utilized as the node-specific information for the network estimation. In step 1, we start with the key genes, S′, defined as those genes with relatively small TADA p-values. In step 2, we further screen the key genes by excluding any elements that are not substantially co-expressed with any other measured genes. This step is taken because the upcoming HMRF model is applied to networks. Genes that are not highly co-expressed with any other genes are not truly functioning in the network. The resulting set, S, establishes the core of the network. In the third step we expand the gene set to V by retrieving all likely neighbors of genes in the set S. The likely partial correlation neighbors of gene j ∈ S are identified based on the absolute correlation |ρ_ij| > τ. The superset V includes all likely risk genes and their neighbors, but excludes all portions of the gene network that are free of genetic signals for risk based on the TADA scores. Similar correlation thresholding ideas have been considered in Butte and Kohane (1999), Luo et al. (2007), Yip and Horvath (2007). Then we apply the neighborhood selection method [Meinshausen and Bühlmann (2006)] for each gene in the set S to decide which genes are the true neighbors of risk genes. Note that the estimated graph does not contain possible edges between nodes in V \ S, but the edges that link nodes in V \ S will not affect the results of our follow-up algorithm, so it is much more efficient to not estimate those edges when we estimate the disease-specific network. In the fourth step we apply the neighborhood selection algorithm to the subnetwork V.

Algorithm 1.

PNS algorithm

1. p-value screening: Exclude any nodes with p-value pi > t. The remaining nodes define S′ = {i : pi ≤ t}.

2. Correlation screening: Construct a graph G′ = {S′, Ω′}, where Ω′ is an adjacency matrix with ${\Omega }_{ij}^{\prime }=I\{\mid {\rho }_{ij}\mid >\tau \}$, where ρij is the pairwise correlation between the ith and jth node. Then exclude all isolated nodes to obtain $S=S^{\prime }\backslash \{j:{\sum }_{i\in S^{\prime }}{\Omega }_{ij}^{\prime }=0\}$.

3. Retrieving neighbors: Retrieve all possible first order neighbors of nodes in S and obtain node set V, where $V=S\cup \{j:\mid {\rho }_{ij}\mid >\tau ,i\in S\}$.

4. Constructing graph: Apply Meinshausen and Bühlmann's (2006) regression-based approach to select the edges among nodes in S and between nodes in S and V/S by minimizing the following d1 individual loss functions separately:

$\left(3.1\right)L_i=\frac{1}{2}{\Vert X_i-{\sum }_{j\in V,j\ne i}{\beta }_{ij}{X}_j\Vert }^2+\lambda {\sum }_{j\in V,j\ne i}\mid {\beta }_{ij}\mid ,i=1,\dots ,d_1$,

where d1 is the number of nodes in S, λ is the regularization parameter. Then the graph Ω of V is constructed as Ωij = 1 – (1 – Eij)(1 – Eji), where matrix E is

$E_{ij}=\{\begin{array}{cc}I\{\mid {\beta }_{ij}\mid >0\},\hfill & i\in S,\hfill \\ 0,\hfill & i\notin S.\hfill \end{array}\phantom{\}}$

5. Return G = (V, Ω).

Setting threshold values in gene screening

The PNS algorithm uses two tuning parameters, t and τ, in the screening stage. The choice of t and τ shall lead to a good reduction in the number of genes entering the network reconstruction step, while keeping most of the important genes. A practical way of choosing t would be to match some prior subject knowledge about the proportion of risk genes. In general, t shall not be too small in order to avoid substantial loss of important genes. The choice of τ is more flexible, depending on the size of the problem and available computational resource. In our autism data the number of genes is very large, therefore, a relatively large value of τ is necessary. The choice of τ = 0.7 has been used for gene correlation thresholding in the literature [see, e.g., Luo et al. (2007), Willsey et al. (2013), Yip and Horvath (2007)]. In our simulation study, we find that the performance of PNS is stable as long as t is not overly small, and is insensitive to the choice of τ. More details are given in Section 4.2.

Choosing the tuning parameter in sparse regression

Finding the right amount of regularization in sparse support recovery remains an open and challenging problem. Meinshausen and Bühlmann (2010) and Liu, Roeder and Wasserman (2010) proposed a stability approach to select the tuning parameter; however, due to the high-dimension-low-sample-size scenario, the subsampling used in this approach reduces the number of samples to an undesirable level. Li et al. (2011) proposed selecting the tuning parameter by controlling the FDR, but the FDR cannot be easily estimated in this context. Lederer and Müller (2014a) suggested an alternative tuning-free variable selection procedure for high-dimensional problems known as TREX. Graphical TREX (GTREX) extends this approach to graphical models [Lederer and Müller (2014b)]. Although this approach produced promising results in simulated data, it relies on subsampling. Consequently, for some data sets the sample size will be a limiting factor.

A parametric alternative relies on an assumption that the network follows a power law, that is, the probability a node connects to k other nodes is equal to p(k) ~ k^−γ. This assumption is often made for gene expression networks [Zhang and Horvath (2005)]. To measure how well a network conforms to this law, assess the square of correlation R² between log p(k) and log(k):

$$R^2={\left(\text{corr}(\log p\left(k\right),\log \left(k\right))\right)}^2.$$ (3.2)

R² = 1 indicates that the estimated network follows the power law perfectly, hence, the larger the R², the closer the estimated network is to achieve the scale-free criteria. In practice, the tuning parameter, λ, can be chosen by visualizing the scatter plot of R² as a function of λ. There is no guarantee that the power law is applicable to a given network [Khanin and Wit (2006)], and this approach will not perform well if the assumption is violated. As applied in the PNS algorithm, the assumption is that the select set of genes in V follow the power law. The PNS subnetwork is not randomly sampled from the full network, as it integrates the p-value and the expression data to select portions of the network rather than random nodes. It has been noted in the literature [Stumpf, Wiuf and May (2005)] that the scale-free property of degree distribution of a random subnetwork may deviate from that of the original full network; however, the deviation is usually small. We find the scale-free criterion suitable for the autism data sets considered in this paper. However, the general performance of PNS and DAWN does not crucially depend on this assumption, as we demonstrate in the simulation study in Section 4.2.

3.2. Hidden Markov random field model

Gene-based tests such as TADA reveal very few genes with a p-value that passes the threshold for genome-wide significance. However, after taking the gene interaction network into consideration, we usually find that some genes with small p-values are clustered. The p-values of those genes are usually not significant individually, but this clustering of small p-values in the network is highly unlikely to happen by chance. To enhance the power to detect risk genes, we adopt a HMRF model to find risk genes by discovering genes that are clustered with other likely risk genes.

First we convert the p-values to normal Z-scores, Z = (Z₁; . . . ; Z_n), to obtain a measure of the evidence of disease association for each gene. These Z-scores are assumed to have a Gaussian mixture distribution, where the mixture membership of Z_i is determined by the hidden state I_i, which indicates whether or not gene i is a risk gene. We assume that each of the Z-scores under the null hypothesis (I = 0) has a normal distribution with mean 0 and variance ${\sigma }_0^2$, while under the alternative (I = 1) the Z-scores approximately follow a shifted normal distribution, with a mean μ and variance ${\sigma }_1^2$. Further, we assume that the Z-scores are conditionally independent given the hidden indicators I = (I₁, . . . , I_n). The model can be expressed as

$$Z_i\sim P(I_i=0)N(0,{\sigma }_0^2)+P(I_i=1)N(\mu ,{\sigma }_1^2).$$ (3.3)

The dependence structure reduces to the dependence of hidden states I_i. To model the dependence structure of I_i, we consider a simple Ising model with probability mass function

$$P(\mathbf{I}=\eta )\propto \exp (b^t\eta +c{\eta }^t\Omega \eta )\text{for all}\eta \in {\{0,1\}}^n.$$ (3.4)

We apply the iterative algorithm (Algorithm 2) to estimate the parameters and the posterior probability of P(I_i|Z).

Algorithm 2.

HMRF parameter estimation

1. Initialize the states of node Ii = 1if Zi > Zthres and 0 otherwise.

2. For t = 1, . . ., T

(a) Update (b̂(t), ĉ(t)) by maximizing the pseudo likelihood

${\prod }_i\frac{\exp \{b{I}_i+c{I}_i{\Omega }_i.\mathbf{I}\}}{\exp \{b{I}_i+c{I}_i{\Omega }_i.\mathbf{I}\}+\exp \{b(1-I_i)+c(1-I_i){\Omega }_i.\mathbf{I}\}}$.

(b) Apply a single cycle of the iterative conditional mode [ICM, Besag (1986)] algorithm to update I. Specifically, we obtain a new ${\widehat{I}}_j^{\left(t\right)}$ based on

$P(I_j\mid \mathbf{Z};{\widehat{\mathbf{I}}}_{-i},{\widehat{b}}^{\left(t\right)},{\widehat{c}}^{\left(t\right)})\propto f(z_i\mid {\widehat{I}}_i)P(I_i\mid {\widehat{\mathbf{I}}}_{-i},{\widehat{b}}^{\left(t\right)},{\widehat{c}}^{\left(t\right)})$.

(c) Update $({\widehat{\mu }}^{(t-1)},{\widehat{\sigma }}_0^{2(t-1)},{\widehat{\sigma }}_1^{2(t-1)})$ to $({\widehat{\mu }}^{\left(t\right)},{\widehat{\sigma }}_0^{2\left(t\right)},{\widehat{\sigma }}_1^{2\left(t\right)})$:

${\widehat{\mu }}^{\left(t\right)}=\frac{{\sum }_{i}P(I_i=1\mid \mathbf{Z},{\widehat{b}}^{\left(t\right)};{\widehat{c}}^{\left(t\right)})Z_i}{{\sum }_{i}P(I_i=1\mid \mathbf{Z},{\widehat{b}}^{\left(t\right)};{\widehat{c}}^{\left(t\right)})}$,

${\widehat{\sigma }}_0^{2\left(t\right)}=\frac{{\sum }_{i}P(I_i=0\mid \mathbf{Z},{\widehat{b}}^{\left(t\right)};{\widehat{c}}^{\left(t\right)})Z_i^2}{{\sum }_{i}P(I_i=0\mid \mathbf{Z},{\widehat{b}}^{\left(t\right)};{\widehat{c}}^{\left(t\right)})}$,

${\widehat{\sigma }}_1^{2\left(t\right)}=\frac{{\sum }_{i}P(I_i=1\mid \mathbf{Z},{\widehat{b}}^{\left(t\right)};{\widehat{c}}^{\left(t\right)}){(Z_i-{\widehat{\mu }}^{\left(t\right)})}^2}{{\sum }_{i}P(I_i=1\mid \mathbf{Z},{\widehat{b}}^{\left(t\right)};{\widehat{c}}^{\left(t\right)})}$.

3. Return $(\widehat{b},\widehat{c},\widehat{\mu },{\widehat{\sigma }}_0^2,{\widehat{\sigma }}_1^2)=({\widehat{b}}^{\left(T\right)},{\widehat{c}}^{\left(T\right)},{\widehat{\mu }}^{\left(T\right)},{\widehat{\sigma }}_0^{2\left(T\right)},{\widehat{\sigma }}_1^{2\left(T\right)})$.

After the posterior probability of P(I_i|Z, I_–i) is obtained, we apply Gibbs sampling to estimate the posterior probability qi = P(I_i = 0|Z). Finally, let q_(i) be the sorted posterior probability in ascending order; the Bayesian FDR correction [Müller, Parmigiani and Rice (2006)] of the lth sorted gene can be calculated as

$${\mathrm{FDR}}_l=\sum _{i=1}^{l}q\left(i\right)/l.$$ (3.5)

Genes with FDR less than α are selected as the risk genes.

In summary, the DAWN algorithm (Algorithm 3) consists of four steps.

Algorithm 3.

DAWN algorithm

1. Obtain gene specific p-values.

2. Estimate the gene network using the PNS algorithm (Algorithm 1).

3. Incorporate the information from steps 1 and 2 into the HMRF model and estimate the parameters of the HMRF model (Algorithm 2).

4. Apply the Bayesian FDR correction to determine the risk genes [equation (3.5)].

The HMRF component of DAWN_α is similar in spirit to what is described here for DAWN, but the implementation in the former algorithm is considerably less powerful due to multi-gene nodes. DAWN_α cannot directly infer risk status of genes from the estimated status of the node.

3.3 Extending the Ising model

Our framework is general and flexible enough to incorporate additional biological information such as the TF network information by naturally extending the Ising model. Under this extended model, we can incorporate a directed network such as the TF network along with the undirected network such as the gene co-expression network. From the microarray gene expression levels, an undirected network could be estimated based on the PNS algorithm. With the TF network information, we could also estimate a directed network that indicates which genes are regulated by specific TF genes. This additional information can be naturally modeled in the Ising model framework by allowing the model parameter to be shifted for particular collection of TF binding sites. The density function of this more general Ising model is as follows:

$$P(\mathbf{I}=\eta )\propto \exp (b{1}^{\prime }\eta +c{\eta }^t\Omega \eta +d{H}^{\prime }\eta ).$$ (3.6)

where H = (h₁, . . . , h_n) is the indicator of TF binding sites, and d > 0 reflects the enhanced probability of risk for genes regulated by TF.

If d > 0, this indicates that the TF binding site covariate is a predictor of risk for diseases. To test whether or not d is significantly larger than zero, we compare the observed statistic d̂ with d obtained under the null hypothesis of no association. To this end, we adopt a smoothed bootstrap procedure which simulates data with the same clustering of the observed genetic signals, but without an association with the TF binding site.

To simulate Z from the null model, we first simulate the hidden states I from the distribution (3.4). We randomly assign initial values of I to each node in the network and the proportion of nodes with I = 1 is r, where r ∈ (0, 1) is a pre-chosen value, for example, 0.1. Then, we apply a Metropolis–Hastings algorithm to update I until convergence. The full bootstrap procedure is described in Algorithm 4.

Algorithm 4.

1. Apply the algorithm to model (3.4) to obtain estimates of the model parameters.

2. Using the estimated null model, simulate I* by the Metropolis–Hastings algorithm, then simulate Z* using equation (3.3).

3. Using model (3.6), estimate the parameters for the simulated data.

4. Repeat steps 2–3 B times, the B copies of estimated d̂ can be used as a reference distribution of the estimated parameter under the null model.

5. Output the p-value $p=\frac{1}{B}{\sum }_{i=1}^{B}I\{{\widehat{d}}_i>d\}$.

For presentation simplicity we describe the idea of incorporating additional subject knowledge into the Ising model for a single TF. The procedure can be straightforwardly extended to incorporate multiple TFs. In this case, the Ising model for the hidden vector I becomes

$$P(\mathbf{I}=\eta )\propto \exp \left(b{1}^{\prime }\eta +c{\eta }^{\prime }\Omega \eta +\sum _{k=1}^K{d}_k{H}_k^{\prime }\eta \right).$$

The bootstrap testing procedure described in Algorithm 4 also carries over in an obvious manner to the multiple TF case.

3.4. More about partial neighborhood selection

In this section we discuss theory that explains why PNS can more precisely estimate edges between risk genes. We find that under the Ising model, nodes with similar properties are more likely to be connected with each other in the network. Therefore, by utilizing this property of the Ising model, we can greatly improve the accuracy of estimating a disease-specific network.

The following theorem suggests that the larger the Z-scores are for the two nodes, the more likely there is an edge connecting those two nodes. Therefore, it is reasonable to adapt the lasso regression to retrieve neighbors of only candidate risk genes, which are the genes that have small p-values. This choice is justified because those genes are more likely to be connected with other genes.

Theorem 3.1

Assume that (Z, I) are distributed according to the HMRF in equations (3.3) and (3.4). Assume that Ω has independent entries. Let Ω′ = {Ω_k1,k2 (k₁, k₂) ≠ (i, j)}. $\mathcal{A}$ be the set of all possible Ω′. Define I_i and I_j as the i th and j th element of I, I′ = (I₁, I₂, . . . , I_d)/{I_i, I_j}, and $\mathcal{B}$ the set of all possible I′. Then for any Ω′ ∈ $\mathcal{A}$ and any I′ ∈ $\mathcal{B}$, P(Ω_ij = 1|Z, Ω′, I′) is an increasing function of Z_i and Z_j.

Theorem 3.1 provides some justification for the p-value thresholding in the PNS algorithm. An important condition here is that I is distributed as an Ising model where the conditional independence is modeled by the binary matrix Ω. In practice, if Ω is estimated from some other data source, then it is possible that Ω may not be relevant to reflect the independence structure of I. This is not the case in our application, as the gene co-expression data is collected from the BrainSpan data for the frontal cortex sampled during the mid-fetal developmental period because it has been shown that this space–time-tissue combination is particularly relevant to autism [Willsey et al. (2013)].

Proof of Theorem 3.1

Let k = 1 represent (I_i, I_j) = (1, 1), k = 2 represent (I_i, I_j) = (1, 0), k = 3 represent (I_i, I_j) = (0, 1), and k = 4 represent (I_i, I_j) = (0, 0). Then

$$\begin{array}{cc}\hfill P({\Omega }_{ij}=1\mid \mathbf{Z},{\Omega }^{\prime },{\mathbf{I}}^{\prime })=& \sum _{k=1}^{4}P({\Omega }_{i,j}=1,(I_i,I_j)=k\mid \mathbf{Z},{\Omega }^{\prime },{\mathbf{I}}^{\prime })\hfill \\ \hfill =& \sum _{k=1}^{4}P({\Omega }_{i,j}=1\mid (I_i,I_j)=k,\mathbf{Z},{\Omega }^{\prime },{\mathbf{I}}^{\prime })P((I_i,I_j)=k\mid \mathbf{Z},{\Omega }^{\prime },{\mathbf{I}}^{\prime })\hfill \\ \hfill =& \sum _{k=1}^{4}P({\Omega }_{i,j}=1\mid (I_i,I_j)=k,{\Omega }^{\prime },{\mathbf{I}}^{\prime })P((I_i,I_j)=k\mid \mathbf{Z},{\Omega }^{\prime },{\mathbf{I}}^{\prime })\hfill \\ \hfill =& M_1({\mathbf{I}}^{\prime },{\Omega }^{\prime })P_1+\sum _{k=2}^4{M}_2({\mathbf{I}}^{\prime },{\Omega }^{\prime })P_k,\hfill \end{array}$$

where M_i(I′, Ω′) = P(Ω_{i, j} = 1|(I_i, I_j) = k, Ω′, I′) and P_k = P ((I_i, I_j) = k|Z, Ω′, I′). Taking a derivative of P(Ω_ij = 1|Z, Ω′, I′) with respect to Z_i, we have

$$\begin{array}{cc}\hfill \frac{\partial P({\Omega }_{ij}=1\mid \mathbf{Z},{\Omega }^{\prime },{\mathbf{I}}^{\prime })}{\partial Z_i}& =M_1({\mathbf{I}}^{\prime },{\Omega }^{\prime })\times \frac{\partial P_1}{\partial Z_i}+M_2({\mathbf{I}}^{\prime },{\Omega }^{\prime })\times \left(\frac{\partial P_2}{\partial Z_i}+\frac{\partial P_3}{\partial Z_i}+\frac{\partial P_3}{\partial Z_i}\right)\hfill \\ \hfill & =M_1({\mathbf{I}}^{\prime },{\Omega }^{\prime })\times \frac{\partial P_1}{\partial Z_i}-M_2({\mathbf{I}}^{\prime },{\Omega }^{\prime })\times \frac{\partial P_1}{\partial Z_i}\hfill \\ \hfill & =(M_1({\mathbf{I}}^{\prime },{\Omega }^{\prime })-M_2({\mathbf{I}}^{\prime },{\Omega }^{\prime }))\times \frac{\partial P_1}{\partial Z_i}.\hfill \end{array}$$

Based on Lemma 3.1, we have M₁(I′, Ω′) – M₂(I′, Ω′) > 0. Based on Lemma 3.2, we have $\frac{\partial P_1}{\partial Z_i}>0$. Thus, we obtain $\frac{\partial P({\Omega }_{ij}=1\mid \mathbf{Z},{\Omega }^{\prime },{\mathbf{I}}^{\prime })}{\partial Z_i}>0$, and P(Ω_ij = 1|Z, Ω′, I′) is an increasing function of Z_i. Similarly, we obtain that P(Ωij = 1|Z, Ω′, I′) is also an increasing function of Z_j.

The theorem above reveals the specific structure of the adjacency matrix for the network in the Ising model setting. This kind of adjacency matrix has more edges in the block of risk genes and fewer edges in the block of nonrisk genes. Thus, given this specific structure and limited sample size, it is reasonable to focus on estimating the edges between genes with small p-values. Therefore, under the Ising model, the proposed PNS algorithm is a more precise network estimation procedure than other existing network estimating procedures, which all ignore the node-specific information.

Lemma 3.1

Under the same conditions as in Theorem 3.1, for any Ω′ ∈ $\mathcal{A}$ and any I′ ∈ $\mathcal{B}$,

$$P({\Omega }_{ij}=1\mid I_i,I_j,{\mathbf{I}}^{\prime },{\Omega }^{\prime })=\{\begin{array}{cc}{M}_1({\mathbf{I}}^{\prime },{\Omega }^{\prime })>P({\Omega }_{ij}=1),\hfill & if{I}_i=I_j=1,\hfill \\ M_2({\mathbf{I}}^{\prime },{\Omega }^{\prime })<P({\Omega }_{ij}=1),\hfill & otherwise.\hfill \end{array}\phantom{\}}$$

Proof

$$\frac{P({\Omega }_{ij}=1\mid I_i=I_j=1,{\mathbf{I}}^{\prime },{\Omega }^{\prime })}{P({\Omega }_{ij}=0\mid I_i=I_j=1,{\mathbf{I}}^{\prime },{\Omega }^{\prime })}=\frac{P({\Omega }_{ij}=1,I_i=I_j=1,{\mathbf{I}}^{\prime },{\Omega }^{\prime })}{P({\Omega }_{ij}=0,I_i=I_j=1,{\mathbf{I}}^{\prime },{\Omega }^{\prime })}=\frac{P(I_i=I_j=1,{\mathbf{I}}^{\prime }\mid {\Omega }_{ij}=1,{\Omega }^{\prime })P({\Omega }_{ij}=1)P\left({\Omega }^{\prime }\right)}{P(I_i=I_j=1,{\mathbf{I}}^{\prime }\mid {\Omega }_{ij}=0,{\Omega }^{\prime })P({\Omega }_{ij}=0)P\left({\Omega }^{\prime }\right)}.$$

Let

$$f(I_i,I_j,{\mathbf{I}}^{\prime }\mid {\Omega }_{ij},{\Omega }^{\prime })=\exp (-b^t\mathbf{I}+c{\mathbf{I}}^t\Omega \mathbf{I}),$$

where I_–i,–j = I′, I_i, = I_i, I_j = I_j. We define

$$\begin{array}{cc}\hfill T_1({\mathbf{I}}^{\prime },{\Omega }_{ij},{\Omega }^{\prime })=& f(I_i=1,I_j=1,{\mathbf{I}}^{\prime }\mid {\Omega }_{ij},{\Omega }^{\prime }),\hfill \\ \hfill T_2({\mathbf{I}}^{\prime },{\Omega }_{ij},{\Omega }^{\prime })=& f(I_i=1,I_j=0,{\mathbf{I}}^{\prime }\mid {\Omega }_{ij},{\Omega }^{\prime }),\hfill \\ \hfill T_3({\mathbf{I}}^{\prime },{\Omega }_{ij},{\Omega }^{\prime })=& f(I_i=0,I_j=1,{\mathbf{I}}^{\prime }\mid {\Omega }_{ij},{\Omega }^{\prime }),\hfill \\ \hfill T_4({\mathbf{I}}^{\prime },{\Omega }_{ij},{\Omega }^{\prime })=& f(I_i=0,I_j=0,{\mathbf{I}}^{\prime }\mid {\Omega }_{ij},{\Omega }^{\prime }).\hfill \end{array}$$

Then we obtain that

$$\begin{array}{cc}\hfill P(I_i=I_j=1,{\mathbf{I}}^{\prime }\mid {\Omega }_{ij}=1,{\Omega }^{\prime })=& \frac{T_1({\mathbf{I}}^{\prime },{\Omega }_{ij}=1,{\Omega }^{\prime })}{{\sum }_{{\mathbf{J}}^{\prime }\in \mathcal{B}}{\sum }_{k=1}^4{T}_k({\mathbf{J}}^{\prime },{\Omega }_{ij}=1,{\Omega }^{\prime })},\hfill \\ \hfill P(I_i=I_j=1,{\mathbf{I}}^{\prime }\mid {\Omega }_{ij}=0,{\Omega }^{\prime })=& \frac{T_1({\mathbf{I}}^{\prime },{\Omega }_{ij}=0,{\Omega }^{\prime })}{{\sum }_{{\mathbf{J}}^{\prime }\in \mathcal{B}}{\sum }_{k=1}^4{T}_k({\mathbf{J}}^{\prime },{\Omega }_{ij}=0,{\Omega }^{\prime })}.\hfill \end{array}$$

It is easy to show that

$$T_1({\mathbf{I}}^{\prime },{\Omega }_{ij}=1)=T_1({\mathbf{I}}^{\prime },{\Omega }_{ij}=0)\times \exp \left\{2c\right\}$$

and

$$T_k({\mathbf{I}}^{\prime },{\Omega }_{ij}=0)=T_k({\mathbf{I}}^{\prime },{\Omega }_{ij}=1),k=2,3,4.$$

Therefore,

$$\frac{P(I_i=I_j=1,{\mathbf{I}}^{\prime }\mid {\Omega }_{ij}=1,{\Omega }^{\prime })}{P(I_i=I_j=1,{\mathbf{I}}^{\prime }\mid {\Omega }_{ij}=0,{\Omega }^{\prime })}=\frac{{\sum }_{{\mathbf{J}}^{\prime }\in \mathcal{B}}{\sum }_{k=1}^4{T}_k({\mathbf{J}}^{\prime },{\Omega }_{ij}=0,{\Omega }^{\prime })}{{\sum }_{{\mathbf{J}}^{\prime }\in \mathcal{B}}\{{\sum }_{k=2}^4{T}_k({\mathbf{J}}^{\prime },{\Omega }_{ij}=0,{\Omega }^{\prime })+T_1({\mathbf{J}}^{\prime },{\Omega }_{ij}=0,{\Omega }^{\prime })\times \exp \left\{2c\right\}\}}\times \frac{T_1({\mathbf{I}}^{\prime },{\Omega }_{ij}=0,{\Omega }^{\prime })\times \exp \left\{2c\right\}}{T_1({\mathbf{I}}^{\prime },{\Omega }_{ij}=0,{\Omega }^{\prime })}=\frac{{\sum }_{{\mathbf{J}}^{\prime }\in \mathcal{B}}\exp \left\{2c\right\}{\sum }_{k=1}^4{T}_k({\mathbf{J}}^{\prime },{\Omega }_{ij}=0,{\Omega }^{\prime })}{{\sum }_{{\mathbf{J}}^{\prime }\in \mathcal{B}}\{{\sum }_{k=2}^4{T}_k({\mathbf{J}}^{\prime },{\Omega }_{ij}=0,{\Omega }^{\prime })+T_1({\mathbf{J}}^{\prime },{\Omega }_{ij}=0,{\Omega }^{\prime })\times \exp \left\{2c\right\}\}}>1\text{if}c>0.$$

Thus, we obtain

$$\frac{P({\Omega }_{ij}=1\mid I_i=I_j=1,{\mathbf{I}}^{\prime },{\Omega }^{\prime })}{P({\Omega }_{ij}=0\mid I_i=I_j=1,{\mathbf{I}}^{\prime },{\Omega }^{\prime })}>\frac{P({\Omega }_{ij}=1)}{P({\Omega }_{ij}=0)},$$

which leads to

$$P({\Omega }_{ij}=1\mid I_i=I_j=1,{\mathbf{I}}^{\prime },{\Omega }^{\prime })=M_1({\mathbf{I}}^{\prime },{\Omega }^{\prime })>\frac{P({\Omega }_{ij}=1)}{P({\Omega }_{ij}=0)+P({\Omega }_{ij}=1)}.$$

Similarly, for any Ω′ ∈ $\mathcal{A}$ and any I′ ∈ $\mathcal{B}$, we obtain

$$\frac{P((I_i,I_j)=k,{\mathbf{I}}^{\prime }\mid {\Omega }_{ij}=1,{\Omega }^{\prime })}{P((I_i,I_j)=k,{\mathbf{I}}^{\prime }\mid {\Omega }_{ij}=0,{\Omega }^{\prime })}=\frac{{\sum }_{{\mathbf{J}}^{\prime }\in \mathcal{B}}{\sum }_{l=1}^4{T}_l({\mathbf{J}}^{\prime },{\Omega }_{ij}=0,{\Omega }^{\prime })}{{\sum }_{{\mathbf{J}}^{\prime }\in \mathcal{B}}\{{\sum }_{l=2}^4{T}_l({\mathbf{J}}^{\prime },{\Omega }_{ij}=0,{\Omega }^{\prime })+T_1({\mathbf{J}}^{\prime },{\Omega }_{ij}=0,{\Omega }^{\prime })\times \exp \left\{2c\right\}\}}<1\text{when}k=2,3,4,$$ (3.7)

where k = 2 means (I_i, I_j) = (1, 0), k = 3 means (I_i, I_j) = (0, 1), and k = 4 means (I_i, I_j) = (0, 0). Then it is easy to obtain

$$P({\Omega }_{ij}=1\mid (I_i,I_j)=k,{\mathbf{I}}^{\prime },{\Omega }^{\prime })=M_k({\mathbf{I}}^{\prime },{\Omega }^{\prime })<\frac{P({\Omega }_{ij}=1)}{P({\Omega }_{ij}=0)+P({\Omega }_{ij}=1)}.$$

From equation (3.7) it is clear that M_k(I′, Ω′) does not depend on k, thus M_k(I′, Ω′) = M2(I′, Ω′) for k = 2, 3, 4.

Based on Lemma 3.1, we know that if a pair of nodes has two risk nodes, then this pair of nodes are more likely to be connected with an edge than the pairs of nodes with only one risk node or no risk nodes.

Lemma 3.2

Under the same conditions as in Theorem 3.1, for any Ω′ ∈ $\mathcal{A}$ and any I′ ∈ $\mathcal{B}$, P(I_i = 1, I_j = 1|I′, Ω′, Z) is an increasing function of Z_i and Z_i.

Proof

We first derive the conditional probability of I_i = I_j = 1 given I′, Ω′ and Z:

$$\begin{array}{cc}\hfill P_1=& P(I_i=1,I_j=1\mid {\mathbf{I}}^{\prime },{\Omega }^{\prime },\mathbf{Z})=P(I_i=1,I_j=1,{\mathbf{I}}^{\prime },{\Omega }^{\prime },\mathbf{Z})∕P({\mathbf{I}}^{\prime },{\Omega }^{\prime },\mathbf{Z})\hfill \\ \hfill =& P(\mathbf{Z}\mid I_i=1,I_j=1,{\mathbf{I}}^{\prime },{\Omega }^{\prime })P(I_i=1,I_j=1,{\mathbf{I}}^{\prime },{\Omega }^{\prime })∕P({\mathbf{I}}^{\prime },{\Omega }^{\prime },\mathbf{Z})\hfill \\ \hfill =& P(Z_i\mid I_i=1)P(Z_j\mid I_j=1)P({\mathbf{Z}}_{-i,-j}\mid {\mathbf{I}}^{\prime })P(I_i=1,I_j=1,{\mathbf{I}}^{\prime },{\Omega }^{\prime })∕P({\mathbf{I}}^{\prime },{\Omega }^{\prime },\mathbf{Z})\hfill \\ \hfill =& P(Z_i\mid I_i=1)P(Z_j\mid I_j=1)P({\mathbf{Z}}_{-i,-j}\mid {\mathbf{I}}^{\prime })P(I_i=1,I_j=1,{\mathbf{I}}^{\prime }\mid {\Omega }^{\prime })P\left({\Omega }^{\prime }\right)∕P({\mathbf{I}}^{\prime },{\Omega }^{\prime },\mathbf{Z})\hfill \\ \hfill =& P(Z_i\mid I_i=1)P(Z_j\mid I_j=1)P({\mathbf{Z}}_{-i,-j}\mid {\mathbf{I}}^{\prime })P(I_i=1,I_j=1,{\mathbf{I}}^{\prime }\mid {\Omega }^{\prime })∕P({\mathbf{I}}^{\prime },\mathbf{Z}\mid {\Omega }^{\prime }).\hfill \end{array}$$

Similarly, we obtain

$$\begin{array}{cc}\hfill P_2& =P(I_i=1,I_j=0\mid {\mathbf{I}}^{\prime },{\Omega }^{\prime },\mathbf{Z})\hfill \\ \hfill & =P(Z_i\mid I_i=1)P(Z_j\mid I_j=0)P({\mathbf{Z}}_{-i,-j}\mid {\mathbf{I}}^{\prime })P(I_i=1,I_j=0,{\mathbf{I}}^{\prime }\mid {\Omega }^{\prime })∕P({\mathbf{I}}^{\prime },\mathbf{Z}\mid {\Omega }^{\prime }),\hfill \\ \hfill P_3& =P(I_i=0,I_j=1\mid {\mathbf{I}}^{\prime },{\Omega }^{\prime },\mathbf{Z})\hfill \\ \hfill & =P(Z_i\mid I_i=0)P(Z_j\mid I_j=1)P({\mathbf{Z}}_{-i,-j}\mid {\mathbf{I}}^{\prime })P(I_i=0,I_j=1,{\mathbf{I}}^{\prime }\mid {\Omega }^{\prime })∕P({\mathbf{I}}^{\prime },\mathbf{Z}\mid {\Omega }^{\prime }),\hfill \\ \hfill P_4& =P(I_i=0,I_j=0\mid {\mathbf{I}}^{\prime },{\Omega }^{\prime },\mathbf{Z})\hfill \\ \hfill & =P(Z_i\mid l_i=0)P(Z_j\mid I_j=0)P({\mathbf{Z}}_{-i,-j}\mid {\mathbf{I}}^{\prime })P(I_i=0,I_j=0,{\mathbf{I}}^{\prime }\mid {\Omega }^{\prime })∕P({\mathbf{I}}^{\prime },\mathbf{Z}\mid {\Omega }^{\prime }).\hfill \end{array}$$

We further define

$$\begin{array}{cc}\hfill C_1=& P({\mathbf{Z}}_{-i,-j}\mid {\mathbf{I}}^{\prime })P(I_i=1,I_j=1,{\mathbf{I}}^{\prime }\mid {\Omega }^{\prime }),\hfill \\ \hfill C_2=& P({\mathbf{Z}}_{-i,-j}\mid {\mathbf{I}}^{\prime })P(I_i=1,I_j=0,{\mathbf{I}}^{\prime }\mid {\Omega }^{\prime }),\hfill \\ \hfill C_3=& P({\mathbf{Z}}_{-i,-j}\mid {\mathbf{I}}^{\prime })P(I_i=0,I_j=1,{\mathbf{I}}^{\prime }\mid {\Omega }^{\prime }),\hfill \\ \hfill C_4=& P({\mathbf{Z}}_{-i,-j}\mid {\mathbf{I}}^{\prime })P(I_i=0,I_j=0,{\mathbf{I}}^{\prime }\mid {\Omega }^{\prime }).\hfill \end{array}$$

Since

$$P(I_i,I_j,{\mathbf{I}}^{\prime }\mid {\Omega }^{\prime })=P(\mathbf{I}\mid \Omega )P({\Omega }_{ij}=1)+P(\mathbf{I}\mid \Omega )P({\Omega }_{ij}=0),$$

it is then clear that C_k, k = 1, . . . , 4 is independent with Z_i, Z_j. Since

$$P_1∕P_2=\frac{C_{1}P(Z_j\mid I_j=1)}{C_{2}P(Z_j\mid I_j=0)}=\frac{C_1}{C_2}\exp \left(\mu Z_j-\frac{{\mu }^2}{2}\right),$$

therefore P₁/P₂ is an increasing function of Z_j and independent with Z_i. Similarly, we obtain P₁/P₃ is an increasing function of Z_i and independent with Z_j, and P₁/P₄ is an increasing function of Z_i and Z_j. Since

$$P_1=\frac{P_1}{P_1+P_2+P_3+P_4}=\frac{1}{1+P_2∕P_1+P_3∕P_1+P_4∕P_1},$$

thus P₁ is an increasing function of Z_i and Z_j.

Lemma 3.2 suggests that a larger value of Z indicates a larger probability of being a risk node. The probability of being a risk node is an increasing function of the Z score, given the risk status of other nodes are fixed.

4. Simulation

In this section we use simulated data to evaluate our proposed models and algorithms and demonstrate the efficacy of our proposed method. We simulate Z-scores and hidden states from the HMRF model as given in (3.3) and (3.4). The gene expression levels are simulated from a multivariate Gaussian distribution. First, we compare the proposed PNS algorithm with other existing high-dimensional graph estimation algorithms. Second, we compare the power to detect the risk genes using graphs estimated using a variety of graph estimation algorithms. Our objective is to determine if we can achieve better risk gene detection when we incorporate the network estimated by PNS into the HMRF risk gene detection procedure. This comparison also sheds light on the advantages of DAWN relative to DAWN_α.

4.1. Data generation

We adopt the B–A algorithm [Barabási and Albert (1999)] to simulate a scale-free network G = (V, Ω), where V represents the list of nodes and the adjacency matrix of the network is denoted as Ω. To obtain a positive definite precision matrix supported on the simulated network Ω, the smallest eigenvalue e of vΩ is first computed, where v is a chosen positive constant. We then set the precision matrix to be vΩ (|e| + u)I_{d × d}, where I_{d × d} the identity matrix, d is the number of nodes, and u is another chosen positive number. Two constants v and u are set as 0.9 and 0.1 in our simulation. Finally, by inverting the precision matrix, we obtain the covariance matrix Σ. Gene expression levels, X₁, . . . , X_n, are generated independently from N(0, Σ). The sample size n is equal to 180 in our simulation.

To simulate Z from (3.3), we first simulate the hidden states I from the Ising model (3.4). Initial values of I are randomly assigned to each node in the simulated graph and we let half of the nodes have initial values I_i = 1. Then, we apply the standard Metropolis–Hastings algorithm to update I with 200 iterations. The parameters in the Ising model (3.4) are set as b = −7 and c = 3 in our simulation.

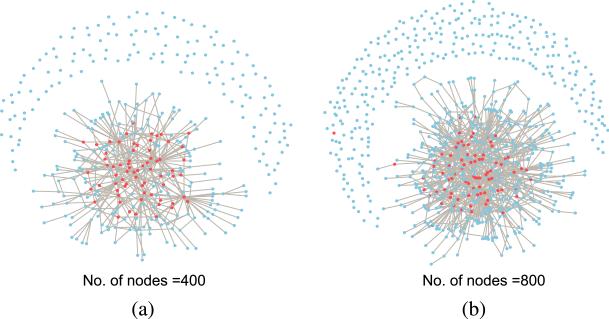
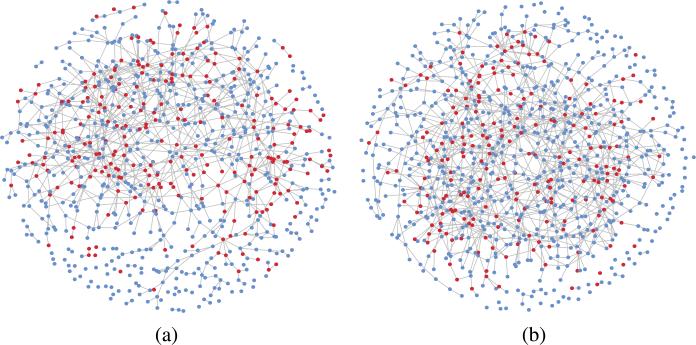
Figure 1 shows the generated scale-free network with the hidden states simulated from the Ising model. The numbers of nodes d are set at 400 and 800, respectively. In Figure 1(a) there are in total 68 nodes with I_i = 1 and in Figure 1(b) there are in total 82 nodes with I_i = 1. After the network and the hidden states embedded in the network are obtained, we simulate z-score Z_i based on model (3.3) with μ = 1.5, σ₀ = 1 and σ₁ = 1.

Fig. 1.

Simulated scale-free network. (a) number of nodes equals 400, (b) number of nodes equals 800.

4.2. Estimation and evaluation

Using the simulated data X₁, . . . , X_n, we first estimate the graph with the PNS algorithm. The p-value threshold t is chosen to be 0.1 and the correlation threshold τ is set at 0.1. Define the important edges as those edges connecting risk nodes. To evaluate the performance of the PNS algorithm in retrieving important edges, we compare the following three graph estimation algorithms:

• PNS: The proposed PNS algorithm.

• Glasso: Graphical lasso algorithm.

• Correlation: Compute the pairwise correlation matrix M from X₁, . . . , X_n, then estimate graph Ω_ij. = I{|M_ij| < τ}.

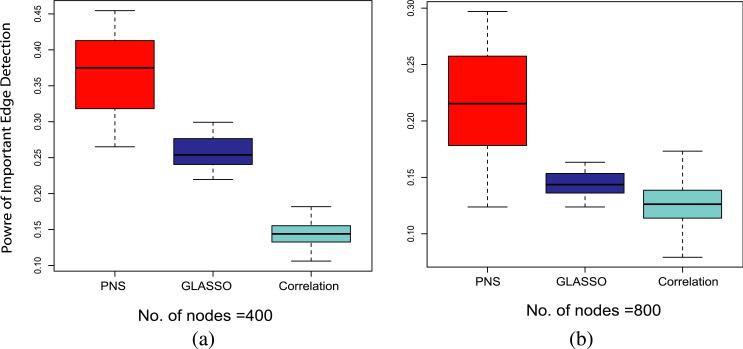
To compare the performance of graph estimation, the FDR is defined as the proportion of false edges among all the called edges. Power is defined as the proportion of true, important edges that are called among all the important edges in the true graph. Figure 2 shows that under the same FDR, PNS retrieves many more important edges than the Glasso and Correlation algorithms. Calling more true edges between risk nodes will improve performance, but calling more false edges will reduce the power of the HMRF algorithm. From the comparison in Figure 2, we see that when calling the same number of false edges, the PNS algorithm calls more true important edges, which suggests that the HMRF model can achieve better power when using the network estimated by the PNS algorithm. We will examine this conjecture by comparing the power of the HRMF model using networks estimated with different algorithms. The tuning parameters for each model are chosen to yield a preset FDR. It is worth noting that here the PNS algorithm does not use the scale-free criterion to choose the sparsity parameter λ. Thus, the good performance of PNS does not really depend on the scale-free assumption.

Fig. 2.

Power of important edge detection. The FDR of the three approaches is set at 0.5.

To evaluate the power of network assisted risk gene detection, we apply the HMRF model using an estimated graph $\widehat{\Omega }$ and the simulated z-score Z. We compare the following four approaches:

• HMRF_PNS: Apply the HMRF algorithm by incorporating the graph estimated by PNS.

• HMRF_Glasso: Apply the HMRF algorithm by incorporating the graph estimated by Glasso. The tuning parameter of Glasso is chosen to make the estimated graph having the same number of edges with $\widehat{\Omega }$, the network estimated by PNS.

• HMRF_oracle: Apply the HMRF algorithm by incorporating the true graph Ω.

• Naive: Classify the nodes only based on the observed z-score Z.

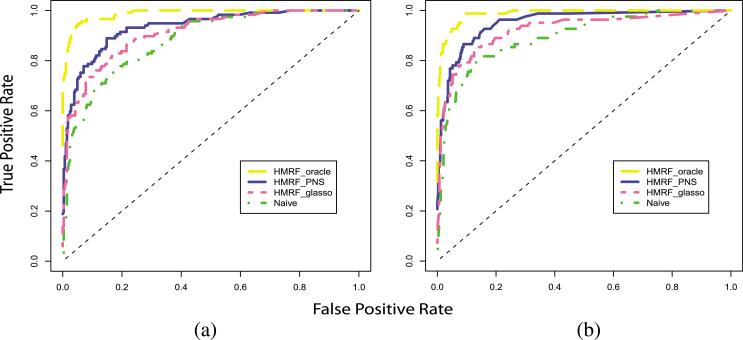
Figure 3 shows the receiver operating characteristic (ROC) curve of the four approaches applied to a single data set. We see that by applying the HMRF model to incorporate the structural information via the PNS algorithm, the accuracy rate of classification can be largely improved. To evaluate the robustness of the proposed algorithm, we repeat the simulation 20 times and compare the true positive rates (TPR) obtained from each approach under the same false positive rate. From Table 1, we reach the same conclusion that HRMF_PNS performs much better than DAWN_α, HMRF_Glasso and the Naive method.

Fig. 3.

ROC curve. (a) number of nodes equals 400, (b) number of nodes equals 800.

Table 1.

True positive rate comparison. The false positive rates are controlled at 0.1

	d = 400	d = 800
DAWN	0.733 (0.02)	0.732 (0.02)
DAWNα	0.663 (0.02)	0.612 (0.03)
HMRF_Glasso	0.670 (0.03)	0.651 (0.01)
HMRF_Oracle	0.934 (0.02)	0.917 (0.01)
Naive	0.585 (0.02)	0.567 (0.01)

This simulation experiment also yields insights into advantages of DAWN over DAWN_α. A key difference between the algorithms is that DAWN_α utilizes an estimated correlation network, while DAWN relies on the PNS partial correlation network. Comparing the two approaches in Figures 2, 3 and Table 1 reveals notable differences. It appears that the correlation network fails to capture a sizable portion of the correct edges of the graph. Consequently, the HMRF has a greater challenge discovering the clustered signal. Overall, the simulations suggest that DAWN performs much better because it uses PNS to fit the graph.

Next, we examine the robustness of our proposed DAWN under different tuning parameters. To generate Table 1, we chose t = 0.1 and τ = 0.1. Now, we vary the tuning parameters t and τ and reevaluate the performance of DAWN. For t we use five different values 0.06, 0.08, 0.1, 0. 12, 0. 14, and for τ we use three different values 0.05,0.1, 0.15. The comparison is made using the same 20 simulated data sets that were used to generate Table 1 (node = 800).

From Table 2 we see that the results of DAWN are not sensitive to the choice of τ. The tuning parameter t does affect the performance of our algorithm. If t is too small, we will not have enough seed genes for constructing the network and too many pairs of key genes are missed. But as long as t is not too small, the performance of our algorithm is robust. Hence, it is reasonable to choose a t that is not too small because in the screening stage we prefer overinclusion. Finally, comparing Tables 1 and 2, we see that for every combination of parameters, DAWN outperforms DAWN_α and HMRF_glasso.

Table 2.

True positive rate comparison of DAWN under different parameters

	t = 0.06	t = 0.08	t = 0.1	t = 0.12	t = 0.14
τ = 0.05	0.665 (0.01)	0.709 (0.01)	0.732 (0.02)	0.717 (0.01)	0.699 (0.01)
τ = 0.1	0.666 (0.01)	0.709 (0.01)	0.732 (0.02)	0.717 (0.01)	0.698 (0.01)
τ = 0.15	0.667 (0.01)	0.708 (0.01)	0.731 (0.02)	0.717 (0.01)	0.698 (0.01)

5. Analysis of autism data

Building on the ideas described in Section 2, Background and Data, we search for genes association with risk for autism. The gene expression data we use to estimate the network was produced and normalized by Kang et al. (2011). Willsey et al. (2013) identified the spatial/temporal choices crucial to neuron development and highly associated with autism. Networks were estimated from the FC during post-conception weeks 10–19 (early fetal) and 13–24 (mid fetal). Thus, we apply PNS to estimate the gene network using brains in early FC and mid FC, respectively. For a given time period, all corresponding tissue samples were utilized. In the early FC period there are 140 observations and in the mid FC period there are 107 observations. To represent genetic association TADA p-values, p_i are obtained from De Rubeis et al. (2014) for each of the genes.

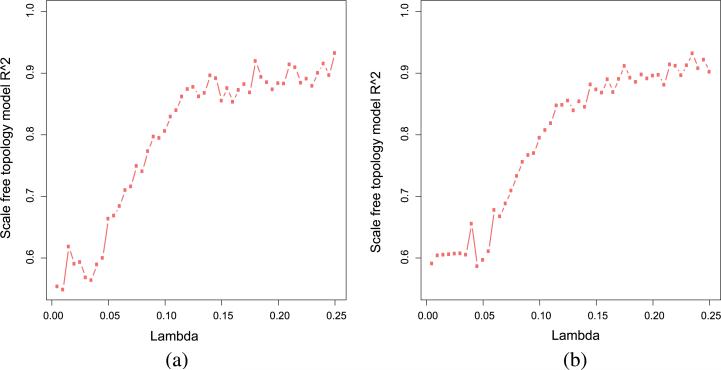
The PNS algorithm is applied to early FC and mid FC separately. The p-value threshold t is chosen to be 0.1 and the correlation threshold τ is set as 0.1. After the screening step, in early FC there are 6670 genes of which 834 genes have p-values less than 0.1, and in mid FC there are 7111 genes of which 897 genes have p-value less than 0.1. We define these genes with p-value less than 0.1 as key genes. To choose the tuning parameter λ, we apply the scale-free criteria and plot the square of correlation R² [equation (3.2)] versus λ in Figure 4. Based on the figure we select, λ = 0.12 because it yields a reasonably high R² value in both periods. The full network of all analyzed genes in early FC contains 10,065 edges of which 1005 edges are between key genes, and the subnetwork of key genes is shown in Figure 5(a). The full network of all analyzed genes in mid FC contains 11,713 edges of which 1144 edges are between key genes, and the subnetwork of key genes is shown in Figure 5(b).

Fig. 4.

Scale-free topology criteria. (a) early FC (b) mid FC.

Fig. 5.

Result of HMRF_PNS algorithm for autism data. (a) early FC (b) mid FC.

After the networks are estimated, we assign z-scores to each node of the network and then apply the HMRF model to the network. The initial hidden states of genes are set as I{p_i < 0.05}. We fix the hidden states of 8 known autism genes as 1. Those 8 known autism genes are ANK2, CHD8, CUL3, DYRK1A, GRIN2B, POGZ, SCN2A and TBR1 based on Willsey et al. (2013). We then compute the Bayesian FDR value [Müller, Parmigiani and Rice (2006)] of each gene based on the posterior probability q_i obtained from the HMRF algorithm. Under the FDR level of 0.1, we obtain 246 significant genes in early FC of which 114 have at least one identified dnLoF mutation. In mid FC we obtain 218 significant genes of which 115 have at least one dnLoF mutation. We combine the significant genes from those two periods and obtain in total 333 genes as our final risk gene list (Supplemental Table 1 [Liu, Lei and Roeder (2015)]). Among them, 146 genes have at least one dnLoF mutation. Comparing to the number of genes discovered by TADA [De Rubeis et al. (2014)] where structural information of the genes was not incorporated, the power of risk gene detection has been substantially improved. The genes in the risk gene list are red in Figure 5. From the figure it is clear that those genes in the risk gene list are highly clustered in the network.

In our risk gene list, in addition to the 8 known ASD genes, there are 10 additional genes that have been identified as ASD genes [Betancur (2011)] (three syndromic: L1CAM, PTEN, STXBP1; two with strong support from copy number and sequence studies: MBD5, SHANK2; and five with equivocal evidence: FOXG1, FOXP1, NRXN1, SCN1A, SYNGAP1). Fisher's exact test shows significant enrichment for nominal ASD genes in our risk gene list (p-value = 2.9 × 10⁻⁶).

Next we compare the performance of DAWN_α and DAWN on the autism data. Ranking the DAWN_α genes by FDR q-value, we retain the top 333 genes for comparison. Autism risk genes are believed to be enriched for histone-modifier and chromatin-remodeling pathways [De Rubeis et al. (2014)]. Comparing the DAWN_α and DAWN gene list with the 152 genes with histone-related domains, we find 9 of these designated genes are on the DAWN_α list (Fisher's exact test p-value = 4.7 × 10⁻²) and 11 are on the DAWN list (p-value = 5.5 × 10⁻³). Thus, DAWN lends stronger support for the histone-hypothesis and, assuming the theory is correct, it suggests that DAWN provides greater biological insights, but this does not prove that DAWN is better at identifying autism risk genes. Using new data from Iossifov et al. (2014), we can conduct a powerful validation experiment. Summarizing the findings from the 1643 additional trios sequenced in this study, we find 251 genes that have one or more additional dnLoF mutations. Based on previous studies of the distribution of dnLoF mutations, we know that a substantial fraction of these genes are likely autism genes [Sanders et al. (2012)]. We find 18 and 24 of these genes are in the DAWN_α and DAWN lists, respectively. If we randomly select 333 genes from the full genome, on average, we expect to sample only 4–5 of the 251 genes. Thus, both lists are highly enriched with these probable autism genes (Fisher's exact test p-value = 2.4 × 10⁻⁶ and 3.4 10⁻¹⁰, resp.). From this comparison we conclude that while both models are successful at identifying autism risk genes, DAWN is more powerful.

We further investigate the robustness of our model to the lasso tuning parameter, λ, by comparing the risk gene prediction set using two additional choices bracketing our original selection. We identified 324, 333 and 243 risk genes with FDR < 0.1 using λ = 0.10, 0.12 and 0.15, respectively. Not surprisingly, the gene lists varied somewhat due to the strong dependence of the model on the estimated network; however, overlap between the first and second list was 281, and overlap between the second and third list was 197. The median TADA p-value for risk genes identified was approximately 0.01 for each choice of λ, suggesting the models were selecting genes of similar genetic information on average. But the model fitted with the strictest smoothing penalty (λ = 0.15) identified a smaller number of genes, and yet it retained some genes with weaker TADA signals (95th percentile TADA p-value 0.3 versus 0.1 for the other smoothing values). This suggests that there might be greater harm in over-smoothing than under-smoothing. De Rubeis et al. (2014) identified 107 promising genes based on marginal genetics scores alone (TADA scores with FDR < 0.3), hence, we also examined consistency of the estimators over this smaller list of likely ASD risk genes. Of these genes, 12 of them do not have gene expression data at this period of brain development and cannot be included in our analysis, reducing our comparison for potential overlap to 95 genes. For the 3 levels of tuning parameters, DAWN identified 82, 82 and 75 genes from this list, respectively. We conclude that although the total number of genes varies, the genes with the strongest signals are almost all captured by DAWN regardless of the tuning parameter chosen. Nevertheless, to obtain a more robust list of risk genes, it might be advisable to use the intersection of genes identified by a range of tuning parameters.

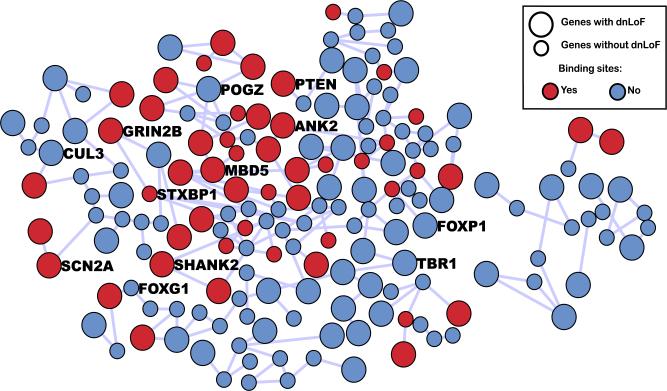
The Ising model allows for the incorporation of numerous covariates such as TF binding sites either individually or en masse. To illustrate, we incorporate the additional information from targets of FMRP [Darnell et al. (2011)]. These target genes have been shown to be associated with autism [Iossifov et al. (2012)], hence, it is reasonable to conjecture that this covariate might improve the power of autism risk gene detection. Indeed, the additional term is significant in the Ising model (p < 0.005 obtained from Algorithm 4 and B is set as 200). Applying model (3.4) to the early FC period, we discovered 242 genes of which 118 have at least one dnLoF mutation. Four of the genes with one dnLoF mutation are newly discovered after we incorporate the TF information. Those four genes are TRIP12, RIMBP2, ZNF462 and ZNF238. Figure 6 shows the connectivity of risk genes after incorporating the TF information.

Fig. 6.

Risk genes identified after incorporating FMRP targets.

6. Conclusion and discussion

In this paper we propose a novel framework for network assisted genetic association analysis. The contributions of this framework are as follows: first, the PNS algorithm utilizes the node specific information so that the accuracy of network estimation can be greatly improved; second, this framework provides a systematic approach for combining the estimated gene network and individual genetic scores; third, the framework can efficiently incorporate additional structural information concerning the dependence between genes, such as the targets of key TFs.

A key insight arises in our comparison of the HMRF model using a variety of network estimation procedures. The Glasso approach tries to reconstruct the whole network, while the PNS approach focuses on estimating only the portions of the network that capture the dependence between disease-associated genes. It might seem counterintuitive that the HMRF model can achieve better power when the network is estimated by the PNS algorithm rather than by other existing high-dimensional network estimation approaches such as Glasso. Why would we gain better power when giving up much of the structural information? Results using the oracle show that HMRF works best when provided with the complete and accurate network (Table 1). The challenge in the high-dimensional setting is that it is infeasible to estimate the entire network successfully. Hence, the PNS strategy of focusing effort on the key portions of the network is superior. With this approach more key edges are estimated correctly relative to the number of false edges incorporated into the network.

While we build on ideas developed in the DAWN_α model [Liu et al. (2014)], the approach presented here extends and improves DAWN_α in several critical directions. In the original DAWN_α model, the gene network was estimated from the adjacency matrix obtained by thresholding the correlation matrix. To obtain a sparse network, DAWN_α grouped tightly correlated genes together into multi-gene supernodes. DAWN uses PNS to obtain a sparse network directly without the need for supernodes. This focused network permits a number of improvements in DAWN. Because each node in the network produced by the PNS algorithm corresponds to a single gene, it is possible to directly apply the Bayesian FDR approach to determine risk genes. In contrast, the DAWN_α required a second screening of genes based on p-values to determine risk genes after the HMRF step. Finally, DAWN is more flexible and allows for the incorporation of other covariates into the model.

The proposed framework is feasible under different scenarios and has a wide application in various problems. In this paper, we extended the Ising model so that the proposed network assisted analysis framework can be applied to incorporate both the gene co-expression network and the gene regulation network. This framework can also be naturally extended to incorporate the PPI network together with the gene co-expression network by simply adding another parameter in the Ising model. These three different types of networks can even be integrated simultaneously to maximize the power of risk gene detection. Moreover, the proposed risk gene discovery framework can be applied not only to ASD but also to many other complex disorders.