Abstract
State-space multivariate dynamical systems (MDS) (Ryali et al., 2011) and other causal estimation models are being increasingly used to identify directed functional interactions between brain regions. However, the validity and accuracy of such methods is poorly understood. Performance evaluation based on computer simulations of small artificial causal networks can address this problem to some extent, but they often involve simplifying assumptions that reduce biological validity of the resulting data. Here, we use a novel approach taking advantage of recently developed optogenetic fMRI (ofMRI) techniques to selectively stimulate brain regions while simultaneously recording high-resolution whole-brain fMRI data. ofMRI allows for a more direct investigation of causal influences from the stimulated site to brain regions activated downstream and is therefore ideal for evaluating causal estimation methods in vivo. We used ofMRI to investigate whether MDS models for fMRI can accurately estimate causal functional interactions between brain regions. Two cohorts of ofMRI data were acquired, one at Stanford University and the University of California Los Angeles (Cohort 1) and the other at the University of North Carolina Chapel Hill (Cohort 2). In each cohort optical stimulation was delivered to the right primary motor cortex (M1). General linear model analysis revealed prominent downstream thalamic activation in Cohort 1, and caudate-putamen (CPu) activation in Cohort 2. MDS accurately estimated causal interactions from M1 to thalamus and from M1 to CPu in Cohort 1 and Cohort 2, respectively. As predicted, no causal influences were found in the reverse direction. Additional control analyses demonstrated the specificity of causal interactions between stimulated and target sites. Our findings suggest that MDS state-space models can accurately and reliably estimate causal interactions in ofMRI data and further validate their use for estimating causal interactions in fMRI. More generally, our study demonstrates that the combined use of optogenetics and fMRI provides a powerful new tool for evaluating computational methods designed to estimate causal interactions between distributed brain regions.
Keywords: Optogenetic fMRI, Causality, Dynamical Systems, Channelrhodopsin
Introduction
State-space multivariate dynamical systems (Daunizeau et al., 2009; Friston et al., 2003; Friston et al., 2008; Ryali et al., 2011; Smith et al., 2009) and other causal estimation models are being increasingly used to investigate how cognitive functions emerge as a result of directed functional interactions between distributed brain regions (Cai et al., 2015; Cooray et al., 2015; Ham et al., 2013; Urner et al., 2013; Vossel et al., 2015; Vossel et al., 2012; Wen et al., 2013; Wen et al., 2012). Validating the performance of these methods in neuroimaging data remains a challenging problem because the true causality is typically not known. Here we take advantage of recently developed optogenetic stimulation techniques with simultaneous high-resolution whole-brain fMRI recordings to investigate whether our state space based multivariate dynamical systems (MDS) (Ryali et al., 2011) models for fMRI can accurately estimate causal functional interactions between distributed brain regions.
Computer simulations of artificial neural networks with a small number of nodes have been thus far the most widely-used strategy for validating causal estimation methods (Havlicek et al., 2015; Schippers et al., 2011; Seth et al., 2013; Smith et al., 2011). However, these simulations do not adequately model neurophysiological and vascular features underlying in vivo fMRI data. Another notable problem with most extant simulation studies is that the dynamical model used for generating test data is also used for validating the estimation procedures. For example, vector autoregressive models have been used to simulate data for validating Granger causal analysis (GCA) (Roebroeck et al., 2005; Schippers et al., 2011). Similarly, data from a generative dynamic causal model (DCM) model was used to investigate the performance of DCM on a four-node network model (Razi et al., 2014), and in a previous study, we used MDS-generated datasets to test MDS algorithms (Ryali et al., 2011). To address this issue, Smith and colleagues used a DCM generative model to simulate multiple test datasets, which were then used to investigate the performance of several causal estimation methods other than DCM (Smith et al., 2011). Additionally, Seth and colleagues used more neurophysiologically realistic simulations to characterize the performance of GCA and clarify its strengths and weaknesses (Seth et al., 2013). More recently, Smith and colleagues demonstrated inherent limitations in testing causal estimations models based on simulated fMRI data that are generated by common underlying models (Smith et al., 2013). Experimental approaches have also been used to validate causal estimation methods. In human fMRI data, this approach has primarily focused on the demonstration of converging evidence from dynamic causal modeling and differential relative timing of brain activation profiles (Katwal et al., 2013; Sridharan et al., 2008; Supekar and Menon, 2012). David and colleagues suggested a more direct approach by using invasive intracranial EEG and fMRI recordings to validate causal estimation methods and identify neural drivers of spontaneous spike-and-wave discharges, albeit in rodent models of epilepsy (David et al., 2008).
A potentially more powerful approach for validation of methods such as MDS is to combine brain stimulation with in vivo imaging to uncover causal interactions between stimulated and target regions. Until recently, technologies to conduct such investigations have been sorely lacking. Here we take advantage of recent developments in optical brain stimulation with simultaneous whole-brain fMRI recording to validate the performance of MDS on experimental data. We used viral transfection to express light sensitive channelrhodopsin-2 (ChR2) proteins in specific brain regions. BOLD fMRI signals were then recorded during optical stimulation, allowing for detection of activation in the stimulated site as well as in downstream functional targets (Kahn et al., 2011; Lee et al., 2010; Shih et al., 2013). ofMRI is an ideal technique for validating dynamic causal estimation methods in vivo. In this study, we used ofMRI to validate MDS procedures for estimating dynamic causal interactions from stimulated “seed” regions in primary motor cortex (M1) to downstream “target” regions.
Two cohorts of ofMRI data were acquired at three different small animal imaging facilities, one by Lee and colleagues at UCLA and at Stanford University (Cohort 1) and the other by Shih and colleagues at University of North Carolina, Chapel Hill (Cohort 2). Both cohorts feature optical stimulation to right primary motor cortex (M1) and significant activation in a single downstream target: thalamus in Cohort 1, and caudate-putamen (CPu) in Cohort 2. We used MDS to investigate causal interactions between M1, the optically stimulated site, and respective downstream target regions that showed significant activation as a result of the stimulation. We hypothesized that MDS would accurately uncover significant causal interactions from the optically stimulated seed region to the downstream target regions. Additional control analyses were then conducted to examine the specificity and stability of the results. In these analyses, we hypothesized that MDS would not detect causal interactions between control regions and downstream targets, and that estimated causal interactions from stimulated to downstream targets would remain stable with the addition of control regions.
Methods
Cohort 1: UCLA/Stanford-ofMRI
ofMRI data was acquired from five adult female Sprague-Dawley rats (250–350g; Charles River Laboratories, Wilmington, MA). Data from two rats were excluded because one did not respond to optical stimulation and the second had movement related artifacts. Of the final three rats included in this study, one was imaged at UCLA and two at Stanford University using identical imaging protocols.
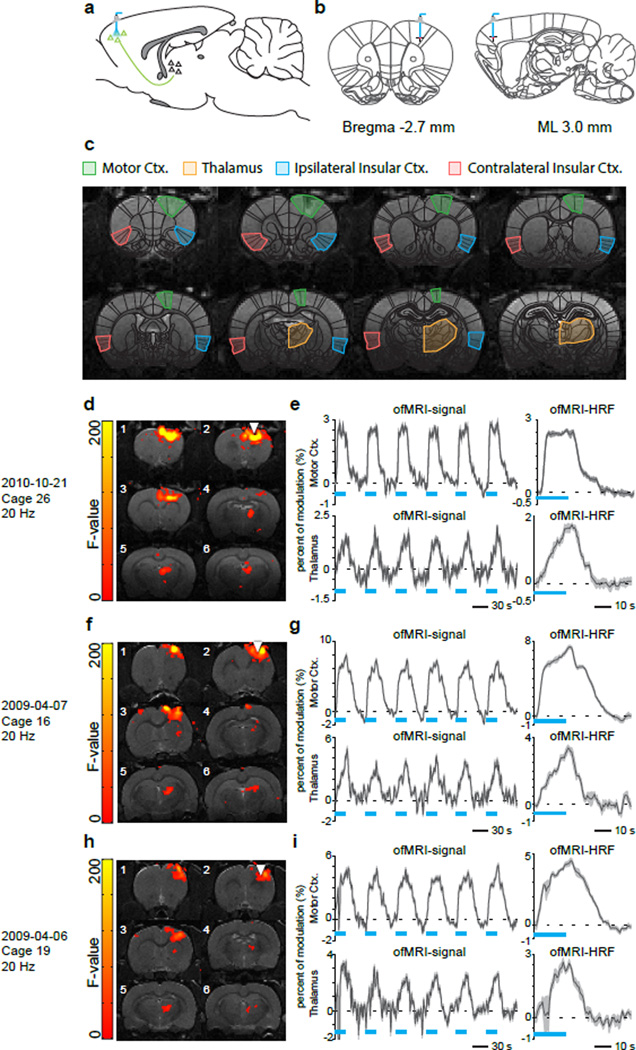
During surgery, M1 was targeted and injected with an adeno-associated virus expressing a ChR2-EYFP fusion protein using coordinates −2.7 mm anteroposterior (AP), +3.0 mm mediolateral (ML) right hemisphere, −2.0 mm and −2.5 mm dorsoventral (DV) (Figure 1a and 1b). Additional surgical procedures and details can be found in our previous ofMRI publications (Lee et al., 2010; Shih et al., 2013). Figure 1c shows anatomical overlays on single subject T1-weighted MRI depicting regions of interest in the current study.
Figure 1. Study design: Cohort 1.
(a, b) Schematic of ofMRI experimental paradigm. Right primary motor cortex (M1) was targeted and injected with adeno-associated virus expressing a Channelrhodopsin2 (ChR2)-EYFP fusion protein. Chronically implanted optic fibers were placed above viral infusion sites. (c) Anatomical overlays on single subject T1-weighted MRI depicting regions of interest in the current study. BOLD signal coherence maps, time courses, and estimated HRFs for Rat 1 (d, e), Rat 2 (f, g), and Rat 3 (h, i).
All ofMRI experiments were conducted three weeks after virus injection for optimal ChR2 expression. The fMRI scans were performed on a 7T small animal MRI system (UCLA: Brucker Biospec, Stanford: Magnex Scientific). All scans used the same 39 mm outer diameter and 25 mm inner diameter custom-designed transmit/receive single-loop surface coil. During the fMRI experiment, animals were artificially ventilated under light anesthesia with a mixture of O2 (35%), N2O (63.5%), isoflurane (1.2–1.5%) and CO2 (3–4%). A block designed fMRI stimulation scheme consisting of six ON-OFF cycles at 20 sec ON and 40 sec OFF for a total of 6 minutes was used. During the ON cycles, optical stimulation was delivered at 20 Hz, with a 5 ms pulse duration. The data were acquired using an interleaved spiral readout Gradient Recalled Echo (GRE) BOLD sequence with 0.5 mm slice thickness and 23 slices. In-plane field of view (FOV) was designed to be 35×35 mm2 and in-plane spatial resolution was 0.5×0.5 mm2. A sliding window reconstruction was then performed to reconstruct the data into 128×128×23 matrix-size, 750 ms temporal resolution images.
After reconstruction, subject motion was corrected by the inverse Gauss-Newton motion correction algorithm (Miao et al., 2013) and 4D fMRI data was analyzed with statistical parameter mapping (SPM) using the general linear model (GLM) with five gamma basis. An F-test was then conducted and active voxels were selected as those with corresponding Bonferroni-corrected p-values less than 0.05. The ROIs were manually selected based on a standard digital rat brain atlas (Schwarz et al., 2006).
Cohort 2: UNC-ofMRI
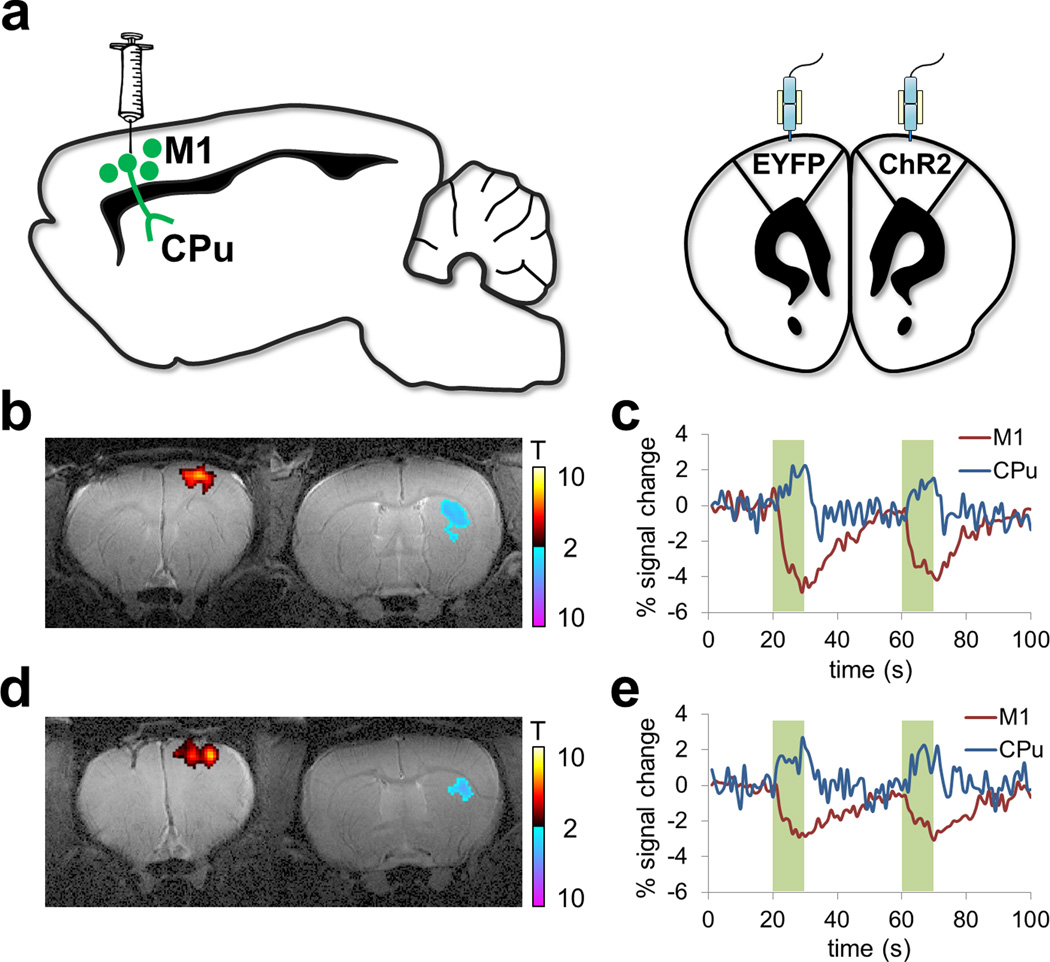
ofMRI data was acquired from two adult male Sprague Dawley rats (300–450 g; Charles River). Rats were deeply anesthetized with isoflurane (2%), and the primary motor cortex was targeted for optogenetics. To preferentially target cortical pyramidal cells, we used an adeno-associated virus carrying the gene encoding ChR2 fused to an enhanced yellow fluorescent protein (EYFP) or only EYFP (all under the calcium/calmodulin kinase IIα promoter) (AAV5-CaMKIIα-ChR2(H134R)-EYFP). Injection volume was 1µl and coordinates were (in mm from bregma and cortical surface): +3.0 AP, +2.5 ML and −1.5 DV (Figure 2a). Injection flow rate was 0.1 µl/min, and an additional 10 minutes were given for virus diffusion prior to needle retraction. Chronically implanted optic fibers were placed 0.5 mm above the virus injection site. A recovery period of at least 3 weeks was given before fMRI to allow for adequate opsin expression.
Figure 2. Study design: Cohort 2.
(a) Schematic of ofMRI experimental paradigm. Rats were deeply anesthetized with isoflurane (2%), and the primary motor cortex was targeted for optogenetics. To preferentially target cortical pyramidal cells, an adeno-associated virus was used carrying the gene encoding channelrhodopsin-2 (ChR2) fused to an enhanced yellow fluorescent protein (EYFP) or only EYFP. Chronically implanted optic fibers were placed above viral infusion sites. (b)–(c), (d)–(e): Representative t-scored functional activation maps from two rats, overlaid on same-subject T2-weighted anatomical images (b, d). Corresponding time-courses of CBV changes in motor cortex and dorsolateral striatum (c, e).
Each rat was endotracheally intubated and ventilated with ~1.5% isoflurane and medical air. The ventilation rate and volume were adjusted to maintain end-tidal CO2 (EtCO2) within a range of 2.6–3.2% and oxygen saturation (SpO2) above 96%. Rectal temperature was maintained at 37±0.5 °C. Dexmedetomidine (0.1 mg/ml) and pancuronium bromide (1.0 mg/ml) were infused intravenously for the duration of the scan. For CBV-weighted MRI, a tail-vein catheter was used to deliver a monocrystalline iron oxide contrast agent at a dose of 30 mg Fe/kg. Single-shot, single-sampled GE-EPI sequences (BW= 300 kHz, TR= 1000 ms, TE= 8.107 ms, 80×80 matrix, FOV= 2.56 × 2.56 cm2, slice thickness= 1 mm) were acquired using a Bruker 9.4T MR scanner and homemade surface coil.
ofMRI was conducted using a homemade fiber optic patch cable, connected to a 473 nm laser (Shanghai Laser & Optics Century, Shanghai, China) outside of the scanner room. Laser wattage was measured as 16–20 mW from the end of the optic fiber. Optical stimulation was presented in an OFF-ON-OFF-ON-OFF design, with an initial rest period of 20 sec, followed by 2 ON-OFF cycles of 10 sec stimulation and 30 sec rest. During the ON cycle, optical stimulation was delivered at 40 Hz, with a 5 ms pulse duration.
Details of the image processing procedures are described fully in (Shih et al., 2013). In brief, the data were co-registered to correct for spatial image drifts over time using SPM’s spatial realignment function. All volumes were co-registered to the temporal mean image to account for spatial translation and rotation using mutual information as the cost metric. Activated brain regions with respect to optical stimulation within each rat were found with GLM using the SPM toolbox. A Bonferroni correction against the total number of brain voxels (p<0.05) was used to correct for multiple comparisons.
MDS for estimating causal interactions in ofMRI data
MDS is a state-space model (Ryali et al., 2011) consisting of a state equation to model the latent “neuronal–like” states of the dynamic network and an observation equation to model BOLD-fMRI signals as a linear convolution of latent neural dynamics and HRF responses. Like DCM, it estimates both intrinsic and experimentally modulated causal interactions between brain regions while accounting for variations in hemodynamic responses in these regions.
The state equation in MDS is a multivariate linear difference equation or a first order multivariate auto regressive (MVAR) model that defines the state dynamics
| (1) |
The model for the observed BOLD responses is a linear convolution model
| (2) |
| (3) |
In Equation (1), s(t) is a M × 1 vector of latent signals at time t of M regions, Cj is a connection matrix ensued by modulatory input vj(t) and J is the number of modulatory inputs. The non-diagonal elements of Cj represent the coupling of brain regions in the presence of vj(t). Therefore, latent signals s(t) in M regions at time t is a bilinear function of modulatory inputs vj(t) and its previous state s(t−1). w(t) is an M × 1 state noise vector whose distribution is assumed to be Gaussian distributed with covariance matrix Q(w(t) ~ N (0, Q)). Additionally, state noise vectors at time instances 1,2, …., T (w(1), w(2) … w(T)) are assumed to be identical and independently distributed (iid). The latent dynamics modeled in equations (1) and (2) give rise to observed fMRI time series represented by Equation (3).
We model the fMRI-BOLD time series in region m as a linear convolution of HRF and latent signal sm (t) in that region. To represent this linear convolution model as an inner product of two vectors, the past L values of sm (t) are stored as a L × 1 vector xm (t) in equation (2).
In equation (3), ym (t) is the observed BOLD signal at time t of m-th region. Φ is a p × L matrix whose rows contain bases for HRF. bm is a 1 × p coefficient vector representing the weights for each basis function in explaining the observed BOLD signal ym (t). Therefore, the HRF in m-th region is represented by the product bmΦ. The BOLD response in this region is obtained by convolving HRF (bmΦ) with the L past values of the region’s latent signal (xm(t)) and is represented mathematically by the vector inner product bmΦ xm(t). Uncorrelated observation noise em(t) with zero mean and variance is then added to generate the observed signal ym (t). em (t) is also assumed to be uncorrelated with w(τ), at all t and τ. Therefore, equation (3) represents the linear convolution between the embedded latent signal xm (t) and the basis vectors for HRF. Here, we use the canonical HRF and its time derivative as bases, as is common in most fMRI studies.
Equations (1–3) together represent a state-space model for estimating the causal interactions in latent signals based on observed multivariate fMRI time series. Crucially, MDS also takes into account variations in HRF as well as the influences of modulatory and external stimuli in estimating causal interactions between the brain regions.
Estimating causal interactions between M regions specified in the model is equivalent to estimating the parameters Cj, j = 1,2‥J. In order to estimate Cj’s, the other unknown parameters Q, and and the latent signal based on the observations , t = 1,2,‥ T, where T is the total number of time samples and S is the number of subjects, need to be estimated. We use a variational Bayes approach (VB) for estimating the posterior probabilities of the unknown parameters of the MDS model given fMRI time series observations for S number of subjects (Ryali et al., 2011). In this analysis we set J = 2 corresponding to two conditions: stimulus ON and stimulus OFF and report the causal interactions between brain regions in the stimulus ON condition. We use the same non-informative hyper-parameters as in our previous study (Ryali et al., 2011). We assume a Gaussian prior distribution on each element of Cj(m, n) with mean 0 and precision Λj(m, n). We assume that each precision parameter Λj(m, n) follows a Gamma distribution with hyper-parameters co and do, which are set to non-informative values of 10−3 each. We also use a Gamma distribution for each diagonal element of the noise precision Q−1 in Equation (1) with hyper-parameters ao and bo set to non-informative values of 10−3 each. We use similar prior distributions for the parameters bm and em(t) in the output Equation (3). The details of VB estimation of these parameters are provided in Appendix B of our previous study (Ryali et al., 2011). We initialized the MDS algorithm using the same procedures as described in (Ryali et al., 2011). The fMRI time time-series for each region m and subject s, is linearly de-trended, its temporal mean removed and normalized by its standard deviation prior to applying MDS.
To test the statistical significance of the estimated causal links, we use the posterior probabilities of the estimated parameters. More specifically, to test the significance of a causal link from n-th region to m-th region we use p(Cj(m, n)|y) which is a normal distribution whose mean and variance are estimated using the VB framework (Ryali et al., 2011). We use this distribution to find the standard normal z-score for the mean value of Cj(m, n) and test its significance at p = 0.05 with a Bonferroni correction for multiple comparisons.
Results
Cohort 1: UCLA/Stanford-ofMRI
In all three rats from Cohort 1, GLM analysis identified significant activations in the stimulated right hemisphere M1 region and a downstream target in the right hemisphere thalamus. Figure 1d shows the significantly activated brain regions in right M1 and thalamus for Rat 1. As shown in Figure 1e, BOLD signals synchronous to the optical stimulus in Rat 1 were observed at both right M1 (white triangle) and the downstream thalamus. Figures 1f,g and 1h,i show the same information for Rat 2 and Rat 3, respectively.
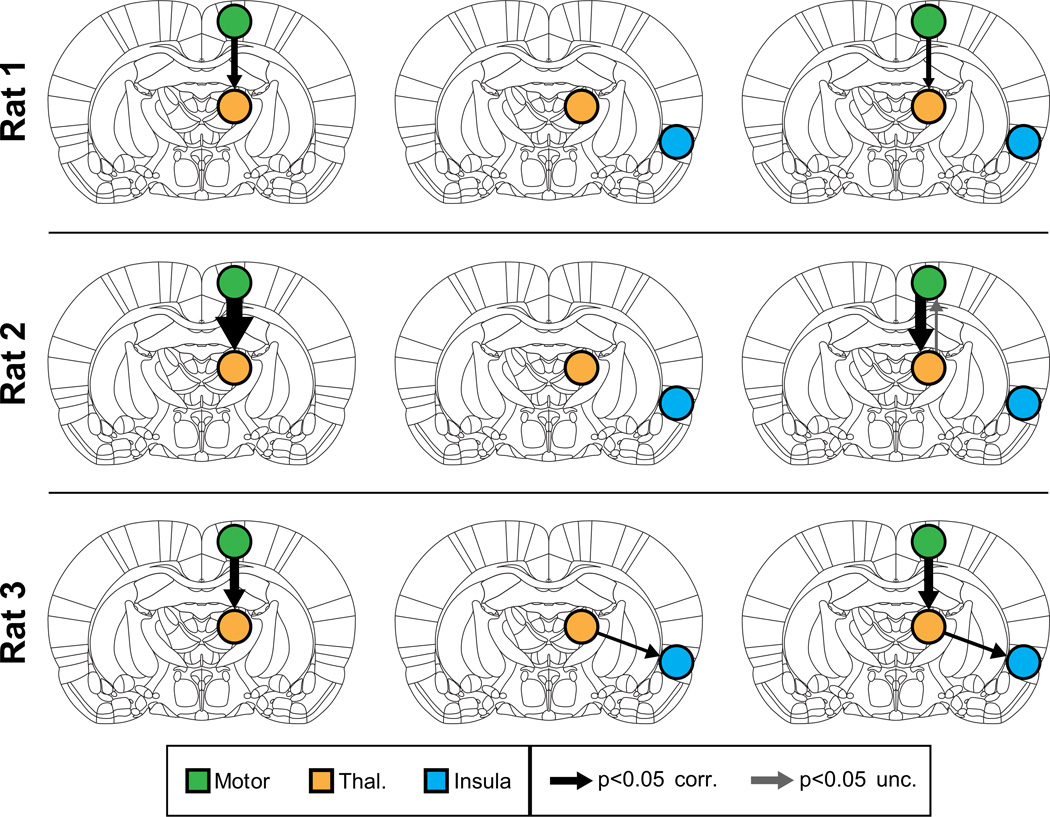
We then applied MDS to examine causal interactions between M1 and thalamus. Mean BOLD signals were extracted from the significantly activated voxels in the right hemisphere M1 and thalamus ROIs. As hypothesized, MDS estimated a highly significant (p < 0.05, Bonferroni corrected) causal drive from M1 to thalamus in Rat 1, Rat 2 and Rat 3, as shown in the left column of Figure 3. Tables S1a, S2a and S3a respectively show the z-scores for the causal directions and their corresponding p-values (shown in parenthesis) for Rat 1, Rat 2 and Rat 3. Significant connections (p < 0.05, Bonferroni corrected) are highlighted in red in these tables. The causal drive in the opposite direction (thalamus to M1) was weak and insignificant (p > 0.05, Bonferroni corrected) in all three rats (Figure 3, left column).
Figure 3. Causal interactions estimated by MDS in Cohort 1.
(Left) Causal interactions between Motor and Thalamus, in all three rats MDS correctly uncovered significant causal drive from M1 to thalamus. (Middle) Analysis with insula as control region. MDS found no casual drive from the control region insula to thalamus in all three rats. (Right) Causal drive from M1 to thalamus was strong and significant even upon inclusion of insula as control region. Thicknesses of the arrows depict the strength of significant causal interactions (z-score).
Next, we performed a control analysis where we examined causal interactions between a right insular cortex “seed” region, which was not activated with the optical stimulation and the same target ROI in the thalamus. Mean BOLD signals were extracted from voxels in an anatomically defined right hemispheric insula ROI. We found no significant causal drive between the insula and the thalamus in Rats 1 and 2 (Figure 3, middle column, and Supplementary Tables S1b, S2b). In Rat 3, we found significant causal interactions from thalamus to insula (Figure 3, middle column and Supplementary Table S1c). However, the strength of this thalamus to insula causal drive was significantly weaker than the strength of causal interactions from M1 to thalamus (p < 0.01).
To demonstrate the stability of our findings, we estimated causal interactions between the three ROIs together using MDS. We found that the causal drive from M1 to thalamus could be detected even with the addition of the insula control region in all three rats (Figure 3, right column, and Supplementary Tables S1c, S2c, S3c).
We then estimated BOLD responses in M1 and thalamus regions using Equations (1–3). Top panels of supplementary Figures S1, S2 and S3 display the estimated quasi-neuronal states for M1 and thalamus (s(t) as defined in Equation (1)) in Rats 1, 2 and 3 respectively. The middle and bottom panels of supplementary Figures S1, S2 and S3 show the estimated and actual BOLD responses in M1 and thalamus for Rats 1, 2 and 3 respectively. We excluded the first 32 sec, which is the length of the canonical HRF response, because BOLD estimates using linear convolution are not reliable due to the zero padding of quasi-neuronal signals in that period. The estimates of quasi-neuronal states suggest that they are closely aligned to stimulus onset (top panels of supplementary Figures S1, S2 and S3) whereas the estimated and actual BOLD responses show a lagged response (middle and bottom panels of supplementary Figures S1, S2 and S3) in all three rats. A comparison between the estimated and actual BOLD responses further revealed that the MDS-estimated BOLD responses for both regions (M1 and thalamus) in all three rats match well with the actual responses (middle and bottom panels of supplementary Figures S1, S2 and S3).
Cohort 2: UNC-ofMRI
In both rats from Cohort 2, GLM analysis identified significant activations in stimulated M1 and downstream target in the Caudate-Putamen (CPu). Figures 2b and 2c show the significantly activated brain regions in the right hemispheric M1 and CPu as well as the associated BOLD signal changes for Rat 1. Figures 2d and 2e show the same information for Rat 2.
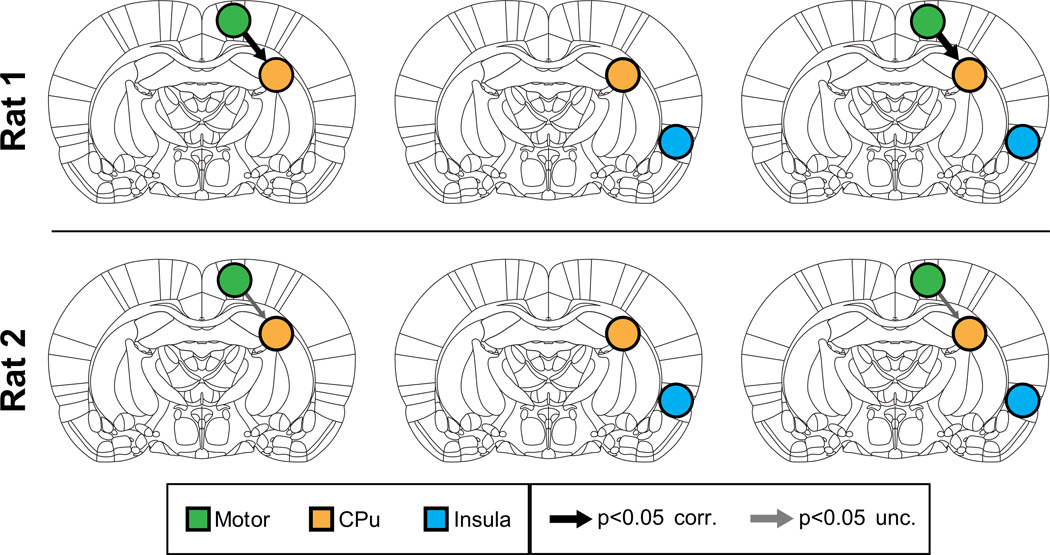
We then applied MDS to examine causal interactions between M1 and CPu. Mean BOLD signals were extracted from the two ROIs centered on the locally maximally activated voxels in M1 and CPu respectively, both with a radius of 1 voxel. All other procedures were similar to those used for analysis of Cohort 1 data. As hypothesized, MDS estimated a causal drive from M1 to CPu in Rat 1 (p < 0.05, Bonferroni corrected) and Rat 2 (p < 0.05, uncorrected), as shown in the left column of Figure 4. Causal interactions in the opposite direction (CPu to M1) were weak and non-significant (p > 0.05, uncorrected) for both rats (Figure 4, left column). Supplementary Tables S4a and S5a respectively show the z-scores for the causal interactions and their corresponding p-values for Rat 1 and Rat 2.
Figure 4. Causal interactions estimated by MDS in Cohort 2.
(Left) Causal interactions between Motor and CPu. In both rats MDS correctly uncovered significant causal drive from M1 to CPu. Middle: MDS found no causal drive from control region insula and CPu. Right: Causal drive from M1 to CPu remained significant even upon inclusion of insula as control region. Thicknesses of the arrows depict the strength of significant causal interactions (z-score).
Next, we performed the same control analyses as those used with Cohort 1. There were no significant causal interactions between the non-stimulated control region and the CPu in either direction in both rats (Figure 4, middle column and Supplementary Tables S4b, S5b).
To demonstrate the stability of our findings, we then examined causal interactions between the three ROIs together using MDS. We found that causal interactions from M1 to CPu could be detected even with the addition of the control region in Rat 1 (p < 0.05, Bonferroni corrected) and Rat 2 (p < 0.05, uncorrected) (Figure 4, right column and Supplementary Tables S4c and S5c). Additionally, the strength of causal interactions from M1 to CPu was still greater than all other causal interactions (Supplementary Tables S4c S5c).
We then examined the estimated quasi-neuronal signals s(t) and BOLD responses in M1 and CPu. The top panels of supplementary Figures S4 and S5 show the estimated quasi-neuronal signals for M1 and CPu while the middle and bottom panels of supplementary Figures S4 and S5 show the estimated BOLD responses in Rats 1 and 2 respectively. The estimates of BOLD responses matched well with their actual BOLD responses and the estimates quasi-neuronal signals showed the expected lag when compared to the respective BOLD responses (middle and bottom panels of supplementary Figures S4 and S5). In this cohort also, the quasi-neuronal states were time locked to the stimulus onsets whereas the estimated and actual BOLD responses were delayed. Note that here also the first 32 sec of BOLD responses are not plotted because of the linear convolution operation.
Discussion
Combining optogenetics and fMRI to evaluate methods for causal estimation
ofMRI is a novel technique for selectively stimulating a brain region and observing causal effects of such stimulation across the entire brain (Kahn et al., 2011; Lee et al., 2010; Shih et al., 2013). Optogenetic stimulation with ChR2 also enables stimulation of a circumscribed cortical region in a temporally precise manner. This spatial and temporal precision as well as the whole-brain coverage provided by ofMRI delivers exceptional spatial and temporal precision for investigating dynamic functional connectivity between distributed regions spanning the entire brain. Although previous studies have used ofMRI to examine functional connectivity of different brain regions (Lee, 2011, 2012), dynamic causal interactions associated with optogenetic stimulation have not been explored yet. In this study, we leveraged the unique capabilities of these technologies and demonstrated how combining optogenetics and fMRI provides us with powerful new tools for validating dynamic causal modeling techniques in ways that were not previously possible.
A particular advantage of optogenetic techniques over other approaches such as forepaw, whisker or visual stimulation (Sanganahalli et al., 2009) is that it can be used to validate causal interactions associated with specific functional circuits and cell-types. Given the complexity of functional connectivity and potential involvement of multiple pathways and cell types (e.g. excitatory vs inhibitory neurons), and neurotransmission within and across different nuclei, it is extremely challenging to study brain mechanisms underlying causal interactions in neural circuits. ofMRI overcomes these weaknesses and provides tools to probe specific functional pathways and causal influences.
Validation of MDS by combining optogenetic stimulation with simultaneous fMRI
We used some of the capabilities of ofMRI to validate MDS-based analytic procedures for estimating dynamic causal interactions in fMRI data. Across two independent cohorts we found that MDS accurately estimated dynamic causal interactions from the stimulated site to downstream target sites. Additional control analyses demonstrated the specificity and stability of causal interactions estimated by MDS. Our findings suggest that MDS state-space models can reliably estimate causal interactions in ofMRI datasets and further validate their use for causal estimation in fMRI. A powerful feature of MDS (Ryali et al., 2011; Smith et al., 2009)) is that it estimates causal interactions in the underlying “quasi-neuronal” signals, rather than the BOLD fMRI data which is subject to delay and dispersion by the HRF. Furthermore, MDS also provides an estimate of this neuronal signal which was found to display two key features: (i) it was time-locked to stimulus onset, and (ii) it showed an earlier onset in the stimulated site with respect to the target site (supplementary Figures S1–S5). These results suggest that MDS deconvolved BOLD responses while estimating causal interactions between brain regions. Crucially, in spite of differences in data acquisition protocol and experimental design, our findings were replicated across two independent cohorts, further validating MDS as a useful technique for investigating causal interactions and the underlying deconvolved “neuronal” signals in fMRI data.
Limitations and future work
The main goal of our study was to investigate whether MDS can accurately estimate causal interactions between brain regions in BOLD fMRI. The small ofMRI sample sizes currently available preclude a direct comparison with other methods including Granger causal analysis (GCA) (Roebroeck et al., 2005), dynamic causal modeling (DCM) (Friston et al., 2003; Friston et al., 2008), directed information transfer measures (Patel et al., 2006) and Bayes Net (Ramsey et al., 2011). Future studies will need to address such comparisons with much larger ofMRI samples than those currently available.
Continued progress in the use of ofMRI for validating brain connectivity methods will require further research on several other fronts as well. More thorough investigation of the effects of stimulation parameters including timing, frequency of stimulation, number of stimulations, and session duration will be needed. In the Cohort 1 dataset, our findings demonstrate that causal interactions from M1 to thalamus were significant in Rat 1, Rat 2 and Rat 3, and moreover they were stable even in the presence of an additional control region (Figure 3, right column). This dataset used a block design with a stimulation duration of 20 sec followed by a 40 sec rest block, resulting in 6 blocks of stimulation with a session duration of about 360 sec (Figure 1). Whether shorter stimulation and rest blocks and event-related paradigms can achieve similar results remains to be investigated. Our analysis of the Cohort 2 dataset suggests preliminarily that even with shorter blocks and session durations MDS can uncover causal interactions in ofMRI data (Figure 4). Further research is needed to determine optimal stimulation timing and session durations for ofMRI studies.
ofMRI may be particularly useful in determining optimal experimental designs for estimation of dynamic causal interactions in noninvasive brain imaging. In conventional GLM analysis of fMRI data, it has been shown that block designs are better suited for detecting activations while event-related designs are more optimal for estimating regional hemodynamic response (Liu et al., 2001). However, no studies have investigated optimal experimental designs for estimating causal interactions in fMRI data; ofMRI may provide a unique tool in this regard. Finally, simultaneous electrophysiological and ofMRI recordings with integrated data analysis and computational modeling are needed for providing critical information about the neurophysiological basis of dynamic causal interactions across distributed brain regions.
Conclusions
Our findings demonstrate that MDS can accurately estimate dynamic causal interactions in ofMRI data. In spite of differences in data acquisition protocol and experimental design, causal interactions from an optically stimulated source region to target sites were replicated across two cohorts and scanners, highlighting the robustness of our findings. Validation of MDS with ofMRI provides further insights into the applicability of state-space causal estimation methods in BOLD-fMRI studies. More generally, our findings suggest that ofMRI provides a powerful new tool for validating dynamic connectivity procedures that are being increasingly used in brain imaging studies.
Supplementary Material
Acknowledgments
This research was supported by grants from the National Institutes of Health (1K25HD074652, and NS071221), and the Li Ka Shing Foundation. We thank Dr. Steve Smith for valuable feedback on the study. We also thank Jonathan Nicholas for the feedback on the manuscript.
Footnotes
MDS analysis scripts and ofMRI data used in this study are available for download from our lab website: scsnl.stanford.edu/documents/MDS_Scripts_and_ofMRI_data.zip
References
- Cai W, Chen T, Ryali S, Kochalka J, Li CS, Menon V. Causal Interactions Within a Frontal-Cingulate-Parietal Network During Cognitive Control: Convergent Evidence from a Multisite-Multitask Investigation. Cerebral Cortex. 2015 doi: 10.1093/cercor/bhv046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooray GK, Sengupta B, Douglas P, Friston K. Dynamic causal modelling of electrographic seizure activity using Bayesian belief updating. Neuroimage. 2015 doi: 10.1016/j.neuroimage.2015.07.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daunizeau J, Friston KJ, Kiebel SJ. Variational Bayesian identification and prediction of stochastic nonlinear dynamic causal models. Physica D. 2009;238:2089–2118. doi: 10.1016/j.physd.2009.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- David O, Guillemain I, Saillet S, Reyt S, Deransart C, Segebarth C, Depaulis A. Identifying neural drivers with functional MRI: an electrophysiological validation. PLoS biology. 2008;6:2683–2697. doi: 10.1371/journal.pbio.0060315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Harrison L, Penny W. Dynamic causal modelling. Neuroimage. 2003;19:1273–1302. doi: 10.1016/s1053-8119(03)00202-7. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Trujillo-Barreto N, Daunizeau J. DEM: a variational treatment of dynamic systems. Neuroimage. 2008;41:849–885. doi: 10.1016/j.neuroimage.2008.02.054. [DOI] [PubMed] [Google Scholar]
- Ham T, Leff A, de Boissezon X, Joffe A, Sharp DJ. Cognitive control and the salience network: an investigation of error processing and effective connectivity. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2013;33:7091–7098. doi: 10.1523/JNEUROSCI.4692-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Havlicek M, Roebroeck A, Friston K, Gardumi A, Ivanov D, Uludag K. Physiologically informed dynamic causal modeling of fMRI data. Neuroimage. 2015;122:355–372. doi: 10.1016/j.neuroimage.2015.07.078. [DOI] [PubMed] [Google Scholar]
- Kahn I, Desai M, Knoblich U, Bernstein J, Henninger M, Graybiel AM, Boyden ES, Buckner RL, Moore CI. Characterization of the functional MRI response temporal linearity via optical control of neocortical pyramidal neurons. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2011;31:15086–15091. doi: 10.1523/JNEUROSCI.0007-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katwal SB, Gore JC, Gatenby JC, Rogers BP. Measuring relative timings of brain activities using fMRI. Neuroimage. 2013;66:436–448. doi: 10.1016/j.neuroimage.2012.10.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee JH. Tracing activity across the whole brain neural network with optogenetic functional magnetic resonance imaging. Frontiers in neuroinformatics. 2011;5:21. doi: 10.3389/fninf.2011.00021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee JH. Informing brain connectivity with optogenetic functional magnetic resonance imaging. Neuroimage. 2012;62:2244–2249. doi: 10.1016/j.neuroimage.2012.01.116. [DOI] [PubMed] [Google Scholar]
- Lee JH, Durand R, Gradinaru V, Zhang F, Goshen I, Kim DS, Fenno LE, Ramakrishnan C, Deisseroth K. Global and local fMRI signals driven by neurons defined optogenetically by type and wiring. Nature. 2010;465:788–792. doi: 10.1038/nature09108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu TT, Frank LR, Wong EC, Buxton RB. Detection power, estimation efficiency, and predictability in event-related fMRI. Neuroimage. 2001;13:759–773. doi: 10.1006/nimg.2000.0728. [DOI] [PubMed] [Google Scholar]
- Miao QY, Tang Y, Kurths J, Fang JA, Wong WK. Pinning controllability of complex networks with community structure. Chaos. 2013;23 doi: 10.1063/1.4816009. [DOI] [PubMed] [Google Scholar]
- Patel RS, Bowman FD, Rilling JK. A Bayesian approach to determining connectivity of the human brain. Human Brain Mapping. 2006;27:267–276. doi: 10.1002/hbm.20182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsey JD, Hanson SJ, Glymour C. Multi-subject search correctly identifies causal connections and most causal directions in the DCM models of the Smith et al. simulation study. Neuroimage. 2011;58:838–848. doi: 10.1016/j.neuroimage.2011.06.068. [DOI] [PubMed] [Google Scholar]
- Razi A, Kahan J, Rees G, Friston KJ. Construct validation of a DCM for resting state fMRI. Neuroimage. 2014;106C:1–14. doi: 10.1016/j.neuroimage.2014.11.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roebroeck A, Formisano E, Goebel R. Mapping directed influence over the brain using Granger causality and fMRI. Neuroimage. 2005;25:230–242. doi: 10.1016/j.neuroimage.2004.11.017. [DOI] [PubMed] [Google Scholar]
- Ryali S, Supekar K, Chen T, Menon V. Multivariate dynamical systems models for estimating causal interactions in fMRI. Neuroimage. 2011;54:807–823. doi: 10.1016/j.neuroimage.2010.09.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanganahalli BG, Bailey CJ, Herman P, Hyder F. Tactile and non-tactile sensory paradigms for fMRI and neurophysiologic studies in rodents. Methods in molecular biology. 2009;489:213–242. doi: 10.1007/978-1-59745-543-5_10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schippers MB, Renken R, Keysers C. The effect of intra- and inter-subject variability of hemodynamic responses on group level Granger causality analyses. Neuroimage. 2011;57:22–36. doi: 10.1016/j.neuroimage.2011.02.008. [DOI] [PubMed] [Google Scholar]
- Schwarz AJ, Danckaert A, Reese T, Gozzi A, Paxinos G, Watson C, Merlo-Pich EV, Bifone A. A stereotaxic MRI template set for the rat brain with tissue class distribution maps and co-registered anatomical atlas: application to pharmacological MRI. Neuroimage. 2006;32:538–550. doi: 10.1016/j.neuroimage.2006.04.214. [DOI] [PubMed] [Google Scholar]
- Seth AK, Chorley P, Barnett LC. Granger causality analysis of fMRI BOLD signals is invariant to hemodynamic convolution but not downsampling. Neuroimage. 2013;65:540–555. doi: 10.1016/j.neuroimage.2012.09.049. [DOI] [PubMed] [Google Scholar]
- Shih YY, Chen YY, Lai HY, Kao YC, Shyu BC, Duong TQ. Ultra high-resolution fMRI and electrophysiology of the rat primary somatosensory cortex. Neuroimage. 2013;73:113–120. doi: 10.1016/j.neuroimage.2013.01.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith JF, Chen K, Pillai AS, Horwitz B. Identifying effective connectivity parameters in simulated fMRI: a direct comparison of switching linear dynamic system, stochastic dynamic causal, and multivariate autoregressive models. Frontiers in neuroscience. 2013;7:70. doi: 10.3389/fnins.2013.00070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith JF, Pillai A, Chen K, Horwitz B. Identification and validation of effective connectivity networks in functional magnetic resonance imaging using switching linear dynamic systems. Neuroimage. 2009 doi: 10.1016/j.neuroimage.2009.11.081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Miller KL, Salimi-Khorshidi G, Webster M, Beckmann CF, Nichols TE, Ramsey JD, Woolrich MW. Network modelling methods for FMRI. Neuroimage. 2011;54:875–891. doi: 10.1016/j.neuroimage.2010.08.063. [DOI] [PubMed] [Google Scholar]
- Sridharan D, Levitin DJ, Menon V. A critical role for the right fronto-insular cortex in switching between central-executive and default-mode networks. Proc Natl Acad Sci U S A. 2008;105:12569–12574. doi: 10.1073/pnas.0800005105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Supekar K, Menon V. Developmental maturation of dynamic causal control signals in higher-order cognition: a neurocognitive network model. PLoS Comput Biol. 2012;8:e1002374. doi: 10.1371/journal.pcbi.1002374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Urner M, Sarri M, Grahn J, Manly T, Rees G, Friston K. The role of prestimulus activity in visual extinction. Neuropsychologia. 2013;51:1630–1637. doi: 10.1016/j.neuropsychologia.2013.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vossel S, Mathys C, Stephan KE, Friston KJ. Cortical Coupling Reflects Bayesian Belief Updating in the Deployment of Spatial Attention. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2015;35:11532–11542. doi: 10.1523/JNEUROSCI.1382-15.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vossel S, Weidner R, Driver J, Friston KJ, Fink GR. Deconstructing the architecture of dorsal and ventral attention systems with dynamic causal modeling. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2012;32:10637–10648. doi: 10.1523/JNEUROSCI.0414-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen X, Liu Y, Yao L, Ding M. Top-down regulation of default mode activity in spatial visual attention. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2013;33:6444–6453. doi: 10.1523/JNEUROSCI.4939-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen X, Yao L, Liu Y, Ding M. Causal interactions in attention networks predict behavioral performance. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2012;32:1284–1292. doi: 10.1523/JNEUROSCI.2817-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.